WYDZIAŁ ETI PG

Katedra Systemów Elektroniki Morskiej

Laboratorium Obwodów i Sygnałów

FILTRY

Opracował: Witold Szkudliński

Gdańsk 2011

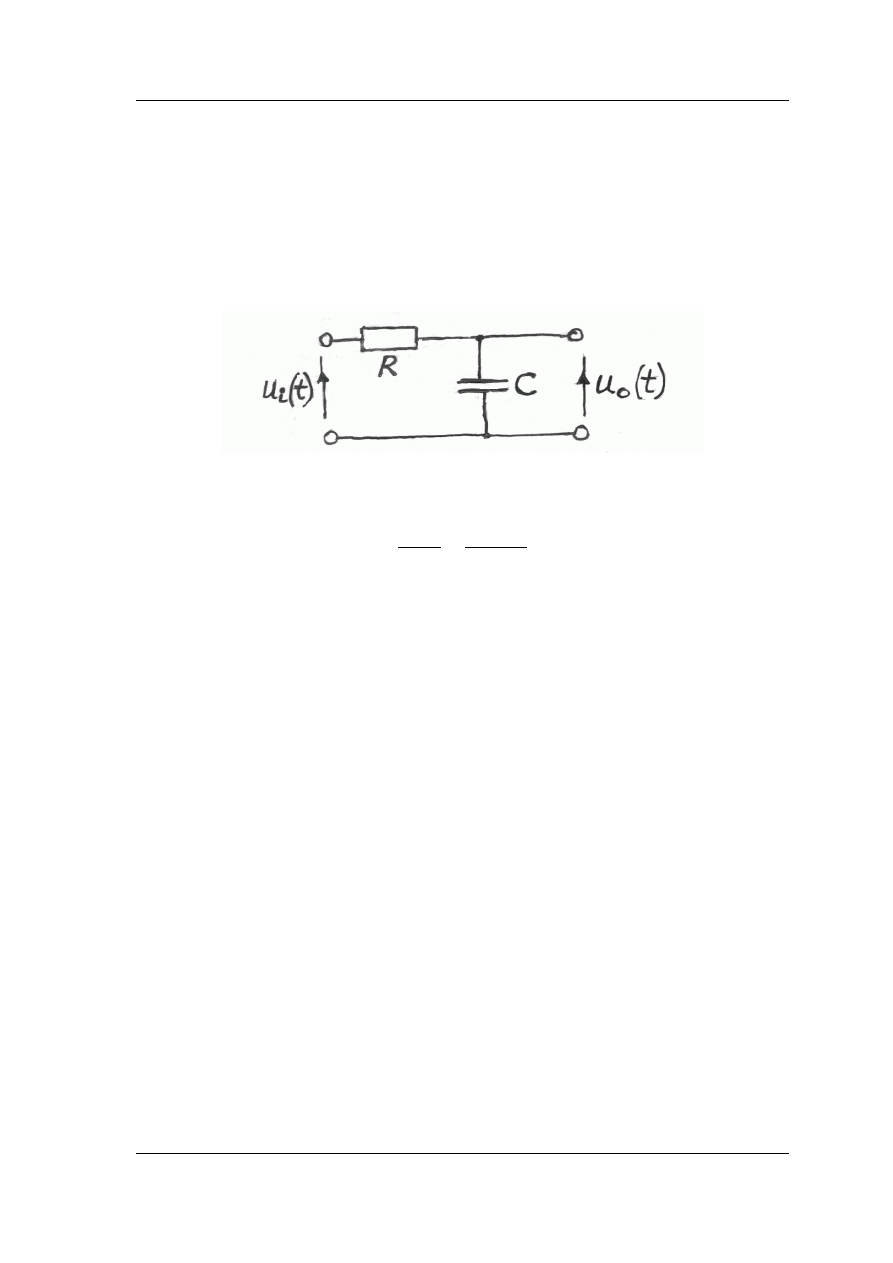
© Witold Szkudliński: FILTRY

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_Filters_2011.pdf Modyfikacje 2010 i 2011: C. Stefański

Katedra Systemów Elektroniki Morskiej

Laboratorium sieciowe 626Ea

Instrukcje LOiS - wersja 2011

2

2.1.

Wstęp

Przetwarzanie sygnału polega w wielu przypadkach na określonym oddziaływaniu

na poszczególne składowe reprezentacji tego sygnału w dziedzinie częstotliwości. Układy
elektryczne, które pozwalają na tego rodzaju oddziaływanie noszą ogólną nazwę filtrów.

Historycznie filtry bazują na zależnych od częstotliwości właściwościach

kondensatora i cewki indukcyjnej. Jeżeli do pojedynczego kondensatora dodamy
rezystor otrzymujemy najprostszy i często stosowany filtr przedstawiony tu na rys. 2.1.

Rys. 2.1. Prosty filtr dolnoprzepustowy RC

Transmitancja napięciowa układu z rys. 2.1 przedstawia się następująco:

=

=

1

1 + ,

(2.1)

gdzie zmienna

= + jest nazywana pulsacją zespoloną (też czasem

(kątową)

częstotliwością zespoloną).

Moduł funkcji (2.1) możemy sobie wyobrazić jako powierzchnię figury rozpiętą

w przestrzeni nad płaszczyzną o współrzędnych

, , które są składowymi zespolonej

zmiennej

= + . Przyjęcie = 0 oznacza, że ograniczamy rozważania do przekroju

figury dokonanego wzdłuż osi

, przy czym zmienną nazywamy pulsacją (też

częstotliwością kątową).

Wiadomo również, że przy sinusoidalnym napięciu wejściowym, napięcie na wyjściu

jest w stanie ustalonym również sinusoidalne zgodnie z zapisem

=

cos

,

=

cos

+ ,

= |

∙

|, = arg

.

(2.2)

Filtr z rys. 2.1 przetwarza wejściową sinusoidę na sinusoidę o tej samej częstotliwości

lecz (potencjalnie) innej amplitudzie i fazie. w tej sytuacji zrozumiałe jest, że przebieg
wejściowy złożony z wielu składowych sinusoidalnych jest przez filtr przetwarzany na
przebieg o (potencjalnie) innym charakterze, gdyż relacje amplitudowe i fazowe
pomiędzy składowymi mogą być dla przebiegu wyjściowego już inne niż na wejściu.

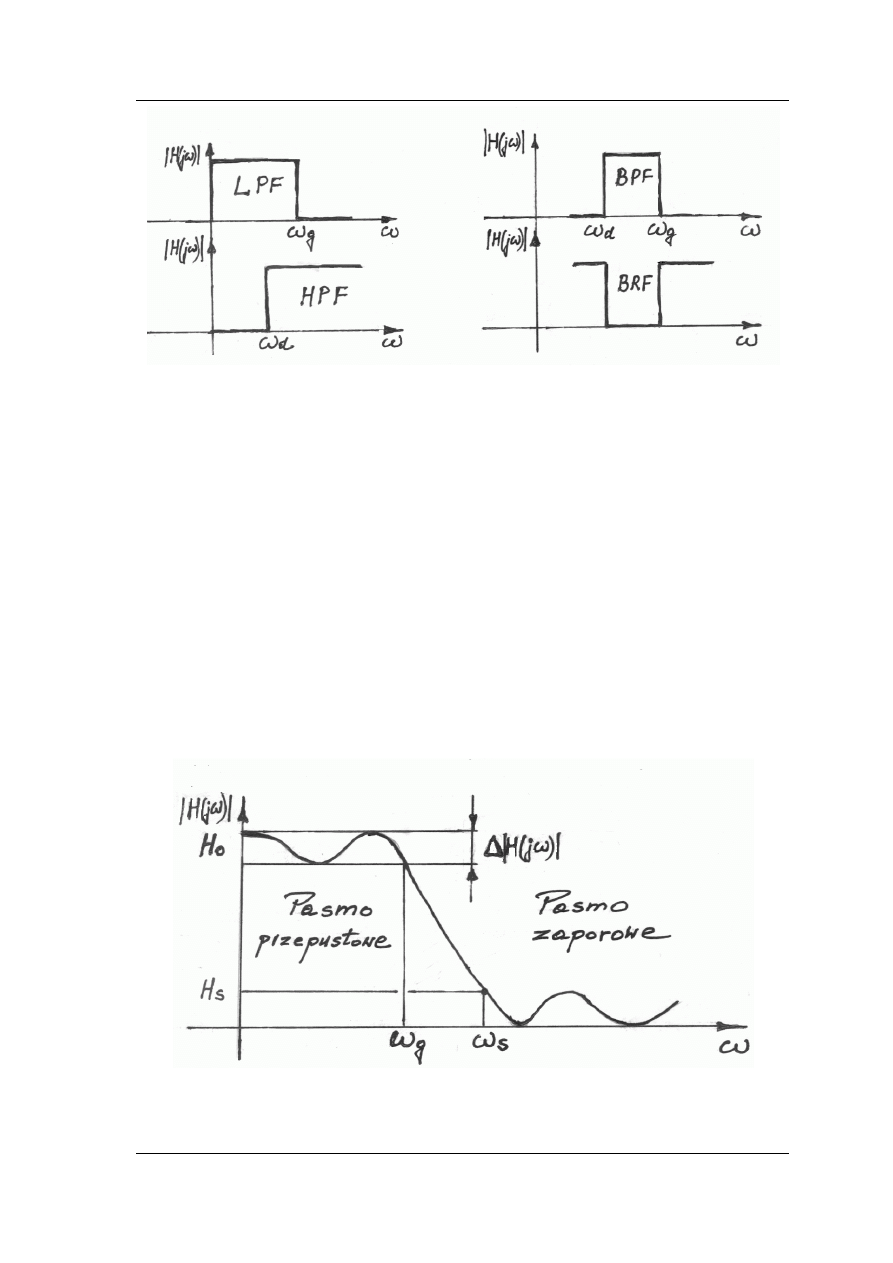
Na rys. 2.2 przedstawiono z grubsza zarysowane charakterystyki amplitudowe

związane z określonymi typami filtrów.

© Witold Szkudliński: FILTRY

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_Filters_2011.pdf Modyfikacje 2010 i 2011: C. Stefański

Katedra Systemów Elektroniki Morskiej

Laboratorium sieciowe 626Ea

Instrukcje LOiS - wersja 2011

3

Rys. 2.2. Typy idealizowanych charakterystyk amplitudowych filtrów

W przypadku filtru dolnoprzepustowego (FDP; ang. LPF – lowpass filter) małe

częstotliwości znajdują się w paśmie przepustowym, a większe częstotliwości w paśmie
zaporowym filtru. z kolei dla komplementarnego z nim filtru górnoprzepustowego (FGP;
ang. HPF – highpass filter) małe częstotliwości są w paśmie zaporowym, a wielkie
w przepustowym. Realizując kaskadę złożoną z odpowiednio dobranych fitrów
dolnoprzepustowego i górnoprzepustowego można uzyskać filtr pasmowo-przepustowy
(FPP; ang. BPF – bandpass filter). Filtr wszechprzepustowy (ang. APF – all-pass filter) nie
zmienia amplitud składników harmonicznych przechodzącego sygnału, ale zmienia
relacje fazowe między tymi składnikami. Układem komplementarnym do filtru
pasmowo-przepustowego jest filtr pasmowo-zaporowy (FPZ; ang. BRF – bandreject filter

lub BSF – band-stop filter

). Wąskopasmowy filtr pasmowo-przepustowy (BRF o wąskim

paśmie) jest często nazywany filtrem typu Notch (ang. Notch filter).

W praktyce, przejście charakterystyk filtrów pomiędzy pasmem przepustowym

i zaporowym nigdy nie jest nieskończenie strome (patrz rys. 2.3). Skończone nachylenie
powoduje pojawienie się dodatkowego pasma na osi częstotliwości, które nazywamy
pasmem przejściowym (ang. TB- transition band).

Rys. 2.3. Przykład realnej charakterystyki filtru LPF

Na rys. 2.3 zostało zdefiniowanych kilka ważnych parametrów filtru:

© Witold Szkudliński: FILTRY

Katedra Systemów Elektroniki Morskiej

• Częstotliwość graniczna

opuszcza przedział zafalowań
w

przypadku np. filtru Butterwortha, którego char

• Tłumienie lub wzmocnienie

• Falowanie w paśmie przepustowym

• Granica pasma zaporowego

po raz pierwszy poziom tłumienia właściwy dla pasma zaporowego.

• Tłumienie w paśmie zaporowym

Wracając jeszcze raz do transmitancji (2.1) możemy jej właściwości określić również

w ten sposób, iż jest to funkcja posiadająca zero

w punkcie

=

!

. Funkcja

położenia bieguna na płaszczyźnie „
płaszczyzny. Żonglując położeniem biegunów
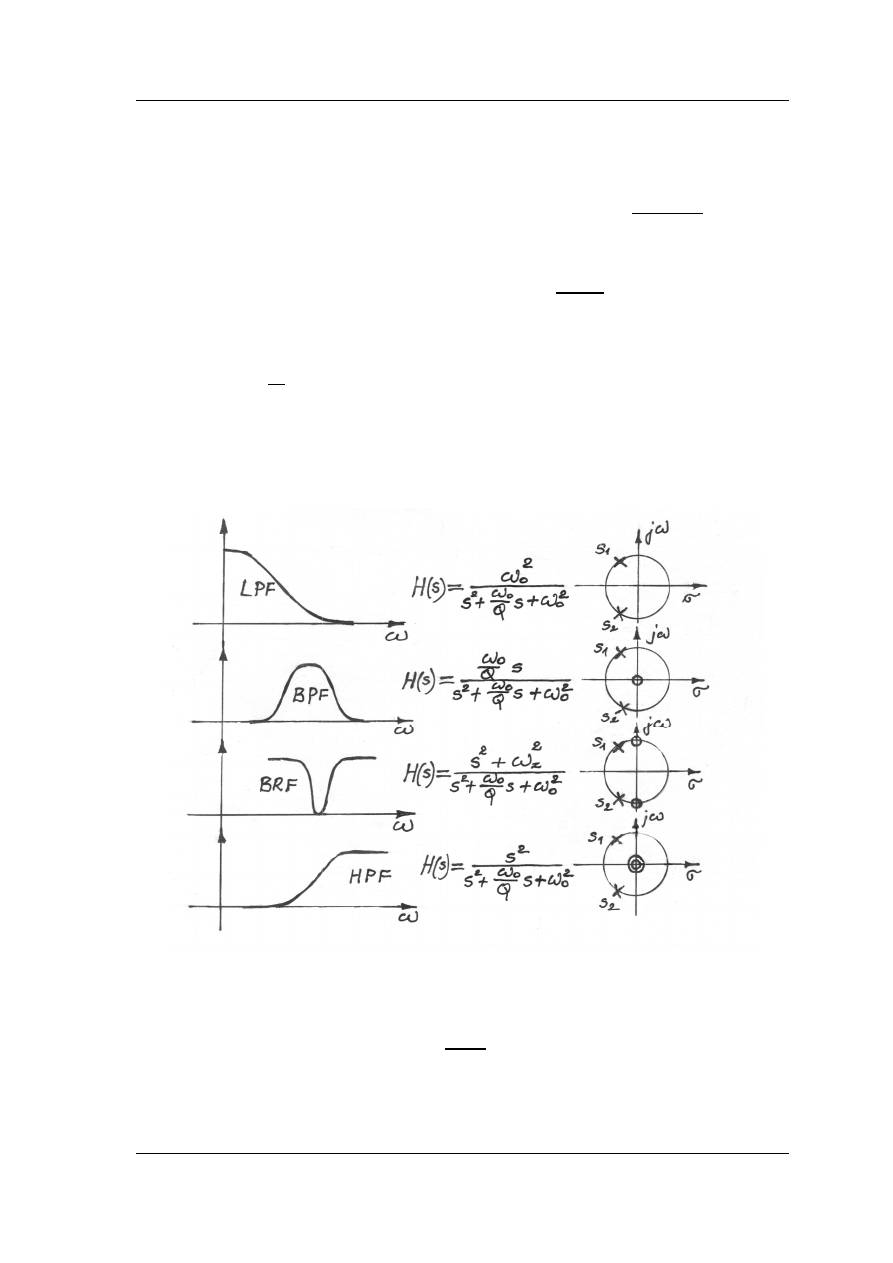
oczywisty wpływamy na właściwości charakterystyk filtru, co możemy prześledzić
przykładzie przedstawionych na rys. 2.4 wykresów charakterystyk filtrów
rzędu) o dwóch biegunach.

Rys. 2.4. Wpływ położenia zer

Dla dolnoprzepustowego

w punkcie

= " mamy

Z kolei transmitancj

niezależnie od jego struktury, zapis

Laboratorium Obwodów

Plik:LOiS_Filters_2011.pdf

Laboratorium sieciowe 626Ea

4

Częstotliwość graniczna (f

g

) jest to częstotliwość przy której charakterystyka

przedział zafalowań w paśmie przepustowym lub spada o 3dB

przypadku np. filtru Butterwortha, którego charakterystyka nie faluje.

lub wzmocnienie w paśmie przepustowym

#

=

paśmie przepustowym

Δ|| = 20log '

|(

|(

Granica pasma zaporowego (f

s

) oznacza częstotliwość, dla której filtr osiąga

po raz pierwszy poziom tłumienia właściwy dla pasma zaporowego.

paśmie zaporowym

"

)

= 20log '

(

*

|(+

,

|

- w [dB].

Wracając jeszcze raz do transmitancji (2.1) możemy jej właściwości określić również

to funkcja posiadająca zero w nieskończoności

. Funkcja

, czyli przekrój wzdłuż osi

położenia bieguna na płaszczyźnie „s” mimo, iż biegun ten leży na drugiej
płaszczyzny. Żonglując położeniem biegunów i zer transmitancji
oczywisty wpływamy na właściwości charakterystyk filtru, co możemy prześledzić
przykładzie przedstawionych na rys. 2.4 wykresów charakterystyk filtrów

biegunach.

2.4. Wpływ położenia zer i biegunów na właściwości filtrów

Dla dolnoprzepustowego filtru pierwszego rzędu z pojedynczym biegunem

mamy

=

"

+ ".

Z kolei transmitancja dolnoprzepustowego filtru drugiego rzędu moż

niezależnie od jego struktury, zapisana w postaci funkcji

Laboratorium Obwodów i Sygnałów (LOiS)

Modyfikacje 2010 i 2011: C. Stefański

Instrukcje LOiS - wersja 2011

jest to częstotliwość przy której charakterystyka

paśmie przepustowym lub spada o 3dB

akterystyka nie faluje.

= |0| w [dB].

'

(+|

/01

(+|

/23

- w [dB]

dla której filtr osiąga

po raz pierwszy poziom tłumienia właściwy dla pasma zaporowego.

[dB].

Wracając jeszcze raz do transmitancji (2.1) możemy jej właściwości określić również

nieskończoności

(

)

∞

=

s

i biegun

wzdłuż osi

, zależy od

iż biegun ten leży na drugiej z osi tej

zer transmitancji

w sposób

oczywisty wpływamy na właściwości charakterystyk filtru, co możemy prześledzić na
przykładzie przedstawionych na rys. 2.4 wykresów charakterystyk filtrów (drugiego

filtrów

pojedynczym biegunem

(2.3)

drugiego rzędu może być,

© Witold Szkudliński: FILTRY

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_Filters_2011.pdf Modyfikacje 2010 i 2011: C. Stefański

Katedra Systemów Elektroniki Morskiej

Laboratorium sieciowe 626Ea

Instrukcje LOiS - wersja 2011

5

4

=

#

4

4

+

#

5 +

#

4

(2.4)

o biegunach

=

+

*

46

+

#

71

86

9

,

=

+

*

46

#

71

86

9

,

gdzie

5 to dobroć, zaś

#

to pulsacja charakterystyczna, czyli standardowe parametry

układu drugiego rzędu.

Realizację filtru rzędu wyższego niż drugi można sobie między innymi wyobrazić jako

połączenie w kaskadę niezależnych od siebie członów rzędu pierwszego (2.3) i drugiego
(2.4). Przykładowo, transmitancje filtrów rzędu trzeciego i piątego możemy przedstawić
jako

:

=

∙

4

;

=

∙

4

<

∙

4

<<

(2.5)

W wyrażeniu (2.5) transmitancje układów drugiego rzędu mogą się różnić co do wartości
parametrów, co zaznaczono różnicując

)

(

2

s

H

za pomocą symboli „prim” oraz „bis”.

2.2.

Dolnoprzepustowe prototypy filtrów

Na wstępie podkreślono, że właściwości transmitancji filtru zależą od położenia jej

biegunów. w literaturze i konstrukcjach praktycznych powszechnie utrwaliły się pojęcia
filtrów Butterwortha, Czebyszewa, Bessela, których właściwości są jednoznacznie
związane z położeniem biegunów na płaszczyźnie „s”. Podstawowe dane na ten temat
zamieszczono tutaj w tablicach (2.1-2.3)

1

. Zamieszczone dane w każdym przypadku

dotyczą filtru dolnoprzepustowego o pulsacji granicznej równej 1 rad/s. Filtr o takich
właściwościach jest na ogół niepraktyczny i dlatego ma znaczenie tylko jako prototyp,
którego parametry trzeba każdorazowo zmienić (skalować) w taki sposób, aby działanie
filtru przenieść w obszar pożądanych częstotliwości. w celu wskazania, że mamy do
czynienia z prototypem pulsację zespoloną w transmitancjach (2.1)-(2.5) oznaczymy
każdorazowo literą „p”.

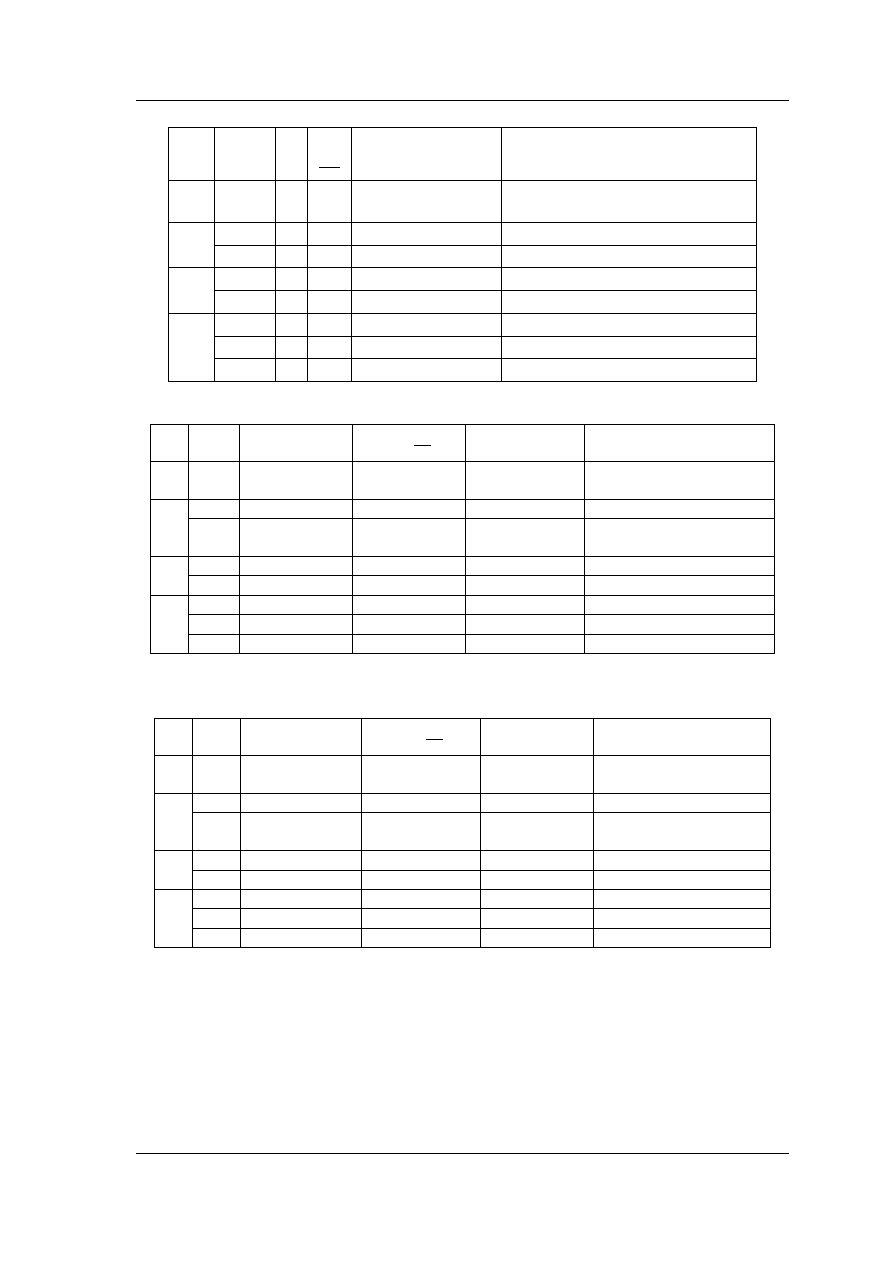
Transmitancje podstawowych ogniw kaskady (2.5) dla prototypu zapiszemy teraz

w postaci

= =

"

>

= + "

>

,

4

= =

>#

4

=

4

+

>#

5

>

= +

>#

4

.

(2.6)

1

Dane zamieszczone w tabl.2.1-2.4 dla rzędów n=4 i 5 otrzymano na podstawie opracowania „ OP-AMP Applications”

pod redakcją Waltera G. Junga, które powstało w firmie Analog Devices w 2002 roku, zaś dla rzędów n=2 i 3
pochodzą z precyzyjnych obliczeń wykonanych w programie MAXIMA przez C. Stefańskiego

© Witold Szkudliński: FILTRY

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_Filters_2011.pdf Modyfikacje 2010 i 2011: C. Stefański

Katedra Systemów Elektroniki Morskiej

Laboratorium sieciowe 626Ea

Instrukcje LOiS - wersja 2011

6

Tablica 2.1. Parametry prototypów filtrów Butterwortha

Rząd

n

Sekcja

"

>

>#

[

@AB

C

]

5

>

Bieguny

2

4

= 1.0 0.70710678118655

=

,4

=-0.70710678118655

±j0.70710678118655

3

= 1.0

=

=-1.0

4

= 1.0

1.0

=

4,:

=-0.5±j0.86602540378444

4

4

<

= 1.0

1.3065

=

,4

=-0.3827±j0.9239

4

<<

= 1.0

0.5412

=

:,8

=-0.9239±j0.3827

5

= 1.0

=

=-1.0

4

<

= 1.0

1.6182

=

4,:

=-0.3090±j0.9511

4

<<

= 1.0

0.6180

=

8,;

=-0.8090±j0.5878

Tablica 2.2. Parametry prototypów filtrów Czebyszewa (1dB)

Rząd

n

Sekcja

"

>

>#

[

@AB

C

]

5

>

Bieguny

2

4

=

0.86233770962438 0.95652007119336

=

,4

= -0.45076822515001

±j0.73514238936096

3

=

0.45135175640551

=

=-0.45135175640551

4

=

0.91070162104782 2.017720343663899

=

4,:

=-0.22567587820275

±j0.88229691180268

4

4

<

=

0.9433

3.5594

=

,4

=-0.1325±j0.9339

4

<<

=

0.5019

0.7845

=

:,8

=-0.3199±j0.3868

5

=

0.280

=

=-0.280

4

<

=

0.9614

5.5559

=

4,:

=-0.0865±j0.9575

4

<<

=

0.6337

1.3988

=

8,;

=-0.2265±j0.5918

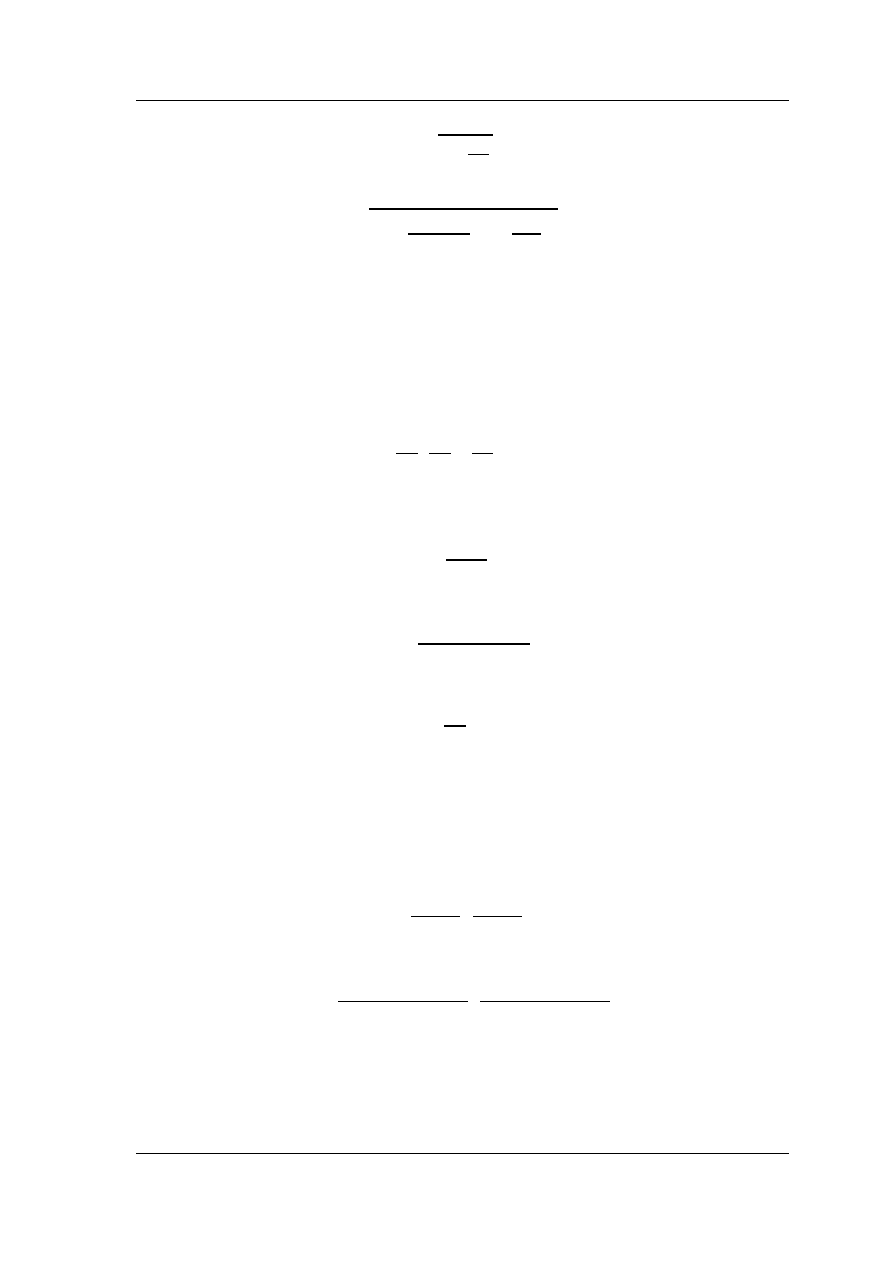
Tablica 2.3. Parametry prototypów filtrów Bessela

Rząd

n

Sekcja

"

>

>#

[

@AB

C

]

5

>

Bieguny

2

4

=

1.272019649514096 0.57735026918963

=

,4

=-1.101601330592162

±j0.63600982475703

3

=

1.322675799910445

=

=1.322675799910445

4

=

1.447617133146987 0.69104662582507

=

4,:

=-1.047409161008936

±j0.99926443628064

4

4

<

=

1.4192

0.5219

=

,4

=-1.3596±j0.4071

4

<<

(=)

1.5912

0.8055

=

:,8

=-0.9877±j1.2476

5

=

1.5069

=

=-1.5069

4

<

=

1.7607

0.9165

=

4,:

=-0.9606±j1.4756

4

<<

=

1.5611

0.5635

=

8,;

=-1.3851±j0.7201

Projektując filtr odpowiedniego typu i rzędu (do rzędu piątego), dane dotyczące

bądź parametrów członów kaskady (

"

>

,

>#

, 5

>

), bądź składowych biegunów można

pobrać z zamieszczonych w literaturze tablic (tutaj 2.1-2.3). Najpierw jednak projektant
filtru musi zdecydować się na którąś ze znanych form realizacji takiego układu. w grę
wchodzą struktury obwodowe LC lub LC w powiązaniu z tzw. rezonatorami (ceramiczne,
kwarcowe, mikropaskowe, SAW), struktury RC plus wzmacniacz operacyjny oraz układy
działające w czasie w sposób nie ciągły tylko przerywany (dyskretny), a wśród nich
układy przełączane C i układy cyfrowe.

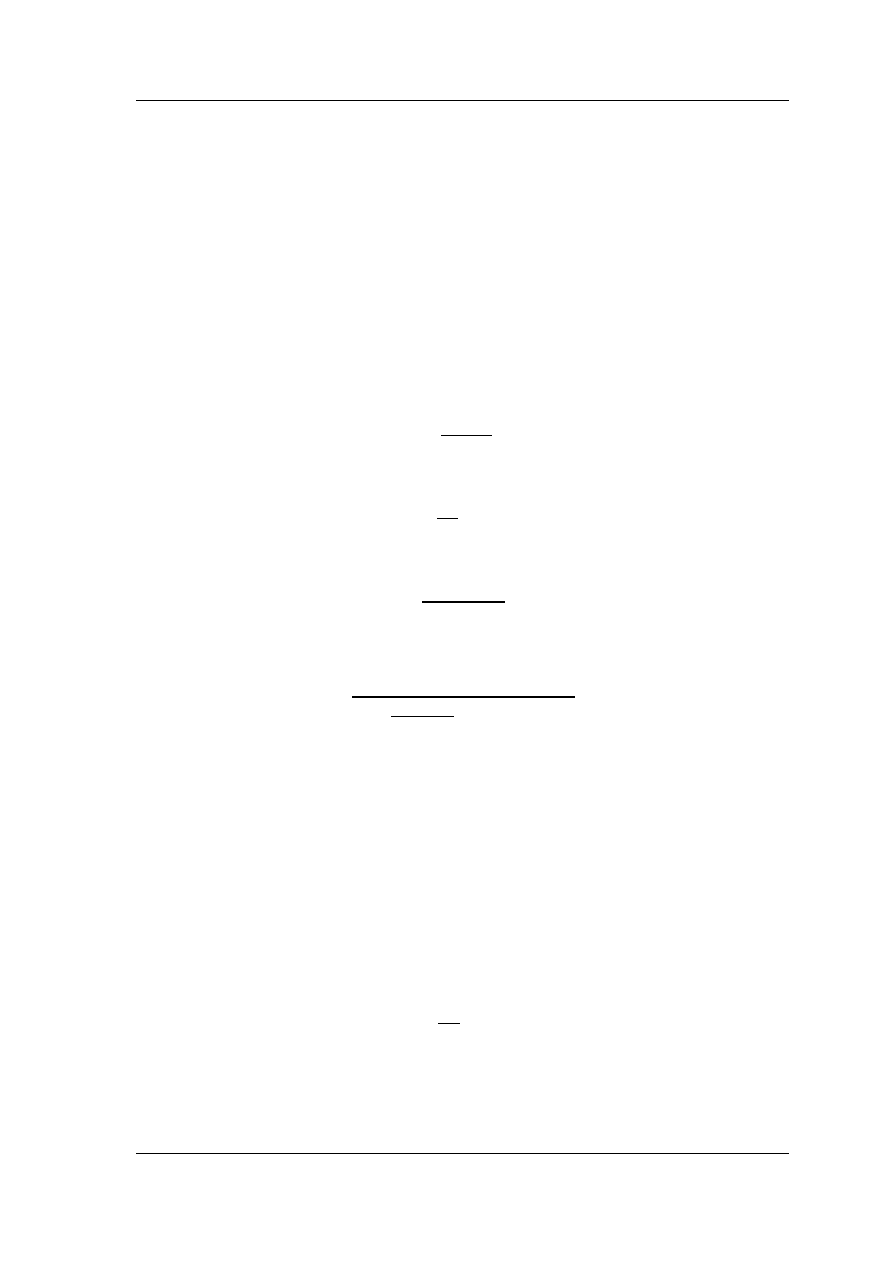
© Witold Szkudliński: FILTRY

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_Filters_2011.pdf Modyfikacje 2010 i 2011: C. Stefański

Katedra Systemów Elektroniki Morskiej

Laboratorium sieciowe 626Ea

Instrukcje LOiS - wersja 2011

7

2.3.

Projektowanie filtrów kaskadowych

Filtrem kaskadowym będziemy dalej nazywali kaskadowe połączenie bloków

o określonych transmitancjach, dające w efekcie transmitancję wypadkową w sposób
przedstawiony wzorem (2.5).

Pierwszy

krok

w projektowaniu

filtru

polega

na

pobraniu

parametrów

odpowiedniego prototypu z tablic 2.1-2.3. Następne operacje zależą od tego, czy filtr
wynikowy ma być filtrem dolnoprzepustowym, górnoprzepustowym, czy też filtrem
pasmowo-przepustowym.

Filtr dolnoprzepustowy
W przypadku filtru dolnoprzepustowego, np. trzeciego rzędu o pulsacji

granicznej

F

, wystarczy w transmitancjach prototypów

)

(

),

(

p

H

p

H

2

1

dokonać

prostego przeskalowania częstotliwości.
Do transmitancji prototypu

= =

"

>

= + "

>

,

(2.7)

podstawiamy

= =

F

.

(2.8)

W wyniku otrzymujemy funkcję, która jest transmitancją pierwszego członu kaskady

F

∙ "

>

+

F

∙ "

>

.

(2.9)

Identyczne podstawienie wprowadzamy do funkcji

4

= otrzymując

4

G

>#

∙

F

H

4

4

+

>#

∙

F

5

>

+ G

>#

∙

F

H

4

.

(2.10)

Po połączeniu filtrów o transmitancjach (2.9) i (2.10) w kaskadę o transmitancji

:

∙

4

powstaje filtr dolnoprzepustowy trzeciego rzędu o pulsacji

granicznej

F

.

W przypadku filtru dolnoprzepustowego innego rzędu niż trzeci postępujemy

w sposób analogiczny, z tym, że dane z tablic 2.1-2.3 dotyczą filtrów tylko do piątego
rzędu.

Filtr górnoprzepustowy
Zamiana transmitancji dolnoprzepustowego prototypu

= na transmitancję filtru

górnoprzepustowego o pulsacji granicznej

g

ω

zachodzi po zastosowaniu nieliniowej

transformacji

=

F

(2.11)

Transformacja (2.11) daje w wyniku

© Witold Szkudliński: FILTRY

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_Filters_2011.pdf Modyfikacje 2010 i 2011: C. Stefański

Katedra Systemów Elektroniki Morskiej

Laboratorium sieciowe 626Ea

Instrukcje LOiS - wersja 2011

8

=

+

F

"

>

,

4

=

4

4

+

F

>#

∙ 5

>

+ I

F

>#

J

4

,

:

=

∙

4

(2.12)

Filtr pasmowo-przepustowy

Dolnoprzepustowy prototyp może również stanowić bazę do utworzenia

transmitancji filtru pasmowo-przepustowego. Zamianę transmitancji prototypu na
transmitancję filtru pasmowo-przepustowego dokonuje się za pomocą nieliniowej
transformacji

= =

#

Δ

+

I

#

+

#

J

(2.13)

gdzie:

#

jest pulsacją środkową zaś

Δ

+

to pasmo filtru na osi

.

Po podstawieniu (2.13) do funkcji przenoszenia prototypu pierwszego rzędu

=

1

= + 1,

otrzymujemy transmitancję filtru pasmowo-przepustowego drugiego rzędu

KL4

Δ

+

4

+ Δ

+

+

#

4

,

(2.14)

Zauważmy, że na podstawie porównania (2.14) z (2.4) mamy

Δ

+

#

5 ,

(2.15)

czyli znany związek szerokości pasma z pulsacją środkową i dobrocią układu (obwodu)
drugiego rzędu.

Teraz podstawimy (2.13) do

4

= o postaci nieco innej niż (2.4). Mianowicie, jeżeli

w mianowniku i liczniku transmitancji drugiego rzędu

4

= mamy wyrażenia o

rzeczywistych współczynnikach, to obydwa bieguny transmitancji drugiego rzędu są
zespolone sprzężone, czyli

4

=

>#

= − =

∙

>#

= − =

∗

.

(2.16)

Po podstawieniu (2.13) otrzymujemy

KL8

>#

Δ

+

4

− =

Δ

+

+

#

4

∙

>#

Δ

+

4

− =

∗

Δ

+

+

#

4

,

(2.17)

Dalsze przekształcenia wykonamy zakładając wąskopasmowość układu

2

#

≫ |=

|Δ

+

.

(2.18)

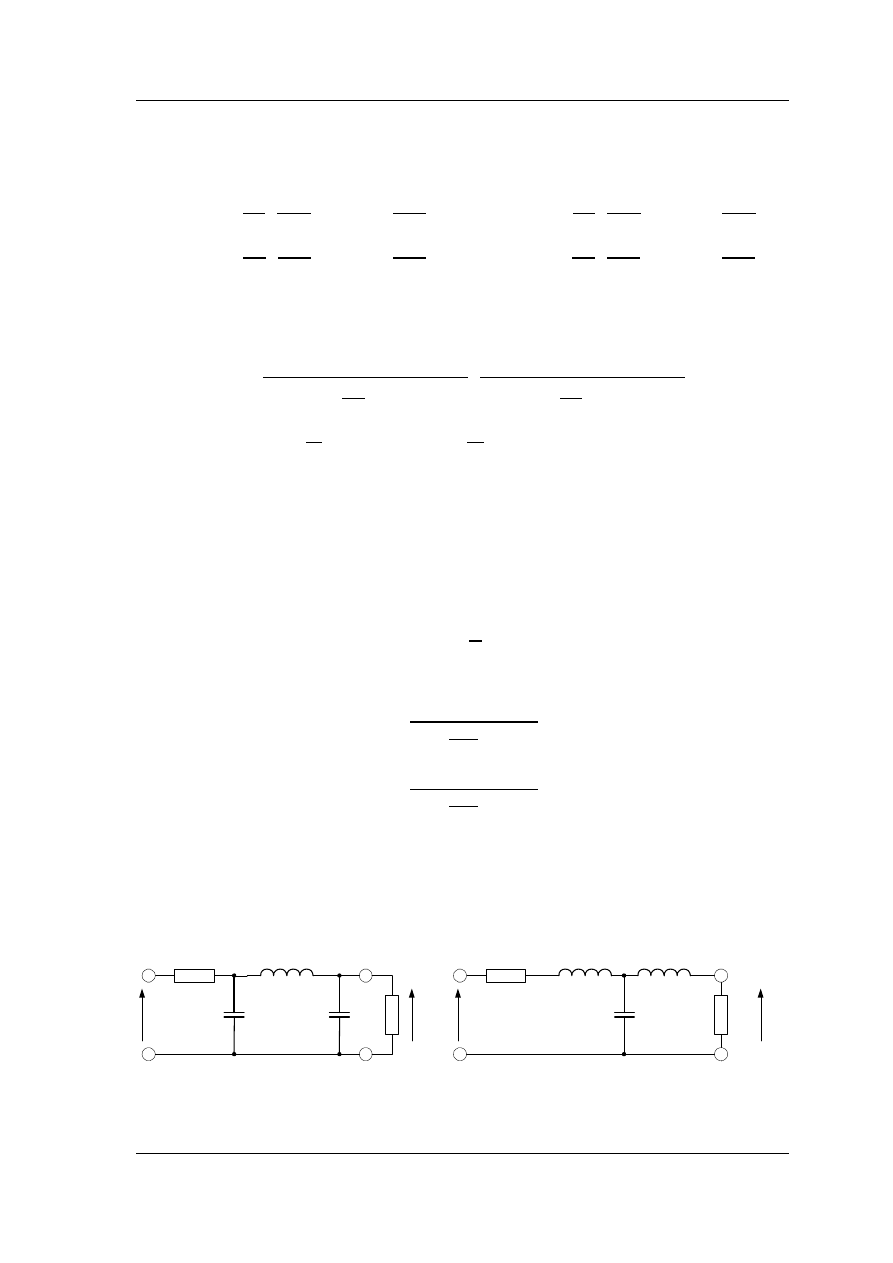
Bieguny transmitancji (2.17) są między innymi uzależnione od położenia biegunów

prototypu, przy czym po przyjęciu symboli na składowe bieguna

=

,

© Witold Szkudliński: FILTRY

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_Filters_2011.pdf Modyfikacje 2010 i 2011: C. Stefański

Katedra Systemów Elektroniki Morskiej

Laboratorium sieciowe 626Ea

Instrukcje LOiS - wersja 2011

9

=

= " O,=

∗

= " + O,

(2.19)

otrzymujemy następujące zapisy przybliżonego położenia obu par

P

,

4

,

:

,

8

Q

biegunów transmitancji

KL8

:

= I1

O

25J

"Δ

+

2 + I

#

OΔ

+

2 J,

4

= I1 +

O

25J

"Δ

+

2 I

#

+

OΔ

+

2 J,

:

= I1 +

O

25J

"Δ

+

2 + I

#

+

OΔ

+

2 J,

8

= I1

O

25J

"Δ

+

2 I

#

OΔ

+

2 J.

Bieguny grupujemy w nowe, tym razem sprzężone pary:

,

8

oraz

4

,

:

i otrzymujemy transmitancję (2.17) w postaci (przybliżonej) iloczynu dwóch funkcji
wymiernych o rzeczywistych współczynnikach

KL8

>#

Δ

+

4

+ I1 − O

25J "Δ

+

+

#

4

∙

>#

Δ

+

4

+ I1 + O

25J "Δ

+

+

#4

4

,

(2.20)

gdzie:

#

#

'1 −

R

46

-,

#4

#

'1 +

R

46

- .

Każdy z członów iloczynu (2.20) może reprezentować oddzielny i niezależny układ

pasmowy drugiego rzędu (patrz wzór 2.4), przy czym układy te muszą być w takim
przypadku połączone w kaskadę

KL8

KL4

<

∙

KL4

<<

.

(2.21)

Pulsacje środkowe obu układów to odpowiednio

#

i

#4

, zaś ich dobroci są takie

same i równe

5

5

4

5

".

(2.22)

Stąd ostateczny zapis członów transmitancji (2.21)

KL4

<

>#

Δ

+

4

+

#

5

+

#

4

,

KL4

<<

>#

Δ

+

4

+

#4

5

4

+

#4

4

.

(2.23)

2.4.

Projektowanie dolnoprzepustowych filtrów RLC

Historycznie

jedną

z pierwszych

i do

dzisiaj

stosowaną

realizacją

dolnoprzepustowego filtru drugiego i wyższych rzędów jest przedstawiona na rys. 2.5
drabinkowa struktura elementów LC.

2

L

o

R

1

C

i

R

3

C

i

R

o

R

1

L

3

L

2

C

i

U

i

U

o

U

o

U

b)

Rys. 2.5. Struktury drabinkowe do realizacji filtrów filtr dolnoprzepustowych RLC

2-go i 3-go rzędu trzeciego: a) struktura typu

S, b) struktura typu T

a)

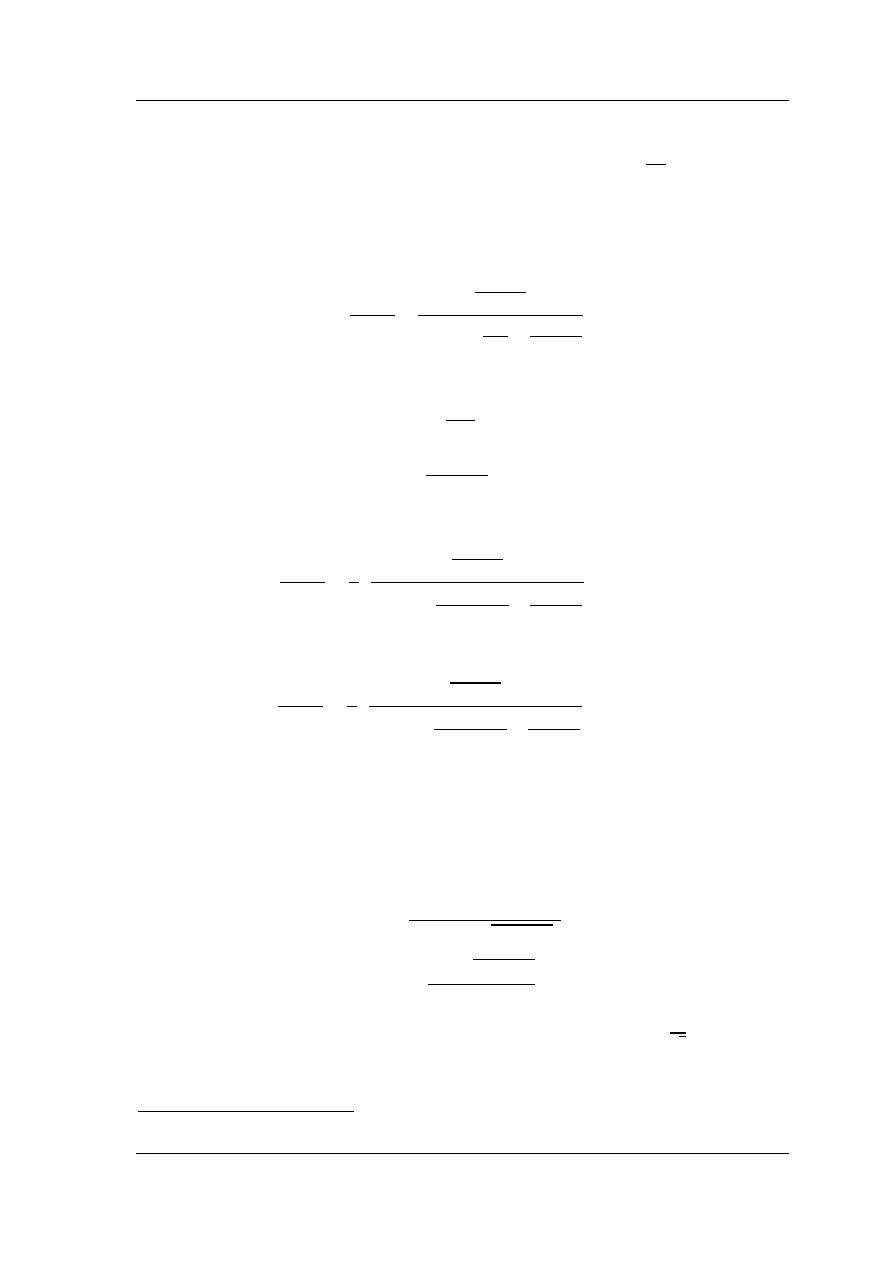
© Witold Szkudliński: FILTRY

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_Filters_2011.pdf Modyfikacje 2010 i 2011: C. Stefański

Katedra Systemów Elektroniki Morskiej

Laboratorium sieciowe 626Ea

Instrukcje LOiS - wersja 2011

10

Weźmiemy pod uwagę kilka wariantów i tak dobierzemy LC, aby parametry filtru

dopasować do danych zawartych w tabl. 2.1-2.3. Uzyskamy w ten sposób prototypy
w postaci struktur drabinkowych, każda o pulsacji granicznej

F

= 1

T

U0V

,

W

.

Jedna cewka i jeden kondensator w połączeniu z rezystorami tworzą prototyp filtru

dolnoprzepustowego rzędu drugiego

1

.

Wariant

= 1Ω,

= ∞, Z

= Z

>

,

= 0,

4

=

>4

, Z

:

= 0:

4

= =

=

= =

1

Z

>

>4

=

4

+ = ∙ 1

Z

>

+ 1

Z

>

>4

.

(2.24)

W wyniku porównania (2.24) z (2.6) otrzymujemy

Z

>

5

>

>#

>4

1

>#

∙ 5

>

.

(2.25)

Wariant

=

= 1Ω (dla T oraz Π):

4

= =

=

= =

1

2 ∙

2

Z

>

>4

=

4

+ = ∙ Z

>

+

>4

Z

>

>4

+ 2

Z

>

>4

typ T

(2.26a)

(dla T

Z

= Z

>

,

4

=

>4

, Z

:

= 0)

4

= =

=

= =

1

2 ∙

2

Z

>4

>

=

4

+ = ∙ Z

>4

+

>

Z

>4

>

+ 2

Z

>4

>

typ Π

(2.26b)

(dla

Π

=

>

,Z

4

= Z

>4

,

:

= 0)

Porównamy teraz transmitancje (2.26) z (2.6), jednak zrobimy to z pominięciem

współczynnika „1/2” w wyrażeniu (2.26), gdyż zmiana tego współczynnika nie zmienia
typu transmitancji.

Po porównaniu otrzymujemy

Z

>

=

>

=

25

>

>#

G1 + \1 25

>4

H

>4

= Z

>4

=

1 + \1 25

>4

>#

∙ 5

>

.

(2.27)

Obie struktury: T(

Z

>

,

>4

) oraz

Π(

>

,

Z

>4

) mogą realizować tylko

5

>

≤

√4

.

1

Gdy nie ma R

o,

to dla obu struktur Π & T dostaniemy taki sam schemat ("znikają" odpowiednio C

1

oraz L

3

) czyli taką

samą transmitancję.

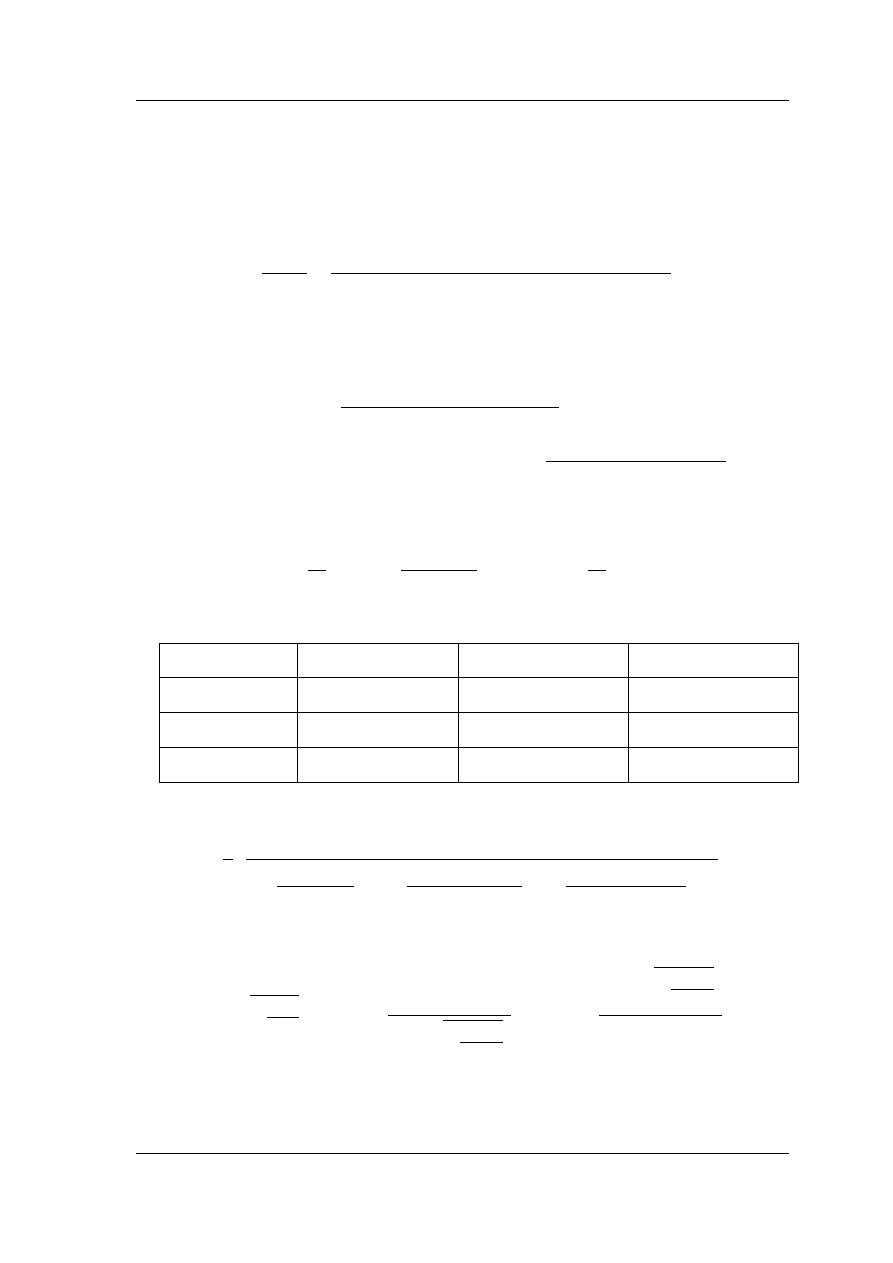
© Witold Szkudliński: FILTRY

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_Filters_2011.pdf Modyfikacje 2010 i 2011: C. Stefański

Katedra Systemów Elektroniki Morskiej

Laboratorium sieciowe 626Ea

Instrukcje LOiS - wersja 2011

11

Cewka i dwa kondensatory, połączone w strukturę typu Π (rys. 2.5a), tworzą filtr

drabinkowy rzędu trzeciego. Rozważania dla struktury z rys. 2.5b pominiemy ze względu
na praktyczną uciążliwość stosowania w obwodzie większej liczby cewek.

Dla prototypu w postaci struktury LC typu

Π rozważymy dwa warianty.

Wariant

= 1Ω,

= ∞,

=

>

, Z

4

= Z

>4

,

:

=

>:

:

:

= =

=

= =

1

=

:

Z

>4

>

>:

+ =

4

Z

>4

>:

+ =G

>

+

>:

H + 1

.

(2.28)

Zauważmy, że chcąc umiejscowić bieguny transmitancji (2.28) w punktach

określonych w tablicach 2.1-2.3 możemy skorzystać z zapisu w postaci iloczynu
transmitancji rzędów pierwszego i drugiego

:

=

= ∙

4

=

−=

∙ |=

4

|

4

= − =

∙ = − =

4

∙ = − =

4

∗

1

_

:

=

:

+ _

4

=

4

+ _

= + 1

(2.29)

Obliczone na podstawie tabl. 2.1-2.3 współczynniki transmitancji (2.29) zawiera tabl.2.4.
Na podstawie porównania (2.28) i (2.29) otrzymujemy

>

_

:

_

4

,Z

>4

_

4

4

_

_

4

− _

:

,

>:

_

−

_

:

_

4

.

(2.30)

Tablica 2.4. Współczynniki mianownika transmitancji trzeciego rzędu

Typ filtru

3

a

2

a

1

a

Butterwoth

1

2

2

Czebyszew (1dB) 2.671361385329835 2.41144730652494

2.759772362609196

Bessel

0.36077726616969 1.232954186460277 1.755672368681211

Wariant

=

= 1Ω,

=

>

, Z

4

= Z

>4

,

:

=

>:

:

:

= =

1

2 ∙

1

=

:

∙ Z

>4

>

>:

2

+ =

4

∙ Z

>4

G

>

+

>:

H

2

+ = ∙ Z

>4

+

>

+

>:

2

+ 1

(2.31)

Porównanie (z pominięciem współczynnika „1/2”) wyrażeń (2.29) z (2.31) daje w wyniku

Z

>4

= _

`

1

aba

4c

9

c

d

9

e

,

>

=

2_

:

_

4`

1

aba

4c

f

g

h9

c

9

9

e

,

>:

=

_

4`

1

aba

4c

f

g

h9

c

9

9

e

Z

>4

. (2.32)

Współczynniki (

_

, _

4

, _

:

) tak samo jak w poprzednim przypadku pobieramy z tabl. 2.4.

© Witold Szkudliński: FILTRY

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_Filters_2011.pdf Modyfikacje 2010 i 2011: C. Stefański

Katedra Systemów Elektroniki Morskiej

Laboratorium sieciowe 626Ea

Instrukcje LOiS - wersja 2011

12

Skalowanie elementów filtru RLC

Niezależnie od rzędu filtru, elementy RLC wyliczone za pomocą wzorów (2.25, 2.27,

2.30, 2.32) dają nam układy, których pulsacje graniczne

F

= 1

T

U0V

,

W

, co w sposób

oczywisty ogranicza możliwości praktycznego zastosowania filtru; równie niepraktyczne
jest obciążanie wejścia lub wyjścia filtru rezystancją 1 om. Użyteczny filtr o pulsacji
granicznej

F

> 1

T

U0V

,

W

uzyskamy poprzez odpowiednie przeskalowanie wartości

elementów prototypu.

Chcąc otrzymać parametry filtru dolnoprzepustowgo RLC o częstotliwości

granicznej

g

f i rezystancji

R

R

i

=

lub

R

R

R

o

i

=

=

, musimy dokonać następującego

przeskalowania wszystkich indukcyjności oraz pojemności struktury prototypowej:

Z =

2jk

F

∙ Z

>

, =

1

2jk

F

∙

>

.

(2.33)

gdzie

Z

>

,

>

to parametry wyliczane ze wzorów (2.25, 2.27, 2.30, 2.32) natomiast

Zi

to te same parametry po przeskalowaniu

1

.

Generalnie, dla

F

≫ 1

T

U0V

,

W

wartości indukcyjności i pojemności ulegają

zmniejszeniu i to zwykle o wiele rzędów wielkości.

2.5.

Odpowiedzi filtru dolnoprzepustowego w dziedzinie czasu

Odpowiedzi układu w dziedzinie czasu są w praktyce badane zwykle przy dwóch

standardowych pobudzeniach pobudzeniu quasi-impulsem Diraca oraz impulsem
w postaci uskoku napięcia.

Odpowiedź impulsowa

Impuls Diraca

m, to nieskończenie krótki impuls o nieskończenie dużej amplitudzie

lecz o jednostkowej powierzchni.

Odpowiedź impulsowa obwodu, oznaczana jako

no, to odpowiedź tego obwodu –

przy braku innych pobudzeń w obwodzie – na pobudzenie idealnym impulsem Diraca

m.

W praktyce, ze zrozumiałych względów, stosuje się zamiast idealnego impulsu Diraca

m po prostu impuls napięciowy lub prądowy o czasie trwania znacznie krótszym od
czasu trwania odpowiedzi; oczywiście otrzymujemy w takim przypadku impuls o
powierzchni różnej od jedności (jest to quasi-impuls Diraca).

Odpowiedź

p na quasi-impuls Diraca o powierzchni q

r

(wyrażonej odpowiednio

w [

s ∙ ] lub [t ∙ ]) można zapisać w postaci

p ≅ q

r

∙ ℎ,

(2.34)

gdzie

ℎ to odpowiedź układu na idealny impuls Diraca m.

Odpowiedź jednostkowa (też skokowa)

Uskok (skok) jednostkowy

1

(zwany też jedynką Heaviside’a) jest ograniczonym

w amplitudzie przebiegiem czasowym, który dla czasu t<0 jest zerowy, a dla czasu t>0
przyjmuje wartość jeden.

Odpowiedź jednostkowa (= odpowiedź skokowa) obwodu, oznaczana jako

wo, to

odpowiedź tego obwodu – przy braku innych pobudzeń obwodzie – na pobudzenie
idealnym uskokiem jednostkowym

1

.

1

Ze wzoru (2.33) wyznaczamy najpierw R (L jest w układzie pomiarowym zadane), a potem C.

© Witold Szkudliński: FILTRY

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_Filters_2011.pdf Modyfikacje 2010 i 2011: C. Stefański

Katedra Systemów Elektroniki Morskiej

Laboratorium sieciowe 626Ea

Instrukcje LOiS - wersja 2011

13

Ponieważ w praktyce trudno o idealny uskok jednostkowy

1

, musimy zadowolić

się jego odpowiednim przybliżeniem. w tym przypadku potrzebny impuls pobudzający
pozwalający uzyskać na wyjściu obwodu odpowiedź „podobną” do odpowiedzi skokowej
musi mieć z kolei znacznie dłuższy czas trwania od trwania w układzie stanu
przejściowego. Jednocześnie nachylenie zbocza impulsu powinno być znacznie większe
od nachylenia zbocza odpowiedzi.

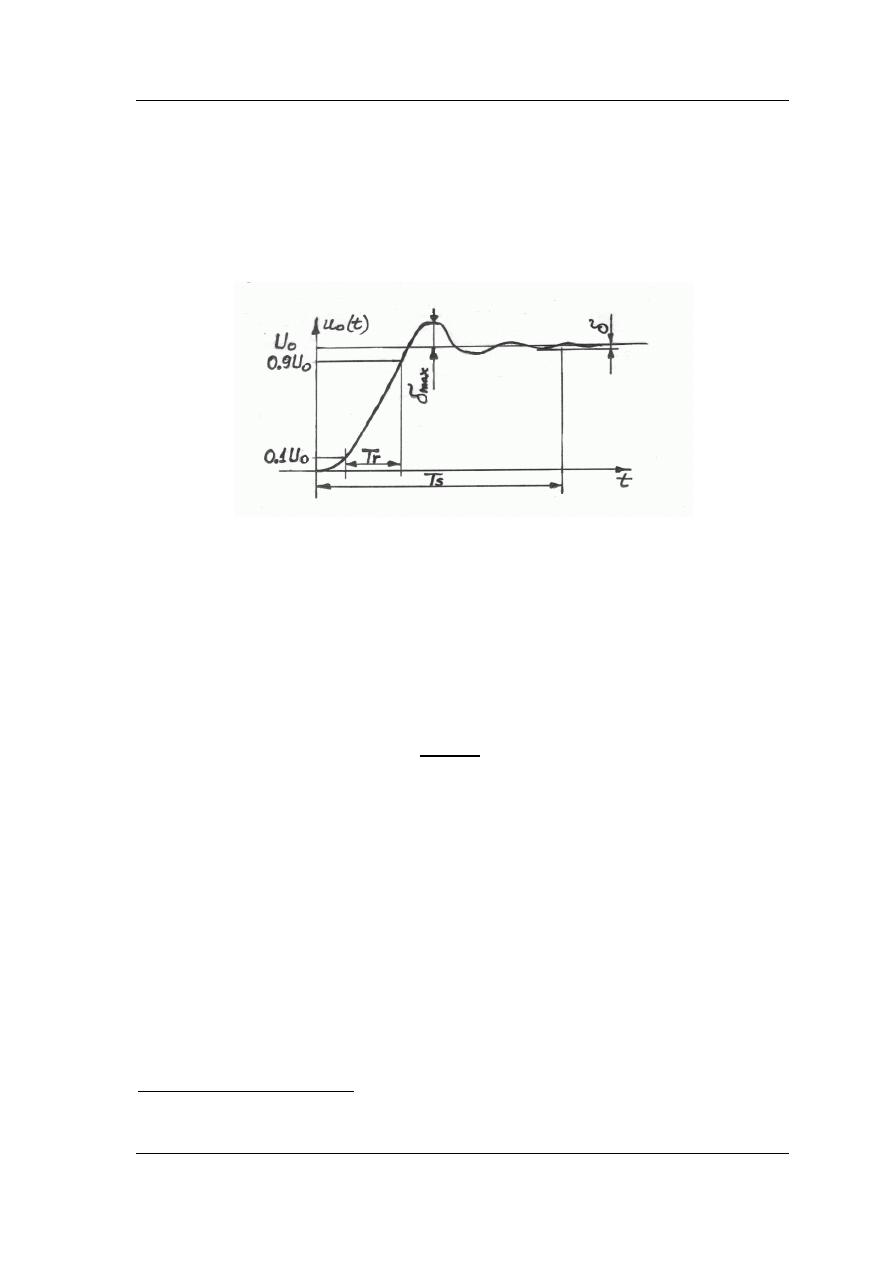
Charakterystyczny kształt odpowiedzi filtru na czoło (uskok) impulsu przedstawia

nam rys. 2.6.

Rys. 2.6. Ogólny charakter odpowiedzi filtru na czoło impulsu prostokątnego

Czas, w którym odpowiedź (startując od zera) zmienia się od 10% do 90% wartości

ustalonej

nazywamy czasem narastania impulsu

x

)

. Następnym parametrem

charakterystycznym jest podawany w procentach parametr

m

ycz

, czyli maksymalny

przerzut odpowiedzi ponad wartość

. Czas

{

|

osiągania przez grzbiet impulsu

wartości

ze względną dokładnością

m (zwykle

%

1

=

δ

) jest kolejnym

z charakteryzujących filtr parametrów.

Wiadomo, że czas

x

)

[s] narastania zbocza odpowiedzi zależy od

}

:~K

[Hz] (

}

:~K

to

tzw. trzydecybelowe pasmo filtru) według wzoru

1

:

x

)

≅

1

j ∙ }

:~K

.

(2.35)

2.6.

Opis badanych układów

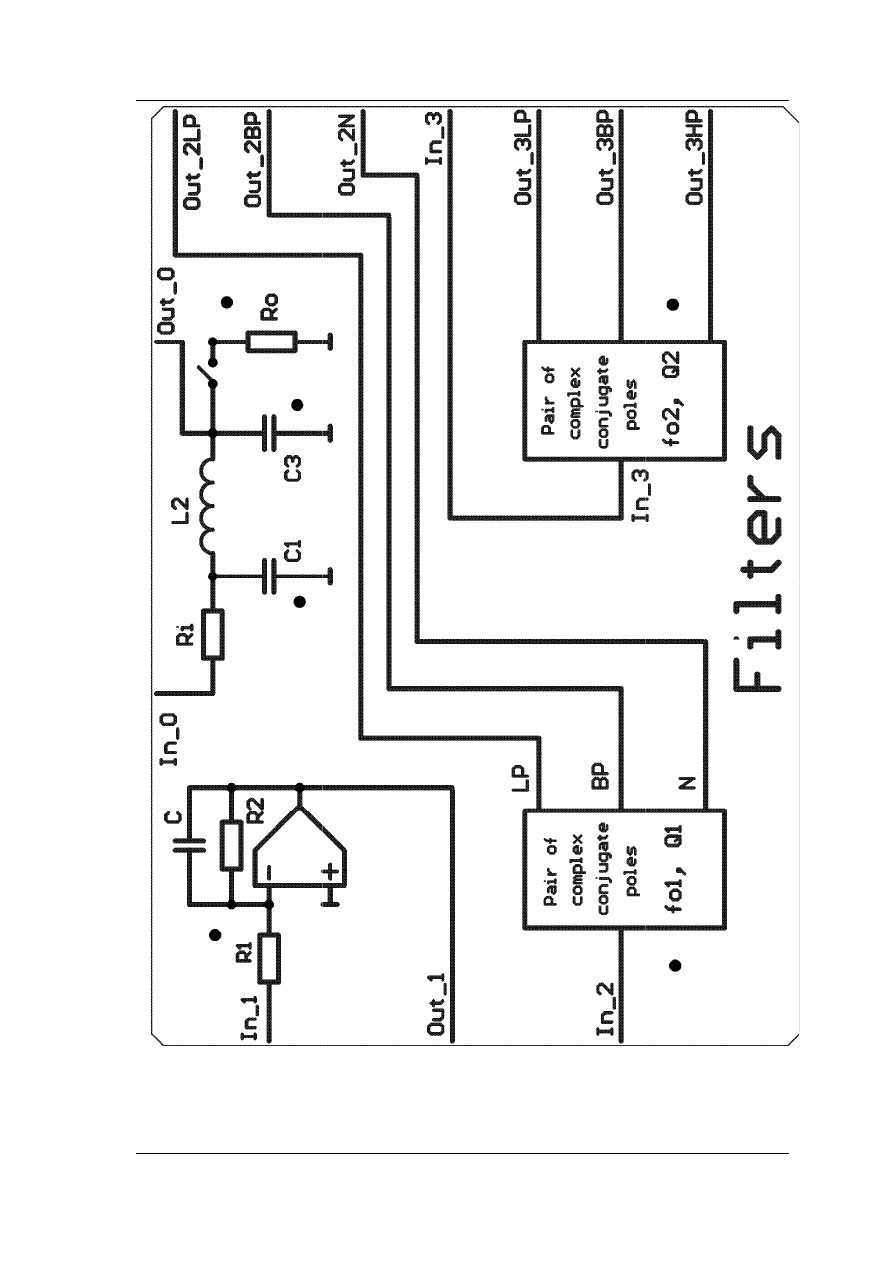
Do dyspozycji wykonawcy ćwiczenia jest pulpit operacyjny przedstawiony na rys.

2.7. Parametry przedstawionych na pulpicie struktur zmieniamy ręcznie bezpośrednio na
pulpicie

(potencjometry

obrotowe)

oraz

za

pomocą

interfejsu

programu

filter_struct.exe

2

.

Na pulpicie widzimy schemat dolnoprzepustowego filtru RLC (In_0

Out_0)

złożonego z cewki L=32mH, kondensatorów

i

4

o pojemnościach przełączanych (za

pomocą programu) w ramach dowolnej sumy elementów zbioru {10nF, 10nF, 5nF, 2nF,
2nF, 1nF, 500pF, 0pF} oraz dwóch rezystorów ręcznie regulowanych

[0.1-10k] i

[0.1-10k];

odłączamy lub dołączamy za pomocą klucza sterowanego z programu.

Dalej, na pulpicie jest do dyspozycji filtr pierwszego rzędu RC (In_1 -> Out_1)

zbudowany w oparciu o wzmacniacz operacyjny. Transmitancja filtru ma postać

1

Patrz materiał ćwiczenia Widma sygnałów okresowych (

plik ze słowem Fourier w nazwie

).

2

Autor dziękuje mgr. inż. Marcinowi Szkudlińskiemu za realizację założeń dotyczących interfejsu użytkownika

i sposobu komunikacji z procesorem na pulpicie operacyjnym.

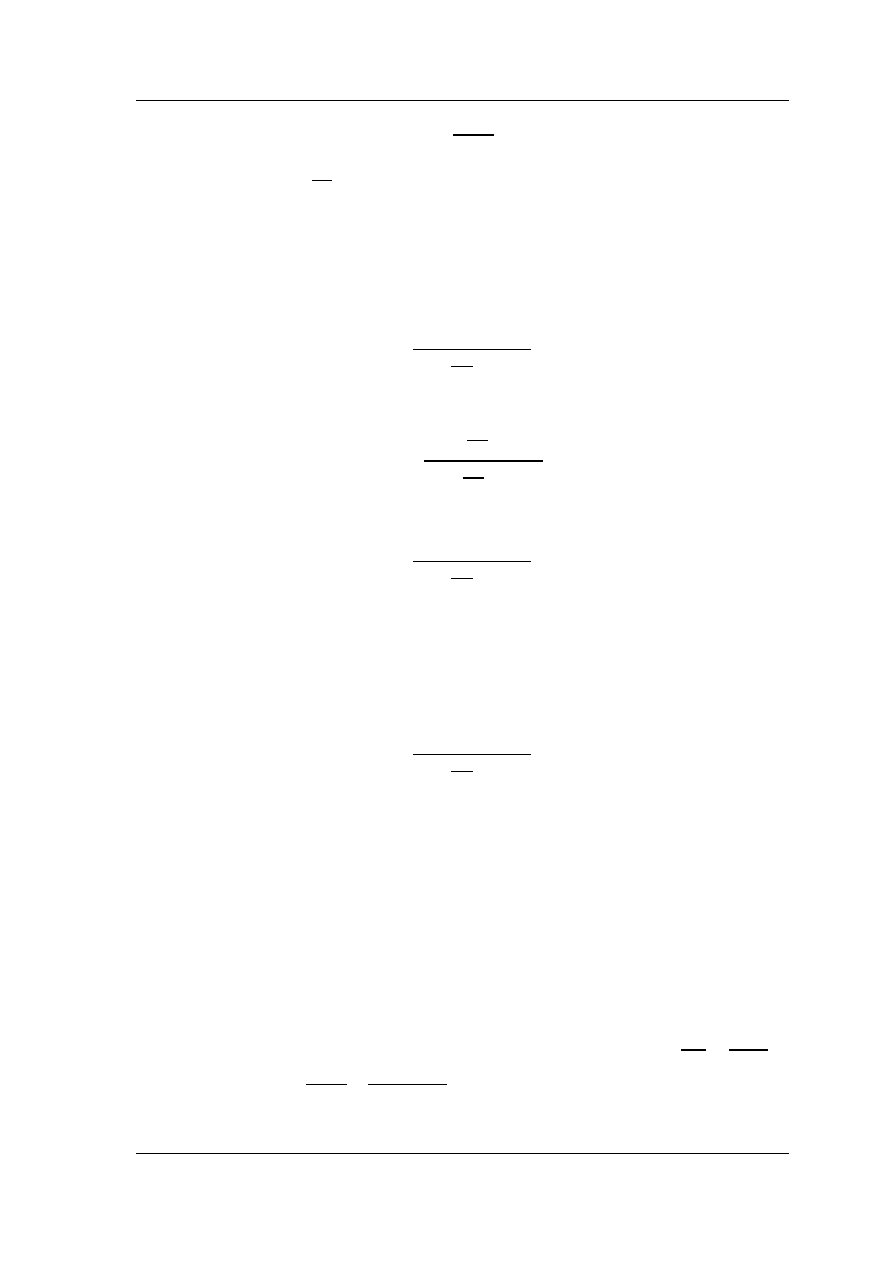
© Witold Szkudliński: FILTRY

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_Filters_2011.pdf Modyfikacje 2010 i 2011: C. Stefański

Katedra Systemów Elektroniki Morskiej

Laboratorium sieciowe 626Ea

Instrukcje LOiS - wersja 2011

14

=

"

+ ",

" =

1

,

= 10[nF],

= 1 … 10[kΩ].

(2.36)

Pojemność C jest stała, zaś rezystancja R

1

=R

2

=R regulowana za pomocą programu

filter_struct w zakresie 1 k

Ω … 11 kΩ.

Pierwszy blok 2-go rzędu (In_2-> Out_2) jest to układ scalony o dużej rezystancji

wejściowej, który realizuje trzy transmitancje:

- do wyjścia Out_2LP

4

=

#

4

4

+

#

5 +

#

4

,

(2.37)

- do wyjścia Out_2BP

4

= 5 ∙

#

5

4

+

#

5 +

#

4

,

(2.38)

- do wyjścia Out_2N

4

=

4

+

#

4

4

+

#

5 +

#

4

.

(2.39)

Następny blok 2-go rzędu (In_3->Out_3) pozwala na realizację transmitancji:

- do wyjścia Out_3LP – wzór (2.37),

- do wyjścia Out_2BP – wzór (2.38),

- do wyjścia Out_3HP

4

=

4

4

+

#

5 +

#

4

.

(2.40)

Parametry

k

#

, 5 obu bloków reguluje się za pomocą programu filter_struct

odpowiednio w zakresie 5.5 kHz … 11 kHz i 0,5 … 64.

Przykłady projektowania dolnoprzepustowego filtru RLC

1)

Pierwszy projekt dotyczy filtru drugiego rzędu o częstotliwości granicznej

k

F

= 10kHz. Do obliczeń pobieramy dane z tablicy analogicznej do tablic 2.1-2.3;

niech te dane wynoszą

>#

= 0.9098, 5

>

= 0.8093. Strukturę drugiego rzędu

o

=

= 1Ω musimy od razu odrzucić, bo realizuje dobroci tylko do wartości

0.707 (patrz wzór 2.27). Struktura z rys. 2.5b o

= 1Ω, Z

>

,

>4

,

= ∞ realizuje

praktycznie każdą wartość dobroci i opisuje się transmitancją postaci (2.24).

Obliczamy parametry prototypu według wzorów (2.25):

Z

>

=

6

h

+

h*

=

#.ˆ#‰:
#.‰#‰ˆ

0.8895[H]

,

>4

+

h*

∙6

h

0.9098∙0.8093

= 1.3581[F].

Obliczone

, Z

>

,

>4

to dopiero elementy prototypu filtru. Parametry filtru

właściwego otrzymujemy przez przeskalowanie parametrów prototypu za pomocą

© Witold Szkudliński: FILTRY

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_Filters_2011.pdf Modyfikacje 2010 i 2011: C. Stefański

Katedra Systemów Elektroniki Morskiej

Laboratorium sieciowe 626Ea

Instrukcje LOiS - wersja 2011

15

wzorów (2.33). Ze wzoru (2.33) nie wyliczamy

Z

, gdyż jest to wielkość z góry znana

(

Z

=32mH, gdyż na pulpicie operacyjnym jest tylko jedna cewka o indukcyjności

32mH właśnie), za to możemy przez przekształcenie tego wzoru otrzymać

= :

= =

2j ∙ k

F

Z

Z

>

=

2j ∙ 10

8

∙ 32 ∙ 10

a:

0.8895

2260[Ω].

Z kolei

4

1

2jk

F

∙

>4

=

1

2j ∙ 10

8

∙ 2.26 ∙ 10

:

∙ 1.3581 9.56[nF].

2)

Drugi projekt dotyczy filtru trzeciego rzędu o częstotliwości granicznej

k

F

10kHz o strukturzeΠ (rys. 2.5a) w wariancie

=

= 1Ω.

Na etapie obliczeń

dotyczących prototypu pulsacja graniczna

F>

prototypu jest zawsze w okolicy

1 T

)c~

Œ

W, zaś

informacja o

g

f

filtru przyda się dopiero przy przeskalowaniu.

Do obliczeń pobieramy

_

:

= 1.9153, _

4

2.3459, _

2.3512, _

#

= 1 z tablicy analogicznej do tabl. 2.4.

Na podstawie wzoru (2.32) otrzymujemy

Z

>4

= 1.4366[H].

Wyliczenie

4c

f

g

h9

c

9

9

daje wynik liczbowy 0.9999 co oznacza, że wyrażenie

'1 −

4c

f

g

h9

c

9

9

- występujące pod pierwiastkiem praktycznie zeruje się.

Uwaga! Nie należy w tym przypadku zrażać się sytuacją, gdy wyrażenie pod pierwiastkiem uzyskamy
w postaci zbliżonej do zera liczby ujemnej, może to bowiem wynikać z przyjmowania do wyliczeń
nieadekwatnej liczby miejsc po przecinku. w takim przypadku również uznamy, że wyrażenie
podpierwiastkowe daje w wyniku zero.

W sytuacji zerowania liczby podpierwiastkowej

1

>

=

>:

=

2_

:

_

4

= 1.632[F].

Pozostaje wykonać operację skalowania. Znowu ze wzoru (2.33) nie wyliczamy

Z

4

, bo – jak poprzednio – wiemy, że

Z

4

32 mH, za to możemy na podstawie tego

wzoru otrzymać

=

=

:

=

2jk

F

Z

4

Z

>4

=

2j ∙ 10

8

∙ 32 ∙ 10

a:

1.4366

1405[Ω].

W następnej kolejności obliczamy pojemności kondensatorów. Na podstawie

(2.33) otrzymujemy

:

1

2jk

F

∙

>

=

1

2j ∙ 10

8

∙ 1.405 ∙ 10

:

∙ 1.632 ≅ 18.5[nF].

2.7.

Pomiar charakterystyki amplitudowej filtru

W definicji transmitancji badanych w ramach ćwiczenia filtrów wielkością wejściową

jest napięcie na gnieździe wejściowym, zaś wielkością wyjściową jest napięcie na
gnieździe wyjściowym. Charakterystyka amplitudowa, czyli moduł transmitancji, to
stosunek (iloraz) amplitudy napięcia wyjściowego do amplitudy napięcia na wejściu
(patrz rys. 2.7). w przypadku struktury RLC musimy się zastanowić nad ewentualnym
wpływem, jaki na pomiar wywiera rezystancja wewnętrzna generatora (R

g

=50

Ω).

W przypadku filtrów kaskadowych ten wpływ jest pomijalny ze względu na duży moduł
impedancji wejściowej bloku filtru (100

kΩ).

1

Dla ułatwienia dodajmy, że

=

:

dla trzeciego rzędu filtrów typu Butterwortha i Czebyszewa obustronnie zakoń-

czonych rezystorami o jednakowych rezystancjach

=

.

© Witold Szkudliński: FILTRY

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_Filters_2011.pdf Modyfikacje 2010 i 2011: C. Stefański

Katedra Systemów Elektroniki Morskiej

Laboratorium sieciowe 626Ea

Instrukcje LOiS - wersja 2011

16

Często moduł transmitancji napięciowej, czyli tzw. częstotliwościową charakterystykę

amplitudową podaje się w postaci unormowanej ( w skali 0-1) lub w skali decybelowej

||

[BŽ]

= 20log||.

(2.41)

2.8.

Pomiar przesunięcia fazowego

Pomiar przesunięcia fazowego jakie wprowadza filtr do sinusoidalnego sygnału,

wiąże się na ogół z większymi trudnościami niż w przypadku pomiaru wprowadzanych
przez filtr zmian amplitudy sinusoidy. w najprostszym przypadku może być dokonany
punkt po punkcie za pomocą generatora sinusoidy o precyzyjnie znanej częstotliwości
oraz dwukanałowego oscyloskopu.

Przesunięcie fazowe

k na częstotliwości k można obliczyć korzystając

z przesunięcia

Δ na osi czasu pomiędzy sinusoidą wyjściową i wejściową filtru.

Mierzymy przesunięcie

Δ, a następnie wyliczamy przesunięcie fazowe w stopniach ze

wzoru

k

Δ

x ∙ 360 = 0.36 ∙ Δ

[C]

∙ k

[‘’“]

[

”

].

(2.42)

2.9.

Przykładowe pytania kontrolne

1)

Na przykładzie charakterystyki amplitudowej dolnoprzepustowego filtru

Czebyszewa objaśnij pojęcia:

• częstotliwości granicznej f

g

,

• wzmocnienia w paśmie przepustowym,
• falowania w paśmie przepustowym.

2)

Po co stosujemy tzw. skalowanie elementów filtru LC i na czym ono polega?

3)

Na przykładzie charakterystyki amplitudowej dolnoprzepustowego filtru

Butterwortha objaśnij pojęcia:

• częstotliwości granicznej f

g

,

• granicy pasma zaporowego f

s

,

• tłumienia w paśmie zaporowym.

4)

Naszkicuj częstotliwościowe charakterystyki amplitudowe Butterwortha dla

trzech przypadków:

• filtru dolnoprzepustowego,
• filtru pasmowo przepustowego,
• filtru górnoprzepustowego,

Na każdej z naszkicowanych charakterystyk zdefiniuj sposób określania pasma
przenoszenia filtru.

5)

Naszkicuj charakterystyczny przebieg - w funkcji czasu - napięcia wyjściowego

dla filtru dolnoprzepustowego pobudzonego na wejściu uskokiem napięcia. Na
rysunku zaznacz definicje:

• czasu narastania czoła impulsu,
• miary przerzutu odpowiedzi.

6)

Kolejne pytania – równie ważne – znajdzie Czytelnik w naszej witrynie

1

.

1

http://www.eti.pg.gda.pl/katedry/ksem/pracownicy/Czeslaw.Stefanski/PomoceDydaktyczne/11_ObwodyIsygnaly_semIII/

© Witold Szkudliński: FILTRY

Katedra Systemów Elektroniki Morskiej

Laboratorium Obwodów

Plik:LOiS_Filters_2011.pdf

Laboratorium sieciowe 626Ea

17

Rys. 2.7. Widok pulpitu operacyjnego

Laboratorium Obwodów i Sygnałów (LOiS)

Modyfikacje 2010 i 2011: C. Stefański

Instrukcje LOiS - wersja 2011