WYDZIAŁ ETI PG

Katedra Systemów Elektroniki Morskiej

Laboratorium Obwodów i Sygnałów

DWÓJNIKI I CZWÓRNIKI

Opracował: Witold Szkudliński

Gdańsk 2011

© Witold Szkudliński: D

WÓJNIKI I CZWÓRNIKI

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_NPorts_2011.pdf Modyfikacje 2011: C. Stefański

Laboratorium OiS

(sieciowe)

KSEM/626Ea

Wersja 2011

-2-

3.1.

Wstęp

Często, niezależnie od struktury wewnętrznej obwodu i liczby elementów w takiej strukturze, jest

nam dogodnie potraktować cały obwód jako element o dwóch końcówkach – dwójnik (ang. two-
terminal) lub element charakteryzujący się występowaniem dwóch wrót (ang. two-port), czyli czwór-
nik (dwuwrotnik); jedne wrota noszą nazwę wejścia , a drugie - wyjścia. Dalszym rozszerzeniem poję-
cia czwórnika jest tzw. wielowrotnik (ang. multi-port), który może mieć więcej niż dwoje wrót.

3.2.

Dwójniki

Najprostsze, jednoelementowe dwójniki to podstawowe elementy obwodów elektrycznych : re-

zystor, kondensator i cewka indukcyjna. Dla początkujących adeptów elektroniki, wymienione ele-
menty są całkowicie i jednoznacznie opisane przez następujący zestaw wyrażeń:

dt

di

L

u

dt

du

C

i

i

R

u

L

L

C

C

R

R

=

=

⋅

=

,

,

.

(3.1)

Trzeba jednak zwrócić uwagę czytelnika, że właściwości rzeczywistych elementów (produkowa-

nych przemysłowo rezystorów, kondensatorów i cewek) są bardziej złożone niż to wynika z (3.1).
Szczególnie trudno idealizować właściwości cewek indukcyjnych, którym poświęcimy kolejny akapit.
Cewka indukcyjna

Zapisany w (3.1) związek między prądem i napięciem dla cewki reprezentuje związane z cewką

zmienne w czasie pole magnetyczne. Jednak przepływ prądu przez wykonane z miedzi zwoje powo-
duje (wskutek skończonej przewodności tego materiału) zamianę energii elektrycznej na ciepło

1

.

Oznacza to, że cewka rzeczywista zachowuje się w pewnym stopniu jak rezystor, podczas gdy opisa-
na trzecim z kolei z wyrażeń (3.1) cewka idealna się nie grzeje. Z kolei ciasno nawinięte (szczególnie
wielowarstwowo) izolowane zwoje sprzyjają powstawaniu w cewce pola elektrycznego, czyli zjawiska
charakterystycznego dla kondensatora. Połączenie opisanych powyżej obserwacji prowadzi do roz-
ważenia zachowania się rzeczywistej cewki w sposób zbliżony do zachowania się w obwodzie elek-
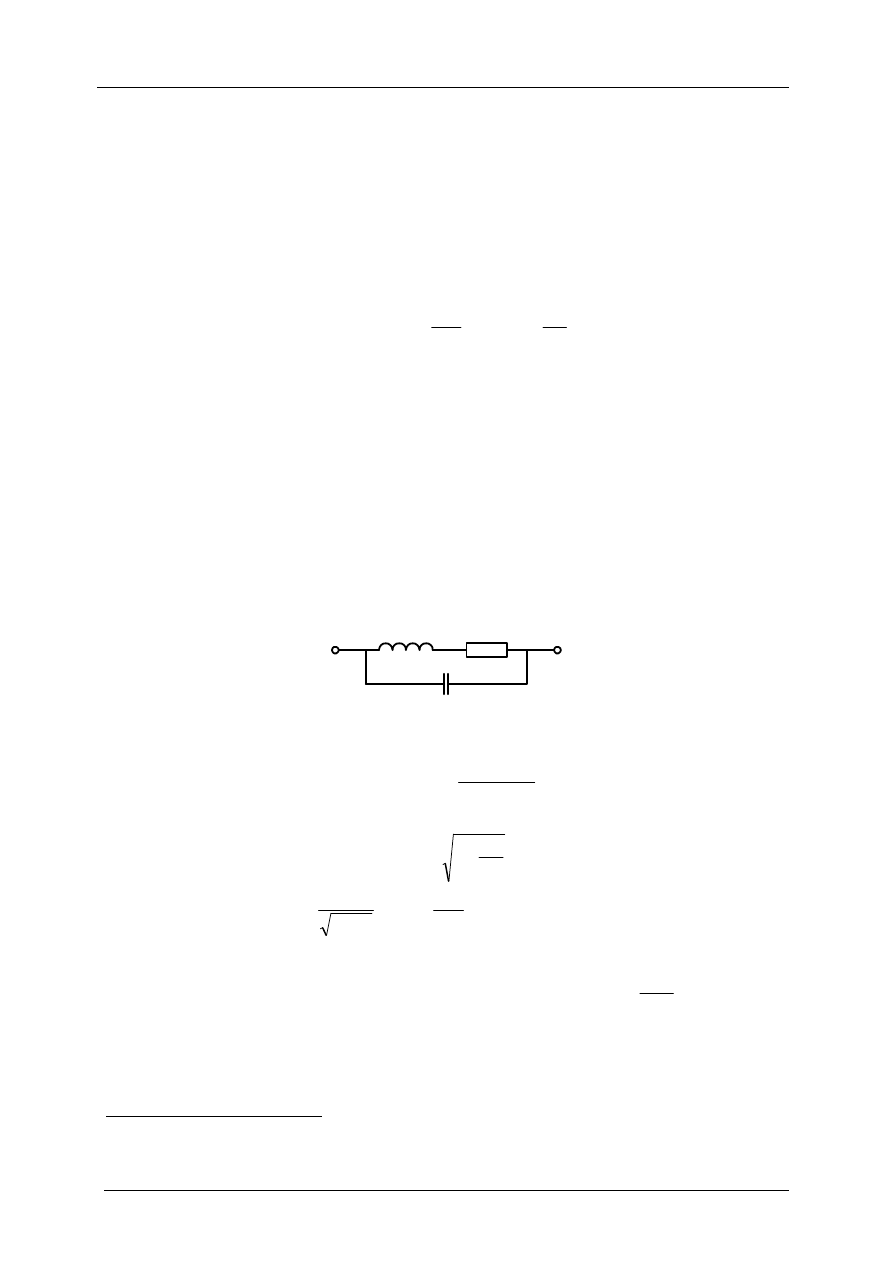
trycznym dwójnika przedstawionego na rys. 3.1.

L

L

R

L

C

•

•

Rys. 3.1. Model elektryczny nieidealnej cewki indukcyjnej

Model cewki (rys. 3.1) ma więc postać równoległego obwodu rezonansowego o admitancji

2

2

2

)

(

L

R

L

R

C

Y

L

L

L

L

ω

ω

ω

ω

+

−

+

=

j

j

j

(3.2)

Podstawowym parametrem obwodu rezonansowego jest częstotliwość rezonansowa

L

r

L

L

L

r

r

R

L

Q

C

L

Q

Y

ω

ω

ω

ω

ω

=

⋅

=

−

=

⇒

=

,

1

,

1

1

0

)}

(

Im{

0

2

0

gdzie

j

(3.3)

Dla większości profesjonalnie wykonanych cewek

1

>>

L

Q

, stąd jako pierwsze przybliżenie dla czę-

stotliwości rezonansowej możemy przyjąć

0

ω

ω

≈

r

, a jako drugie













−

≅

L

r

Q

2

1

1

0

ω

ω

.

Impedancja dwójnika z rys. 3.1 jest dla częstotliwości rezonansowej rzeczywista i wynosi

(

)

L

L

r

R

Q

Z

⋅

+

=

1

)

(

2

ω

j

(3.4)

1

Straty w miedzianym uzwojeniu rosną ze wzrostem częstotliwości przepływającego prądu sinusoidalnego. W przypadku

zwojów nawiniętych na ferromagnetycznym rdzeniu dochodzą jeszcze straty energii w tym materiale.

© Witold Szkudliński: D

WÓJNIKI I CZWÓRNIKI

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_NPorts_2011.pdf Modyfikacje 2011: C. Stefański

Laboratorium OiS

(sieciowe)

KSEM/626Ea

Wersja 2011

-3-

Czyli dla prądu sinusoidalnego o częstotliwości rezonansowej cewka zachowuje się jak rezystor
o rezystancji wynikającej ze wzoru (3.4); rezystancja ta jest często nazywana rezystancją dynamiczną
obwodu z rys. 3.1.
Z kolei dla częstotliwości dużo większej od częstotliwości rezonansowej cewka zachowuje się jak kon-
densator

r

L

C

Y

ω

ω

ω

ω

>>

≈

,

)

(

j

j

(3.5)

W przypadku używania dla cewki modelu z rys. 3.1, impedancja cewki dla częstotliwości dużo mniej-
szej od częstotliwości rezonansowej

L

R

Z

≅

)

(

ω

j

,

(3.6)

gdy

r

ω

ω

<<

.

Jednak pomiar rezystancji cewki dla prądu stałego (

0

=

ω

) często daje zaskakujący wynik

L

DC

R

R

<<

.

(3.7)

Sytuacja taka zachodzi dlatego, że w modelu z rys. 3.1, ܴ

௅

reprezentuje straty energii , a straty energii

w uzwojeniu oraz w rdzeniu na którym uzwojenie jest nawinięte rosną ze wzrostem częstotliwości.
Stąd wniosek, że prosty model cewki z rys. 3.1 często nie przedstawia dostatecznie dobrze jej wła-
ściwości dla częstotliwości dalekich od częstotliwości rezonansowej.

3.3.

Czwórniki

Istnieją obwody, które, niezależnie od liczby elementów wewnątrz struktury, jest dogodnie trak-

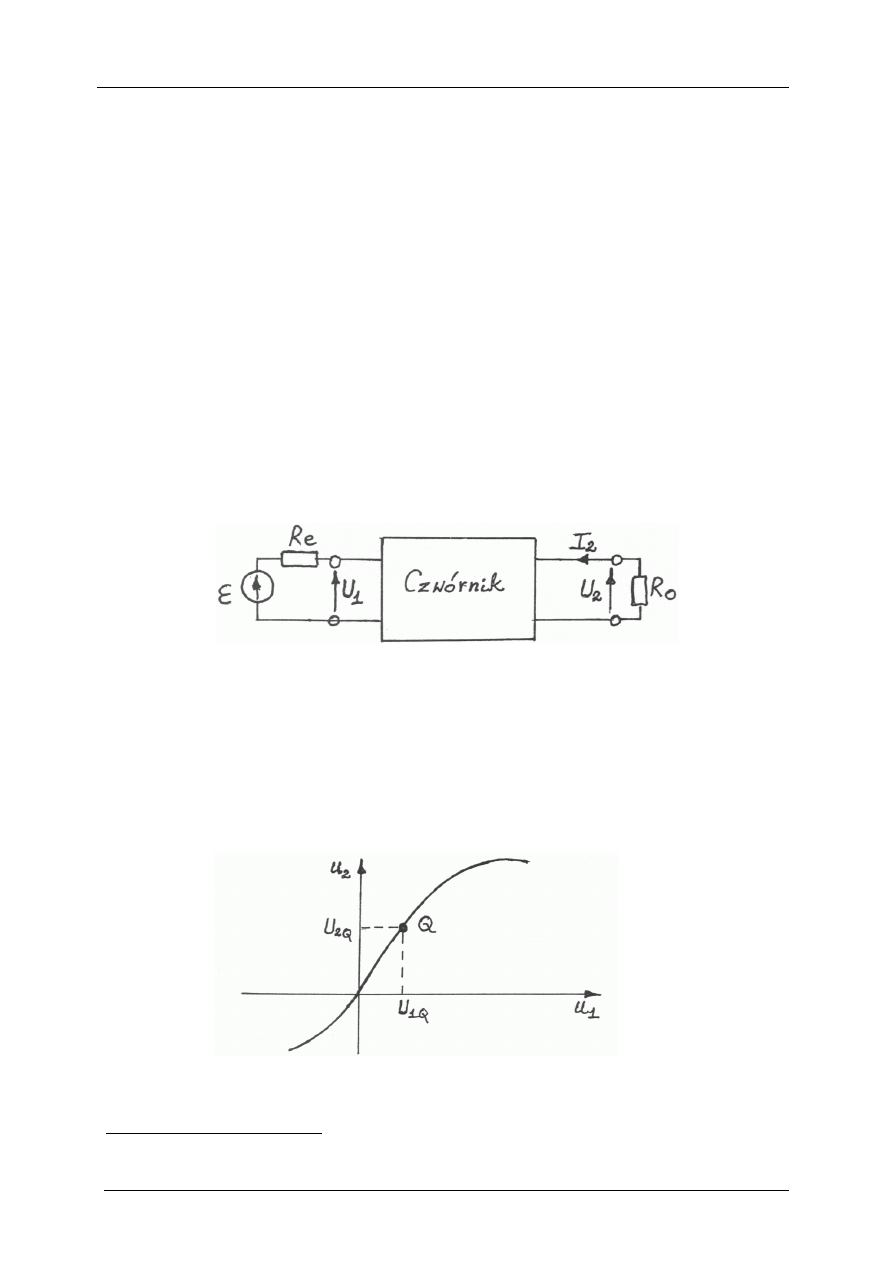
tować w sposób przestawiony symbolicznie na rys. 3.2.

Rys. 3.2. Rysunek obustronnie obciążonego czwórnika

Interesują nas właściwości obwodu (czwórnika) obserwowane na dwóch wrotach (dwóch parach
końcówek) przy czym poszukiwane właściwości określamy jako różnego rodzaju relacje zespolonych
amplitud prądów i napięć przy pobudzeniu sinusoidalnym.
W poprzednim rozdziale założyliśmy a priori, że rozpatrywane dwójniki (cewka i rezonator piezoelek-
tryczny) to elementy liniowe. Trzeba dodać, że takie podejście nie zawsze jest uprawnione i wystar-
czające. Tego rodzaju uwaga odnosi się również (a nawet częściej) do czwórników, toteż spróbujmy
teraz przeprowadzić elementarne rozważania dla czwórnika, o którym wiemy, że nie jest liniowy.

Załóżmy, że dla czwórnika pomierzyliśmy jego charakterystykę statyczną

u

2

=f(u

1

)

przedstawioną tu

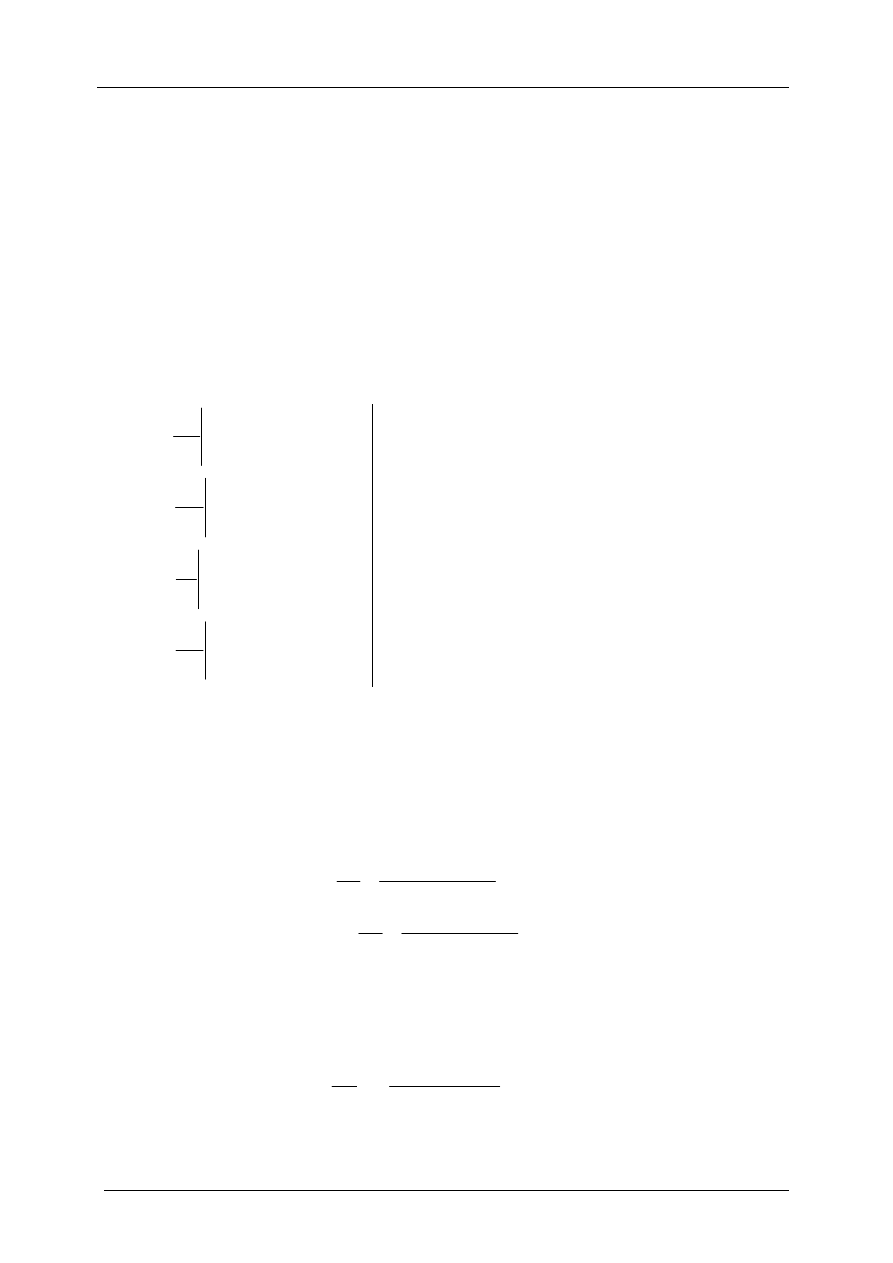
na rys. 3.3

2

.

Rys. 3.3. Przykładowa charakterystyka statyczna

)

(

1

2

u

f

u

=

nieliniowego czwórnika

2

Charakterystyka statyczna czyli wynik badania napięciem quasistałym

© Witold Szkudliński: D

WÓJNIKI I CZWÓRNIKI

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_NPorts_2011.pdf Modyfikacje 2011: C. Stefański

Laboratorium OiS

(sieciowe)

KSEM/626Ea

Wersja 2011

-4-

Kiedy mamy do czynienia z czwórnikiem nieliniowym, to jednym z istotnych objawów tego stanu
rzeczy jest pokazane na rys. 3.3 odchylenie charakterystyki statycznej od linii prostej. Globalna nie-
liniowość charakterystyki nie oznacza iż nie można na niej wyszukać i wykorzystać odcinków pra-
wie-liniowych (quasiliniowych). Na przykładowej charakterystyce z rys. 3.3 wybrano punkt

Q

, w

otoczeniu którego mamy do czynienia z odcinkiem charakterystyki o prawie stałym i niezerowym
nachyleniu. Odstępstwa krzywej w otoczeniu punktu Q (punktu pracy) od liniowości będziemy sza-
cowali korzystając z rozkładu funkcji

)

(

1

u

f

w szereg Taylora

.......

)

(

)

(

)

(

2

1

1

3

2

1

1

2

1

1

1

2

2

+

−

+

−

+

−

=

−

Q

Q

Q

Q

U

u

k

U

u

k

U

u

k

U

u

(3.8)

Na drodze eksperymentalnej wygodnym sposobem zbadania nieliniowości w sposób ilościowy

jest wprowadzenie na wejście czwórnika napięcia sinusoidalnego. Musimy jednocześnie pamiętać o
konieczności zapewnienia właściwego punktu pracy. Często robimy to w ten sposób, że na wejście
czwórnika wprowadzamy napięcie

t

U

U

t

u

i

i

Q

ω

cos

)

(

1

1

+

=

(3.9)

Analitycznie, po podstawieniu (3.11) do szeregu (3.10) otrzymujemy

.......

..........

3

cos

2

cos

cos

)

(

)

(

)

(

3

3

4

1

2

2

2

1

3

3

4

3

1

2

2

2

1

2

2

+

+

+

+

+

+

+

+

=

−

=

t

U

k

t

U

k

t

U

k

U

k

U

k

U

t

u

t

u

i

i

i

i

i

i

i

i

Q

o

ω

ω

ω

(3.10)

Widzimy, że pobudzenie sinusoidą układu, który nie jest liniowy, owocuje pojawieniem się na wyjściu
wielu sinusoid o częstotliwościach będących całkowitą wielokrotnością częstotliwości pobudzenia.
Dodatkowo mamy do czynienia w przebiegu wyjściowym ze zmianą składowej stałej w stosunku do
wyjściowej współrzędnej punktu pracy

Q

U

2

.

Niezależnie od wynikających z powyższych zapisów rezultatów przekształceń, zmiany napięcia wyj-
ściowego w otoczeniu punktu pracy można także zapisać w postaci

.....

3

cos

2

cos

cos

)

(

3

2

1

0

+

+

+

+

=

t

U

t

U

t

U

U

t

u

i

o

i

o

i

o

o

o

ω

ω

ω

(3.11)

Bazując na wyrażeniach (3.9-3.11) możemy zdefiniować współczynniki zniekształceń nieliniowych
drugiego i trzeciego rzędu

1

2

2

o

o

d

U

U

h

=

,

1

3

3

o

o

d

U

U

h

=

(3.12)

Oprócz współczynników

3

2

,

d

d

h

h

, równie często jest używany globalny współczynnik zniekształceń

nieliniowych ( THD-total harmonic distortion):

.

..........

2

4

2

3

2

2

+

+

+

=

d

d

d

d

h

h

h

h

(3.13)

Powszechnie liczbowe wartości współczynników zniekształceń są podawane w procentach lub w
decybelach:

d

dB

d

d

d

h

h

h

h

log

20

,

100

]

[

[%]

⋅

=

⋅

=

(3.14)

Powróćmy ponownie do wyrażenia (3.10) przedstawiającego napięcie wyjściowe jako wynik

podstawienia pobudzenia (3.9) do opisującego czwórnik szeregu Taylora .

Zauważmy, że wystarczy odpowiednio ograniczyć

i

U

, aby uzyskać efekt pomijalnego znaczenia skła-

dowych o częstotliwościach

,....

3

,

2

i

i

ω

ω

Oznacza to, że zawsze istnieje taka wartość

im

U

, że dla

wszystkich

im

i

U

U <

(3.15)

składowe o amplitudach

3

3

4

1

3

2

2

2

1

2

,

im

o

im

o

U

k

U

U

k

U

=

=

(3.16)

stają się dla nas niemierzalne, a tym samym subiektywnie pomijalne; to samo dotyczy wszystkich
następnych składowych wyrażenia (3.13).

© Witold Szkudliński: D

WÓJNIKI I CZWÓRNIKI

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_NPorts_2011.pdf Modyfikacje 2011: C. Stefański

Laboratorium OiS

(sieciowe)

KSEM/626Ea

Wersja 2011

-5-

Składową zmienną napięcia wyjściowego w przypadku spełnienia warunku (3.15) możemy przedsta-
wić jako

t

U

k

t

u

i

i

o

ω

cos

)

(

1

≅

(3.17)

zaś badany czwórnik określić jako quasiliniowy.
Do opisu czwórnika liniowego (quasiliniowego) mamy do dyspozycji funkcje określane ogólnie jako:
impedancje, admitancje oraz transmitancje. W szczególności dla czwórników wspomniane funkcje
wprowadza się również pod postacią tzw. macierzy czwórnikowych:

[ ]

[ ]

[ ]

h

y

z

,....,

,

.

Definicje związane z macierzą

[ ]

h

dla przypadku sinusoidalnego stanu ustalonego w czwórniku li-

niowym są następujące

2

22

1

21

2

2

12

1

11

1

U

h

I

h

I

U

h

I

h

U

+

=

+

=

(3.18)

gdzie

2

2

1

1

,

,

,

I

U

I

U

to amplitudy zespolone reprezentujące sinusoidalne przebiegi o pulsacji

i

ω

.

Zinterpretujmy kolejno wszystkie elementy macierzy [h].

0

1

1

11

2

=

=

U

I

U

h

(3.19)

h

11

ma sens impedancji wejściowej czwórnika mierzonej

przy zwartym wyjściu,

0

2

1

12

1

=

=

I

U

U

h

(3.20)

h

12

przedstawia możliwości transmisji przebiegu

napięciowego wstecz, z wyjścia na otwarte wejście,

0

1

2

21

2

=

=

U

I

I

h

(3.21)

h

21

ma sens wzmocnienia prądowego przy zwartym

wyjściu czwórnika,

0

2

2

22

1

=

=

I

U

I

h

(3.22)

h

22

to z kolei admitancja wyjściowa czwórnika,

którego wejście jest otwarte.

Bezpośrednio z definicji (3.19-3.22) można ustalić metodykę pomiaru parametrów macierzy [h]. Usta-
lając warunki pomiarowe, w przypadkach (3.20) i (3.22) przekładamy źródło sygnału sinusoidalnego z
wejścia na wyjście oraz w każdym przypadku pamiętamy, aby zostały zachowane zawsze te same
współrzędne punktu pracy

Q

na charakterystyce statycznej; współrzędne punktu pracy najłatwiej

utrzymać separując składowe stałe i zmienne (zwarcia potrzebujemy tylko dla składowej sinusoidalnej
czyli zmiennej w czasie) za pomocą kondensatora o odpowiednio dużej pojemności.

Parametry macierzy

[

h

]

czwórnika nie zależą od rezystancji

R

e

oraz

R

o

, ale już impedancja wejściowa

Z

in

oraz impedancja wyjściowa

Z

out

są od tych wielkości zwykle silnie uzależnione:

o

o

in

R

h

R

h

h

I

U

Z

⋅

+

⋅

+

=

=

22

11

1

1

1

}

det{

(3.23)

e

e

out

R

h

h

R

h

I

U

Z

⋅

+

+

=

=

22

11

2

2

}

det{

(3.24)

Impedancja wejściowa (3.23) i wyjściowa (3.24) należą do wielkości określających właściwości
czwórnika w warunkach roboczych. Oprócz nich do tej grupy należą pojęcia wzmocnienia (tłumie-
nia) napięciowego , prądowego lub mocy.
Transmitancja napięciowa wynosi

o

u

G

h

h

h

U

U

H

11

21

1

2

}

det{

+

−

=

=

(3.25)

© Witold Szkudliński: D

WÓJNIKI I CZWÓRNIKI

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_NPorts_2011.pdf Modyfikacje 2011: C. Stefański

Laboratorium OiS

(sieciowe)

KSEM/626Ea

Wersja 2011

-6-

Moduł transmitancji (wzmocnienie napięciowe

u

A

) będzie określał nam relację pomiędzy amplitu-

dami sinusoidalnych napięć na wejściu i wyjściu, zaś faza wektora

u

H

odzwierciedla przesunięcie

fazowe sinusoidy wyjściowej w stosunku do przebiegu odniesienia, którym jest sinusoida na wej-

ściu. W przypadku, gdy

1

<

u

A

mówimy, że czwórnik nie wzmacnia, tylko tłumi sygnał napięciowy.

Transmitancja prądowa

o

i

R

h

h

I

I

H

22

21

1

2

1 +

−

=

−

=

(3.26)

Moduł

i

H

to wzmocnienie prądowe

i

A

obciążonego czwórnika .

Wzmocnienie napięciowe efektywne

E

U

A

ue

2

=

(3.27)

Zwróćmy uwagę, że

ue

u

A

A =

tylko w przypadku

0

=

e

R

.

Wzmocnienie mocy

zwykłe

in

out

P

P

P

A =

(3.28)

i efektywne

e

out

P

P

Pe

A =

Występujące we wzorach (3.28) moce to

e

e

in

in

o

out

G

E

P

G

U

P

G

U

P

⋅

=

⋅

=

⋅

=

2

4

1

2

1

2

1

2

2

2

1

,

,

(3.29)

gdzie

e

in

o

G

G

G

,

,

to odpowiednie konduktancje (

}

/

1

Re{

in

in

Z

G =

Podkreślmy, że w każdych warunkach pomiarowych nie mogą zostać zmienione współrzędne punktu
pracy

Q

czwórnika, co najłatwiej uzyskać blokując przepływ prądu stałego za pomocą kondensato-

ra o odpowiednio dużej pojemności.

Tłumik rezystorowy

Profesjonalne obwody do tłumienia napięcia mogą między innymi mieć postać przedstawionego na
rys. 3.4 czwórnika o strukturze typu ”T”.

•

•

1

R

2

R

3

R

1

I

2

I

2

U

1

U

Rys. 3.4. Tłumik rezystorowy typu „T”

Przedstawiony tłumik jest czwórnikiem o symetrycznej budowie strukturalnej, a przyjmując R

1

=R

3

otrzymujemy również elektryczną symetrię czwórnika .
W przypadku tłumika ważnym parametrem jest rezystancja charakterystyczna R

c

:

ot

zw

c

R

R

R =

(3.30)

przy czym rezystancje pod pierwiastkiem to rezystancja zwarciowa (zwarte wyjście) i rezystancja

rozwarciowa (otwarte wyjście); dla

3

1

R

R

=

mamy

2

1

1

1

,

2

1

R

R

R

R

R

ot

G

G

zw

+

=

+

=

+

(3.30a)

Rezystancja charakterystyczna

R

c

ma tę ciekawą właściwość, że włączona na wyjście tłumika za-

pewnia rezystancję wejściową równą również R

c

.

Po obciążeniu układu z rys. 3.4 rezystancją charakterystyczną R

c

, współczynnik wnoszonego przez

tłumik tłumienia napięcia wejściowego

c

zw

c

zw

ot

zw

ot

zw

R

R

R

R

R

R

R

R

u

u

−

+

=

−

+

=

=

1

1

1

1

2

1

α

(3.31)

© Witold Szkudliński: D

WÓJNIKI I CZWÓRNIKI

Laboratorium OiS

(sieciowe)

Rys. 3.5

Do celów projektowych potrzebujemy wzorów, z których możemy otrzymać wartości rezystancji
(R

1

,R

2

,R

3

) tłumika na podstawie założonych: tłumienia

przekształceniach wyrażeń (3.30 i

1

,

1

1

R

R

R

c

⋅

+

−

=

α

α

Poza sferą akademicką współczynnik tłumienia podaje się najczęściej w dB
rach)

α

=

dB

Dwa tłumiki o tłumieniach

1

α

i

α

α

=

Czwórnik z tranzystorem bipolarnym

Tranzystor bipolarny w konfiguracji wspólny

kowe tworzą popularny czwórnik noszący nazwę wtórnika emiterowego.

Zasadnicze elementy wtórnika to
polegającą na polaryzacji i zabezpieczeniu
zmiennego. Przy zerowym napięciu wejściowym
emitera jest praktycznie zerowy. Jeżeli napięcie to wzrośnie i przekroczy poziom ok. +0.7
do czynienia z przepływem prądu

jednocześnie napięciem wyjściowym

jest pozbawione składowej stałej
(3.15) rozważany wtórnik emiterowy
U

1Q

≥0.7 V . Dla quasiliniowego wtórnika emiterowego można narysować przedstawiony na rys. 3.7

WÓJNIKI I CZWÓRNIKI

Laboratorium Obwodów

Plik:LOiS_NPorts_2011.pdf Modyfikacje 2011

KSEM/626Ea

-7-

3.5. Wykres zmian tłumienia

α zgodnie ze wzorem (3.31)

Do celów projektowych potrzebujemy wzorów, z których możemy otrzymać wartości rezystancji

) tłumika na podstawie założonych: tłumienia

α

oraz rezystancji charakterystycznej R

(3.30 i 3.31) otrzymujemy

3

1

1

2

1

1

1

R

R

R

R

ot

zw

ot

zw

R

R

R

R

=

⋅

−

−

−

=

dla

Poza sferą akademicką współczynnik tłumienia podaje się najczęściej w dB lub rzadziej w Np. (nep

α

α

α

ln

,

log

20

=

Np

i

2

α

, połączone kaskadowo, dają łącznie tłumienie

2

1

α

α

⋅

,

2

,

1

,

dB

dB

dB

α

α

α

+

=

tranzystorem bipolarnym

Tranzystor bipolarny w konfiguracji wspólny-kolektor plus widoczne na rys. 3.10

kowe tworzą popularny czwórnik noszący nazwę wtórnika emiterowego.

.
.

.

.

.

V

U

CC

5

+

=

F

C

b

µ

2

.

2

2

=

D

Ω

= k

R

E

1

p

C

1

u

'

2

u

''

2

u

E

B

C

.

.

B

R

Ω

=

k

R

B

100

+

nF

C

b

100

1

=

uF

8

.

6

Rys. 3.6. Schemat wtórnika emiterowego z tranzystorem npn

to tranzystor i rezystor R

E

. Reszta elementów pełni pomocniczą

zabezpieczeniu tranzystora oraz oddzieleniu obwodów prądu stałego i

Przy zerowym napięciu wejściowym u

1

, prąd płynący w tranzystorze od kolektora do

emitera jest praktycznie zerowy. Jeżeli napięcie to wzrośnie i przekroczy poziom ok. +0.7

prądu i w efekcie ze spadkiem napięcia na rezystorze

wyjściowym

,

2

u

. Napięcie wyjściowe

,

,

2

u

różni się od poprzedniego

stałej w czasie. Dla napięcia wejściowego postaci

emiterowy jest czwórnikiem quasiliniowym w otoczeniu

wtórnika emiterowego można narysować przedstawiony na rys. 3.7

Laboratorium Obwodów i Sygnałów (LOiS)

Modyfikacje 2011: C. Stefański

Wersja 2011

Do celów projektowych potrzebujemy wzorów, z których możemy otrzymać wartości rezystancji

oraz rezystancji charakterystycznej R

c

. Po

(3.32)

lub rzadziej w Np. (nepe-

(3.33)

, połączone kaskadowo, dają łącznie tłumienie

(3.34)

3.10 elementy dodat-

Rys. 3.6. Schemat wtórnika emiterowego z tranzystorem npn

pełni pomocniczą rolę

oddzieleniu obwodów prądu stałego i

, prąd płynący w tranzystorze od kolektora do

emitera jest praktycznie zerowy. Jeżeli napięcie to wzrośnie i przekroczy poziom ok. +0.7 V, to mamy

rezystorze R

E

; napięcie to jest

od poprzedniego tym, że

(3.9) przy założeniu

otoczeniu punktu pracy

wtórnika emiterowego można narysować przedstawiony na rys. 3.7

© Witold Szkudliński: D

WÓJNIKI I CZWÓRNIKI

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_NPorts_2011.pdf Modyfikacje 2011: C. Stefański

Laboratorium OiS

(sieciowe)

KSEM/626Ea

Wersja 2011

-8-

małosygnałowy schemat zastępczy dla dostatecznie małych częstotliwości wejściowej składowej si-
nusoidalnej. Otrzymujemy w ten sposób czwórnik na podstawie którego możemy określić wszystkie
właściwości wtórnika dla takiej składowej.

be

g

be

m

U

g

be

U

E

R

1

u

2

u

.

.

.

.

Rys. 3.7. Małosygnałowy schemat zastępczy wtórnika dla małych częstotliwości.

Na rys. 3.7, tranzystor jest reprezentowany przez rezystor

g

be

i prądowe źródło sterowane. Tran-

skonduktancja źródła sterowanego

g

m

dla tranzystora w temperaturze pokojowej jest bardzo prosto

związana z prądem emitera w punkcie pracy

]

{

40

]

[

mA

I

mS

g

EQ

m

⋅

≅

(3.35)

Z kolei konduktancja g

be

dla niezbyt dużych prądów (0-10 mA) może być w przybliżeniu wyznaczana

na podstawie zależności

0

β

m

be

g

g ≅

(3.36)

gdzie

0

β

, to popularny parametr, który można określić jako wzmocnienie prądowe tranzystora w

konfiguracji wspólny emiter.
Dla czwórnika z rys. 3.7 można , jak dla wielu innych czwórników , znaleźć zdefiniowane wzorami
(3.19-3.22) parametry czwórnikowe typu [h]. Otrzymujemy

E

R

be

h

h

h

r

h

1

22

0

21

12

11

)

1

(

1

=

+

−

=

=

=

β

(3.37)

Parametry robocze omawianego czwórnika (wtórnika) można znaleźć korzystając ze wzorów (3.25-
3.29) lub na podstawie definicji parametrów roboczych oraz rys. 3.4 i 3.11. Otrzymujemy

m

be

m

be

e

E

out

o

E

E

E

be

in

E

be

m

E

be

m

u

g

r

g

r

R

R

R

R

R

R

R

r

I

U

R

R

g

g

R

g

g

U

U

A

1

1

,

)

1

(

)

(

1

)

(

'

'

0

1

1

'

'

1

2

≈

+

+

=

=

+

+

=

=

+

+

+

=

=

β

(3.38)

gdzie R

e

to rezystancja źródła sygnału (patrz rys. 3.2)

Jeszcze raz podkreślmy, że w każdych warunkach pomiaru parametrów roboczych nie mogą zostać
zmienione współrzędne punktu pracy

Q

czwórnika, co najłatwiej uzyskać blokując przepływ prądu

stałego przez ܴ

o

za pomocą kondensatora o odpowiednio dużej pojemności.

Transformator

Transformator idealny to czwórnik opisany układem dwóch równań :

1

2

1

2

1

i

n

i

u

n

u

⋅

−

=

⋅

=

(3.39)

gdzie parametr „݊” nazywa się przekładnią transformatora.
Dla transformatora idealnego, obciążonego rezystorem R

o

rezystancja wejściowa wynosi

2

n

R

R

o

in

=

(3.40)

© Witold Szkudliński: D

WÓJNIKI I CZWÓRNIKI

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_NPorts_2011.pdf Modyfikacje 2011: C. Stefański

Laboratorium OiS

(sieciowe)

KSEM/626Ea

Wersja 2011

-9-

Transformator rzeczywisty to obiekt zbudowany z dwóch lub więcej cewek indukcyjnych sprzężo-
nych magnetycznie. Strumienie magnetyczne mogą się zamykać przez powietrze, jednak sprzężenie
jest bardziej efektywne jeśli droga strumieni wspólnych cewek wypada całkowicie lub częściowo we-
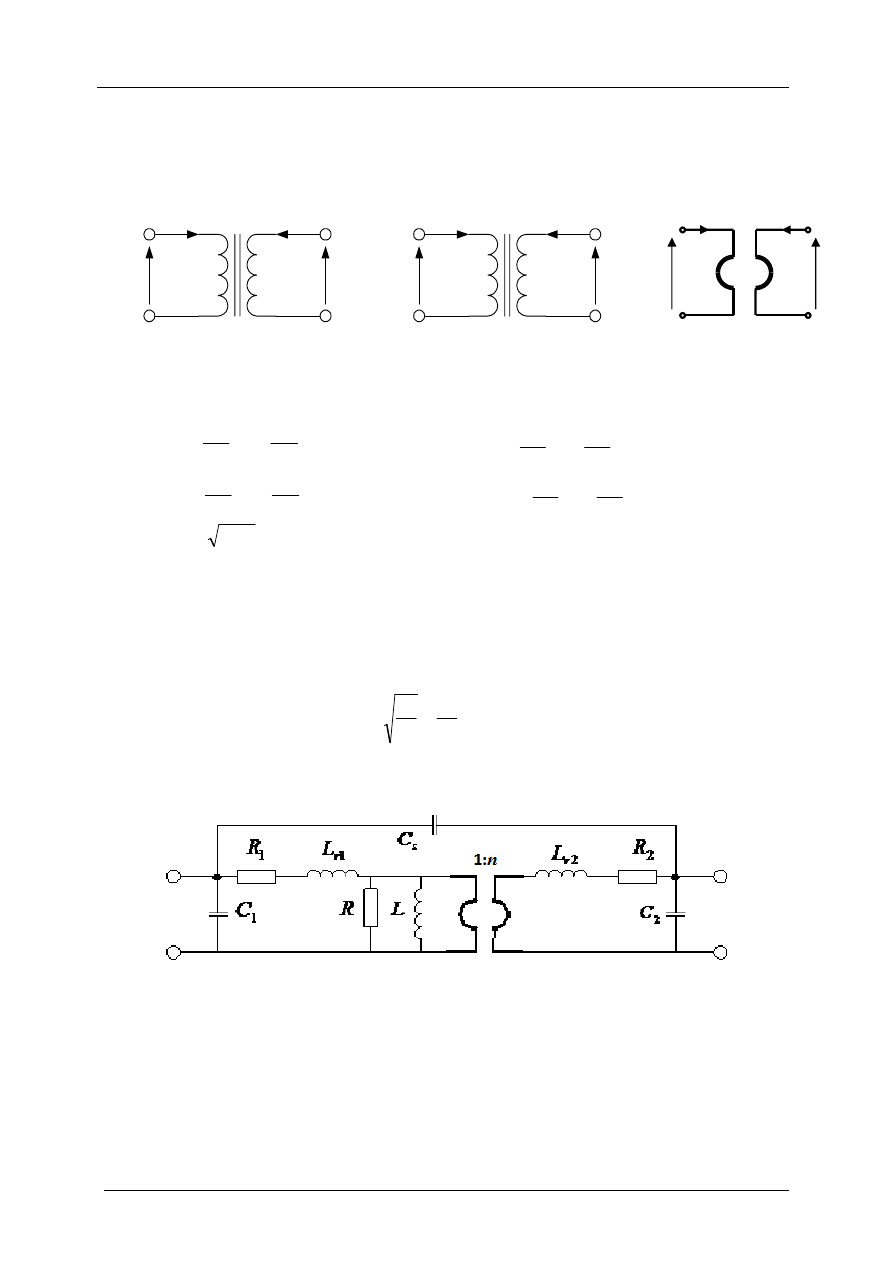
wnątrz rdzenia z materiału ferromagnetycznego. Sprzężenie magnetyczne dwóch cewek przedsta-
wiamy graficznie na sposoby pokazane na rys. 3.8

1

i

2

i

1

i

2

i

1

u

1

u

2

u

2

u

a)

b)

1

L

1

L

2

L

2

L

. .

.

.

c)

Rys. 3.8. Symboliczne rysunki transformatora: a) nieodwracającego, b) odwracającego, c) idealnego

Przedstawione na rys. 3.8a) i 3.8b) cewki sprzężone można w pierwszym przybliżeniu (pomijając
przede wszystkim straty) opisać za pomocą następujących układów równań:

dt

di

L

dt

di

M

u

dt

di

M

dt

di

L

u

2

2

1

2

2

1

1

1

+

=

+

=

dla rys. 3.8a

dt

di

L

dt

di

M

u

dt

di

M

dt

di

L

u

2

2

1

2

2

1

1

1

+

−

=

−

=

dla rys. 3.8b (3.41)

gdzie

1

0

,

2

1

≤

<

=

k

L

L

k

M

; k nosi nazwę współczynnika sprzężenia uzwojeń .

Indukcyjności własne uzwojeń są wprost proporcjonalne do kwadratu z liczby nawiniętych na rdzeniu
(karkasie) zwojów. Znak indukcyjności wzajemnej (+/- M) zależy od kierunku nawinięcia uzwojenia
wtórnego w relacji do uzwojenia pierwotnego. Dla uzwojeń nawiniętych w tym samym kierunku
mamy sytuację z rys. 3.8 a .
Dla cewek o dostatecznie dużych bezstratnych indukcyjnościach i w pełni ze sobą sprzężonych (k=1),
równania (3.40) można w granicy przekształcić do równań (3.39) dla transformatora idealnego; wtedy

1

2

1

2

n

n

L

L

n

=

=

(3.42)

gdzie n

1

i n

2

to liczba zwojów w odpowiednich uzwojeniach.

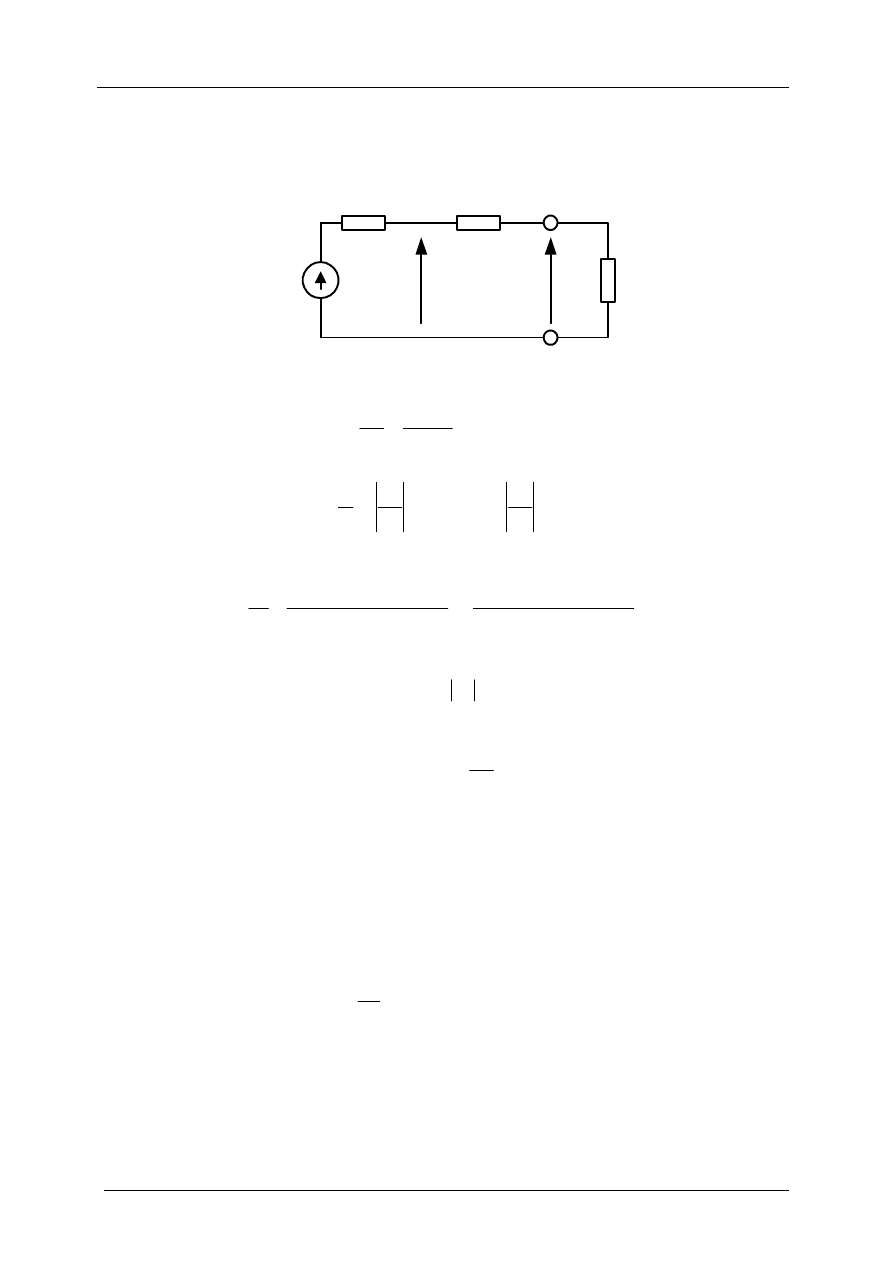
Po uwzględnieniu strat w uzwojeniach (R

1

, R

2

) i rdzeniu (R) oraz pojemności między-zwojowych, mo-

del zastępczy transformatora przyjmuje postać przedstawioną na rys. 3.9.

Transformator idealny

Rys. 3.9. Liniowy model transformatora rzeczywistego

Indukcyjność L (rys. 3.9) jest nazywana indukcyjnością główną, zaś pozostałe dwie to indukcyjności
rozproszenia., przy czym:

2

2

1

1

1

)

1

(

,

)

1

(

,

L

k

L

L

k

L

L

k

L

r

r

⋅

−

=

⋅

−

=

⋅

=

(3.43)

Niewątpliwie, w przypadku sprzężenia uzwojeń poprzez rdzeń ferromagnetyczny, indukcyjności roz-
proszenia są w stosunku do indukcyjności głównej bardzo małe.

1:n

u

1

u

2

i

2

i

1

© Witold Szkudliński: D

WÓJNIKI I CZWÓRNIKI

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_NPorts_2011.pdf Modyfikacje 2011: C. Stefański

Laboratorium OiS

(sieciowe)

KSEM/626Ea

Wersja 2011

-10-

3.4.

Wybrane zagadnienia dotyczące pomiarów. Sposób pomiaru admitancji (im-

pedancji)

Admitancję lub impedancję wejściową będziemy mierzyli wykorzystując przedstawiony na rys.

3.10 obwód, w którym pomiędzy generator i badany obiekt wtrącamy rezystor o znanej rezystancji

R.

e

R

R

x

Y

1

U

2

U

t

E

t

e

ω

cos

)

(

=

)

(t

e

Rys. 3.10. Obwód do pomiaru admitancji i impedancji

Znana rezystancja R tworzy łącznie z mierzoną admitancją dzielnik napięcia, dla którego

x

Y

G

G

U

U

+

=

1

2

(3.44)

Po przekształceniach otrzymujemy















+















−

=

ϕ

ϕ

sin

1

cos

1

2

1

2

1

U

U

U

U

R

Y

x

j

(3.45)

gdzie

ϕ

to przesunięcie fazowe pomiędzy sinusoidalnymi napięciami

)

(

1

t

u

i

)

(

2

t

u

.

Jak wiemy impedancja jest odwrotnością admitancji. Zatem

(

)

(

)

(

)

2

2

2

2

}

Im{

})

(Re{

}

Im{

}

Im{

}

Re{

}

Re{

1

x

x

x

x

x

x

x

x

Y

Y

Y

Y

Y

Y

Y

Z

+

+

+

=

=

j

(3.46)

Nieco inny sposób pomiaru impedancji wejściowej polega na użyciu w obwodzie z rys. 3.10 rezy-

stora R, którego rezystancja wypełnia warunek

x

Z

R >>

(3.47)

W takim przypadku pomiar impedancji sprowadza się do pomiaru transmitancji napięciowej zgod-
nie ze wzorem

1

2

U

U

R

Z

x

⋅

≅

(3.48)

Pomiar przesunięcia fazowego

Pomiar przesunięcia fazowego, jakie wprowadza np. czwórnik do sinusoidalnego sygnału, wiąże

się na ogół z większymi trudnościami niż w przypadku pomiaru wprowadzanych przez filtr zmian am-
plitudy sinusoidy. W najprostszym przypadku może być dokonany punkt po punkcie za pomocą gene-
ratora sinusoidy o precyzyjnie znanej częstotliwości oraz dwukanałowego oscyloskopu. Przesunięcie
fazowe na częstotliwości

f

można obliczyć korzystając z przesunięcia

t

∆

na osi czasu pomiędzy

sinusoidą wyjściową i wejściową filtra. Mierzymy przesunięcie

t

∆

, a następnie wyliczamy przesunię-

cie fazowe w stopniach:

]

[

36

.

0

360

)

(

]

[

]

[

°

⋅

⋅

=

=

kHz

s

f

t

T

t

f

µ

∆

∆

Φ

(3.49)

3.5. Opis pulpitu operacyjnego

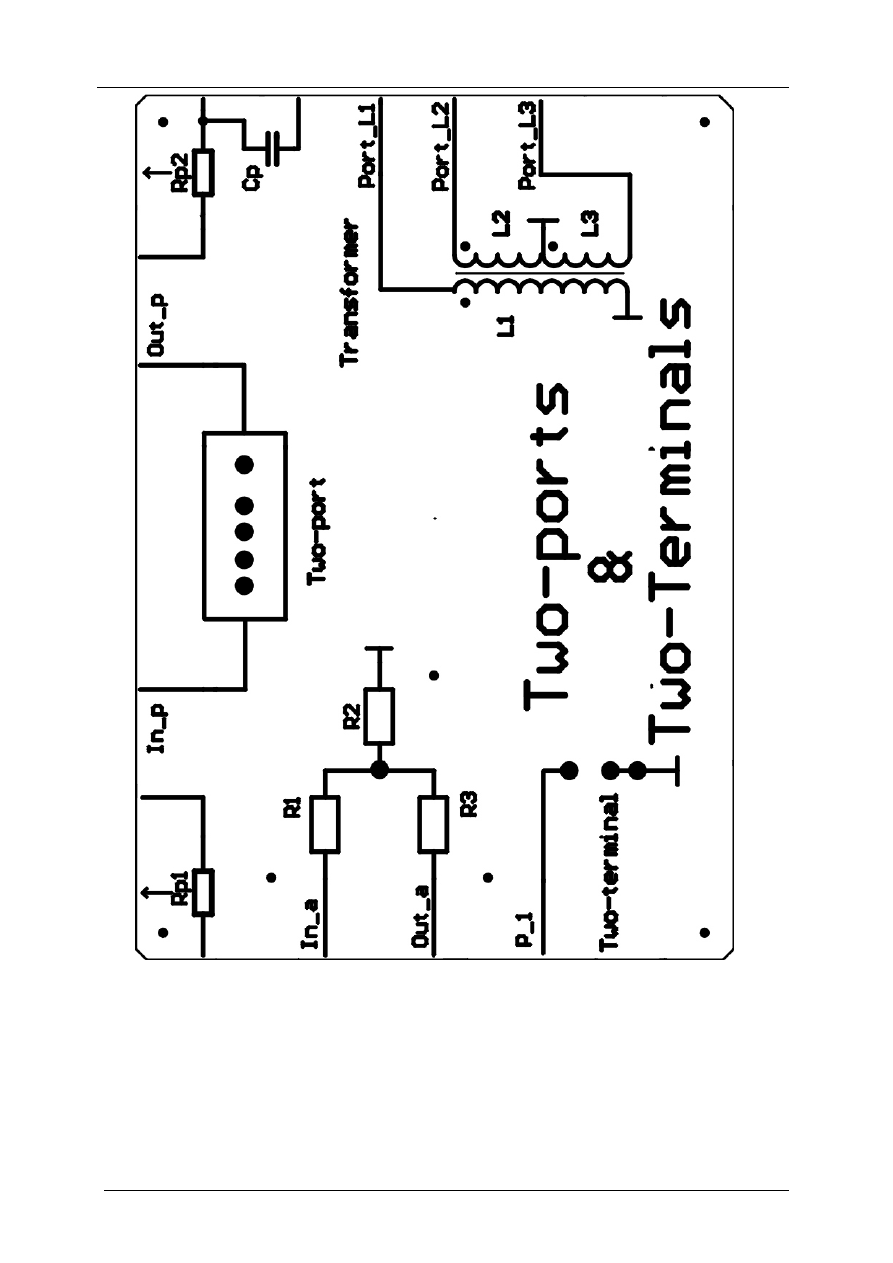
Do dyspozycji wykonawcy ćwiczenia jest pulpit operacyjny przedstawiony na rys. 3.11.

Zawiera on transformator o dwóch uzwojeniach wtórnych z przeciwstawnymi kierunkami nawinięcia.
Mamy zatem możliwość badania zarówno transformatora nieodwracającego (rys. 3.8a), jak i odwra-
cającego (rys. 3.8b). Wiadomo, że wszystkie uzwojenia transformatora zostały nawinięte na rdzeniu
pierścieniowym z materiału ferromagnetycznego F-2001 (

φ40mm). Drugim z układów do badania jest

© Witold Szkudliński: D

WÓJNIKI I CZWÓRNIKI

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_NPorts_2011.pdf Modyfikacje 2011: C. Stefański

Laboratorium OiS

(sieciowe)

KSEM/626Ea

Wersja 2011

-11-

tłumik rezystorowy o strukturze typu „T” (rys. 3.4). Rezystory R

1

,R

3

tłumika to wieloobrotowe poten-

cjometry (0-200 om). Rezystor R

2

jest wieloobrotowym potencjometrem o rezystancji płynnie zmien-

nej w zakresie (0-500om).
W górnej części pulpitu umiejscowiono potencjometry: R

p1

(0-22kom) i R

p2

(0-100om). Rezystor R

p2

można użyć bezpośrednio lub w połączeniu w szereg z kondensatorem C

p

= 6.8uF. Specjalne gniazda

(trzy i pięciostykowe) umożliwiają podłączenie różnego typu dwójników oraz czwórników.

W czasie zajęć mamy do dyspozycji następujące dwójniki:
• Cewki indukcyjne, ponumerowane
Zestaw dostępnych czwórników zawiera:

• Czwórnik z tranzystorem o schemacie jak na rys. 3.6 (tylko wyjście

'

2

u

).

3.5.

Przykładowe pytania kontrolne

1)

Przedstawić model elektryczny rzeczywistej cewki indukcyjnej. Jak się wyraża rezystancja dyna-

miczna oraz dobroć takiej cewki dla częstotliwości rezonansowej ?

2) Podać definicje elementów macierzy hybrydowej [h] i napisać równania wiążące napięcia i prądy

wrót poprzez wyrazy tej macierzy.

3) Naszkicować schemat blokowy czwórnika z prądami i napięciami wrotowymi, a następnie korzysta-

jąc z rysunku podać definicje:

• impedancji wejściowej,
• parametrów czwórnikowych

h

22

oraz h

12

.

4) Naszkicować schemat blokowy czwórnika z prądami i napięciami wrotowymi, a następnie korzy-

stając z rysunku podać definicje:

• impedancji wyjściowej,
• parametrów czwórnikowych

h

11

oraz h

21

.

5) Objaśnić (rysunek, opis idei) metodę pomiaru nieznanej impedancji Z

x

lub admitancji Y

x

, polegającą

na wtrąceniu rezystora o znanej rezystancji.

6) Naszkicować symbol idealnego transformatora łącznie z prądami i napięciami wrotowymi, a na-

stępnie podać równania opisujące właściwości tego elementu.

7) Jakie macierze (wymienić nazwy przynajmniej trzech, nie licząc macierzy hybrydowej) mogą opi-

sywać czwórnik liniowy (bądź quasiliniowy)?

8) Kolejne pytania – równie ważne – znajdzie Czytelnik w naszej witrynie

3

.

3

http://www.eti.pg.gda.pl/katedry/ksem/pracownicy/Czeslaw.Stefanski/PomoceDydaktyczne/11_ObwodyIsygnaly_semIII/

© Witold Szkudliński: D

WÓJNIKI I CZWÓRNIKI

Laboratorium Obwodów i Sygnałów (LOiS)

Plik:LOiS_NPorts_2011.pdf Modyfikacje 2011: C. Stefański

Laboratorium OiS

(sieciowe)

KSEM/626Ea

Wersja 2011

-12-

Rys. 3.11. Widok pulpitu operacyjnego