
WYDZIAŁ ETI PG
Katedra Systemów Elektroniki Morskiej
Laboratorium Obwodów i Sygnałów
WIDMA SYGNAŁÓW OKRESOWYCH
Opracował: Marek S. Makowski
Gdańsk 2011

© Marek S. Makowski: W
IDMA SYGNAŁÓW
OKRESOWYCH
Laboratorium Obwodów i Sygnałów (LOiS)
Plik:LOiS_Spectrum_2011.pdf Modyfikacja 2011: M. Makowski, C. Stefański
F
Laboratorium OiS
(sieciowe)
KSEM/626Ea
Wersja 2011
2/12
1.
WPROWADZENIE
Sygnały okresowe tworzą ważną klasę sygnałów elektrycznych wykorzystywanych w
teorii sygnałów i obwodów oraz pomiarach i testach układów i urządzeń. W zakresie
teorii operujemy sygnałami okresowymi jako pewnymi abstraktami matematycznymi
w tym sensie, że są sygnałami wszechtrwającymi. W pomiarach i eksperymentach z
natury rzeczy mamy do czynienia z sygnałami w pewnym przedziale czasu. Warunki
pomiaru dobierane są w ten sposób, że po pobudzeniu odpowiedź układu jest bardzo
bliska odpowiedzi w stanie ustalonym t.j. tak jak przy pobudzeniu sygnałem wszech-
trwającym. Bardzo ważną metodą badawczą w stanie ustalonym jest analiza fourie-
rowska
inaczej widmowa bądź częstotliwościowa. W trakcie ćwiczenia, podczas sy-
mulacji a następnie pomiarów student zapozna się z widmami wybranych sygnałów
okresowych oraz wpływem kształtu, proporcji i symetrii sygnału na składniki widma.
2.
PODSTAWY TEORETYCZNE
2.1.
Reprezentacja sygnałów za pomocą zbioru sygnałów ortogonal-
nych. Uogólniony szereg Fouriera.
Rozważmy zbiór zupełny funkcji czasu g
1
(t), g
2
(t), …, g
n
(t), które są wzajemnie
ortogonalne w przedziale <t
1
, t
2
>, t.z.n. [patrz iloczyn skalarny ]
∫
≠
=
2
1
0
)
(
)
(
t
t
i
j
i
j
dt
t
g
t
g
dla
(2.1)
∫
=
=
2
1
)
(
)
(
t
t
j
i
j
i
j
K
dt
t
g
t
g
dla
Załóżmy, że dowolny sygnał x(t) będzie aproksymowany w przedziale <t
1
, t
2
> liniową
kombinacją k tych funkcji, czyli sumą ważoną, gdzie C
r
tworzy zbiór pewnych sta-
łych.
∑
=
≈
k
r
r
r
t
g
C
t
x
1
)
(
)
(
( 2.2)
W celu najlepszej (w sensie pewnej miary błędu) aproksymacji musimy znaleźć od-
powiednie wartości stałych C
r.
Wygodna jest miara średniokwadratowa. Średni błąd
kwadratowy definiowany jest następująco
∑
∫
=
−
−
=
k
r
r
r
t
t
dt
t
g
C
t
x
t
t
1
2
1
2
)]
(
)
(
[
1
2
1
ε
(2.3)
Aby błąd ten był najmniejszy trzeba by wszystkie pochodne cząstkowe błędu ε
względem kolejnych stałych C były zerowe, t.j. aby dla każdego r
0
=
r
C
∂
ε
∂
(2.4)
Rozwiązanie prowadzi do wzoru na j-tą stałą C:
∫
=
t
t
j
j
j
dt
t
g
t
x
K
C
1
)
(
)
(
1
(2.5)
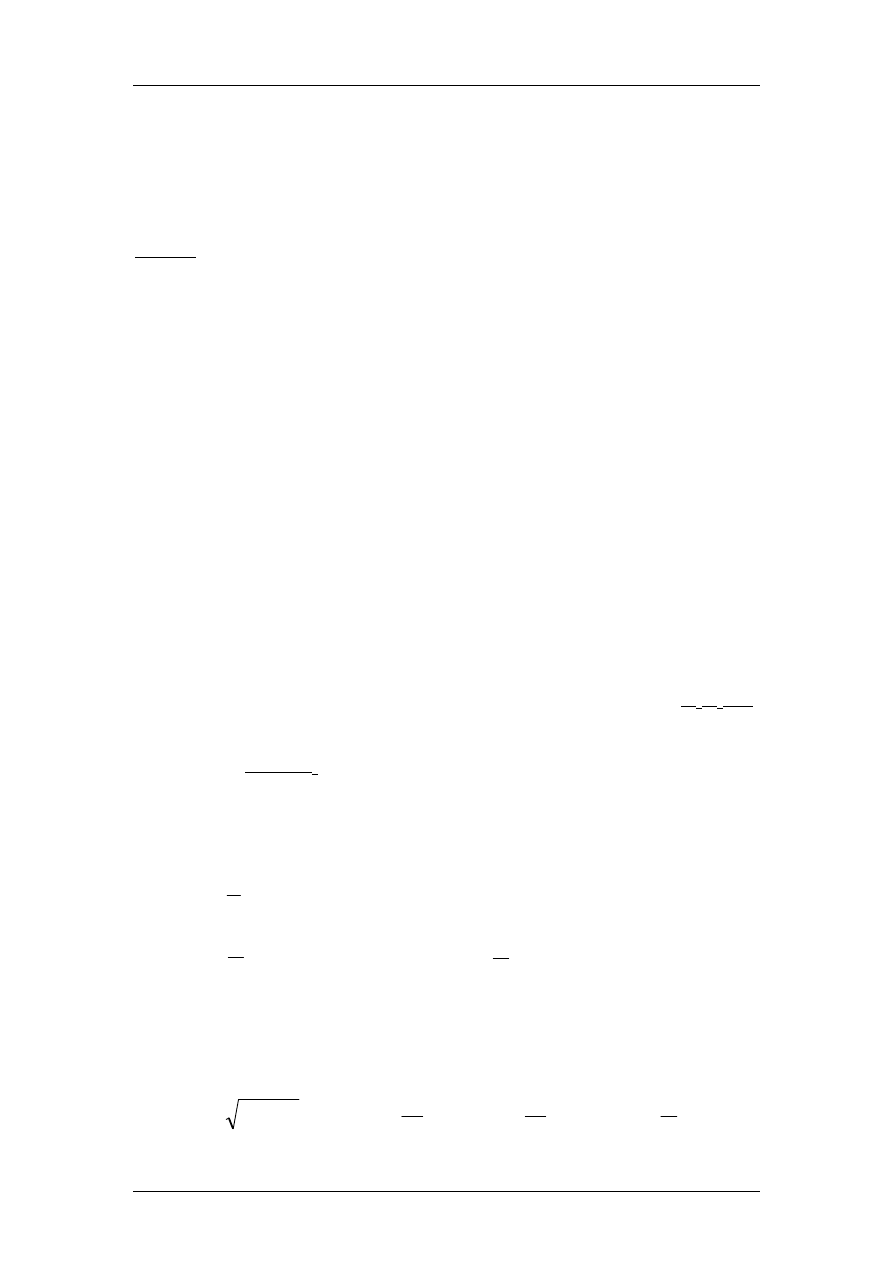
© Marek S. Makowski: W
IDMA SYGNAŁÓW
OKRESOWYCH
Laboratorium Obwodów i Sygnałów (LOiS)
Plik:LOiS_Spectrum_2011.pdf Modyfikacja 2011: M. Makowski, C. Stefański
F
Laboratorium OiS
(sieciowe)
KSEM/626Ea
Wersja 2011
3/12
Można pokazać, że przy tak dobranych współczynnikach błąd maleje przy wzroście
liczby wyrazów k (2.2). W granicy, gdy k
→ ∞ błąd maleje do zera. Wówczas x(t)
opisuje się szeregiem nieskończonym:
∑
∞
=
=
1
)
(
)
(
r
r
r
t
g
C
t
x
(2.6)
Szereg ten nazywany jest uogólnionym szeregiem Fouriera.
Uwaga .
Znamy wiele zbiorów funkcji {g
r
}, które znajdują zastosowanie w opisanym
zagadnieniu aproksymacji. Przykładowo: funkcje trygonometryczne, wykładnicze w
klasycznej analizie widmowej sygnałów ale również: wielomiany Legendre’a, funk-
cje Haara, Walsha i inne [patrz
→
→
→
→ n.p. J. Szabatin: “Teoria Sygnałów”].
2.2.
Sygnał okresowy
Definicja (sygnał okresowy). Sygnałem okresowym nazywamy sygnał x(t) spełniają-
cy dla każdego czasu t równość:
x
(t) = x(t +T) ;
T
> 0
(2.7)
Obserwacje. Liczbę T nazywamy okresem sygnału. Najmniejsza liczba T spełniająca
(2.7) to okres podstawowy.
Sygnał (2.7) jest sygnałem wszechtrwającym t.j. określonym w przedziale cza-
su (
− ∞, + ∞). Zakładamy dalej, że x(t) jest rzeczywistą funkcją czasu.
2.3.
Szereg trygonometryczny Fouriera
2.3.1. Szereg trygonometryczny Fouriera sygnału impulsowego (w przedziale skoń-
czonym
).
Rozpatrzmy najpierw pewną funkcję czasu x(t) w przedziale domkniętym <t
o
, t
o
+T>.
Można pokazać, że zbiór funkcji harmonicznych t.j. zawierający elementy a
k
cosk
ω
o
t
i b
k
sink
ω
o
t jest domkniętym zbiorem ortogonalnym i aproksymuje funkcję x(t) w tym
przedziale gdy T = 2
π/
ω
o
.
Sygnał x(t) można zatem rozwinąć w trygonometryczny szereg Fouriera:
)
sin
cos
(
)
(
1
t
k
b
t
k
a
a
t
x
o
k
k
o
k
o
ω
ω
∑
+∞
=
+
+
=
(2.8)
gdzie:
∫
+
=
T
t
t
o
o
o
dt
t
x
T
a
)
(
1
-
jest wartością średnią x(t) (inaczej składową stałą),
∫
+
=
T
t
t
o
k
o
o
tdt
k
t
x
T
a
ω
cos
)
(
2
,
∫
+
=
T
t
t
o
k
o
o
tdt
k
t
x
T
b
ω
sin
)
(
2
.
(2.9)
Szereg (2.8) można przedstawić w alternatywych postaciach:
∑
+∞
=
+
+
=
1
)
cos(
)
(
k
kn
o
k
o
t
k
c
a
t
x
ϕ
ω
,
∑
+∞
=
+
+
=
1
)
sin(
)
(
k
k
o
k
o
t
k
c
a
t
x
ψ
ω
(2.10)
Pomiędzy współczynnikami szeregów (2.8 ) i (2.10) zachodzą związki:
2
,
2
2
π
ϕ
ψ
ϕ
ϕ
+
=
−
=
=
+
=
k
k
k
k
k
k
k
k
k
k
k
c
b
c
a
b
a
c
sin
i
cos
,
(2.11)
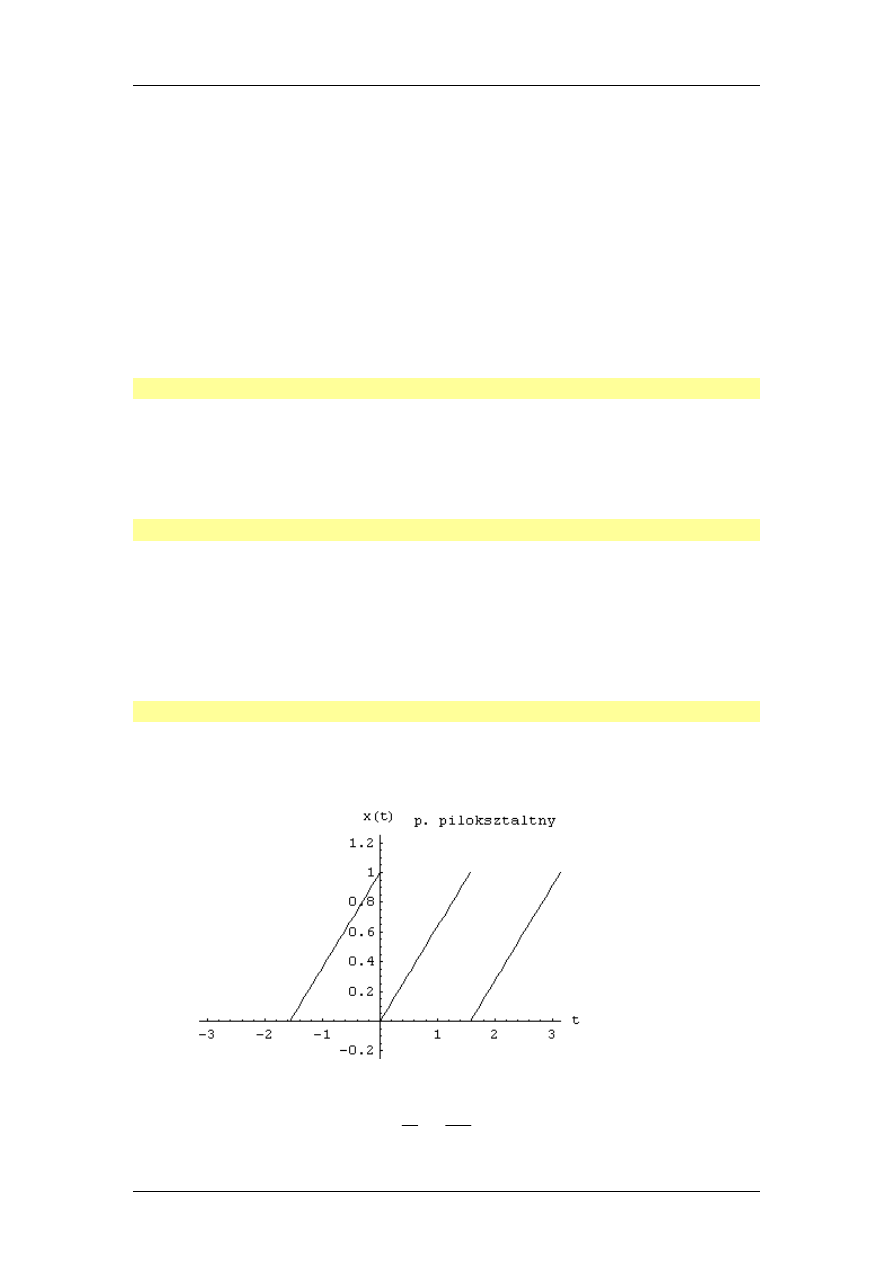
© Marek S. Makowski: W
IDMA SYGNAŁÓW
OKRESOWYCH
Laboratorium Obwodów i Sygnałów (LOiS)
Plik:LOiS_Spectrum_2011.pdf Modyfikacja 2011: M. Makowski, C. Stefański
F
Laboratorium OiS
(sieciowe)
KSEM/626Ea
Wersja 2011
4/12
2.3.2. Szereg trygonometryczny Fouriera sygnału okresowego (w przedziale nie-
skończonym
).
Szeregi (2.8) oraz (2.10) są zbieżne do sygnału (impulsowego) x(t) jedynie w prze-
dziale czasu o długości T . Poza tym przedziałem, z uwagi na okresowość (z okresem
T
) funkcji aproksymujących, przebieg z przedziału podstawowego jest powtarzany.
Tak więc jeżeli sygnał x(t) jest sygnałem okresowym o okresie T to szeregi Fouriera
(2.8) i (2.10) są zbieżne do tego sygnału w przedziale (-
∞, ∞).
2.3.3. Szereg trygonometryczny: przykłady i zadania.
Przykład 1.
Rozwinąć w trygonometryczny szereg Fouriera sygnał x(t) = cos
ω
o
t
.
Dostajemy natychmiast, (bez obliczeń !):
a
0
= 0, a
1
= 1 , alternatywnie: a
o
= 0, c
1
= 1,
ϕ
1
= 0.
Przykład 2.
Wyznaczyć współczynniki trygonometrycznego szeregu Fouriera sygnału
x
(t) = cos20t + 2cos22t.
Obliczenia rozpoczynamy od wyznaczenia okresu podstawowego sygnału x(t).
T
=
π
(lub inaczej
ω
o
= 2) [patrz
→
→
→
→ materiał semestru 2-go].
Konsekwentnie: a
10
= 1, a
11
= 2, a
0
= 0.
Zadanie i Przykład 3.
Rozwinąć w szereg Fouriera przebieg piłokształtny na rysunku:
Sygnał jest okresowy z okresem T =
π/2 , (ω
0
= 2
π/T = 4).
Segment
x
T
(t) sygnału x(t) w przedziale (0,
π/2) dany jest wzorem:
t
A
t
T
A
t
x
T
π
2
)
(
=
=
(2.12)

© Marek S. Makowski: W
IDMA SYGNAŁÓW
OKRESOWYCH
Laboratorium Obwodów i Sygnałów (LOiS)
Plik:LOiS_Spectrum_2011.pdf Modyfikacja 2011: M. Makowski, C. Stefański
F
Laboratorium OiS
(sieciowe)
KSEM/626Ea
Wersja 2011
5/12
Bez obliczeń, z obserwacji x(t), mamy a
0
= A/2. Natomiast po podstawieniu
x
T
(t) do wzorów (2.9) i scałkowaniu przez części dostajemy:
,...
3
,
2
,
1
1
,
,
0
oraz
gdzie
=
=
−
=
=
k
A
k
A
b
a
k
k
π
(2.13)
∑
∞
=
−
=
1
4
sin
1
1
2
1
)
(
k
t
k
k
t
x
π
(proszę sprawdzić ten wynik)
(2.14)
2.3.4 Wpływ symetrii sygnału na współczynniki trygonometrycznego
szeregu Fouriera.
W przykładzie (Zadanie 3) obserwujemy, że współczynniki a
k
= 0 dla k > 0, co ozna-
cza, że w rozwinięciu w trygonometryczny szereg Fouriera nie występują składniki
kosinusoidalne. Wynika to z nieparzystości sygnału x(t).
Każdy sygnał nieparzysty zawiera tylko składniki nieparzyste czyli sinusoidalne. Po-
dobnie każdy sygnał parzysty zawiera tylko składniki parzyste czyli kosinusoidalne
Wpływ tej i innych symetrii sygnału można podsumować w zestawieniu:
Symetria
Definicja
a
0
a
k
b
k
Parzystość
x
(- t) = x(t)
Może być
dowolne
a
k
b
k
= 0
Nieparzystość
x
(- t) = - x(t)
a
0
= 0
a
k
= 0
b
k
Nieparzystość ukryta
a
0
≠ 0
a
k
= 0
b
k
Antysymetryczność
x
(t + T/2) = - x(t)
a
0
= 0
a
2k
= 0
B
2k
= 0
Antysymetria ukryta
a
0
≠ 0
a
2k
= 0
B
2k
= 0
2.4.
Szereg wykładniczy (zespolony) Fouriera. Widmo prążkowe (dys-
kretne)
Można wykazać, że zbiór funkcji wykładniczych postaci:
}
{
0
t
k
ω
j
e
(2.15)
dla k = 0,
±1, ±2, ±3, …jest, podobnie jak zbiór funkcji trygonometrycznych, zbiorem
ortogonalnym w przedziale [por. p. 2.3.1].
Sygnał x(t) można zatem rozwinąć w wykładniczy szereg Fouriera:
∑
∞
−∞
=
=
k
t
jk
k
e
X
t
x
0
)
(
ω
(2.16)
gdzie:
dt
e
t
x
T
X
T
t
t
t
jk
k
∫
+
−
=
0
0
0
)
(
1
ω
(2.17)
jest k-tym (zespolonym) współczynnikiem wykładniczego szeregu Fouriera.
Podobnie gdy sygnał x(t) jest okresowy z okresem:

© Marek S. Makowski: W
IDMA SYGNAŁÓW
OKRESOWYCH
Laboratorium Obwodów i Sygnałów (LOiS)
Plik:LOiS_Spectrum_2011.pdf Modyfikacja 2011: M. Makowski, C. Stefański
F
Laboratorium OiS
(sieciowe)
KSEM/626Ea
Wersja 2011
6/12
0
2
ω
π
=
T
(2.18)
wówczas szereg wykładniczy (zespolony) Fouriera jest zbieżny do tego sygnału w
przedziale (-
∞, ∞).
Komentarz.
Szereg (2.16) można otrzymać z szeregu rzeczywistego (2.8) (trygonome-
trycznego) wykorzystując tożsamości Eulera [por. n.p. J.Osiowski, J.Szabatin, t.II,
rozdz. 5.1.2].
Spostrzeżenie.
Warto odnotować, że choć poszczególne składniki sumy (2.16) są ze-
spolone
, to wartość tej sumy dla każdej chwili t jest rzeczywista. Wynika to z faktu, że
we wzorze (2.16) dla dowolnego k (k ≠ 0) sumujemy (parami) składniki z indeksami k
ujemnymi i dodatnimi. Mając powyższe na uwadze można porównawczo zauważyć,
ż
e:
szeregi trygonometryczne (2.8) i (2.10) (dla sygnałów o wartościach rzeczywistych)
mają współczynniki rzeczywiste oraz k
∈
{ 0, 1, 2, 3, …., +
∞),
szereg wykładniczy (zespolony) (2.16) (dla sygnałów o wartościach rzeczywistych)
ma współczynniki na ogół zespolone oraz k
∈
{-
∞, …, -3, -2, -1 , 0, 1, 2, 3, …., +∞),
Przypomnijmy, że z rozkładem sygnału w szereg Fouriera wiąże się pojęcie widma
sygnału.
2.4.1.
Definicja (Widmo zespolone)
Widmem (zespolonym) sygnału okresowego x(t) nazywamy dyskretny zbiór
{X
k
; k = 0,
±1, ±2, ±3, …} współczynników rozwinięcia tego sygnału w ze-
spolony szereg Fouriera.
Mając na uwadze, że:
k
X
k
k
X
X
arg
j
e
=
(2.19)
2.4.2.
Definicja (Widmo Amplitudowe i Fazowe).
Zbiór {
|X
k
|} nazywamy widmem amplitudowym, a zbiór {argX
k
} widmem fa-
zowym.
Widmo sygnału okresowego jest zbiorem przeliczalnym na osi pulsacji (okre-
ś
lonym dla dyskretnych pulsacji k
ω
0
), z tego względu nazywane jest widmem
dyskretnym
lub prążkowym. Z uwagi na k
∈
( -
∞, +∞) widmo (2.19) nazywa-
my widmem dwustronnym, a składniki widma o ujemnych indeksach (pulsa-
cjach) nie mają interpretacji fizycznej
(ale mają interpretację wskazową)
.
Komentarz nt interpretacji wyników symulacji i pomiarów w laboratorium.
O ile podczas wykładu, ze względów klarowności pojęciowej, jednolitych
i łatwiejszych obliczeń posługujemy się częściej szeregiem Fouriera w postaci zespo-
lonej, o tyle w warunkach laboratoryjnych, przy pomiarach widma mamy do czynie-
nia z rozbiciem sygnału w szereg rzeczywisty. Symulatory elektroniczne z kolei (np.
PSPICE i Micro-Cap) zazwyczaj funkcjonują w ten sposób, że obliczenia (we-
wnętrzne) oparte są na postaci zespolonej (wyznaczane jest widmo dwustronne), a
wyniki prezentowane są w postaci składników rzeczywistych (jako widmo jedno-
stronne
).
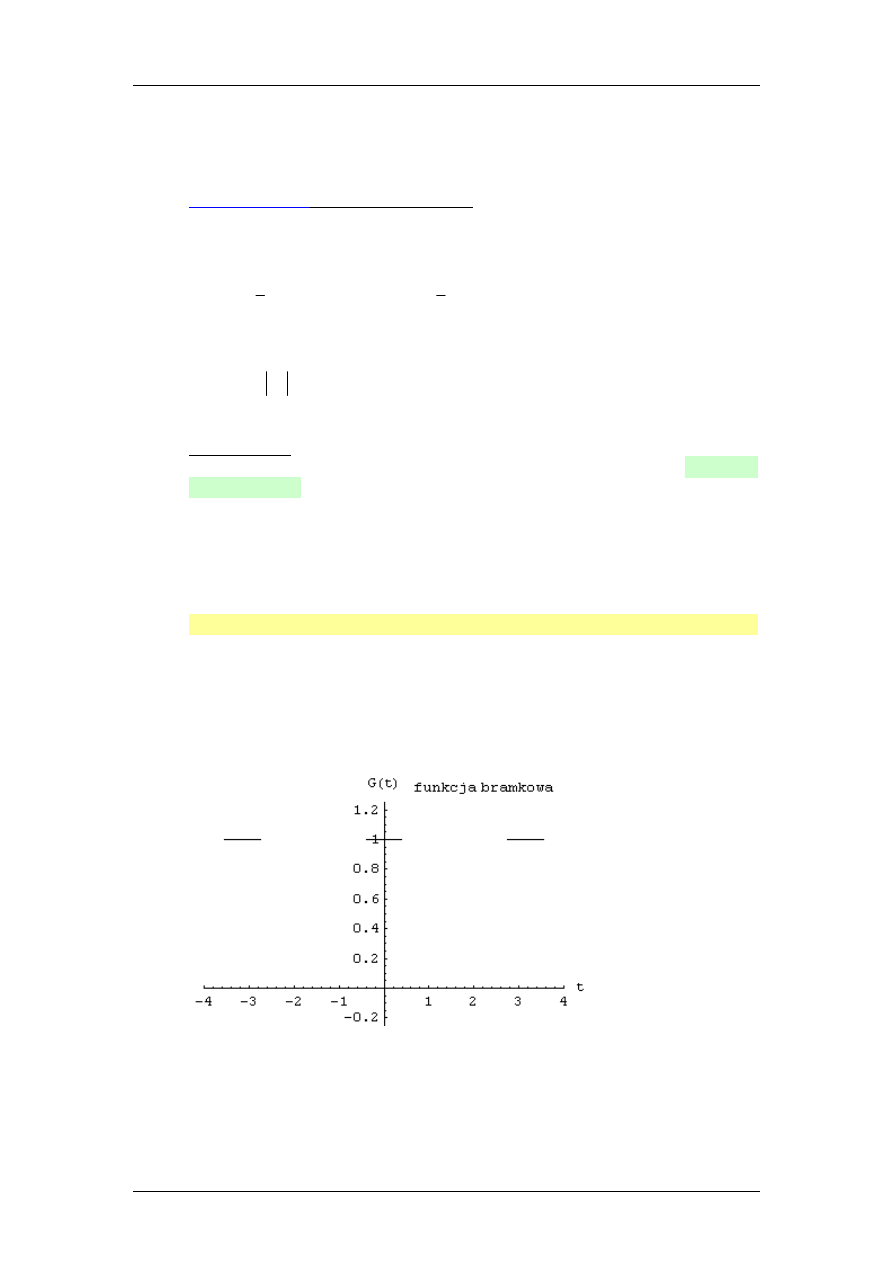
© Marek S. Makowski: W
IDMA SYGNAŁÓW
OKRESOWYCH
Laboratorium Obwodów i Sygnałów (LOiS)
Plik:LOiS_Spectrum_2011.pdf Modyfikacja 2011: M. Makowski, C. Stefański
F
Laboratorium OiS
(sieciowe)
KSEM/626Ea
Wersja 2011
7/12
Zarówno w symulacjach oraz pomiarach dostajemy wprost w tym ćwiczeniu jedynie
widma amplitudowe.
W tej sytuacji student może skorzystać z wzorów pomocniczych.
----------------------------------------------------------------------------------------------
back to link ↓
Wzory pomocnicze. Współczynniki szeregów trygonome-
trycznego rzeczywistego i wykładniczego zespolonego powiązane są zależno-
ś
ciami, które wynikają z porównania postaci (2.9), (2.11) oraz (2.17) i (2.19):
)
,
(
2
)
arg(
2
)
(
)
(
),
(
2
1
2
1
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
o
o
a
b
arctg
jb
a
F
c
F
F
b
F
F
a
b
a
F
b
a
F
a
F
−
=
−
=
=
−
=
+
=
+
=
−
=
=
−
−
−
ϕ
j
j
j
oraz
(2.20)
Spostrzeżenie.
(Funkcje rzeczywiste) Jeżeli f(t) jest funkcją rzeczywistą czasu
(tak założyliśmy w p.2.2 i to jest przypadek praktyki inżynierskiej i pomiarów
w laboratorium) to współczynniki a
k
oraz b
k
są rzeczywiste natomiast współ-
czynnik F
-k
jest sprzężony względem F
k
tj.:
F
-k
= F
*
k
oraz a
0
=F
0
, a
k
= 2ReF
k
, b
k
= -2ImF
k
, dla k > 0 (2.21)
----------------------------------------------------------------------------------------------
2.4.3. Szereg zespolony, widma: przykłady
Przykład 4. Funkcja bramkowa. Rozwinięcie idealizowanego (prostokątnego)
sygnału okresowego w szereg zespolony Fouriera.
Widma: amplitudowe i fazowe. Wpływ symetrii sygnału na widmo.
Rozwinąć w wykładniczy (zespolony) szereg Fouriera funkcję bramkową f(t)
[oznaczana zwykle G(t) od ang. Gate = bramka] jak na rysunku. Narysować
widmo zespolone sygnału f(t) oraz widma amplitudowe i fazowe.
gdzie:
τ
=
π/4 – czas trwania impulsu (
przykładowo
),
T
=
π – okres powtarzania (
przykładowo
),
A
=1 – wysokość impulsu (
inaczej „amplituda”
),
© Marek S. Makowski: W
IDMA SYGNAŁÓW
OKRESOWYCH
Laboratorium Obwodów i Sygnałów (LOiS)
Plik:LOiS_Spectrum_2011.pdf Modyfikacja 2011: M. Makowski, C. Stefański
F
Laboratorium OiS
(sieciowe)
KSEM/626Ea
Wersja 2011
8/12
D
=
τ/ T – tzw. współczynnik wypełnienia (
czas trwania do okresu powtarzania
).
back to link
↓
Po obliczeniach otrzymujemy wzór ogólny na k-ty współczynnik zespo-
lonego szeregu Fouriera:
F
k
= AD Sa(k
π
D
),
F
k
square
(D = ½) = ½ A Sa(½k
π
)
(2.22)
gdzie
Sa(x) =
x
x
sin
to tzw. funkcja próbkowa, inaczej oznaczana sinc
Spostrzeżenie
. Współczynniki (2.22) są rzeczywiste, gdyż f(t) w przykładzie jest funk-
cją parzystą. Spostrzeżenie to oraz inne można uogólnić jak w zestawieniu poniżej.
Symetria sygnału
F
k
Parzystość
Rzeczywiste
Nieparzystość
Urojone
Nieparzystość ukryta
F
o
– rzeczywiste, F
k
– urojone (k
≠
0)
Brak symetrii:
sygnał nie jest parzysty ani nieparzysty
Zespolone
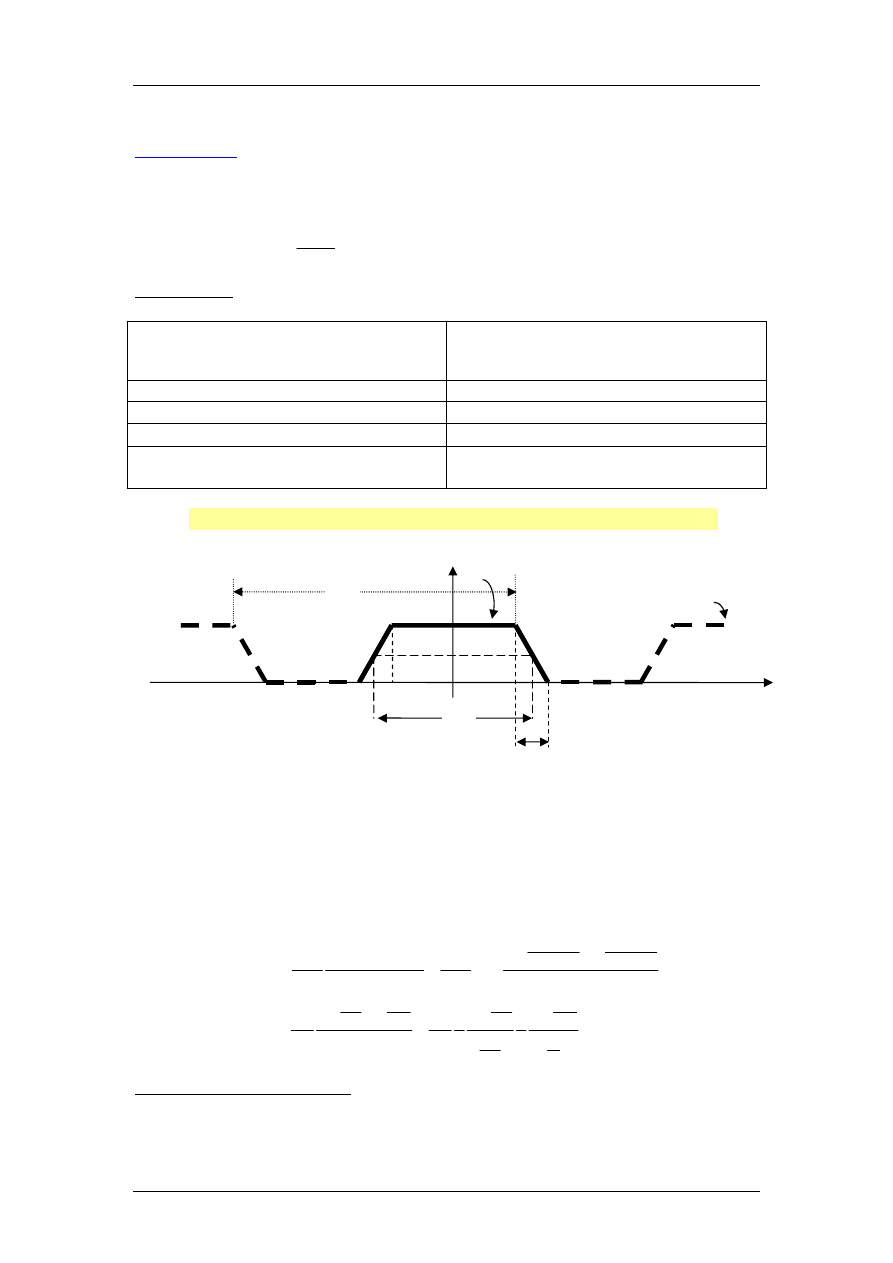
Przykład 5. Impuls zegarowy. Rozwinięcie realistycznego (trapezowego) sy-
gnału okresowego w szereg zespolony Fouriera. Widmo sygnału. Dyskusja.
A)
f(t) to pojedynczy, parzysty impuls trapezowy, gdzie:
A – wysokość impulsu,
τ – czas trwania mierzony w połowie wysokości impulsu,
t
r
– czas narastania (opadania),
a
=
τ/2 – t
r
/2 = ½(
τ – t
r
),
b
=
τ/2 + t
r
/2 = ½(
τ + t
r
),
Transformata Fouriera
1
:
2
2
sin
2
1
2
2
sin
2
4
2
sin
2
sin
4
2
)
(
sin
2
)
(
sin
2
)
(
2
cos
cos
2
)]
(
[
2
2
2
ω
ω
ωτ
ωτ
τ
ω
ω
ωτ
ω
ω
ω
ω
ω
ω
r
r
r
r
t
t
A
t
t
A
b
a
b
a
a
b
A
b
a
a
b
A
t
f
=
=
−
+
−
−
=
−
−
=
F
F
F
F
1
W powyższym przykładzie korzysta się ze znajomości transformaty Fouriera sygna-
łu nieokresowego (por. materiał przedmiotu Przetwarzanie Sygnałów, sem.3). Stu-
dent może wyznaczyć widmo sygnału okresowego wprost ze wzoru (2.17)
f
(t)
t
0
τ
t
r
A
-a
-b
T
f
T
(t)

© Marek S. Makowski: W
IDMA SYGNAŁÓW
OKRESOWYCH
Laboratorium Obwodów i Sygnałów (LOiS)
Plik:LOiS_Spectrum_2011.pdf Modyfikacja 2011: M. Makowski, C. Stefański
F
Laboratorium OiS
(sieciowe)
KSEM/626Ea
Wersja 2011
9/12
Po uporządkowaniu dostajemy:
=
=
2
2
)
(
)]
(
[
r
t
Sa
Sa
A
j
F
t
f
ω
ωτ
τ
ω
F
F
F
F
(2.23)
B)
Rozpatrzmy następnie sygnał f
T
(t): powtarzający się z okresem T ciąg impulsów trapezo-
wych j.w.
Wzór na k-ty współczynnik zespolonego szeregu Fouriera okresowego sygnału zegarowego
wyraża się poprzez
F
F
F
F
–transformatę pojedynczego impulsu po podstawieniu
ω
= k
ω
o
i po-
dzieleniu otrzymanego wyrażenia przez T;
otrzymujemy:
)
(
)
(
)
(
)
(
2
2
)
(
2
2
2
2
τ
π
τ
π
π
π
π
π
ω
τ
ω
τ
ω
r
t
r
r
t
T
k
T
k
r
o
o
o
k
D
k
Sa
D
k
ADSa
D
k
Sa
D
k
ADSa
Sa
ADSa
t
k
Sa
k
Sa
T
A
T
jk
F
F
=
=
=
=
=
(2.24)
gdzie:
T
≥ τ + t
r
– okres
ω
o
= 2
π/T – pulsacja podstawowa
D
=
τ/T ≠ 0 – współczynnik wypełnienia
D
r
= t
r
/T – współczynnik narastania
Sa(.) = sin(.)/(.) – funkcja próbkowa, w przypadku sygnału okresowego – obwiednia widma.
Dyskusja
Widmo sygnału okresowego jest przeliczalnym zbiorem współczynników F
k
zespolo-
nego szeregu Fouriera, gdzie k = 0,
±1, ±2, …
W przykładzie z sygnałem zegarowym jak na rysunku widmo jest zbiorem dyskretnym liczb
rzeczywistych; ich obrazem graficznym są punkty wpisane w obwiednie typu Sa(.).
Analiza: miejsca zerowe obwiedni.
Przy ustalonych współczynnikach D, D
r
wyznaczamy zbiory liczb {k
o
} oraz {k
or
} dające
przejścia obwiedni widma przez zero:
Sa(k
o
πD) Sa(k
or
πD
r
) = 0, stąd
Sa(k
o
πD) = 0 lub Sa(k
or
πD
r
) = 0, czyli
k
o
πD =
±
n
π
lub k
or
πD
r
=
±
m
π,
n
, m = 1, 2, 3, …
k
o
=
±
n
/D
lub k
or
=
±
m
/D
r
o ile
D
, D
r
≠ 0.
W szczególności mamy pierwsze pary miejsc zerowych obwiedni gdy:
k
o
=
±
1/D
lub k
or
=
±
1/D
r
(2.25)
Uwaga.
Liczby k
o
oraz k
or
ogólnie biorąc nie muszą być całkowite. Te spośród nich, które są
całkowite wyznaczają numery zerujących się harmonicznych w widmie.
Spostrzeżenie.
Zmieniając proporcje sygnału zegarowego (czyli D, D
r
) mamy kontrolę nad
obecnością w widmie określonych harmonicznych. Można więc postawić zadanie odwrotne
czyli zadanie syntezy: skonstruować taki sygnał zegarowy aby „znikały” zadane harmoniczne
(również ich całkowite wielokrotności).
Przykład. Wyznaczyć sygnał zegarowy, w którego widmie nie wystąpią 2-ga i 3-cia harmo-
niczna.

© Marek S. Makowski: W
IDMA SYGNAŁÓW
OKRESOWYCH
Laboratorium Obwodów i Sygnałów (LOiS)
Plik:LOiS_Spectrum_2011.pdf Modyfikacja 2011: M. Makowski, C. Stefański
F
Laboratorium OiS
(sieciowe)
KSEM/626Ea
Wersja 2011
10/12
back to link
↓
Rozwiązanie.
(2.26)
k
o
=
±
2 stąd D = ½
k
or
=
±
3 stąd D
r
= 1/3
W widmie otrzymanego sygnału nie występuje 2-ga harmoniczna oraz jej całkowite wielo-
krotności czyli wszystkie parzyste harmoniczne. Spośród pozostałych (nie licząc zerowej
harmonicznej tj. składowej stałej sygnału) nieparzystych harmonicznych znika dodatkowo 3-
cia harmoniczna, 9-ta, 15-ta itd.
Spostrzeżenie
. Otrzymany sygnał jest najlepszą aproksymacją sygnału kosinusoidalnego sy-
gnałem trapezowym.
2
Przykład 6. Widmo zespolone fali trójkątnej.
Widmo unipolarnej, parzystej fali trójkątnej o wartości międzyszczytowej (wyso-
kości) A można uzyskać ze wzoru (2.24) dla fali trapezowej, kładąc:
t
r
=
τ
(czas narastania = czas trwania) oraz
D
=
τ/T = ½
dostajemy
)
2
1
(
2
1
2
π
k
ASa
F
triangle
k
=
(2.27)
Przykładowe pytania kontrolne
A1. Podaj definicję sygnału okresowego.
A2. Co to jest widmo sygnału okresowego ?
A3. Co to jest szereg Fouriera sygnału okresowego?
A4. Zapisz i objaśnij ogólną postać szeregu Fouriera z użyciem trygonometrycznego
formalizmu matematycznego.
A5. Zapisz i objaśnij ogólną postać szeregu Fouriera z użyciem wykładniczego for-
malizmu matematycznego.
A6. Jaka jest różnica między szeregiem rzeczywistym (trygonometrycznym), a zespo-
lonym Fouriera? Jak można przejść z jednej reprezentacji na drugą (podać wzory oraz
tok postępowania, z jakich zależności/tożsamości matematycznych można tu skorzy-
stać?).
A7. Objaśnij pojęcia widma amplitudowego i fazowego sygnału okresowego. Narysuj
widma przykładowego sygnału w układach współrzędnych, oznaczając osie.
Kolejne pytania – równie ważne – znajdzie Czytelnik w Naszej Witrynie
3
.
2
Można pokazać, że dla dowolnego okresowego sygnału odcinkami stałego – odcinkami linio-
wego amplitudy kolejnych harmonicznych, dla dostatecznie dużego k, maleją, względem am-
plitudy 1-szej harmonicznej, szybciej niż z numerem harmonicznej (choć wolniej niż z kwa-
dratem numeru harmonicznej). Stąd powyższe spostrzeżenie.
3
http://www.eti.pg.gda.pl/katedry/ksem/pracownicy/Czeslaw.Stefanski/PomoceDydaktyczne/11_ObwodyIsygnaly_semIII/
© Marek S. Makowski: W
IDMA SYGNAŁÓW
OKRESOWYCH
Laboratorium Obwodów i Sygnałów (LOiS)
Plik:LOiS_Spectrum_2011.pdf Modyfikacja 2011: M. Makowski, C. Stefański
F
Laboratorium OiS
(sieciowe)
KSEM/626Ea
Wersja 2011
11/12
3.
PRZYGOTOWANIE DO ĆWICZENIA
[Fourier]:
Projekt-Obliczenia-Symulacje
1-sza godzina zajęć poświęcona będzie m.in. nauce/przypomnieniu obsługi progra-
mów symulacyjnych. Poniższe zadania (punkty 1-5) studenci wykonują w pierwszej
części zajęć poświęconych widmom sygnałów okresowych. W ramach przygotowania
do zajęć wymaga się od studentów wykonania w domu częściowych obliczeń
i (w zależności od umiejętności) symulacji. W laboratorium wyniki pośrednie studen-
ci zapisują lokalnie na komputerach w swoich katalogach (Pulpit lub Moje Doku-
menty, Moje Obrazy itd.). Ostateczne wyniki w wersji elektronicznej, po ew. dyskusji
z Prowadzącym muszą być przesłane na konto Sprawdzającego ćwiczenie (na adres
pocztowy podany przez Prowadzącego). Na serwerze laboratoryjnym i/albo w Naszej
Witrynie
są dostępne materiały, oprogramowanie i narzędzia do ćwiczeń.
Tylko przesłane wyniki elektroniczne + część papierowa będą oceniane.
Obliczenia ze wzorów
[1-sza godzina zajęć]
A1. Wyznaczyć i narysować
korzystając ze wzoru (2.22)
widmo zespolone (widmo am-
plitudowe oraz fazowe) parzystej fali prostokątnej (D = 50%). Na rysunkach oznaczyć osie u-
kładu współrzędnych oraz charakterystyczne punkty.
Z widma zespolonego wyznaczyć widmo rzeczywiste wg zależności
(2.20) oraz (2.21)
. Na-
rysować to widmo.
A2. Powtórzyć obliczenia i wykresy z p.A1 dla przebiegu prostokątnego o współczynniku
wypełnienia D = 1/3 i D = 2/3. Opisać konstrukcję wykresów.
A3. Wyznaczyć i narysować korzystając ze wzoru (2.24) widmo zespolone (widmo amplitu-
dowe oraz fazowe) przebiegu zegarowego o proporcjach wg
(2.26)
. Na rysunkach oznaczyć
osie, charakterystyczne punkty. Opisać konstrukcje wykresów.
A4. Wyznaczyć i narysować widmo zespolone fali trójkątnej. Skorzystać ze wzorów ogól-
nych, niniejszej instrukcji i/lub literatury. Przedyskutować podobieństwa i różnice z widmem
fali prostokątnej. Jak z widma prostokąta dostać widmo trójkąta ?
Symulacje komputerowe
[2-ga godzina zajęć]
A5. Przeprowadzić symulacje w programie Micro-Cap kolejno sygnałów z punktów
A.1– A.4. Obejrzeć widma tych sygnałów. W razie potrzeby już w trakcie zajęć skorzy-
stać z materiałów pomocniczych na stanowisku pomiarowym i/lub pomocy prowadzące-
go.
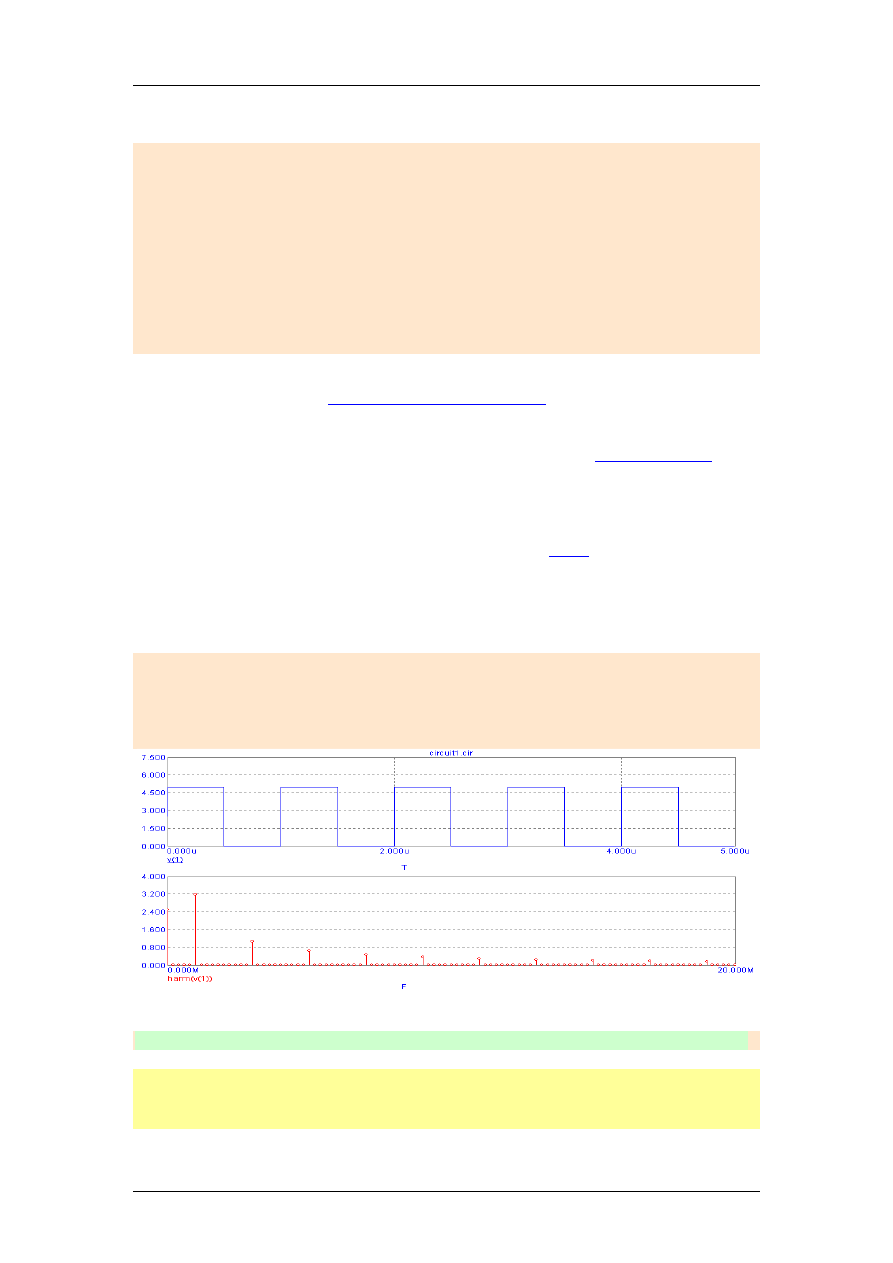
Widmo amplitudowe fali prostokątnej (symulacja Micro-Cap ver.9)
Pomiary widm …
[dwie godziny kolejnych zajęć]
Dalsze wskazówki dotyczące przebiegu zajęć, dokumentacji oraz opraco-
wania wyników podane są w Formatce Sprawozdania (oddzielny doku-
ment) oraz wskazane przez Prowadzącego w trakcie zajęć.

© Marek S. Makowski: W
IDMA SYGNAŁÓW
OKRESOWYCH
Laboratorium Obwodów i Sygnałów (LOiS)
Plik:LOiS_Spectrum_2011.pdf Modyfikacja 2011: M. Makowski, C. Stefański
F
Laboratorium OiS
(sieciowe)
KSEM/626Ea
Wersja 2011
12/12
Tabela pomocnicza
x
wynosi y dB
↕
↕
↕
↕
y
= 20log
10
(x)
x
0
1 (z definicji)
0.5 = 1*1/2
√
√√
√1.13136 ≈≈≈≈ 1.063
1 = 3 - 2
√
√√
√2/1.25 ≈≈≈≈ 1.13136
2 = 20 - 18
10/8 = 1.25
3
√
√√
√2 ≈≈≈≈ 1.4142 (z wiedzy ogólnej)
6 = 3 + 3
√
√√
√2√√√√2 = 2
9
2√
√√
√2 ≈≈≈≈ 2.8284
10 = 9 + 1
2√
√√
√2 *√√√√2/1.25 = 4/1.25 = 3.2
12 = 6 + 6
4 = 2*2
14 = 20 - 6
10/2 = 5
18
2
3
= 8
20
10 (z definicji)
40
100
60
1000
Wyszukiwarka
Podobne podstrony:
LOiS NPorts 2011
LOiS TLine 2011
LOiS Filters 2011
2011 2 KOSZE
higiena dla studentów 2011 dr I Kosinska
Plan pracy na 2011 pps
W 8 Hormony 2010 2011
wm 2011 zad 2
Zawal serca 20 11 2011
PRK 23 10 2011 org
PIW 4z 2011
pmp wykład podmioty 2011 2012
perswazja wykład2 2011 Zasady skutecznej perswazji Petty & Cacioppo
więcej podobnych podstron