
X L V I I I K O N F E R E N C J A N AU K O W A
KOMITETU INŻ YNIERII LĄ DOWEJ I WODNEJ PAN
I KOMITETU NAUKI PZITB
Opole – Krynica
2002
Janusz NICZYJ
1
OPTYMALIZACJA NIEZAWODNOŚ CIOWA PŁ ASKICH
UKŁ ADÓ W KRATOWYCH ZA POMOCĄ ZBIORÓ W ROZMYTCH
1. Wprowadzenie
Teoria zbioró w rozmytych została zainicjowana przez Lotfi Asker Zadeha na początku lat
sześ ć dziesiątych, [1]. Od kiedy Munro w 1979 r. [2] wprowadził koncepcje rozmytoś ci do
optymalizacji konstrukcji wiele prac zostało opublikowanych w zakresie optymalnego
projektowania konstrukcji. Sformułowane programowanie matematyczne można
sklasyfikować na trzy modele: rozmyte programowanie liniowe (FLP), rozmyte
programowanie celu (FGP) i rozmyte programowanie nieliniowe (FNLP).
Mö ller i inni w pracy [3] z 2001 r. przedstawili nową koncepcje bezpieczeństwa konstrukcji
w któ rej nieprecyzyjnoś ć danych wejś ciowych i parametró w modeli przyjmuje się w postaci
rozmytych zmiennych losowych, czy samych zmiennych losowych i rozmytych. Poprzez zmienne
rozmyte zamodelowano rozmytą powierzchnię graniczną stanu. Rozszerzono metode
niezawodnoś ci pierwszego rzędu (First Order Reliability Method - FORM) dlaś rodowiska
rozmytego, proponując rozmytą metodę pierwszego rzędu (Fuzzy First Order Reliability Method –
FFORM) i rozmyty wspó łczynnik niezawodnoś ci. W pracy [4] Royset i inni przedstawili
optymalne projektowanie konstrukcji na bazie niezawodnoś ci. Rozpatrywano trzy problemy
polegające na: minimalizacji początkowych kosztó w projektu i spodziewanych kosztó w awarii,
minimalizacji kosztó w projektu spełniającego ograniczenia projektowe i niezawodnoś ć; i
maksymalizacji niezawodnoś ci przy spełnieniu ograniczeń konstrukcyjnych i związanych z
kosztami. Funkcje celu i/lub zbió r ograniczeń są sprzężone z ogó lnym wspó łczynnikiem
bezpieczeństwa lub prawdopodobieństwem awarii układu lub jego elementó w. Zastosowano
metody pozwalające na rozprzężenie obliczeń związanych z niezawodnoś cią i optymalizacją.
2. Podejmowanie rozmytej decyzji
Yu i Xu w [5] przestawili wielokryterialną rozmytą optymalizacje i trzy metody
podejmowania rozmytej decyzji dla uzyskania optymalnego rozwiązania: metoda przecięć
rozmytych funkcji celu i ograniczeń, wypukła decyzja, iloczyn decyzji.
1
Dr inż., Wydział Budownictwa i Architektury Politechniki Szczecińskiej

142
2.1. Decyzja przecię ć funkcji celu i ograniczeń
Decyzja przecięć funkcji celu ( C
~ ) i ograniczeń ( G~ ) ma postać (nadkreś lenie oznacza
rozmytoś ć danego zbioru):
C
~
G
~
D
~
Ç
=
. W przypadku wielokryterialnej rozmytej
optymalizacji, mamy
I
I
p
j
j
q
k
k
.
C
~
C
~
,
G
~
G
~
1
1
=
=
=
=
(1)
Funkcja przynależnoś ci decyzji ma więc postać
( )
( )
( )
.
μ
μ
μ
~
~
~
þ
ý
ü
î
í
ì
Ù
Ù
þ
ý
ü
î
í
ì
Ù
=
£
£
£
£
x
x
x
p
k
C
p
j
G
q
k
D
1
1
(2)
Decyzja optymalna wybierana jest z rozmytej przestrzeni decyzyjnej D
~ charakteryzowanej
przez funkcje przynależnoś ci
D
~
μ tak by znaleźć optymalny punkt x* któ ry maksymalizuje
D
~
μ , czyli
( )
( )
.
μ
max
μ
~
*
~
x
x
D
R
X
D
n
Î
=
Podstawiając ró wnanie (2) do tej zależnoś ci otrzymujemy
( )
( )
( )
.
μ
,
μ
min
max
μ
~
~
,
*
~
þý
ü
îí
ì
=
Î
x
x
x
j
k
n
C
G
j
k
R
X
D
(3)
Stosując koncepcje wartoś ci progowej
l
i metody poziomó w przecięć C
l
można napisać
ró wnoważne ró wnanie powyższej zależnoś ci w postaci
( )
( )
( )
[ ]
.
,
λ
,
λ
μ
,
λ
μ
λ
max
μ
~
~
*
~
þ
ý
ü
î
í
ì
Î
³
³
=
Î
1
0
x
x
x
jk
k
n
C
G
R
X
D
(4)
Problem rozmytej wielokryterialnej optymalizacji można transformować do problemu
rozwiązania jednokryterialnej nierozmytej optymalizacji, typu;
znaleźć max
D
~
μ (x) =
l
, 0
£
l
£
1
spełniającego ograniczenia
( )
λ
μ
~
³
x
k
G
, k = 1, ... , q
( )
λ
μ
~
³
x
j
C
, j = 1, ... , p. (5)
2.2. Decyzja wypukła
Decyzje wypukłą przedstawiamy w postaci
C
G
D
~
β
~
α
~
+
=
gdzie
a
i
b
są wspó łczynnikami
spełniającymi następujące warunki
a
+
b
=1,
a
³
0,
b
³
0. Dla okreś lonych założeń projektowych
dla funkcji przynależnoś ci elementó w składowych wagi
a
k
i
b
j
są dane i można funkcje
przynależnoś ci decyzji przedstawić w następującej postaci
( )
( )
( )
,
μ
β
μ
α
μ
~
~
~
x
x
x
p
j
C
j
G
q
k
k
D
j
k
å
å
=
=
+
=
1
1
(6)
gdzie
a
k
i
b
j
spełniają warunki
,
β
α
p
j
j
q
k
k
1
1
1
=
+
å
å
=
=
a
k
³
0, k = 1, .. , q
b
j
³
0, j = 1, ... , p. (7)
Problem rozmytej wielokryterialnej optymalizacji można transformować do problemu
rozwiązania jednokryterialnej nierozmytej optymalizacji, typu:

143
znaleźć max
( )
,
~
μ
x
D
spełniającego ograniczenia g
j
(x)
£
C
j
g
, j = 1, ... , m-1
(8)
g
j
(x)
³
C
j
d
, j = m, ... , p.
W metodzie tej decyzja ma charakter ś redniej arytmetycznej w któ rym wagi funkcji celu i
ograniczeń są okreś lane przez decydenta.
2.3. Iloczyn decyzji
Decyzja związana z podejś ciem iloczynowym ma postać
C
G
D
~
~
~
·
=
. Funkcja przynależnoś ci
decyzji ma postać
( )
( )
( )
(
)
p
q
p
j
C
q
k
G
D
x
x
x
j
k
+
=
=
ú
ú
û
ù
ê
ê
ë
é
×
=
Õ
Õ
1
1
1
~
~
~
μ
μ
μ
.
(9)
Problem rozmytej wielokryterialnej optymalizacji można transformować do problemu
rozwiązania jednokryterialnej nierozmytej optymalizacji, typu;
znaleźć max
( )
,
~
μ
x
D
spełniającego ograniczenia g
j
(x)
£
C
j
g
, j = 1, ... , m-1
(10)
g
j
(x)
³
C
j
d
, j = m, ... , p.
W metodzie tej decyzja ma charakter ś redniej geometrycznej.
3. Rozmyte wielokryterialne programowanie liniowe (FMOLP)
Problem wielokryterialnego programowania liniowego (fuzzy multiobjective linear
programming-FMOLP) zawierający rozmyte parametry w funkcjach celu i w ograniczeniach
można przedstawić w postaci [6]
znaleźć max f(x,ã )
@
{f
1
(x,ã
1
), ..., f
k
(x,ã
k
)},
spełniającego ograniczenia x
Î
X(ũ) = { x
Î
R
N
½
g
i
(x,ũ
i
)
å
=
=
n
j
j
ij
x
b
1
£
ũ
i
, (11)
i=1,2,...,m, x
j
³
0, j=1,2,...,n},
gdzie i-ta liniowa funkcja celu ma postać f
i
(x,ã
i
) = (c
i
+ ã
i
c
i
’) x, a obszar dopuszczalny x(ũ)
przyjmujemy jako zbió r zwarty. W ró wnaniach (11) x jest n-wymiarowym wektorem
zmiennych decyzyjnych, ã
i
(i=1,...,k) n-wymiarowe wektory rozmytych parametró w, c
i
i c
i
’
n-wymiarowe wektory i-tej funkcji celu, ũ
i
(i=1,2,...,m) – rozmyte parametry wchodzące w
prawe strony ograniczeń g
i
(x,ũ
i
).
Punkt x*
Î
X(u*) jest rozwiązaniem optymalnym problemu
a
-wielokryterialnego w
sensie
a
-Pareto, wtedy i tylko wtedy gdy nie istnieje inny punkt x
Î
X(u), taki, że f
i
(x,ã )
³
f
i
(x*,a
i
*), i=1,...,k, i nieró wnoś ć ta jest spełniona przynajmniej dla jednego punktu i, dla
któ rego odpowiadające wartoś ci parametró w (a*,u*) nazywamy optymalnymi parametrami
otrzymanymi dla
a
-poziomu.
4. Rozmyte wielokryterialne programowanie nieliniowe (FMONLP)
Głó wne założenia związane z wielokryterialnym programowaniem nieliniowym z rozmytymi
parametrami przedstawił w swej pracy Orlovski [7]. Sakawa i Yano [8] wprowadzili
koncepcje
a
-Pareto optymalnoś ci rozmytego programowania parametrycznego.

144
Hussein i Maaty [9] przedstawiają problem rozmytego wielokryterialnego
programowania nieliniowego (fuzzy multiobjective nonlinear programming-FMONLP)
zawierającego rozmyte parametry w funkcji celu w postaci
znalezienia min f(x,ã )
@
{f
1
(x,ã
1
), ..., f
n
(x,ã
n
)}, (12)
spełniającego ograniczenia x
Î
X = { x
Î
R
n
½
g
i
(x)
£
0, i=1,2,...,m},
gdzie ã
j
= (ã
j1
, ..., ã
jp
), j=1,2, ..., n jest wektorem rozmytych parametró w, któ re mogą być
zdefiniowane przez liczby rozmyte.
Wektor x
*
Î
X będzie efektywnym rozmytym
a
-rozwiązaniem problemu FMNOLP
wtedy i tylko wtedy jeżeli nie istnieje inne x
Î
X takie, że
( )
( )
( )
( )
(
)
( )
Î
³
ïþ
ï
ý
ü
ïî
ï
í
ì
£
<
£
Î
å
=
a
a
m
,
,
,
,...,
,
,
...,
,
,
,
|
*
*
*
1
1
1
~
,
1
n
n
n
n
j
j
j
j
j
a
a
x
f
a
x
f
a
x
f
a
x
f
a
x
f
a
x
f
R
a
n
j
p
j
(13)
5. Rozmyta wielokryterialna optymalizacja niezawodno ściowa
Sformułowanie zagadnienia wielokryterialnej optymalizacji rozmytej polegające na
wyznaczeniu wektora zmiennych decyzyjnych x minimalizującego wektorową funkcje celu
f(x) i spełniającego rozmyte ograniczenia noś noś ci g
j
(x) i niezawodnoś ci konstrukcji,
P
f,s
£
o
f
P
~
można przedstawić w następującej postaci:
znaleźć wektor x = [x
1
, x
2
, ... , x
n
]
T
minimalizujący f(x) = [f
1
(x),..., f
k
(x)]
T
,
(14)
oraz spełniający ograniczenia g
j
(x)
Î
G
~ , j=1, 2, . ., m, oraz P
f,s
£
o
f
P
~
.
gdzie G
~ oznacza zbió r rozmytych ograniczeń projektowych, P
f,s
i
o
f
P
~
, jest odpowiednio
prawdopodobieństwem awarii i dopuszczalnym rozmytym prawdopodobieństwem awarii
konstrukcji. Rozmyty zbió r wszystkich ograniczeń
å
=
=
m
j
j
G
~
G
~
1
,
j
G
~ = { g
j
(x):
j
g
m
(x)>0}, j=1, ..., m (15)
Ograniczenie to oznacza, że g
j
(x) jest elementem zbioru rozmytego
j
G
~ gdy funkcja
przynależnoś ci tego ograniczenia jest większa od zera, czyli
j
g
m
(x)>0.
Rozmyty obszar dopuszczalny jest więc rozpatrywany jako iloczyn (przecięcie) wszystkich
ograniczeń problemu (pkt 2.1.), to znaczy
I
m
j
j
G
~
D
~
=
,
( )
x
D
~
μ
= min {
j
G
~
μ
(g
j
(x))}>0, j=1, ..., m. (16)
Funkcja przynależnoś ci tego zbioru oznacza, że wektor x jest jednym z rozwiązań
dopuszczalnych gdy w minimalnym choć by stopniu spełnia wszystkie przyjęte ograniczenia.
Zbió r rozwiązań dopuszczalnych,
D
R
~
~
Ì
, wyznaczony zgodnie z zasadami
podejmowania decyzji rozmytych, Yu i Xu [5], jest więc przecięciem rozmytych ograniczeń i
rozmytych funkcji celu
ïþ
ï
ý
ü
ïî
ï
í
ì
Ç
ïþ
ï
ý
ü
ïî
ï
í
ì
Ç
ïþ
ï
ý
ü
ïî
ï
í
ì
=
=
=
=
I
I
I
n
l
P
m
j
j
g
k
i
i
f
l
f
R
1
1
1
)
x
(
)
x
(
)
x
(
~
μ
μ
μ
,
,
,
,
(17)

145
Wielkoś ci rozmyte są okreś lone odpowiednio poprzez funkcje przynależnoś ci
m
f
,
m
g
i
m
Pf
.
Rozwiązanie optymalne x
*
wybrane ze zbioru rozwiązań dopuszczalnych cechuje się
największą wartoś cią funkcji przynależnoś ci (3), czyli
R
~
μ (x
*
) =
R
~
x
max
Î
l
j
i
,
,
min {
i
f
m
(x),
j
g
m
(x),
m
Pf,l
(x)},
x
Î
R
~ (18)
Zagadnienie wielokryterialnej optymalizacji rozmytej można zatem przedstawić jako
problem max-min tzn. maksymalizacji minimalnej wartoś ci parametru
l
. Wtedy tradycyjne
programowanie kompromisowe w poró wnaniu z optymalizacją rozmytą z operatorem
decyzyjnym ‘min’ łączącym funkcje celu (18) prowadzi do tych samych wynikó w.
Sformułowanie parametryczne programowania matematycznego ułatwia wprowadzenie
metody
a
-przekrojó w.
a
-przekrojem zbioru rozmytego A
Í
X, oznaczanym przez
a
A
,
nazywamy następujący zbió r nierozmyty
a
A
=
{
}
,
α
)
(
μ
:
³
Î
x
X
x
A
[ ]
1
,
0
Î
"
a
.
Wprowadzenie metody
a
-przekrojó w pozwala sprowadzić rozwiązanie zagadnienia
wielokryterialnej optymalizacji rozmytej do optymalizacji skalarnej nierozmytej z dolnymi i
gó rnymi ograniczeniami brzegowymi i polega na
znalezieniu wektora x
minimalizującego wektorową funkcję celu f(x),
spełniającego ograniczenia g
j,
a
d
(x)
£
g
j,
a
(x)
£
g
j,
a
g
(x), j=1,2,...,m,
i maksymalizującego
a
l
,
przy spełnieniu ograniczeń
α
f
l
μ
(x)
³
a
l
, i=1, ... , k;
j
g
μ
(x)
³
a
l
, j=1, ... , m
α
Pf
l
μ
(x)
³
a
l
, l=1, ... , n (19)
x
d
s
£
x
s
£
x
g
s
a
,
l
a
Î
[0, 1].
Rozwiązanie układu (19), x
l
a
, zależy od
a
okreś lającego poziom osiągnięcia przez rozmyte
wielkoś ci wartoś ci dopuszczalnych oraz od maksymalizowanej wielkoś ci
l
prowadzącej do
ogó lnego rozwiązania kompromisowego uwzględniającego wszystkie rozmyte funkcje celu i
ograniczeń spełnione na poziomie dopuszczalnym
a
.
6. Funkcje przynależności obciążeń , naprę żeń i prawdopodobień stwa awarii
Funkcję przynależnoś ci obciążeń przyjęto w postaci funkcji tró jkątnej, funkcja
przynależnoś ci naprężeń granicznych g
j
=
j
σ~
w poostaci trapezowej [10]. Funkcje
przynależnoś ci funkcji celu oraz dopuszczalnego prawdopodobieństwa awarii, P
f
o
mają
podobne postacie
,
)
(
,
)
(
,
)
(
)
(
,
μ
max
α
,
α
,
max
α
,
α
,
min
α
,
min
α
,
max
α
,
α
,
max
α
,
min
α
,
α
,
α
ï
ï
ï
î
ïï
ï
í
ì
>
£
<
-
-
£
=
i
i
i
i
i
i
i
i
i
i
i
f
f
x
f
dla
f
x
f
f
dla
f
f
x
f
f
f
x
f
dla
i
0
1
ï
ï
ï
î
ï
ï
ï
í
ì
>
£
<
-
-
£
=
g
α
,
f
α
,
f
g
α
,
f
α
,
f
d
α
,
f
d
α
,
f
g
α
,
f
α
,
f
g
α
,
f
d
α
,
f
α
,
f
α
P
P
)
(
P
dla
,
P
)
(
P
P
dla
,
P
P
)
(
P
P
P
)
(
P
dla
,
μ
f
x
x
x
x
0
1
(20)
gdzie:
)
(
f
),
(
f
max
α
,
i
min
α
,
i
x
x
- są odpowiednio najlepszą i najgorszą wartoś cią funkcji celu, a
)
(
P
),
(
P
g
α
,
f
d
α
,
f
x
x
- dolną i gó rną wartoś cią prawdopodobieństwa awarii; wielkoś ci te są
ograniczeniami w rozważanej rozmytej optymalizacji na poziomie
a
.

146
7. Funkcje celu
Jako funkcje celu przyjęto minimalną masę konstrukcji i minimalne przemieszczenie węzła
obciążonego siłą, mianowicie:
α
,
f
1
(x) =
r
s
n
=
å
1
x
s
l
s,
å
=
×
=
=
n
s
s
g
α
g
α
,
s
s
α
),
(
α
,
x
E
)
P
(
N
N
w
)
(
f
1
6
2
x
l
s
, (21)
gdzie: x
s
, l
s
, N
s
oznaczają odpowiednio: przekró j, długoś ć i siłę w s-tym elemencie natomiast
P
g
a
i P
d
a
są odpowiednio gó rną i dolną wartoś cią obciążenia na poziomie
a
.
Ograniczenia naprężeń osiowych w elementach rozciąganych oraz ś ciskanych przy
uwzględnieniu wyboczenia prętó w można wyrazić wzorem:
g
( )
( )
g
α
.
j
α
,
j
α
,
j
σ
σ
£
=
x
x
, g
( )
( )
2
2
j
j
α
,
j
α
,
j
l
x
β
E
π
σ
-
£
=
x
x
, (22)
gdzie I=
b
x
j
2
opisuje zależnoś ć pomiędzy momentem bezwładnoś ci i polem przekroju
poprzecznego pręta, przy stałej wartoś ci
b
ró wnej 0,45.
8. Analiza niezawodności kratownic
W analizie niezawodnoś ci konstrukcji składających się z n elementó w przyjęto, że układ traci
swoje własnoś ci użytkowe gdy staje się mechanizmem. Przyjęto, że układ składa się z
elementó w mających własnoś ci sprężysto-plastyczne. Konstrukcje kratowe są układami
składającymi się z wielu elementó w, a więc ich niezawodnoś ć jest funkcją niezawodnoś ci
elementó w. Przyjęto, że każdy element ma ten sam stopień ważnoś ci i to samo dopuszczalne
prawdopodobieństwo awarii. Margines bezpieczeństwa dla k-tej postaci zniszczenia można
przedstawić w następujący sposó b
( )
å
=
-
=
=
I
i
α
α
i
e
i
α
i
α
k
P
x
R
c
M
g
1
x
,
k = 1, ... , K (23)
gdzie: c
i
a
- stała obliczeniowa, R
i
e
– wytrzymałoś ć obliczeniowa elementu, P
a
- obciążenie
zewnętrzne, I – liczba elementó w, któ rych uszkodzenie doprowadza do k-tej postaci
zniszczenia. Natomiast prawdopodobieństwo awarii konstrukcji w przypadku k-tej postaci
zniszczenia można przedstawić następująco:
P
k
a
= P(M
k
a
<0),
k = 1, ... , K
(24)
W pracy rozważano tylko te postacie zniszczenia, któ re dominują przy tworzeniu się
mechanizmu. W ogó lnym przypadku istnieje korelacja pomiędzy postaciami awarii i trudno
jest uzyskać rozwiązanie z powyższego ró wnania. Dlatego też często oblicza się gó rną i
dolną granicę P
f
wykorzystując zależnoś ci podane przez Ditlevsena
(
)
(
)
(
)
(
)
(
)
,
,
max
,
max
α
α
α
α
α
α
α
α
ï
ï
ï
î
ïï
ï
í
ì
<
Ç
<
-
<
£
÷
÷
ø
ö
ç
ç
è
æ
ïþ
ï
ý
ü
ïî
ï
í
ì
<
Ç
<
-
<
+
<
³
®
å
å
å
å
=
= <
+
=
-
=
K
i
j
i
K
i
i
j
i
K
i
i
i
j
j
i
i
i
f
M
M
P
M
P
M
M
P
M
P
M
P
P
1
1
1
1
1
0
0
0
0
0
0
0
0
(25)
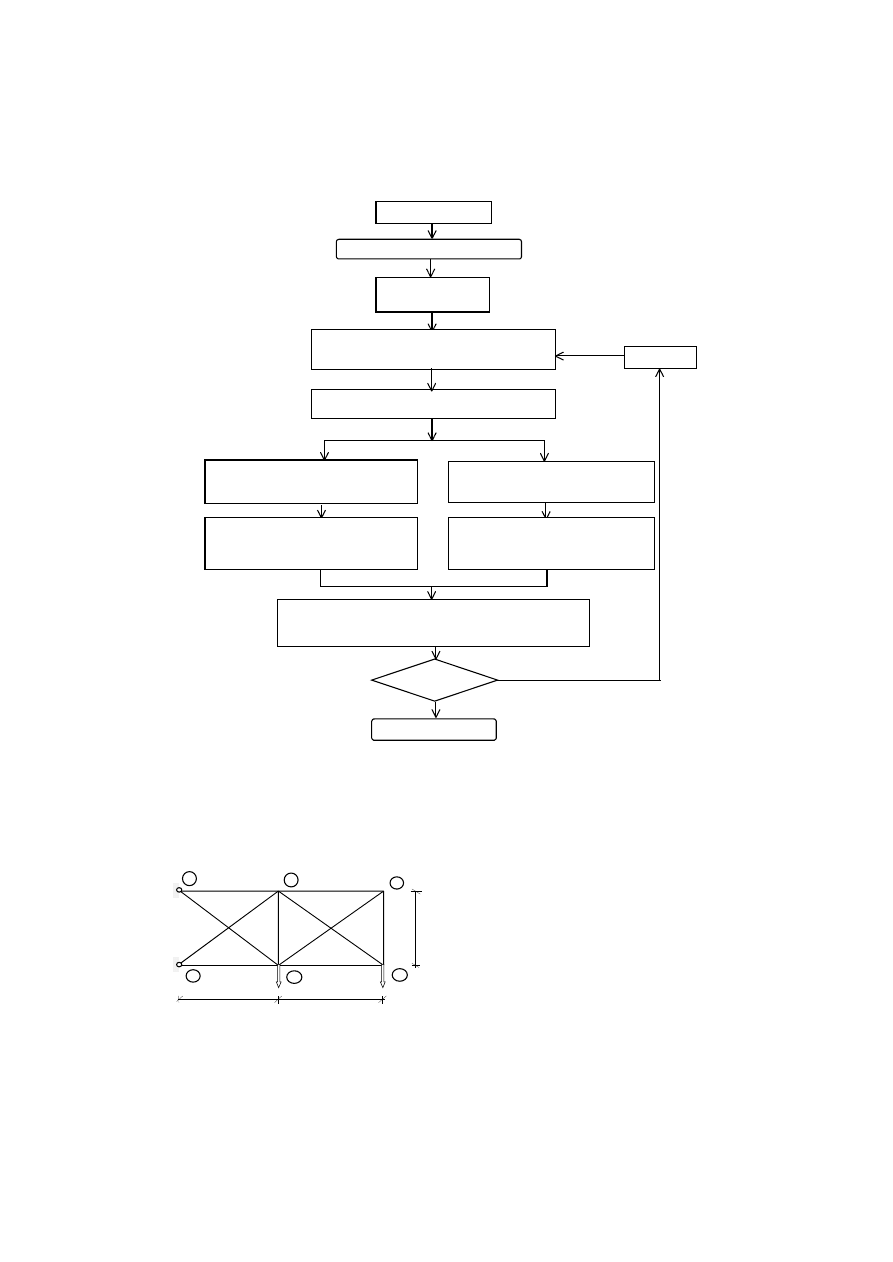
147
Rys. 1. Schemat optymalzacji niezawodnoś ciowej układu
9. Przykład optymalizacji i niezawodności kratownicy
Rozpatrzono przykład optymalizacji płaskiej aluminiowej kratownicy 10-prętowej (rys.2),
module sprężystoś ci E = 6.895E3 kN/cm
2
, i
długoś ci L = 914.4 cm. Rozmycie obciążenia
przyjęto w granicach 10 % w stosunku do
wartoś ci ś cisłej P
1
=P
2
=444.52 kN. Jako
zmienne decyzyjne przyjęto pola przekrojó w
poprzecznych prętó w zmieniających się w
przedziale x
d
s
=0.254cm
2
£
x
s
£
x
g
s
=101.6cm
2
.
Funkcje celu okreś lone są wzorami (21).
Dopuszczalne prawdopodobieństwo awarii
konstrukcji P
o
f
=1.0E-4. W przypadku
ograniczenia związanego z naprężeniami
L
P
2
P
1
2
3
1
6
7
8
9
10
4
5
L
L
3
4
5
6
1
2
Rys.2
Obliczenie max
l
k
a
z ograniczeniami
l
k
a
£
( )
k
x
P
f
α
μ
,
l
k
a
£
( )
k
x
f
i
α
μ
Wektor zmiennych decyzyjnych - x
k
DANE WEJŚ CIOWE
START
Inicjalizacja
x
o
,
a
,
k=0
Wyznaczenie sił w prętach z uwzlędnieniem
ograniczeń na napręż enia (22)
Obliczenie prawdopodobień stwa
awarii P
f,
a
(x
k
) - (24), (25)
Obliczenie funkcji celu
f
1,
a
(x
k
), f
2,
a
(x
k
) - (21)
Obliczenie funkcji przynależ noś ci
( )
k
x
P
f
α
μ
- (20)
Obliczenie funkcji przynależ noś ci
( )
k
x
f
i
α
μ
- (20)
l
k
a
<
l
k-
1
a
STOP
Tak
Nie
x
k+1
=
x
k

148
przyjęto 20 % ró żnicę w stosunku do wartoś ci granicznej. Marginesy bezpieczeństwa (23)
dla czterech ś cieżek zniszczenia przedstawiono w tab.1.
Tablica 1. Marginesy bezpieczeństwa dla czterech ś cieżek zniszczenia
Ścieżki
zniszczenia
M
k
a
<0
1
+
-7
+*
[0.512 R
1
x
1
a
-(P
1,
a
+P
2,
a
)]<0
Ç
[0.236 R
7
x
7
a
+0.333 R
1
x
1
a
-(P
1,
a
+P
2,
a
)]<0
10
-
-9
+
[1.763 R
10
x
10
a
-(P
1,
a
+P
2,
a
)]<0
Ç
[0.707 R
9
x
9
a
+0.706 R
1
x
1
a
-(P
1,
a
+P
2,
a
)]<0
3
-
-7
+
[0.488 R
1
x
1
a
-(P
1,
a
+P
2,
a
)]<0
Ç
[0.707 R
7
x
7
a
+R
1
x
1
a
-(P
1,
a
+P
2,
a
)]<0
7
+
-8
-
[0.676 R
1
x
1
a
-(P
1,
a
+P
2,
a
)]<0
Ç
[0.354 R
7
x
7
a
+0.353 R
1
x
1
a
-(P
1,
a
+P
2,
a
)]<0
*)
(+) i (–) oznaczają odpowiednio siły rozciągające i ś ciskające w elementach
Literatura
[1] ZADEH L.A., Fuzzy sets. Information Control, 8, 1965, pp.338-353.
[2] MUNRO J., Uncertainty and fuzziness in engineering decision-making, In: Proc. First
Canadian Seminar on Systems Theory for Civil Engineering, Calgary, 1979, pp.113-133.
[3] MÖ LLER B., GRAF W., BEER M., SICKERT J.-U., Fuzzy probabilistic method and its
application for the safety assessment of structures, 2
nd
European Conference on
Computational Mechanics, ECCM-2001, Cracow, Poland, 2001, Proc. on CD-Rom, 1-20.
[4] ROYSET J.O., Der KIUREGHIAN A., POLAK E., Reliability-based optimal structural
design by the decoupling approach, Reliability Engineering and System Safety, 2001,
Vol.73, pp.213-221.
[5] YU M., XU G., Multiobjective fuzzy optimization of structures based on generalized
fuzzy decision-making, Computers and Structures, 1994, Vol.53, No.2, pp.411 -417.
[6] SAAD O.M., Stability on multiobjective linear programming problems with fuzzy
parameters, Fuzzy Sets and Systems, 1995, Vol.74, pp.207-215.
[7] ORLOVSKI S., Multiobjective programming problems with fuzzy parameters, Control
Cybernetics, 1984, Vol.13, pp.175-183.
[8] SAKAWA M., YANO H., Interactive decision making for multiobjective nonlinear
programming with fuzzy parameters, Fuzzy Sets and Systems, 1989, Vol29, pp.315-326.
[9] HUSSEIN M.L., MAATY M.A.A., The stability notions for fuzzy nonlinear
programming problem, Fuzzy Sets and Systems, 1997, Vol.85, pp.319-323.
[10] NICZYJ J., Optymalne i niezawodne projektowanie kratownic z zastosowaniem zbioró w
rozmytych, XL Konf. Naukowa KILiW PAN i KN PZITB, Krynica, 1999, T.1, s.127-134.
RELIABILITY-BASED OPTIMIZATION OF PLANE TRUSSES
BY FUZZY SETS
Summary
In this paper an optimum design procedure for minimizing structural mass and vertical
deflections of loaded joint subject to reliability constraints is discussed. The fuzzy
optimization technique based on the principle of intersection of fuzzy decision used for the
multiobjective fuzzy optimization of trusses. The
a
-cut approach and
l
-formulation are used
to express the optimization in a parametric form.
Wyszukiwarka
Podobne podstrony:
Optymalizacja niezawodnościowa płaskich układów kratowych za pomocą zbiorów rozmytych
Optymalizacja niezawodnościowa płaskich układów kratowych za pomocą zbiorów rozmytych
Metoda projektowania układów regulacji za pomocą linii pierwiastkowych
MODELOWANIE UKŁADÓW KOMBINACYJNYCH ZA POMOCĄ FUNKTORÓW LOGICZNYCH
MODELOWANIE UKŁADÓW KOMBINACYJNYCH ZA POMOCĄ FUNKTORÓW LOGICZNYCH SCHEMAT
Metoda projektowania układów regulacji za pomocą linii pierwiastkowych
SYMULACJA PRACY UKŁADÓW FIZYCZNYCH ZA POMOCĄ PAKIETU
pomiaru temperatury za pomocą czujników i układów elektronicznyc
sciaga rozwiazywanie ukladow rownan liniowych za pomoca wzorow cramera, Matematyka
pomiaru temperatury za pomocą czujników i układów elektronicznyc
Czy rekrutacja pracowników za pomocą Internetu jest
Leczenie za pomocą MIBG
Instrukcja do ćw 06 Sterowanie pracą silnika indukcyjnego za pomocą falownika
Badanie za pomocą ankiety, Psychologia
Dziwny obiekt w okolicy Słońca uchwycony za pomocą koronagrafu SOHO, W ஜ DZIEJE ZIEMI I ŚWIATA, ●txt
więcej podobnych podstron