32

O

d samego początku należy podkreślić, że prowadzo-
ne poniżej rozważania mają charakter teoretyczny

i nie naruszają zasad stosowanego w praktyce wymiaro-
wania konstrukcji mostowych, a to przynajmniej z dwóch
powodów.
Po pierwsze, zawsze dążymy do uzyskania pełnego połą-
czenia pomiędzy składowymi elementami, jakimi są beto-
nowa płyta i stalowa belka. Projektowanie dźwigarów ze-
spolonych z podatnym zespoleniem nie jest celowe. Przy
czym przez podatne zespolenie rozumie się tu podatny
sposób połączenia zupełnie odmienny od wytworzonego
poprzez zastosowanie tzw. łączników wiotkich. Podczas
wymiarowania zaprojektowana liczba łączników wiotkich
zapewnia pełne, sztywne połączenie pomiędzy płytą
a belką. Dopiero w przypadku zaistnienia błędu, tj. wtedy
gdy liczba łączników byłaby mniejsza od normowych
wymogów, powstałoby połączenie podatne. Tak więc
na ogół nie należy kojarzyć łączników wiotkich z rozważa-
nym tu połączeniem podatnym. Nie jest to niezbędne, ale
dla porządku należy też dodać, że efektywność dźwigara
mostowego w jego sensie użytkowym jest najwyższa przy
pełnym, tj. sztywnym połączeniu.
Po drugie, stan podatnego połączenia występuje rzadko
i może wynikać ze zmęczenia materiału stref kotwienia
wokół łączników, co jest w praktyce inżynierii mostowej
równoważne z osiągnięciem bądź przekroczeniem stanu
granicznego nośności elementu, uznawanym za sytu-
ację awaryjną, a co za tym idzie – wymagającą szybkiej
naprawy lub co najmniej ograniczenia obciążeń danego
elementu.
Wykazawszy rzadkość wystąpienia stanu podatnego
połączenia, dodajmy, że istnieją nieuwzględniane podczas
normowego wymiarowania zapasy nośności złącza
pomiędzy elementami poprzez pominięcie np. sił adhezji
betonu ze stalą czy nawet po ścięciu łączącej warstwy
adhezyjnej znacznych sił tarcia wynikających z ciężaru
płyty betonowej.
Wobec tylu rezerw i przemyślanych działań rodzi się
pytanie, dlaczego podejmowany jest temat łączników
podatnych? Odpowiedź jest trywialna. Nawet wtedy gdy
stosujemy sprawdzone rozwiązania, interesuje nas ich
zrozumienie, które, jeśli zaistnieje, zazwyczaj jest stoso-
wane również w dziedzinach pokrewnych. Tak też było
w przypadku rozpoznania laboratoryjnego mechanizmu
połączenia podatnego i stworzenia jego teoretycznego
obrazu, który następnie został zastosowany do projekto-
wania współczesnych elementów zespolonych, nazywa-
nych powszechnie kompozytami.
W artykule zawarto przegląd literatury pod kątem po-
szukiwania pierwszych sformułowań po to, by uzupełnić
lukę w polskich publikacjach, w których pewne formuły
problemu pojawiają się znikąd.

Przegląd bibliografi czny

Jak wiadomo, pierwsze publikacje z dziedziny dźwiga-
rów zespolonych pochodzą z końca XIX w., a ich autora-
mi są inżynierowie austriaccy, niemieccy i francuscy (1).

Dla polskich inżynierów podstawową pracą była mono-
grafi a K. Sattlera (1). Dziś, po latach, czytając tę „biblię”,
możemy odczuć rozczarowanie, a nawet zażenowanie
jej stylem, językiem i metodami analizy, tym niemniej
przez autorów polskich prac pozycja ta jest traktowana
jako podstawowa. Skądinąd wiadomo, że książka jest
bardzo trudno dostępna, a odnaleziony przez autora
niniejszego artykułu egzemplarz w bibliotece Poli-
techniki Śląskiej zawierał fi szkę z niewieloma wpisami.
W okresie badań cech dźwigarów zespolonych stal-be-
ton podejmowano problemy pełnego zespolenia w ten
czy inny sposób, zawsze jednak zgodnie z klasycznym
założeniem Bernoulli-Naviera o zachowaniu płaskiego
przekroju poprzecznego belki zespolonej, poczynając
od konfi guracji początkowej poprzez aktualne, praktycz-
nie aż do wytrzymałości materiałów belki defi niowanej
w różny sposób.
W latach 40. XX w. odnotowujemy już prace dotyczące
połączenia podatnego. Pełne opracowanie teoretyczne
znajdujemy w monografi i Rżanicyna (2). O wiele później-
sza książka tego autora (3) jest podsumowaniem głównie
prac teoretycznych autora i innych autorów radzieckich,
przy czym Rżanicyn nie ograniczył się do wąskiej dzie-
dziny belek mostowych, jest nawet odwrotnie – nie
ma mowy o mostach. W książce znajdujemy rozwiąza-
nia analityczne belek i płyt wielowarstwowych, w tym
w granicznym przypadku belek dwuelementowych.
Rozpatrywane są połączenia sztywne i podatne sprężyste,
ale także lepko-sprężyste. Omówiono w sposób szczegó-
łowy wszystkie technicznie możliwe, ale także statycznie
dopuszczalne warunki brzegowe końców belek. W po-
łączeniach podatnych uwzględniono w powierzchni
styku, dalej nazywanej interfejsem, poślizg (slip) i pionowe
rozsunięcie elementów (up lift). Do kompletu problemów
inżynierskich rozpatrzonych w tej książce należy dodać,
że w monografi i znajdziemy także rozwiązania stabilności,
drgań, belki, płyty na podłożach reologicznych. Bogactwo
i kompletność mechaniki struktur wielowarstwowych
jest odwrotnie proporcjonalne do popularności książki
w Polsce. Praca jest niemal niecytowana. Sympatycznym
wyjątkiem jest jej przywołanie przez prof. Kubika w jego
monografi i dotyczącej mechaniki płyt warstwowych.
W pracach (2, 3) znajdziemy wzory opisujące krzywiznę
i zależności na siły normalne w elementach belki zespolo-
nej podatnie, przy czym krzywizna jest tu dana w sposób
uwikłany, będąc stanem pośrednim pomiędzy graniczny-
mi przypadkami zespolenia, tj. wariant całkowitego braku
współpracy w interfejsie oraz wariant pełnego zespolenia.
Przejdźmy teraz do drugiej kluczowej pozycji w zakresie
podatnego połączenia – jest to praca Newmarka, Siessa
i Viesta (4). O ile w monografi ach Rżanicyna znajdujemy
jedynie teorie mechaniki, to (4) jest artykułem zawierają-
cym opis przeprowadzonych badań laboratoryjnych belek
mostowych z łącznikami prętowymi z główkami w ska-
lach 1:1 oraz 1:2, analizę wyników eksperymentalnych,
propozycję standardowego stanowiska badawczego
oraz teorię wymiarowania wraz z przykładem rachunków

Sztywność na zginanie
dźwigara zespolonego
podatnie typu stal-beton

Sławomir Karaś

Katedra Dróg i Mostów, Politechnika Lubelska

Sztywność
na zginanie belki
zespolonej typu
stal-beton nie
została w litera-
turze przedmiotu
dostatecznie
przedyskuto-
wana. Stosując
teorię translacji
osi zerowych
odkształceń
elementów
składowych
belki, przed-
stawiono dwa
możliwe warianty
sztywności
na zginanie.
Analiza na pozio-
mie odkształceń
umożliwia
zastosowanie
wyników tak
w zakresie
sprężystym, jak
i plastycznym.
W artykule
dokonano
także przeglądu
podstawowych
prac z zakresu
rozważanego
przedmiotu.

m o s t y

m a t e r i a ł y i t e c h n o l o g i e

33

do belki swobodnie podpartej obciążonej siłą skupioną.
W artykule czytamy także, że zamieszczona w nim teoria
powstała w roku 1943, co jest dla nas ważne w kontekście
poszukiwania pierwszych rozwiązań.
Rozwinięcie koncepcji Newmarka znajdziemy w artyku-
le Seracino, Oehlers i Yeo (5), w którym wprowadzono
współczynnik zwiększający (Magnifying Factor – MF)
do wyznaczania krzywizny belki w przypadku podatnego
zespolenia. Tę samą metodykę znajdujemy w pracy (6),
przy czym tu załączono obliczenia w przypadku belki
ciągłej. Seracino i Oehlers wprowadzili także pojęcie
punktów ogniskowych połączenia podatnego (Par-
tial-Interaction Focal Points – PIFP). Punkty ogniskowe
powstają na wykresie linii dystrybucji odkształceń belki
zespolonej w miejscach przecięć w wariantach braku ze-
spolenia i pełnego zespolenia. Dodatkowo czytamy tam,
że Seracino udowodnił w swej pracy doktorskiej, że punk-
ty ogniskowe są niezależne od formy i siły połączenia
w interfejsie, przy czym dowód obejmuje przypadek
założeń wprowadzonych przez Newmarka.
Jako kolejny fragment przeglądu literaturowego przywo-
łajmy artykuły (7, 8), w których wprowadzono koncepcję
opisu mechanizmu belki zespolonej poprzez wprowa-
dzenie translacji osi zerowych odkształceń elementów
składowych belki zespolonej. To ujęcie generuje geome-
tryczne miary podatności nie tylko interfejsu, ale także
stref zakotwienia łączników w łączonych elementach,
dodatkowo stwarza możliwość wyznaczenia sztywności
giętej przekroju belki w funkcji geometrycznych miar po-
datności. Przywoływana teoria, podobnie jak u Rżanicyna
i Newmarka, dotyczy belki Bernoulliego i obejmuje proste
związki wytrzymałości materiałów. W końcowej części
artykułu zamieszczono oszacowanie sztywności belki
zespolonej wg tej koncepcji.
Współczesne możliwości zastosowania procedur kom-
puterowych umożliwiają analizy numeryczne bardziej
złożonych modeli konstrukcji. Jako przykłady można
podać analizę sprężystą problemu brzegowo-początko-
wego belki Timoshenko (9) i płyty (10), przy czym – jak się
wydaje – są to przypadki nazbyt zaawansowane nume-
rycznie, by mogły mieć zastosowanie w zagadnieniach
inżynierskich wymiarowania belek mostowych.
Eksperymentalne wyznaczenie wielkości poślizgu i unie-
sienia pionowego w interfejsie jest problemem złożonym
i technicznie trudnym ze względu na małe wartości tych
deformacji. W artykule (4) podano wartość poślizgu jako
równą ~2E-4 m, a w (11) dla belki swobodnie podpartej
o rozpiętości 10 m wartość poślizgu pomierzono jako
równą 4,5E-4 m, tu także wyznaczono proporcję krzywizn
w wariantach podatnego połączenia i sztywnego o wy-
miarze 690/610 = 1,13.

Bardzo ważnym artykułem z punktu widzenia teo-
rii translacji zerowych osi odkształceń jest praca (12),
w której poza poślizgiem pomierzono także pochylenia
przekrojów poprzecznych elementów składowych belki
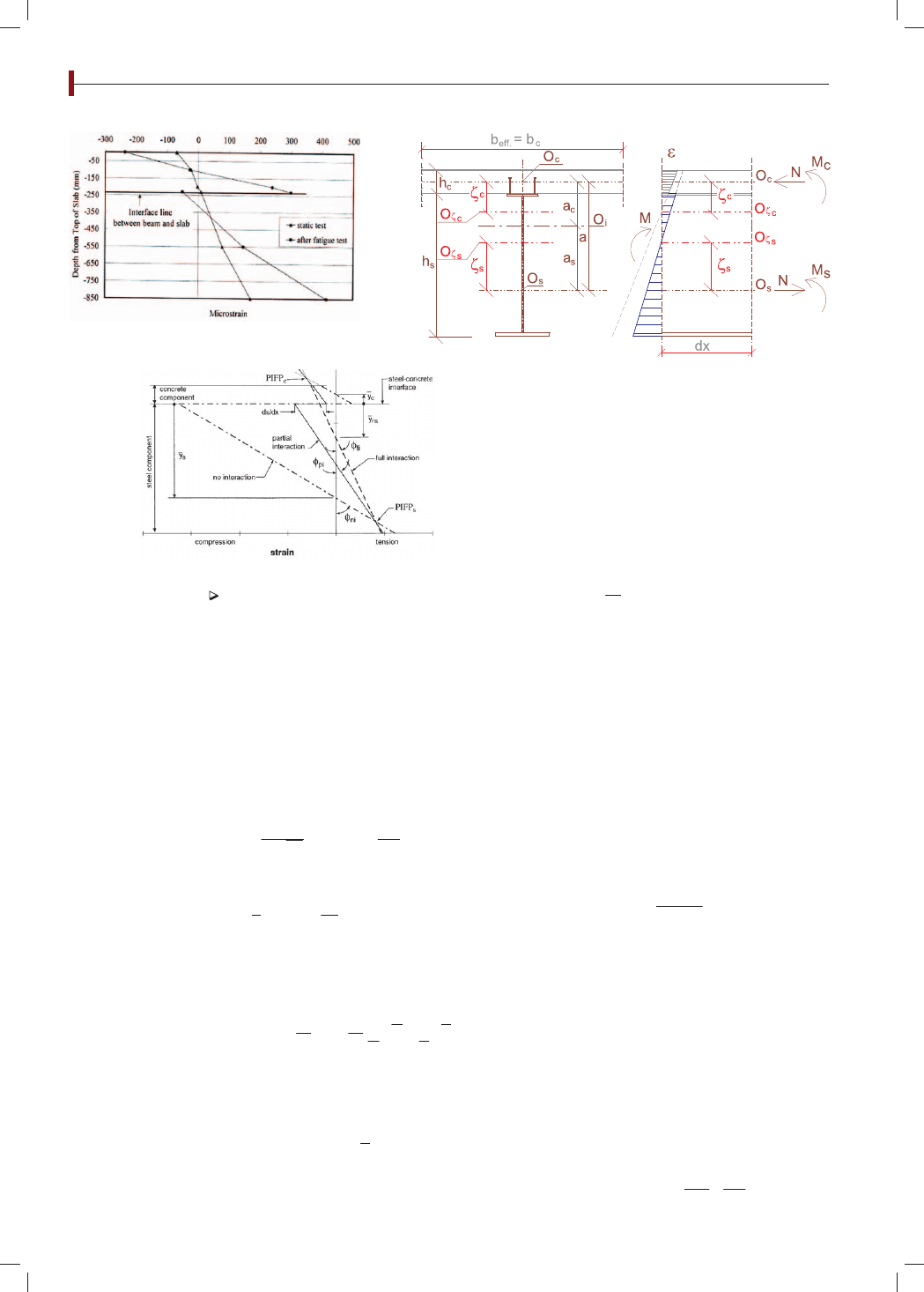
zespolonej. Z zamieszczonej reprodukcji na rys. 1 wynika,

że pochylenia te nie są równoległe, co jest odejściem
od teorii Rżanicyna-Newmarka (R-N), a co odpowiada
założeniom w pracach (7, 8).
Przegląd problematyki z zakresu połączenia podatnego
w dźwigarach zespolonych znajdziemy w monografi ach
(13, 14).
Na zakończenie odnotujmy, że w Eurokodzie 4 w punkcie
1.5.2.1 znajdujemy warunek uwzględniania wpływu pośli-
zgu w interfejsie do podstawowych oszacowań.

Podstawy teorii

belek zespolonych

z połączeniem podatnym

Na użytek przedstawienia problemu wprowadźmy zało-
żenia i oznaczenia stosowane w dalszych rozważaniach.
Rozpatrujemy belkę zespoloną typu stal-beton przedsta-
wioną na rys. 2. Uwzględniamy poślizg w interfejsie, pomi-
jając rozsunięcie elementów. Zagadnienie jest sprężyste.
Stosujemy oznaczenia:
– O

c

, O

s

, O

i

– środki mas i poziome osie przez nie przecho-

dzące odpowiednio w przypadku elementu betonowe-
go, stalowego oraz dźwigara zespolonego,

– E

c

A

c

= EA

c

, E

s

A

s

= EA

s

– sztywności na ściskanie-rozciąga-

nie elementów betonowego i stalowego,

– EA – podwojona średnia harmoniczna

EA

c

i EA

s

,

– E

c

J

c

=

EJ

c

, E

s

J

s

= EJ

s

, E

s

J

i

= EJ

i

– sztywności gięte elemen-

tów betonowego, stalowego oraz dźwigara zespolone-
go, słuszne są także poniższe relacje,

– ∑EJ = EJ

c

+ EJ

s

, EJ

i

= ∑EJ + a

2

EA,

– 

c

, 

s

– oznaczają dodatnie miary translacji (przesunięć)

zerowych linii odkształceń elementów betonowego
i stalowego,

– ε

c

, ε

s

, ε

c

, ε

s

– są to odpowiednio odkształcenia w betonie

i stali oraz w interfejsie w betonie i stali,

– γ = u

c

– u

s

– poślizg w interfejsie jako różnica przemiesz-

czeń w betonie i w stali,

– ρ

c

, ρ

s

– promienie krzywizn w osiach przechodzących

przez środki mas przekrojów poprzecznych odpowied-
nio elementu betonowego i stalowego,

– inne stosowane oznaczenia są typowe i przez to oczy-

wiste w zakresie problemu.

W obu podstawowych pracach (3, 4), tj. teorii R-N, zasto-
sowano postulat Bernoulli-Naviera, co oznacza, że po-
czątkowo płaska powierzchnia przekroju poprzecznego
pozostanie płaska po deformacji oraz że pochylenia
powierzchni elementów składowych płyty betonowej
i belki stalowej są jednakowe (zwróćmy uwagę, że to zało-
żenie nie ma zastosowania w przypadku belki pokazanej
na rys. 2, na którym widać wyraźnie różnicę pochyleń
powierzchni elementów składowych). Konsekwencją zało-
żeń R-N jest wyrażenie:

EJ

Na

M

EJ

M

1

EJ

M

1

s

s

s

c

c

c

6

¸¸

¹

·

¨¨

©

§

U

¸¸

¹

·

¨¨

©

§

U

[1]

34

które można nazwać warunkiem równości krzywizn ele-
mentów składowych, przy czym ściśle mamy tu równość
krzywizn osi elementów składowych. Równania równo-
wagi zagadnienia płaskiego prowadzą nas do związku:

M = M

c

+ M

s

+ Na

[2]

jednakże [2] pokrywa się w całości z [1] i nie jest istotne.
Siłę osiową N znajdujemy z rozwiązania równania róż-
niczkowego rzędu drugiego (tutaj o stałych współczynni-
kach):

M

N

N

2

//

'

O

,

[3]

gdzie

.

const

EA

EJ

EJ

k

i

2

6

O

,

.

const

EJ

a

k

6

'

,

.

const

k

przy czym mamy tu uwzględnione następujące relacje
pomiędzy wielkościami statycznymi i deformacjami:

–

k

W

J

– jeśli

/

N

dx

dN

W

jest liniowym rozkładem siły ścinającej w interfejsie,

a k = const. jest charakterystyką (modułem) połączenia-
podatności,

– gęstość liniowa poślizgu jest proporcjonalna do różnicy

odkształceń elementów składowych w interfejsie

s

c

s

c

/

u

u

dx

d

dx

d

H

H

J

J

Rozwiązanie równania [3] można przedstawić w formie:

x

f

0

N

x

f

0

N

d

f

x

M

x

N

/

/

x

0

T

T

T

'

³

[4]
jeśli

x

sh

1

x

f

O

O

. [4.1]

Alternatywnie, jak to jest w przypadku belek, równanie [3]
można zastąpić formą o rzędzie wyższym o dwa (2):

q

N

N

//

2

'

O

IV

[5]

gdzie q jest rozkładem obciążenia wzdłuż osi belki. W tym
przypadku rozwiązanie znajdujemy w formie:

x

0

N

0

N

d

g

x

q

x

N

/

x

0

T

T

T

'

³

x

g

0

N

x

g

0

N

///

/

//

,

[6]

gdy

x

x

sh

1

x

g

3

O

O

O

.

[6.1]

Nadmieńmy, że postacie [4] i [6] rozwiązań różnią się
nieznacznie od podanych w (3) z racji zastosowania
rachunku operatorowego, a dokładniej transformacji Car-
sona-Laplace’a jako metody rozwiązania, przy czym takie
formy czytelnie uwzględniają warunki brzegowe proble-
mu. W (3) rozwiązanie równania [3] uzyskano, stosując
warunek minimum zagadnienia Euler-Poissona na pracę
sił wewnętrznych wieloelementowej belki zespolonej.
W przypadku zmienności charakterystyki podatności
k wzdłuż osi belki równanie różniczkowe będzie klasyfi ko-
wane inaczej, tj. jako równanie o zmiennych współczyn-
nikach. Kilka przykładów różnych zmienności rozwiązał
Jasim (15, 16). Warianty różnych zmienności geometrii
przekroju poprzecznego belki zespolonej omówiono
w (3).
Ugięcie belki zespolonej tak u Newmarka (4), jak i u Rżani-
cyna (3) wyznaczono z równania na krzywiznę ze wzoru:

EJ

Na

M

y

//

6

[7]

Patrząc na wzór [7], widać, że w rzeczywistości sztywność
na zginanie w klasycznym rozumieniu tego terminu nie
jest uwzględniona. W przypadku podatnego zespolenia
spodziewamy się, że sztywność na zginanie jest wartością
pośrednią pomiędzy sztywnością przy pełnym połącze-
niu EJ

i

, a sztywnością przy braku połączenia pomiędzy

elementami składowymi ∑EJ. Równanie [7] jest wyrazem
poszukiwania ugięcia belki zespolonej podatnie za pomo-
cą zastępczego schematu składającego się z belki dwu-
elementowej bez interakcji w interfejsie przy obciążeniu
zredukowanym (M-Na) zamiast rzeczywistego obciążenia
o wartości M. W (2) Rżanicyn analizował alternatywne
równanie powstałe przez połączenie równań [4] i [7] i po
kilku elementarnych przekształceniach doprowadzone
do następującej postaci:

2

i

//

2

//

EJ

M

EJ

M

y

y

O

6

O

IV

[8]

Rys. 1. Rozkład odkształceń.
Źródło: (12), za zgodą Ch-S. Shim

Rys. 3. Zmienność odkształceń.
Źródło: (4) w uzgodnieniu z R. Seracino

Rys. 2. Teowy dźwigar zespolony z połączeniem podatnym

m o s t y

m a t e r i a ł y i t e c h n o l o g i e

35

Postać [8] jest wyrazem powyższej dyskusji. Taką samą formę
znajdujemy w zupełnie współczesnym podręczniku (14).
Rozwiązanie równania [8] można podać następująco:

d

g

EJ

1

g

EJ

x

M

x

y

//

i

2

x

0

T

»

»

¼

º

«

«

¬

ª

T

6

T

O

T

³

>

@

x

g

0

T

x

g

0

M

EJ

1

/

6

x

g

0

y

x

g

0

y

x

0

y

0

y

///

/

//

/

[9]

Finalizując dyskusję nad teorią R-N (3, 4), wykorzystajmy
względną miarę różnic pomiędzy wynikami teoretyczny-
mi i eksperymentalnymi podanymi w (4) w tablicy 3. Błąd
wynosił tylko 2-7%! Można zatem powiedzieć – to działa!,
ale z drugiej strony kilka wątpliwości w zakresie formuło-
wania teorii dalej pozostaje.
Modyfi kacją teorii R-N są prace Seracino, Oehlersa i innych
(5, 6). Pomimo że punkty ogniskowe (PIFP) są widoczne
na rysunkach w pracy Newmarka (4), to dopiero w (5) zo-
stały one zdefi niowane i wykorzystane jako narzędzie
analityczne (rys. 4). Ponieważ konsekwentnie stosowane
są założenia metody R-N, to także na rys. 3 widać rów-
noległość linii przekrojów poprzecznych w wariantach
podatnego połączenia i braku współpracy pomiędzy ele-
mentami, co wynika z przyjęcia, że krzywizny elementów
składowych są sobie równe.

Seracino wykazał, że dla dowolnego połączenia podat-
nego elementów składowych linie rozkładu odkształceń
będą przechodzić przez punkty ogniskowe (PIFP). Kolejną
innowacją w (5) było wprowadzenie współczynnika
zwiększającego krzywiznę (MF) belki zespolonej z ele-
mentami połączonymi w sposób pełny tak, by uzyskiwać
krzywiznę odpowiadającą belce zespolonej z połącze-
niem podatnym. Współczynnik MF zdefi niowano nastę-
pująco:

//

.

fi

//

.

pi

y

y

MF

(w artykule (4) mamy

MF

y

y

//

.

fi

//

.

pi

) [10]

gdzie

i

//

.

fi

EJ

M

y

.

//

.

pi

y

znajdujemy przez całkowanie równania

EJ

a

k

M

y

/

///

.

pi

6

J

[10.1]

będącego wersją warunków [4] lub [7]. Na pierwszy rzut
oka wprowadzony współczynnik MF nie wnosi nic nowe-
go, jednakże trzeba dodać, że autorzy wprowadzają jed-
nocześnie interesującą uproszczoną metodę wyznaczania
MF, co dowartościowuje całość postępowania. Podano
tam sekwencję kroków uwzględniającą MF, przy ustalo-
nych dla danego przekroju punktach ogniskowych (PIFP),
prowadzącą do wyznaczenia rozkładów odkształceń
i naprężeń.

Wprowadzone udoskonalenia metody R-N nie odpowia-
dają na pytanie, jaka jest sztywność dźwigara zespolone-
go z łącznikami podatnymi. W artykułach (5, 6) stosowane
są założenia teorii R-N, co w konsekwencji powoduje,
że deformacje są liczone przy sztywnościach wyrażonych
równorzędnie charakterystykami statycznymi i geome-
trycznymi wikłającymi gdzieś w swych związkach sztyw-
ność na zginanie.
W polskich publikacjach, pomimo że mostowymi dźwi-
garami zespolonymi różnego typu zajmowało się wielu
autorów, z trudem znajdujemy oryginalne koncepcje
z zakresu teorii połączeń podatnych. Na ogół są to prze-
niesienia na tzw. grunt polski rezultatów zagranicznych.
Pierwszą istotną informację tego typu znajdujemy
w eleganckiej w sensie technicznym pracy, minimono-
grafi i prof. H. Czudka (17). Tam autor podał rozwiązania
zagadnień brzegowych belki zespolonej na podstawie
cytowanych prac radzieckiego uczonego N.N. Strieleckije-
go (18, 19). Monografi a Strieleckijego (18) została wydana
12 lat później po pracy Rżanicyna (2), co w konsekwencji
niniejszych rozważań przesuwa ją w cień za Rżanicynem,
choć trzeba dodać, że zawiera kilka oryginalnych i cie-
kawych elementów. W latach 50. XX w. stosowano taki
rodzaj zapisu, w którym w zakresie ustalonego zwyczaju
we wzorach stosowano oznaczenia wielkości w sensie
integralnym (skończone) z wielkościami nieskończe-
nie małymi. Tak jest w pracach Rżanicyna, Newmarka
i Strieleckijego, a co za tym idzie również w pracy Czudka.
W najpopularniejszej obecnie polskiej monografi i napi-
sanej przez K. Furtaka (20) zamieszczono rysunki z (17)
i przepisano wzory. Kilka lat upłynęło i można by się zapy-
tać, dlaczego przy kolejnych wznowieniach wzory te nie
uległy korekcie, poprzez zastosowanie precyzyjnego
współczesnego zapisu w relacjach różniczkowych? Spra-
wiłoby to nie tylko łatwość czytania, ale również oddaliło
wątpliwości co do błędności wyrażeń.
Oryginalność podejścia odnajdujemy w pracy Machelskie-
go i Toczkiewicza (21), w której autorzy rozpatrują dźwigar
zespolony z połączeniem podatnym, na zupełnie innej
drodze niż zaprezentowana w (7, 8) otrzymano jedną
z miar podatności wynikającą z analiz w (7).

Metoda translacji

zerowych osi odkształceń

łączonych elementów

Tak jak już wzmiankowano wcześniej, teoria R-N nale-
ży do teorii uproszczonych, przy czym najsilniejszym
założeniem jest równość krzywizn łączonych elementów.
Stosując znany wzór z wytrzymałości materiałów, mamy

EJ

/

M

y

1

//

|

U

. Przedyskutujmy wprowadzone

założenie, posiłkując się rys. 4, przy czym 4a pokazuje dwa
niepołączone elementy dźwigara zespolonego z wryso-
wanymi jednakowymi krzywiznami, a 4b obrazuje te same
dwa elementy składowe w wariancie pełnego połączenia
w interfejsie, tj. o równych krzywiznach włókien dolnych
betonu i włókien górnych stali.

Piśmiennictwo
1. Sattler K.: Theorie der Ver-

bundkonstruktionen. Ernst
u. Sohn, Berlin 1953.

2. Ржаницын А.Р.: Теориа со-

ставных стержней стро-
ителных конструкций.
Стройиздат 1948.

3. Ржаницын А.Р.: Состав-

ные стержни и пластинкн.
Стройиздат 1986.

4. Newmark N.M., Siess C.P.,

Viest I.M.: Tests analysis
of composite beams with in-
complete interaction. Proc.
Soc. Experimental Stress
Analysis, 9/1951.

5. Seracino R., Oehlers D.J.,

Yeo M.F.: Partial-interaction
fl exural stresses in compo-
site steel and concrete bridge
beams. Engineering Struc-
tures 2001; 23:1186-93.

6. Seracino R., Chow T. Lee,

Tze C. Lim, Jwo Y. Lim:
Partial interaction stresses
in continuous composite
beams under serviceability
loads. „Journal of Construc-
tional Steel Research” ,
2004, 1525-1543.

7. Карась С.: Новый метод

расчета составных балок.
Дороги i Мости, випуск 8,
Kiev 2008.

8. Karaś S.: The new concept

of composite girder elastic-
ity analysis. VIII Konferenc-
ja naukowa „Konstrukcje
zespolone”, Zielona Góra
2008.

9. Berczyński S., Wróblewski T.:

Vibration of Steel-Concrete
Composite Beams. Using the
Timoshenko Beam Model.
Journal of Vibration and
Control, 11: 829-848, 2005.

36

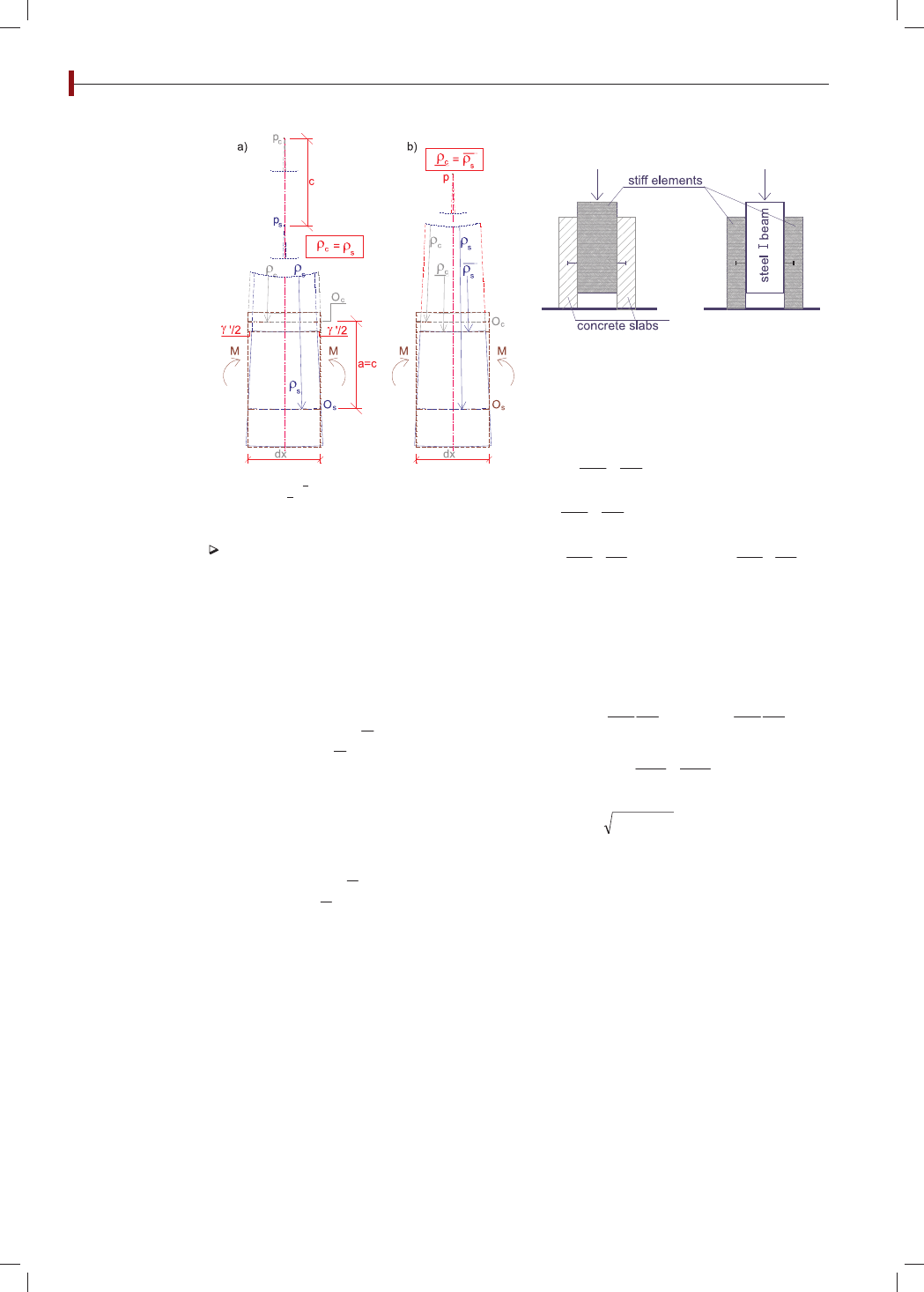
Z rys. 4a widać, że poślizg w interfejsie występuje od sa-
mego początku, jeśli jest słuszne założenie o równości
krzywizn osi środków mas elementów, tj. gdy:

1

s

1

c

U

U

[i]

co oznacza, że takie założenie jest dalekie od rzeczywiste-
go pełnego połączenia w interfejsie. Chcąc skorygować
ten błąd, należy w miejsce (i) wprowadzić opis odpowia-
dający stanowi z rysunku 4b w następującej postaci:

1

s

1

c

a

U

U

[ii]

lub alternatywnie:

s

c

U

|

U

[11]

ale w tym przypadku odchodzimy od założenia [i].
W sensie stricte teoretycznym założenie stosowane tak
przy pełnym połączeniu, jak i w połączeniu podatnym
w interfejsie jest znacznie słabsze niż warunek [11]. W tym
miejscu wprowadźmy inne założenie w miejsce [1], kładąc
w wariancie pełnego połączenia zgodność odkształceń
w interfejsie:

s

c

H

H

[12]

W rzeczywistości warunek [12] odpowiada sytuacji z ry-
sunku 4b, co więcej, to założenie odpowiada warunkowi
zgodności odkształceń. Przyjmując tę koncepcję, przejdź-
my do rozpatrzenia podatnego połączenia pokazanego
na rys. 1. Wprowadzamy następujące rozumowanie: osie
zerowych odkształceń elementów belki zespolonej ule-
gają przesunięciu – translacji – z ich pozycji wyjściowych
w wariancie braku połączenia do ich aktualnego stanu
w wariancie połączenia podatnego, przy czym granicz-
nym położeniem jest pokrycie się tych osi w wariancie
pełnego połączenia w miejscu odpowiadającym osi mas
dźwigara zespolonego.
W konsekwencji tego założenia wprowadzono na rys. 1.
oznaczenia 

c

i 

s

(22) oznaczające translacje odpowiednio

osi zerowych odkształceń odpowiednio płyty betonowej
i belki stalowej. Teraz możemy także przyjąć, że 

c

i 

s

są geometrycznymi miarami podatności stref zakotwień
łączników w sąsiedztwie interfejsu odpowiednio w betonie
i stali.

W sensie rachunkowym dysponujemy dwoma warunka-
mi defi niującymi dwie osie zerowych odkształceń oraz
trzecim warunkiem równowagi:

o

]

H

c

c

c

c

c

c

y

EJ

M

EA

N

0

c

H

0

EJ

M

EA

N

c

c

c

c

]

,

[13]

o

]

H

s

s

s

s

s

s

y

EJ

M

EA

N

0

EJ

M

EA

N

s

s

s

s

0

s

]

H

[14]

oraz

N

a

M

M

M

s

c

, [2]

przy czym y

c

, y

s

są rzędnymi lokalnych układów kartezjań-

skich o początkach na przesuniętych osiach 

c

i 

s

. Korzy-

stając z [2, 13, 14], wyznaczamy niewiadome problemu
w formie:

c

c

c

c

EJ

EA

N

M

]

,

s

s

s

s

EJ

EA

N

M

]

,

1

s

2

s

c

2

c

i

i

a

M

N

»

»
¼

º

«

«
¬

ª

]

]

[15-17]

gdzie

.

.

.

EA

/

EJ

i

.

[17.1]

Zestawiając teorię R-N z prezentowaną tutaj, spostrzega-
my, że warunek [3] znika. Ugięcie i sztywność na zginanie
są teraz funkcjami dystrybucji wprowadzonych miar
geometrycznych podatności 

c

(x), 

s

(x). W konsekwencji

warunków [13, 14] odchodzimy także od sztucznego za-
łożenia o zgodności pochyleń przekrojów poprzecznych
elementów składowych, co jest krokiem w stronę sytuacji
bardziej ogólnej niż przypadek ich zgodności.
Wprowadzone przez Seracino-Oehlersa punkty ognisko-
we mogą posłużyć z dobrym przybliżeniem do wyzna-
czenia pochyleń przekrojów poprzecznych elementów
składowych belki zespolonej, co pokazano w materiale
konferencyjnym (8). Także w tej pracy przedstawiono
funkcyjną zależność siły normalnej N od M, 

c

, 

s

, które

mogą być stałe lub zmienne wzdłuż osi dźwigara zespolo-
nego w zakresach wyrażonych odpowiednio jako:

c

c

a

0

d

]

d

and

s

s

a

0

d

]

d

, [18]

dodatkowo, w przypadku elementów: płyta betonowa
– belka stalowa, ograniczenia te interpretujemy następu-
jąco:
– 

(.)

= a

(.)

– wariant pełnej współpracy jednej ze stref ma-

teriałowych,

10. Sapountzakis E.J.: Dynamic

analysis of composite steel-
concrete structures with
deformable connection.
Computers and Structures
82 (2004), 717-729.

11. Leon R.T., Viest I.M.: Theo-

ries of incomplete interac-
tion in composite beams.
Proceedings Composite
Construction in Steel and
Concrete III, Irsee, Germa-
ny, 9-14 June 1996, 858-
70.

12. Shim Ch-S., Lee P., Chang S.:

Designing of shear connec-
tion in composite steel and
concrete bridges with pre-
cast decks. „Journal of Con-
structional Steel Research”,
57, 2001.

13. Johnson R.P.: Composite

structures of steel and con-
crete. Blackwell Pub., Third
Ed., 2004.

14. Oehlers D.J., Bradford M.A.:

Elementary behavior
of composite steel & con-
crete structural members.
Butterworth-Heinemann,
1999, Oxford GB.

15. Jasim N.A.: Defl ections

of partially composite
beams with linear con-
nector density. „Journal
of Constructional Steel
Research” 49 (1999),
241-254.

16. Jasim N.A.: Computation

of defl ections for continu-
ous composite beams with
partial interaction. Proc In-
stn Civ Engrs Structs and
Bldgs 1997;122:347-54.

Rys. 5. Propozycja stanowiska laboratoryjnego do wyznaczania podatności stref kotwienia
łączników w betonowej płycie i belce stalowej

Rys. 4. Wyłączne zginanie: a) brak połączenia ρ

c

= ρ

s

,

b) pełne połączenie ρ

c

= ρ

s

m o s t y

m a t e r i a ł y i t e c h n o l o g i e

37

– 

(.)

= 0 – przypadek braku współdziałania odpowiedniej

strefy materiałowej,

– przy 

c

= 0 oraz 

s

= 0 – brak zespolenia,

– jeśli 

c

= a

c

i 

s

= a

s

– pełne zespolenie.

Porównując przesunięcia 

c

, 

s

z modułem połączenia

k stosowanym w pracy Newmarka i innych, moduł należy
rozdzielić na dwa elementy składowe odpowiadające
strefom zakotwień łączników w betonie i stali wg wzoru

s

c

k

1

k

1

k

1

,

, [19]

przy czym, jeśli k = ∞, to mamy pełne połączenia, a przy
k = 0 występuje brak połączenia pomiędzy elementami
składowymi. Związek pomiędzy k

c

, k

s

i 

c

, 

s

ma postać

liniową. Konsekwencja rozdzielania modułu k jest pro-
pozycją modyfi kacji testu wprowadzonego w pracy (4),
poprzez objęcie badaniem podatności zakotwienia łącz-
ników w jednym i drugim elemencie dźwigara zespolone-
go, co pokazano na rys. 5.

Sztywność na zginanie

dźwigara z podatnym

zespoleniem

Sztywność elementu na zginanie, rozciąganie, skręca-
nie itd. jest jego cechą materiałowo-geometryczną.
Stąd do wyznaczenia tej cechy stosujemy iloczyn cha-
rakterystyki geometrycznej przekroju elementu przez
cechę odkształcalności, najczęściej nazywaną modu-
łem. Ponownie przypomnijmy, że w teorii R-N oraz jej
modyfikacjach nie występuje stricte sztywność na zgi-
nanie dźwigara zespolonego. W koncepcji związanej
z translacją zerowych osi odkształceń taka możliwość
istnieje. Stosując konsekwentnie twierdzenie Ste-
inera (7), można wyznaczyć moment bezwładności
względem osi O

i

- O

i

(rys. 1), przy czym jest to oś środ-

ków masy elementów składowych belki w wariancie
pełnego zespolenia. Niestety nie jest to banalne
zadanie, a to dlatego, że przy całej dyscyplinie wyzna-
czania momentu bezwładności i stosowania reguły
Steinera możliwe są dwie opcje, różniące się stopniem



c

, 

s

. Przypadek pierwszy daje nam rezultat liniowy

względem 

c

, 

s

, podczas gdy drugi zawiera translacje

w kwadratach w takich oto postaciach:

s

s

s

c

c

c

I

i

a

EA

a

EA

EJ

EJ

]

]

6

,

[20]

oraz:

2

s

s

2

c

c

II

i

EA

EA

EJ

EJ

]

]

6

[21]

Obie postacie spełniają przejścia graniczne odpowiednio
do wariantu pełnego zespolenia i braku zespolenia.

Porównajmy dwie postacie momentów bezwładności

I

i

EJ

(20) oraz

II

i

EJ

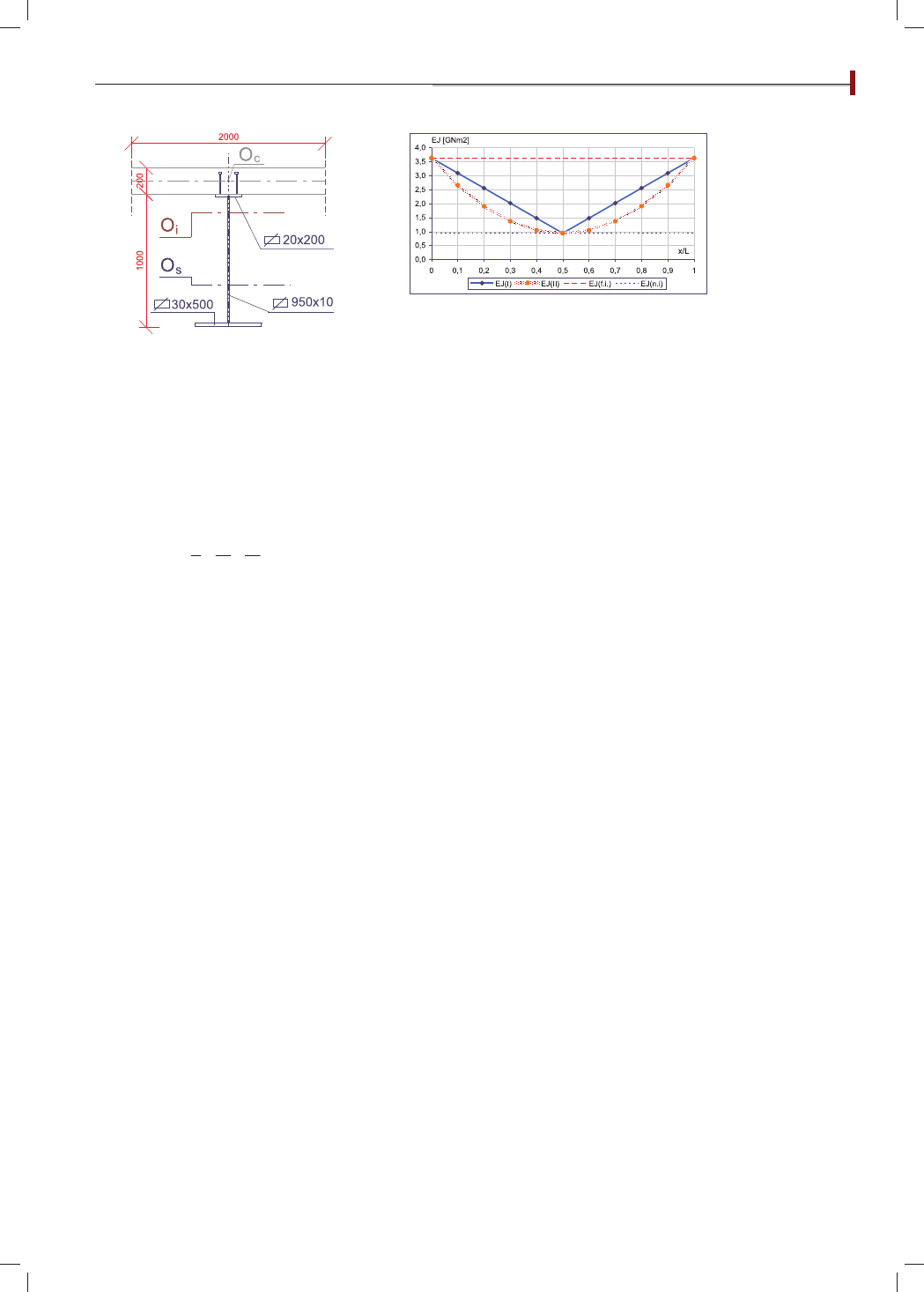
(21) w przypadku typowego dźwi-

gara mostowego, którego wymiary przekroju poprzeczne-
go pokazano na rys. 6.

Wprowadzamy parametry bezwymiarowe:
μ

c

= 

c

/a

c

oraz μ

s

= 

s

/a

s

, przy czym 0 ≤ μ

c

= μ

s

≤ 1 [22-23]

Przyjęto często stosowany rozstaw łączników w belkach
swobodnie podpartych – przy podporach zagęszczony,
w środku belki – bez łączników. Pomiędzy skrajem belki
a jej osią następuje liniowa zmienność gęstości łączników,
co odpowiada interpretacji, że na skrajach belki mamy
pełne zespolenie, a w jej środku brak zespolenia. Przyj-
mując E=E

s

, znajdujemy w przypadku pełnego zespole-

nia EJ

i

= 3,625 GNm

2

, a w osi przy braku zespolenia jest

∑EJ = 0,942 GNm

2

. Na rys. 7 przedstawiono zmienność

sztywności na zginanie. Widoczne są liniowa i kwadrato-
wa forma dystrybucji sztywności wzdłuż osi belki, odpo-
wiednio wg wzorów [20, 21].
Na dzień dzisiejszy brak jest kryterium wskazującego
na przypadek [20] czy [21]. Konieczne są dalsze analizy
oraz adekwatne badania laboratoryjne. Jest przy tym
oczywiste, że wyrażenie [21] jest bezpieczniejsze w sensie
projektowym.

Podsumowanie

Przedstawiona tu koncepcja opisu dźwigara zespolo-
nego była publikowana w wielu miejscach podczas
konferencji poświęconych konstrukcjom zespolonym
w Zielonej Górze (2008 r.), Krakowie (2009 r.), Pilani
(2009 r.), przy czym istotna krytyka miała miejsce w Kijo-
wie (2008 r.), gdzie podczas ostrej dyskusji uznano prawi-
dłowość proponowanego podejścia i w konsekwencji
treść doniesienia konferencyjnego została opublikowa-
na (7) z recenzją prof. Diektiara – doktoranta Rżanicyna.
Tym niemniej odczuwalny jest niedostatek dyskusji
zaprezentowanego problemu i może niniejszy artykuł
wypełni te lukę, co jest życzeniem autora.
Najważniejszym elementem zaprezentowanej koncepcji
jest odejście od założenia o równości krzywizn, które
ogranicza rozpatrywania do przypadku równoległości
kątów pochyleń przekrojów poprzecznych łączonych
elementów w dźwigarze zespolonym.
Kolejnym atutem, poza możliwością wprowadzenia mo-
mentu bezwładności przekroju poprzecznego dźwigara
z połączeniem podatnym, jest poziom prowadzonej ana-
lizy w zakresie odkształceń. Z praktyki żelbetu, ale także
mostowych dźwigarów zespolonych wynika, że odkształ-
cenia mają dystrybucję liniową aż do zniszczenia dźwiga-
ra, przy czym dystrybucja naprężeń może być nieliniowa.
Zatem udało się osiągnąć poziom analizy liniowej przy
dalszych otwartych możliwościach z zakresu rozkładów
naprężeń.
Na zakończenie przywołajmy początkowe stwierdzenie
– podatność w interfejsie w dźwigarach mostowych jest
niepożądana.



Rys. 6. Dźwigar zespolony (mm)

Rys. 7. Zmienność sztywności na zginanie

17. Czudek H.: Konstrukcje

zespolone w mostownic-
twie metalowym. WPW,
11/1969.

18. Strieleckij N.N.: Issledo-

vanie robory i rascziot
na procznost mostowych
objedinionnych balok.
WNIITS, 1960.

19. Strieleckij N.N.: Stale że-

laznobetonnyje mosty.
„Transport”, Moskwa 1965.

20. Furtak K.: Mosty zespolone.

PWN, 1999.

21. Szmygin B.: Semiotyka

w analizie zabytków archi-
tektury. Teka Komisji Urba-
nistyki i Architektury PAN,
t. XXVIII, Kraków, 1996.

22. Machelski Cz., Toczkie-

wicz R.: Podatność połą-
czenia stalowego dźwigara
z płytą betonową w mo-
stach zespolonych. „Drogi
i Mosty” 3/2005.