Odpowiedzi do ćwiczenia Extremum

..................................

..................................

ENERG.11/...........................

imię i nazwisko

numer zestawu

grupa

Zad 1

x

i

y

i

S

(a, b) = ...........................................................................

∂S

∂a

= .............................................

∂S

∂b

= .............................................

∂

2

S

∂a

2

= ..............................

∂

2

S

∂b∂a

= ..............................

∂

2

S

∂a∂b

= ..............................

∂

2

S

∂b

2

= ..............................

Rozwiązaniem układu

∂S

∂a

=

∂S

∂b

= 0 jest a = ..............., b = ................

Ponieważ wartość wyróżnika D(a, b) =

∂

2

S

∂a

2

∂

2

S

∂b∂a

∂

2

S

∂a∂b

∂

2

S

∂b

2

= ............... jest ...............,

więc extremum ...............

Ponieważ wartość

∂

2

S

∂a

2

= ............... jest ..............., więc ekstremum jest ...............

Otrzymujemy prostą regresji ..............................

Sprawdzenie na kalkulatorze statystycznym:

r

= ..............., A = ..............., B = ................

Szkic prostej regresji na tle punktów:

y

0

5

10

15

x

0

2

4

6

8

10

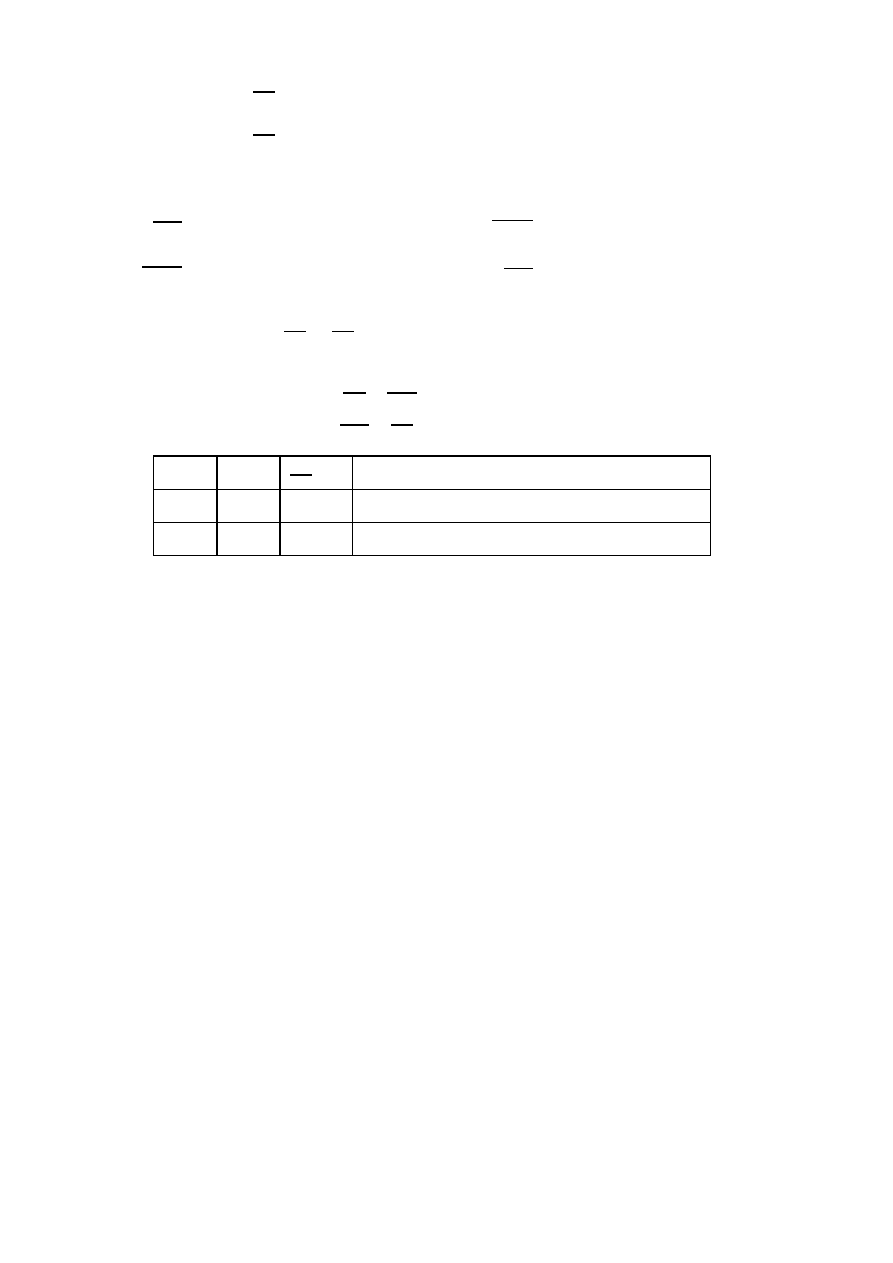
Zad 2

f

(x, y) = ...........................................................................

∂f
∂x

= ............................................................

∂f

∂y

= ............................................................

∂

2

f

∂x

2

= ..............................

∂

2

f

∂x∂y

= ..............................

∂

2

f

∂y∂x

= ..............................

∂

2

f

∂y

2

= ..............................

Rozwiązaniem układu

∂f
∂x

=

∂f

∂y

= 0 są punkty

P

1

= (..............., ...............) oraz P

2

= (..............., ...............).

Wyróżnik wynosi D(x, y) =

∂

2

f

∂x

2

∂

2

f

∂y∂x

∂

2

f

∂x∂y

∂

2

f

∂y

2

= ..............................

punkt

D

(P

i

)

∂

2

f

∂x

2

(P

i

)

wniosek

P

1

P

2