2013-05-30
1
Zasada Huygensa
(czyt. Hojhensa)
Omówione wcześniej zjawiska można obserwować, ale
czy można je przewidywać?
Zasadę która to umożliwia sformułował holenderski fizyk,
matematyk i astronom, Christian Huygens (1629-
1695). Uzasadnia ona poprzednie wnioski dotyczące
rozchodzenia się fal.
Zasada ta określa sposób konstrukcji czoła fali w chwili
późniejszej na podstawie znajomości czoła fali w chwili
wcześniejszej przy dodatkowym założeniu, że wiemy w
którą stronę czoło fali się przesuwa.
22
Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/
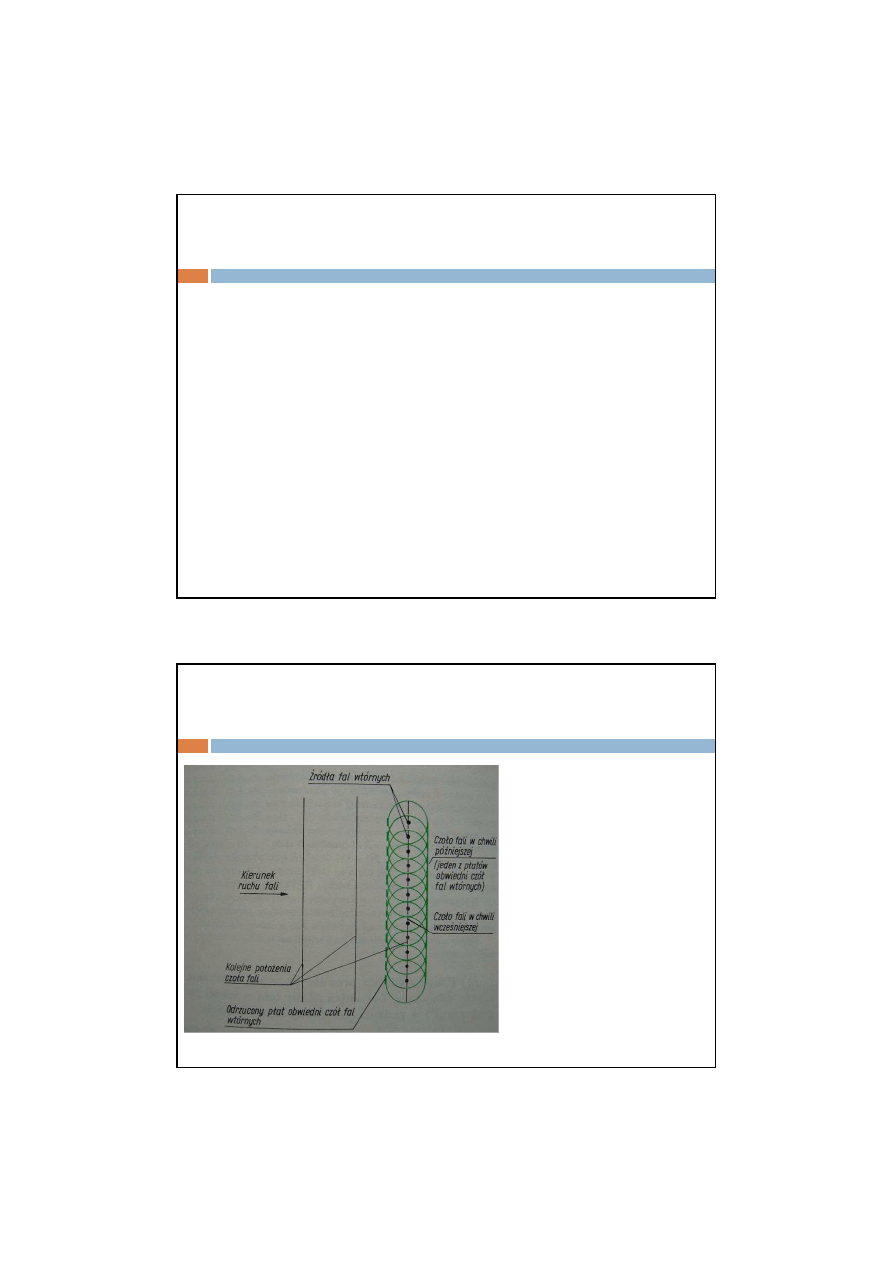
Zasada Huygensa
Czoło fali w chwili
późniejszej można
zbudować przyjmując,
że każdy punkt
ośrodka, do którego
dotarło czoło fali w
chwili wcześniejszej jest
źródłem kulistej fali
wtórnej o tej samej
częstości jak fala
pierwotna.
Obwiednia czół fal
wtórnych jest szukanym
czołem fali w chwili
późniejszej.
23
Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/
2013-05-30
2
Zasada Huygensa - wnioski
1.
Czoło fali w chwili późniejszej jest płaszczyzną
równoległą do czoła fali w chwili wcześniejszej.
Jest to równoważne temu, że promień fali jest linią
prostą.
24
Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/
Zasada Huygensa - wnioski
2.
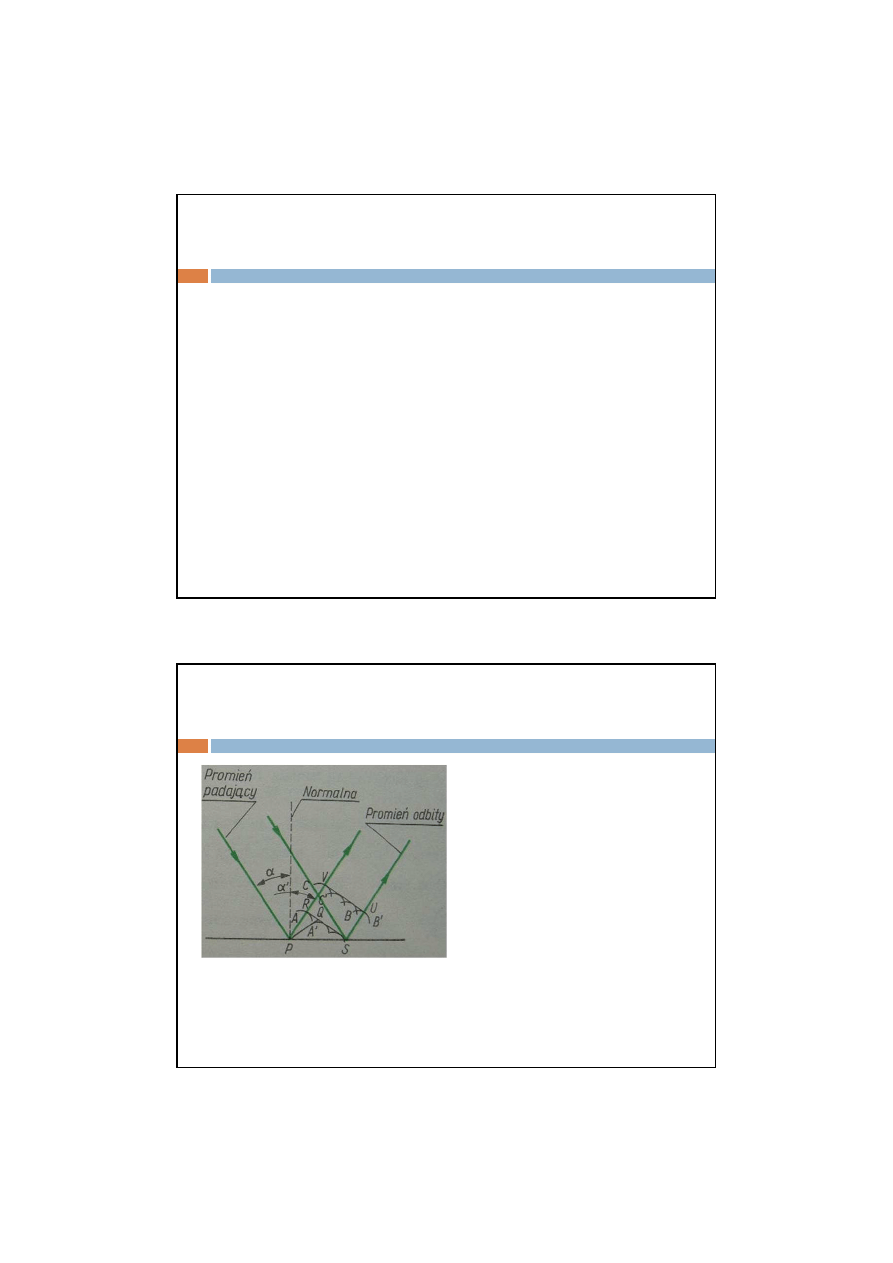
Podczas odbicia promień
padający, normalna do
płaszczyzny odbijającej i
promień odbity leżą w
jednej płaszczyźnie, przy
czym kąt padania jest
równy katowi odbicia.
PQ – czoło fali padającej w chwili, gdy punkt
P dochodzi do powierzchni odbijającej. Punkt
Q w tym czasie zmierza do punktu S. Łuk AA’
zakreślony z punktu P promieniem PR=QS
przedstawia czoło fali wtórnej z punktu P.
25
Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/
2013-05-30
3
Zasada Huygensa - wnioski
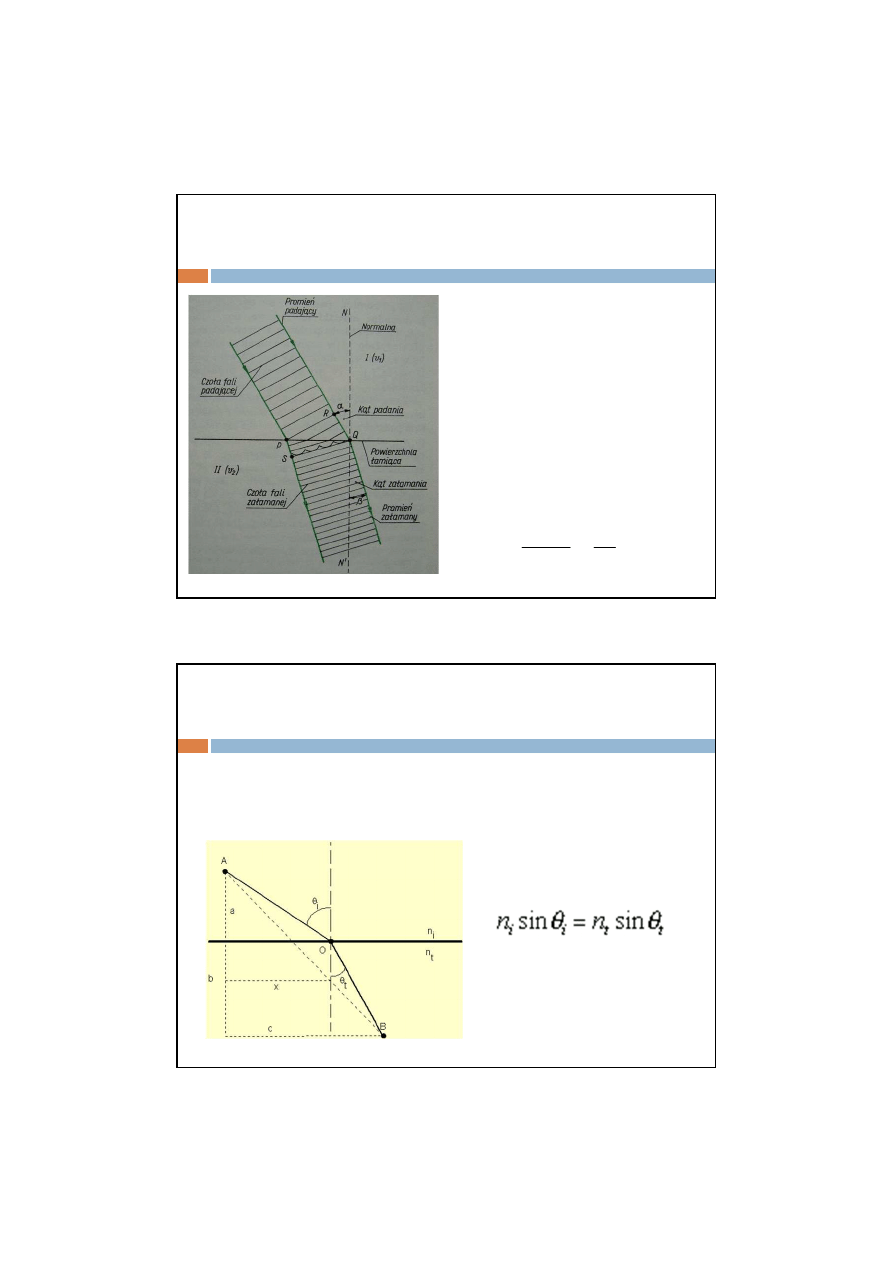
3.
Promień padający na powierzchnię
rozdzielającą dwa jednorodne
ośrodki izotropowe, normalna do
powierzchni łamiącej w punkcie
padania i promień załamany leżą
w jednej płaszczyźnie, przy czym
stosunek sinusa kąta padania do
sinusa kąta załamania nie zależy
od kąta padania, ani od kąta
załamania i jest równy stosunkowi
prędkości fali padającej i
załamanej.
2
1
sin
sin
v
v
=
β
α
26
Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/
Zasada Fermata
Zaburzenie falowe rozchodzi się po takiej drodze,
aby czas przejścia miedzy dwoma punktami był
najkrótszy.
27
Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/
2013-05-30
4
Dyfrakcja
Zjawiska objawiające się odstępstwami od
prostoliniowego biegu promieni nosi nazwę
dyfrakcji (ugięcia) fal.
Dyfrakcja jest nieodłącznym zjawiskiem przy
propagacji fal w ośrodku z przeszkodami.
28
Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/
Dyfrakcja
Intuicyjny przebieg fali przez otwór w przeszkodzie. W rzeczywistości mamy do
czynienia zawsze z dyfrakcją. Efekt jak na rysunku powyżej można jedynie obserwować
w przypadku gdy rozmiar otworu bądź przeszkody jest dużo większy niż długość fali.
29
Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/
2013-05-30
5
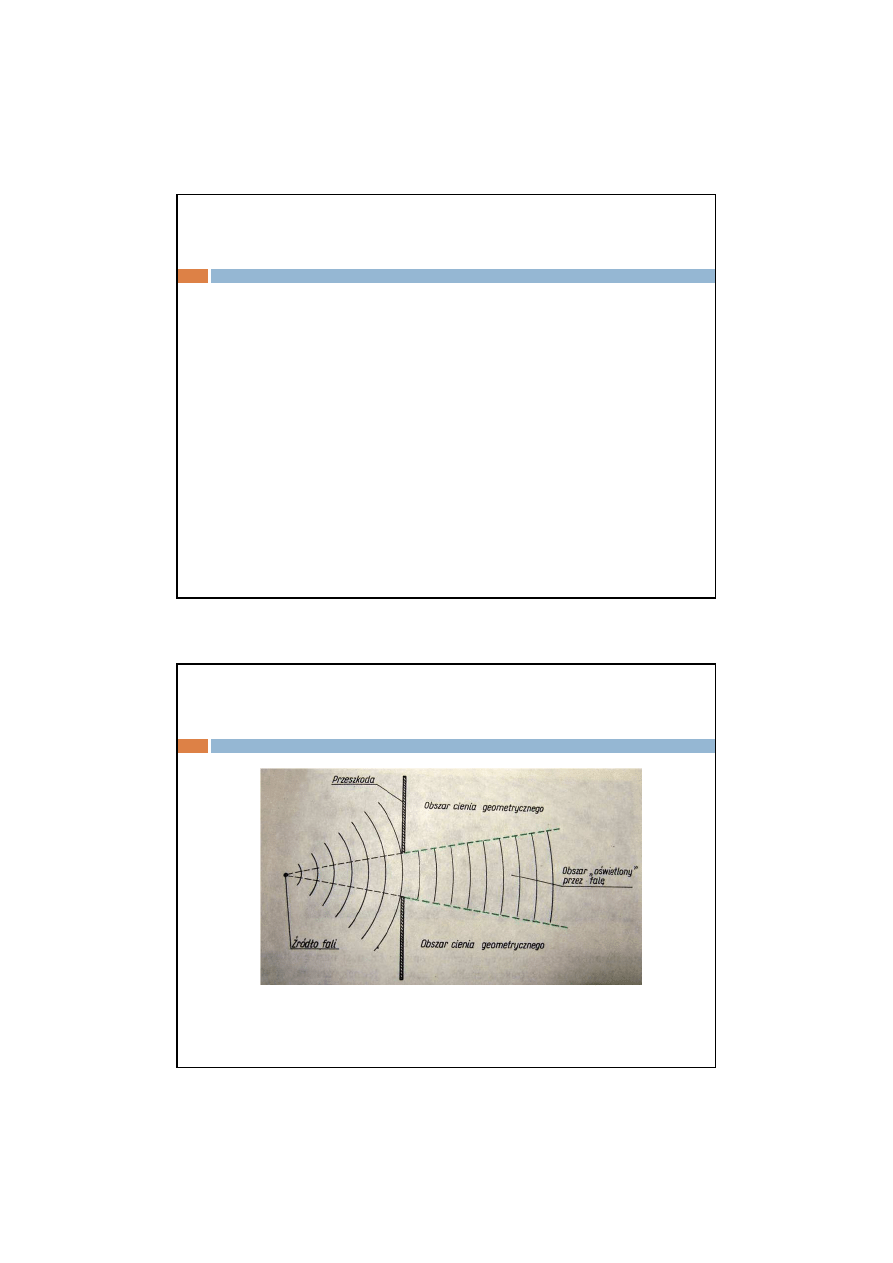
Dyfrakcja
Jeśli długość fali jest porównywalna z rozmiarami
otworu, to również w obszarze cienia geometrycznego
obserwuje się ruch falowy.
30
Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/
Dyfrakcja
Największe odstępstwa od intuicyjnych oczekiwań występują gdy
przeszkoda – otwór jest znacznie mniejsza od długości fali.
Za otworkiem mamy fale praktycznie doskonale kolistą.
31
Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/
2013-05-30
6
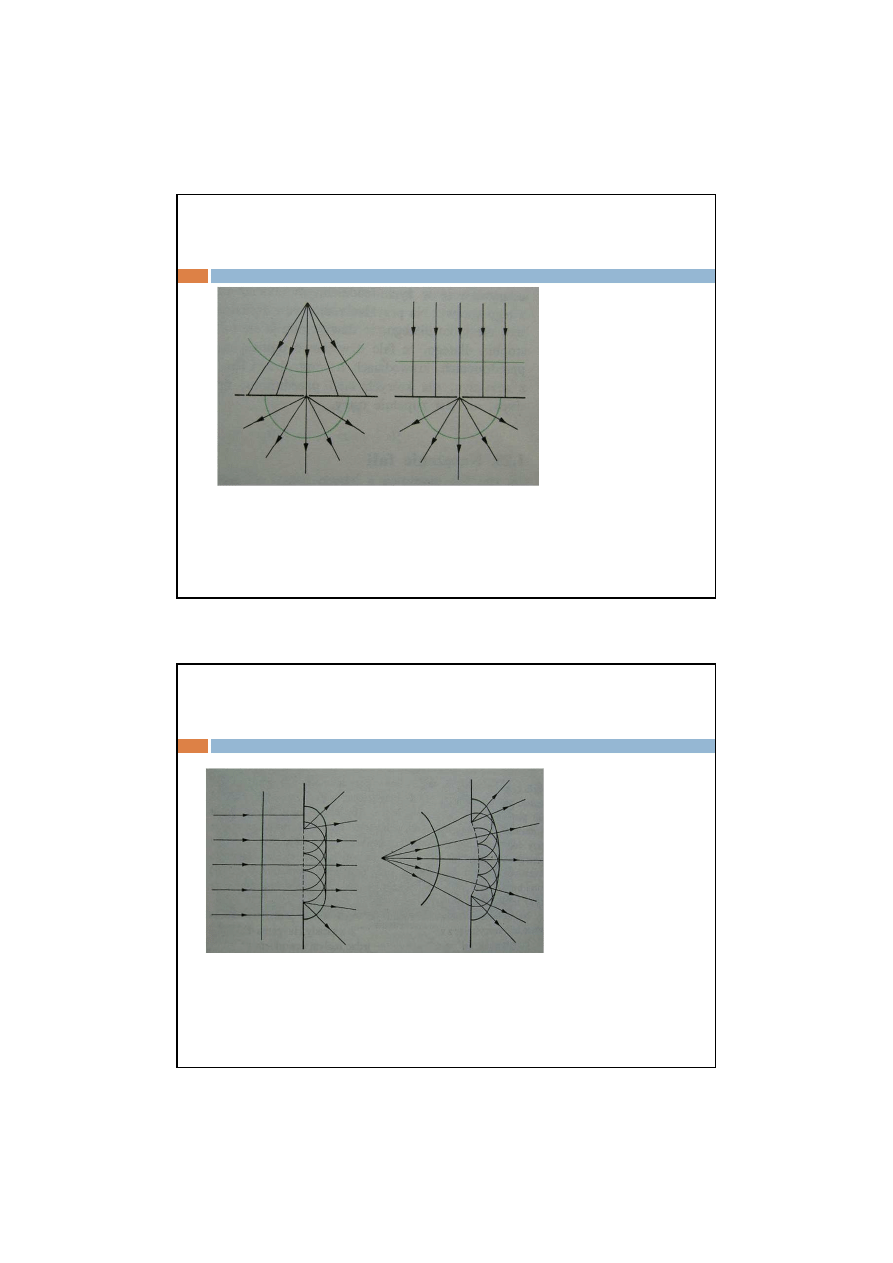
Dyfrakcja
Powstawanie fali za
przeszkodą z bardzo
małym otworkiem w
przypadku gdy fala
padająca jest falą kolistą i
w przypadku gdy fala
padająca jest falą płaską.
Za otworkiem powstaje w
obu przypadkach fala
kolista.
Fala za otworkiem jest suma nieskończenie wielu fal wtórnych, wysyłanych przez
nieskończenie wiele źródeł punktowych mieszczących się w otworku. Fale wtórne wysyłane
przez każdy punk otworka niewiele się od siebie róznią dlatego za otworkiem mamy falę
kolistą
32
Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/
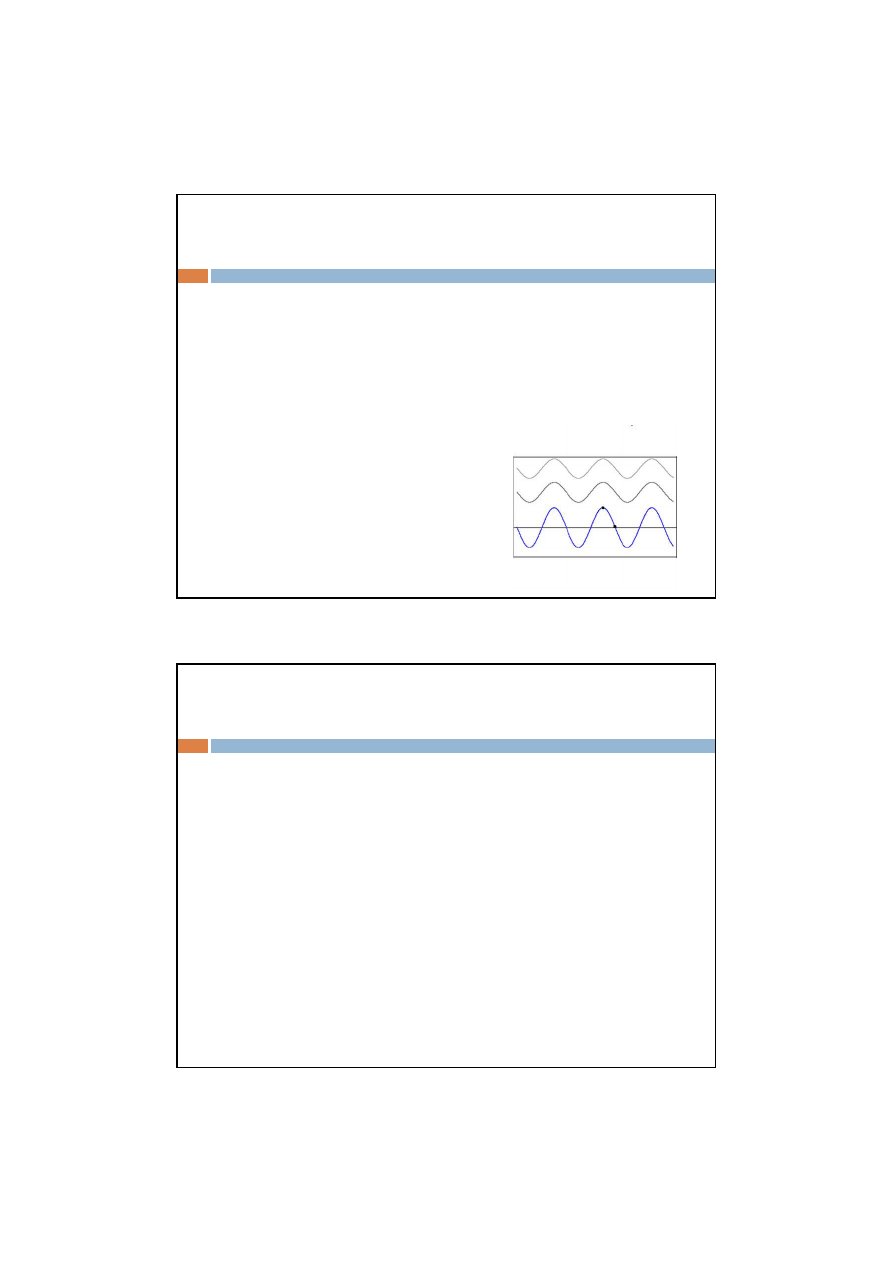
Dyfrakcja
Powstawanie fali za
przeszkodą z większym
otworkiem w przypadku
gdy fala padająca jest
falą płaską i w przypadku
gdy fala padająca jest
falą kolistą.
Fale wtórne wychodzą z punktów rozmieszczonych na dość dużym obszarze w porównaniu z
długością fali. Za otworem mamy do czynienia z falą o złożonym kształcie czoła zależnym
od rodzaju fali padającej.
33
Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/
2013-05-30
7
Interferencja fal
Definicja:
Tworzenie się fali wypadkowej w wyniku nakładania się
fal składowych (ograniczamy się do przypadków gdy
spełniona jest zasada superpozycji). Nakładanie się fal
prowadzi do ich wzmocnienia lub osłabienia w
poszczególnych miejscach w zależności od różnicy faz.
Rodzaje interferencji:
Interferencja destruktywna – wygaszenie
interferencyjne
Interferencja konstruktywna –
wzmocnienie interferencyjne
34
Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/
Interferencja fal
Warunkiem uzyskania interferencji jest spójność
interferujących fal.
Fale nazywamy spójnymi, jeżeli różnica ich faz
∆ϕ
nie
zależy od czasu.
Wzmocnienie
∆ϕ
=2k
π
∆
s=2k
λ
/2
Osłabienie
∆ϕ
=(2k+1)
π
∆
s=(2k+1)
λ
/2
35
Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/
2013-05-30
8
Ruch harmoniczny
Każda fala periodyczna składa się z szeregu
nakładających się fal harmonicznych.
Fale harmoniczne wytwarzane są przez
źródła poruszające się ruchem harmonicznym.
Ruch harmoniczny zachodzi wtedy, gdy siła
powodująca ruch jest wprost proporcjonalna
do wychylenia i skierowana przeciwnie.
36
Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/
Ruch harmoniczny
Równanie ruchu harmonicznego:
)
(
)
(
t
x
k
t
F
⋅
−
=
współczynnik sprężystości
Wychylenie ciała z poło
ż
enia równowagowego powoduje,
ż
e zaczyna na nie
działa
ć
siła zwrotna F(t)
- skierowana przeciwnie do wychylenia (st
ą
d „-”
w równaniu) i tym samym staraj
ą
ca si
ę
zawróci
ć
je ponownie do poło
ż
enia
równowagowego.
Drgania opisane powyższym równaniem
nazwiemy harmonicznymi, a drgające ciało
oscylatorem harmonicznym.
37
Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/
2013-05-30
9
Ruch harmoniczny
Przykłady ruchu harmonicznego:
ciało na sprężynie (niewielkie wychylenia)
wahadło matematyczne (niewielkie wychylenia)
wahadło fizyczne (niewielkie wychylenia)
obciążona szklanka pływająca w wodzie
ciecz w U-rurce
38
Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/
Ruch harmoniczny
Równanie ruchu harmonicznego – rozwiązanie:
x
k
a
m
−
=
0
=
+
x
m
k
a
2
ω
=
m
k
y
podstawiam
0
2
=
+
x
a
ω
)
sin(
)
(
ϕ
ω
+
=
t
A
t
x
amplituda drgań
maksymalne
wychylenie
początkowa
faza drgań
częstość (pulsacja) drgań
własnych
ruch harmoniczny jest ruchem okresowym sinusoidalnym
faza drgań
39
Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/
2013-05-30
10
Ruch harmoniczny
)
(
)
(
t
x
k
t
F
⋅
−
=
)
sin(
)
(
ϕ
ω
+
=
t
A
t
x
40
Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/
m
k
=
2
ω
pulsacja (kołowa częstość
drgań własnych)