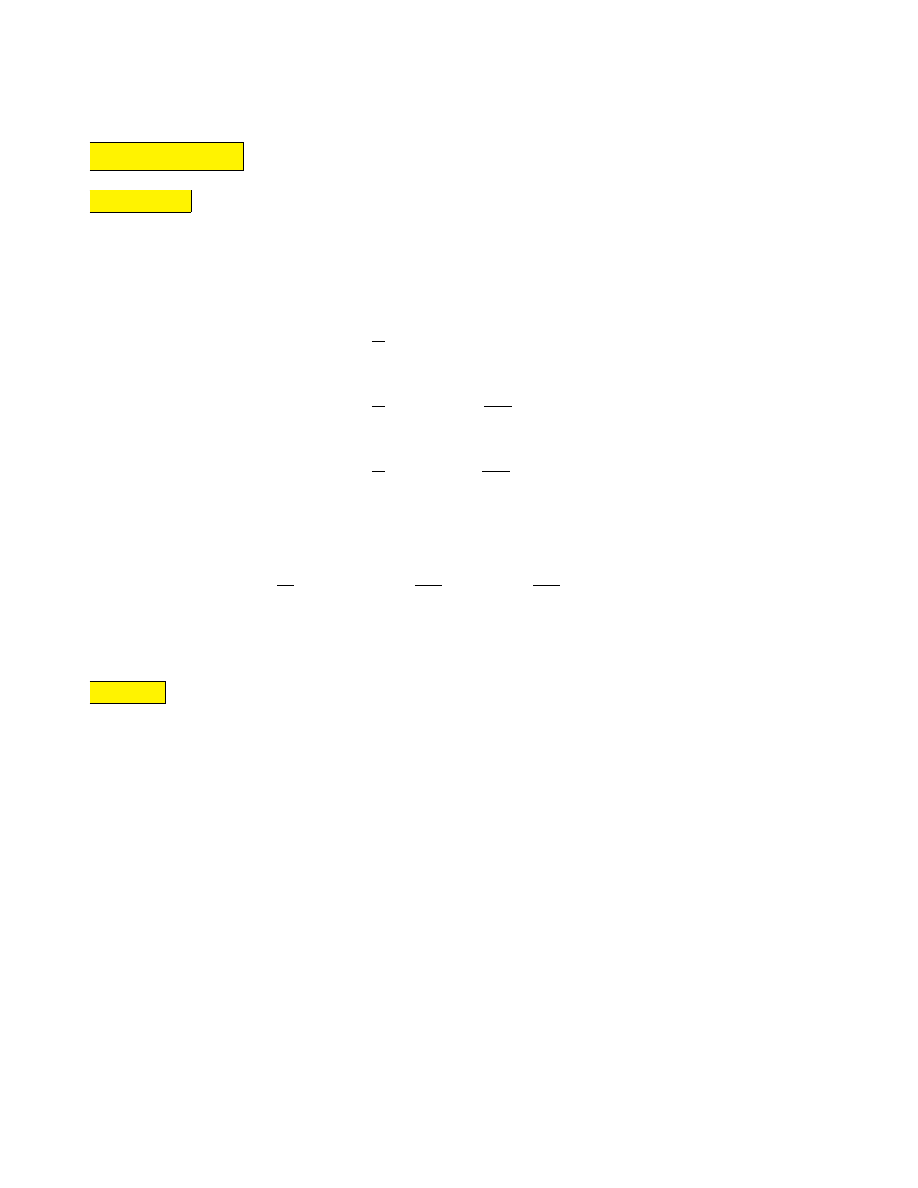
Rachunek prawdopodobieństwa MAP1064
Wydział Elektroniki, rok akad. 2008/09, sem. letni
Wykładowca: dr hab. A. Jurlewicz
Wykład 2: Szeregi Fouriera
Definicja.
Niech f (t) będzie funkcją określoną na
R
, okresową o okresie 2T
(tzn. f (t + 2T ) = f (t) dla każdego t ∈
R
) oraz całkowalną na przedziale [−T, T ].
Definiujemy ciągi (a
n
), (b
n
):
a
0
=
1
T
T
Z
−T
f (t)dt,
a
n
=
1
T
T
Z
−T
f (t) cos
nπt
T
dt,
b
n
=
1
T
T
Z
−T
f (t) sin
nπt
T
dt,
n = 1, 2, . . .
Szereg postaci
a
0
2
+
∞
X
n=1
a
n
cos
nπt
T
+ b
n
sin
nπt
T
nazywamy
szeregiem Fouriera funkcji f (t)
.
Uwaga.
• Jeżeli f (t) jest funkcją parzystą na przedziale [−T, T ], to b
n
= 0 dla każdego
n = 1, 2, . . . i w szeregu Fouriera tej funkcji nie występują sinusy.
• Jeżeli f (t) jest funkcją nieparzystą na przedziale [−T, T ], to a
n
= 0 dla każdego
n = 0, 1, 2, . . . i w szeregu Fouriera tej funkcji nie występują cosinusy i wyraz po-
czątkowy.
1
Twierdzenie:
Załóżmy, że f (t) określona na
R
, ograniczona, okresowa o okresie 2T spełnia warunki
Dirichleta tzn.
(1) przedział [−T, T ] można podzielić na skończoną ilość przedziałów takich, że f (t)
jest ciągła i monotoniczna na wnętrzu każdego z nich;
(2) dla każdego t mamy
f (t) =
f (t−) + f (t+)
2
,
gdzie granice f (t±) = lim
x→t±
f (x) są właściwe.
Wtedy dla każdego t mamy
f (t) =
a
0
2
+
∞
X
n=1
a
n
cos
nπt
T
+ b
n
sin
nπt
T
gdzie po prawej stronie równości znajduje się szereg Fouriera funkcji f .
Uwaga.
• Warunek (2) jest spełniony w każdym punkcie ciągłości funkcji f . W punktach nie-
ciągłości oznacza on, że zakładamy występowanie jedynie nieciągłości pierwszego
rodzaju i że jako wartość funkcji w takim punkcie przyjmujemy średnią arytmetycz-
ną granic jednostronnych.
• Teza twierdzenia zachodzi także, gdy przyjmiemy inne założenia o funkcji f , np.
zamiast (1) założyc można, że f jest kawałkami klasy C
1
(ciągła lub nieciągła).
2
Zespolony szereg Fouriera:
Inna postać szeregu Fouriera to
f (t) =
∞
X
n=−∞
c
n
e
in
πt
T
,
gdzie
c
n
=
1
2T
T
Z
−T
f (t)e
−in
πt
T
dt.
(Symbol e
ix
oznacza liczbę zespoloną cos x + i sin x w tzw. postaci wykładniczej.)
Zauważmy, że c
0
=
a
0
2
, c
n
=
a
n
− ib
n
2
oraz c
−n
=
a
n
+ ib
n
2
dla n 1.
Interpretacja:
t - czas
f (t) - sygnał okresowy
(c
n
) - widmo sygnału f
cos
nπt
T
, sin
nπt
T
to funkcje okresowe o okresie
2T
n
. Mają ν =
n
2T
okresów
w odcinku [0, 1], czyli częstotliwość ν Hz (ν okresów na sekundę).
3
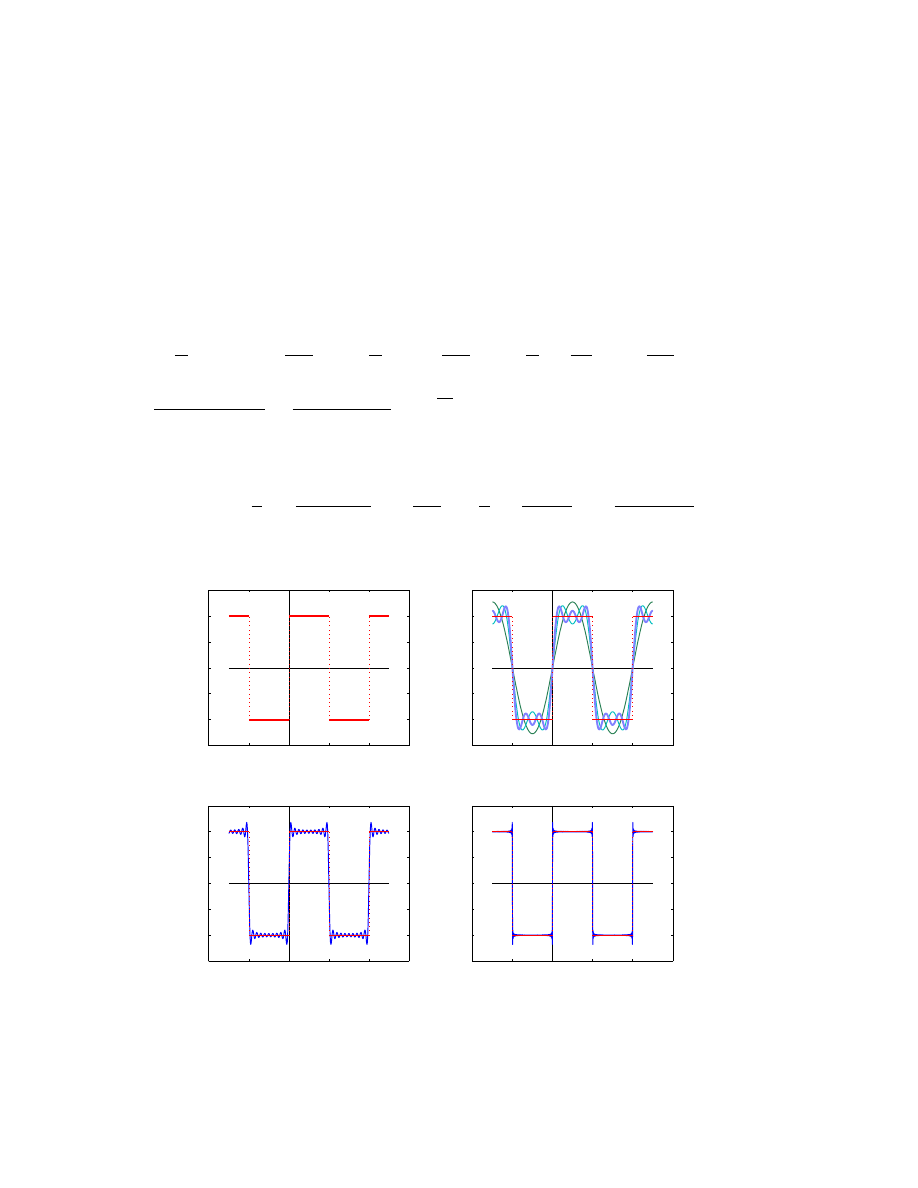
Przykład 1:
Sygnał o przebiegu prostokątnym, okresowy o okresie 2T :
f (t) =
1 dla 0 < t < T
−1 dla −T < t < 0
0 dla t = −T, 0, T.
• Funkcja ta spełnia warunki Dirichleta.
• Na przedziale [−T, T ] jest to funkcja nieparzysta.
Zatem a
n
= 0 dla każdego n = 0, 1, . . ..
Obliczamy b
n
:
b
n
=
1
T
T
Z
−T
f (t) sin
nπt
T
dt =
2
T
T
Z
0
sin
nπt
T
dt =
2
T
−
T
nπ
cos
nπt
T
T
0
=
=
2(1 − cos(nπ))
nπ
=
2(1 − (−1)
n
)
nπ
=
(
4
nπ
dla n = 2k − 1
0 dla n = 2k
, k = 1, 2, . . .
• Zatem sygnał prostokątny rozwija się w następujący szereg Fouriera:
f (t) =
2
π
∞
X
n=1
1 − (−1)
n
n
sin
nπt
T
=
4
π
∞
X
k=1
1
2k − 1
sin
(2k − 1)πt
T
!
−2
−1
0
1
2
3
−1.5
−1
−0.5
0
0.5
1
1.5
−2
−1
0
1
2
3
−1.5
−1
−0.5
0
0.5
1
1.5
−2
−1
0
1
2
3
−1.5
−1
−0.5
0
0.5
1
1.5
−2
−1
0
1
2
3
−1.5
−1
−0.5
0
0.5
1
1.5
sygnal o przebiegu prostokatnym
suma czesciowa szeregu Fouriera tego sygnalu
ilosc skladnikow N=1, 2, 3
suma czesciowa szeregu Fouriera tego sygnalu
ilosc skladnikow N=10
suma czesciowa szeregu Fouriera tego sygnalu
ilosc skladnikow N=100
4
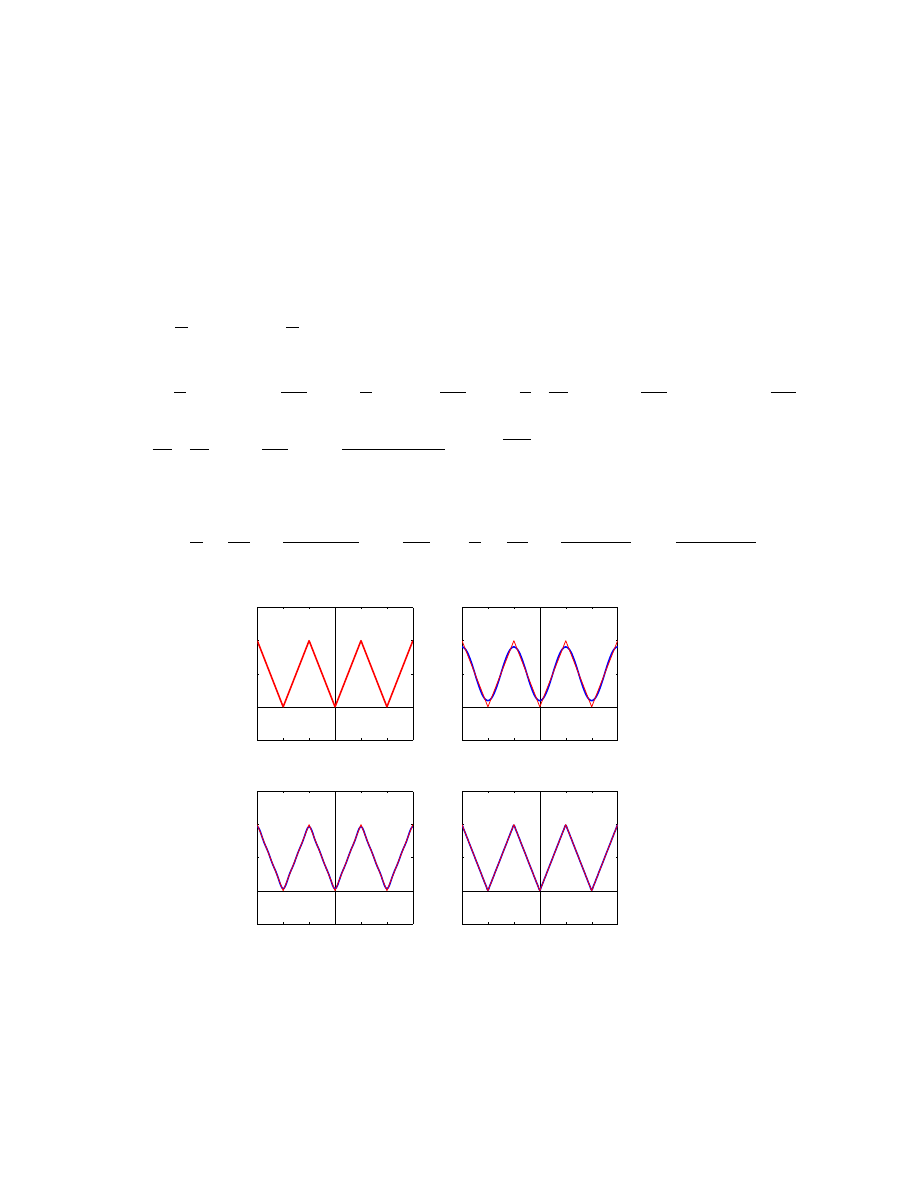
Przykład 2:
Sygnał trójkątny, okresowy o okresie 2T :
f (t) =
(
t dla 0 < t ¬ T
−t dla −T ¬ t < 0.
• Funkcja ta spełnia warunki Dirichleta.
• Na przedziale [−T, T ] jest to funkcja parzysta.
Zatem b
n
= 0 dla każdego n = 1, 2, . . ..
Obliczamy a
n
:
a
0
=
1
T
T
Z
−T
f (t)dt =
2
T
T
Z
0
tdt = T
a
n
=
1
T
T
Z
−T
f (t) cos
nπt
T
dt =
2
T
T
Z
0
t cos
nπt
T
dt =
2
T
T
nπ
t sin
nπt
T
T
0
−
T
Z
0
sin
nπt
T
dt
=
=
2
nπ
T
nπ
cos
nπt
T
T
0
=
2T ((−1)
n
− 1)
n
2
π
2
=
(
−
4T
n
2
π
2
dla
n = 2k − 1
0
dla
n = 2k
, k = 1, 2, . . .
• Zatem sygnał trójkątny rozwija się w następujący szereg Fouriera:
f (t) =
T
2
+
2T
π
2
∞
X
n=1
1 − (−1)
n
n
2
cos
nπt
T
=
T
2
−
4T
π
2
∞
X
k=1
1
(2k − 1)
2
cos
(2k − 1)πt
T
!
−3
−2
−1
0
1
2
3
−0.5
0
0.5
1
1.5
−3
−2
−1
0
1
2
3
−0.5
0
0.5
1
1.5
−3
−2
−1
0
1
2
3
−0.5
0
0.5
1
1.5
−3
−2
−1
0
1
2
3
−0.5
0
0.5
1
1.5
sygnal trojkatny
suma czesciowa szeregu Fouriera tego sygnalu
ilosc skladnikow N=1
suma czesciowa szeregu Fouriera tego sygnalu
ilosc skladnikow N=3
suma czesciowa szeregu Fouriera tego sygnalu
ilosc skladnikow N=10
5
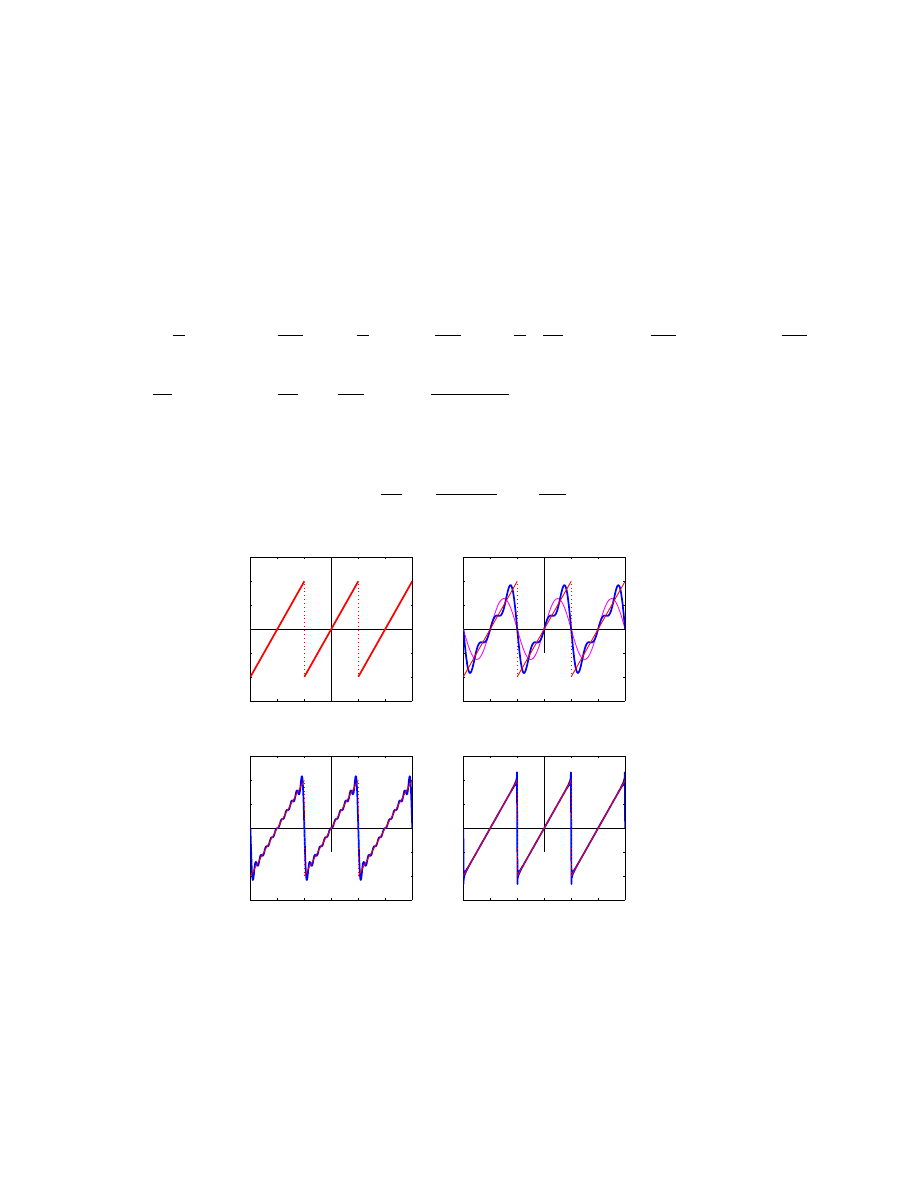
Przykład 3:
Sygnał o przebiegu piłowym, okresowy o okresie 2T :
f (t) =
(
t dla −T < t < T
0 dla t = −T, T.
• Funkcja ta spełnia warunki Dirichleta.
• Na przedziale [−T, T ] jest to funkcja nieparzysta.
Zatem a
n
= 0 dla każdego n = 0, 1, . . ..
Obliczamy b
n
:
b
n
=
1
T
T
Z
−T
f (t) sin
nπt
T
dt =
2
T
T
Z
0
t sin
nπt
T
dt =
2
T
T
nπ
−t cos
nπt
T
T
0
+
T
Z
0
cos
nπt
T
dt
=
=
2
nπ
−(−1)
n
T +
T
nπ
sin
nπt
T
T
0
=
2T (−1)
n+1
nπ
• Zatem sygnał piłowy rozwija się w następujący szereg Fouriera:
f (t) =
2T
π
∞
X
n=1
(−1)
n+1
n
sin
nπt
T
−3
−2
−1
0
1
2
3
−1.5
−1
−0.5
0
0.5
1
1.5
−3
−2
−1
0
1
2
3
−1.5
−1
−0.5
0
0.5
1
1.5
−3
−2
−1
0
1
2
3
−1.5
−1
−0.5
0
0.5
1
1.5
−3
−2
−1
0
1
2
3
−1.5
−1
−0.5
0
0.5
1
1.5
sygnal o przebiegu pilowym
suma czesciowa szeregu Fouriera tego sygnalu
ilosc skladnikow N=1, 3
suma czesciowa szeregu Fouriera tego sygnalu
ilosc skladnikow N=10
suma czesciowa szeregu Fouriera tego sygnalu
ilosc skladnikow N=100
6