Łukasz Skrodzki, gr. I6Y3S1

1/7

Warszawa, dn. 15.01.2008r.

Wojskowa Akademia Techniczna

im. Jarosława Dąbrowskiego

w Warszawie

Laboratorium przedmiotu

'Wprowadzenie do automatyki'

zajęcia 6

Temat:”Modelowanie układów dynamicznych w środowisku MATLAB -

SIMULINK”

Słuchacz

:

Łukasz Skrodzki

grupa

:

I6Y3S1

rok akademicki

:

2007/2008

semsetr:

III

prowadzący

:

mgr inż. Małgorzata Rudnicka – Schmidt

data przeprowadzenia ćwiczenia

: 15.01.2008r.

Łukasz Skrodzki, gr. I6Y3S1

2/7

I. Zadanie

Dla danych wartości: k, T i ξ :

1/ wyznaczyć:
- współczynniki: b

0

, a

0

, a

1

,

- macierze: A, B, C, D,
- bieguny: p

1

, p

2

2/ stosując pakiet SIMULINK zbudować modele badanego układu:
a/ model analogowy - wykorzystując elementy podstawowe:
integrator (blok Integrator), sumator, wzmacniacz (blok Gain),
b/ model odpowiadający opisowi w przestrzeni stanów

(blok State - Space),

c/ model transmitancyjny w dwóch postaciach:

- transmitancji Laplace’a (wykorzystać blok Transfer Fcn),
- transmitancji w postaci zero - biegunowej (blok Zero - Pole)

3/ podać na wejście układu sygnał skokowy (blok Step)
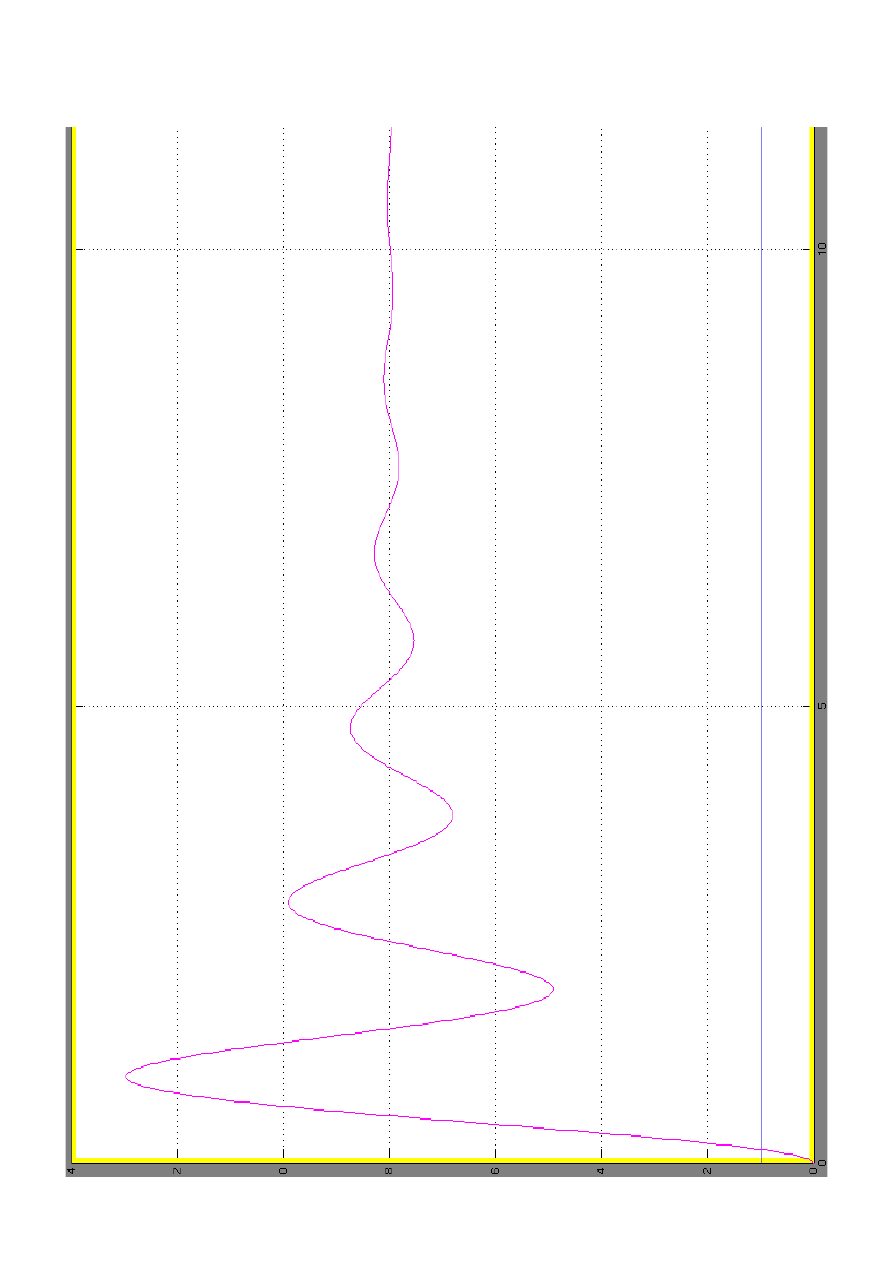
4/ zarejestrować sygnał wejściowy i odpowiedź skokową układu we
wszystkich czterech modelach układu (blok Scope),
4.1/ narysować na wspólnym wykresie sygnał wejściowy oraz
odpowiedzi otrzymane w wyniku symulacji (funkcja plot), wykorzystując
dane zapisane w przestrzeni roboczej MATLABa (blok To
Workspace, lub Out)
6/ zbadać wpływ współczynnika tłumienia ξ na charakter odpowiedzi
skokowej, zarejestrować odpowiedź skokową dla czterech wartości
współczynnika tłumienia:
ξ=0.1

ξ=0.3

ξ=0.6

ξ=1.2

7/ zbadać wpływ stałej czasowej T na charakter odpowiedzi skokowej,
zarejestrować odpowiedź skokową dla czterech wartości stałej
czasowej T:

T=0.2

T=0.4

T=0.7

T=1.5

II. Metoda wykonania:

Dane do zadnia:

k = 8.0

T = 0.3

ksi = 0.15

Ad 1:

Do wyznaczenia współczynników b

0

, a

0

, a

1

porównałem dwa równania:

1

2

2

2

+

+

=

Ts

s

T

k

)

s

(

H

ξ

0

1

2

0

a

s

a

s

b

)

s

(

H

+

+

=

Łukasz Skrodzki, gr. I6Y3S1

3/7

Zgodnie z nimi szukane współczynnki mają następujące wartości:

a

0

=

1

T

2

a

1

=

2 

T

b

0

=

k

T

2

czyli po podstawieniu znanych wartości:

a

0

=

1



0.3

2

=

11.1

a

1

=

2∗0.15

0.3

=

0.3
0.3

=

1

b

0

=

8.0



0.3

2

=

88. 8

Macierze A, B, C, D mają postać:

A=

{

0

1

−

a

0

−

a

1

}

B=

{

0
1

}

C={b

0

0}

D={0}

czyli zgodnie z danymi z zadania:

A=

{

0

1

−

11.1 −1

}

B=

{

0
1

}

C={88.8 0}

D={0 }

Bieguny p

1

, p

2

wyliczyłem obliczając pierwiastki równania w mianowniku transmitancji:

T

2

s

2



2 T s1

Pierwiastkami tego równania są dwie liczbe zespolone sprzężone:

p

1

=−

0.50003.2956i

p

2

=−

0.5000−3.2956i

Ad 2:

Łukasz Skrodzki, gr. I6Y3S1

4/7

Łukasz Skrodzki, gr. I6Y3S1

5/7

Ad 3:

W kolejnym punkcie należało zmieniać współczynnik tłumienia i umieścić wykresy dla
różnych wartości tego współczynnika na jednym wykresie. Wykres ten przedstawia się
następująco:

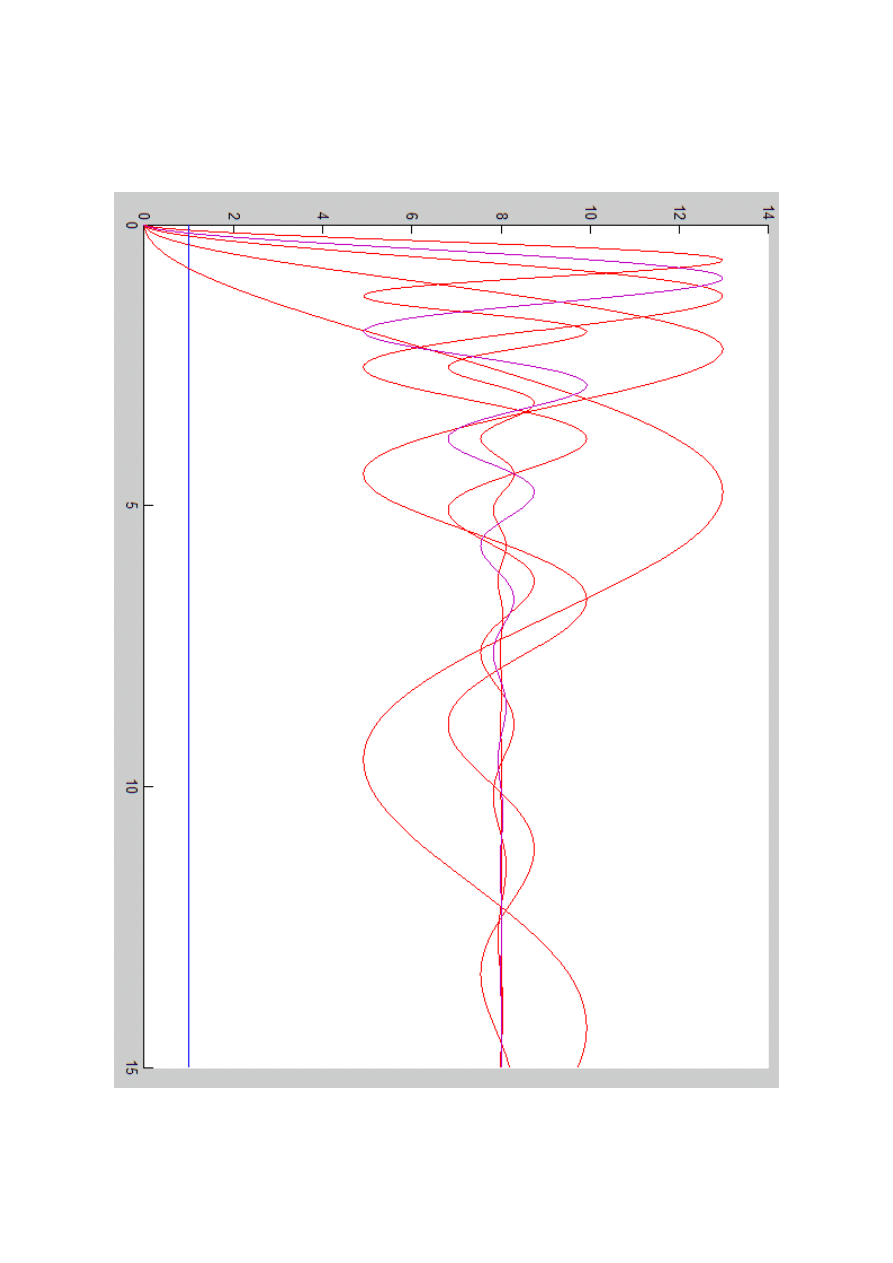
Łukasz Skrodzki, gr. I6Y3S1

6/7

Ad 4:

W kolejnym punkcie zadaniem było zmienianie stałej czasowej i umieszczenie

kolejnych wykresów odpowiedzi skokowej na wspólnym rysunku:

Łukasz Skrodzki, gr. I6Y3S1

7/7

Ad 5:

Wpływ współczynnika tłumienia i stałej czasowej na wykresy odpowiedzi skokowej

jest znaczący. Widać, że wraz ze wzrostem wartości współczynnika tłumienia zwiększa się
również wartość bezwzględna wartości minimalnej i maksymalnej tej odpowiedzi.
Natomiast sam czas potrzebny na wygaszenie sygnału również się zwiększa.

Przy zmianie satałej czasowej natomiast wartości maksymalne i minimalne wykresu

nie zmieniają wartości znacznie dłuższy jest natomiast czas potrzebny na wygaśnięcie
odpowiedzi.