Łukasz Skrodzki, gr. I6Y3S1

1/10

Warszawa, dn. 22.01.2008r.

Wojskowa Akademia Techniczna

im. Jarosława Dąbrowskiego

w Warszawie

Laboratorium przedmiotu

'Wprowadzenie do automatyki'

zajęcia 7

Temat:”

Badanie stabilności liniowego układu regulacji

”

Słuchacz

:

Łukasz Skrodzki

grupa

:

I6Y3S1

rok akademicki

:

2007/2008

semsetr:

III

prowadzący

:

mgr inż. Małgorzata Rudnicka – Schmidt

data przeprowadzenia ćwiczenia

: 22.01.2008r.

Łukasz Skrodzki, gr. I6Y3S1

2/10

I. Zadanie

1.

Układ statyczny

Transmitancja układu otwartego ma postać:

)

1

s

T

)(

1

s

T

)(

1

s

T

(

k

)

s

(

H

3

2

1

+

+

+

=

1.1

Należy zbudować model badanego układu, jako wymuszenie

zastosować generator skoku jednostkowego.

1.2

Zmieniając wartość k współczynnika wzmocnienia układu otwartego należy
znaleźć współczynnik wzmocnienia granicznego k

gr

. Jest to wartość

wzmocnienia, przy której w odpowiedzi skokowej układu zamkniętego
występują niegasnące drgania.

1.3

Zmieniając k od ok. 0.1k

gr

do k

gr

zmierzyć:

- wartość ustaloną sygnału wyjściowego y

ust

,

- wartość maksymalną sygnału wyjściowego y

max

,

- czas regulacji t

r

.

1.4

Dla wartości k z punktu 1.3 wyznaczyć bieguny transmitancji

układu zamkniętego.

2.

Układ astatyczny

Transmitancja układu otwartego ma postać:

s

)

1

s

T

)(

1

s

T

(

k

)

s

(

H

2

1

+

+

=

2.1 Należy zbudować model badanego układu. Jako wymuszenie
zastosować generator skoku jednostkowego.
2.2

Zmieniając wartość współczynnika wzmocnienia k układu otwartego należy
znaleźć współczynnik wzmocnienia granicznego k

gr

.

2.3

Zmieniając k od ok. 0.1k

gr

do k

gr

zmierzyć:

- czas regulacji t

r

,

- wartość maksymalną sygnału wyjściowego y

max

.

2.4 Zmienić wymuszenie na liniowo rosnące. Zmierzyć uchyb

ustalony dla wartości k z punktu 2.3.

Uwaga: W celu uzyskania wymuszenia liniowo rosnącego należy zastosować
blok Ramp z biblioteki Sources. Aby zmierzyć uchyb ustalony, blok Out
lub To Workspace należy podłączyć za węzeł sumacyjny.

2.5

Dla wartości k z punktu 2.3 wyznaczyć bieguny transmitancji

układu zamkniętego.

Łukasz Skrodzki, gr. I6Y3S1

3/10

II. Metod rozwiązania

1)Układ statyczny:

Moje dane to:

T1 = 0.25

T2 = 0.40

T3 = 0.75

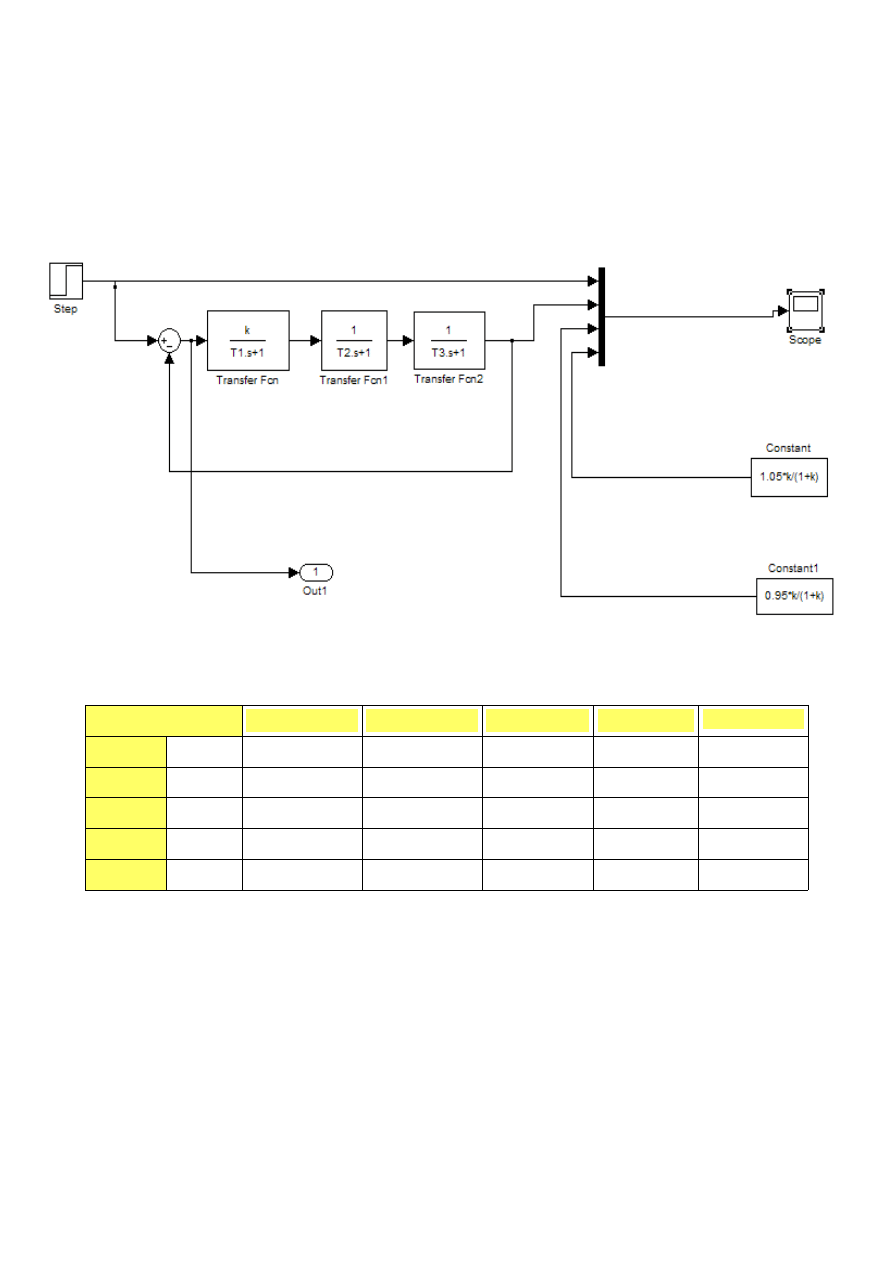
Schemat badanego układu:

Dla przedstawionego układu i wymienionych powyżej danych graniczny współczynnik
wzmocnienia ma wartość

k

gr

=

9.98

.

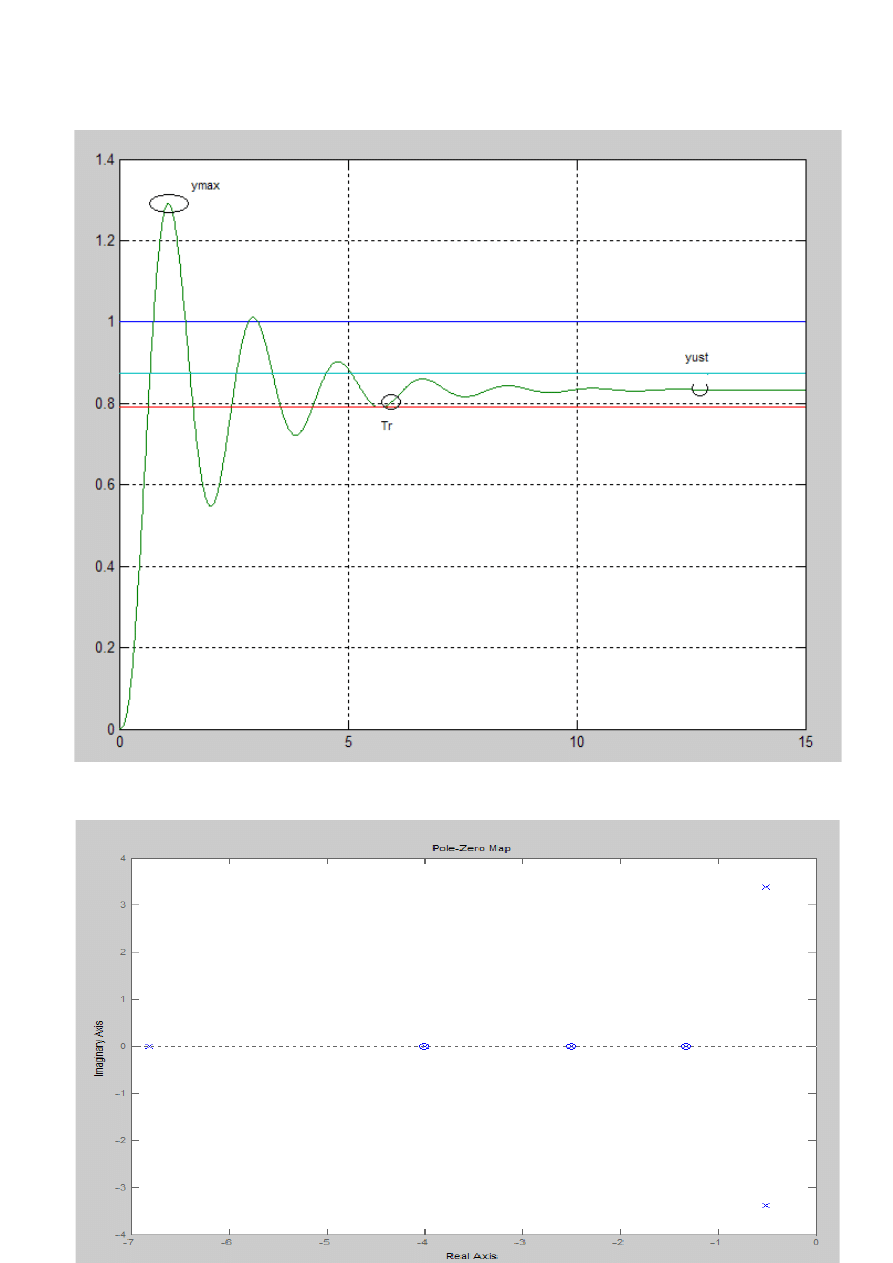
Dla k = 0.5 k

gr

= 4.99 wykres odpowiedzi skokowej przedstawia się następująco:

k

y

ust

y

max

e

ust

t

r



0.1

k

gr

0,998

0.50

0,5495

0,50

2,53

0,099

0.2

k

gr

1,996

0.6682

0,8246

0,318

3,076

0,234

0.5

k

gr

4,99

0.8351

1,2896

0,1649

5,8449

0,544

0.7

k

gr

6,896

0.8752

1,4892

0,1248

10,196

0,702

0.8

k

gr

7,984

0.8897

1,5677

0,1103

15,991

0,7535

Bieguny transmitancji układu zamkniętego to:
P1 = -6.8140
P2 = -0.5097 + 3.3854i
P3 = -0.5097 - 3.3854i
P4 = -4.0000
P5 = -2.5000
P6 = -1.3333

Łukasz Skrodzki, gr. I6Y3S1

4/10

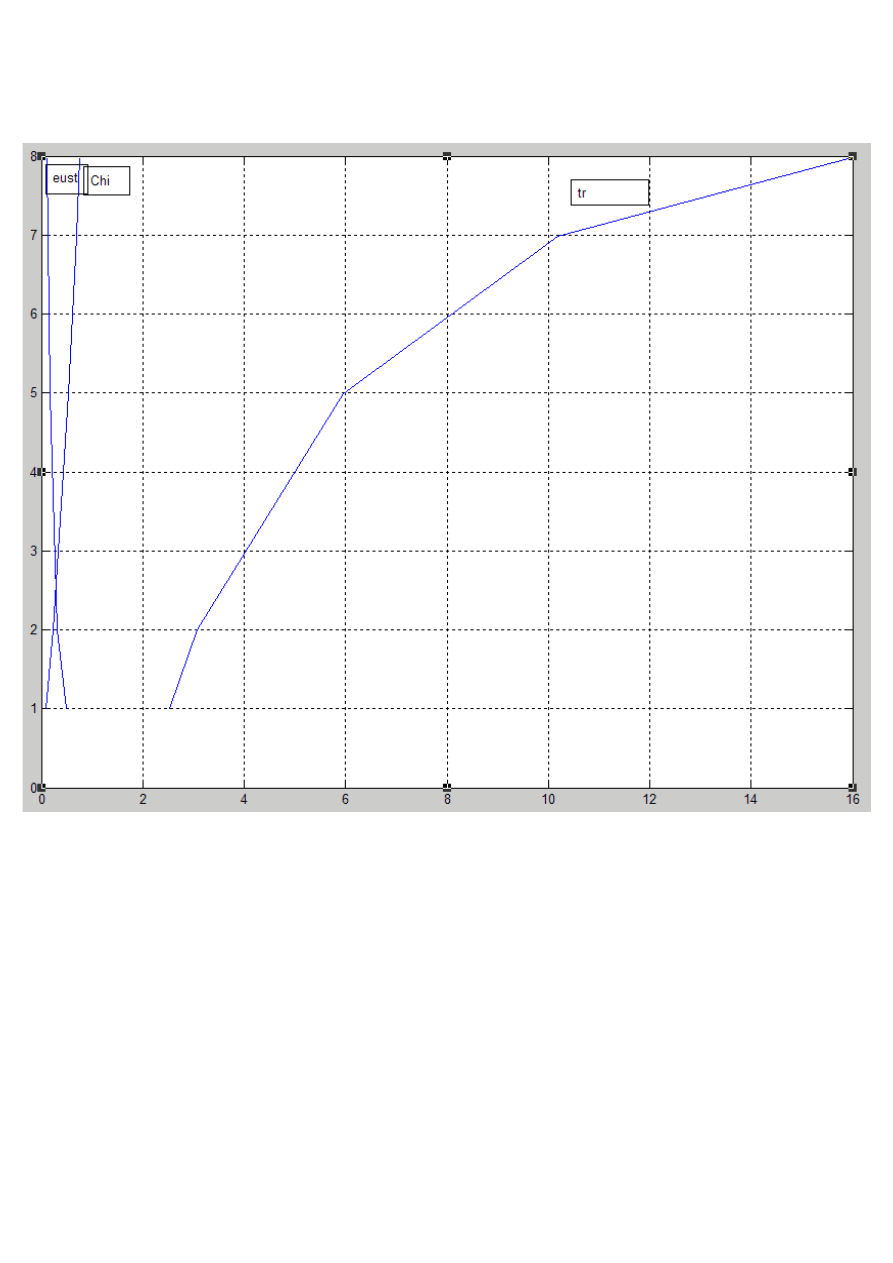
Wykres położenia biegunów transmitancji:
Zależności na wspólnym wykresie:

Łukasz Skrodzki, gr. I6Y3S1

5/10

Łukasz Skrodzki, gr. I6Y3S1

6/10

2)Układ astatyczny:
Moje dane:
T1 = 0.05

T2 = 1.5

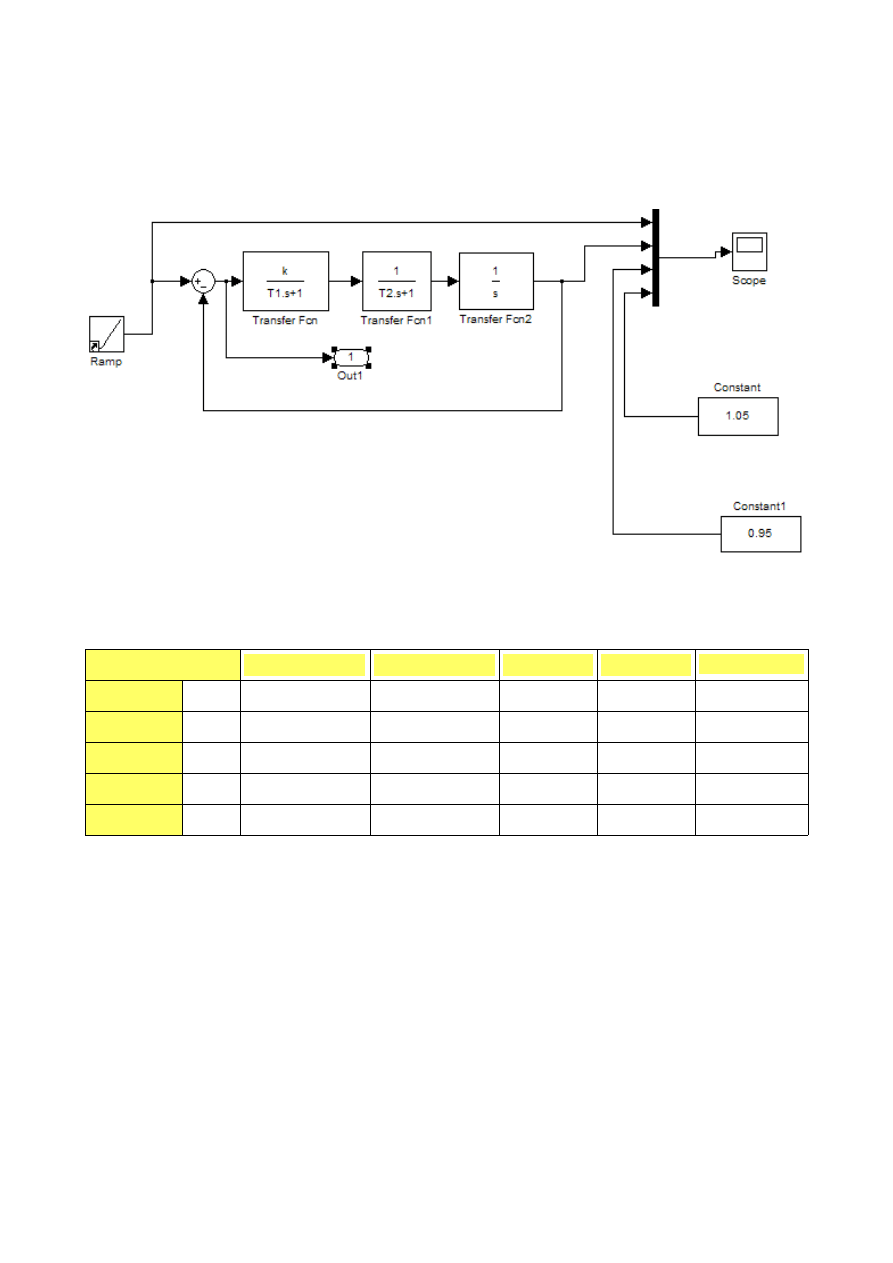
Schemat układu:

Graniczny współczynnik wzmocnienia dla tego układu ma wartość 20.71

k

y

max

y

ust

e

ust

t

r



0.1 k

gr

2,07

1,4345

0.5613

0.4387

9.2512

0.6087

0.3 k

gr

6,21

1,6979

0.7931

0.2069

12.8687

0.5389

0.5 k

gr

10,35

1,8214

0.8625

0.1375

18.3525

0.5265

0.7 k

gr

14,49

1,8944

0.9064

0.0936

30.89

0.5215

0.8 k

gr

16,56

1,9200

0.9211

0.0789

47.9455

0.5200

Bieguny tej transmitancji to:
P1 = 0
P2 = -20.3564
P3 = -20.0000
P4 = -0.4885 + 2.5575i
P5 = -0.4885 - 2.5575i
P6 = -1.3333

Łukasz Skrodzki, gr. I6Y3S1

7/10

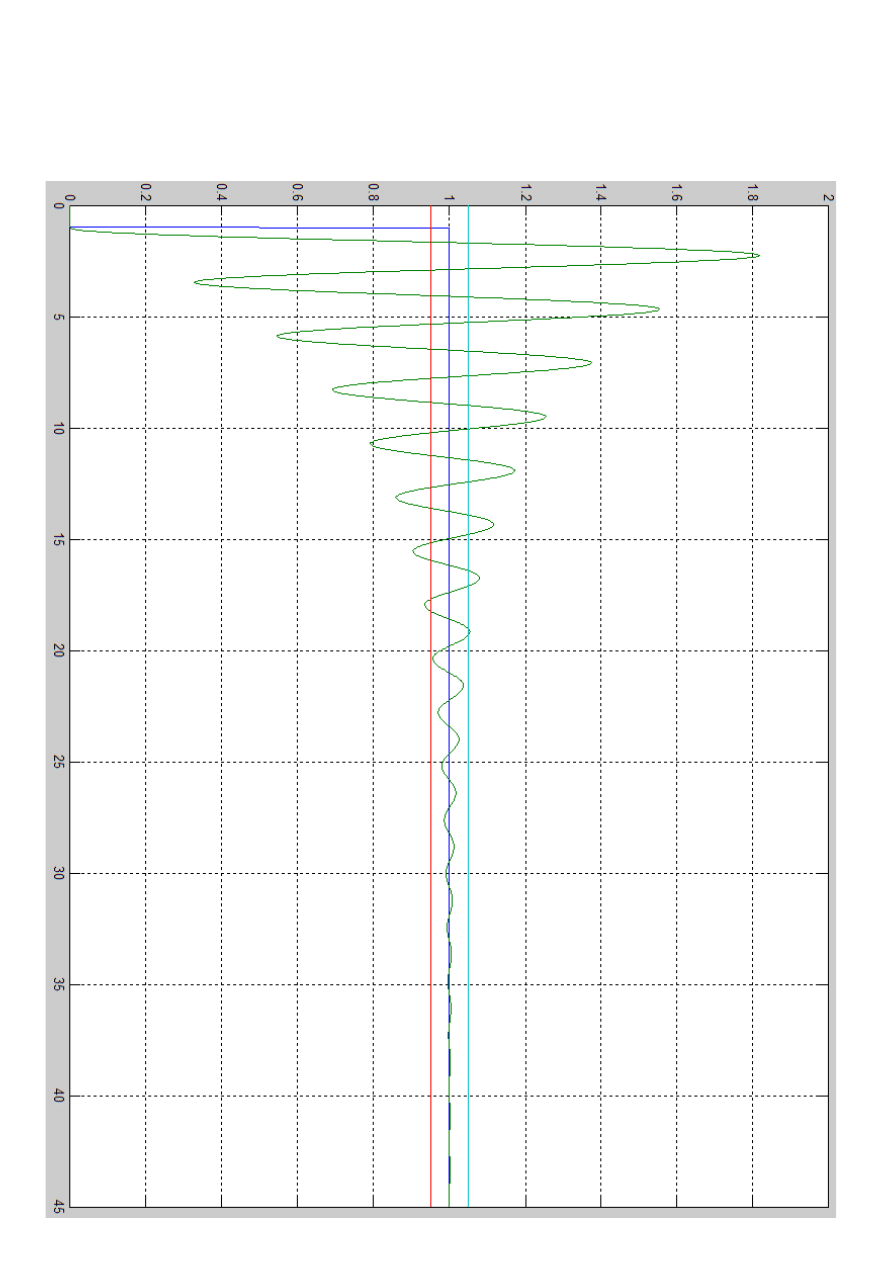
Wykres odpowiedzi skokowej układu dla k = 0.5 *

k

gr

Łukasz Skrodzki, gr. I6Y3S1

8/10

Położenie biegunów transmitancji:

Łukasz Skrodzki, gr. I6Y3S1

9/10

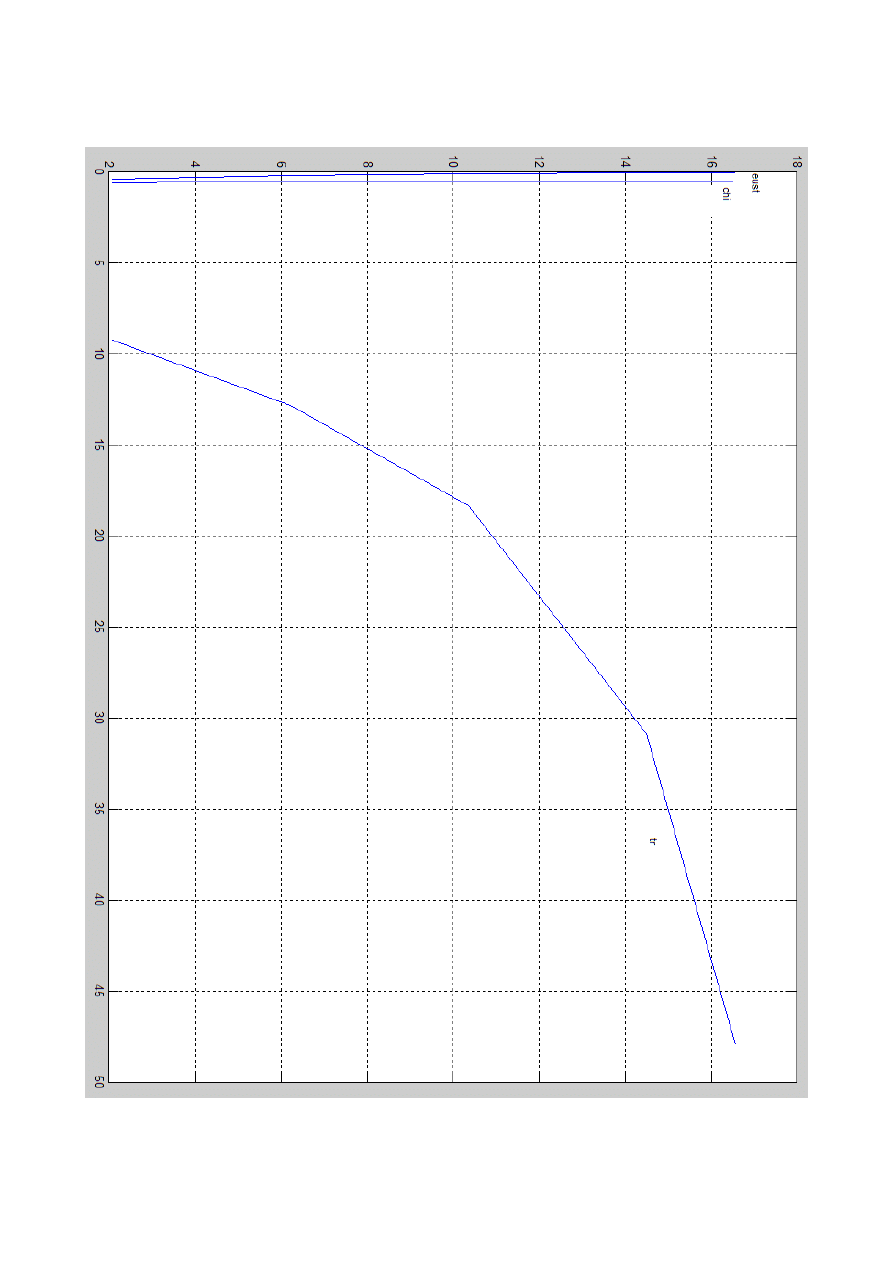
Wykres zależności od k:

Łukasz Skrodzki, gr. I6Y3S1

10/10

Wnioski:

Widać, że dla k równego k granicznemu układ zachowuje się stabilnie i oscyluje

wciąż utrzymuje się wokół tej samej wielkości. Przy zmniejszaniu k w stosunku do k
granicznego wpółczynnik przeregulowania zmniejsza się dążąc do ½. Natomiast w miarę
zmniejszania k uchyb ustalony rośnie, przy jednoczesnym zwiększaniu się wielkości czasu
regulacji układu.