Autor: Martin Slota
Zdroj: http://www.zones.sk
Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú
č
ely a akéko
ľ
vek verejné
publikovanie je bez predchádzajúceho súhlasu zakázané.
1/5
MATURITNÉ PRÍKLADY Z MATEMATIKY
M
ATURITNÝ OKRUH
10:
P
OLYNOMICKÉ FUNKCIE
1. príklad (110/2)
Zadanie: Ur
č
te parameter
R
p
∈
tak, aby rovnica
0
9
2
=
−
+
−
p
px
x
mala dva korene, ktorých rozdiel je
šes
ť
.
Riešenie:
Korene, ktoré h
ľ
adáme si ozna
č
íme
(
)
2
1
2
1
,
x
x
x
x
>
. Pre tieto korene musí plati
ť
, že:
(
) (
)
2
1
x
x
x
x
−
⋅
−
0
=
(
)
2
1
2
1
2
x
x
x
x
x
x
+
⋅
+
−
0
=
Teraz je zo zadania zrejmé, že:
2
1
x
x
+
p
=
2
1
x
x
9
−
=
p
2
1
x
x
−
2
1
6
6
x
x
+
=
⇒
=
Výsledok už teraz dostaneme jednoduchým dosadzovaním a úpravami:
2
1
x
x
9
2
1
−
+
=
x
x
(
)
2
2
6
x
x
⋅
+
9
6
2
2
−
+
+
=
x
x
2
2
2
6
x
x
+
3
2
2
−
=
x
3
4
2
2
2
+
+
x
x
0
=
(
) (
)
1
3
2
2
+
⋅
+
x
x
0
=
3
3
1
2
=
⇒
−
=
x
x
0
=
⇒ p
5
1
1
2
=
⇒
−
=
x
x
4
=
⇒ p
Rovnica
0
9
2
=
−
+
−
p
px
x
má dva korene, ktorých rozdiel je šes
ť
, ak
0
=
p
alebo
4
=
p
.
2. príklad (110/11)
Zadanie: Na
č
rtnite graf funkcie
3
4
5
12
7
:
x
x
x
y
f
+
−
=
.
Riešenie:
Defini
č
ný obor funkcie je
( )
R
f
D
=
, funkcia je spojitá.
Nulové body funkcie:
( )
(
)
(
)(
)
⇒
−
−
=
+
−
⋅
=
+
−
=
4
3
12
7
12
7
3
2
3
3
4
5
x
x
x
x
x
x
x
x
x
x
f
nulové body sú 0, 3, 4
Lokálne extrémy:
( )
(
)
(
)
⇒
−
−
=
+
−
⋅
=
+
−
=
′
5
18
2
5
36
28
5
36
28
5
2
2
2
2
3
4
x
x
x
x
x
x
x
x
x
x
f
MLE sú 0; 3,6; 2
Lokálne maximum:
[ ]
16
,
2
Lokálne minimum:
[
]
197
,
11
;
6
,
3
−
Konvexnos
ť
a konkávnos
ť
, inflexné body:
( )
(
)
(
)
⇒
−
−
=
+
−
⋅
=
+
−
=
′′
5
6
3
20
72
84
20
72
84
20
2
2
3
x
x
x
x
x
x
x
x
x
x
f
MIB sú 0; 3; 1,2
0
3,6
2
+
+
–
+
0
3
1,2
–
+
–
+
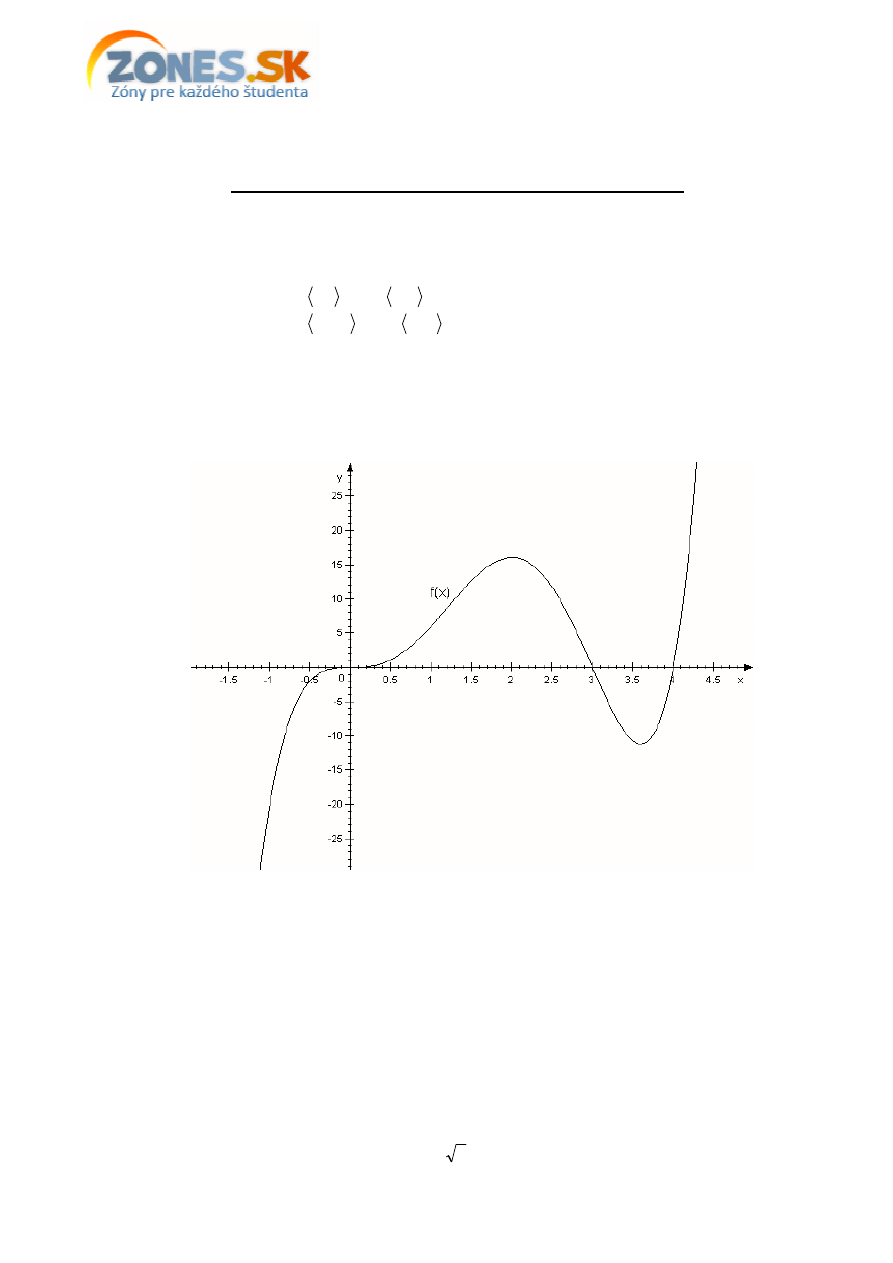
Autor: Martin Slota
Zdroj: http://www.zones.sk
Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú
č
ely a akéko
ľ
vek verejné
publikovanie je bez predchádzajúceho súhlasu zakázané.
2/5
MATURITNÉ PRÍKLADY Z MATEMATIKY
M
ATURITNÝ OKRUH
10:
P
OLYNOMICKÉ FUNKCIE
Funkcia je konvexná na
2
,
0
a na
∞
,
3
Funkcia je konkávna na
0
,
∞
−
a na
3
;
2
,
1
Inflexné body:
[ ] [
] [ ]
0
,
3
,
70912
,
8
;
2
,
1
,
0
,
0
Asymptoty v
:
∞
±
( )
( )
−∞
=
∞
=
−∞
→
∞
→
x
f
x
f
x
x
lim
lim
Graf:
3. príklad (110/13)
Zadanie: V rovnici
0
2
3
=
+
+
px
x
ur
č
te
R
p
∈
tak, aby rovnica mala viacnásobný kore
ň
a potom ur
č
te
všetky jej korene.
Riešenie:
Ke
ď
že rovnica je tretieho stup
ň
a, môžem ma
ť
maximálne trojnásobný kore
ň
. Budeme teda
uvažova
ť
dve situácie – že má trojnásobný a že má dvojnásobný kore
ň
:
a) Trojnásobný kore
ň
:
1
x
(
)
3
1
x
x
−
0
=
3
1
2
1
2
1
3
3
3
x
x
x
x
x
x
−
+
−
0
=
Ke
ď
porovnáme odvodenú rovnicu so zadanou, zistíme, že
1
x
by malo by
ť
rovné 0 (
č
len
2
x
v zadanej rovnici nie je) a zárove
ň
aj
3
2
−
. Tento postup teda nevedie k vyriešeniu príkladu.

Autor: Martin Slota
Zdroj: http://www.zones.sk
Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú
č
ely a akéko
ľ
vek verejné
publikovanie je bez predchádzajúceho súhlasu zakázané.
3/5
MATURITNÉ PRÍKLADY Z MATEMATIKY
M
ATURITNÝ OKRUH
10:
P
OLYNOMICKÉ FUNKCIE
b) Dvojnásobný kore
ň
1
x
a jednonásobný kore
ň
:
2
x
(
) (
)
2
2
1
x
x
x
x
−
⋅
−
0
=
(
)
(
)
2
2
2
1
1
2
2
x
x
x
xx
x
−
⋅
−
−
0
=
2
1
2
2
1
2
2
2
1
1
2
3
2
2
x
x
x
xx
x
x
xx
x
x
x
−
+
−
+
−
0
=
(
)
(
)
2
1
2
2
1
2
1
2
2
1
3
2
2
x
x
x
x
x
x
x
x
x
x
−
+
+
−
−
+
0
=
Ke
ď
teraz porovnáme rovnice, zistíme, že:
3
2
2
1
2
2
2
2
0
2
2
1
2
1
2
1
3
1
2
1
2
1
2
2
1
−
=
⇒
+
=
−
=
⇒
=
⇒
=
⇒
=
−
−
=
⇒
=
−
−
p
x
x
x
p
x
x
x
x
x
x
x
x
x
Rovnica
0
2
3
=
+
+
px
x
má viacnásobný kore
ň
, pokia
ľ
3
−
=
p
. Jej kore
ň
mi sú potom dvojnásobný
kore
ň
1 a jednonásobný kore
ň
–2.
4. príklad (111/22)
Zadanie: Riešte v R rovnicu
0
4
12
11
11
12
4
2
3
4
5
=
+
+
+
+
+
x
x
x
x
x
.
Riešenie:
Ke
ď
že táto recipro
č
ná rovnica je nepárneho stup
ň
a, musíme najprv nájs
ť
jeden jej kore
ň
a dosta
ť
sa delením polynómov k recipro
č
nej rovnici párneho stup
ň
a. Kore
ň
om recipro
č
nej rovnice
nepárneho stup
ň
a je vždy 1 alebo –1. V našom prípade je to o
č
ividne
1
1
−
=
x
. Teraz rovnicu
vydelíme:
(
)
(
)
4
8
3
8
4
1
:
4
12
11
11
12
4
2
3
4
2
3
4
5
+
+
+
+
=
+
+
+
+
+
+
x
x
x
x
x
x
x
x
x
x
Vzniknutú rovnicu si najprv upravíme a potom použijeme tzv. Lagrangeovu substitúciu:
(
)
0
2
5
2
1
4
0
5
8
4
0
3
8
2
4
1
0
3
1
8
1
4
0
4
8
3
8
4
0
4
8
3
8
4
2
2
2
2
2
2
2
3
4
=
+
⋅
−
⋅
=
−
+
=
+
+
−
⋅
+
=
=
+
+
⋅
+
+
⋅
=
+
+
+
+
=
+
+
+
+
y
y
y
y
y
y
x
x
y
x
x
x
x
x
x
x
x
x
x
x
x
Teraz už iba dopo
č
ítame
:
x
1.
⇒
<
0
D
v R nie je riešenie
2.
0
2
2
2
2
2
1
1
2
2
=
+
−
=
+
=
+
x
x
x
x
x
x
(
)
0
2
1
2
2
0
2
5
2
5
2
2
2
5
1
2
2
=
+
⋅
+
⋅
=
+
+
−
=
+
−
=
+
x
x
x
x
x
x
x
x

Autor: Martin Slota
Zdroj: http://www.zones.sk
Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú
č
ely a akéko
ľ
vek verejné
publikovanie je bez predchádzajúceho súhlasu zakázané.
4/5
MATURITNÉ PRÍKLADY Z MATEMATIKY
M
ATURITNÝ OKRUH
10:
P
OLYNOMICKÉ FUNKCIE
Riešením rovnice teda je
−
−
−
=
2
1
,
2
,
1
K
.
5. príklad (112/28)
Zadanie: Ur
č
te kubickú funkciu, ktorá má v bode
[ ]
6
,
4
lokálne maximum a v bode
[ ]
1
,
6
lokálne
minimum.
Riešenie:
Všeobecne takúto kubickú funkciu môžeme zapísa
ť
takto:
( )
0
1
2
2
3
3
a
x
a
x
a
x
a
x
f
+
+
+
=
.
Jej prvá derivácia by potom bola:
( )
1
2
2
3
2
3
a
x
a
x
a
x
f
+
+
=
′
. Pre prvú deriváciu funkcie zárove
ň
platí,
že dáva nulovú hodnotu v bodoch 4 a 6 (sú v nich lokálne extrémy). Takže:
( )
(
) (
)
k
a
k
a
a
k
a
k
a
k
a
k
kx
kx
x
x
k
a
x
a
x
a
x
f
k
24
5
24
10
2
3
24
10
6
4
2
3
1
2
3
3
1
2
3
2
1
2
2
3
=
−
=
=
⇒
⇒
⇒
=
−
=
=
⇒
⇒
⇒
+
−
=
−
⋅
−
⋅
=
+
+
=
′
Teraz ešte využijeme poznatok o funk
č
ných hodnotách lokálnych extrémov funkcie:
( )
( )
0
1
2
2
3
3
0
1
2
2
3
3
6
6
6
1
6
4
4
4
6
4
a
a
a
a
f
a
a
a
a
f
+
⋅
+
⋅
+
⋅
=
=
+
⋅
+
⋅
+
⋅
=
=
Rovnice od
č
ítame a dosadíme za á
č
ka:
(
)
4
15
3
4
5
24
2
5
20
3
152
5
2
20
152
5
1
2
3
=
=
−
⋅
+
−
⋅
+
⋅
=
−
+
+
=
−
k
k
k
k
k
a
a
a
Dosadením dostávame:
134
360
300
80
6
4
4
4
6
90
24
4
75
5
4
5
3
0
0
0
1
2
2
3
3
1
2
3
−
=
+
+
−
=
+
⋅
+
⋅
+
⋅
=
=
=
−
=
−
=
=
=
a
a
a
a
a
a
k
a
k
a
k
a

Autor: Martin Slota
Zdroj: http://www.zones.sk
Používanie materiálov zo ZONES.SK je povolené bez
obmedzení iba na osobné ú
č
ely a akéko
ľ
vek verejné
publikovanie je bez predchádzajúceho súhlasu zakázané.
5/5
MATURITNÉ PRÍKLADY Z MATEMATIKY
M
ATURITNÝ OKRUH
10:
P
OLYNOMICKÉ FUNKCIE
Funkcia sp
ĺň
ajúca podmienky je teda:
( )
134
90
4
75
4
5
2
3
−
+
−
=
x
x
x
x
f
.
Wyszukiwarka
Podobne podstrony:
Polynomicke funkcie
L 3 Complex functions and Polynomials
Matematyka cw8 Badanie funkci Wykres funkcji
POLSKA PIASTÓW, Czym byly grody jakie funkcie pelnily, Czym byly grody jakie funkcie pelnily
Goniometricke funkcie
Exponencialne a logaritmicke funkcie
brychkov+yu a %2c+prudnikov+a p +integral%27nye+preobrazovanija+obobshchyonnyh+funkcij+%28smb%2c+nau
Funkcie
całki, CALKI, Całki funkci elementarnych:
Mitologia funkcie i rodzaje, Mit jest opowieścią, która przedstawia, organizuje wierzenia danej społ
calki, Ca˙ki funkci elementarnych:
Minimalizacja funkci
Wartość średnia funkci
L 3 Complex functions and Polynomials
Matematyka cw8 Badanie funkci Wykres funkcji
Bezhanov K A , i dr Programma i zadanija po teorii funkcij kompleksnogo peremennogo (3 kurs FRTK i F
Betcke T OPTIMAL SCALING OF GENERALIZED AND POLYNOMIAL EIGENVALUE PROBLEMS
Turbiner Lie Algebraic Approach 2 the Theory of Polynomial Solutions (1992) [sharethefiles com]
USPRAWNIANIE FUNKCI PERCEPCYJNO MOTORYCZNEJ
więcej podobnych podstron