1
OSCYLATOR DRGA
Ń
HARMONICZNYCH
(NIETŁUMIONYCH)
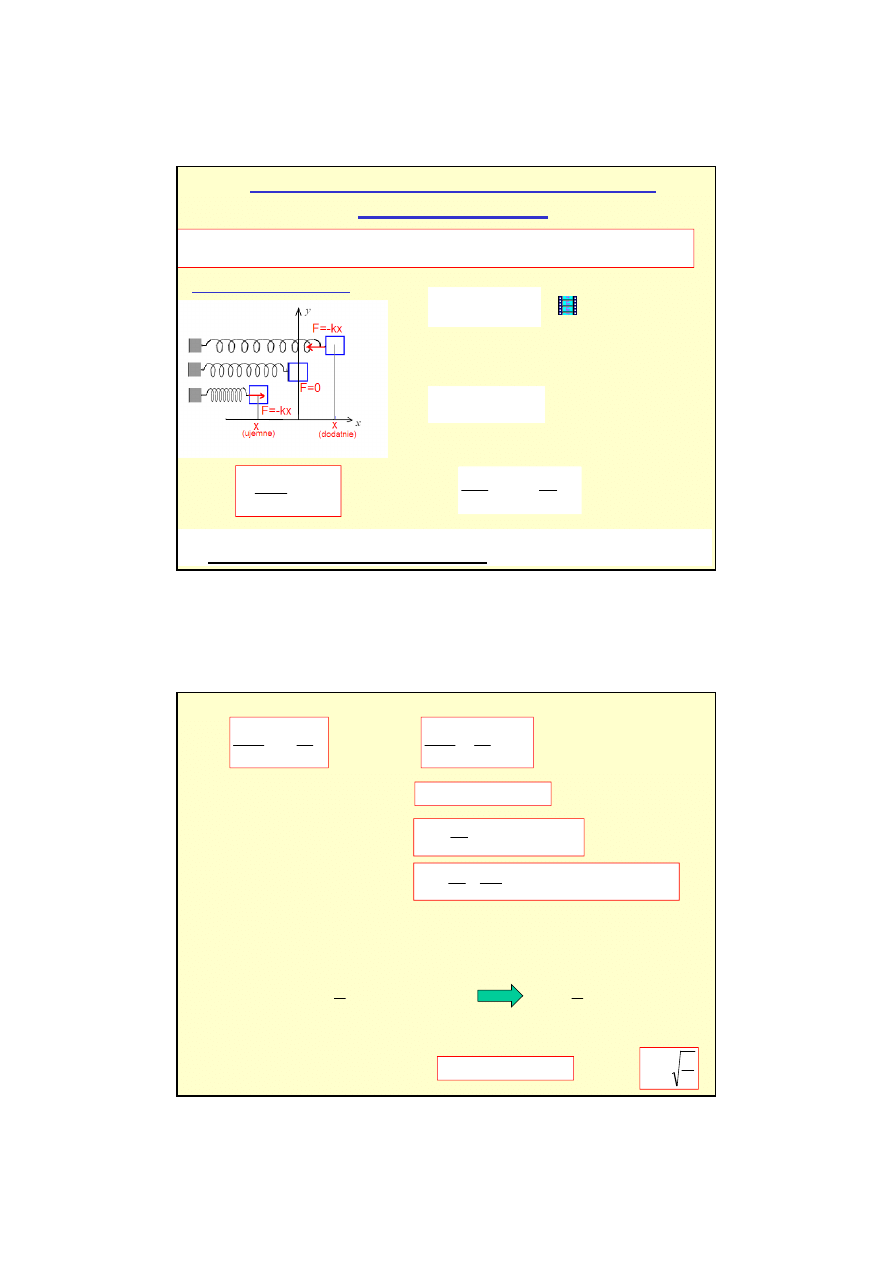
x
k
F
−
=
Sił
ą
harmoniczn
ą
(spr
ęż
ysto
ś
ci) nazywamy sił
ę
działaj
ą
c
ą
na ciało, proporcjonaln
ą
do przesuni
ę
cia tego ciała od pocz
ą
tku układu i skierowan
ą
ku pocz
ą
tkowi układu.
x
k
ma
−
=
Korzystamy z drugiej zasady
dynamiki Newtona:
Masa na spr
ęż
ynie
x
k
t
x
m
−
=
2
2
d
d
Czyli:
Aby znale
źć
kinematyczne równanie ruchu x(t) trzeba rozwi
ą
za
ć
równanie ró
ż
niczkowe
tzw. równanie oscylatora drga
ń
harmonicznych.
=
t
t
d
x
d
x
f
t
d
x
d
,
,
2
2
równanie
ró
ż
niczkowe
(II rz
ę
du):
równanie ruchu
(II zas dyn. Newtona)
x
m
k
t
d
x
d
−
=
2
2
(*)
inaczej:
0
2
2
=
+
x
m
k
t
d
x
d
)
cos(
)
(
0
ϕ
ω
+
=
t
A
t
x
)
sin(
)
0
0
ϕ
ω
ω
+
−
=
=
t
A
t
d
x
d
(t
v
Zgadujemy rozwi
ą
zanie postaci:
Obliczamy pierwsz
ą
:
i drug
ą
pochodn
ą
:
(przy okazji obliczyli
ś
my pr
ę
dko
ść
i przyspieszenie)
)
(
)
cos(
2
0
0
2
0
2
2
t
x
ω
t
Aω
dt
x
d
dt
d
a(t)
−
=
+
−
=
=
=
ϕ
ω
v
Rozwi
ą
zanie ogólne równania
Podstawiamy do równania oscylatora drga
ń
harmonicznych:
0
)
cos(
)
cos(
0
0
2
0
=
+
+
+
−
ϕ
ω
ϕ
ω
t
A
m
k
t
Aω
m
k
ω
=
0
(*)
to:
)
cos(
)
(
0
ϕ
ω
+
=
t
A
t
x
gdzie:
m
k
ω
=
2
0
2
Ogólniej mo
ż
emy zapisa
ć
,
ż
e rozwi
ą
zaniem równania oscylatora drga
ń
harmonicznych postaci:
)
cos(
)
(
0
ϕ
ω
+
=
t
A
t
x
0
2
0
2
2
=
+
x
ω
dt
x
d
jest funkcja:
0
ω
gdzie:
zale
ż
y od układu drgaj
ą
cego
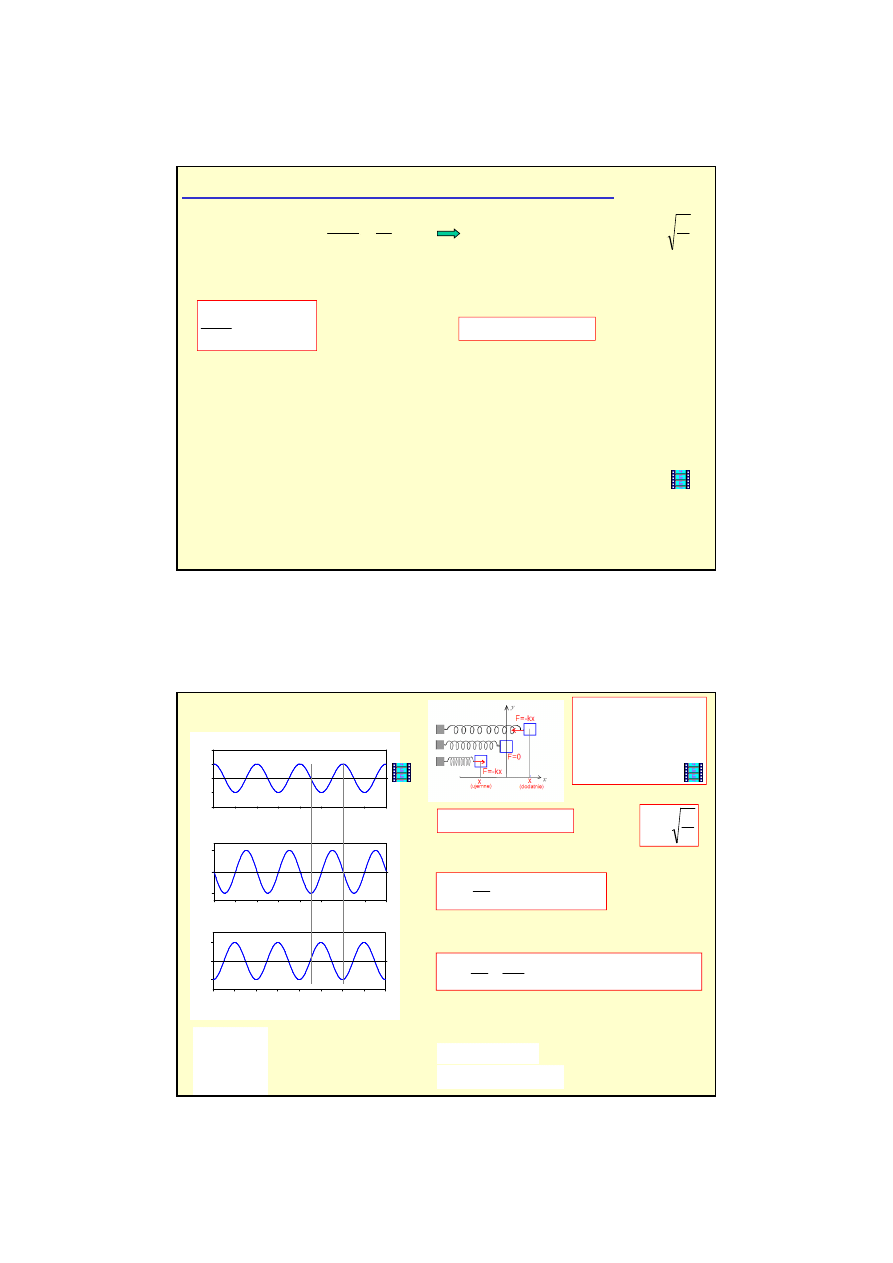
Dla oscylatora drga
ń
harmonicznych okres drga
ń
nie zale
ż
y od amplitudy
A
.
0
/
2
ω
T
π
=
Okres drga
ń
wynosi
, cz
ę
stotliwo
ść
drga
ń
definiujemy jako:
0
/
2
ω
T
π
=
π
2
/
/
1
0
ω
T
f
=
=
(jednostka cz
ę
stotliwo
ś
ci drga
ń
1 Hz = 1 s
-1
)
Dla spr
ęż
yny mieli
ś
my:
0
d
d
2
2
=
+
x
m
k
t
x
m
k
ω
=
0
)
cos(
)
(
0
ϕ
ω
+
=
t
A
t
x
Ogólne równanie oscylatora drga
ń
harmonicznych
Je
ś
li ruch ciała opisany jest powy
ż
szym równaniem ró
ż
niczkowym to
znamy jego rozwi
ą
zanie.
)
sin(
)
0
0
ϕ
ω
ω
+
−
=
=
t
A
t
d
x
d
(t
v
m
k
ω
=
0
)
cos(
)
(
0
ϕ
ω
+
=
t
A
t
x
gdzie:
Interpretacja rozwi
ą
zania:
A - amplituda ruchu
ωt + φ - fazą drgań
ω
0
=2
π
/T – częst. kątowa
T- okres drgań
φ - faza początkowa
Stałe A i
φ
s
ą
wyznaczone
przez warunki pocz
ą
tkowe:
)
cos(
)
0
(
ϕ
A
x
=
)
sin(
)
0
0
ϕ
ω
A
(
−
=
v
t
A
-A
T
T/2
x(t)
0
0
2T
3T
v
max
T
T/2
v(t)
0
0
2T
3T
T
T/2
0
0
2T
3T
-v
max
a
max
-a
max
a(t)
t
t
2
0
max
0
max
max
Aω
a
Aω
A
x
=
=
=
v
φ=0
)
(
)
cos(
2
0
0
2
0
2
2
t
x
ω
t
Aω
dt
x
d
dt
d
a(t)
−
=
+
−
=
=
=
ϕ
ω
v
3
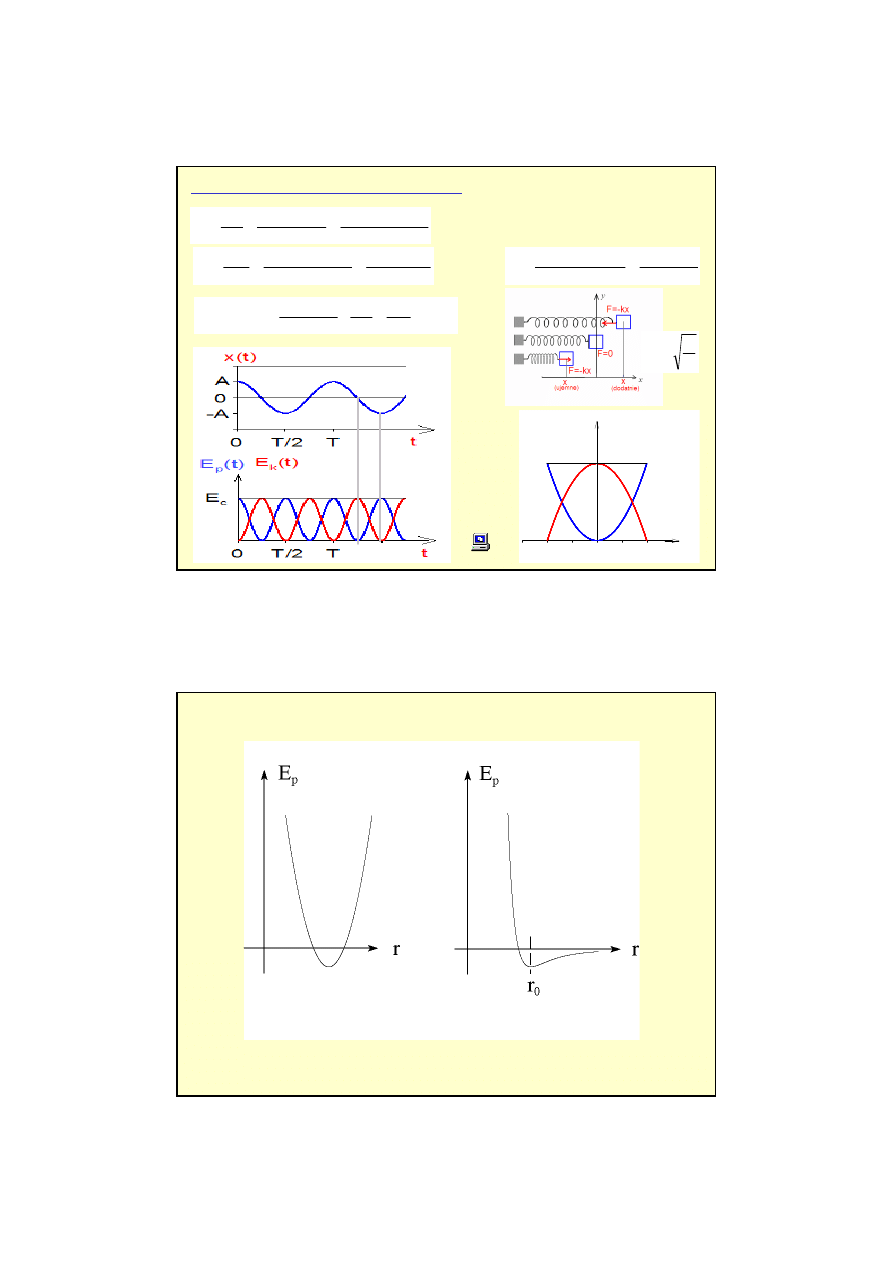
Energia w ruchu harmonicznym
2
cos
2
cos
2
0
2
2
2
0
0
2
2
2
t
A
m
t
A
k
x
k
E
p
ω
ω
ω
=
=
=
t
A
(t)
0
0
sin
ω
ω
−
=
v
t
A
t
x
0
cos
)
(
ω
=
k
m
=
2
0
ω
2
sin
2
sin
2
0
2
2
0
2
2
2
0
2
t
kA
t
A
m
m
E
k
ω
ω
ω
=
=
=
v
2
)
(
2
)
cos
1
(
2
2
0
2
2
x
A
k
t
kA
E
k
−
=
−
=
ω
inaczej:
.
2
2
2
)
(
2
2
2
2
const
A
k
x
k
x
A
k
E
E
E
p
k
c
=
=
+
−
=
+
=
-A
E
p
(t)
0
x
E
k
(t)
E
c
A
lub
m
k
ω
=
0
cz
ę
stotliwo
ść
drga
ń
atomów: f
≅≅≅≅
10
14
Hz
Przykład 1.
atomy w sieci krystalicznej
4
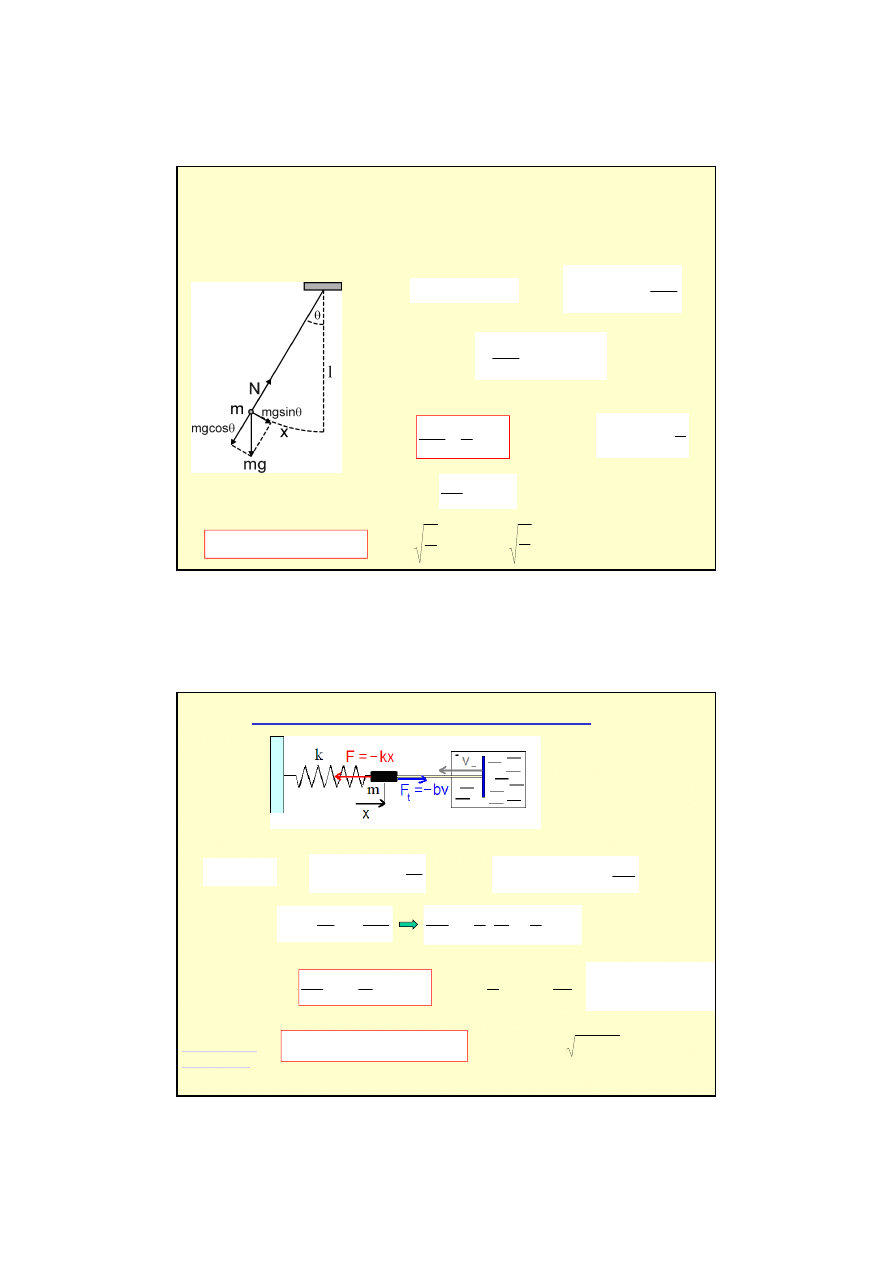
Przykład 2.
wahadło matematyczne
ciało o masie punktowej,
zawieszone na cienkiej,
niewa
ż
kiej, nierozci
ą
gliwej nici
składowa siły
powoduj
ą
ca
ruch:
2
2
d
d
t
x
m
ma
F
=
=
θ
sin
d
d
2
2
mg
t
x
m
−
=
θ
sin
mg
F
−
=
II zasada dynamiki
Newtona:
czyli:
rozwiazanie równania oscylatora
drga
ń
harmonicznych:
)
cos(
)
(
0
0
ϕ
ω
+
=
t
x
t
x
l
g
=
0
ω
g
l
T
π
2
=
0
2
2
=
+
x
l
g
d t
x
d
poniewa
ż
:
l
x
=
≈
θ
θ
sin
0
2
0
2
2
=
+
x
ω
d t
x
d
dla małych wychyle
ń
θ
:
dt
dx
b
b
F
x
t
−
=
−
=
v
x
k
F
s
−
=
siły działaj
ą
ce na ciało:
2
2
d t
x
d
m
ma
F
F
F
t
s
=
=
+
=
II zasada dynamiki Newtona:
0
2
2
x =
m
k
+
dt
dx
m
b
+
d t
x
d
2
2
d t
x
d
= m
dt
dx
-kx -b
inaczej:
równania oscylatora
drga
ń
harmonicznych
tłumionych (r. ruchu)
0
2
2
0
2
2
x =
+ ω
dt
dx
β
+
d t
x
d
2m
b
=
β
m
k
=
2
0
ω
β
ω
ω
2
2
-
=
0
rozwi
ą
zanie:
(dodatek 1)
)
+
t
(
Ae
=
x
t
ϕ
ω
β
cos
−
(
ββββ
- współczynnik tłumienia,
ω
0
-cz
ę
st. k
ą
towa drga
ń
własnych)
gdzie:
RUCH HARMONICZNY TŁUMIONY
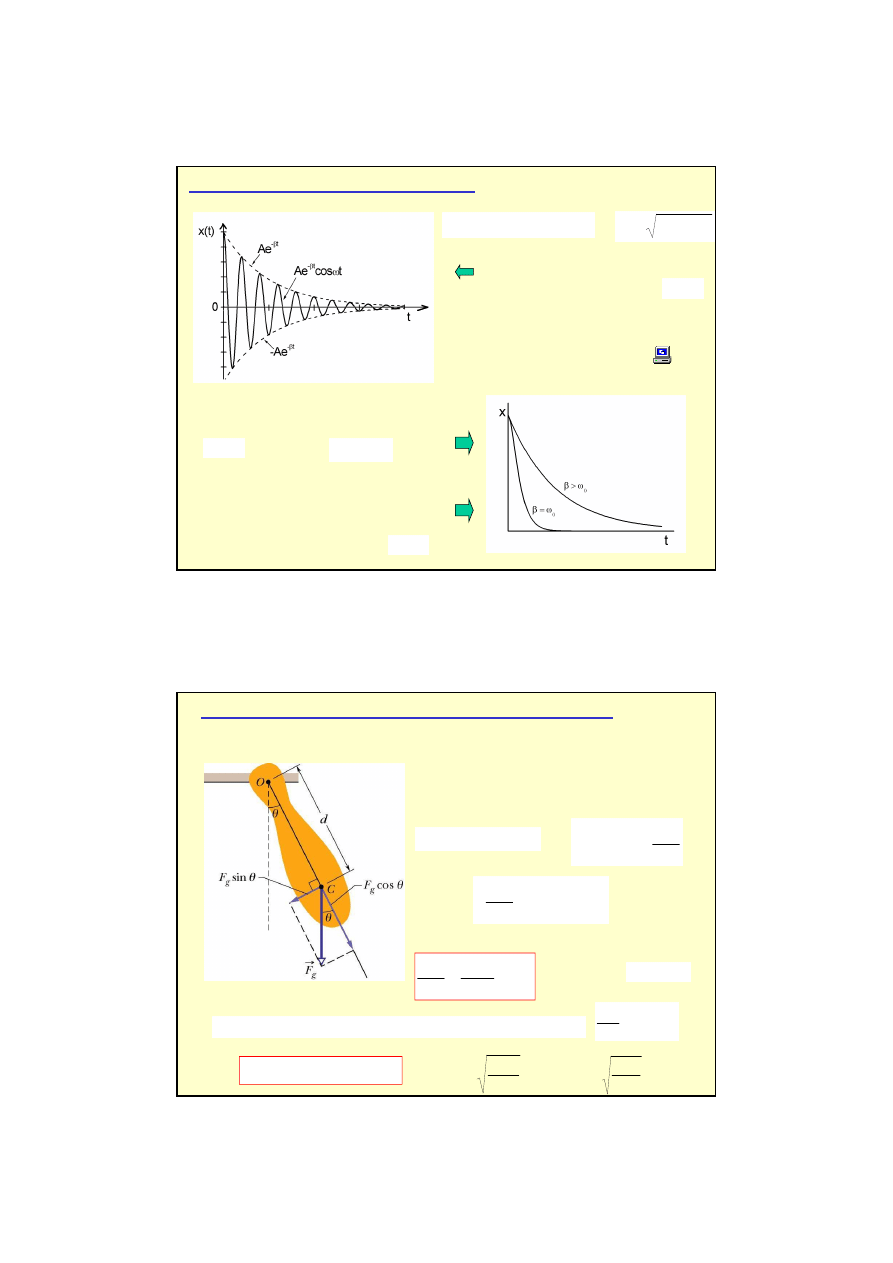
5
2
2
0
β
ω
ω
−
=
Oscylacyjny charakter ruchu zachowany
zostaje dla
słabego tłumienia.
β
ω
>
0
Gdy tłumienie (opór) stanie si
ę
dostatecznie
du
ż
e ruch przestaje by
ć
ruchem drgaj
ą
cym,
a ciało wychylone z poło
ż
enia równowagi
powraca do niego
asymptotycznie.
β
ω
<
0
Szczególny przypadek odpowiada sytuacji,
gdy mówimy wtedy o tłumieniu
krytycznym.
β
ω
=
0
t
e
A
x
β
−
=
)
+
t
(
Ae
=
x
t
ϕ
ω
β
cos
−
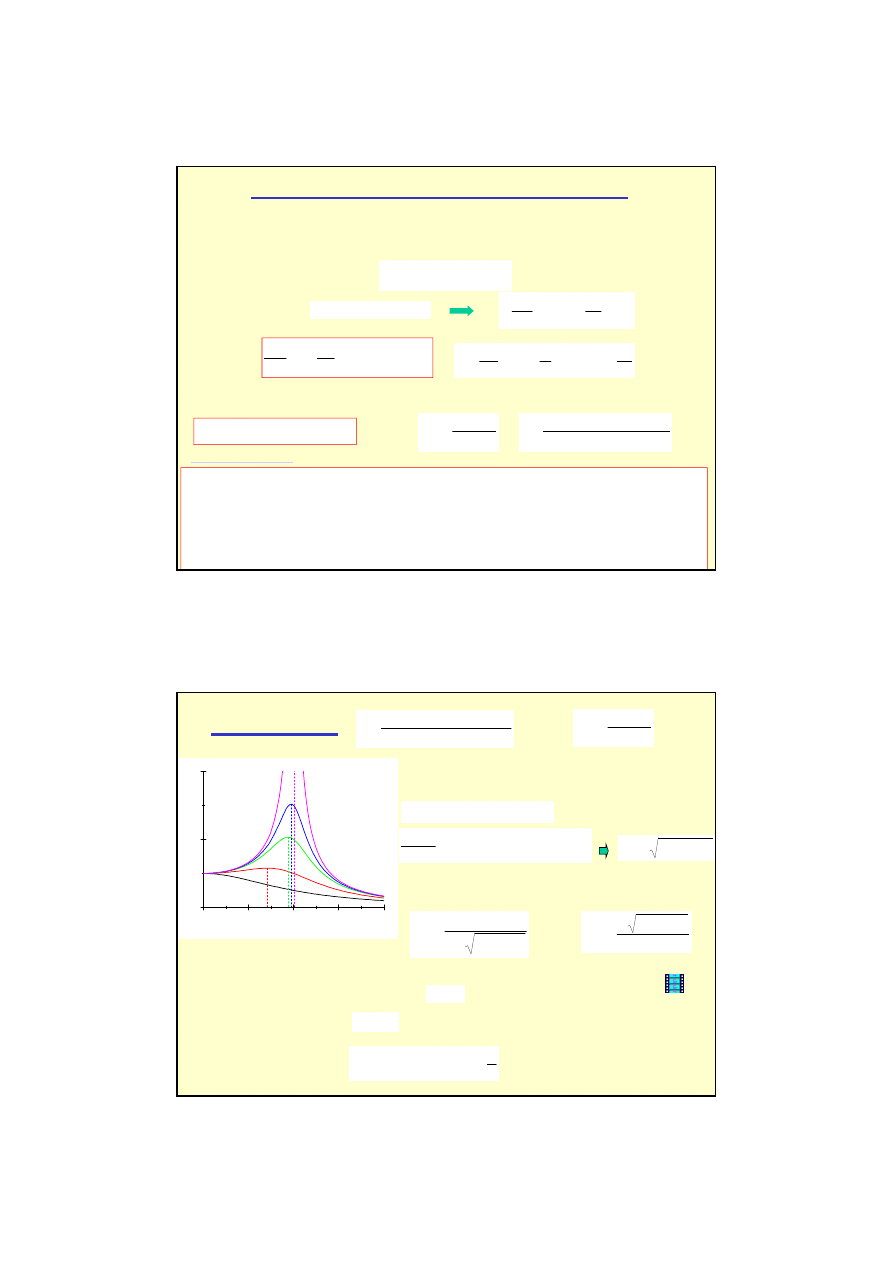
Oscylator tłumiony - wnioski
Przykład ruchu (1): Wahadło fizyczne
moment siły
powoduj
ą
cy
ruch:
2
2
d
d
t
I
I
M
θ
ε
=
=
θ
θ
sin
d
d
2
2
mgd
t
I
−
=
θ
sin
d
mg
M
−
=
II zasada dynamiki
Newtona dla bryły
sztywnej:
czyli:
dla małych wychyle
ń
θ
:
0
d
d
2
2
=
+
θ
θ
I
mgd
t
poniewa
ż
:
θ
θ
≈
sin
rozwi
ą
zanie równania oscylatora drga
ń
harmonicznych:
)
cos(
)
(
0
0
ϕ
ω
θ
θ
+
=
t
t
I
mgd
=
0
ω
mgd
I
T
π
2
=
0
d
d
2
0
2
2
=
+
θ
ω
θ
t
PRZYKŁADY RUCHU BRYŁY SZTYWNEJ
6
Je
ż
eli chcemy podtrzyma
ć
drgania to musimy działa
ć
odpowiedni
ą
sił
ą
zewn
ę
trzn
ą
F(t)
Sił
ę
tak
ą
nazywamy sił
ą
wymuszaj
ą
c
ą
:
t
F
t
F
ω
sin
)
(
0
=
Równanie ruchu:
)
(t
F
b
x
k
ma
+
−
−
=
v
F(t)
t
d
x
d
b
x
k
t
d
x
d
m
+
−
−
=
2
2
t
ω
α
x
ω
t
d
x
d
β
t
d
x
d
sin
2
0
2
0
2
2
=
+
+
m
F
m
k
m
b
0
0
2
0
oraz
,
2
=
=
=
α
ω
β
układ jest pobudzany z cz
ę
sto
ś
ci
ą
ω
ró
ż
n
ą
od cz
ę
sto
ś
ci własnej
ω
0
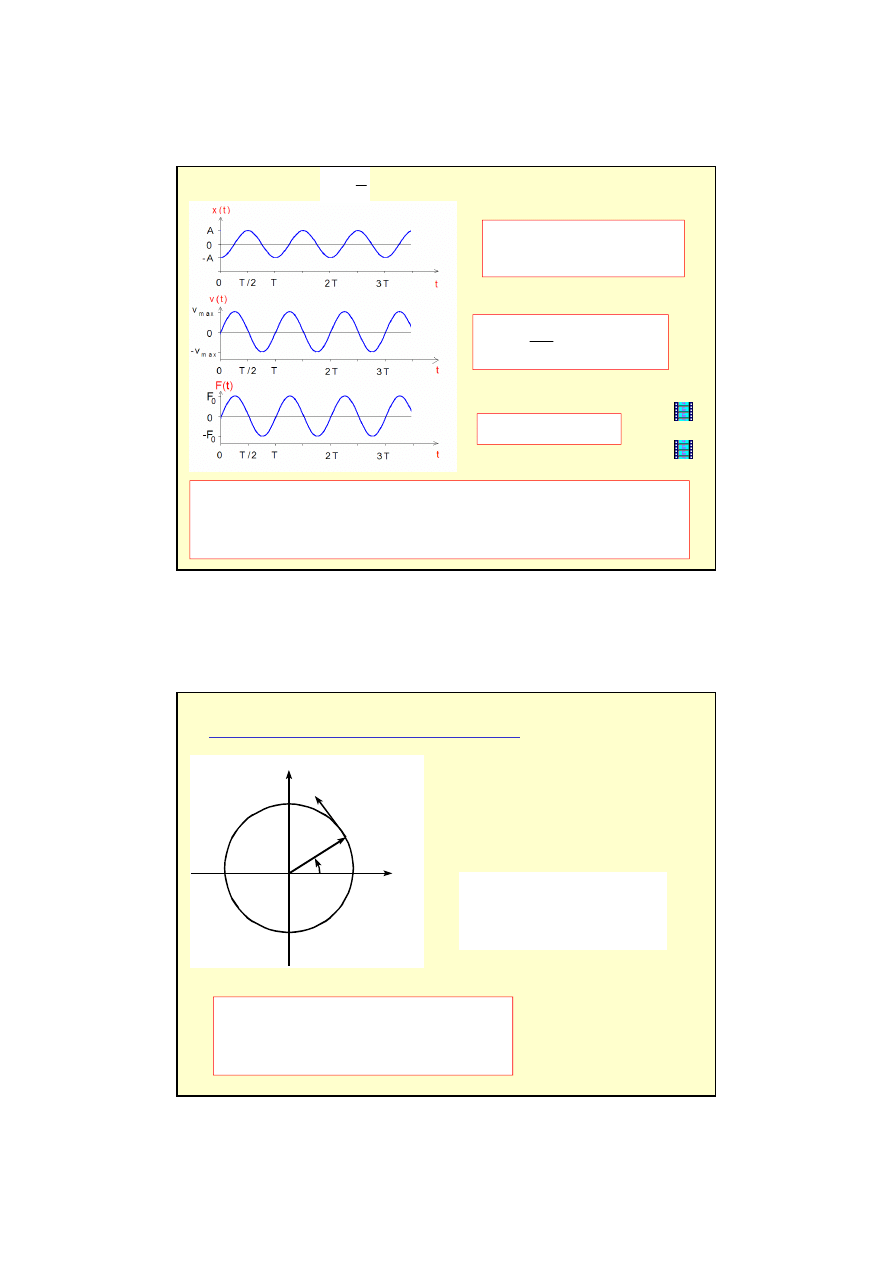
DRGANIA WYMUSZONE I REZONANS
)
sin(
)
(
ϕ
ω
+
=
t
A
t
x
2
2
0
2
ω
ω
βω
ϕ
−
−
=
tg
2
/
1
2
2
2
2
2
0
0
]
4
)
[(
ω
β
ω
ω
α
+
−
=
A
gdzie:
WNIOSKI:
•Drgania (wymuszone) w stanie ustalonym odbywaj
ą
si
ę
z cz
ę
sto
ś
ci
ą
siły
zewn
ę
trznej, a nie z cz
ę
sto
ś
ci
ą
własn
ą
•Amplituda i faza zale
żą
od relacji pomi
ę
dzy cz
ę
sto
ś
ci
ą
wymuszaj
ą
c
ą
ω
, a cz
ę
sto
ś
ci
ą
własn
ą
ω
0
oraz od współczynnika tłumienia
(patrz dodatek 2)
ω
0
A
ω
β
4
β
3
β
2
β
1
β
0
= 0
β
0
<β
1
<β
2
<β
3
<β
4
)
..... rezonans
2
/
1
2
2
2
2
2
0
0
]
4
)
[(
ω
β
ω
ω
α
+
−
=
A
Dla drgań nietłumionych ( ) :
2
ππππ
ϕϕϕϕ
ϕϕϕϕ
−
→
⇒
−∞
→
tg
0
→
β
1)
∞
→
r
A
2)
Gdy siła wymuszaj
ą
ca osi
ą
ga
odpowiedni
ą
cz
ę
stotliwo
ść
:
2
2
0
2
β
ω
ω
−
=
r
2
2
2
2
2
0
4
)
(
)
(
ω
β
ω
ω
ω
+
−
=
f
0
8
)
(
4
)
(
2
2
2
0
=
+
−
−
=
ω
β
ω
ω
ω
ω
ω
d
df
2
2
0
0
2
β
ω
β
α
−
=
r
A
to amplituda drgań gwałtownie
rośnie:
β
β
ω
ϕ
2
2
0
2
−
−
=
tg
2
2
0
2
ω
ω
βω
ϕ
−
−
=
tg
7
)
sin(
)
(
0
t
F
t
F
ω
=
)
cos(
)
2
/
sin(
)
(
t
A
t
A
t
x
ω
π
ω
−
=
−
=
)
sin(
d
d
)
(
t
A
t
x
t
ω
ω
=
=
v
2
π
ϕ
−
=
Co oznacza warunek:
•Siła wymuszająca jest w tej samej fazie co prędkość ciała (ma ten sam kierunek i zwrot
co prędkość) – cały czas działa konstruktywnie i przyspiesza ciało.
•Siła tłumiąca miała zawsze zwrot przeciwny do prędkości - działa destruktywnie
powodując opóźnienie.
?
)
sin(
sin
)
cos(
cos
ϕ
ω
α
ϕ
ω
α
+
=
=
+
=
=
t
A
r
y
t
A
r
x
α
(t)=
ω
t +
ϕ
r=A
x
y
r
α(
α(
α(
α(
t)
Ruch harmoniczny a ruch po okr
ę
gu
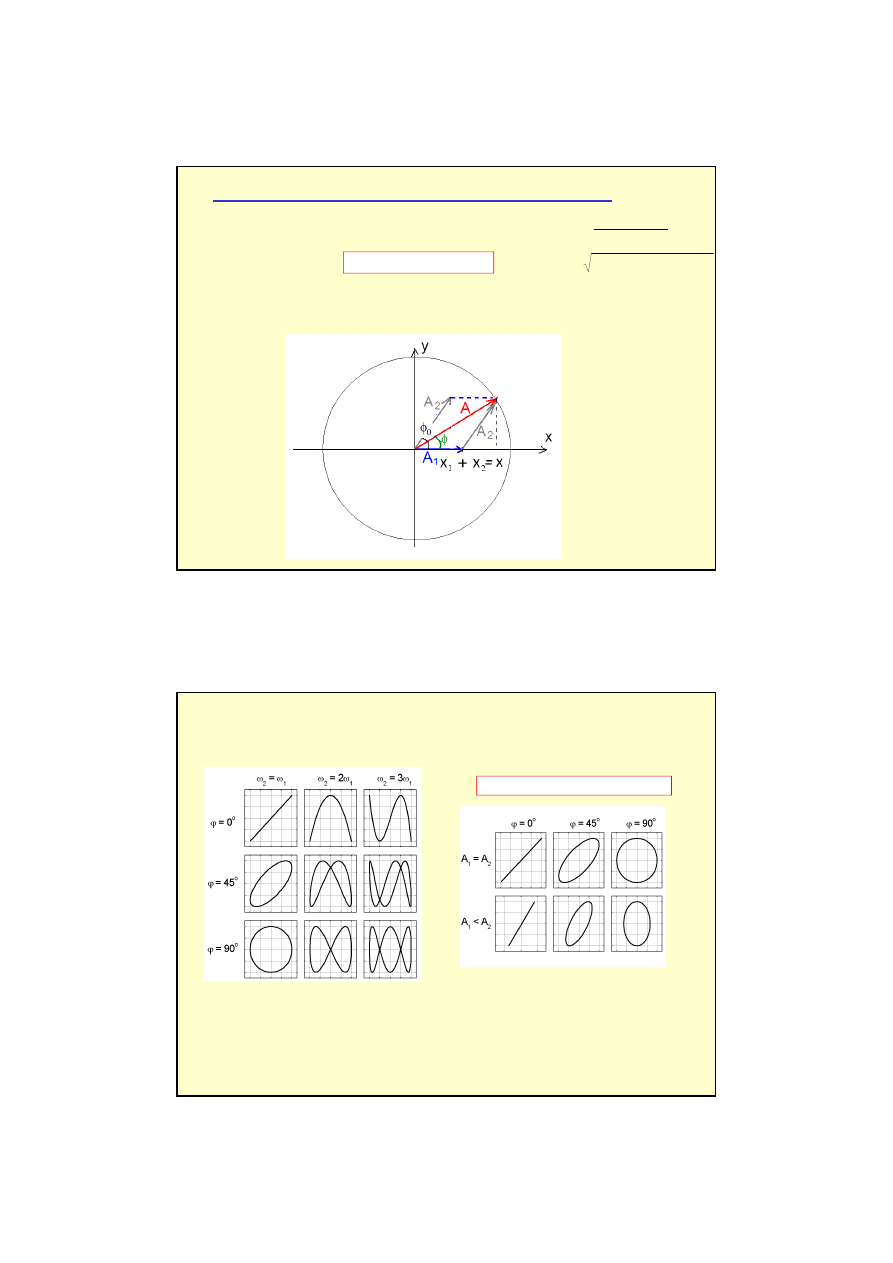
8
)
cos(
;
cos
0
2
2
1
1
ϕ
ω
ω
+
=
=
t
A
x
t
A
x
Superpozycja drga
ń
:
Drgania równoległe:
)
cos(
2
1
ϕ
ω
+
=
+
=
t
A
x
x
x
ró
ż
nica faz
φ
0
= 0
maksimum; ró
ż
nica faz
φ
0
=
π
minimum
SKŁADANIE DRGA
Ń
HARMONICZNYCH
0
2
1
2
2
2
1
0
2
1
0
2
cos
2
cos
sin
ϕ
ϕ
ϕ
ϕ
A
A
A
A
A
A
A
A
tg
+
+
=
+
=
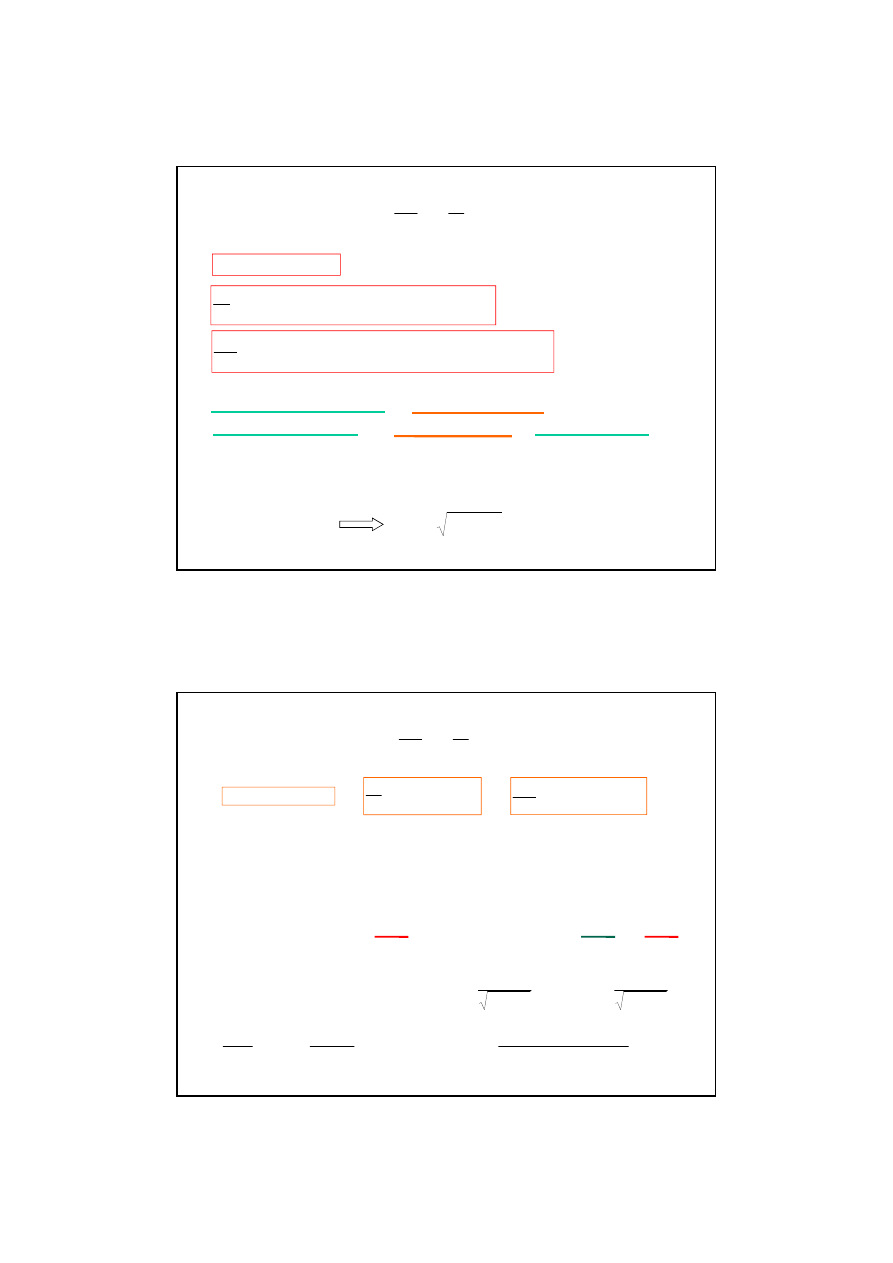
Drgania prostopadłe:
)
cos(
;
cos
2
2
1
1
ϕ
ω
ω
+
=
=
t
A
y
t
A
x
Krzywe Lissajous
9
0
d
d
2
d
d
2
0
2
2
=
+
+
x
t
x
t
x
ω
β
)
+
t
(
Ae
=
x
t
ϕ
ω
β
cos
−
)
+
t
(
e
A
)
+
t
(
e
A
=
t
x
t
t
ϕ
ω
ω
ϕ
ω
β
β
β
sin
cos
d
d
−
−
−
−
)
+
t
(
e
A
)
+
t
(
e
A
=
t
x
t
t
ϕ
ω
βω
ϕ
ω
ω
β
β
β
sin
2
cos
)
(
d
d
2
2
2
2
−
−
+
−
[
]
0
cos
sin
cos
2
sin
2
cos
)
(
2
0
2
2
=
+
−
−
+
+
+
−
−
−
−
−
−
)
+
t
(
Ae
)
+
t
(
e
A
)
+
t
(
e
A
)
+
t
(
e
A
)
+
t
(
e
A
t
t
t
t
t
ϕ
ω
ω
ϕ
ω
ω
ϕ
ω
β
β
ϕ
ω
βω
ϕ
ω
ω
β
β
β
β
β
β
0
cos
)
2
(
2
0
2
2
2
=
+
−
−
−
)
+
t
(
e
A
t
ϕ
ω
ω
β
ω
β
β
2
2
0
2
β
ω
ω
−
=
2
2
0
β
ω
ω
−
=
Rozwi
ą
zanie równania:
Dodatek 1:
Rozwi
ą
zanie równania:
Dodatek 2:
t
x
t
x
t
x
ω
α
ω
β
sin
d
d
2
d
d
0
2
0
2
2
=
+
+
)
sin(
)
(
ϕ
ω
+
=
t
A
t
x
)
cos(
d
d
ϕ
ω
ω
+
=
t
A
t
x
)
sin(
d
d
2
2
2
ϕ
ω
ω
+
−
=
t
A
t
x
(
)
t
t
A
t
A
ω
α
ϕ
ω
βω
ϕ
ω
ω
ω
sin
)
cos(
2
)
sin(
0
2
2
0
=
+
+
+
−
ϕ
ω
ϕ
ω
ϕ
ω
ϕ
ω
ϕ
ω
ϕ
ω
sin
sin
cos
cos
)
cos(
sin
cos
cos
sin
)
sin(
t
t
t
t
t
t
−
=
+
+
=
+
(
)
[
]
(
)
[
]
t
t
A
t
A
ω
α
ω
ϕ
βω
ϕ
ω
ω
ω
ϕ
βω
ϕ
ω
ω
sin
cos
cos
2
sin
sin
sin
2
cos
0
2
2
0
2
2
0
=
+
−
+
−
−
2
2
0
2
cos
sin
ω
ω
βω
ϕ
ϕ
ϕ
−
−
=
=
tg
2
/
1
2
2
2
2
2
0
0
]
4
)
[(
ω
β
ω
ω
α
+
−
=
A
ϕ
ϕ
ϕ
ϕ
ϕ
2
2
1
1
cos
1
sin
tg
tg
tg
+
=
+
=
Wyszukiwarka
Podobne podstrony:
IMIR materialu drgania id 21187 Nieznany
IMIR materiału drgania
drgania, AGH Imir materiały mix, Studia
Zad 25 10 11, AGH Imir materiały mix, Studia
IMIR materiały fale
IMIR materiały grawitacja
termo 1, AGH Imir materiały mix, Studia
matmascigi, AGH Imir materiały mix, Studia
sprawko M4, AGH Imir materiały mix, Studia
pnom sprawko, AGH Imir materiały mix, Studia
laborka-cw3 (1), AGH Imir materiały mix, Studia
Tob zagadnienia opracowane, AGH Imir materiały mix, Studia
sprawko M4 (1), AGH Imir materiały mix, Studia
IMIR materialy grawitacja
ankietaONR, AGH Imir materiały mix, Studia
IMIR materialy prad id 211874 Nieznany
więcej podobnych podstron