1 Matematyka zbiory liczbowe

mówimy też mnogość, a dział matematyki, którego zadaniem jest badanie ogólnych
własności zbiorów nazywa się teorią mnogości. Pojęcia zbioru nie definiuje się w teorii
mnogości, traktując je jako pojęcie pierwotne.

Zbiór liczbowy to zbiór, którego elementami są liczby.

Przedmioty, które należą do danego zbioru, nazywamy jego elementami.

Podstawowym pojęciem teorii mnogości jest pojęcie należenia elementu do zbioru. Zdanie
orzekające, że element a należy do zbioru A zapisujemy w sposób następujący:

∈A

Jeśli chcemy zaznaczyć, że element a nie należy do zbioru A, piszemy

∉A

Zbiory oznaczamy wielkimi literami: A, B, ..., a ich elementy małymi literami: a, b,

...

Najczęściej zbiór określamy wymieniając wszystkie jego elementy, np. {2, 4, 7}, lub

podając warunki, jakie spełniają elementy tego zbioru, np. {x

∈R: 3 < x < 10}. W obu

przypadkach używamy zapisu nawiasu klamrowego { }. Ogólnie zbiór, którego
wszystkimi elementami są x

, x

, ..., x

, oznaczamy {x

, x

, ..., x

Ze względu na ilość elementów zbiory dzielimy na:

o zbiory skończone - zawierające ściśle określoną liczbę elementów (np. zbiór

dzielników liczby 6),

o zbiory nieskończone - zawierające nieskończoną ilość elementów (np. zbiór

liczb parzystych).

Zbiory skończone definiujemy najczęściej wymieniając wprost wszystkie jego

elementy, natomiast w przypadku zbiorów nieskończonych zazwyczaj określamy warunek,
który muszą spełniać wszystkie jego elementy.

Relacje między zbiorami

Relacje między zbiorami określamy następująco:

Równość zbiorów

Zbiory A i B nazywamy równymi wtedy i tylko wtedy, gdy każdy element zbioru A

jest elementem zbioru B i na odwrót.

A = B

⇔ ∀ x (x∈A ⇔ x∈B).

Inkluzja zbiorów

Jeżeli każdy element zbioru A jest elementem zbioru B, to mówimy, że A jest

podzbiorem B i zapisujemy A

⊂B. A nazywamy podzbiorem B, zbiór B zaś nadzbiorem

zbioru A. Symbol

⊂ nazywamy znakiem inkluzji.

Matematyka – Zarządzanie

______________________________________________________________________________________

___________________________________________________________________

Dr inż. Wanda Gryglewicz-Kacerka

Państwowa Wyższa Szkoła Zawodowa we Włocławku

⊂ B jeżeli (x∈A ⇒ x∈B)

Jeśli A nie jest podzbiorem B, piszemy A

⊄ B.

Zbiory rozłączne

Zbiory, których iloczyn jest zbiorem pustym, nazywamy rozłącznymi.

A ∩ B = Ø

Iloczyn kartezjański

Zbiór A×B nazywamy iloczynem kartezjańskim zbiorów A i B jeśli:

A×B = {(x, y): x

∈A ∧ y∈B}

Dla dowolnych zbiorów A, B, C zachodzi:

⊂A

jeżeli A

⊂B i B⊂C, to A⊂C

jeżeli A

⊂B i B⊂A, to A = B

Prawa rachunku zbiorów A i B:

przemienność sumy zbiorów

∪ B = B ∪ A

przemienność iloczynu zbiorów

A ∩ B = B ∩ A

łączność sumy zbiorów

∪ B) ∪ C = A ∪ (B ∪ C)

łączność iloczynu zbiorów

(A ∩ B) ∩ C = A ∩ (B ∩ C)

rozdzielność iloczynu względem sumy zbiorów

A ∩ (B

∪ C) = (A ∩ B) ∪ (A ∩ C)

rozdzielność sumy względem iloczynu zbiorów

∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

prawa de Morgana dla zbiorów

(A ∩ B)' = A'

∪ B'

∪ B)' = A' ∩ B'

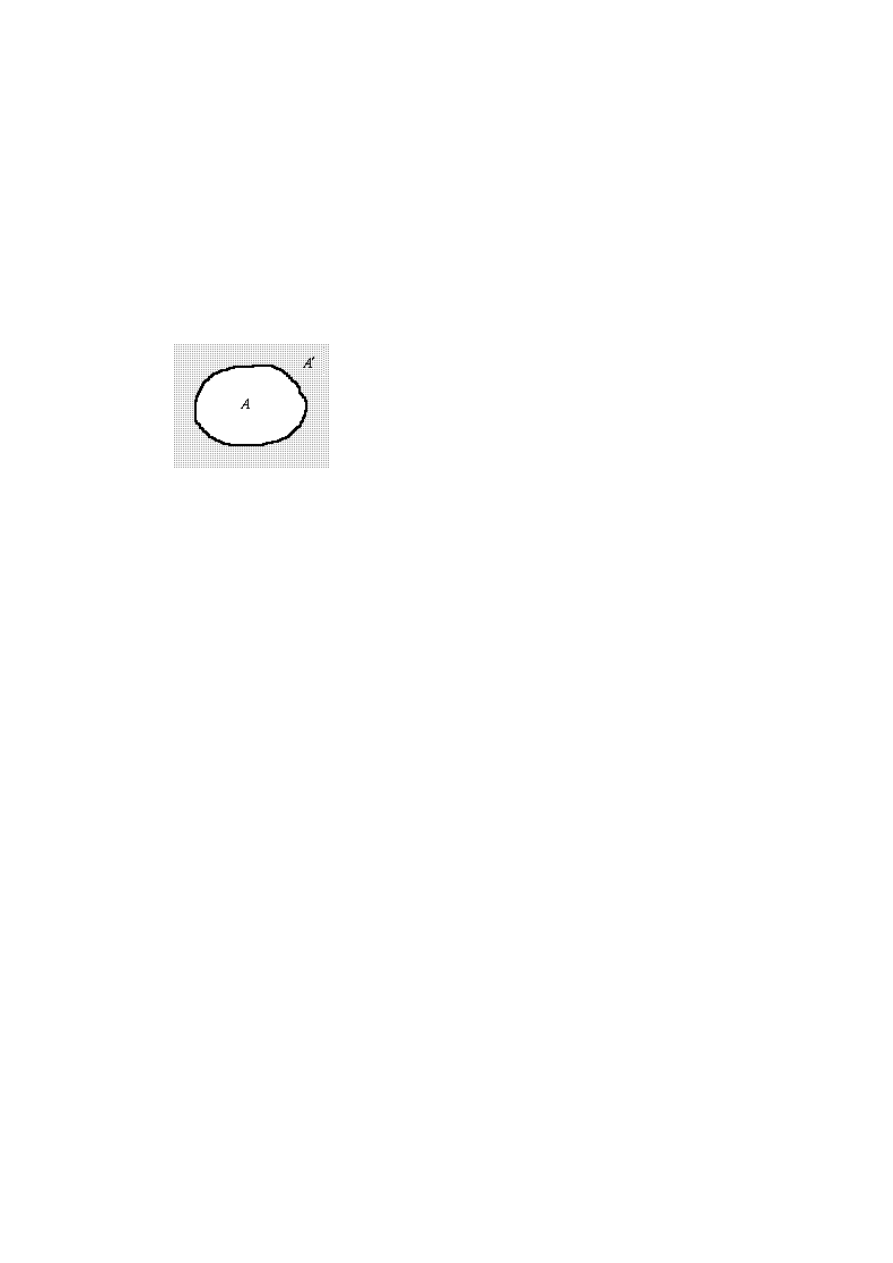
Przestrzeń - dopełnienie zbioru

Matematyka – Zarządzanie

______________________________________________________________________________________

___________________________________________________________________

Dr inż. Wanda Gryglewicz-Kacerka

Państwowa Wyższa Szkoła Zawodowa we Włocławku

Często w algebrze zbiorów mamy do czynienia ze zbiorami, które są podzbiorami

pewnego ustalonego zbioru, który nazywamy przestrzenią:

Nich X będzie przestrzenią.

Dopełnieniem zbioru A

⊂ X nazywamy zbiór X\A i oznaczamy symbolem A'

A' jest zatem zbiorem tych wszystkich elementów przestrzeni X, które nie są

elementami zbioru A. Jeżeli przestrzeń X jest ustalona, to z definicji dopełnienia zbioru
wynika, że dla każdego A

⊂ X i każdego x∈X spełniony jest warunek (x∈A') ⇔ (x∉A).

Dopełnienie zbioru A' można przedstawić graficznie jako obszar zacieniowany:

Dla dowolnego podzbioru A przestrzeni X zachodzi:

∪ A = X

X ∩ A = A

X' = 0

0' = X

(A')' = A

Moc zbioru

Georg Cantor, twórca teorii mnogości, określał moc zbioru jako pewne

uporządkowanie. Moc zbioru określa wielkość danego zbioru, a zbiory mają tę samą moc,
gdy mają tyle samo elementów. Określeniem mocy zbioru jest liczba kardynalna tego
zbioru. Liczba kardynalna zbioru skończonego jest równa liczbie jego elementów.

Równość mocy zbiorów określamy jako równoliczność.

Zbiory X i Y nazywamy równolicznymi, jeśli istnieje funkcja różnowartościowa

f:X→Y przekształcająca zbiór X na Y. Równoliczność zbiorów zapisujemy X ~ Y.

Dla dowolnych zbiorów X, Y, Z, zachodzi:

o X ~ X
o X ~ Y

⇒ Y ~ X

o (X ~ Y)

∧ (Y ~ Z) ⇒ X ~ Z

Zamiast mówić, że dane zbiory są równoliczne, można również mówić, że zbiory te

są równej mocy lub że mają tę samą liczbę kardynalną.

Posługując się pojęciem równoliczności można zdefiniować pojęcia zbiorów

skończonego i nieskończonego.

Matematyka – Zarządzanie

______________________________________________________________________________________

___________________________________________________________________

Dr inż. Wanda Gryglewicz-Kacerka

Państwowa Wyższa Szkoła Zawodowa we Włocławku

Zbiór nieskończony to zbiór, który jest równoliczny z pewnym swoim właściwym

podzbiorem. Liczbę kardynalną nazywamy nieskończoną, gdy jest mocą pewnego zbioru
nieskończonego.

Zbiór skończony, to zbiór, który nie jest nieskończony. Moc zbioru skończonego

wyraża się zawsze pewną nieujemną liczbą całkowitą.

Zbiory przeliczalne i nieprzeliczalne

Zbiór przeliczalny:
Zbiór A ≠ 0 jest przeliczalny wtedy i tylko wtedy, gdy jest on zbiorem wyrazów

pewnego ciągu nieskończonego, czyli wtedy i tylko wtedy, gdy istnieje funkcja f
przekształcająca zbiór wszystkich liczb naturalnych na zbiór A.

Zbiór przeliczalny zatem to zbiór skończony lub równoliczny ze zbiorem wszystkich

liczb naturalnych. Zbiory przeliczalne nieskończone są równej mocy. Moc zbiorów
przeliczalnych nieskończonych oznaczamy symbolem

ℵ0 (czytaj: alef zero).

Przykłady zbiorów przeliczalnych:

o podzbiór zbioru przeliczalnego jest zbiorem przeliczalnym,
o

suma dowolnej skończonej ilości zbiorów przeliczalnych jest zbiorem
przeliczalnym,

o produkt kartezjański zbiorów przeliczalnych jest zbiorem przeliczalnym,
o

zbiór wszystkich liczb całkowitych jest zbiorem przeliczalnym,

zbiór wszystkich liczb wymiernych jest zbiorem przeliczalnym,

zbiór wszystkich ciągów skończonych o wyrazach należących do ustalonego
zbioru przeliczalnego jest zbiorem przeliczalnym,

zbiór wszystkich wielomianów jednej zmiennej o współczynnikach
wymiernych jest przeliczalny,

zbiór wszystkich liczb algebraicznych jest przeliczalny.

Zbiór nieprzeliczalny:
Zbiór nieprzeliczalny to zbiór, który nie jest przeliczalny.
Zbiór liczb rzeczywistych przedziału <0, 1> jest zbiorem nieprzeliczalnym, gdyż nie

istnieje ciąg o wyrazach z przedziału <0, 1>, taki że każda liczba rzeczywista z tego
przedziału jest wyrazem ciągu.

Jeżeli zbiór A jest nieprzeliczalny i A

⊂ B, to B jest również zbiorem

nieprzeliczalnym. Z twierdzenia tego wynika, że zbiór wszystkich liczb rzeczywistych jest
nieprzeliczalny.

Moc zbioru wszystkich liczb rzeczywistych nazywamy continuum i oznaczamy

symbolicznie

ℭ.

Zbiór wszystkich liczb niewymiernych oraz zbiór wszystkich liczb przestępnych jest

zbiorem nieprzeliczalnym.

Matematyka – Zarządzanie

______________________________________________________________________________________

___________________________________________________________________

Dr inż. Wanda Gryglewicz-Kacerka

Państwowa Wyższa Szkoła Zawodowa we Włocławku

Rodzaje zbiorów liczbowych

Wyodrębniamy następujące zbiory liczbowe:

o Liczby naturalne,
o Liczby całkowite,
o Liczby wymierne,
o Liczby rzeczywiste,
o Liczby zespolone,
o Wektory,
o Macierze.

Liczby naturalne, całkowite, wymierne, rzeczywiste i zespolone nazywamy także

obiektami skalarnymi. Przyjmiemy oznaczenia:

o liczby naturalne (natural numbers)

o liczby całkowite

Z (C)

o liczby wymierne (rational numbers)

o liczby rzeczywiste (real numbers)

o liczby niewymierne (irrational numbers)

R\Q

Każda liczba rzeczywista jest reprezentowana jako punkt na osi liczbowej oraz

każdemu punktowi na osi odpowiada dokładnie jedna liczba.

Rysunek 1 Reprezentacja zbiorów liczbowych na osi liczbowej

Liczby naturalne

Definiując zbiór liczb naturalnych musimy oprzeć się o pojęcia pierwotne, jakimi są:

stała 0,

relacja równości,

jednoargumentowa funkcja n' zadająca następnik liczby naturalnej n.

N = 0, 1, 2, 3, 4, 5, 6, 7, 8, ...

Liczby naturalne to liczby używane powszechnie do liczenia i ustalania kolejności.

Pojęcie liczby jest jednym z najstarszych i najbardziej abstrakcyjnych pojęć, jednak
niewiedza na temat czym liczby są, nie przeszkadza nam sprawnie się nimi posługiwać.
Liczby naturalne można ustawić w ciąg nieskończony (po kolei jedna za drugą).

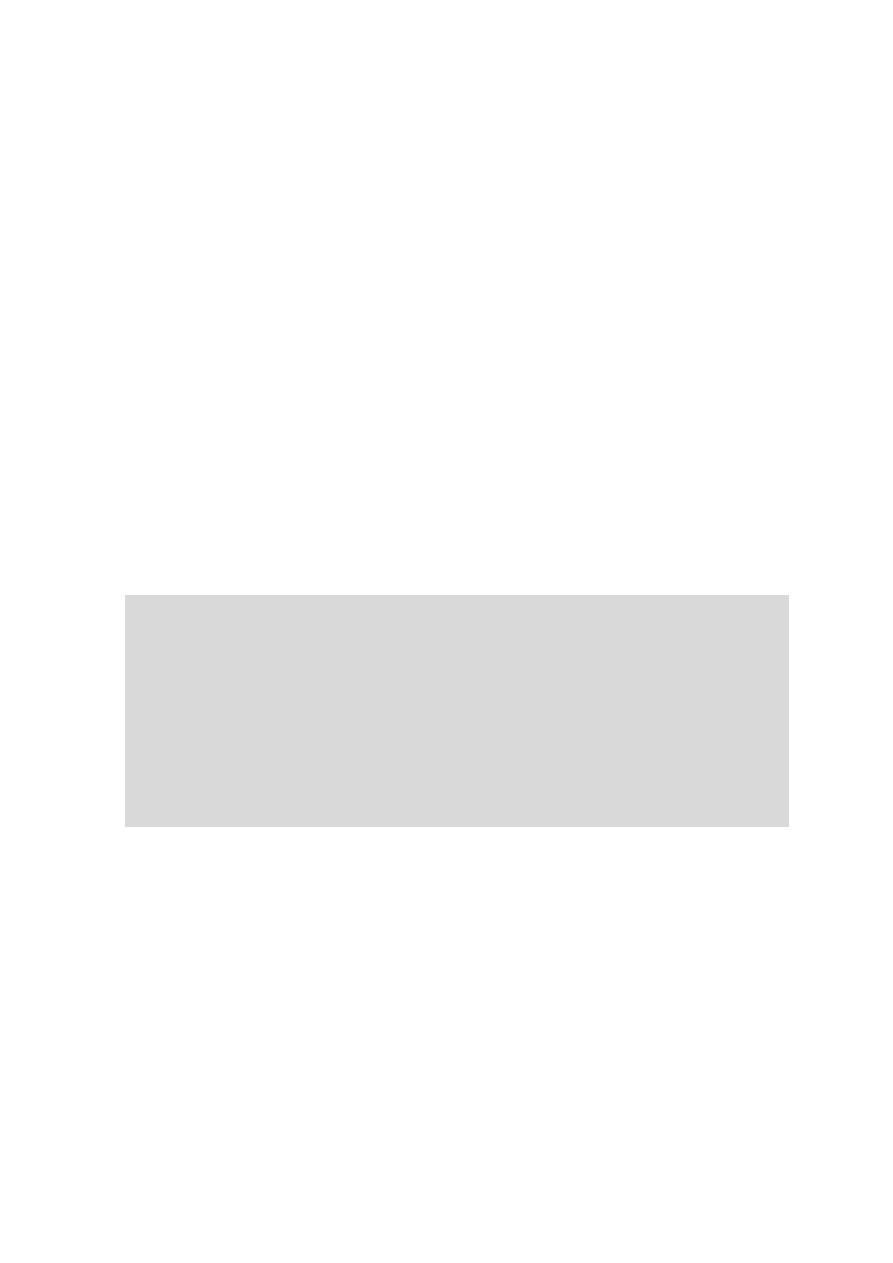
Matematyka – Zarządzanie

______________________________________________________________________________________

___________________________________________________________________

Dr inż. Wanda Gryglewicz-Kacerka

Państwowa Wyższa Szkoła Zawodowa we Włocławku

Dysponując jedynką, łatwo jest otrzymać wszystkie inne liczby naturalne. Trzeba tylko
cierpliwie dodawać ... Zbiór liczb naturalnych oznaczamy symbolem N.

Zbiór liczb naturalnych N jest najmniejszym zbiorem, spełniającym następujące

warunki:

1. 0

∈ N,

2. Jeśli n

∈ N, to n + 1 ∈ N

Czy zero jest liczbą naturalną?

To zależy od definicji. Czasem matematycy przyjmują, że zero jest liczbą naturalną,

a czasem zaczynają od jedynki. Przy określaniu kolejności jest obojętne, czy liczby
naturalne będą się zaczynać od 0, 1, czy od jakiejkolwiek innej z liczb. Przy określaniu
liczebności sensowne jest, żeby liczby naturalne zaczynały sie od zera, czyli od mocy
zbioru pustego. Natomiast jako przedmiot badań teorii liczb, zero okazuje się wyjątkiem i
do większości twierdzeń i definicji trzeba dodać zastrzeżenia, że coś jest różne albo
większe od zera.

Ile jest liczb naturalnych?

Liczb naturalnych jest nieskończenie wiele.

(Podanie ścisłej definicji zbioru liczb naturalnych nie było proste i zajęło

matematykom wiele czasu. Giuseppe Peano zaproponował następujące warunki, które
definiują zbiór liczb naturalnych:

- istnieje liczba naturalna 0,

- każda liczba naturalna ma swój następnik,

- zero nie jest następnikiem żadnej liczby naturalnej,

- różne liczby naturalne mają różne następniki,

- jeśli zero ma daną własność i następnik dowolnej liczby naturalnej ma tę własność,

to każda liczba naturalna ma tę własność (zasada indukcji matematycznej).)

Definicja i własności operacji dodawania i mnożenia w zbiorze liczb naturalnych jest

następująca:

Definicja indukcyjna (dodawania dwóch liczb naturalnych) składa się z dwóch

części. Najpierw definiujemy dodawanie dla elementu 0. Część druga definicji ma postać
implikacji, w której zakładamy, że zostało zdefiniowane działanie dla dwóch liczb
naturalnych i z tego wnioskujemy jak wygląda dodawanie danej liczby do następnika
drugiej.

Dodawanie liczb naturalnych

Dodawanie w zbiorze liczb naturalnych jest określone następująco:

Matematyka – Zarządzanie

______________________________________________________________________________________

___________________________________________________________________

Dr inż. Wanda Gryglewicz-Kacerka

Państwowa Wyższa Szkoła Zawodowa we Włocławku

Określmy dodawanie dla elementu 0: 0 + n = n dla każdego n należącego do
zbioru N,

Załóżmy, że jest określone dodawanie liczb m i n, wynik tego dodawania
oznaczmy przez (m + n ). Wówczas dodawanie m' i n określone jest
następująco: m' + n = (m + n)' dla każdych n, m należących do N.

Następnik liczby n utożsamiany jest z liczbą n+1, co oznacza, że:

(m + 1)+n=(m + n)+1.

Własność (1) określa, ile wynosi dodanie 0 do dowolnego n.
Własność (2) pokazuje, jaki jest wynik dodawania następnika m do n gdy znana jest

suma m + n. Taki zapis oznacza, że dodanie liczby m do n równe jest m - krotnemu
dodaniu do niego jedności.

W przypadku m = 0, wtedy zgodnie z definicja dodawania liczb naturalnych

określamy dodawanie kolejnych liczb jako:

1 + n= 0' + n = (0 + n)' = n'

(np. 1+1 = 0' + 1 = (0 + 1)' = 1' = 2)

2 + n = 1' + n = (1 + n)' = n''

(np. 2 + 1 = 1' + 1 = (1 + 1)' = 2' = 3)

Mnożenie liczb naturalnych

Mnożenie w zbiorze liczb naturalnych jest określone następująco:

Określmy mnożenie dla elementu 0: 0 × n = 0, dla każdego n



Załóżmy, że jest określone mnożenie liczb m i n, i wynik oznaczymy przez m× n.
Wówczas mnożenie liczb m' i n określone jest następująco: m'× n = (m× n) + n dla
każdych m, n



Mnożenie liczby m przez n polega na m-krotnym dodaniu liczby n do siebie.

Niech m = 0

1 × n = 0' × n = (0 × n) + n = 0 + n = n

2 × n = 1' × n = (1 × n) + n = n + n

...

Własności dodawania i mnożenia są następujące:
m + (n + k) = (m + n) + k (łączność),
m + n = n + m (przemienność),
m × (n + k) = m × n + m × k (rozdzielność),
m × n = n × m (przemienność),

(m × n) × k = m × (n × k) (łączność),

m × 1 = m (istnienie jedynki)

Matematyka – Zarządzanie

______________________________________________________________________________________

___________________________________________________________________

Dr inż. Wanda Gryglewicz-Kacerka

Państwowa Wyższa Szkoła Zawodowa we Włocławku

(m' = m + 1) Þ (m = n' dla pewnej liczby n),

dla każdej pary m, n liczb naturalnych: m = n lub m = n + k dla pewnego k lub n =

m + k dla pewnego k,

Porządek w zbiorze liczb naturalnych

Porządek w zbiorze liczb naturalnych jest zdefiniowany w następujący sposób:
m < n wtedy, gdy istnieje liczba naturalna k ¹ 0 taka, że m + k = n.

Wtedy, m jest liczbą mniejszą od liczby n, np.: 5<7, bo istnieje k = 2, takie że 5 + 2 =

Twierdzenie o uporządkowaniu
Dla każdej pary liczb naturalnych mamy:

m = n lub m > n lub m < n.

Powyższe twierdzenie mówi zatem, że dowolne dwie liczby albo są sobie równe albo

jedna z nich jest większa od drugiej.

Liczby całkowite

Z = { ..., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ... }

Próżno szukać wśród liczb naturalnych takiej, która jest wynikiem odejmowania

liczby większej od mniejszej. Można oczywiście uznać, że takie działanie nie ma sensu.
Taka była mniej więcej postawa uczonych w starożytnej Grecji.

Obecnie liczby ujemne już są akceptowane. Liczby całkowite razem z liczbami

naturalnymi (oraz zerem) tworzą zbiór liczb całkowitych rozciągający się od minus do plus
nieskończoności. Zbiór liczb całkowitych można więc zdefiniować, jako rozszerzenie
zbioru liczb naturalnych o wszystkie wyniki operacji odejmowania liczb naturalnych od
zera.

Zbiór liczb całkowitych jest najmniejszym podzbiorem zbioru wszystkich liczb

rzeczywistych, spełniający następujące warunki:

1. 0

∈ Z,

2. Jeśli c

∈ Z, to c + 1 ∈ Z i c - 1 ∈ Z

Liczbami całkowitymi nazywamy więc wszystkie liczby naturalne, zero oraz

wszystkie liczby przeciwne do naturalnych. Zbiór wszystkich liczb całkowitych
oznaczamy literą Z lub C.

Liczby przeciwne

Liczbą przeciwną do liczby a jest liczba (-a)

Matematyka – Zarządzanie

______________________________________________________________________________________

___________________________________________________________________

Dr inż. Wanda Gryglewicz-Kacerka

Państwowa Wyższa Szkoła Zawodowa we Włocławku

Liczbą przeciwną do liczby dodatniej jest liczba ujemna, a liczbą przeciwną do

liczby ujemnej jest liczba dodatnia. Liczbą przeciwną do zera jest zero.

Porównywanie liczb całkowitych

Porównując liczby całkowite należy pamiętać, że:

- liczba dodatnia jest zawsze większa od liczby ujemnej,

- z dwóch liczb ujemnych większa jest ta, która leży bliżej zera na osi liczbowej,

- liczba zero jest większa od każdej liczby ujemnej.

[W starożytności ani rachmistrze babilońscy czy egipscy, ani greccy myśliciele oraz

arabowie nie mieli ogólnej idei liczb ujemnych. Pierwszymi, którzy stosowali ilości
ujemne, byli matematycy indyjscy. W VI i VII w. n. e. Używali ich dla potrzeb
rachunkowych, mianowicie długi zapisywano jako wartości ujemne. Na zachodzie liczby
ujemne pojawiły się dopiero w XV wieku jako osobne byty numeryczne, którym jednak
odmawiano istnienia w postaci liczb. Otrzymały nazwę numeri absurdi i nie były uważane
za możliwe rozwiązanie równania. Dopiero w XVII wieku angielski matematyk John
Wallis zastosował współrzędne ujemne do punktów krzywej.]

Liczby całkowite są rozszerzeniem zbioru liczb naturalnych i są zdefiniowane

następująco:

Dla każdej liczby n



N rozpatrujemy formalnie liczbę - n, którą będziemy nazywali

ujemną liczbą całkowitą.

Z - zbiór liczb całkowitych, definiujemy poprzez podanie określeń porządku i

operacji mnożenia i dodawania.

Relację mniejszości w zbiorze liczb naturalnych oznaczmy teraz przez <Z w celu

zaznaczenie, że odnosi się ona do tego właśnie zbioru.

Definicja

W zbiorze liczb całkowitych dodawanie obliczamy tak jak w zbiorze liczb

naturalnych. W zależności od wartości liczb rozpatrzymy następujące :

Obie liczby są liczbami naturalnymi, wtedy

m +Z n = m+ n, gdy m, n



Obie liczby są liczbami całkowitymi ujemnymi

m +Z n = - ( k + l), gdy m = -k, n = -l i k, l



o Jedna liczba jest dodatnia, a druga ujemna

m +Z n = u



N, takie, że m = p+ u gdy m



n = -p i m



p dla pewnego p



o m +Z n = - w, gdzie w



N takie, że m = p+ w gdy m



N, n = -p i p >m dla

pewnego p



Przykład:

Matematyka – Zarządzanie

______________________________________________________________________________________

___________________________________________________________________

Dr inż. Wanda Gryglewicz-Kacerka

Państwowa Wyższa Szkoła Zawodowa we Włocławku

(-5) + (3) = - (5-3)

2 + (-1) = 1 ponieważ 2 = 1 + 1

2 + (-5) = -3 ponieważ 5 = 2 + 3

W zbiorze liczb całkowitych określamy mnożenie liczb całkowitych wykorzystując

definicję mnożenia liczb naturalnych. Rozpatrujemy następujące przypadki:

Obie liczby są dodatnie m × Z n = m × n, gdy m, n



Jedna liczba jest dodatnia, a druga ujemna m × Z n = - (m × p), gdy m



N, n

= -p, dla p



Obie liczby są ujemne m × Z n = k × l, , gdy m = -k, n = -l, dla pewnych k,
l



Odejmowanie liczb całkowitych definiujemy jako działanie odwrotne do

dodawania:

m - n = u wtedy, gdy m = n + u.

Zbiór liczb całkowitych stanowi rozszerzenie zbioru liczb naturalnych. Można w nim

wykonywać działanie odejmowania liczb, które nie zawsze było wykonalne w zbiorze
liczb naturalnych. Natomiast zbiór ten nie jest zamknięty na działanie dzielenia dwóch
liczb, tzn. że istnieją liczby całkowite, których iloraz nie należy do tego zbioru. Zbiorem
liczbowym, w którym działanie dzielenia dwóch liczb całkowitych jest wykonalne jest
zbiór liczb wymiernych.

Liczby wymierne

Liczby wymierne

Q = { x : x = p/ q , p

∈ Z , q ∈ N }

Liczby, które można zapisać w postaci ułamka (przy czym w liczniku są liczby

całkowite, a w mianowniku - naturalne prócz zera), nazywa się liczbami wymiernymi.

Liczbę x nazywamy liczbą wymierną, gdy x = p/q dla pewnych liczb całkowitych

p i q, gdzie q ≠ 0.

Zbiór liczb wymiernych oznaczamy literą Q. Każda liczba całkowita i każda liczba

naturalna jest liczbą wymierną. W odróżnieniu od liczby całkowitej, liczba wymierna nie
jest w zasadzie wielokrotnością jednostek. Wraz z liczbami wymiernymi pojęcie ilości
ulega zmianie, przechodzimy od wyliczania do wymiaru.

W życiu codziennym często znajdujemy się w sytuacji, gdy musimy jakąś całość

podzielić na części. Wtedy to każdą z tych części możemy zapisać w postaci ułamka. Jedna
z czterech części - to

1/4 , dwie z trzech części - to 2/3.

W każdym

Matematyka – Zarządzanie

______________________________________________________________________________________

___________________________________________________________________

Dr inż. Wanda Gryglewicz-Kacerka

Państwowa Wyższa Szkoła Zawodowa we Włocławku

ułamku wyróżniamy licznik, który liczy i mianownik, który określa na ile części

została podzielona całość. Licznik od mianownika oddzielony został kreską ułamkową,
która zastępuje nam dzielenie.

Ułamek to liczba oznaczająca część całości.

Zapisujemy a/b , gdzie a oznacza licznik ułamka, b oznacza mianownik ułamka.

[ Współczesny sposób zapisu ułamków pochodzi od matematyków hinduskich,

zapisywali oni licznik i mianownik, nie używając jednak kreski rozdzielającej. Dodanie
kreski rozdzielającej zawdzięczamy Arabom tłumaczącym dzieła Hindusów. W Europie
jako pierwszy w swoich pracach znane do dziś oznaczenie ułamków publikuje włoski
matematyk Fibonacci. ]

Ułamki dzielimy na właściwe i niewłaściwe.

Ułamek właściwy - to taki ułamek, w którym licznik jest mniejszy od mianownika.

Ułamki właściwe są mniejsze od 1.

Przykłady:

4/5, 1/7, 3/8

Ułamek niewłaściwy - to taki ułamek, w którym licznik jest większy od mianownika

lub równy mianownikowi. Ułamki niewłaściwe są większe lub równe 1.

Przykłady:

5/3, 12/12, 15/7

Ułamki niewłaściwe przedstawione w postaci całości i ułamka właściwego

nazywamy liczbami mieszanymi.

Przykład:

5/3= 5:3=1 r. 2= 1

Porównywanie ułamków zwykłych

Trudniej jest porównać dwa ułamki zwykłe od dwóch liczb naturalnych, na które

wystarczy, że zerkniemy okiem, a już potrafimy wskazać większą z nich. W przypadku
dwóch ułamków o jednakowych licznikach lub mianownikach porównywanie nie jest
trudne. W przypadku ułamków o różnych licznikach i różnych mianownikach, należy
sprowadzić te ułamki do wspólnego mianownika lub licznika, bo w przeciwnym wypadku
wskazanie większej może być kłopotliwe.

Jeżeli ułamki zwykłe mają takie same mianowniki to ten jest większy, który ma

większy licznik.

Matematyka – Zarządzanie

______________________________________________________________________________________

___________________________________________________________________

Dr inż. Wanda Gryglewicz-Kacerka

Państwowa Wyższa Szkoła Zawodowa we Włocławku

Jeżeli ułamki zwykłe mają takie same liczniki to ten jest większy, który ma mniejszy

mianownik.

Jeżeli ułamki nie mają ani równych liczników, ani równych mianowników, to

można sprowadzić ułamki do wspólnego mianownika lub licznika za pomocą operacji
rozszerzania.

Przykłady:

2/5< 3/5 ,

8/10> 3/10

5/12< 5/10 ,

1/3> 1/4 ,

3/4 =3·3/4·3 = 9/12 ,
4/6 =4·2/6·2 = 8/12 ,
9/12> 8/12 , a więc 3/4> 4/6

Czasami interesuje nas tylko równość dwóch ułamków, chcemy wiedzieć, że albo są

równe albo nie. Nie musimy ich skracać ani rozszerzać, aby się tego dowiedzieć. Jeśli są
równe, to zachodzi proporcja i wtedy iloczyn wyrazów skrajnych jest równy iloczynowi
wyrazów środkowych.

Jeżeli ułamki są równe, to iloczyn licznika pierwszego ułamka i mianownika

drugiego ułamka jest równy iloczynowi mianownika pierwszego ułamka i licznika
drugiego ułamka.

Przykład:

2/5= 8/20 , to 2 · 20 = 8 · 5

[ Ogólne pojęcie stosunku dwóch liczb zostało wprowadzone przez pitagorejczyków

w VI w. p.n.e. Poprzedzający ich Babilończycy i Egipcjanie używali jedynie ułamków z
licznikiem 1. Słowo ułamek pochodzi od wywodzącego się z łaciny fractio, przekładu z
arabskiego kasr - złamany, a zatem ułamki to liczby złamane, gdzie mianownik określa,
licznik liczy.]

Działania na ułamkach zwykłych
Pewną trudnością w wykonywaniu działań na ułamkach jest sprowadzenie ułamków

do wspólnego mianownika. Będzie to potrzebne zarówno przy dodawaniu, jak i
odejmowaniu ułamków, które mają różne mianowniki. Aby sprowadzić ułamki do
wspólnego mianownika, należy znaleźć dowolną metodą wspólną wielokrotność
mianowników tych ułamków. Najlepiej jeśli będzie to najmniejsza wspólna wielokrotność.
Rozszerzamy każdy z ułamków i tak oto ułamki mają takie same mianowniki.

Przykład:
Chcemy aby ułamki 5/12 oraz 4/9 miały takie same mianowniki.

Matematyka – Zarządzanie

______________________________________________________________________________________

___________________________________________________________________

Dr inż. Wanda Gryglewicz-Kacerka

Państwowa Wyższa Szkoła Zawodowa we Włocławku

Najlepszy mianownik to najmniejszy mianownik, znacznie ułatwione są wtedy

dalsze rachunki. Szukamy najmniejszej wspólnej wielokrotności liczb 12 i 9. Można to
zrobić wypisując po prostu kolejne wielokrotności tych liczb:

W12 = {12, 24, 36, 48}

W9 = {9, 18, 27, 36}

Najmniejszą wspólną wielokrotnością liczb 12 i 9 jest liczba 36, czyli naszym

wspólnym mianownikiem będzie 36. Teraz należy rozszerzyć oba ułamki. Ułamek 5/12
rozszerzamy przez 3, a ułamek 4/9 rozszerzamy przez 4. W wyniku otrzymujemy dwa
ułamki o mianowniku 36, a mianowicie 15/36 oraz 16/36.

Dodawanie i odejmowanie ułamków zwykłych
Jeżeli ułamki mają takie same mianowniki to dodajemy liczniki, a mianownik

zostawiamy bez zmian.

2/7 + 3/7 = 5/7

Jeżeli chcemy dodać liczby mieszane, dodajemy całości do całości, a ułamki do

ułamków:

2 3/8 + 5 2/8 = 7 5/8

Jeżeli ułamki zwykłe mają różne mianowniki, to najpierw należy sprowadzić ułamki

do wspólnego mianownika, a potem dodać liczniki, pozostawiając mianownik bez zmian.

Dodawanie ułamków jest przemienne i łączne.
Aby odjąć ułamki o jednakowych mianownikach, odejmujemy ich liczniki, a

mianownik zostawiamy bez zmian.

7/10 - 4/10 = 3/10

Jeżeli chcemy odjąć liczby mieszane, odejmujemy całości od całości, a ułamki od

ułamków:

4 3/5 - 1 2/5 = 3 1/5

Aby odjąć ułamki o różnych mianownikach, najpierw sprowadzamy je do wspólnego

mianownika, następnie odejmujemy.

Oznaczenia: 1/2 - ułamek zwykły , 1/2, 2[2/3] - liczba mieszana 2 2/3,

Mnożenie i dzielenie ułamków zwykłych
Aby pomnożyć liczbę naturalną przez ułamek (lub odwrotnie), mnożymy licznik

ułamka przez tę liczbę, a mianownik zostawiamy bez zmian.

Przykład

4* 3/5 = 12/5 = 2 2/5

Jeżeli chcemy pomnożyć dwa ułamki, mnożymy licznik pierwszego ułamka przez

licznik drugiego i mianownik pierwszego ułamka przez mianownik drugiego.

Przykład

Matematyka – Zarządzanie

______________________________________________________________________________________

___________________________________________________________________

Dr inż. Wanda Gryglewicz-Kacerka

Państwowa Wyższa Szkoła Zawodowa we Włocławku

2/3 · 3/5 = 6/15 = 2/5

Podczas mnożenia jeśli to możliwe można stosować skracanie ułamków. Należy

pamiętać, aby skracając zawsze wybierać jedną liczbę z licznika, drugą z mianownika.

Jeżeli chcemy pomnożyć przez siebie dwie liczby mieszane, to obie zamieniamy na

ułamki niewłaściwe i mnożymy licznik przez licznik, a mianownik przez mianownik.

Przykład

2 1/5 · 1 2/3 = 11/5 · 5/3 = 55/15 = 3· 10/15 = 3 2/3

Mnożenie ułamków jest przemienne i łączne.

Odwrotność liczby

Jeżeli iloczyn dwóch liczb jest równy 1 , to mówimy, że jedna liczba jest

odwrotnością drugiej.

4/3 jest odwrotnością 3/4 , liczba 5 jest odwrotnością 1/5 .

Aby podzielić dwie liczby należy dzielną pomnożyć przez odwrotność dzielnika.
Przykład:

1/5 : 2/3 = 1/5 · 3/2 = 3/10

Liczby niewymierne

Są liczby, których nie można przedstawić w postaci ilorazu dwóch liczb

całkowitych. Nazywamy je liczbami niewymiernymi. Liczb niewymiernych jest całe
mnóstwo - dużo więcej niż wszystkich możliwych liczb wymiernych. [Natknęli się na nie
pitagorejczycy, rozważając długości przekątnych kwadratu. ]

Liczby niewymierne to liczby, które nie są wymierne. Liczbę niewymierną nie

można przedstawić w postaci ułamka, a rozwinięcie dziesiętne liczby niewymiernej jest
nieskończone i nieokresowe.

Przykłady liczb niewymiernych: π, e, pierwiastek z 2,…….

[ Istnienie liczb niewymiernych bardzo zaskoczyło pitagorejczyków, którzy uważali,

że liczby są składnikami wszystkich bytów, których głównym zadaniem jest
przedstawianie wymiarów wielkości geometrycznych. Stało się to za sprawą twierdzenia
samego Pitagorasa i najważniejszej figury starożytnego świata - kwadratu.

I tak w kwadracie o boku długości 1, korzystając z twierdzenia Pitagorasa - długość

przekątnej musi być taka, aby jej kwadrat równał się 2. Pitagorejczycy udowodnili że nie
istnieje żadna taka liczba wymierna, której kwadrat wynosi 2. A więc przekątna i bok
kwadratu nie mają żadnej wspólnej miary. Są niewspółmierne. A mimo to jesteśmy w
stanie je zobaczyć.

Matematyka – Zarządzanie

______________________________________________________________________________________

___________________________________________________________________

Dr inż. Wanda Gryglewicz-Kacerka

Państwowa Wyższa Szkoła Zawodowa we Włocławku

Wielkości geometryczne wymykające się numeryczności zostały określone mianem

alogon - niewyrażalnych. Grecy rozwinęli teorię dotyczącą wyłącznie wielkości
geometrycznych, ustalili proporcje między wielkościami, ale odmówili im prawa do miana
liczb. Dopiero dwa tysiące lat później byty te przyłączyły się do grona liczb, a ta, której
kwadrat wynosi 2 i od której wszystko się zaczęło została nazwana liczbą niewymierną -
pierwiastkiem kwadratowym z 2. ]

Liczby rzeczywiste

Zbiór liczb rzeczywistych R to najmniejsze powiększenie zbioru liczb wymiernych,

w którym każdy ciąg rosnący i ograniczony z góry ma swoją granicę.

Zbiór liczb rzeczywistych zawiera wszystkie pierwiastki liczb naturalnych.

Pierwiastek z dwójki

jest liczbą rzeczywistą odpowiadającą długości przekątnej

kwadratu jednostkowego. Działania w zbiorze liczb rzeczywistych spełniają te same
własności co w zbiorze liczb wymiernych.

Liczby rzeczywiste nie będące liczbami wymiernymi nazywamy liczbami

niewymiernymi.

Można udowodnić, że √2, √3, √4, są liczbami niewymiernymi.
Liczby rzeczywiste wygodnie jest utożsamiać z punktami na prostej. Każdemu

punktowi prostej odpowiada jedna i tylko jedna liczba rzeczywista, i na odwrót. Liczba
rzeczywista opisuje bowiem odległość opatrzoną kierunkiem, wskazanym przez jej znak,
mierzoną za pomocą pewnej ustalonej jednostki.

Zbiór wszystkich liczb wymiernych i niewymiernych nazywa się zbiorem liczb

rzeczywistych.

Pojęcie liczby rzeczywistej obejmuje wszystkie rodzaje liczb używane w codziennej

praktyce: liczby naturalne, liczby całkowite, ułamki, pierwiastki, itp. Zbiór liczb
rzeczywistych oznaczany jest symbolem R.

Liczby rzeczywiste oznaczają ciągłość.

[Bezsilność liczb wymiernych w wyrażaniu wszystkich miar wielkości,

spowodowało, że rozbudowano pole liczb. W IX wieku arabski uczony Al-Farabi
poszerzył pojęcie liczby o liczby wymierne i niewymierne dodatnie. Dwa wieki później
matematyk arabski Omar Chajjam sformuował ogólną teorię liczby. Do liczb wymiernych
dodał takie elementy, aby wszystkie wielkości mogły zostać zmierzone. ]

Pojęcie liczb rzeczywistych możliwe jest dzięki osi ukierunkowanej. Zrozumienie

ciągłości liczb rzeczywistych, może ułatwić fakt, że wypełniają one całkowicie oś, nie
pozostawiając żadnej "dziury". Znak + lub - ma za zadanie wskazać kierunek na osi, liczba
bez znaku określa zaś długość.

Strukturę liczb niewymiernych wyjaśnimy na przykładzie liczby √2. Obliczenie jej

na kalkulatorze daje wynik: 1,4142135.

Matematyka – Zarządzanie

______________________________________________________________________________________

___________________________________________________________________

Dr inż. Wanda Gryglewicz-Kacerka

Państwowa Wyższa Szkoła Zawodowa we Włocławku

Czy jest to jednak dokładna wartość ? łatwo przekonać się że nie, gdyż podnosząc

liczbę 1,4142135 do kwadratu otrzymamy liczbę 1,9999998, która jest bliska liczbie 2, ale
jest jednak od niej mniejsza.

Dokładnej wartości 2 nie otrzymamy również zmieniając ostatnią cyfrę liczby

1,4142135 na 6, gdyż po podniesieniu do kwadratu otrzymamy wartość 2,0000001, tym
razem większą od 2.

Obliczenia przy użyciu kalkulatora z większą dokładnością dadzą podobny rezultat,

choć odchyłka od 2 będzie teraz mniejsza. Zmiana cyfry na ostatnim miejscu po przecinku
nie przyniesie również efektu.

Mamy tu do czynienia z pewną prawidłowością, a nie użyciem kalkulatora o zbyt

małej dokładności. Jest to cecha liczby √2 i wszystkich innych liczb niewymiernych - nie
dają się zapisać jako liczba ze skończoną ilością liczb po przecinku.

---------------------------------------------------------------------------------------------------

ZADANIA

Zadanie 1

Uzasadnij wybór.

Zadanie 2

Zadanie 3

Zadanie 4

Zadanie 5

Zadanie 6

Zadanie 7

Matematyka – Zarządzanie

______________________________________________________________________________________

___________________________________________________________________

Dr inż. Wanda Gryglewicz-Kacerka

Państwowa Wyższa Szkoła Zawodowa we Włocławku

Zadanie 8

Zadanie 9

Zadanie 10

Zadanie 11

Zadanie 12

Zadanie 13

Zadanie 14

Zadanie 1

Zadanie 15

Wyznacz elementy zbioru A = {1, 2, 3, ...,10}

Wyznacz elementy zbioru A = {x

∈N: 3 < x < 10}

Wyznacz elementy zbioru A = {x

∈N: x < 0}

Wyznacz elementy zbioru A = {x

∈N: x ≤ 5}

Wyznacz elementy zbioru A = {x

∈C: -5 < x ≤ 3}.

Wyznacz elementy zbioru A = {x

∈C: x2 < 10}.

Uwaga:

Matematyka – Zarządzanie

______________________________________________________________________________________

___________________________________________________________________

Dr inż. Wanda Gryglewicz-Kacerka

Państwowa Wyższa Szkoła Zawodowa we Włocławku

Przyjmiemy oznaczenia:

o Liczby naturalne

Liczby całkowite

Z (lub C)

o Liczby wymierne

o Liczby rzeczywiste

o Liczby niewymierne

R\Q

(wykład strona 6)