Metody probabilistyczne i statystyka koło nr 1 13.12.2010

Jest tego całkiem sporo więc pewnie zamiast krótkiego manuala wyjdzie niemała powieść.
Na poczatek może jakieś małe ogarnięcie w tym jakie są rodzaje zadań.

1. „Proste” prawdopodobieństwo.
2. Prawdopodobieństwo przedstawione graficznie.
3. Prawdopodobieństwo zależne.
4. Zmienna typu skokowego
5. Zmienna typu ciągłęgo.

UWAGA: W niektórych punktach będzie potrzebna umiejętność całkowania, której sam nie
posiadam zbyt dobrze. Najlepiej skonsultujcie się z jakims sensei z matematyki lub dobrze
całkującego.
UWAGA2: Wszystkie zadania są z ćwiczeń.
Pierwszy punkt już miałem ogarnięty Ci co sciągnęli ćwiczenie pierwsze napisane na kompie,
które wrzucałem wraz z wykładem to mogą pominąć to i przejść od strony trzeciej. Resztę
zapraszam do dalelszej lektury.

Wzór

P  A=

k
n

[ P(A) – prawdopodobieństwo zajścia zdarzenia A; k – zdarzenia sprzyjające

(ilość możliwości w których te zdarzenie się spełnia); n- ilość możliwych zdarzeń.] Stosujemy gdy
spełnione są następujące warunki:

–

zdarzenia są jednakowo możliwe (jest taka sama szansa na ich spelnenie)

–



- zbiór skończony (możemy policzyć ilość elementów)

Sposoby liczenia prawdopodobieństwa:
1 Permutacje
P

n

=n!

2 Kombinacje C

k
n

=



n
k



=

n !

k !n−k ! nieistotna kolejność losowań

n- ilość możliwych zdarzeń
k-\zdarzenia sprzyjające

3.Wariacje bez powtórzeń W k

n

=

n !



n−k !

kolejność istotna. Bez zwracań.

4.Wariacje z powtórzeniami

V k

n

=

n

k

n- ile miejsc k- ile osób/przedmiotów

kolejność istotna. Ze zwracaniem.
Zadania

1. Z 5 kul bialych i 4 czerwonych losujemy 4 kule. Jakie jest prawdopodobieństwo

wylosowania 2 bialych i 2 czerwonych kul ?

2. W sposób losowy przestawiamy litery AAAEKMMTTY. Jakie jest prawdopodobieństwo

ulozenia sowa MATEMATYKA?

3. Przy okrąglym stole ustawiono 10 osób. Jakie jest prawdopodobieństwo, że 2 wylosowane

osoby będą siedzialy obok siebie?

4. W sposób losowy przestawiamy cyfry {0,1,2,3,4,5,6,7,8,9}. Jakie jest prawdopodobieństwo

że 1 i 2 będą obok siebie dokladnie w takiej kolejności.

5. W 10-cio piętrowym budynku windą jedzie 7 osób. Jakie jest prawdopodobieństwo, że

żadne z 2 osób nie wysiądą na tym samym piętrze?

6. Losowo rozmieszczono n kul w n komórkach. Jakie jest prawdopodobieństwo, że dokladnie

1 komórka jest pusta?\

Rozwiązania

By Perez

Strona 1 z 13

Metody probabilistyczne i statystyka koło nr 1 13.12.2010

1. Musimy obliczyć k i n. Naszym A jest wylosowanie 2 kul bialych i 2 czarnych. Wiemy że:
kolejność nie ma znaczenia (nie przypisujemy nic do niczego) nie ma powtórzeń, wszystkich kul

jest 9 a wylosować musimy 4, a więc n=



ilość wszystkich kul

ilosc kul do wylosowania



, a więc n=



9
4



=

9 !

4 !9−4!

licząc dalej wychodzi

1×2×3×4×5×6×7×8×9
1×2×3×41×2×3×4×5

jak widać możemy skrócić 2×7×9=14×9=126 .

Polowa roboty z glowy. Teraz musimy obliczyć k. wiemy że z 5 kul bialych potrzebujemy 2 kul i z
4 czarnych potrzebujemy 2 kolejnych kul . Oczywiście dalej nie przypisujemy nic i nie ma
powtórek. Więc stosujemy taki sam wzór. Zauważ jednak, że pomiędzy losowaniem 2 kul bialych a
2 czarnych występuje w zadaniu spójnik „i”. Oznacza to, że pomiędzy jednym a drugim wzorkiem

wystąpi mnożenie. No to do roboty k =



5

2



×



4
2



=

5!

2 !×3 !

=

4×5

2

=

¿

3×4

2

=

10×6=60

Ostatni krok. Podstawienie do wzorku tego co jest na początku.

P  A=

60

126

=

10

21

. I koniec :)

2.Dobrze mamy literki zadanie jest banalne. Po szybkim obliczeniu ich ilości wiemy, że jest ich 10
jeżeli wiemy ile jest miejsc i obliczając n mozemy sobie powkladac tak gdzie chcemy to n=10 !
Już tlumacze dlaczego. Mając 10 liter mozemy na miejsce pierwsze wsadzić dowolną literkę, po
tym mamy 9 liter i możemy je zamontować w 9 a nie 10 miejsc, bo 10 jest już zajęte przez pierwszą
literkę itd. na koniec mamy coś takiego 10 9 8 7 6 5 4 3 2 1. Musimy wstawić coś między te liczby
przy czymś takim wstawiamy ZAWSZE mnożenie. Ostatecznie

10×9×8×7×6×5×4×3×2×1=10 ! . Teraz musimy z tego czegoś ulożyć MATEMATYKA.

Zasada jest bardzo prosta. Zliczamy ilosć i dorzucamy silnie. Mamy 3 literkli A 2 M i 3 T, a więc

k =3!×2 !×2 !=6×4=24 . Na zakończenie wstawiamy do wzoru P  A=

24

10!

. Proste

prawda ?
3.Liczba n liczymy tak samo jak w poprzednim zadaniu, czyli n=10! Wyliczenie k już nie jest takie
proste. Odejmijmy 2 osoby z 10. Wynik to osoby nieważne dla nas więc zastosujmy tutaj to samo
co przy n. Więc pierwszym czolonem liczby k jest 8! Idźmy dalej. Czy mamy powiedziane w jakiej

kolejności maja siedźieć te osoby ? NIE. Więc użyjmy na nich permutacji. Kolejny
czon to 2!. Aby zrozumiec ostatni czlon potrzebujemy obrazka . To coś niebieskie to
nasz stolik. Te kreski to miejsca siedzące. Osoba pierwsza z pary może sobie wybrać
dowolne siedzenie a osoba 2 musi siąść obok niego więc może siaść na 10 miejscach. I
dlatego ostatnią liczbą jest 10. tak więc

k =8 !×2!×10

. Na zakończenie standard.

P  A=

8!×2 !×10

10 !

. UWAGA. Można zauważyć, że 10 i 8! z licznika można sktócić z 10! z

mianownika. Po skróceniu wynik wygląda tak : P  A=

2
9

Koniec.

4.Liczba n to już wiadomo od razu. n=10! Teraz z k znowu będzie męczenia się. Od razu zróbmy
ot samo co w poprzednim zadaniu. 8! Mamy podane dokladne ulożenie liczb więc nie permutujemy
ich. Teraz ostatnia sprawa. Musimy zaznaczyć, że nie mamy dokladnego ulokowania tych liczb, a
więc musimy policzyc w ilu miejscach może stanąć 1 tak żeby warunek byl spelniony. Stworzmy
szablon sytuacji _ _ _ _ _ _ _ _ _ _ mamy 10 miejsc sprawdźmy gdzie jedynka może stać (może
stać w tylko w tym miejscy gdzie jest co najmniej jedno miejsce za nią) od razu rzuca się w oczy
miejsce 10 na którym nie może stać, bo nie ma nic za tym miejscem. Tak więc ostatnia liczbą jest

By Perez

Strona 2 z 13

Metody probabilistyczne i statystyka koło nr 1 13.12.2010

liczba 9, a k wyglada tak :

k =8 !×9=9 !

. Na koniec oczywistość.

P  A=9

!

10

!=

1

10

5. Liczba n jest najzwyklejszą wariacją, ponieważ nie mamy żadnych ograniczeń (w poprzednich
zadaniach nie mogliśmy wstawić 2 osób/liczb w te samo miejsce). Więc kierując się wzorem
wariacji mamy n=10

7

. teraz policzmy k. Pierwsza osoba może wysiąść gdzie chce czyli na 10

piętrach. Druga już tylko na 9 bo na jednym z 10 już wysiadla jedna osoba. Itd. ostatecznie k
wygląda tak: k =10×9×8×7×6×5×4 . Pamiętajmy o tym , że mamy tylko 7 osób a pięter jest

10. więc musimy napisać tylko 7 liczb. Teraz formalność

P  A=

10×9×8×7×6×5×4

10

7

6. Tutaj dla lepszego zrozumienia zmienię n z zadania na q i odpowiednia zindeksuje.
q

1

- ilość komórek, a q

2

– ilość kulek. Teraz obliczymy n. N obliczamy tak samo jak w poprzednim

zadaniu. Z tego samego powodu więc

n=q

1

q

2

. Teraz liczba k. Jak wiemy z zadania obie te

wielkości są identyczne sobie. Więc żeby była jedna komórka wolna a druga z 2 kulkami. Więc z q

1

musimy odjąć 2. a więc pierwszym elementem jest (n-2). Kolejnym będzie n czyli komórka pusta, a

ostania będzie



n
2



.Ostatecznie będzie tak:

k =n−2×n×



n
2



.

Wszystko. Koniec punktu pierwszego. Cieszcie się i radujcie.

Teraz bierzmy się za prawdopodobieństwo przedstawione graficznie.
Na początek jakiś mały wstęp. Jeśli jest mowa o odcinku jakimkolwiek (najcześciej przedział 0,1).
to wtedy żeby dobrze zrozumieć jak wygląda dany obszar prawdopodobieństwa potrzebujemy
wykresu. (będzie zapewne wymagany)

Na początek jedno zadanko.
Z odcinka <0,1> wybrano losowo i niezależnie 2 punkty x i y, które dzielą ten odcinek na 3 odcinki.
Znaleźć prawdopodobieństwo, że z tych 3 odcinkót można zbudować trójkąt.
Na pocątek oznaczmy omegę czy zbiór wszystkich zdarzeń w tym zadaniu. Skoro jest mowa o
odcinku musimy napisać to troszke po logicznemu.

={

x , y : x∈〈0,1〉∧ y∈〈0,1〉}=〈0,1〉×〈0,1〉 - praktycznie  będzie wyglądać tak samo w

każdym zadaniu.

Teraz mały powrót do przeszłości. Pamietacie prawa konstrukcji trójkąta? Trójkąt zbudujemy wtedy
i tylko wtedy gdy suma dwóch mniejszych boków jest WIĘKSZA od boku największego. Trzeba to
jakoś teraz napisać. Pamiętajcie jeśli nie mamy miar boków to długosć boku to koniec – poczatek.
Stwórzmy A (zdarzenie sprzyjające dla nas, czyli takie przy którym stworzone boki dadzą nam
trójkąt) .Opiszmy to sobie najpierw tak ogólnie.
Mamy 3 możliwości wylosowania punktu. x>y , y>y i x=y. Ta trzecia możliwosć odpada, ponieważ
mamy mieć odcinek podzielony na 3 części a jak mamy x=y to jest wtedy podział na 2 odcinki.
Więdź idźmy dalej w podział gdzie
x<y
będziemy mieć 3 długości boków
x
y-x
1-y
Teraz musimy opisać te 3 boki tak, żeby kazdy miał szanse być tym największym.
x+(y-x)>(1-y)

(y-x)+(1-y)>x

x+(1-y)>(y-x)

By Perez

Strona 3 z 13

Metody probabilistyczne i statystyka koło nr 1 13.12.2010

Następnie podział kolejny
y<x. Trzy boki to: y, (x-y) oraz (1-y). A zależności:
y+(x-y)>(1-y)
(x-y)+(1-y)>y
y-(1-x)>(x-y)
Na koniec napiszmy to w funkcji działającej po x,y

A={ x , y :

{

x y−x 1− y 



y− x1− y x

x1− y  y− x

}

∨

{

y x− y1−x 



x− y1−x  y

y1−x  x− y 

}

}

wygląda to jak wygląda, ale jak każdy wie możemy to matematycznie poskracać. Napisze jak to
wygląda po skróceniu, bo skracanie to każdy potrafi.

A={ x , y :

{

y

1
2

yx −

1
2

y

x−1

2

}

∨

{

x

1
2

y

1

2

y

1

2

}

}

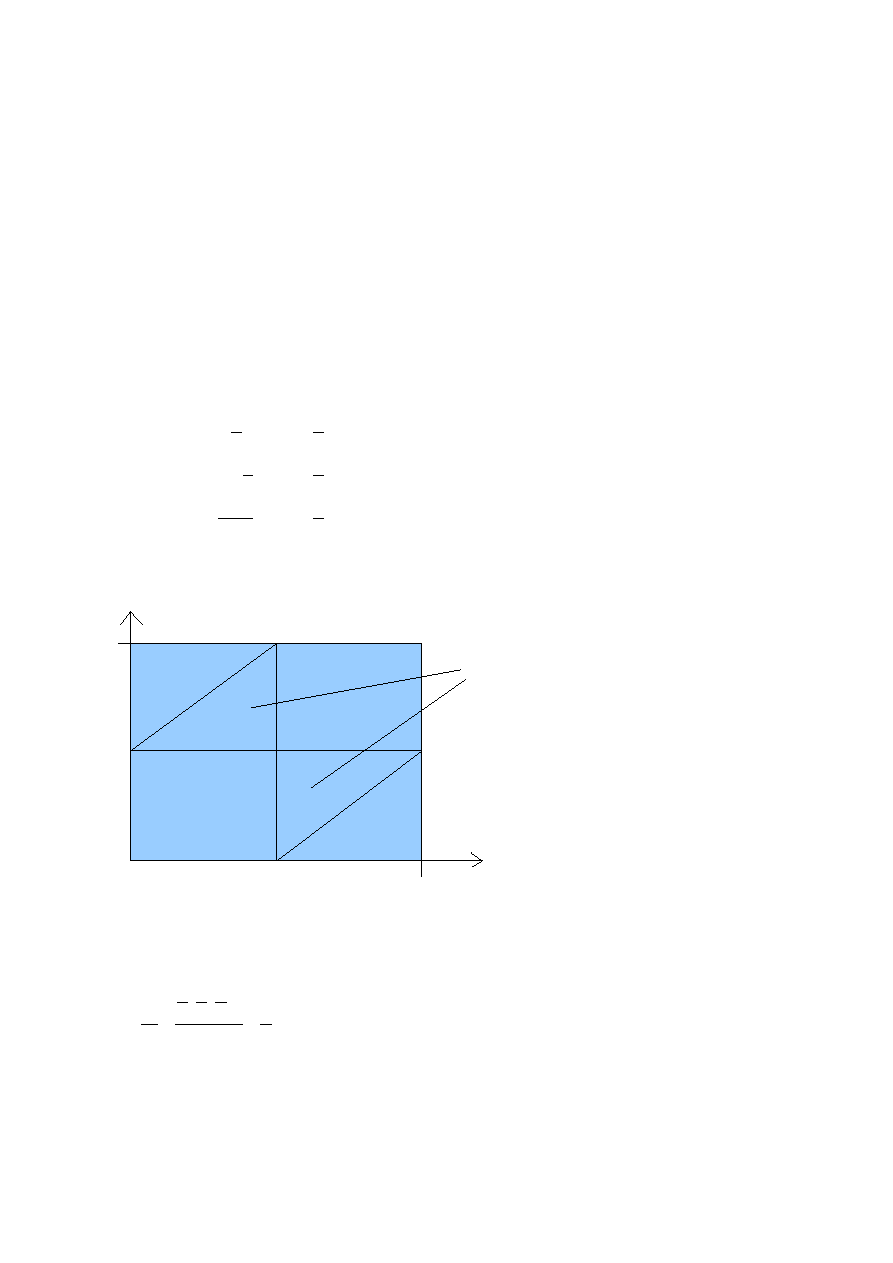
Jak zauważyliście to bedą proste pomykające po  Narysujmy w koncu tą  .

Ten niebiski prostokąt to  . te linie to są funkcje podane przez nasze skrócone A.

PAMIĘTAJCIE:  to obszar naszych działań więc zbiorem zdarzeń wszystkich jest pole tego
kwadrata.

P  A

A



=

1
2

⋅

1
2

⋅

1
2

⋅

2

1⋅1

=

1

4

Koniec zadania. Myślicie, że to takie proste. Otórz nie, bo wiecie pewnien kretyn wymyślił całki i
nie wiedział co z nimi zrobić to wcisnął je tam gdzie się tylko dało. Kolejne zadanie udowodni wam
to.

By Perez

Strona 4 z 13

x

y

1

1

Teraz musimy zamalowac odpowiedni obszar
patrząc na nierówności. Wszystko wskazuje
na to że tymi obszaremi są. (Ja ich nie
zamaluje bo mam lenia dziś.) Policzmy sobie
teraz P(A).

Metody probabilistyczne i statystyka koło nr 1 13.12.2010

ZADANIE II
Kwadratu  równego [0,1]x [0,1] wybieramy punkt o współrzędnych p,q. Jakie jest
prawdopodobieństwo, że równanie x

2



pxq=0 Będzie miało 2 pierwiaski zespolone [Gdy Δ

jest ujemna]



0 - nasz warunek, że delta musi być ujemna. Jak pamiętamy wzorek na Δ z

liceum/technikum to musimy przekonwertować go na nasze niewiadome i zamienić go z Δ w naszej
nierówności. Będzie to wyglądać tak:

P

2

−

4q0

Teraz opiszmy zbiór wszystkich zdarzeń 

={

p , q : p ∈[0,1]∧q∈[0,1]}=[0,1]×[0,1] - jak dobrze zauważycie  wygląda tak samo

jak w poprzednim zadaniu.
Teraz stwórzmy zbiór zdarzeń sprzyjających A- zdarzenie przy którym równanie x

2



pxq=0

Będzie miało 2 pierwiaski zespolone, czyli wtedy kiedy Δ będzie ujemna i po ot właśnie
rozpisywaliśmy Δ na początku zadania.

A={ p , q: p

2

−

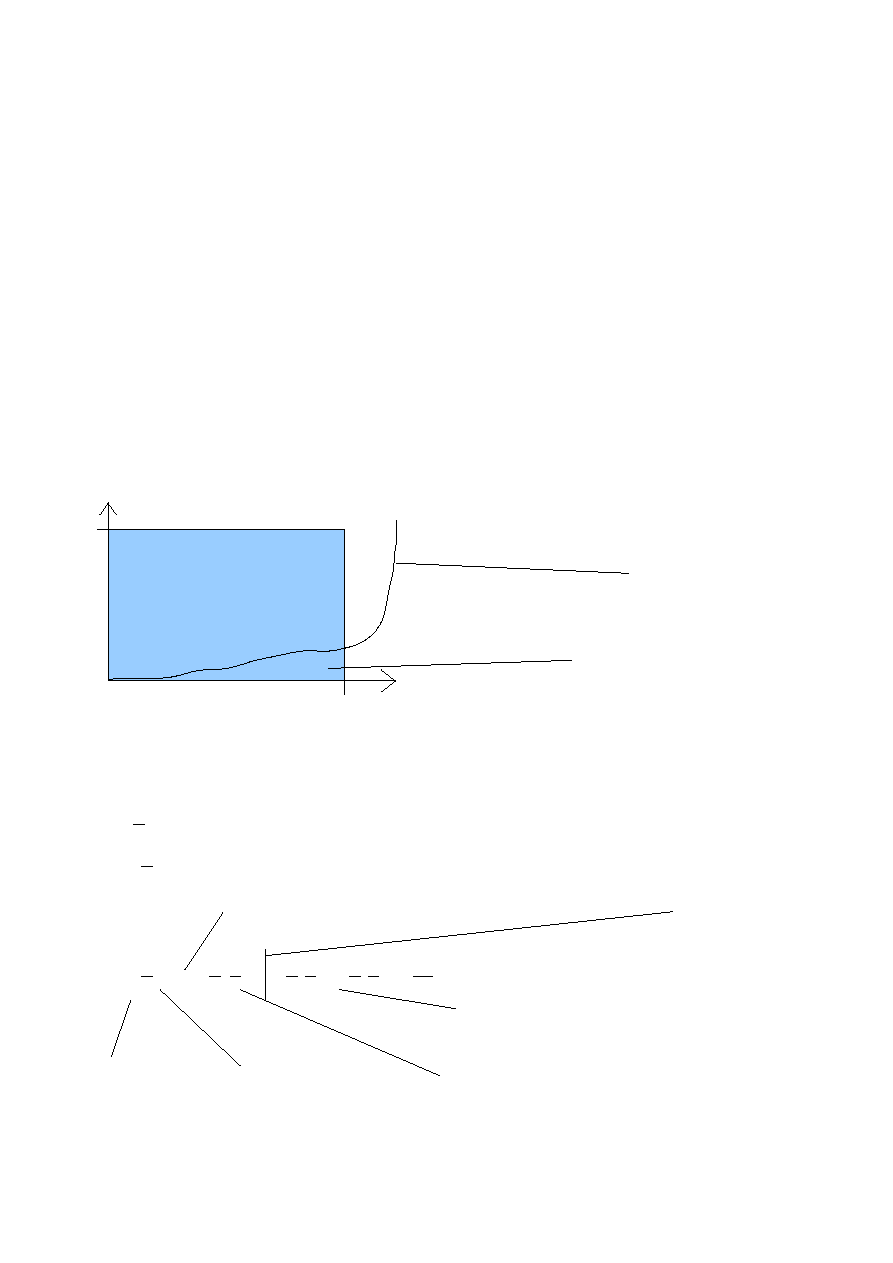
4q≤0} No to teraz jakiś wykresik zróbmy, żeby wiedzieć co będziemy liczyć.

Ale najpierw uławtwy sobie nierówność.

p

2

−

4q0

p

2



4q

q

1

4

p

2

Nie zostaje nam nic innego jak scałkować tego potworka. Oczywiście całkujemy

tylko

1
4

p

2

, ponieważ to jest odpowiedzialne nam za położenie krzywej na układzie

współrzędnych.

S=

∫

0

1

1
4

p

2

dp=

1
4

⋅

1

3

p

3

=

1
4

⋅

1
3

1

3

−

1
4

⋅

1
3

0

3

=

1

12

By Perez

Strona 5 z 13

S

Uznajmy, że ta
krzywa to jest nasz
wykres Δ

S to nasze zdarzenie
przeciwne do A, a ze względu
na to, że jest „łatwiejsze” do
policzenia to bierzemy się za
nie

1
0

Liczba na dole oznacza
skąd całkowanie się
zaczyna na górze
pokazuje gdzie kończymy
całkowanie

To musi być zawsze. Przez to pokazujemy po
jakiej zmiennej idzie całkowanie.

Funkcja do
całkowania

Ta magiczna kreska
jest zastępowana
przez przez tego
fikusa na początku
zawsze wstawaimy to
na końcu

Podstawiamy w miejsce
zmiennej najpierw liczbę z góry
kreski i potem odejmujemy to
samo tylko zamiest zmiennej
wpisujemy liczbę z dołu kreski

Zwiększamy wykładnik o 1 i tworzymy ułamek którego
mianownik jest aktualnym wykładnikiem

Metody probabilistyczne i statystyka koło nr 1 13.12.2010

Na koniec zostaje nam obliczenie prawdopodobieństwa.

P  A=

1−S



=

1−

1

12

1

=

11
12

UWAGA 1: S tutaj jest zdarzeniem przeciwnym do A i dlatego tak to liczyliśmy. Inne zaznaczenie
zdarzenie przeciwnego jest takie. A
UWAGA 2: Możemy dostać możliwość obliczenia 2 połączonych prawdopodobieństw.Wtedy
używamy następującego wzorku:

P  A∪B= P  AP  B−gdy jest mowa o zdarzeniu jednym LUBdrugim

P  A∩B=P  A⋅P  B−gdy jest mowa o zdarzeniu jednym ORAZ i drugim

Kojeny punkt możemy uznać za ukończony.

TERAZ PUNKT NR 3 Prawdopodobieństwo warunkowe.
Na wstepie może jakieś wzorki. Myślę, że te powinny starczyc ewentualnie dopisze jakieś podczas
robienia zadań.

P  B/ A=

P  B∩A

P  A

−

prawdopodobieństwo B jest zależne od A

P A

i

/

B=

P  A

j

⋅

P  B∖ A

∑

i

P



A

i

⋅

P  B∖ A

i

−

wzór Baysa

Zadanie I Firma produkuje 98% wyrobu odpowiadającego normie. Wśród wyrobów jest 75%
wyrobu pierwszego gatunku. Oblicz prawdopodobieństwo , że wylosowany produkt jest pierwszego
gatunku.
UWAGA: Nie jestem pewniem swoich notatek z tego zadania, jeśli będzie błąd to dajcie znać i nie
linczujcie mnie. W tłumaczeniu a dlaczego tak? Posłużyłem się wykipedią.
Dobra wiadomość przy tym zadaniu nie musimy liczyć naszej ulubionej  . Teraz wystarczą
tylko nam prawdopodobienstwa 2 zdarzeń, które mamy tutaj opisane i potem odpowiednio
zadziałać na nich.
Zdarznia
A- wylosowano element spełniający norme
B- wylosowano element pierwszego gatunku

P(A)=0,98 – zamieniamy procenty odpowiadnio w pradowpodobienstwo.
100%=1 w pradowpodobieństwie.
P(B/A)=0,75
teraz:
( B n A ) - wyrób jest pierwszego gatunku i spelnia norme
teraz z prawd. warunkowego:

P  B/ A=P  B∩A/ P  A→ P  B∩ A= P  B/ A⋅P  A=0.75⋅0,98=0,735

ale B⊂A więc : P  A∩B = P  B∩ A=P  B zatem : P  B=0,735

koniec.
Teraz zadanie II.
Pewna metoda do wykrywnia uszkodzeniń daje następujące wyniki. Jeżeli urządzenie ma defekt to
metoda wykrywa go w 90% i niewykrywa w 10% przypadków. Jeśli urządzenie nie ma defektu to
mimo to w 1% metoda informuje o nim. W partii jest 2% elementów majacych defekt. Jakie jest
prawdopodobieństwo, że wybrane urządzenie rozpoznane jako uszkodzone jest rzeczywiście

By Perez

Strona 6 z 13

Metody probabilistyczne i statystyka koło nr 1 13.12.2010

uszkodzone?
No to znow zabawa w literki.
A- wylosowano urządzenie z defektem.
B – metoda wykryła defekt.
Teraz musimy ustalić co wiemy.
Wiemy:
ile jest urządzeń z defektem – 2%.
ile jest urzędzen bez defektu - 98%
ile metoda wykrywa urządzeń mających defekt – 90%
ile metoda nie wykrywa defektu mimo że urządzenie je ma – 10%
ile metoda wyrywa defekt mimo jego braku – 1%
Teraz opiszmy to sobie w języku prawdopodobieństwa.
P(A)=0,02

P  

A=0,98

P(B/A)=0,9

P  B/ A=0,1

P  B/ A=0,01

(specjanie powiększyłem, żeby było widać kreskę które mówi nam że jest to

zdarznie przeciwne do B)

Nie wiemy tylko jakie jest prawdopodobienstwo, że wybrane urzadzenie jest uszkodzone i, że
metoda pokazuje, że jest defekt i to nam będzie trzeba policzyć
musimy policzyc coś takiego

P  A/ B=

P  A∩ B

P  B

tylko, że nie mamy P(B). Ale nic straconego mamy P(B/A) i P(B/ A )

oraz mamy P(A) i P(

A

) i oczywiście jest wzorek żeby policzyć B. Zróbmy to.

P  B=P  A⋅P B / AP  A⋅P  B/ A=0,2⋅0,90,98⋅0,01=0,0278

A góra ułamka to : P  B/ A⋅P  A=0,9⋅0,02=0,018

ostatecznie:

0,018

0,0278

=

0,64748201 koniec zadania i punktu III.

Teraz bierzmy się za kolejny punkt czyli zmienne losowe typu skokowego.
Na wstęp kilka wzorkó które trzeba znać wkraczając tutaj.
Wartość oczekiwana m

m=

∑

i

x

i

⋅

p

i

- mnożymy wartość x z jego prawdopodobieństwem i dodajemy z kolejnym

mnozeniem x-a z jego prawdopodobieństwem.
Wariancja 

2

oraz odchylenie standartowe





2

=

∑

i



x

i

−

m

2

⋅

p

i

=



∑

i



x

i

−

m

2

⋅

p

i

Modalna – takie x_i dla którego p jest największe.
Mediana takie x_i spełniające następujacy warunek.

P x

i

≤

1
2

≤

P ≤ x

i



Dystrybuanta f(x)

f  x =P  X x 

By Perez

Strona 7 z 13

Metody probabilistyczne i statystyka koło nr 1 13.12.2010

do obliczania dystrybuant różnych innych

F  x = P  x P a≤b=F b−F a 

Teraz zadanko.
Mamy następujący rozkład zmiennej losowej typu skokowego.

x

i

p

i

-1

0,05

1

0,12

3

0,13

5

c

7

0,16

9

0,13

11

0,09

a) obicz wartość c
b) Wartość oczekiwaną,wariancję i odchylenie standartowe, mediane i modalną tej zmiennej
losowej
c)podać dystrybuantę tej zmiennej losowej
d)oblicz

P5 P 1 P=7 P19 P 1≤9 P 1≤8 P−1≤≤10

a) jak dobrze wiemy suma wszystkich p musi wyjść 1 skoro nie wiemy ile jest c to musimy
zsumować wszystko i odjąc od 1, a więc:

c=1−0,050,120,130,160,130,09=0,32 no to mamy punkt a z głowy.

b)
wartość oczekiwana m. Nic prostrzego jak wkopać wszystko do wzoru.

m=−1⋅0,051⋅0,123⋅0,135⋅0,327⋅0,169⋅0,1311⋅0,09=−0,050,121,60,391,121,170,99=5,34

Teraz wariancja. Najlepiej do niej dorzucić tabelkę z policzonymi x

i

−

m oraz z ich potegą.

x

i

x

i

−

m



x

i

−

m

2

-1 -1-5,34=-6,34

40,2

1

1 - 5,34 = -4,34

18,84

3

3 – 5,34 = -2,34

5,47

5

5 – 5,34 = - 0, 34

0,12

7

7 – 5,34 = 1,66

2,76

9

9 – 5,34 = 3,66

13,4

11 11 - 5,34 = 5,66

32,04

Ok to teraz kopiemy to do wzoru



2

=

40,20⋅0,0518,84⋅0,125,47⋅0,130,12⋅0,322,76⋅0,1613,4⋅0,1332,04⋅0,09

więc liczac dalej wychodzi



2

=

2,012,660,710,040,441,742,88=10,08

By Perez

Strona 8 z 13

Metody probabilistyczne i statystyka koło nr 1 13.12.2010

odchylenie standartowe to po prostu pierwiastkujemy wyliczoną wariancję.

=



10,08=3,17

modalna

m

o

=

5 , bo 5 ma największe p ztego rozkładu zmiennej losowej typu skokowego

teraz mediana mamy takiego potworka

Teraz jedyne co nam zostało to obliczyć daną wartość ja sugeruje zeby liczyć watrości najbliższe
wartości oczekiwanej, ale to tylko moja sugestia nie musicie się nią sugerować, ja policze teraz dla
wszystkich od -1 zaczynając a kończąc na medianie.

P −1≤

1
2

≤

P ≤−1=P 0≤

1
2

≤

P 0,05 NIE

P 1≤

1

2

≤

P ≤1= P 0,05≤

1

2

≤

P 0,17 NIE

P 3≤

1

2

≤

P ≤3=P 0,17≤

1
2

≤

P 0,3 NIE

P 5≤

1
2

≤

P ≤5=P 0,3≤

1
2

≤

P  0,62 TAK

c)dystrybuanta zmiennej tej – najpierw opis potwor

f  x =P  X −1=0 f  x =P  X 7=0,62

f  x =P  X 1=0,05 f  x=P  X 9=0,78

f  x =P  X 3=0,17 f  x= P  X 11=0,01

f  x =P  X 5=0,3 f  x= P  X ≥11=1

Na koniec pozostaje nam obliczyć te kilka wzorków.

P 5 P 1 P =7 P 19 P 1≤9 P 1≤8 P −1≤≤10

Potrzebujemt do tego wszystkich dystrybuant i tabelki z p

i

.

P5=0,3− ponieważ jest takawartośc dystrybuanty dla5

By Perez

Strona 9 z 13

Tutaj sumujemy wszystkie p
które w tabelce są NAD
wybraną zmienna

Tutaj wpisujemy to
co jest z lewej +
wartość p rzy danej
zmiennej losowej

Jeśli ten warunek
zostanie spełniony to
ten x jest medianą

P x

i

≤

1
2

≤

P ≤x

i



To działa tak samo jak
pierwszy człon przy
liczeniu mediany, czyli
bierzemy te p które
jest NAD w tabelce

f  x =P  X  x

Ten X to w sumie jest
to samo co ksi (albo
jak kto woli tornado)

Metody probabilistyczne i statystyka koło nr 1 13.12.2010

P1 - tego tak prosto nie obliczymy. Trzeba pokombinować troszkę. O wiele łatwije będzie

nam policzyć zdarzenie przeciwne do niego (ze względu na znak nierówności, ale wtedy pojawia
się kolejny problem. P≤1 A to nie pasuje nam do wzoru. Więc dlatego możemy zrobić taki
myk. Żeby pozbyć się nierówności łagodnej to musimy w

x

i

zwiększyć i o 1[wybrać kolejną wartość ] a więc obliczenie będzie wyglądać tak:

P1=1−P≤1=1−P 3=1−0,17=0,83

Kolejne proste

P=7=0,16 teraz małe wytłumaczenie dlaczego 0,16 a nie 0,62. Ponieważ kiedy mamy znak

równości to wybieramy wartość p, jeśli mamy znak nierówności to wtedy wybieramy F(x).

P19=P 3≤9=0,78−0,17=0,61 Teraz słowo wyjaśnienia.

Jeśli chcemy zmienić nier owność łagodną na ostrą to należy w x

i

zwiększyć i o 1 i podem

podstawiić do wzoru.

P1≤9=P 3≤9=0,78−0,17=0,73

P1≤≤8=P 19=0,75

P−1≤≤10=P−1≤11=0,91−0=0,91

UWAGA: jeśli wynik wyjdzie ci na większy od 1 lub ujemny to masz coś źle policzone.

Koniec punktu przedostatniego.
Na zakończenie zmienna losowa typu ciągłego.
UWAGA: w tym punkcie jest duuużo całkowania, lae na szczęście najprostrze jesgo
przypadki.

Standardowo wzorki na początek.

DYSTRYBUANTA

F  x=

∫

−∞

x

f t dt

WARTOŚĆ OCZEKIWANA:

M=

∫

−∞

∞

x f  x dx

WARIANCJA



2

=

∫

−∞

∞



x−m

2

f  x dx

ODCHYLENIE STANDARDOWE

=



∫

−∞

∞



x−m

2

f  x dx

MEDIANA

Funkcja gęstości przyjmuje wartość

1
2

MODALNA
MAX DLA FUNKCJI GĘSTOŚCI.

Teraz zadanko.

By Perez

Strona 10 z 13

Metody probabilistyczne i statystyka koło nr 1 13.12.2010

Dana jest funkcja gęscośći f  x=

{

cx dla1≤x≤3

0 dla pozostałych

}

a) dla jakiej c f(x) jest funkcja gęstości dla 
b) wyznaczyć dystrybuantę dla 
c) wyznaczyć jej wartość oczekiwaną odchylenie standardowe i medianę.
d)obliczyć

P2

P≤1,5

P 0.5

P1,52.5

P 25

P=2,5

a) funkcja gęstości do rozkładu zmiennej losowej typu ciągłego musi spełniać 2 warunki

1. f  x ≥0

∫

−∞

∞

f  x dx=1

więc możemy (i musimy) wywnioskować, że c jest większe równe 1, ponieważ gdyby był zerem to
całkowanie byłoby 0.
Teraz patrząc na funkcję gęstości mamy 2 podziały. Pierwszy to przediał 1-3 a drugi to reszta.
Musimy opisać to w całce.

–

pierwsza całka [−∞ , 1]

–

druga całka [1 , 3]

–

trzecia całka [3 , ∞]

no to całkujmy.

∫

1

3

cx dx=1

c

∫

1

3

x dx=1

c

1
2

x

2

=

1

c

1
2

3

2

−

c

1
2

1=1

4c=1

c=

1
4

f  x=

{

1
4

x dla 1≤x≤3

0 dla pozostałych

}

tak teraz wygląda nasz naowa funkcja gęstości i na jej podstawie

By Perez

Strona 11 z 13

∫

−∞

1

0 dx

∫

1

3

cx dx

∫

3

∞

0=1

Tytaj ratuje nas od
całkowania 0 lub
mówiąc inaczej brak
zmiennej do całkowania

Jedyna co będziemy
całkować to właśnie tą
środkową i robimy to
analogicznie jak całke
opisaną kilka stron wyżej

3

1

Metody probabilistyczne i statystyka koło nr 1 13.12.2010

obliczymy DYSTRYBUANTĘ.

F  x=

∫

−∞

x

f t dt

Tutaj musimy zrobić podział na 3 przypadki, ponieważ nasza funkcja specyficznie zachowuje się w
odpowiednich przedziałach.
-x<1
- 1≤x≤3
-x>3
łapmy się na pierwszy przediał
x<1

F  x=

∫

−∞

x

0 dt=0 całka idzie po przedziale takim właśnie ze względu na wzór a zachowaniem

funkcji jest tutaj 0 które w magiczny sposób niszczy całkę.
Następny przypadek.
1<x<3

F  x=

∫

−∞

1

0 dt

∫

1

3

1
4

t dt=0

1
8

t

2

=

1
8

x

2

−

1
8

teraz pewnie każdy zapyta mnie co przy magicznej

kresce robi na górze x a nie 3. Otóż x jest równy 3 i niestety musimy tak to zamienić.
Ostatni wariant
x>3

F  x=

∫

−∞

1

0 dt

∫

1

3

1
4

t dt

∫

3

∞

0 dt=0

1
8

t

2



0=

1
8

9−

1
8

=

1

Ostatenie dystrybuanta wygląda tak :

F  x=

{

0 dla x1

1
8

−

1
8

dla1≤x≤3

1 dla x3

}

Następna do ostrzału idzie WARTOŚĆ OCZEKIWANA

m=

∫

−∞

1

x 0 dx

∫

1

3

1
4

x dx

∫

3

∞

x 0 dx=0

1
4

∫

1

3

x

2

dx0=

1

12

x

3

=

1

12

⋅

27−

1

12

⋅

1=

27
12

−

1

12

=

13

6

Wszystko liczymy tak jak podawałem kilka stron temu. Najlepiej potrenujcie sobie sami z takimi
całkami.
WARIANCJA ze względu na to ze nic nie dzieje się w przedziałach x<1 oraz x>3 możemy je
pominąć w całkowaniu



2

=

∫

1

3



x− 13

6



2

1
4

x dx= 1

4

∫

1

3



x

2

−

2⋅13

6



169

36



x dx= 1

4

∫

1

3



x

3

−

13

3

x

2



169

36

x dx= 1

4



1
4

x

4

−

13

9

x

3



169

72

x

2



licząc dalej

1
4



81

4

−

39

169

8

−

1
4



1
4

−

13

9



169

72

=

11
36

ODCHYLENIE STANDARTOWE

=



11
36

=



11

6

By Perez

Strona 12 z 13

x

1

3

1

3

1

3

1

Metody probabilistyczne i statystyka koło nr 1 13.12.2010

MEDIANA

F  x=

1
2

1
8

x

2

−

1
8

=

1
2

x

2

−

1=4 x

2

=

5

x=



5∨x =



−

5

I na koniec musimy policzyć te nasze cudeńka małe.

P2=F 2=

1
8

⋅

2

2

−

1
8

=

3

8

P ≤1,5=F 1,5=

1
8

⋅

9
4

−

1
8

=

5

32

P0.5=1−P≤0.5=1−F 0,5=1−0=1

P1,52.5=F 2,5−F 1,5=

1
8

⋅

6,25−

5

32

=

1
2

P 25=F 5−F 2=1−

1
8

⋅

4−

1
8

=

1−

5
8

=

3
5

P =2,5=0

Ostatnie kilka słów komentarza.
W zmiennej typu ciągłego nie mają znacznia czy nierówność jest łagodna czy ostra. Jeśli mamy
odwrotną nierówność (przypadek 3) to zamieniamy strone , zmieniamy na łagodną oraz
odejmujemy od 1 (bo tworzymy zdarzenie przeciwne do podanego) Przypadek ostatni- niestety jest
takie prawo, bo trafienie w ciągu liczb rzeczywistych jednej liczby ma znikome
prawdopodobieństwo, które można pominąć.

KONIEC.

By Perez

Strona 13 z 13