
LOKALNA GRUPA GALAGTYK
NAZWA
TYP GALAKTYKI
JASNOŚ Ć logM/M
¤
Duż y Obłok Magellana
JrI
10
Mały Obłok Magellana
JrI
9.3
Andromeda
Sb
11.5
M32
E2
F5
9.5
9.8
Trójk¹ t M33
Se
E
E
JrI
Jr
10.1
9
9
8.4
8.5
Skultor
E0
E0
6.5
7.3
Lew I
E4
6.6
Lew II
E1
6.0
Dragon
E0
5
Mała Niedź wiedzica
E0
5
Maffei
S0
11.3
ASTRONOMIA POZAGALAKTYCZNA
Typy galaktyk
Klasyfikacja Hubbla.
Eliptyczne
E
0
, E
1
, E
2
..........E
7
Spiralne S
0
bez poprzeczki S
a
, S
b
, S
c
z poprzeczką SB
a
, SB
b
, Sb
c
n = (a - b) 10/a

KOSMOLOGIA
Zasady kosmologiczne
Wszechś wiat jest jednakowy dla każ dego obserwatora
Zasada Antropiczna
Ś cisła zasada Kosmologiczna
MODELE KOSMOLOGICZNE
WSZECHŚ WIATA
1.Definicja Wszechś wiata.
2.Galaktyki, Clustry.
3.Zasada kosmologiczna.
4.Dlaczego niebo jest ciemne.
5.Rozbieganie się galaktyk
Prawo Hubbla
6.Modele kosmologiczne.
Lemaitre Fridmana
7.Model Hoyle’a.
8.Promieniowanie reliktowe T= 2.7 K
9.Testowanie modeli kosmologicznych.
PARADOKS OLBERTSA
dr
ω
Czy Wszechś wiat jest ograniczony?
O
R
j const
fot
s cm
=
⋅
3
ω =
S
R
2
ν ω
= ⋅
⋅
R
dx
2
dI
j
R
= ⋅
ν
2
I
R dR
R
R
r
r
=
= ⋅
= ⋅
∞
∞
∫
ω
ω
ω
2
2
0
0
0
zatem proporcjonalnie do r
r
I
=∞ →∞
Niebo powinno być jasne nawet w nocy
Clustry d
Mpc
≈
50
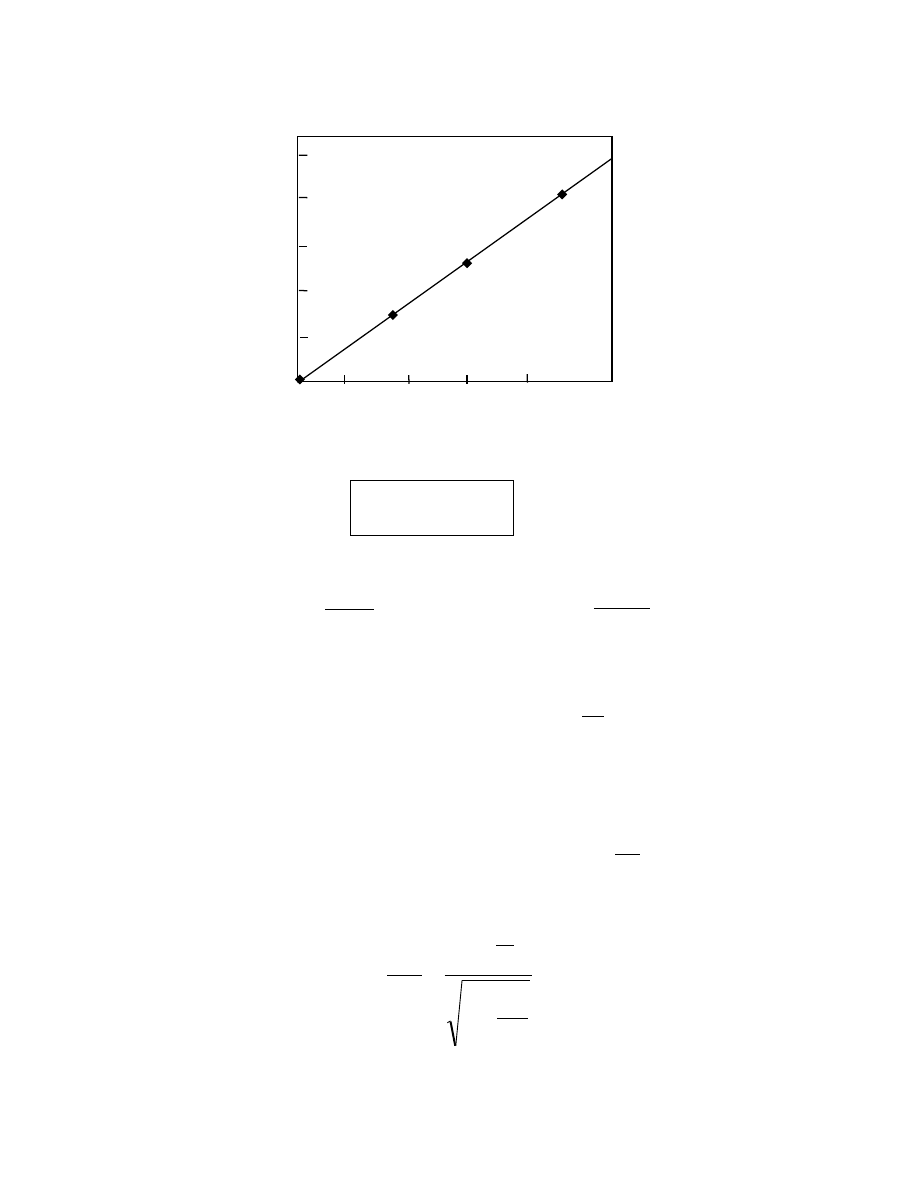
Prawo HUBBLA
ν
r
[km/s] 75
Hydra
60
45
Bootes
30
Corona Bolearis
15
Virgo
500
1000 1500 2000
[10
6
lat ś wietlnych]
ϑ
= ⋅
H R
(
)
H
km
s Mpc
≈
⋅
500
BYŁ O!!!
; H
km
s Mpc
= −
⋅
50 100
Ograniczonoś ć Wszechś wiata
υ
→
c;
c = H
⋅
R
max
= H
⋅
R
ph;
R
c
H
cm
ph
= =
⋅
6 2 10
28
.
H
≈
500 km s
-1
Mpc
-1
(było !!!)
H = 50
÷
100 km s
-1
Mpc
-1
Ograniczonoś ć
Wszechś wiata
ϑ
→
c
c = H R
max
= H R
ph
R
c
H
cm
ph
=
=
⋅
6 2 10
28
.
z
c
c
=
=
+
−
−
∆
λ
λ
υ
υ
1
1
1
2
2
Czy Prawo Hubbla jest zrozumiale w ś wietle zasady kosmologicznej?
l = R(t) l
0;
( )
( )
l t
l
R t
= ⋅
0
( )
υ
= = ⋅
⋅
=
⋅
⋅
dl
dt
l
R
R
R
l t
0
υ
r
= H
⋅
r;
( )
( )
H
R t
R t
=
⋅
Dla chmury punktó
w materialnch gdy zachodzi warunek
GM
lc
2
1
<
(Nevtona opis grawitacji)
Jak okreś lić R(t)
F
GM
r
= −
2
a
GM
r
x
=
=
2
..
d l
dt
GM
l
l
2
2
2
=
∗
.
→
l l
GM l
l
.. .
.
⋅ =
2
d
dt
l
GM
d
dt l
2
2
1
.
=
l
GM
l
K
.
2
2
=
−
( )
M
l
t
=
4
3
3
π ρ
( )
l
G
l
t
l
K
.
2
3
2
4
3
=
−
π ρ
( )
( )
( ) ( )
l
l
G
t
K
l
t
t l t
.
2
2
2
0
3
8
3
1
=
−
⋅ =
πρ
ρ
ρ
( ) ( )
ρ
ρ
t
t
l
=
0
3
( )
l
l
G
t
l
K
l
.
2
2
0
3
2
8
3
=
−
π
ρ
( )
( )
l
G
t
l
K
l
R t
l
.
2
0
0
8
3
=
−
=
⋅
π
ρ
( )
( )
( )
R t
G
t
R t
K
.
2
0
8
3
=
−
π
ρ
→ całkowita energia

MODELE FRIDMANA
Gdy k = 0
R(t)
R
∼
t
2/3
model E_S
t
gdy k > 0 E
g
> E
k
R(t)
( )
R
G
t
k
max
=
8
3
0
π ρ
t
gdy k < 0 E
g
< E
k
R(t)
R
∼
t
R
∼
t
2/3
t
Opis dokładny
Odległoś ć w czasoprzestrzeni zapisuje się ds
2
= g
αβ
dx
α
dx
β
Tensor metryczny g
αβ
powią zany jest z rozkładem materii opisywanym za pomocą
tensora energii pędu T
αβ
,
równaniami pola Einskina
G
R
g
R
G
c
T
αβ
αβ
αβ
αβ
π
=
−
=
1
2
8
4
gdzie
R R
=
α
α
jest skalarem krzywizny
R
R
αβ
ασβ
σ
=
jest tensorem Ricciego
g
αβ
nosi nazwę tensora Einsteina
Dla dalekich odległoś ci od masy, przewidywania ogólnej teori względnoś ci powinny
pokrywać się z wynikami Newtona, warunek ten jest spełniony gdy ds
2
wynosi
ds
r
r
c dt
dr
r
r
r
d
d
g
g
2
2
2
2
2
2
2
2
1
1
= −
−
−
−
+
(
)
(
sin
)
θ
θ φ
( )
ds
c dt
R t du
2
2
2
=
−
(
)
(
)
du
dr
kr
r d
d
2
2
2
2
2
2
2
1
=
−
+
+
θ
θ ϕ
sin
k
→
krzywizna przestrzeni
k = 1
→
zamknięta
k = -1
→
otwarta
k = 0
→
płaska
R
R
R
R
Gp
c
kc
R
c
.
.
2
2
2
2
2
2
2
8
+
+
= −
+
π
Λ
( )
R
R
G
t
kc
R
c
c
sta
.
2
2
2
2
8
3
−
= − −
+
−
π ρ
λ
Λ
ła kosmologiczna
;
ρ
0
0
0
2
= −
R
R H
..
ρ
π
kryt
H q
G
.
=
3
8
0
2
0
= ~2x10
-29
gramów/cm
3
Model Hoyl’a
Ś cisła zasada kosmologiczna
ρ
=constans
Idea nieustannego stwarzania materii
Promieniowanie reliktowe wyklucza taka moż liwoś ć
Testy na modeli kosmologicznych
Hubbla; Zliczanie ź ródeł; N=4/3
πρ
r
3
J(r)=L
/
4π
r
2
Zatem r=constant J
-2
Liczba ź ródeł o strumieniu większym od J będzie
N(>J) = const
ρ
J
-3/2
TEST HUBBLA
L - moc promieniowania - luninancja
(
)
f
L
R l
z
=
+
4
1
0
2
0
2
2
π
bo energia maleje 1 + z razy
( )
( )
( )
dN
d
f
dt l R R t
n
l f R R t
t
Ω
〉 =
〉 =
−
∫
0
2
0
3
1
0
2
0
4
0
4
0
[
]
α
π
Metody okreslania pola magnetycznego w przestrzeni kosmicznej
•
Rotacja płaszczyzny polaryzacji Faradaya
•
polaryzacja ś wiatła gwiazd -Devisa
•
Effekt Zemana
Rotacja Faradaya
n
p
g
2
2
1
1
= −
±
(
)
(
) cos
ν
ν
ν
ν
θ
θ
∠
→
( , )
l B
∆
n
p
g
=
ν ν
ν
θ
2
3
cos
;
∆
∆
ϕ
π
ν
=
2
n
c
;
∆
θ
π ν ν
ν
θ
=
p
g
c
dl
2
2
cos
rotacja
θ
π
ν
ν ν
θ
=
∫
c
dl
p
l
g
2
2
0
cos
θ
λ
π
= ⋅
∫
8 1 10
5
2
0
1
.
N B dl
e
B
N B dl
N dl
e
e
π
≈
∫
∫
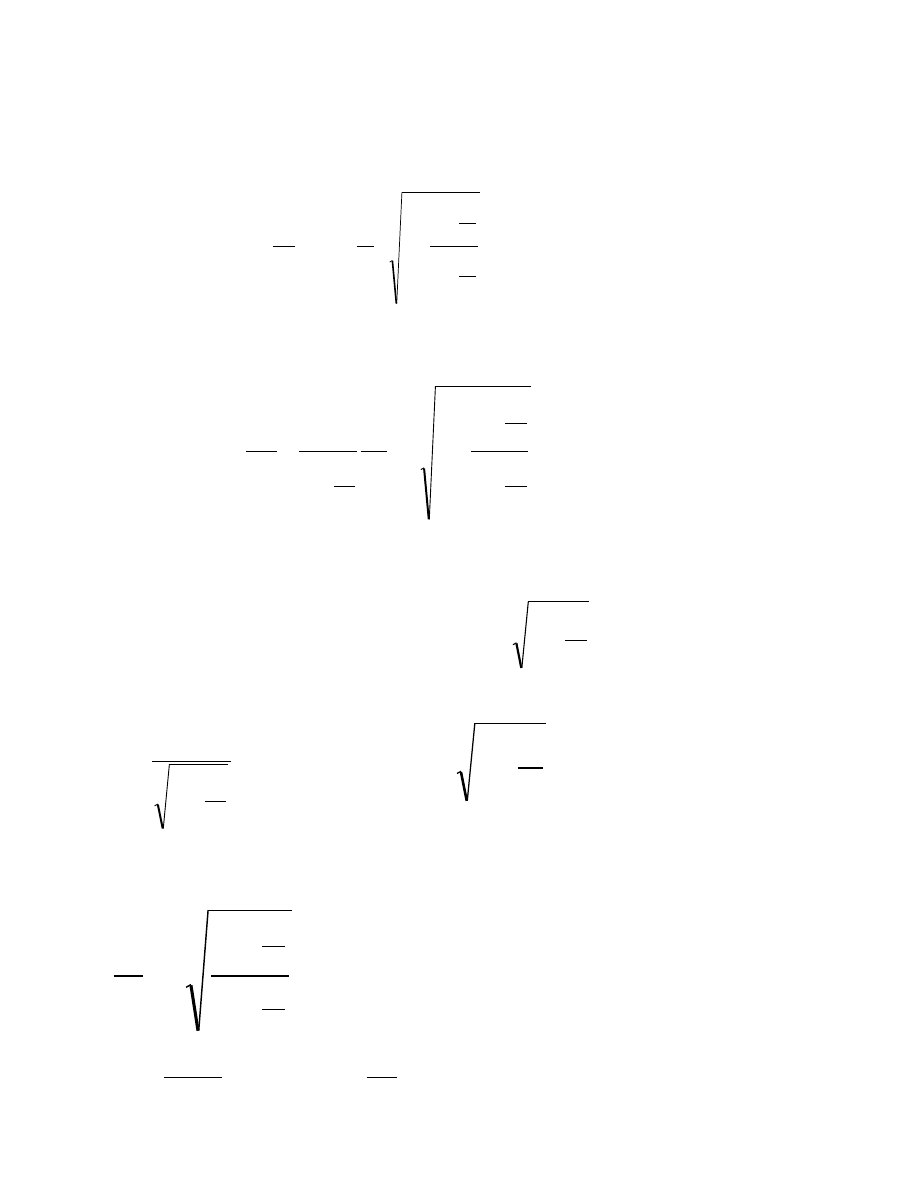
RADIALNY RUCH W POLU
GRAWITACYJNYM
υ
r
g
g
g
o
dr
dt
c
r
r
r
r
r
r
=
=
−
⋅ −
−
−
(
)
1
1
1
1
gdy obserwator w ro
gdy r
→
rg
υ
→
0
υ
τ
=
=
−
=
−
−
−
dR
d
r
r
dr
dt
c
r
r
r
r
g
g
g
o
1
1
1
1
1
gdy obserwator w r
gdy r
→
rg
υ
→
c
dt
c d
dR
2
2
2
=
−
τ
;
c d
r
r
c dt
g
τ
=
−
1
dR
dr
r
r
g
=
−
1
;
d
r
r
dt
g
τ
=
−
1
λ
λ
λ λ
λ
λ
λ
o
g
o
g
o
o
r
r
r
r
g
gdzie r
GM c
z
z
=
−
−
=
=
+ =
−
1
1
2
1
2
/
;
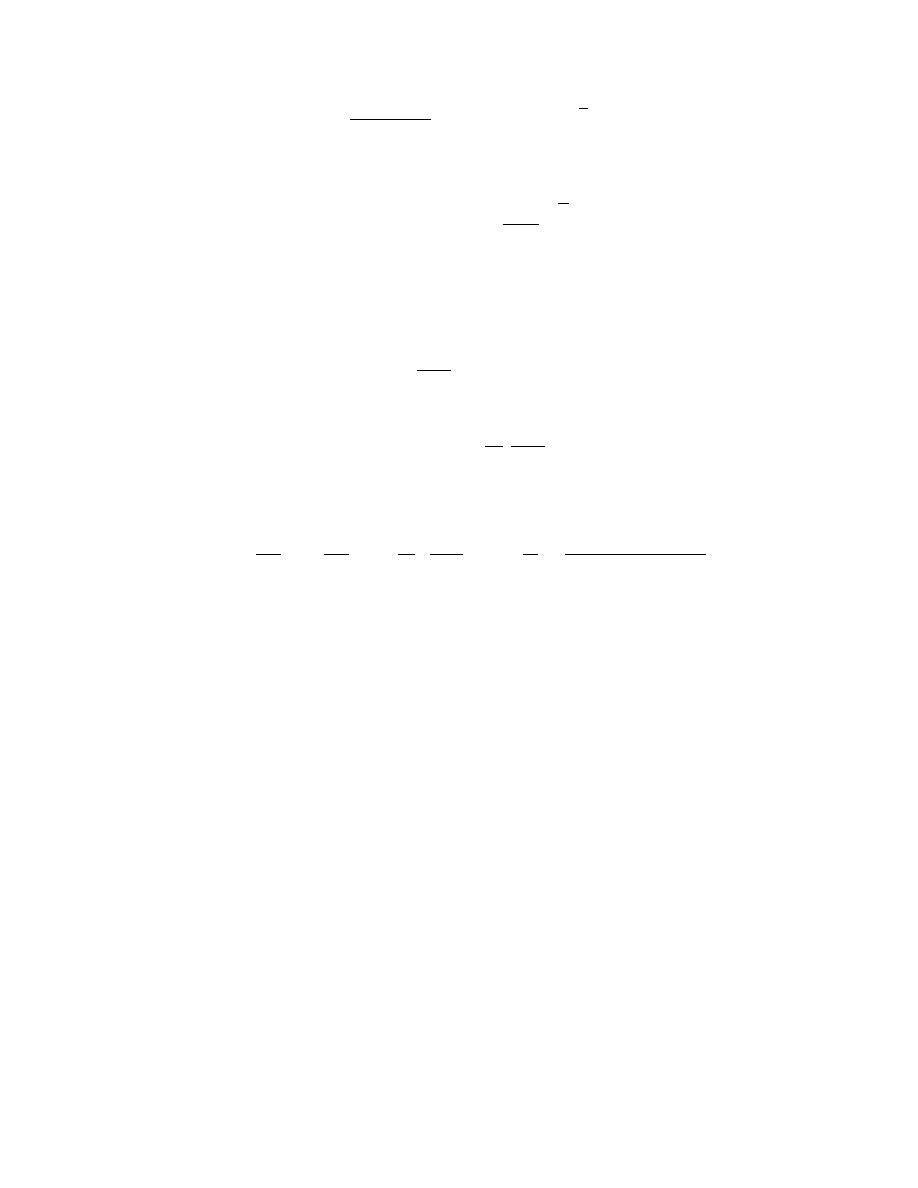
ν
π
p
e
e
e
e N
E m
A
N
H
=
=
⋅
(
)
.
2
0
3
1
2
2
4
9 1
10
ν
ν
ν
→
=
−
grup
p
c[
(
)]
1
1
2
ν
g <<
ν
ν
~ 10
2 -
10
3
MHz
ν
ν
p
<<
1
ν
ν
ν
grup
p
c
=
−
[
(
) ]
1
1
2
2
ν
ν
ν
ν
π ε
ν
−
=
=
+
= +
∫
∫
∫
a
p
l
l
e
e
dl
dl
c
l
c
e
m c
N dl
[
(
) ]
1
1
2
8
0
0
2
2
2
0
2
Wyszukiwarka
Podobne podstrony:
wykl5
05 md wykl5
GRUCZOŁY DOKREWNE wykł5
wykł5 podm wykon
Ak wykł5, Antropologia kulturowa, Wykład z antropologii
Wykl5
biochem-wykl5, STUDIA, biochemia
wykl5 Elektronika
podstawy finansow wykl5
SOUP wykl5
wykl5
wykł5 nadobowiazkowy
~$Metrol wielk geometr wykł5 2009
Metrol wielk geometr wykł5 2009
więcej podobnych podstron