1

SOCZEWKI

OKULAROWE

cz. 1

JEDNOOGNISKOWE

SOCZEWKI SFERYCZNE

Marek ZAJĄC, ©2002

SOCZEWKA SFERYCZNA













−

−

=

Φ

2

1

1

1

1

)

1

(

r

r

n

[1 dpt.] =[1/m]

ZDOLNOŚĆ ZBIERAJĄCA = MOC OPTYCZNA

R

n

n

s

n

s

n

)

'

(

'

'

−

+

=

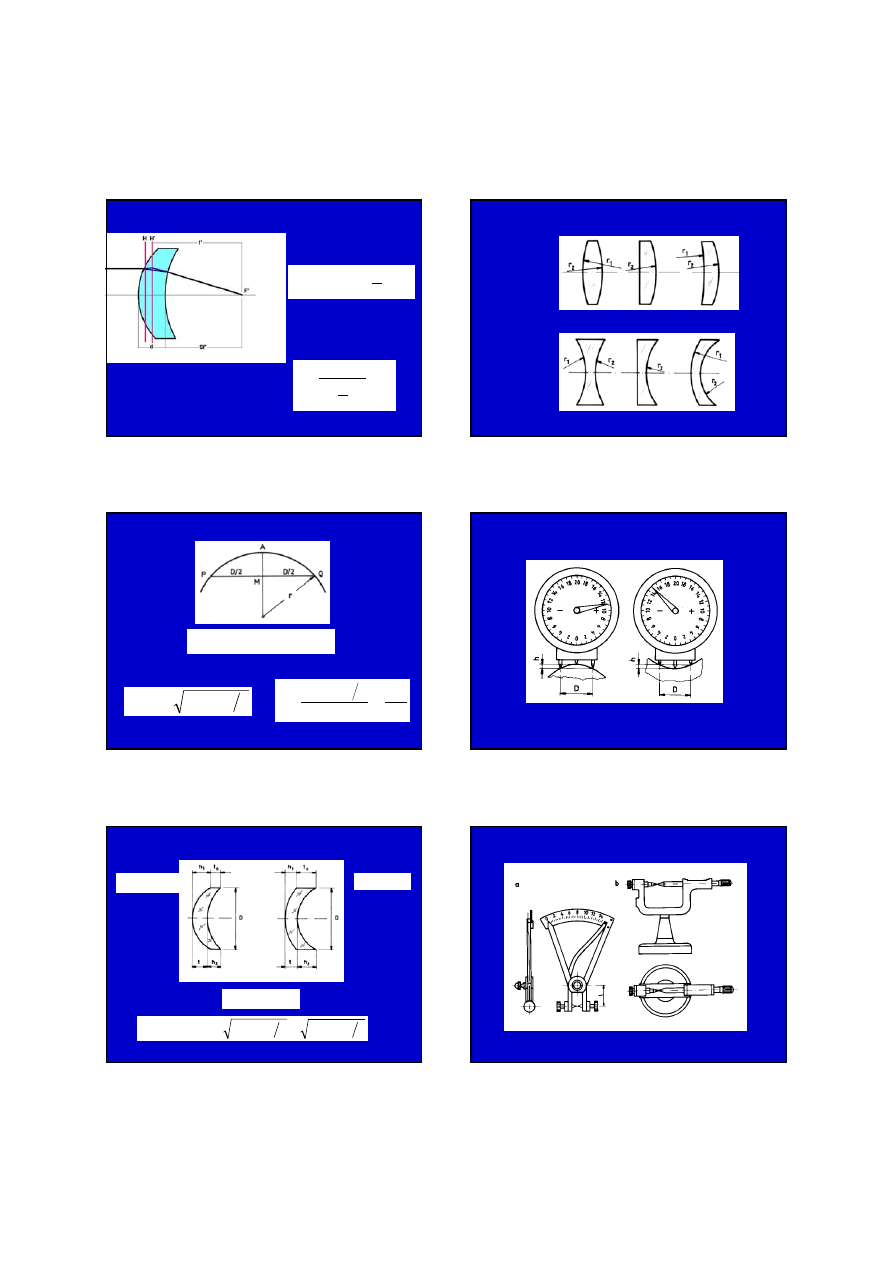
SFERYCZNA POWIERZCHNIA ODWZOROWUJĄCA

Φ

=

=

−

'

'

)

'

(

f

n

R

n

n

'

'

0

f

s

s

n

s

→

→

∞

→

1

1

1

)

1

(

R

n

−

=

Φ

2

2

1

)

1

(

R

n

−

=

Φ

ZDOLNOŚĆ ZBIERAJĄCA (MOC OPTYCZNA)

Jaka moc wypadkowa?

MOC SOCZEWKI SFERYCZNEJ

MOC SOCZEWKI SFERYCZNEJ

2

1

Φ

+

Φ

=

Φ

Moc sferometryczna

2

MOC SOCZEWKI SFERYCZNEJ

Moc właściwa

Moc czołowa

2

1

2

1

Φ

Φ

−

Φ

+

Φ

=

Φ

n

d

2

1

1

1

Φ

+

Φ

−

Φ

=

Φ

n

d

Odległości:
f’ - ogniskowa obrazowa
Sf’- zbiegowa (czołowa)

SOCZEWKI SFERYCZNE

dodatnie

ujemne

r1>0,

r2<0

r1=

∞, r2<0

r1<r2<0

r1=

∞, r2>0

r1<0,

r2>0

r1>r2>0

(

)

2

2

2

)

2

/

(D

h

r

r

+

−

=

4

2

2

D

r

r

h

−

−

=

h

D

h

D

h

r

8

2

4

2

2

2

≈

+

=

PROMIEŃ KRZYWIZNY POWIERZCHNI SFERYCZNEJ

SFEROMETR ZEGAROWY

PROMIEŃ KRZYWIZNY POWIERZCHNI SFERYCZNEJ

SOCZEWKI MENISKOWE

2

1

0

h

h

t

t

−

+

=

4

4

2

2

2

2

2

1

2

1

0

D

r

D

r

r

r

t

t

−

+

−

−

−

+

=

mm

t

5

,

1

≥

mm

t

5

,

1

0

≥

POMIAR GRUBOŚCI SOCZEWKI

GRUBOŚĆ SOCZEWKI

3

Soczewka meniskowa

niech:

n=1.66

niech:

SOCZEWKA SFERYCZNA

dptr

0

,

2

+

=

Φ

dptr

1

,

7

2

−

=

Φ

dptr

1

,

9

)

1

,

7

(

0

,

2

2

1

=

−

−

=

Φ

−

Φ

=

Φ

(

)

mm

m

n

r

53

,

72

0725275

,

0

1

,

9

1

66

,

1

1

1

1

≈

=

−

=

Φ

−

=

(

)

mm

m

n

r

96

,

93

0939577

,

0

1

,

7

66

,

1

1

1

2

2

≈

=

−

−

=

Φ

−

=

Soczewka dodatnia

Φ

=+2,0 dptr., meniskowa

r

1

= 72,53 mm

r

2

= 93,96 mm.

średnica D = 70 mm,
grubość na brzegu t

0

= 1,5 mm.

grubość w środku

SOCZEWKA SFERYCZNA

mm

h

0036

,

9

4

70

53

,

72

53

,

72

2

2

1

=

−

−

=

mm

h

7621

,

6

4

70

96

,

93

96

,

93

2

2

2

=

−

−

=

mm

mm

t

75

,

3

7415

,

3

7621

,

6

0036

,

9

5

,

1

≈

=

−

+

=

2

1

2

1

Φ

Φ

−

Φ

+

Φ

=

Φ

n

d

Moc właściwa

2

1

1

1

Φ

+

Φ

−

Φ

=

Φ

n

d

Moc czołowa

2

1

Φ

+

Φ

=

Φ

Moc sferometryczna

dptr

1

,

9

1

=

Φ

dptr

1

,

7

2

−

=

Φ

n=1,66

Soczewka meniskowa dodatnia

t

0

=3,75 mm

dptr

c

20

,

2

190997

,

2

)

1

,

7

(

1

,

9

66

,

1

00375

,

0

1

1

,

9

≈

=

−

+

−

=

Φ

dptr

15

,

2

14596

,

0

2

)

1

,

7

(

1

,

9

66

,

1

00375

,

0

)

1

,

7

(

1

,

9

+

≈

+

=

−

⋅

⋅

−

−

+

=

Φ

dptr

00

,

2

)

1

,

7

(

1

,

9

+

=

−

+

=

Φ

Soczewka meniskowa

dptr

0

,

10

0

,

4

0

,

6

1

2

−

=

−

−

=

Φ

−

Φ

=

Φ

dptr

0

,

6

−

=

Φ

dptr

0

,

4

1

+

=

Φ

niech:

n=1.523

mm

m

n

r

0

,

131

131

,

0

0

,

4

1

523

,

1

1

1

1

≈

=

−

=

Φ

−

=

mm

m

n

r

3

,

53

10523

,

0

0

,

10

523

,

1

1

1

1

2

≈

=

−

−

=

Φ

−

=

niech:

SOCZEWKA SFERYCZNA

Soczewka ujemna

Φ

=-6,0 dptr. , meniskowa

r

1

= 131,0 mm

r

2

= 52,2 mm.

średnica D = 60 mm,
grubość w środku t = 1,5 mm.

mm

h

4814

,

3

4

60

131

131

2

2

1

≈

−

−

=

mm

h

2445

,

9

4

0

6

3

,

52

3

,

52

2

2

2

≈

−

−

=

mm

h

h

t

t

3

,

7

2631

,

7

2445

,

9

4814

,

3

5

,

1

2

1

0

≈

=

+

−

=

+

−

=

grubość na brzegu

SOCZEWKA SFERYCZNA

(

)

(

)

dptr

96

,

5

039396

,

0

6

10

4

523

,

1

0015

,

0

10

4

−

≈

+

−

=

−

⋅

⋅

−

−

+

=

Φ

(

)

dptr

c

98

,

5

98418

,

5

10

4

523

,

1

0015

,

0

1

4

−

≈

−

=

−

+

−

=

Φ

2

1

2

1

Φ

Φ

−

Φ

+

Φ

=

Φ

n

d

Moc właściwa

2

1

1

1

Φ

+

Φ

−

Φ

=

Φ

n

d

Moc czołowa

2

1

Φ

+

Φ

=

Φ

Moc sferometryczna

dptr

0

,

4

1

+

=

Φ

dptr

0

,

10

2

−

=

Φ

n=1.523

Soczewka meniskowa ujemna

(

)

dptr

00

,

6

10

4

−

=

−

+

=

Φ

t

0

=1.5 mm

4

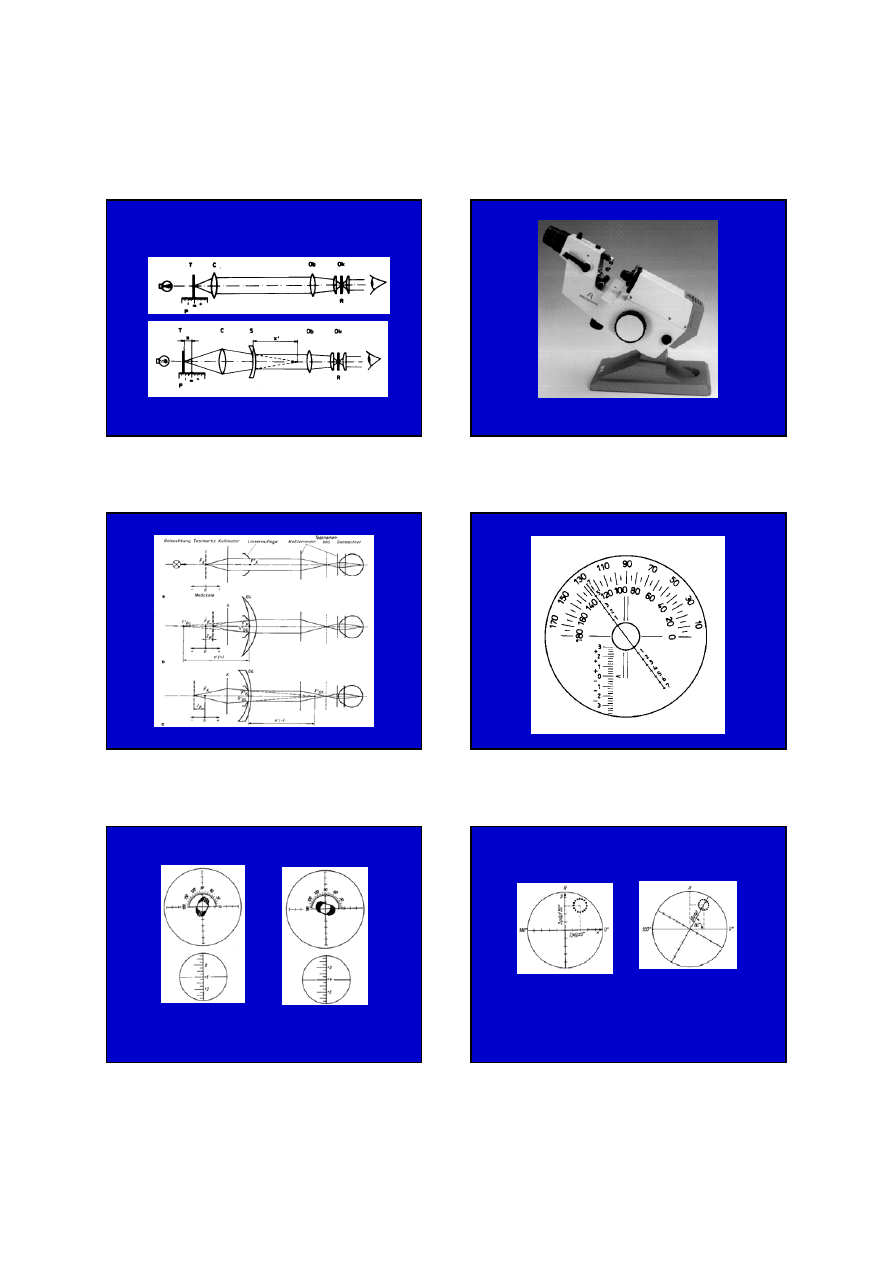
DIOPTROMIERZ LUNETOWY

POMIAR MOCY SOCZEWKI

DIOPTROMIERZ LUNETOWY

POMIAR MOCY SOCZEWKI

POMIAR MOCY SOCZEWKI

DIOPTROMIERZ LUNETOWY

SKALA DIOPTROMIERZA LUNETOWEGO

POMIAR MOCY SOCZEWKI

DIOPTROMIERZ LUNETOWY
pomiar mocy soczewki astygmatycznej

POMIAR MOCY SOCZEWKI

DIOPTROMIERZ LUNETOWY
pomiar mocy pryzmatycznej

POMIAR MOCY SOCZEWKI

5

DIOPTROMIERZ LUNETOWY
pomiar mocy części do dali i naddatku

POMIAR MOCY SOCZEWKI

Metoda „wklęsła”

Metoda „wypukła”

DIOPTROMIERZ LUNETOWY
pomiar mocy części do dali i naddatku

POMIAR MOCY SOCZEWKI

POMIAR MOCY SOCZEWKI

DIOPTROMIERZ PROJEKCYJNY

POMIAR MOCY SOCZEWKI

DIOPTROMIERZ PROJEKCYJNY

POMIAR MOCY SOCZEWKI

DIOPTROMIERZ AUTOMATYCZNY

POMIAR MOCY SOCZEWKI

DIOPTROMIERZ AUTOMATYCZNY (Humphrey Lens Analyser)

1 - źródło światła,
2 - pryzmat czworościenny,
3 - soczewka kolimująca,
4 - przysłona sektorowa,
5 - silnik,
6 - pryzmat odbijający,
7 - czterootworowa przysłona,
8 - układ odwzorowujący,
9 - zwierciadło,
10 - przysłona,
11 - detektor kwadrantowy,
12 - badana soczewka,

6

Sprawdzenie mocy soczewki metodą neutralizacji

POMIAR MOCY SOCZEWKI

Dopuszczalne odchyłki mocy soczewek sferycznych według
PN-86/Z-53090

zakres mocy

dopuszczalna odchyłka mocy czołowej

(dioptrii)

(dioptrii)
grupa I

grupa II

do 3,0

0,06

0,12

3,25 do 6,0

0,09

0,12

6,5 do 9,0

0,12

0,18

9,5 do 12,0

0,18

0,18

12,5 do 20,0

0,25

0,25

ponad 20,0

0,25

0,35

TOLERANCJE WYMIAROWE

Materiał

Szkło

klasyczne

(„mineralne”)

CR39

(„plastik”)

Szkło o dużym

współcz. załamania

(„high index”)

Współcz. załamania

n [-]

1,523

1,50

1,80

Liczba Abbego

ν [-]

58,6

47

ok. 30

Gęstość

ρ [g/cm3]

2,62

1,32

3,0

Promień zewnętrzny

r1 [mm]

52,3

48,0

80,0

Promień wewnętrzny

r2 [mm]

74,7

68,6

111,43

Grubość w środku

t [mm]

5,17

4,95

3,73

Strzałka zewnętrzna

h

1

[mm]

9,46

10,53

5,84

Strzałka wewnętrzna

h

2

[mm]

6,29

7,58

4,17

Objętość soczewki

V [cm

3

]

24,83

19,93

15,74

Masa soczewki

m [g]

65,02

26

47

Współczynnik odbicia

R [%]

4,3

3,78

8

Uwagi

lekkie

płaskie,

konieczna warstwa

przeciwodblaskowa

SOCZEWKI OKULAROWE - PORÓWNANIE MATERIAŁÓW

Φ = +3,0 dptr, D = 60 mm, t

0

= 2 mm

ABERRACJE SOCZEWEK

ABERRACJE SOCZEWEK

Aberracja CHROMATYCZNA

Aberracje MONOCHROMATYCZNE

Opis aberracji monochromatycznychwedług
Seidela (aberracje III-rzędowe):

•

aberracja SFERYCZNA

•

KOMA

•

ASTYGMATYZM

•

KRZYWIZNA POLA

•

DYSTORSJA

( )

( )

[

]













ρ

−

ρ

−

λ

=

λ

Φ

=

Φ

2

1

1

1

1

n

R

R

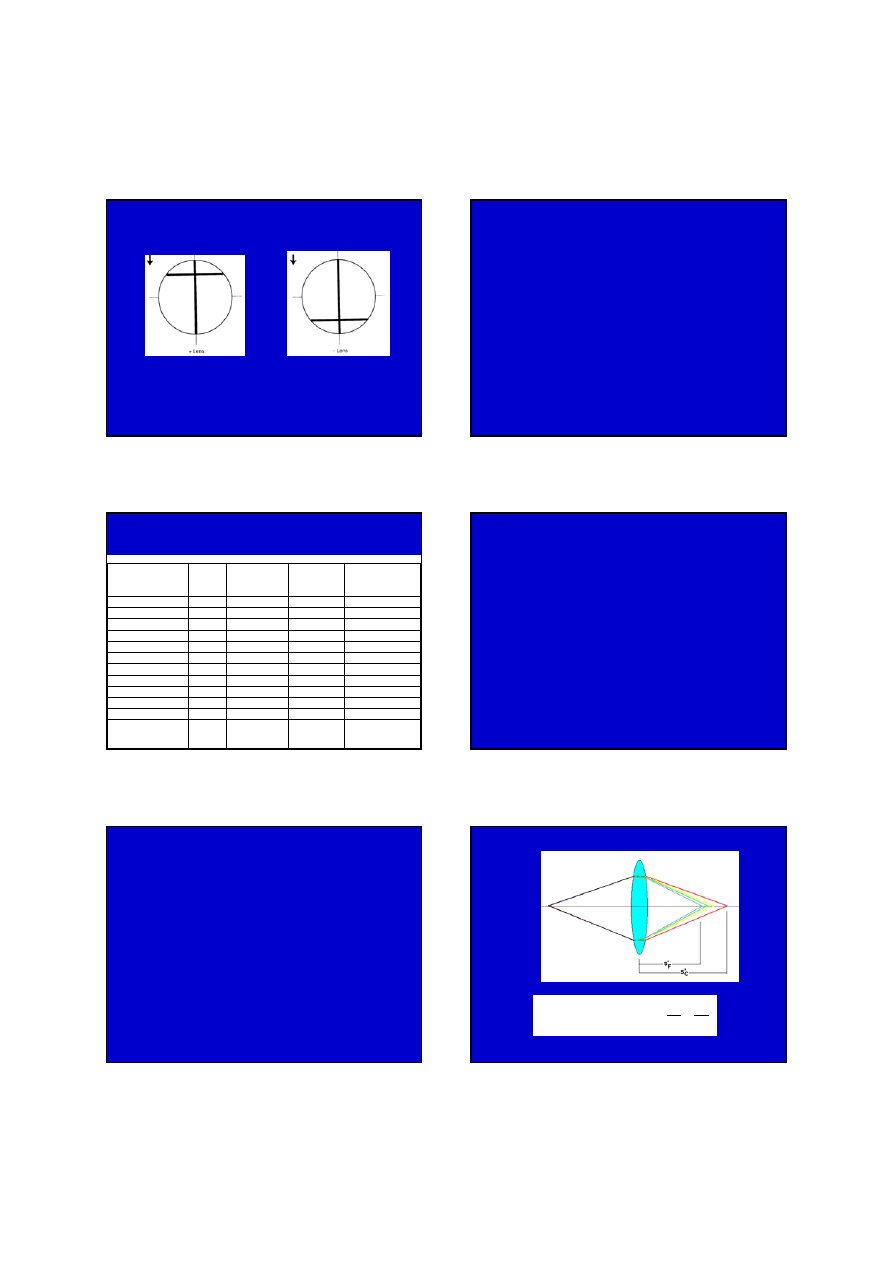
ABERRACJA CHROMATYCZNA

Aberracja chromatyczna podłużna pojedynczej soczewki

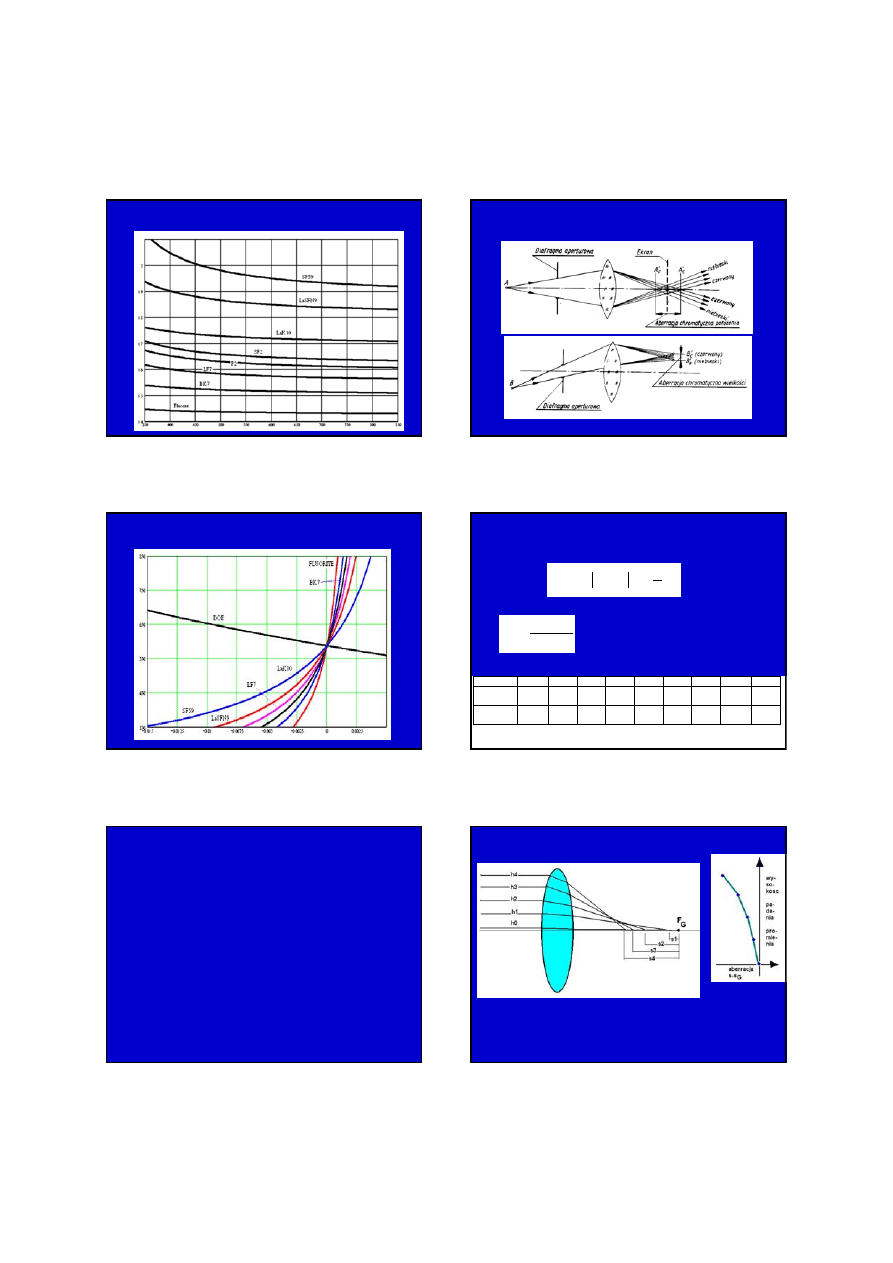
7

ABERRACJA CHROMATYCZNA

właściwości dyspersyjne materiałów optycznych

ABERRACJA CHROMATYCZNA

ABERRACJA CHROMATYCZNA

Aberracja chromatyczna podłużna pojedynczej soczewki

ABERRACJA CHROMATYCZNA

właściwości dyspersyjne materiałów optycznych

0

1

1

2

Φ

ν

=

Φ

−

Φ

=

∆Φ

λ

λ

C

F

d

R

n

n

n

−

−

=

ν

1

<— liczba Abbego

Glass

Fluorite FK54

BK7

LF7

F2

SF2

LaK10 LaSFN9 SF59

Refractive
index n

1.4339

1.437

1.517

1.575

1.620

1.648

1.720

1.850

1.952

Abbe
number ν

95.140

90.702

64.162 41.490 36.366 25.767 50.410 32.169

20.363

λ

F

=486.1 nm

λ

d

=587.6 nm

λ

C

=656.3 nm

ABERRACJE SOCZEWEK

Aberracja CHROMATYCZNA

Aberracje MONOCHROMATYCZNE

Opis aberracji monochromatycznychwedług
Seidela (aberracje III-rzędowe):

•

aberracja SFERYCZNA

•

KOMA

•

ASTYGMATYZM

•

KRZYWIZNA POLA

•

DYSTORSJA

ABERRACJE ODWZOROWANIA

ABERRACJA SFERYCZNA
zależy od 4. potęgi apertury,
nie zależy od kata polowego

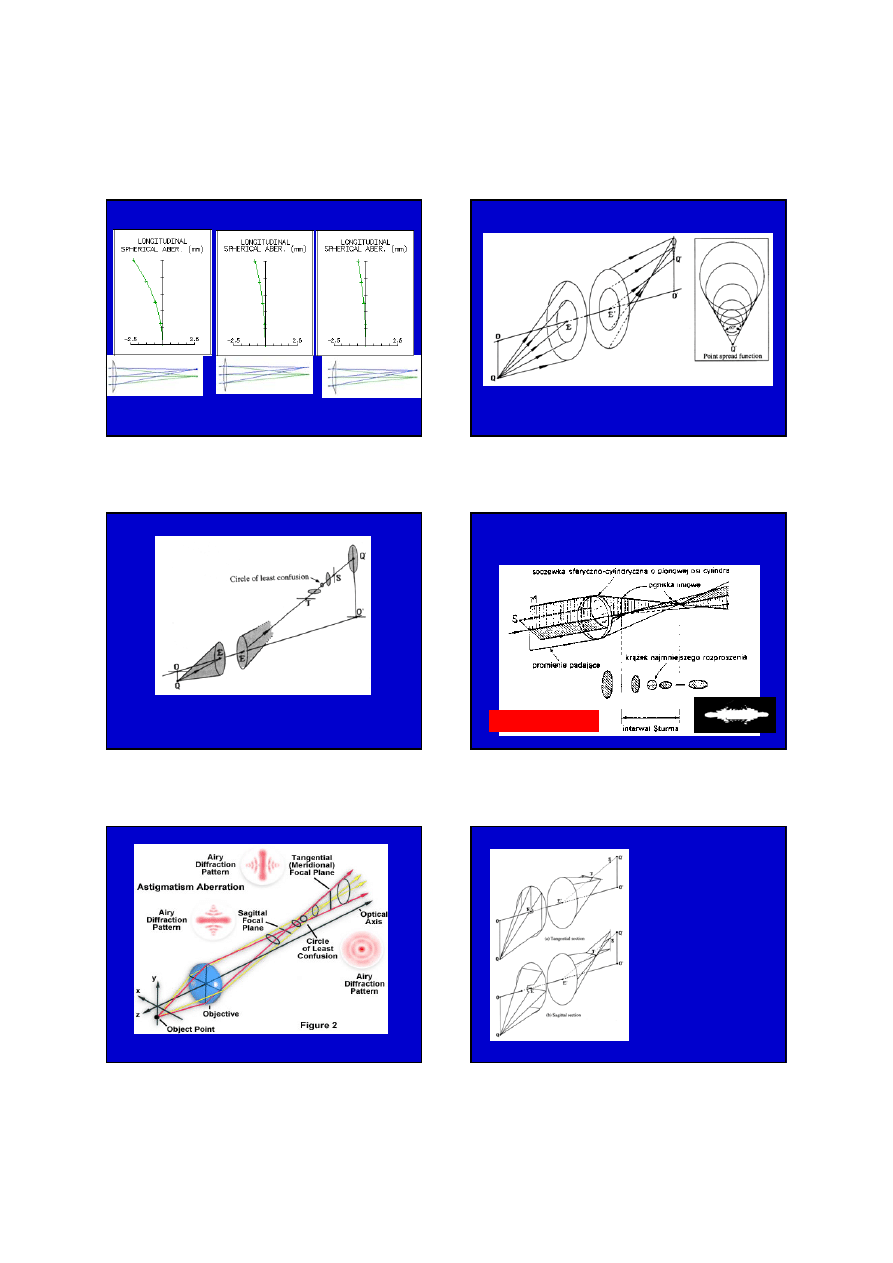
8

ABERRACJA SFERYCZNA

zależy od kształtu soczewki

ABERRACJE ODWZOROWANIA

ABERRACJE ODWZOROWANIA

KOMA

(zależy od 1. potęgi kata pola widzenia

od 3. potęgi apertury)

ABERRACJE ODWZOROWANIA

ASTYGMATYZM I KRZYWIZNA POLA
zależą od 2. potęgi kata pola widzenia

od 2. potęgi apertury)

ASTYGMATYZM

ABERRACJE ODWZOROWANIA

ASTYGMATYZM

ABERRACJE ODWZOROWANIA

ABERRACJE ODWZOROWANIA

ASTYGMATYZM I
KRZYWIZNA POLA
zależą od
2. potęgi kata pola
widzenia
od 2. potęgi apertury)

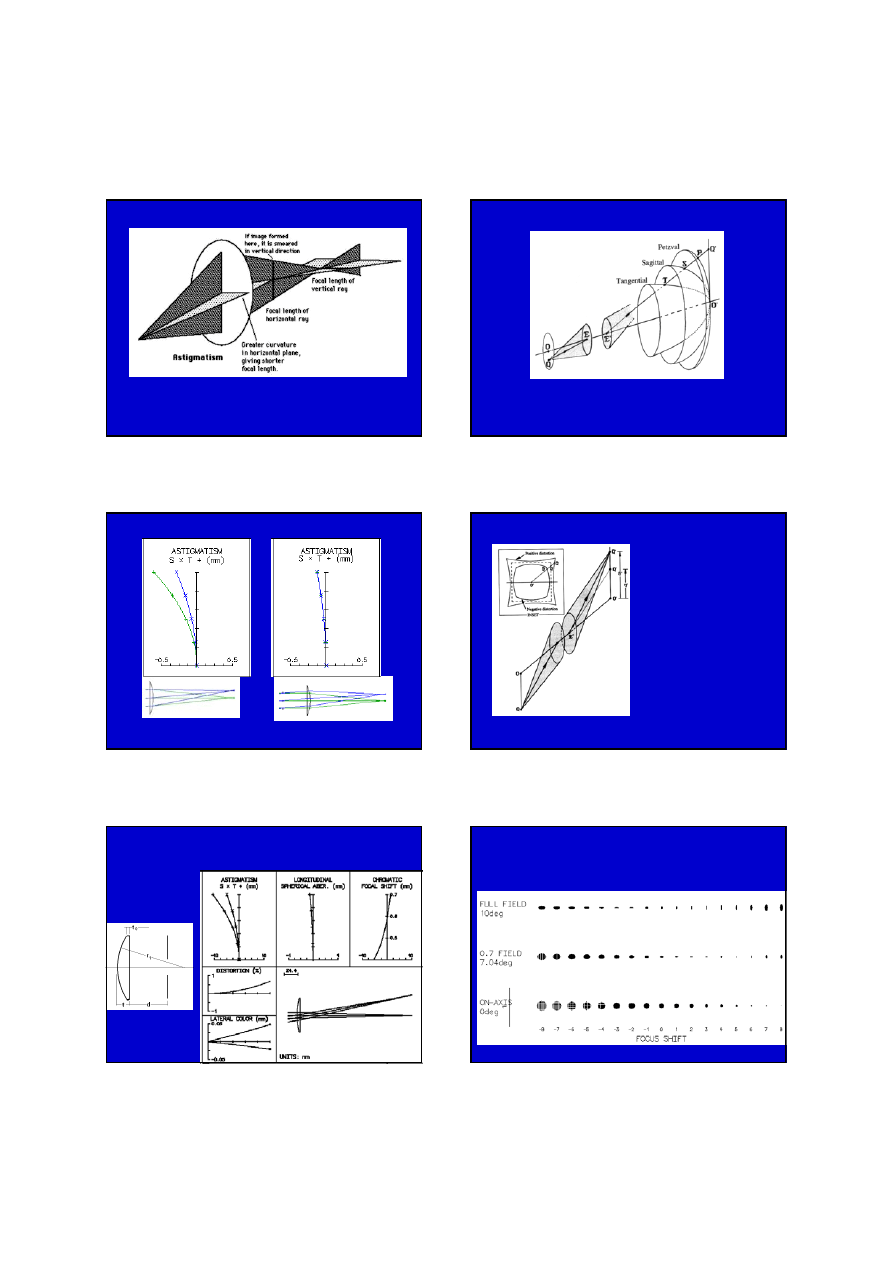
9

ASTYGMATYZM

ABERRACJE ODWZOROWANIA

ABERRACJE ODWZOROWANIA

ASTYGMATYZM I KRZYWIZNA POLA

ASTYGMATYZM

zależy od położenia źrenicy

ABERRACJE ODWZOROWANIA

ABERRACJE ODWZOROWANIA

DYSTORSJA
zależy od
3. potegi kąta pola widzenia
i 1. potegi kąta aperturowego,
zniekształca obraz,
nie psuje ostrości

Soczewka 1:
r

1

=104.6 mm, n=1.532,

r

r

2

=

∞, t=5,9 mm, D=60 mm, t

0

=1,5 mm, d=25 mm

Soczewka 1:
r

1

=104.6 mm, n=1.532,

r

r

2

=

∞, t=5,9 mm, D=60 mm, t

0

=1,5 mm, d=25 mm

10

Soczewka 2:
r

1

=40.94 mm, n=1.532, r

2

= 61,35mm, t=6,75 mm, D=60 mm, t

0

=1,5 mm, d=25 mm

Soczewka 2:
r

1

=40.94 mm, n=1.532, r

2

= 61,35mm, t=6,75 mm, D=60 mm, t

0

=1,5 mm, d=25 mm

Projektowanie soczewek

okularowych

Aberracje układu okulary-oko

WSPÓŁPRACA OKA Z OKULARAMI

Jak jest usytuowana soczewka okularowa względem oka?

LOKALIZACJA SOCZEWKI WZGLĘDEM OKA

Kąt pantoskopowy ramki

Odległość
wierzchołkowa

WSPÓŁPRACA OKA Z OKULARAMI

Odległość do obrocia oka

WSPÓŁPRACA OKA Z OKULARAMI

Gdzie jest źrenica układu okulary-oko?

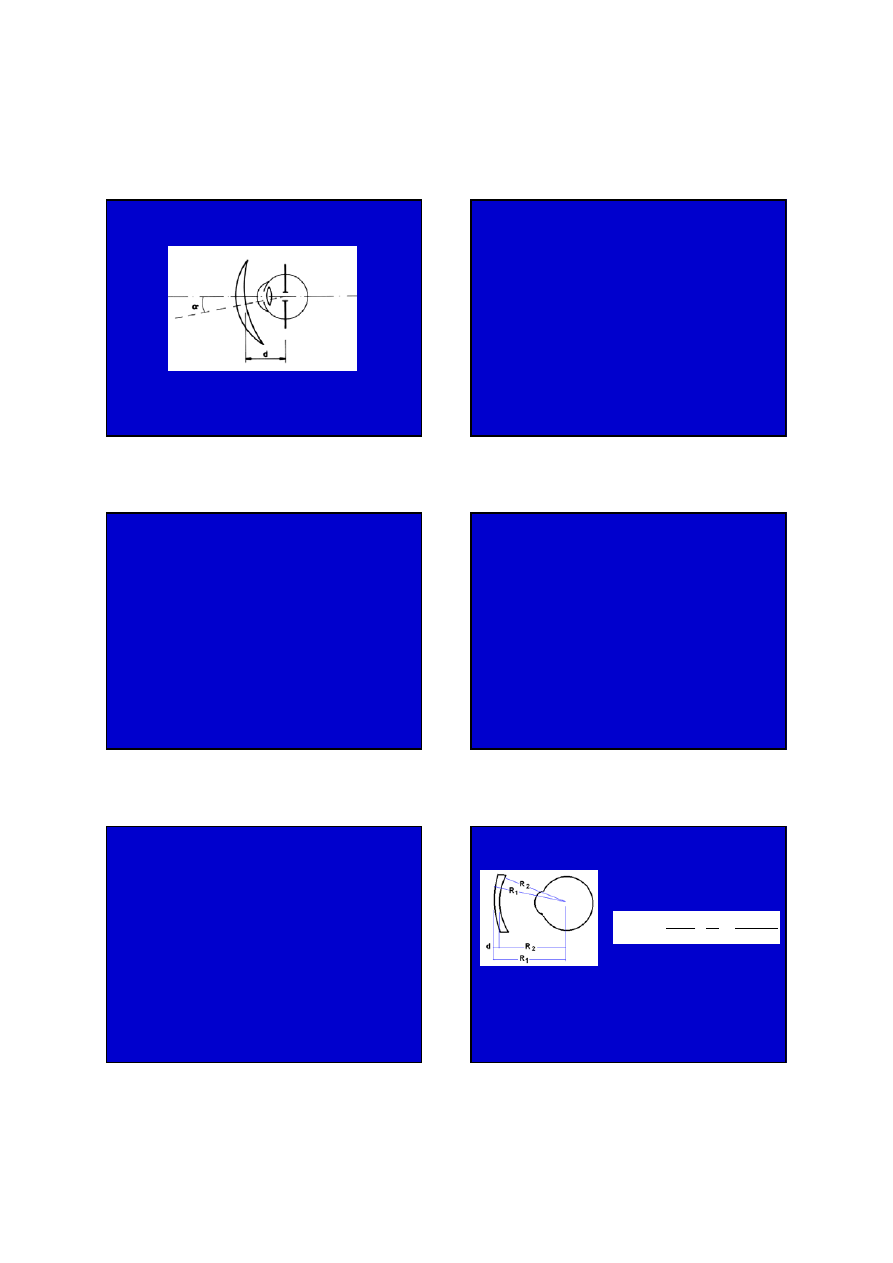
11

WSPÓŁPRACA OKA Z OKULARAMI

Gdzie jest źrenica układu okulary-oko?

PROJEKTOWANIE SOCZEWEK OKULAROWYCH

KRYTERIA:
• jakość obrazu (małe aberracje)
• estetyka (płaskie)
• wygoda (lekkie)
• względy technologiczne (niewiele krzywizn bazowych)

ABERRACJE
• chromatyczna - duża liczba Abbego
• monochromatyczne:

• sferyczna, koma - mała apertura, zaniedbywalne,
• dystorsja - nie psuje ostrości
• krzywizna pola - kompensowana przez akomodację
• astygmatyzm (wiązek pozaosiowych) NAJWAŻNIEJSZA

PROJEKTOWANIE SOCZEWEK OKULAROWYCH

KOREKCJA ASTYGMATYZMY SOCZEWEK OKULAROWYCH

• WOLLASTON - pierwsze uwagi o możliwości korekcji,

• OSTWALD (1898) - pierwsze rozwiązanie,

• TSCHERNING (1904) - dokładne rozwiązanie,

• T.GUTKOWSKI, T. WAGNEROWSKI (lata 30. - 40.),
• H.MELANOWSKI, J. BARTKOWSKA (lata 50.- 60.)

PROJEKTOWANIE SOCZEWEK OKULAROWYCH

Kształt soczewki określony przez
*MOC:

Φ = Φ

1

+

Φ

2

, WYGIĘCIE:

Ψ = Φ

1

-

Φ

2

, GRUBOŚĆ: d

*Powierzchnia bazowa - pierwsza lub druga,
*Niewielka liczba powierzchni bazowych,
*Minimalizowany astygmatyzm (krzywizna pola)
*Rodzaje:

płasko-wypukłe, płasko-wklęsłe - duże aberracje
dwuwypukłe, dwuwklęsłe - tylko w kasetach próbnych,
peryskopijne (małe moce):

dodatnie: powierzchnia bazowa druga,

Φ

2

=-1,25 dptr,

ujemne: powierzchnia bazowa pierwsza,

Φ

1

=+1,25 dptr,

meniskowe

dodatnie powierzchnia bazowa druga

Φ

2

=-6,0 dptr,

ujemne - powierzchnia bazowa pierwsza

Φ

1

=+6,0 dptr.

sferocylindryczne

dodatnie - pierwsza powierzchnia toryczna,
ujemne - druga powierzchnia toryczna

PROJEKTOWANIE SOCZEWEK OKULAROWYCH

przykłady konstrukcji soczewek

•PUNKTALNE - projekt ROHR, wykonanie ZEISS 1911

(od +7.78 dptr. do -24.68 dptr., dla każdej mocy inna krzywizna),

•KATRAL

(dla oczu bezsoczewkowych),

•ORTHOGON - BAUSCH & LOMB 1928,

(mniej krzywizn bazowych,astygmatyzm <0.25 dptr. dla całego pola),

•TILLYER - AMERICAL OPTICAL COMPANY 1926

(19 krzywizn bazowych, częściowo skorygowana krzywizna pola),

•PUNKTAL - ZEISS 1946-47

(dla dali i bliży, astygmatyzm <0.1 dptr. dla kąta 15

o

, <0.2 dptr. dla

całego pola),

•UNIVIS - UNIVIS Inc. 1963

(kąt 30

o

, przednia powierzchnia sferyczna, druga toryczna),

•itd.

PROJEKTOWANIE SOCZEWEK OKULAROWYCH

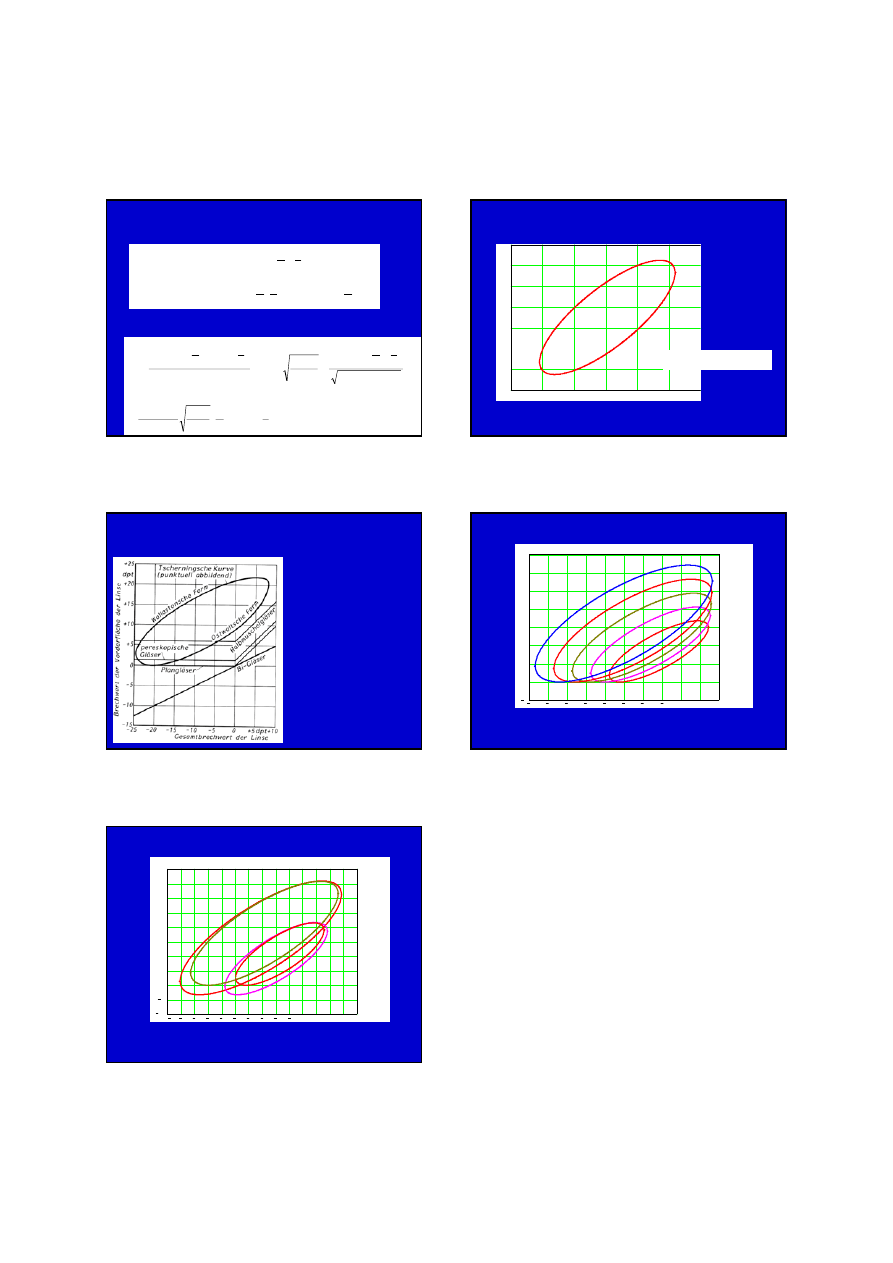
Soczewka aplanatyczna OSTWALDA (1898)

d[mm] 1,5 2,0

2,5

3,0

10,0

n
1,5

-1,28

-1,74 -2,22 -2,72 -13,3

1,6

-1,53

-2,09 -2,67 -3,28 -16,0

1,7

-1,78

-2,43 -3,11 -3,82 -18,7

1,8

-2,04

-2,78 -3,56 -4,36 -21,3

R

2

=25-28 mm,

R

1

=R

2

+d

d=1,5 mm

2

2

2

2

)

1

(

1

1

)

1

(

R

n

d

R

d

R

n

−

−

≈













−

+

−

=

Φ

12

PROJEKTOWANIE SOCZEWEK OKULAROWYCH

ROZWIĄZANIA ZAGADNIENIA KOREKCJI ASTYGMATYZMU

1.

SOUTHAL (1937), BARTKOWSKA (1961):

0

1

)

1

(

1

1

)

1

(

2

)

2

(

)

1

(

1

1

)

1

(

)

2

(

)

2

(

2

2

1

2

2

1

=









−

+

Φ

+









−

−

Φ

−

−

−

−

Φ























 +

−

+

Φ

+

−

Φ

+

L

n

n

s

L

n

n

n

s

L

n

s

n

n

2.

GUTKOWSKI, WAGNEROWSKI (1944-1950)

0

1

)

1

(

1

2

2

3

)

1

(

2

)

2

3

)(

2

(

1

1

)

1

(

2

2

2

3

2

3

1

)

1

(

1

)

1

(

2

2

2

2

2

2

=

























+

−

+

−

−

−

−

























−

+











 +

−

−

+

−

Ψ

+

























−









+

−

−

+

Φ

s

n

L

n

n

n

n

n

n

n

s

L

n

n

n

n

s

n

L

n

PROJEKTOWANIE SOCZEWEK OKULAROWYCH

ROZWIĄZANIA ZAGADNIENIA KOREKCJI ASTYGMATYZMU

Φ

Φ1

Elipsa TSCHERNINGA

0

1

2

1

=

−

Φ

−

Φ

C

B

A

Różne konstrukcje
soczewek okularowych

PROJEKTOWANIE SOCZEWEK OKULAROWYCH

ROZWIĄZANIA ZAGADNIENIA KOREKCJI ASTYGMATYZMU

PROJEKTOWANIE SOCZEWEK OKULAROWYCH

ROZWIĄZANIA ZAGADNIENIA KOREKCJI ASTYGMATYZMU

Elipsy Tscherninga dla soczewek okularowych przeznaczonych do dali
umieszczonych 13 mm przed okiem a wykonanych ze szkła o różnych
współczynnikach załamania.

40

35

30

25

20

15

10

5

0

5

10

5

0

5

10

15

20

25

30

35

n=1,8

n=1,7

n=1,6

n=1,5

n=1,4

[dptr.]

[dptr.]

Φ

Φ1

PROJEKTOWANIE SOCZEWEK OKULAROWYCH

ROZWIĄZANIA ZAGADNIENIA KOREKCJI ASTYGMATYZMU

Elipsy Tscherninga dla soczewek okularowych przeznaczonych do dali
i do bliży umieszczonych tuż przed okiem lub w odległości e = 13 mm
przed okiem

10

5

0

5

10

15

20

25

30

35

40

50 45 40 35 30 25 20 15 10 5

0

5

10 15 20

e=0

e=13 mm

do dali

do bliży

do dali

do bliży

[dptr.]

Φ1

[dptr.]

Φ