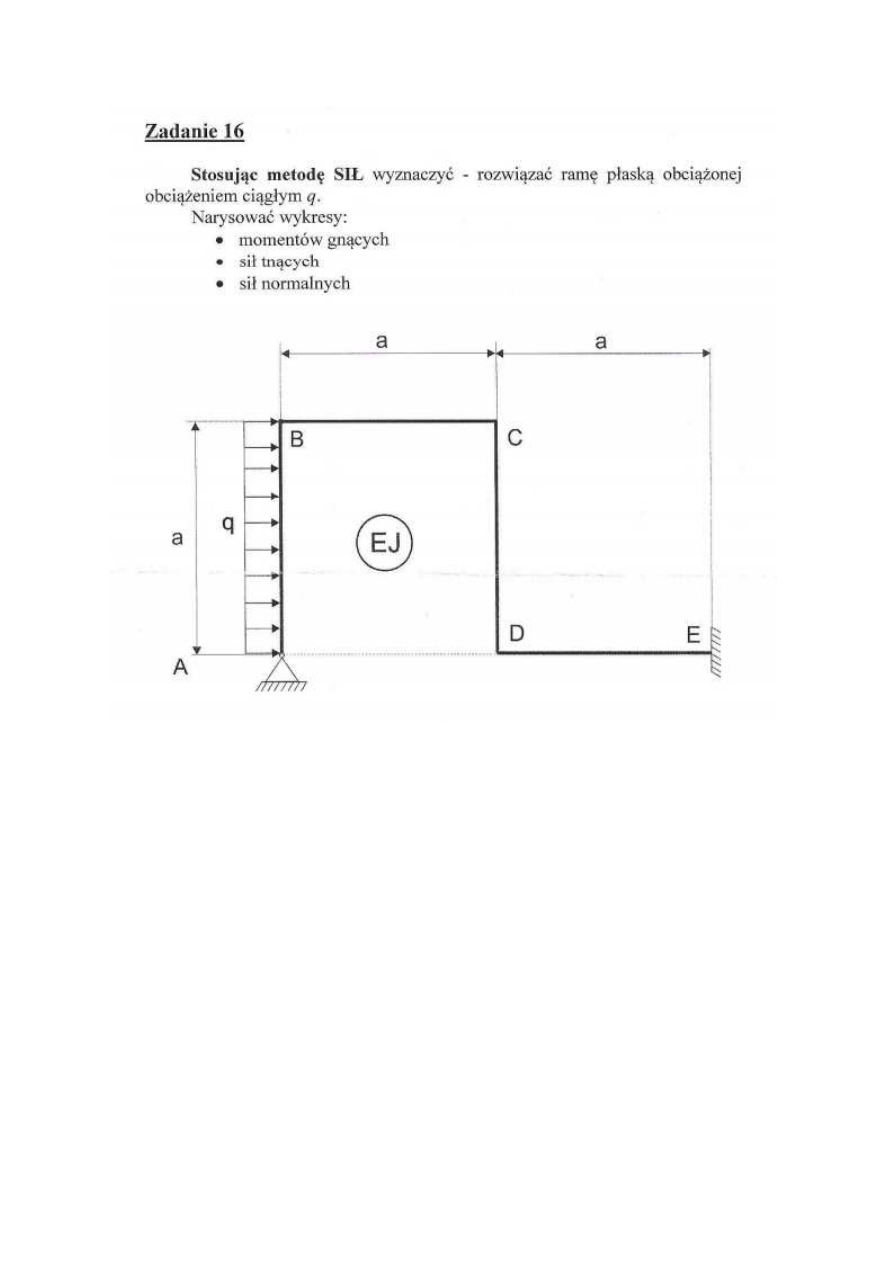
•

 

Rama jest dwukrotnie statycznie niewyznaczalna: 

 

•

 

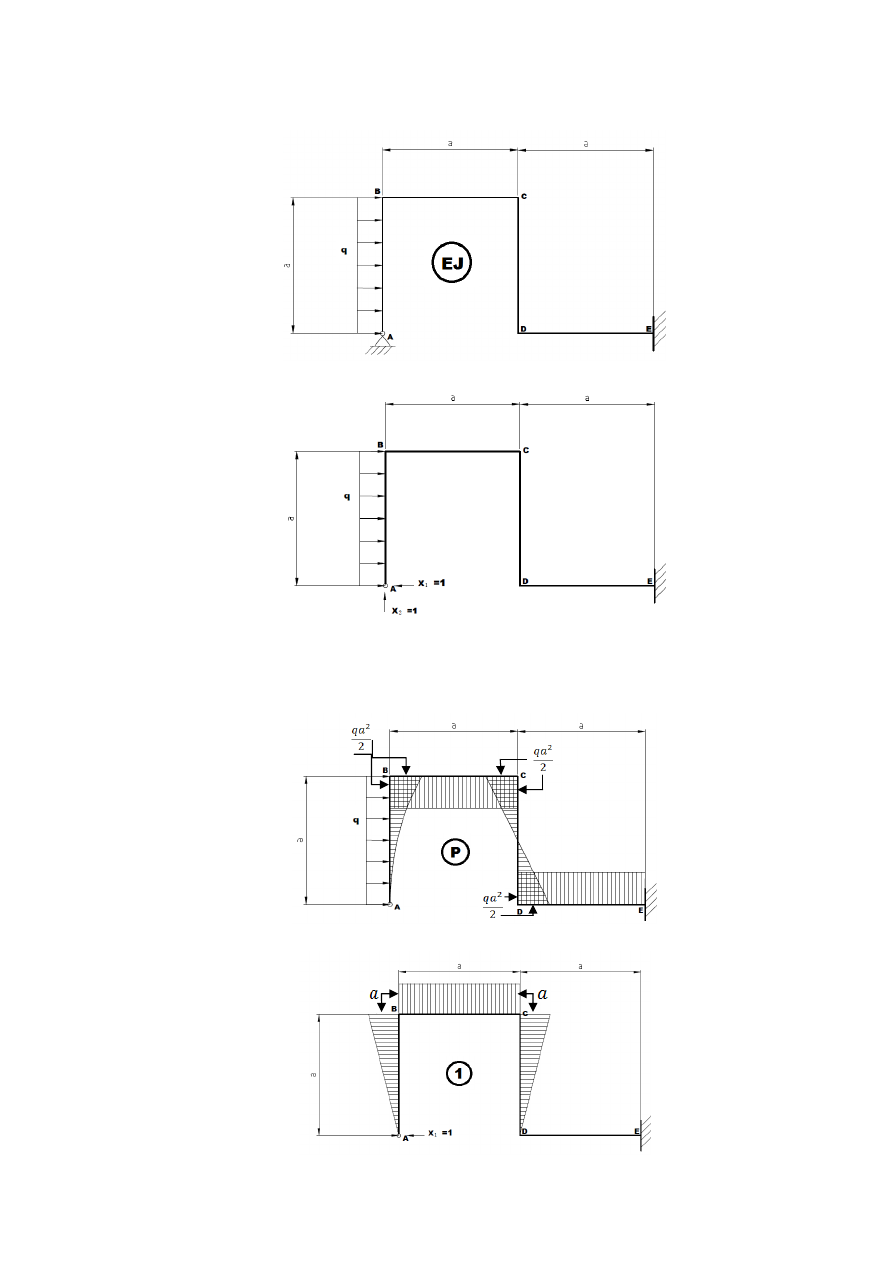
Układ uwolniony (podstawowy): 

 

•

 

Równania kanoniczne dla rozważanej ramy mają postać: 

δ

11

X

1

+ δ

12

X

2

+ δ

1P

=0 

δ

21

X

1

+ δ

22

X

2

+ δ

2P

=0 

•

 

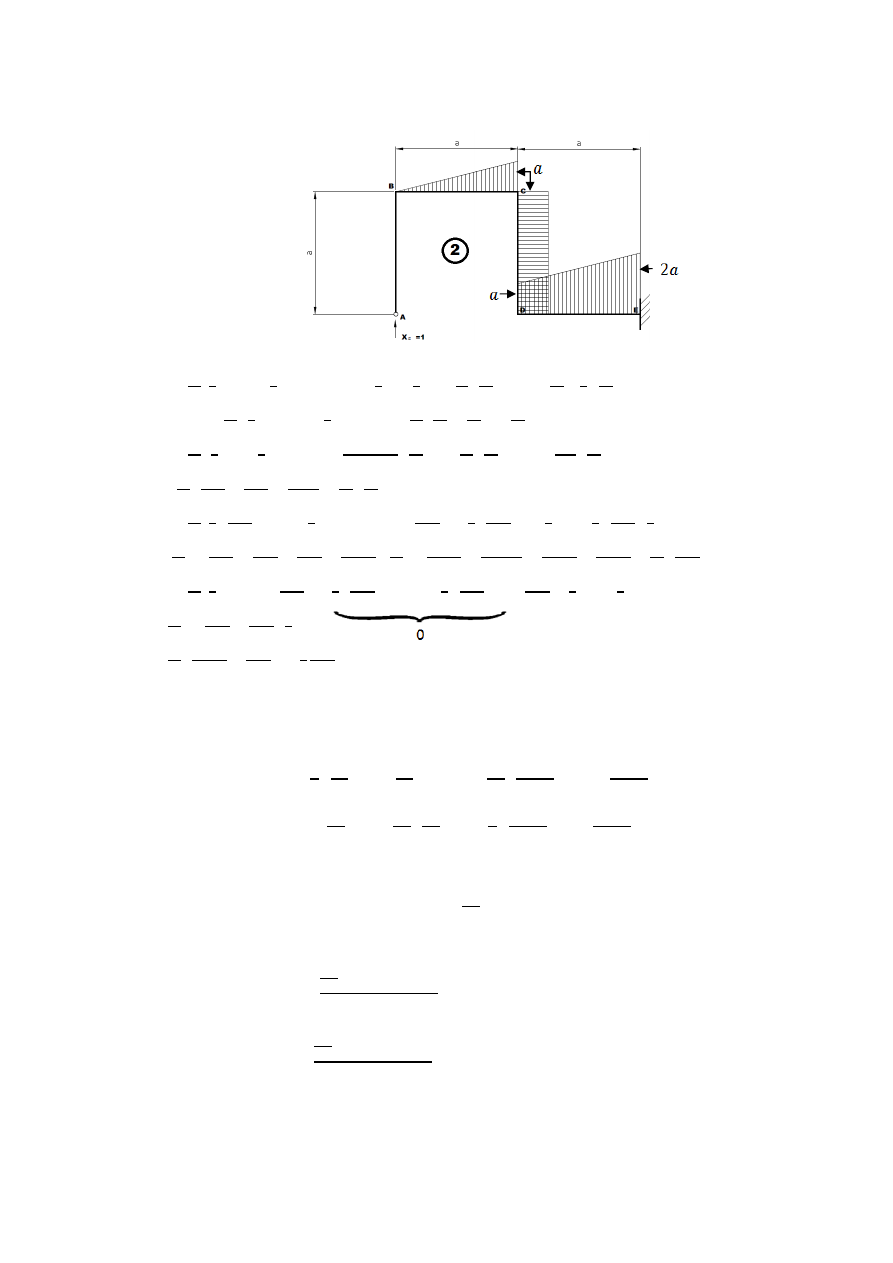
Wykresy momentów gnących wywołanych obciążeniem ciągłym: 

 

•

 

Wykresy momentów gnących wywołanych siłą jednostkową X

1

: 

 

•

 

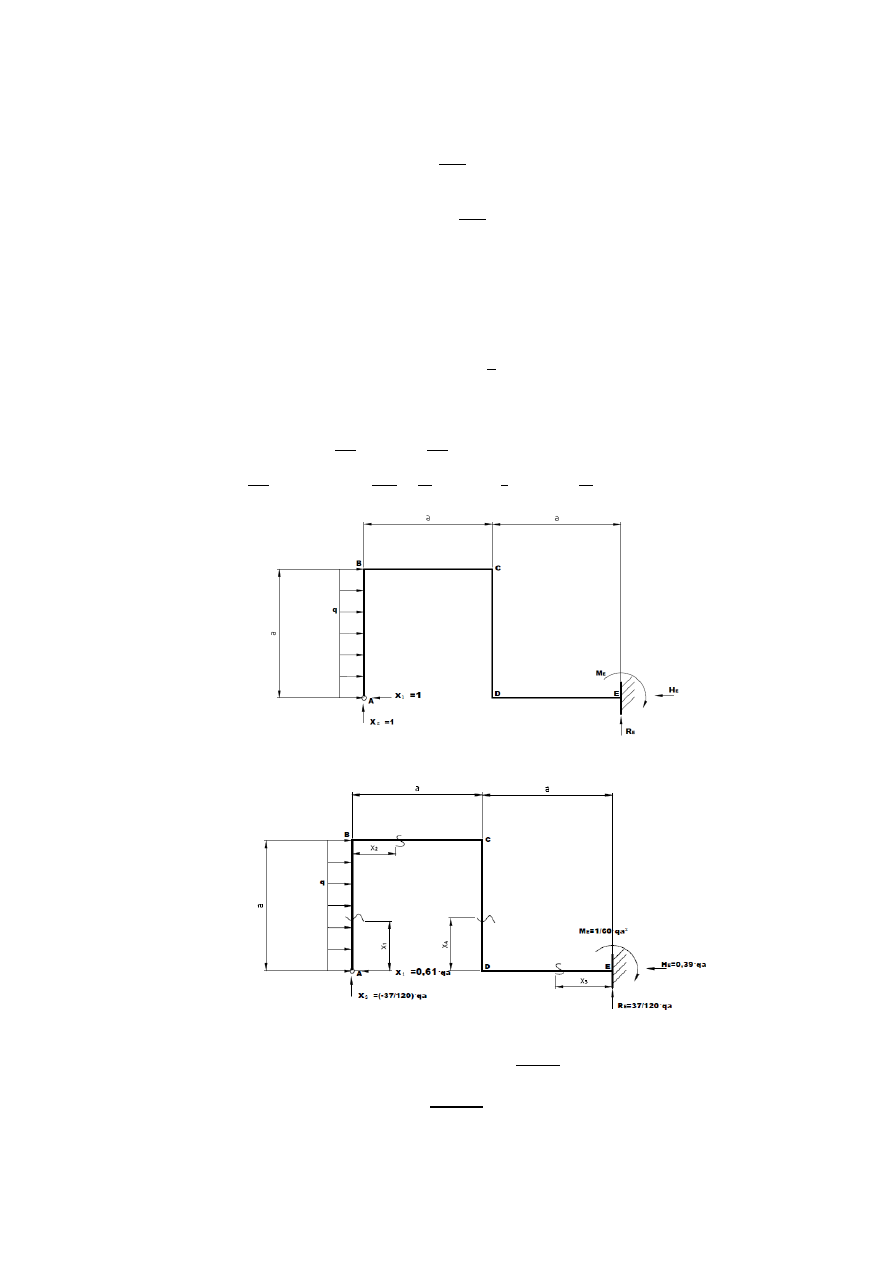
Wykresy momentów gnących wywołanych siłą jednostkową X

2

: 

 

•

 

Współczynniki układu równań kanonicznych są następujące: 

δ

11

=

ଵ

ாூ

ଵ

ଶ

∙

 ∙  ∙

ଶ

ଷ

∙

 + 

ଶ

∙

 +

ଵ

ଶ

ଶ

∙

ଶ

ଷ

∙

=

ଵ

ாூ

௔

య

ଷ

+

ଷ

+

௔

య

ଷ

=

ହ

ଷ

∙

௔

య

ாூ

 

δ

12

=δ

21

=

ଵ

ாூ

ଵ

ଶ

∙

ଶ

∙

 +

ଵ

ଶ

∙

ଶ

∙

 =

ଵ

ாூ

௔

య

ଶ

+

௔

య

ଶ

 =

௔

య

ாூ

 

δ

22

=

ଵ

ாூ

ଵ

ଶ

∙

ଶ

∙

ଶ

ଷ

∙

 + 

ଷ

+

௔∙ሺ௔ାଶ∙௔ሻ

ଶ

∙

ଵସ

ଽ

∙

=

ଵ

ாூ

௔

య

ଷ

+

ଷ

+

ଷ௔

మ

ଶ

∙

ଵସ

ଽ

∙

= 

=

ଵ

ாூ

ଶ∙௔

య

଺

+

଺∙௔

య

଺

+

ଵସ∙௔

య

଺

= 

ଵଵ

ଷ

∙

௔

య

ாூ

 

δ

1P

=

ଵ

ாூ

ଵ

ଷ

∙

௤∙௔

మ

ଶ

∙

 ∙ −

ଷ

ସ

∙

 + 

ଶ

∙

−

௤∙௔

మ

ଶ

 +

ଵ

ଶ

∙

௤∙௔

య

ଶ

∙

−

ଶ

ଷ

 +

ଵ

ଶ

∙

௤∙௔

య

ଶ

∙

ଵ

ଷ

∙

 = 

= 

ଵ

ாூ

−

௤∙௔

ర

଼

−

௤∙௔

ర

ଶ

−

௤∙௔

ర

଺

+

ଶ∙௤∙௔

ర

ଶସ

=

ଵ

ாூ

−

ଷ∙௤∙௔

ర

ଶସ

−

ଵଶ∙௤∙௔

ర

ଶସ

−

ସ∙௤∙௔

ర

ଶସ

+

ଶ∙௤∙௔

ర

ଶସ

=-

ଵ଻

ଶସ

∙

௤∙௔

ర

ாூ

 

δ

2P

=

ଵ

ாூ

ଵ

ଶ

∙

ଶ

∙

−

௤∙௔

మ

ଶ

 +

ଵ

ଶ

∙

௤∙௔

య

ଶ

∙

− +

ଵ

ଶ

∙

௤∙௔

య

ଶ

∙

 +

௤∙௔

య

ଶ

∙

ଵ

ଶ

∙

 +

ଵ

ଶ

∙ 2 ∙

= 

=

ଵ

ாூ

−

௤∙௔

ర

ସ

+

௤∙௔

య

ଶ

∙

ଷ

ଶ

∙

 = 

=

ଵ

ாூ

ଷ∙௤∙௔

ర

ସ

−

௤∙௔

ర

ସ

 =

ଵ

ଶ

௤∙௔

ర

ாூ

 

               

•

 

Po podstawieniu współczynników do układu równań kanonicznych otrzymamy: 

5

3

∙

ଷ

∙

ଵ

+

ଷ

∙

ଶ

+

−

17

24

∙

 ∙ 

ସ

 

= 0/∙

3 ∙

ଷ

ଷ

∙

ଵ

+

11

3

∙

ଷ

∙

ଶ

+

1

2

∙

 ∙ 

ସ

= 0/∙

6 ∙

ଷ

 

 

5 ∙ 

ଵ

+ 3 ∙

ଶ

−

17

8

∙

 ∙  = 0

6 ∙

ଵ

+ 22 ∙

ଶ

∙ 3 ∙

 ∙  = 0

 

ଵ

=

17

8

∙

 ∙  − 3 ∙ 

ଶ

5

= 0,425 ∙

 ∙  − 0,6 ∙ 

ଶ

 

6 ∙

17

8

∙

 ∙  − 3 ∙ 

ଶ

5

 + 22 ∙ 

ଶ

+ 3 ∙

 ∙  = 0 

2,55 ∙

 ∙  − 3,5 ∙ 

ଶ

+ 22 ∙

ଶ

+ 3 ∙

 ∙  = 0 

18,4 ∙

ଶ

= −5,55 ∙

 ∙  

ଶ

= −

37

120

∙

 ∙  

ଵ

= 0,425 ∙

 ∙  − 0,6 ∙ −

37

120

 ∙  ∙  = 0,61 ∙  ∙  

•

 

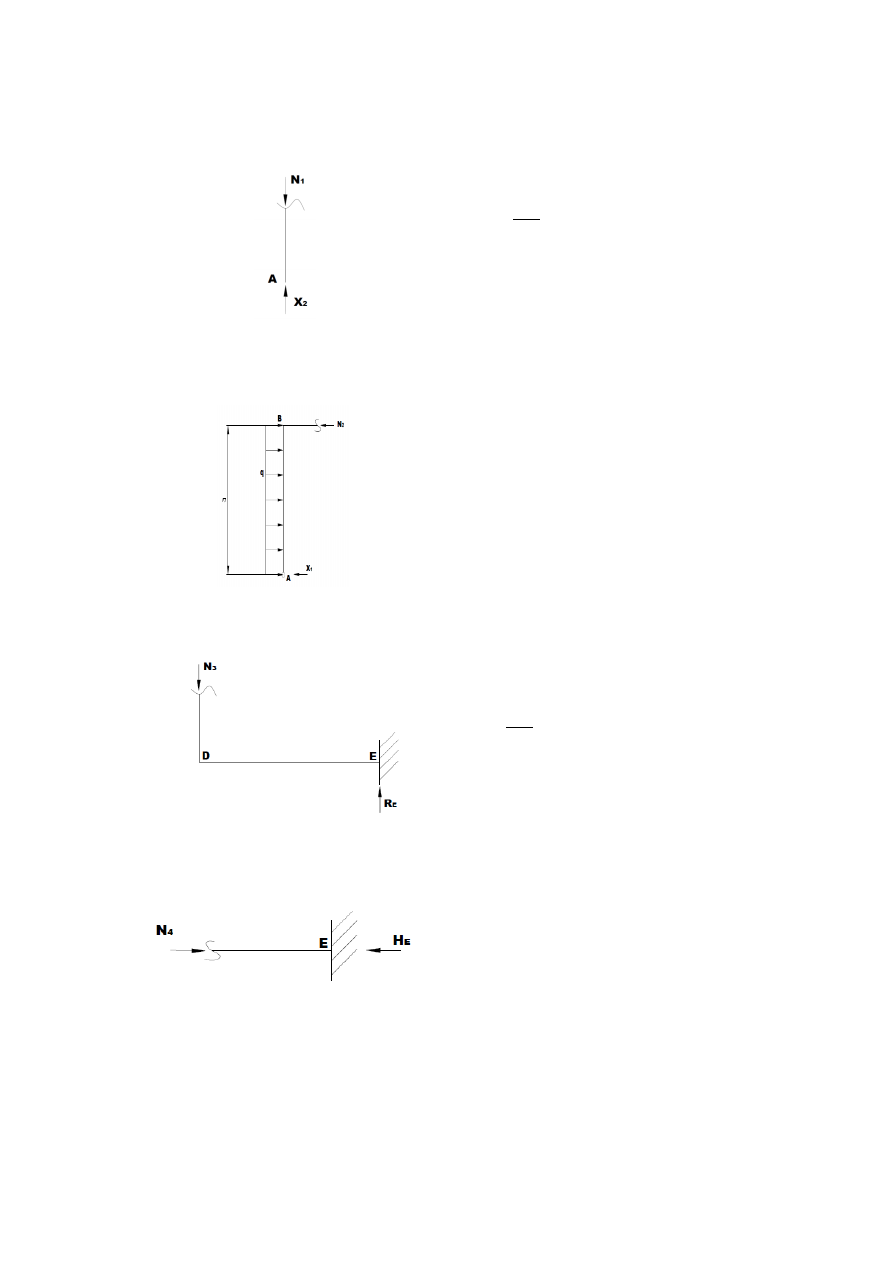
Równania równowagi: 

 

௫

= 0 ∶

−

ଵ

−

ா

+

 ∙  = 01 

 

௬

= 0 ∶

ଶ

+

ா

= 0

2 

 

ா

= 0 ∶

−

ா

−

 ∙  ∙

2

−

ଶ

∙ 2 ∙

 = 03 

 

z

1: 

ா

=

 ∙  − 0,61 ∙  ∙  = 0,39 ∙  ∙  

z  

2:

ா

= −

ଶ

= −

−

ଷ଻

ଵଶ଴

∙

 ∙  =

ଷ଻

ଵଶ଴

∙

 ∙  

z  

3:

ா

=

ଷ଻

ଵଶ଴

∙

 ∙  ∙ 2 ∙  −

௤∙௔

మ

ଶ

=

ଷ଻

଺଴

∙

 ∙ 

ଶ

−

ଵ

ଶ

∙

 ∙ 

ଶ

=

଻

଺଴

∙

 ∙ 

ଶ

 

 

•

 

Momenty gnące i siły tnące: 

 

0 ≤

ଵ

≤

 

ଵ

 = 

ଵ

∙

ଵ

−

 ∙ 

ଵ

ଶ

2

 

ଵ

 =

 

ଵ

 

ଵ

=

ଵ

−

 ∙ 

ଵ

 

 

0 ≤

ଶ

≤

 

ଶ

 = −

 ∙ 

ଶ

2

+

ଶ

∙

ଶ

+

ଵ

∙

 

ଶ

 =

 

ଶ

 

ଶ

=

ଶ

= −

37

120

∙

 ∙  

0 ≤

ଷ

≤

 

ଷ

 = 

ா

∙

ଷ

−

ா

 

ଷ

 = −

 

ଷ

 

ଷ

= −

ா

= −

37

120

∙

 ∙  

0 ≤

ସ

≤

 

ସ

 = 

ா

∙

 − 

ா

∙

ସ

−

ா

 

ସ

 = −

 

ସ

 

ସ

=

ா

= 0,39 ∙

 ∙  

 

I 

ଵ

|

௫

భ

ୀ଴

= 0 

ଵ

|

௫

భ

ୀ௔

= 0,61 ∙

 ∙ 

ଶ

−

 ∙ 

ଶ

2

= 0,11 ∙

 ∙ 

ଶ

 

ଵ

|

௫

భ

ୀ௫

బ

= 0 

ଵ

−

 ∙ 

଴

= 0 

଴

=

ଵ

= 0,61 ∙

 

ଵ

|

௫

భ

ୀ଴,଺ଵ௔

= −

 ∙ 

ଶ

∙ 0,18605 + 0,3721 ∙

 ∙ 

ଶ

= 0,18605 ∙

 ∙ 

ଶ

 

ଵ

|

௫

భ

ୀ଴

=

ଵ

= 0,61 ∙

 ∙  

ଵ

|

௫

భ

ୀ௔

= 0,61 ∙

 ∙  −  ∙  = 0,39 ∙  ∙  

 

II 

ଶ

|

௫

మ

ୀ଴

= −

 ∙ 

ଶ

2

+ 0,61 ∙

 ∙ 

ଶ

= 0,11 ∙

 ∙ 

ଶ

 

ଶ

|

௫

మ

ୀ௔

= 0,11 ∙

 ∙ 

ଶ

+

−

37

120

 ∙  ∙ 

ଶ

= −

119

600

∙

 ∙ 

ଶ

 

ଶ

|

௫

మ

ୀ଴

=

ଶ

|

௫

మ

ୀ௔

=

ଶ

= −

37

120

∙

 ∙  

 

III 

ଷ

|

௫

య

ୀ଴

= −

ா

= −

7

60

∙

 ∙ 

ଶ

 

ଷ

|

௫

య

ୀ௔

=

37

120

∙

 ∙ 

ଶ

−

7

60

∙

 ∙ 

ଶ

=

23

120

∙

 ∙ 

ଶ

 

ଷ

|

௫

య

ୀ଴

=

ଷ

|

௫

య

ୀ௔

= −

ா

= −

37

120

∙

 ∙  

 

IV 

ସ

|

௫

ర

ୀ଴

=

37

120

∙

 ∙ 

ଶ

−

7

60

∙

 ∙ 

ଶ

=

23

120

∙

 ∙ 

ଶ

 

ସ

|

௫

ర

ୀ௔

=

37

120

∙

 ∙ 

ଶ

− 0,39 ∙

 ∙ 

ଶ

−

7

60

∙

 ∙ 

ଶ

= −

119

600

∙

 ∙ 

ଶ

 

ସ

|

௫

ర

ୀ଴

=

ସ

|

௫

ర

ୀ௔

=

ா

= 0,39 ∙

 ∙  

•

 

Siły normalne: 

 

Pręt A-B: 

 

−

!

ଵ

+

ଶ

= 0 

!

ଵ

=

ଶ

= −

37

120

∙

 ∙  

 

 

 

 

 

 

 

Pręt B-C: 

 

 

 ∙  − 

ଵ

−

!

ଶ

= 0 

!

ଶ

=

 ∙  − 0,61 ∙  ∙  = 0,39 ∙  ∙  

 

 

 

 

 

 

Pręt C-D: 

 

ா

−

!

ଷ

= 0 

!

ଷ

=

ா

=

37

120

∙

 ∙  

 

 

 

 

Pręt D-E:  

 

!

ସ

−

ா

= 0 

!

ସ

=

ா

= 0,39 ∙

 ∙  

 

 

 

 

 

 

 

 

•

 

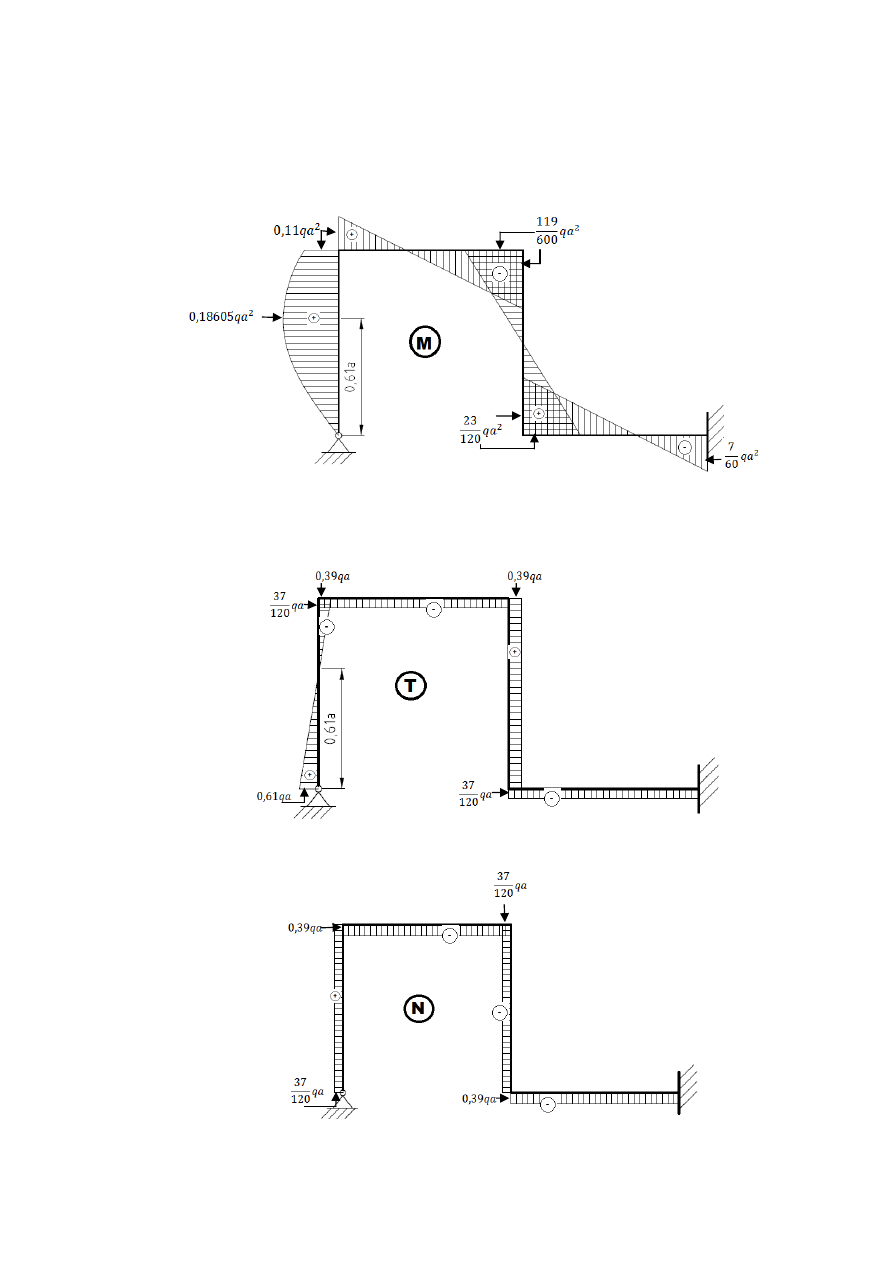
Wykresy: 

 

Momentów gnących: 

 

 

 

 

 

 

Sił tnących:  

 

 

 

 

 

Sił normalnych: