Projekt „Informatyka – inwestycją w przyszłość”

współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego

Biuro Projektu:

Politechnika Radomska im. Kazimierza Pułaskiego

26-600 Radom, ul. Chrobrego 27, pok. nr 44, tel. [phone]

www.zamawiane.pr.radom.pl; e-mail: [e-mail]

Zajęcia wyrównawcze z fizyki -Zestaw 6

dr M.Gzik-Szumiata

Ruch obrotowy bryły sztywnej. Prędkość liniowa i prędkość kątowa, moment bezwładności, moment
siły, przyspieszenie kątowe, moment pędu.

Zadanie 1. Znajdź środek masy układu trzech cząstek o masach m

1

= 1 kg, m

2

= 2 kg i m

3

= 3 kg,

umieszczonych w wierzchołkach równobocznego trójkąta o boku a = 1 m.

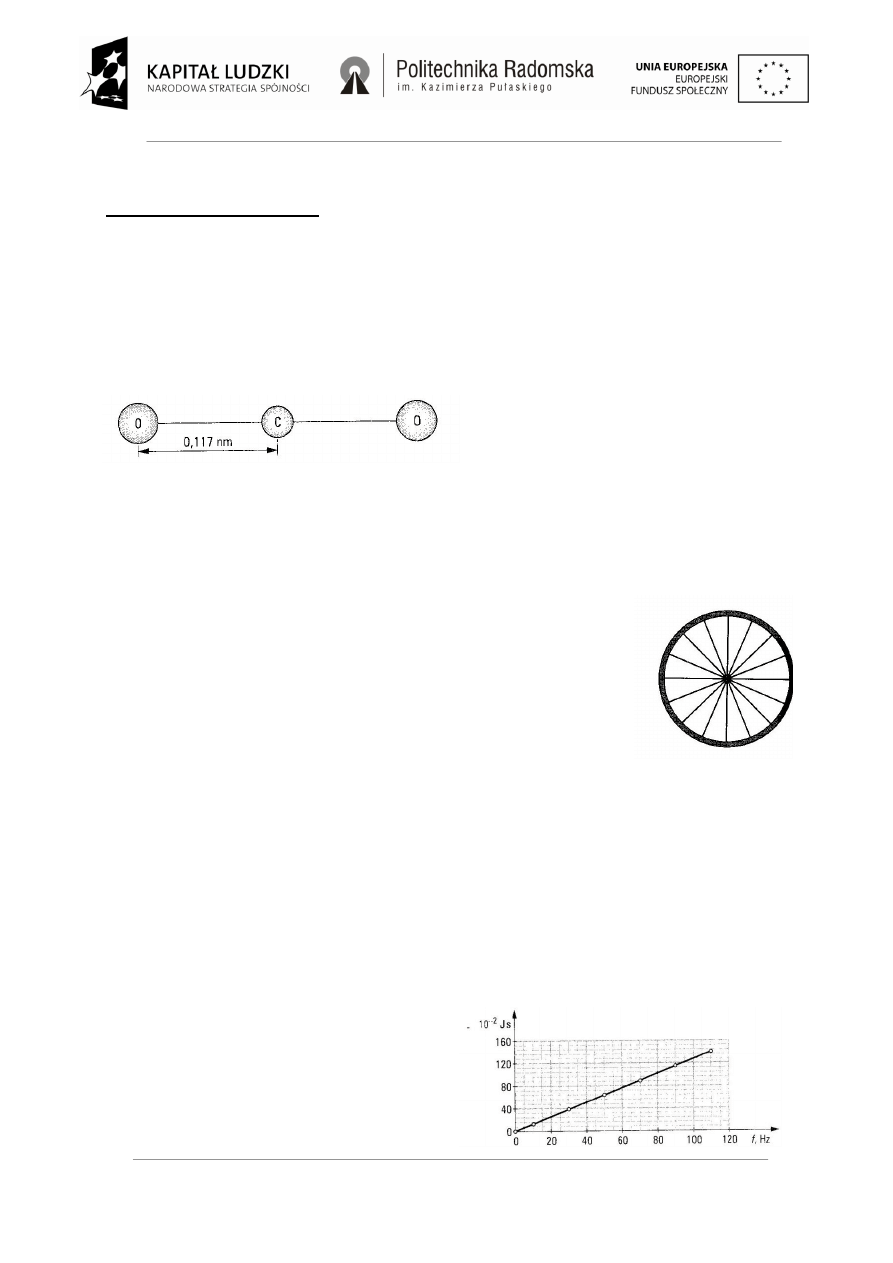
Zadanie 2. Na rysunku przedstawiono model cząsteczki CO

2

(dwutlenku węgla). Masa atomu tlenu

wynosi 2,66·10

-26

kg, a węgla 1,99·10

-26

kg.

1. Oblicz moment bezwładności cząsteczki CO

2

względem osi przechodzącej przez jej środek masy.

2. Moment pędu cząsteczki CO

2

obracającej się względem osi przechodzącej przez jej środek masy

jest równy 3,9·10

-44

J·s, a energia kinetyczna ruchu obrotowego ma wartość 18,35·10

-32

J. Oblicz

częstotliwość obrotu cząsteczki dwutlenku węgla.

Zadanie 3. Na rysunku przedstawiono koło kolarskie. Koło to jest cienką
obręczą o promieniu 40 cm i masie 100g, zespoloną 16 szprychami o masie 5
g każda. Na krawędzi obręczy umieszczono oponę (drugą cienką obręcz) o
masie 100 g.

-Oblicz moment bezwładności koła kolarskiego względem osi obrotu.

Zadanie 4. Podczas wirowania w typowej pralce automatycznej następuje wypływ wody z bębna
wewnętrznego do zewnętrznego, z którego jest ona odpompowywana na zewnątrz. Osiągnięcie
prędkości kątowej o wartości 10 obrotów na sekundę przy zapełnionym bębnie pralki zajmuje 5s.
Moment bezwładności pełnego bębna z woda wynosi 0,9 kg·m

2

. Zakładając, że moment

bezwładności zapełnionego bębna jest stały (podczas rozpędzania), oblicz :

-średnie przyspieszenie kątowe, średni moment sił, końcową energię ruchu obrotowego, końcowy
moment pędu.

Zadanie 5. W myjni samochodów szczotki
czyszczące umocowane są na obracającym się
walcu. Na wykresie przedstawiono zależność
momentu pędu obracającego się walca od jego
częstotliwości.

L

Projekt „Informatyka – inwestycją w przyszłość”

współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego

Biuro Projektu:

Politechnika Radomska im. Kazimierza Pułaskiego

26-600 Radom, ul. Chrobrego 27, pok. nr 44, tel. [phone]

www.zamawiane.pr.radom.pl; e-mail: [e-mail]

Oblicz pracę, jaką należy wykonać, by zatrzymać walec obracający się z częstotliwością 50 Hz.

Zadanie 6. Z równi pochyłej o wysokości 2 m i kącie nachylenia 30

o

stacza się bez poślizgu walec o

masie 1 kg i promieniu 5 cm.

a)Oblicz przyspieszenie , z jakim stacza się walec z równi pochyłej.

b) Oblicz przyspieszenie kątowe, z jakim obraca się walec.

c)Oblicz wartość prędkości środka masy tego walca u podstawy równi.

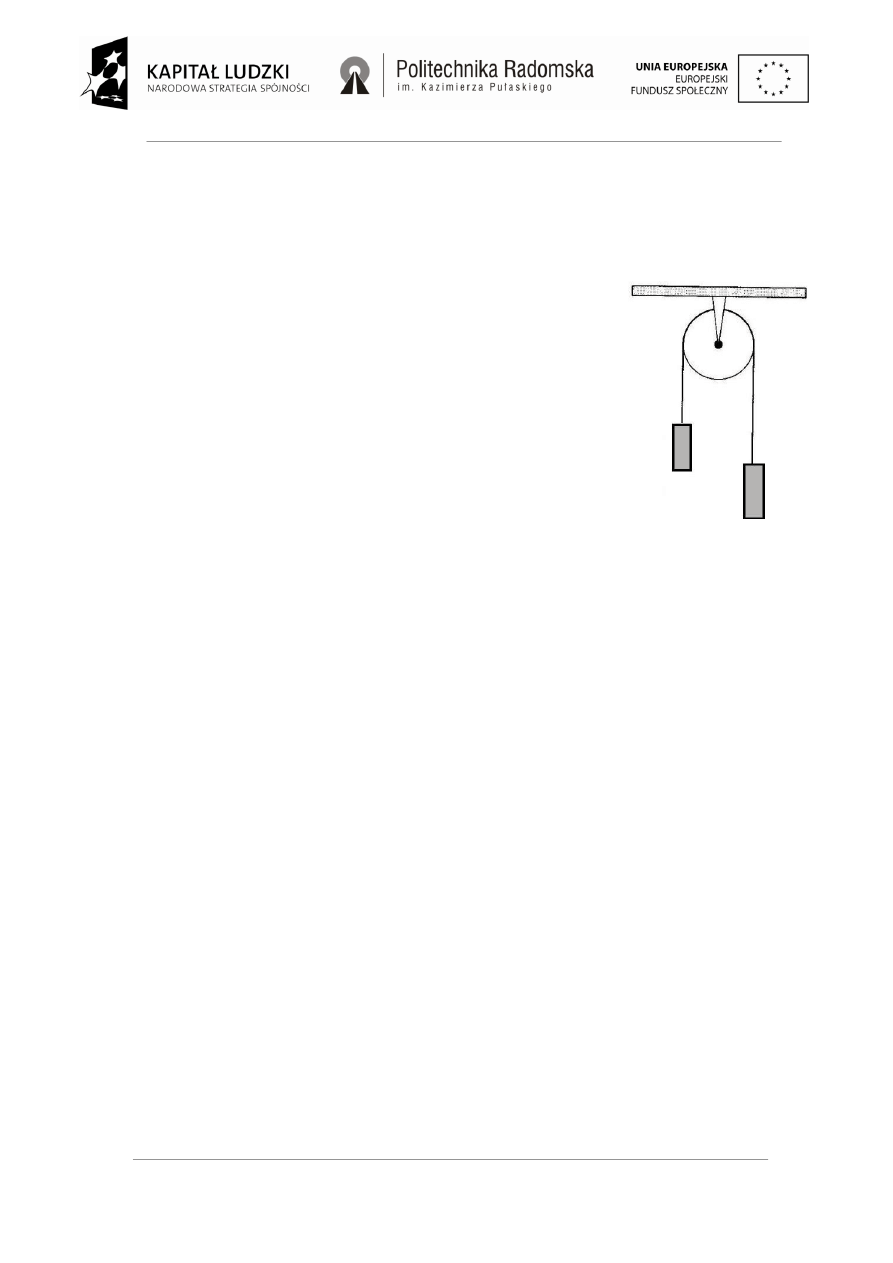
Zadanie 7. Na rysunku przedstawiono układ składający się z bloczka w
kształcie walca o promieniu R i masie M, nieważkiej linki oraz dwóch
ciężarków o masie m

1

i m

2

przymocowanych do obu końców linki

przerzuconej przez bloczek przy czym spełniony jest warunek m

1

> m

2

-Oblicz wartość przyspieszenia, z którym poruszają się ciężarki.
-Oblicz wartość siły naprężenia linki.

Zadanie 8. Pręt metalowy o długości 1 m i masie 2 kg zawieszono na jednym z jego końców.
Następnie odchylono pręt o kąt od pionu o kąt 90

o

i puszczono. Obliczyć, jaką prędkość liniową

będzie miał swobodny koniec pręta przechodząc przez położenie równowagi?

m

1

m

2