
POLITECHNIKA POZNANSKA
INSTYTUT KONSTRUKCJI BUDOWLANYCH
Zaklad Mechaniki Budowli
C W I C Z E N I E nr 3
W
YZNACZANIE
S
IŁ
W
EWNĘTRZNYCH
W
R
AMACH
wykonał: Damian Ziółkowski
Politechnika Poznańska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2003/2004
www.ikb.poznan.pl/anita.kaczor
wykonał Damian Ziółkowski
2
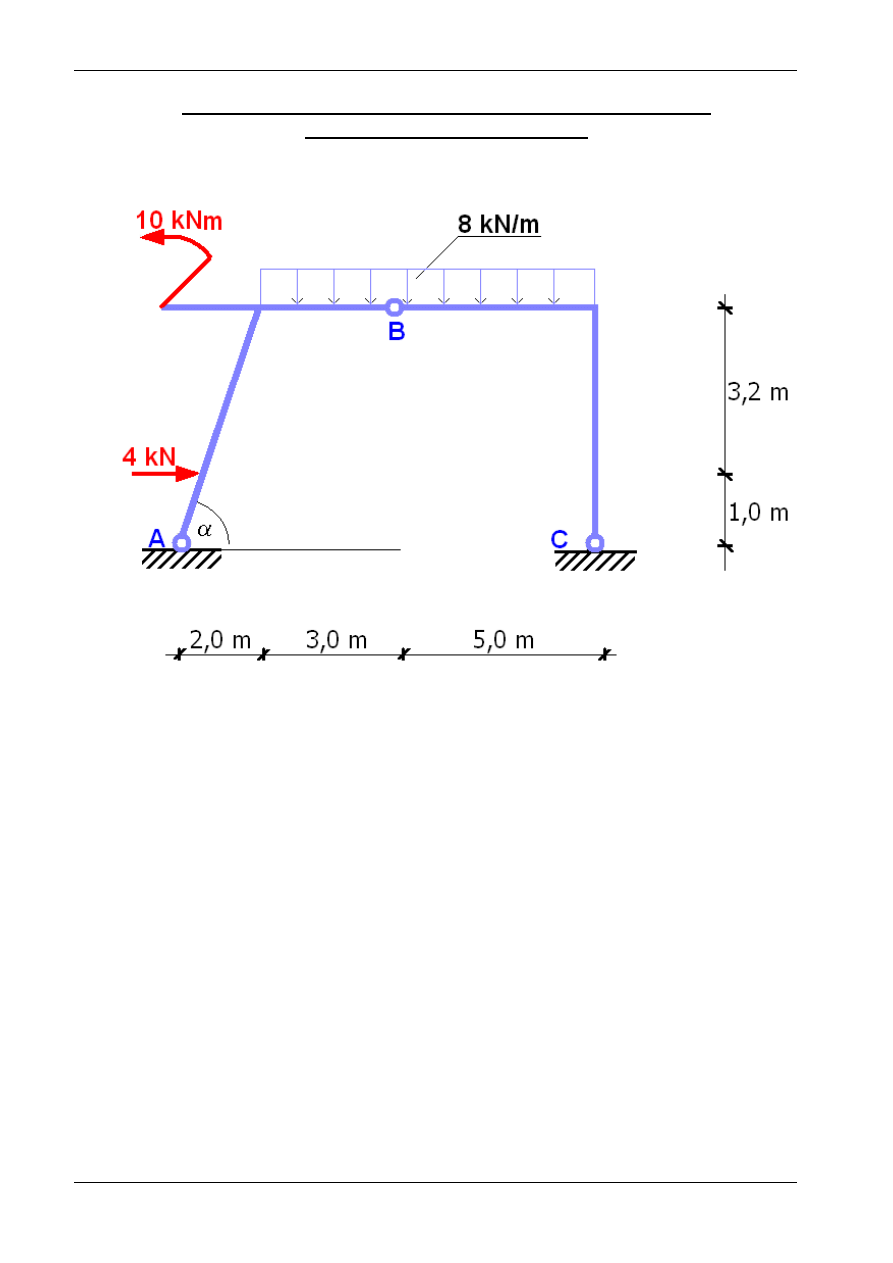
WYZNACZYĆ SIŁY ZEWNĘTRZNE I WEWNĘTRZNE
W NASTĘPUJĄCEJ RAMIE:
1. Analiza geometrycznej niezmienności i statycznej wyznaczalności:
a) warunek konieczny:
)
r
r
r
(
t
r
t
s
C
B
A
+
+
−
=
−
=
3
3
2
2
2
2
=
=
=
=
C
B
A
r
r
r
t
0
6
6
2
2
2
2
3
=
−
=
+
+
−
⋅
=
)
(
s
b) warunek dostateczny:
Tarcza AB połączona jest z podłożem przegubem A oraz z tarczą BC przegubem B.
Tarcza BC połączona jest z podłożem przegubem C oraz z tarczą AB przegubem B.
Przeguby A, B, C nie leżą na jednej prostej, a więc układ tarcz AB i BC tworzy układ
trójprzegubowy, geometrycznie niezmienny.
Politechnika Poznańska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2003/2004
www.ikb.poznan.pl/anita.kaczor
wykonał Damian Ziółkowski
3
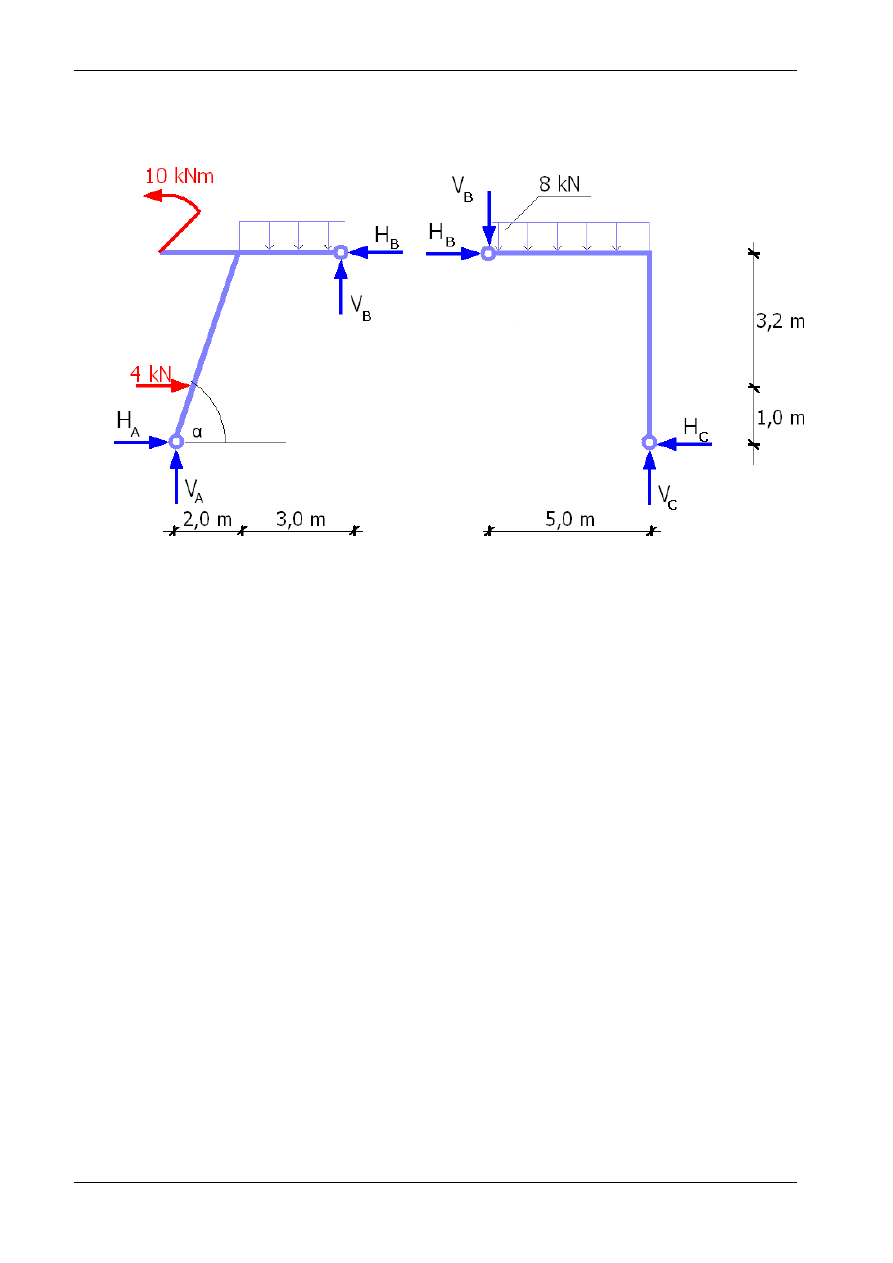
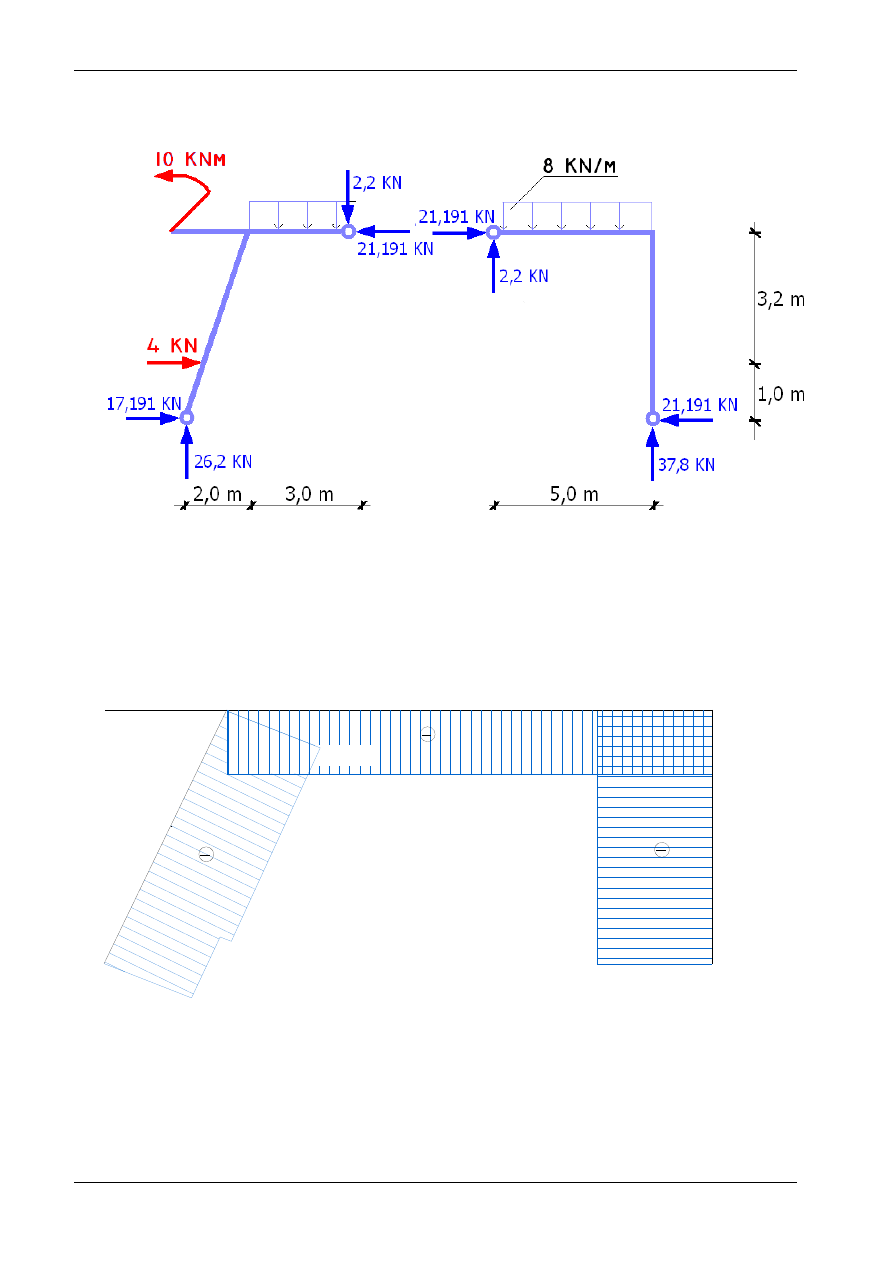
Uwolnienie układu od więzów:
sin
α
= 0,9029
cos
α
= 0,4300
0
∑
=
C
A
M
0
10
6
8
8
1
4
10
=
⋅
−
⋅
⋅
+
⋅
+
−
=
∑
C
C
A
V
M
V
C
= 37,800 kN
0
∑
=
C
C
M
0
10
4
8
8
1
4
10
=
⋅
+
⋅
⋅
−
⋅
+
−
=
∑
A
C
C
V
M
V
A
= 26,200 kN
0
∑
=
L
B
M
0
2
4
5
5
1
3
8
2
3
4
10
=
⋅
−
⋅
+
⋅
⋅
−
⋅
−
−
=
∑
,
H
V
,
,
M
A
A
L
B
H
A
= 17,191 kN
0
∑
=
L
X
0
4
=
−
+
=
∑
B
A
L
H
H
X
H
B
= 21,191 kN
0
∑
=
L
Y
0
3
8
=
⋅
−
+
=
∑
B
A
L
V
V
Y
V
B
= -2,200 kN
0
∑
=
P
X
0
=
−
=
∑
C
B
P
H
H
X
H
C
= 21,191 KN
SPRAWDZENIE WYNIKÓW:
0
4
=
−
+
=
∑
C
A
C
H
H
X
0
8
8
=
⋅
−
+
=
∑
C
A
C
V
V
Y
0
2
4
5
5
3
3
8
1
4
10
=
⋅
−
⋅
−
⋅
⋅
+
⋅
+
−
=
∑
,
H
V
,
M
B
B
L
A
Politechnika Poznańska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2003/2004
www.ikb.poznan.pl/anita.kaczor
wykonał Damian Ziółkowski
4
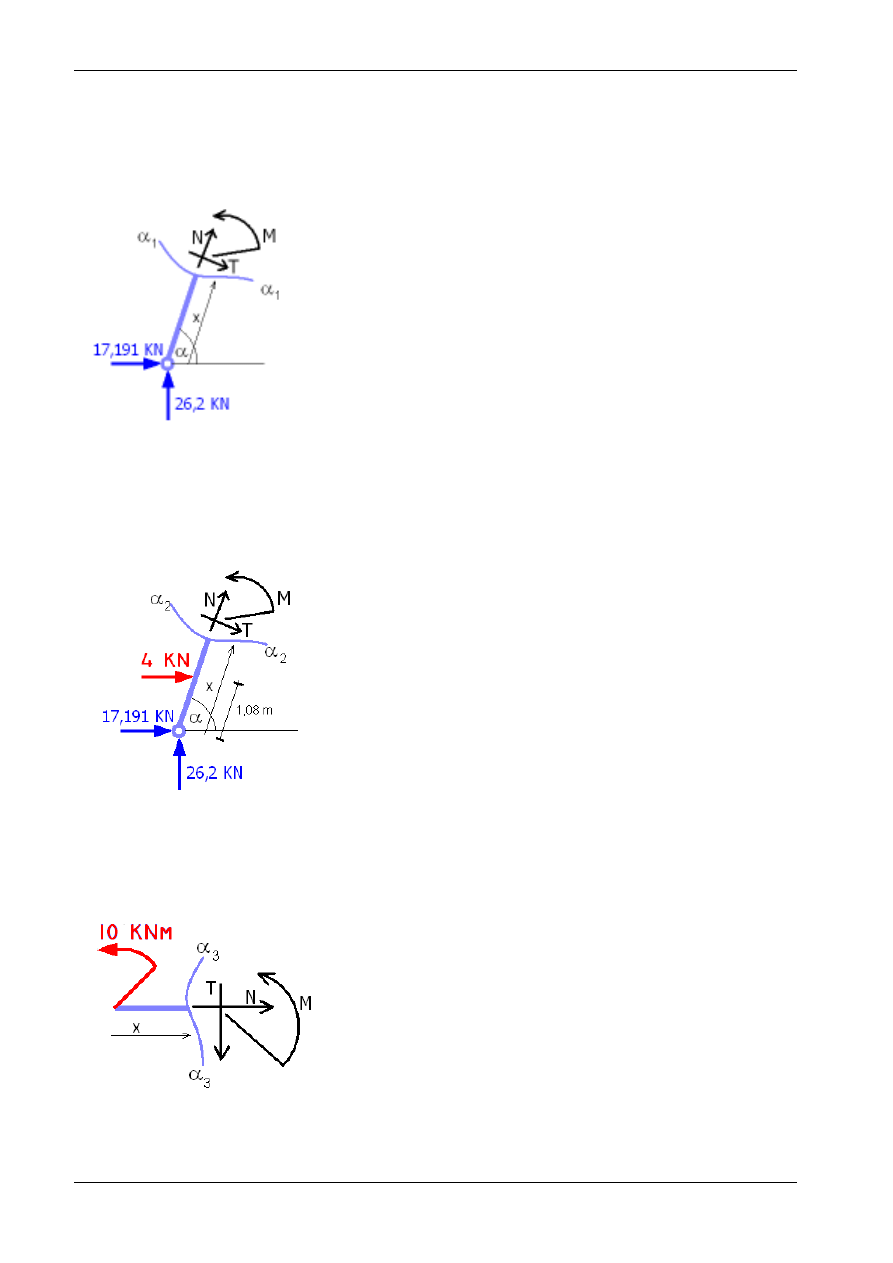
2. Wyznaczanie sił wewnętrznych:
α
1
-α
1
α
2
-α
2
α
3
-α
3
kN
x
N
046
,
31
cos
191
,
17
sin
2
,
26
)
(
−
=
⋅
−
⋅
−
=
α
α
kN
x
T
258
,
4
sin
191
,
17
cos
2
,
26
)
(
−
=
⋅
−
⋅
=
α
α
kNm
M
kNm
M
x
x
x
x
M
719
,
4
)
108
,
1
(
0
)
0
(
258
,
4
cos
191
,
17
cos
2
,
26
)
(
=
=
−
=
⋅
⋅
−
⋅
⋅
−
=
α
α
kNm
x
M
x
T
x
N
10
)
(
0
)
(
0
)
(
−
=
=
=
kN
x
N
765
,
32
cos
4
cos
191
,
17
sin
2
,
26
)
(
−
=
⋅
−
⋅
−
⋅
−
=
α
α
α
kN
x
T
870
,
7
sin
4
sin
191
,
17
cos
2
,
26
)
(
−
=
⋅
−
⋅
−
⋅
=
α
α
α
kNm
M
kNm
M
x
x
x
x
x
M
609
,
32
)
652
,
4
(
719
,
4
)
108
,
1
(
002
,
4
870
,
7
sin
4
sin
191
,
17
cos
2
,
26
)
(
−
=
=
+
−
=
⋅
⋅
−
⋅
⋅
−
⋅
⋅
=
α
α
α
Politechnika Poznańska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2003/2004
www.ikb.poznan.pl/anita.kaczor
wykonał Damian Ziółkowski
5
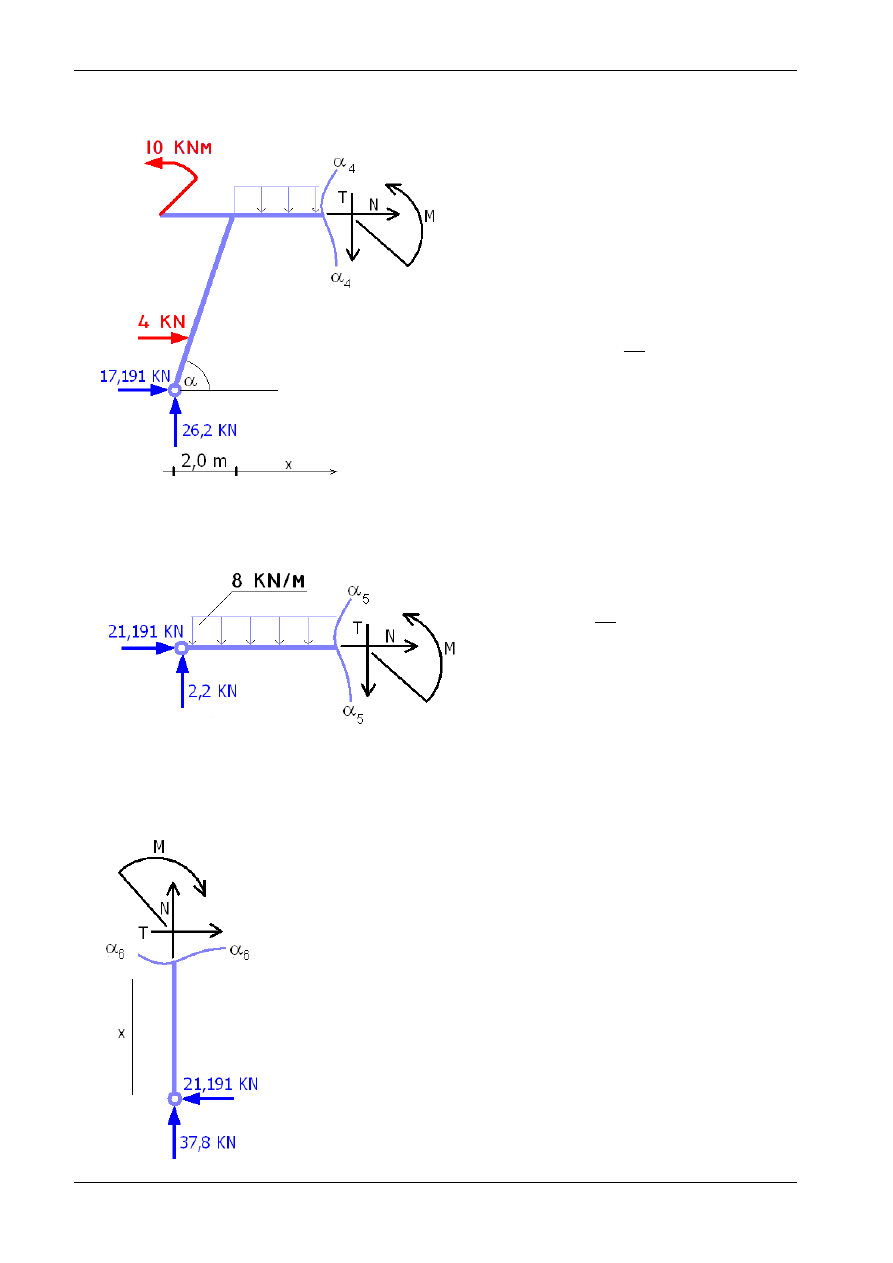
α
4
-α
4
α
5
-α
5
α
6
-α
6
kN
T
kN
T
x
x
x
x
x
M
x
x
T
kN
x
N
2
,
2
)
3
(
2
,
26
)
0
(
602
,
42
2
,
26
4
2
,
3
4
2
,
4
191
,
17
2
8
10
)
2
(
2
,
26
)
(
8
2
,
26
)
(
191
,
21
4
191
,
17
)
(
2
2
=
=
−
+
−
=
=
⋅
−
⋅
−
−
−
+
=
−
=
−
=
−
−
=
kNm
x
M
m
x
x
x
T
kN
T
kN
T
x
x
x
M
x
x
T
kN
x
N
e
e
301
,
0
)
(
275
,
3
0
8
2
,
26
0
)
(
800
,
37
)
5
(
200
,
2
)
0
(
2
8
2
,
2
)
(
8
2
,
2
)
(
191
,
21
)
(
3
2
=
=
⇒
=
−
⇒
=
−
=
=
−
=
−
=
−
=
kNm
M
kNm
M
x
x
M
kN
x
T
kN
x
N
002
,
89
)
2
,
4
(
0
)
0
(
191
,
21
)
(
191
,
21
)
(
8
,
37
)
(
−
=
=
−
=
=
−
=
kNm
M
kNm
M
0
)
3
(
602
,
42
)
0
(
=
−
=
kNm
M
kNm
M
89
)
5
(
0
)
0
(
−
=
=
Politechnika Poznańska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2003/2004
www.ikb.poznan.pl/anita.kaczor
wykonał Damian Ziółkowski
6
3. Zestawienie sił zewnętrznych:
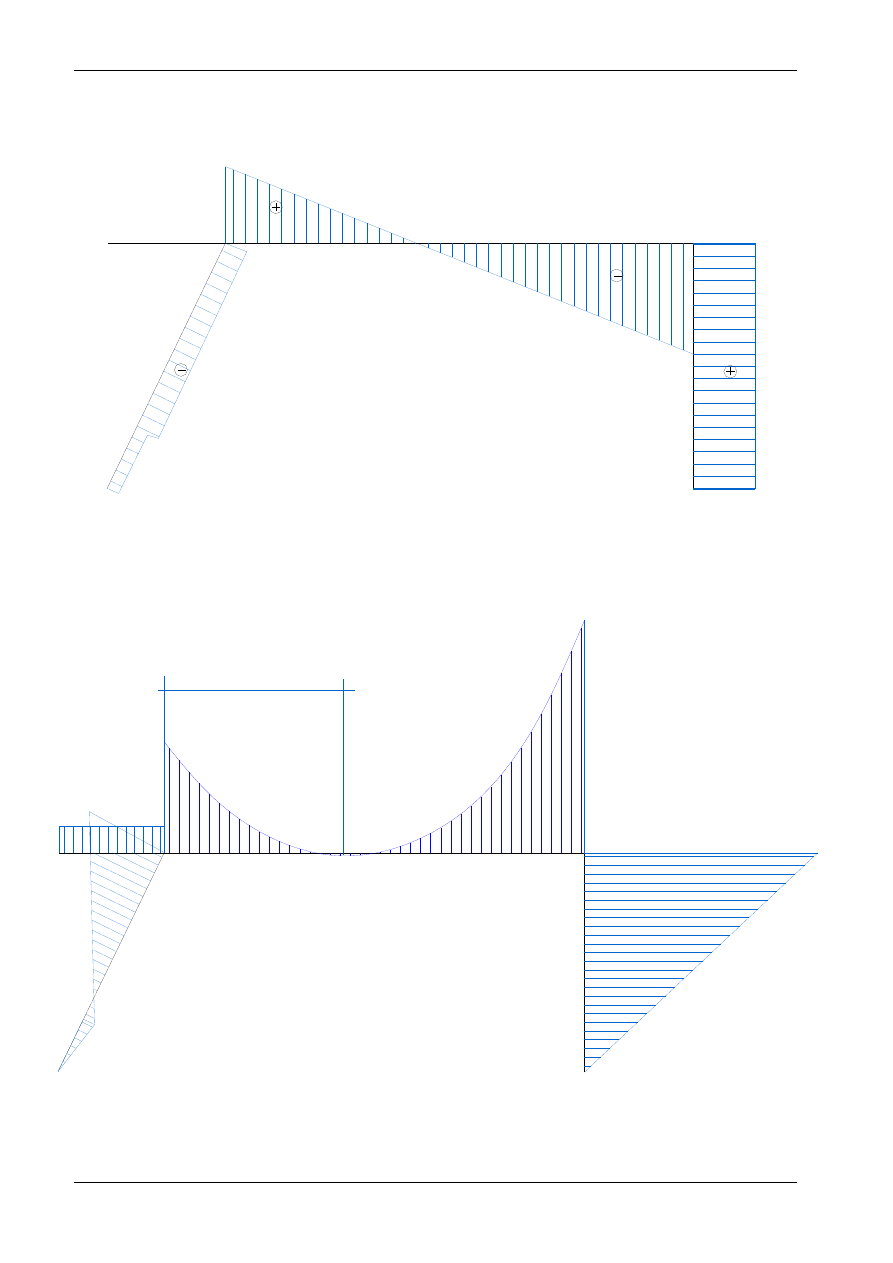
4. Wykresy sił wewnętrznych:
-31,046
-37,8
-32,765
-21,191
N
[kN]
Politechnika Poznańska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2003/2004
www.ikb.poznan.pl/anita.kaczor
wykonał Damian Ziółkowski
7
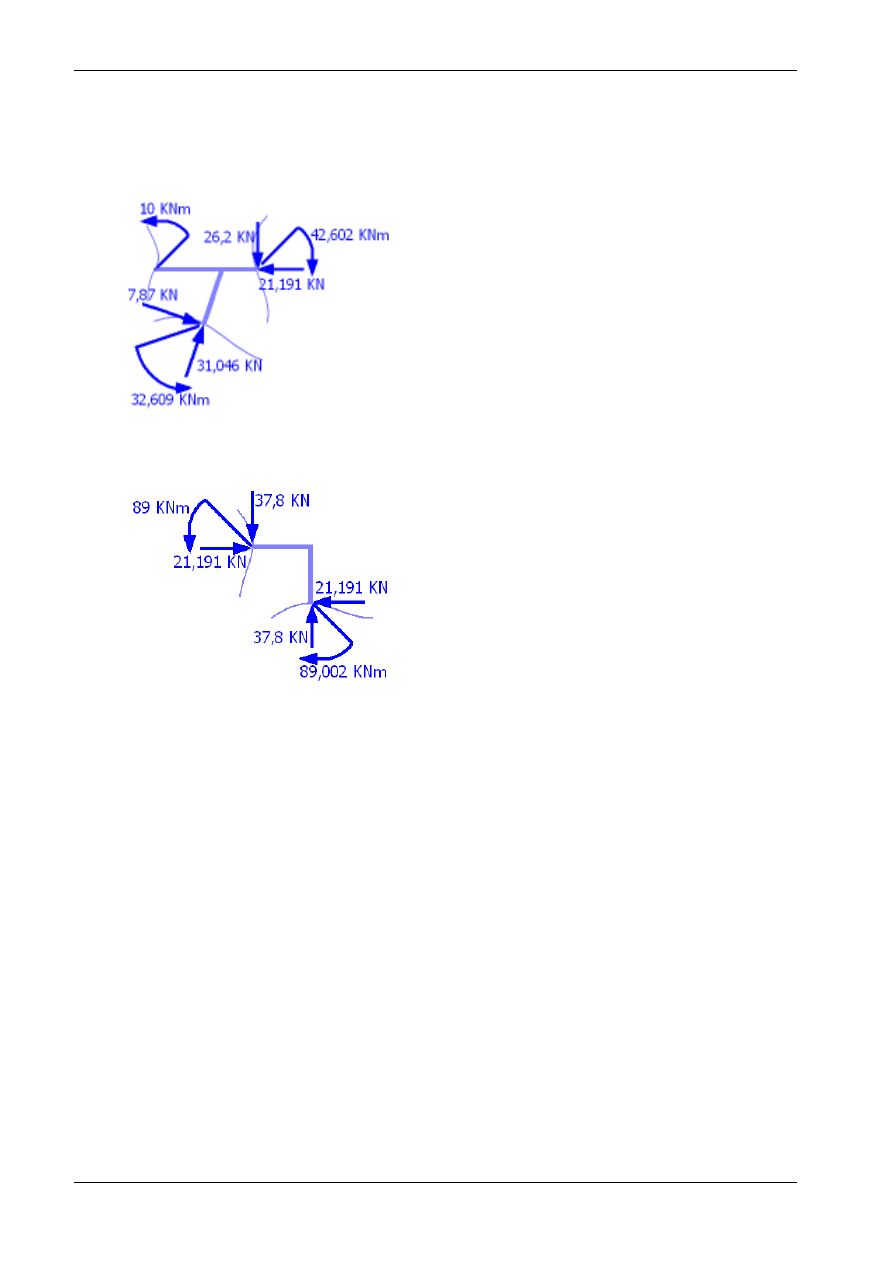
4,719
-32,609
-10
min=0,303
3,275 m
-89
-89
M
[kNm]
-7,870
-4.258
26,2
-37,8
21,191
T
[kN]
Politechnika Poznańska
→
Instytut Konstrukcji Budowlanych
→
Zakład Mechaniki Budowli
2003/2004
www.ikb.poznan.pl/anita.kaczor
wykonał Damian Ziółkowski
8
5. Równowaga sił wewnętrznych w węźle:
0
191
,
21
sin
87
,
7
cos
765
,
32
≈
−
⋅
+
⋅
=
∑
α
α
X
0
2
,
26
cos
87
,
7
sin
765
,
32
≈
−
⋅
+
⋅
=
∑
α
α
Y
0
007
,
0
602
,
42
609
,
32
10
≈
=
−
+
=
∑
M
0
191
21
191
21
=
−
=
∑
,
,
X
0
8
37
8
37
=
−
=
∑
,
,
Y
002
,
0
002
,
89
89
−
=
−
=
∑
M
Wyszukiwarka
Podobne podstrony:
Projekt 2 (Damiana Ziółkowskiego)
Projekt 1 (Damiana Ziółkowskiego)
Projekt 2 (Damiana Ziółkowskiego)
Projekt 1 (Damiana Sierockiego)
Projekt 1 (Damiana Sierockiego)
Projekt 1 (Damiana Sierockiego)
Projekt 1 (Damiana Sierockiego)
Projekt 2 (Damiana Sierockiego)
Projekt Damian kopia1
Projekt Damian doc
napęd elekt nr20, Przwatne, Studia, semestr 5, Studia Pulpit, napedy projekty, projekty got, projekt
naped teoria, Przwatne, Studia, semestr 5, Studia Pulpit, napedy projekty, projekty got, projekty od
napęd elektry proj, Przwatne, Studia, semestr 5, Studia Pulpit, napedy projekty, projekty got, proje
napęd elektry nr9, Przwatne, Studia, semestr 5, Studia Pulpit, napedy projekty, projekty got, projek
mój projekt----kkk, Przwatne, Studia, semestr 5, Studia Pulpit, napedy projekty, projekty got, proje
Napęd elektr. proj, Przwatne, Studia, semestr 5, Studia Pulpit, napedy projekty, projekty got, proje
naped-proj, Przwatne, Studia, semestr 5, Studia Pulpit, napedy projekty, projekty got, projekty od D
więcej podobnych podstron