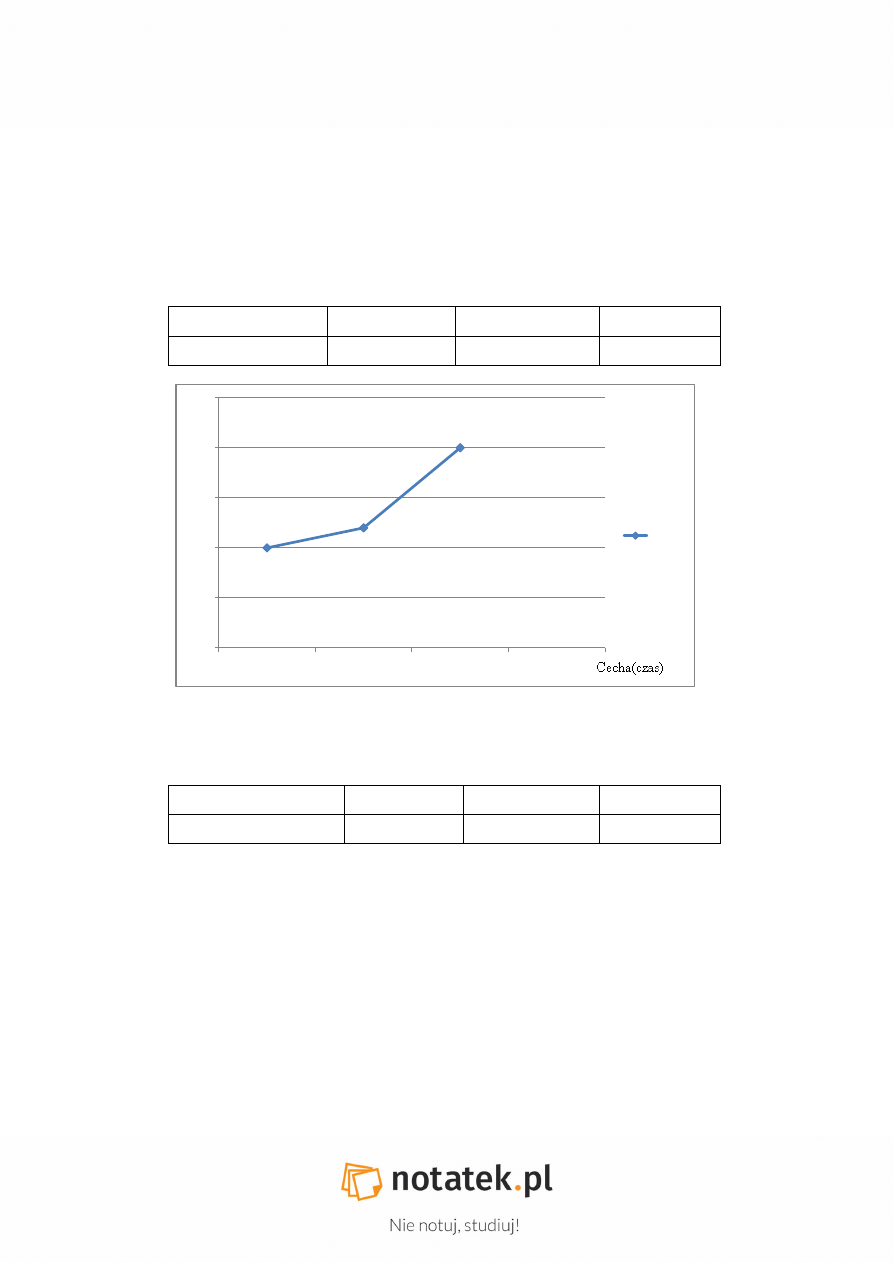
1)

Czasowe

– przedstawienie rozwoju zjawisk w czasie z uwzględnieniem

I

momentów – ściśle określonego momentu w czasie

TABLICA

1 stycznia A.D

1950

1951

1952

Liczba chorych

100

120

200

II okresów
-

pewnego podziału czasu

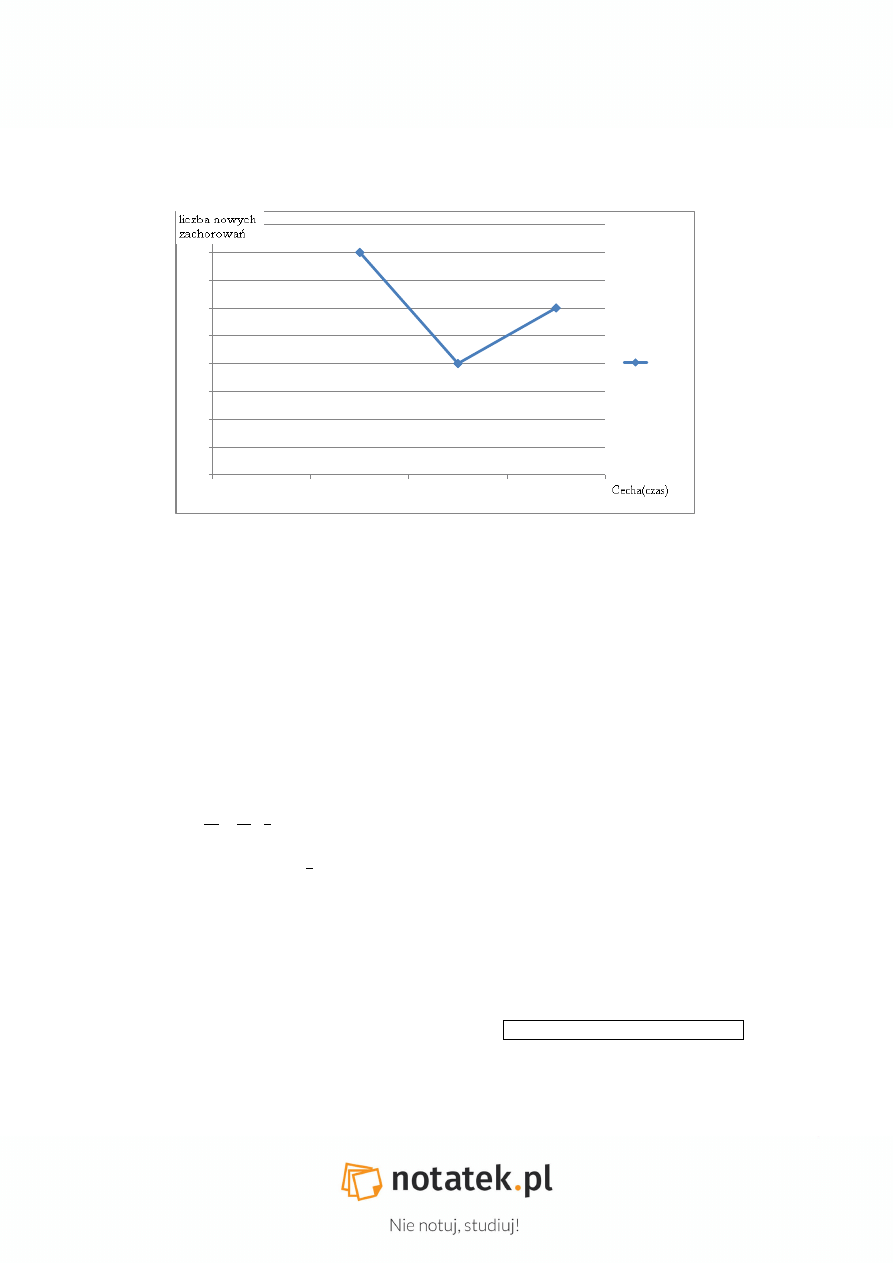
TABLICA

lata

<1950-1955)

<1955-1960)

<1960-1965)

Liczba nowych zachorowań

80

40

60

0

50

100

150

200

250

1950

1951

1952

Seria 1

Liczba chorych

OPISOWA ANALIZA STRUKTURY ZJAWISK MASOWYCH

Typy rozkładów empirycznych jednej zmiennej (mieszanej)

-

Podstawowe pojęcia

Częstość względna

lub wskaźnik struktury – stosunek (ułamkowy/procentowy) liczby

jednostek posiadających określoną wartość lub wariant cechy do liczby wszystkich jednostek
poddanych badaniu. Przykład :

n

o

= 30

– liczba jednostek posiadających wartość x

o

pewnej cechy

N = 70

– liczba wszystkich jednostek poddanych badaniu

Rozwiązanie:

W=

�

=

30

70

=

3

7

Wp = W x 100% =

3

7

x 100% ≈ 42,8571…. % -

częstość względna postaci

procentowej

dla wartości cechy

Rozkład empiryczny (cechy) zmiennej

– przyporządkowanie kolejnym wartościom lub

wariantom ( cechy) zmiennej x

o

odpowiadającym im liczb n

i

lub częstości względnych w

i

albo

(wp)i jednostek posiadających daną wartość lub wariant x

i.

Przykład

0

10

20

30

40

50

60

70

80

90

1950

1955

1960

1965

Seria 1

Częstość względna

Czas x

i

trwania schorzenia Liczba jednostek n

i

(lata)
1 -------------------------------

 2

2 --------------------------------> 0
3 -------------------------------

 1

4 -------------------------------

 4

5 -------------------------------

 2

6 -------------------------------

 0

7 -------------------------------

 0

8 -------------------------------

 1

Typy rozkładów empirycznych zmiennej mierzalnej (najczęściej spotykane)

Rozkłady empiryczne

I cechy skokowej

II cechy ciągłej

a)jednostronne b)wielostonne



1)symetryczne 2)miarkowanie 3)skrajnie

Symetryczne symetryczne

i)normalne
ii)leptokustyczne
iii)platokustyczne

i)prawoskośne

ii)lewoskośne

a) Jednostronne

mają jedno maksimum, tzn. liczebności skupiają się wokół (są

najwyższe w sąsiedztwie) dokładnie jednej wartości zmiennej x

I

W

i

(wp)i

2

10

20 %

0

0 %

1

10

10 %

4

10

40 %

2

10

20 %

0

0 %

0

0 %

1

10

10 %

http://notatek.pl/podstawy-statystyki-z-demografia-wyklad-3?notatka