Wrocław, 04.01.2014 r.

Wyznaczanie współczynnika tarcia

statycznego

Wykonał:

Jakub Kubacki

Prowdzący:

Andrzej Koźmic

1

Wstęp teoretyczny

Zjawisko tarcia jest niezbędne do zajścia jakiegokolwiek ruchu. Występuje powszech-
nie w przyrodzie i często nie zdajemy sobie sprawy z jej obecności. Jej wartość zależy
od materiału, z jakiego wykonano stykające się ciała, a także siły nacisku. Ta nato-
miast zależy od kąta nachylenia do poziomu oraz od sił zewnętrznych działających
na ciało. Siłą nacisku nazywamy siłę prostopadłą do powierzchni, po której porusza
się ciało. Źródłem siły tarcia są nierówności występujące na powierzchni stykających
się ciał. W idealnej sytuacji, kiedy powierzchnie styku są idealnie gładkie, tarcie nie
występuje. Zestawienie tych dwóch sytuacjach prezentuje Rysunek. 1.

Rys. 1.

Zasadniczo wyróżnia się kilka rodzajów tarcia:

• Tarcie kinetyczne związane z ruchem ciała. Wektor tej siły zwrócony jest

przeciwnie do wektora przesunięcia. Siła tarcia kinetycznego hamuje ruch. Jej
wartość jest proporcjonalna do wartości siły nacisku i wyraża się wzorem:

T

=

µF

N

(1)

Gdzie F

N

to siła nacisku, a µ to współczynnik tarcia, pozbawiony jednostki

i zależny od rodzaju stykających się powierzchni.

• Tarcie statyczne występuje pomiędzy ciałem nieruchomym a powierzchnią

na której się znajduje. Można zauważyć, że wartość tarcia statycznego jest
większa od kinetycznego.

• Tarcie toczone jest to siła występująca przy toczeniu przedmiotów typu kula

czy walec. Jej wartość jest mniejsza niż w przypadku przesuwania.

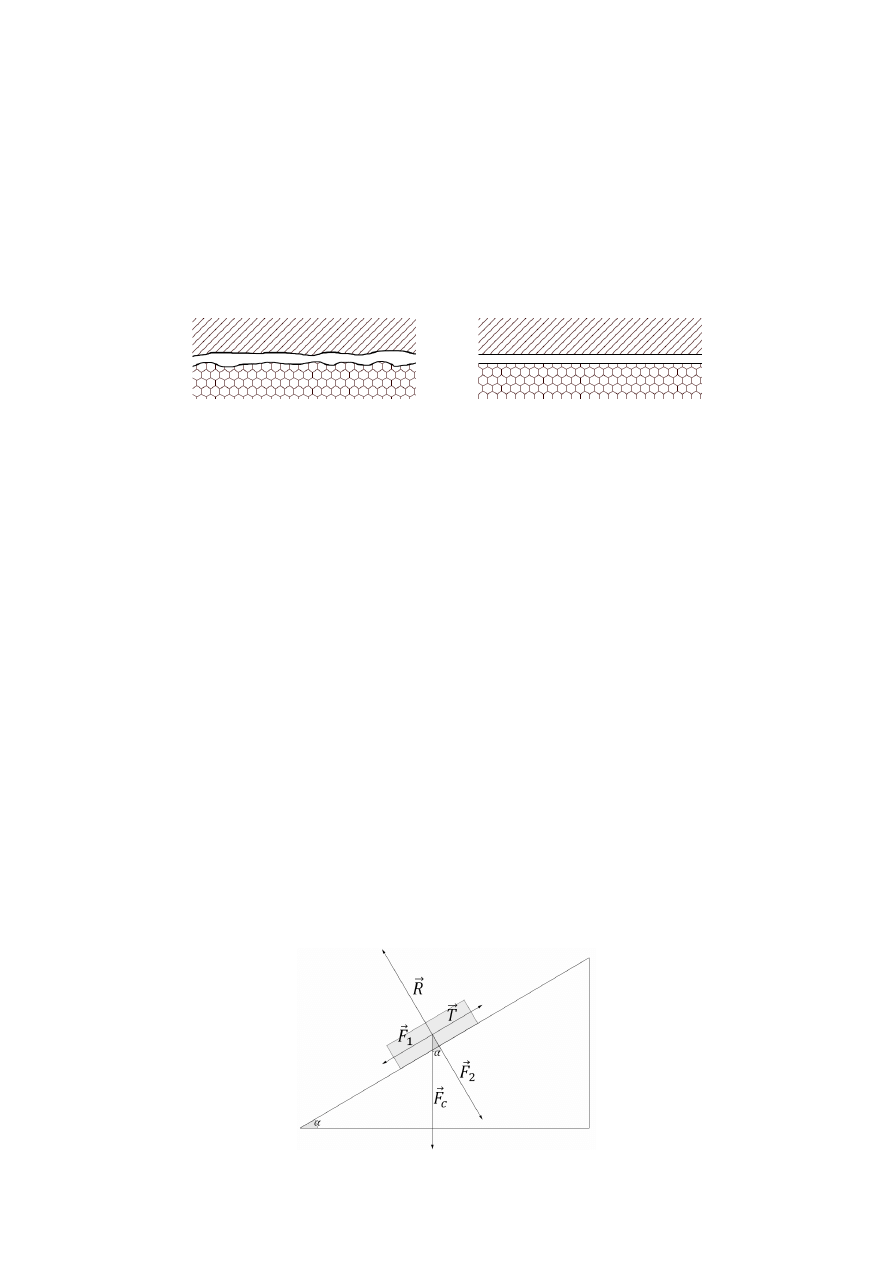
Rysunek 2. przedstawia rozkład sił działających na ciało znajdujące się na równi
pochyłej.Wszystkie siły działające na ciało się równoważą, zgodnie z II Zasadą Dyna-
miki Newtona ciało pozostaje w spoczynku. Natomiast III ZDN głosi, że wszystkie
oddziaływania są wzajemne. Dla przykładu kiedy ciało na Rysunku 2. oddziałuje
na podłoże siłą nacisku wywołaną przez grawitacje, podłoże reaguje siłą ~

R.

Rys. 2.

1 / 3

Na powyższym rysunku siłą prostopadłą do podłoża jest ~

F

2

i równoważy ona siłę

reakcji ~

R. Siła ~

F

1

równoważy siłę ~

T . Natomiast siły ~

F

1

i ~

F

2

są składowymi siły

ciężkości ~

F

c

. Natomiast stosunek ich wartości opisuje wzór:

F

1

F

2

=

tan α

Z definicji siły ~

T wiemy również:

T

=

µF

2

T

=

F

1

Stąd:

µ

=

F

1

F

2

=

tan α

(2)

2

Pomiary

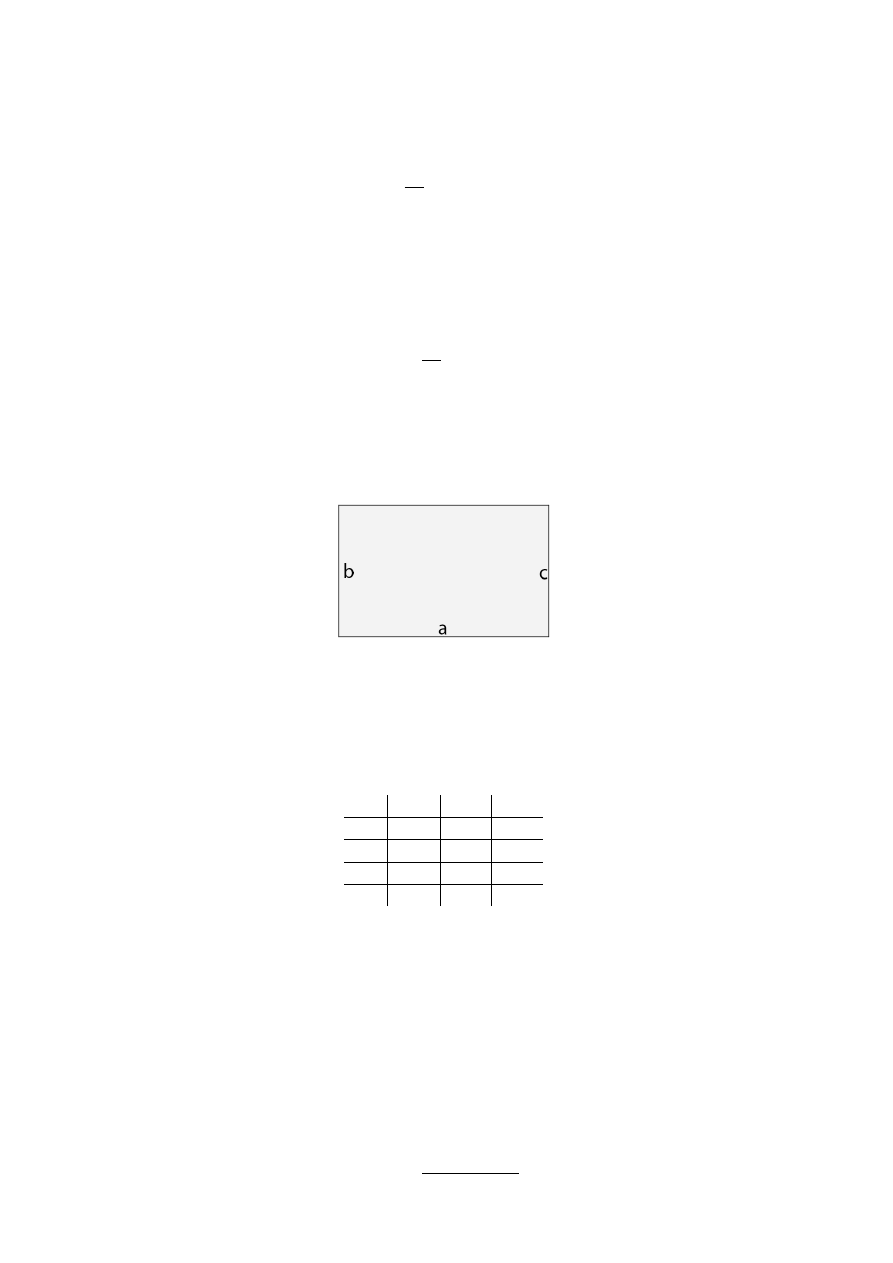
Drewniany klocek w kształcie prostopadłościanu, którego krawędzie oznaczono wg. Ry-
sunku 3.

Rys. 3.

Krawędź b była pokryta filcem, c gumą a krawędź a nie była pokryta niczym. Klocek
stawiano na równi pochyłej, wykonanej z metalu, z zamocowanym kątomierzem, na
różnych krawędziach. Następnie regulowano kąt nachylenia tak, by klocek pozosta-
wał w spoczynku. Wyniki pomiaru zapisano w tabeli:

Lp.

a

[

◦

]

b

[

◦

]

c

[

◦

]

1.

25

15

30

2.

20

15

25

3.

20

15

30

4.

25

15

30

Tabela 1.

Działka elementarna kątomierza wynosiła

∆

^ =

5

◦

Średnie wartości poszczególnych

kątów wynoszą:
a

śr.

= (

23 ± 5

)

◦

b

śr.

= (

15 ± 5

)

◦

c

śr.

= (

29 ± 5

)

◦

Ponieważ tangens nie jest funkcją liniową, nie przyjmę wartości tan 5

◦

za wartość

niepewności

∆µ. Obliczam ją jako niepewność pomiaru pośredniego z metody Naj-

mniej Korzystnego Przypadku. Posługując się wzorem 3. oraz danymi z tabeli 2. W
celu porównawczym wyliczę również niepewność względną ze wzoru 4.

∆µ

=

µ

max

− µ

min

2

(3)

2 / 3

W

=

∆x

x

śr.

100%

(4)

a

b

c

x

śr.

[

◦

]

22,50

15,00

28,75

x

max.

[

◦

]

27,50

20,00

33,75

x

min.

[

◦

]

17,50

10,00

23,75

µ

x

śr.

0,42

0,27

0,55

µ

x

max.

0,52

0,36

0,67

µ

x

min.

0,32

0,18

0,44

Tabela 2.

W powyżesz tabeli x oznacza kolejną kolumnę

(

a, b, c

)

. Na podstawie tabeli 2.

wyliczam:

µ

a

=

0, 4 ± 0, 2

W

a

=

50%

µ

b

=

0, 3 ± 0, 1

W

b

=

33,

(

33

)

% ≈ 40%

µ

c

=

0, 6 ± 0, 2

W

c

=

33,

(

33

)

% ≈ 40%

3

Wnioski

Ze wszystkich zbadanych materiałów współczynnik tarcia pomiędzy gumą a równią
pochyłą jest największy. Nie bez znaczenia pozostaje też fakt, że guma mogła zwil-
gotnieć i stać się bardziej „klejąca”.
Pomiary obarczone są również dużą niepewnością. Która sięga nawet 50%. Najpew-
niej wynika to z niedokładności kątomierza. Celem zwiększenia dokładności wyniku
powtórzyłbym doświadczenie, lecz zamiast korzystać z kątomierza, zmierzyłbym od-
powiednie długości równi (np. linijką).

3 / 3