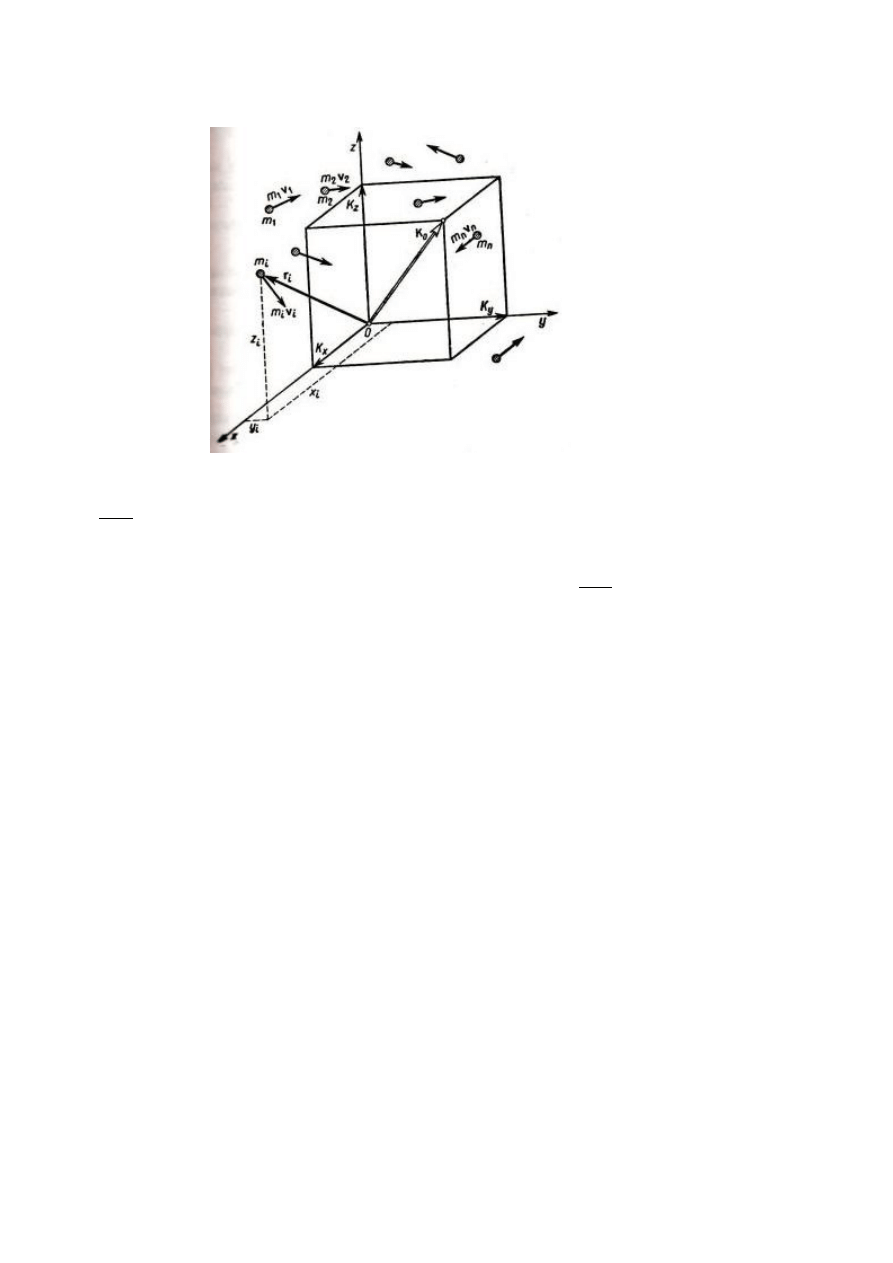
40. Zasada zachowania krętu dla układu punktów materialnych

dK

O

dt

=

∑

i

=1

i

=n

M

iO

, gdzie M

iO

=r

i

×P

i

. Załóżmy, że

∑

i

=1

i

=n

M

iO

=0 (na układ punktów

materialnych nie działają siły zewnętrzne albo działają takie siły których momenty względem

pewnego nieruchomego bieguna O są równe zeru). Z tego wynika

dK

O

dt

=0 ⇒ K

O

=const.

W przypadku gdy momenty wszystkich sił zewnętrznych układu punktów materialnych względem
pewnego nieruchomego bieguna O są równe zeru, wówczas kręt układu względem tego bieguna nie
ulega zmienie.

41. Współczynnik restytucji, jak obliczamy energię uderzenia.

Współczynnik restytucji jest to pewna stała wzynaczana doświadczalnie (charakterystyczna dla
każdego materiału) określająca związek miedzy impulsami sił pierwszego i drugiego okresu
uderzania.

S ' '

=k⋅S '

, 0

k 1 .

k=1 oznacza zderzenie idealnie sprężyste, k=0 oznacza zderzenie idealnie niesprężyste.

Energia uderzenia jest to różnica energi kinetycznej przed uderzeniem i po.

T =T −T ' (nie wiem czy to o to chodzi :/)

42. Na czym polega zasada Hamiltona (zasda najmniejszego działania)

Zasada Hamiltona - zasada najmniejszego działania, podstawowa zasada wariacyjna w mechanice
głosząca, że spośród wielu możliwych ruchów układu mechanicznego fizycznie realizowany jest
ten, w którym działanie S przyjmuje najmniejszą wartość.

44. Częstość drgań swobodnych nietłumionych w układach o dwóch stopniach swobody

Częstośc: 

i

=

1



i

,



1

=

2



k

1

,



2

=

2



k

2

, gdzie k

1

=−k

2

=k . k – stała opisująca ruch, można

wyliczyc ją z równań różniczkowych: q

1

1

=

1

1

cos

 k

1

t



1

 , q

2

1

=

2

1

cos

 k

1

t



1

 , gdzie



1

,



2

,

 - amplitudy współrzędnych q1 i q2.

46. Jak obliczamy energię straconą przy uderzeniu?

Energię straconą przy uderzeniu obliczamy z różnicy energii kinetycznych przed zderzeniem i po.

Np dla uderzenia prostego i środkowego 2 ciał:

T =T −T ' =

1
2

1−k

2



m

1

m

2

m

1

m

2

v

1

−v

2



2

47. Uderzenie proste i środkowe mas

Uderzenie dwóch ciał materialnych nazywamy prostym, gdy prędkości punktów, w których stykają
się ciała są skierowane wzdłuż wspólnej normalnej do powierzchni obu ciał. Jeżeli wspomniana
normalna, zwana normalną uderzenia, przechodzi przez środki mas uderzających o siebie ciał, to
uderzenie nosi nazwę uderzenia środkowego.