1

Dr inż. Czesław Rybicki

Inżynieria złożowa

1.

Równanie bilansu masowego dla złóż gazu

Metoda bilansu masy jest podstawowym narzędziem inżynierii złożowej

pozwalającym analizować i prognozować charakter przebiegu eksploatacji

złóż ropy i gazu. Technika ta pozwala na oszacowanie m.in.: zasobów

początkowych gazu w złożu, ciśnienia początkowego, zasobów gazu w

złożu w dowolnym okresie jego eksploatacji, aktualnego średniego

ciśnienia złożowego. Istotą metody jest zastosowanie zasady zachowania

masy w odniesieniu do złoża traktowanego jako zbiornik o jednorodnym

ciśnieniu i temperaturze [Dake, 1978].

Na podstawie zasady zachowania masy można zapisać:

p

i

n

n

n





(1)

gdzie:

n – bieżąca ilość moli gazu w złożu,

n

i

– początkowa ilość moli gazu w złożu,

n

p

– ilość moli gazu wydobyta ze złoża.

Metodę bilansu masy można zastosować po pewnym okresie eksploatacji

dla którego znana jest ilość wydobytego medium i ciśnienie złożowe.

Analizując przy pomocy tego równania dane z przebiegu eksploatacji

można m. in. ocenić warunki energetyczne eksploatacji złoża.

Mimo oczywistości tego równania w praktyce występują problemy ze

spełnieniem tej zależności. Wynikają one z faktu, że w równaniu tym

dokładnie znana jest jedynie ilość wydobytego gazu. Nie są znane

dokładnie ani pierwotne zasoby ani ilość gazu pozostałego w złożu.

Dodatkowym problemem jest możliwa zmiana objętości przestrzeni

porowej, bądź wskutek dopływu wody, bądź wskutek zaciskania się por

skał.

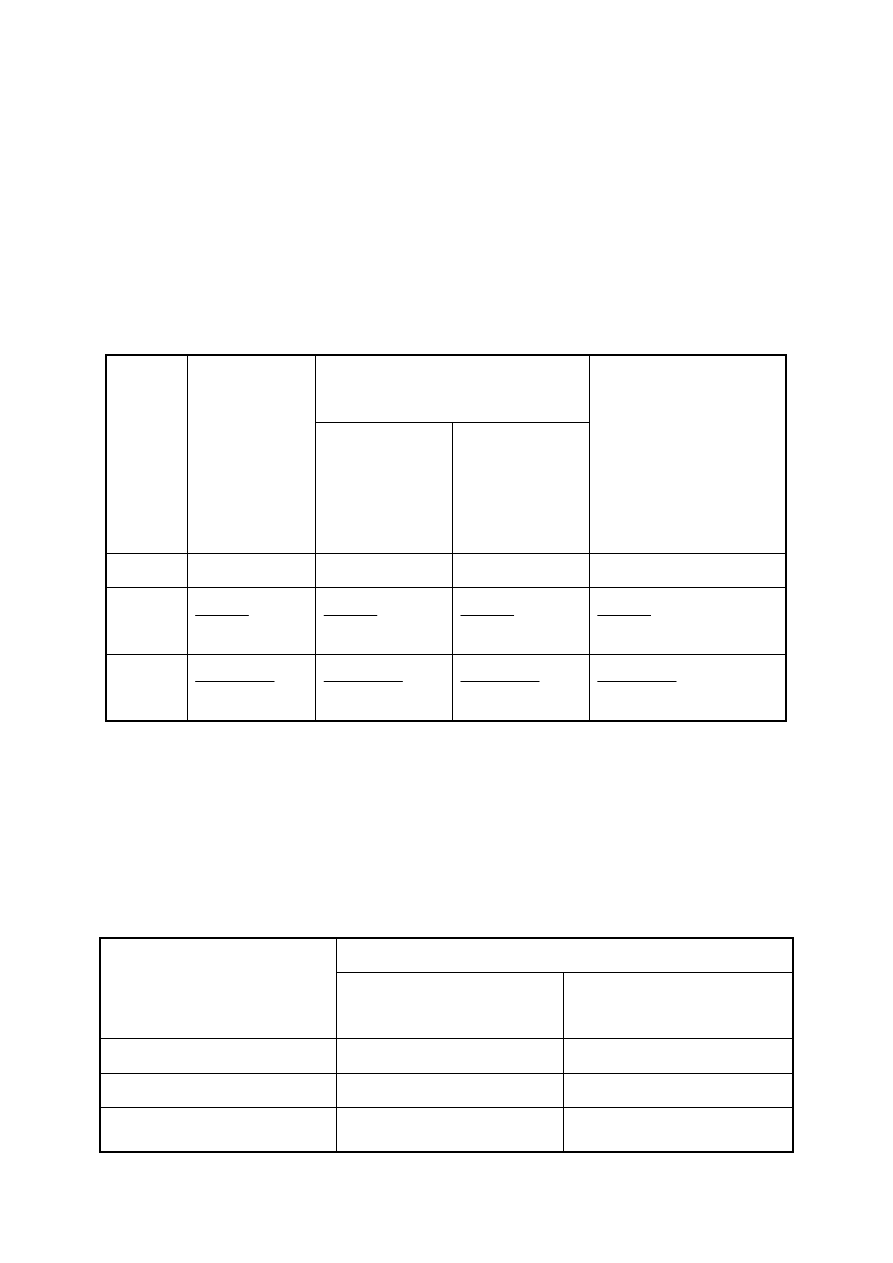
2

Zakładając stałą objętość złoża, wówczas objętość ekspansji płynów

złożowych powinna być równa objętości płynów wydobytych w wyniku

eksploatacji.

Człony objętości ekspansji wyrażone zostały w warunkach

powierzchniowych oraz złożowych dla ciśnienia początkowego i bieżącego,

co przedstawiono w tabeli 1.1.

Tab. 1.1. Człony równania objętości ekspansji złożowej.

Płyn/

skała

Objętość

odniesiona

do

warunków

powie-

rzchniowych

Objętość

w

warunkach

złożowych

Objętość ekspansji

płynów złożowych i

złoża

początkowyc

h

końcowych

Gaz

G

GB

gi

GB

g

G∙(B

g

-B

gi

)

Woda

p

w

wi

V S

B



p

w

wi

wi

V S

B

B





p

w

w

wi

V S

B

B





p

w

w

wi

wi

V S

(B

B )

B







Skała

p

mi

V (1

)

B



 



p

mi

mi

V (1

)

B

B



 





p

m

mi

V (1

)

B

B



 





p

m

mi

mi

V (1

)

(B

B )

B





 





G – zasoby gazu w złożu,

B

gi

, B

g

- współczynniki objętościowe gazu, odpowiednio przy ciśnieniu

początkowym i bieżącym,

Człony objętości płynów wydobytych przeliczono z warunków

powierzchniowych na warunki złożowe, co przedstawiono w tabeli 1.2.

Tab. 1.2. Człony równania objętości wydobytych płynów.

Płyn

Objętość płynów wydobytych

W

warunkach

powierzchniowych

W

warunkach

złożowych

Gaz

G

p

G

p

B

g

Woda

W

p

W

p

B

w

Dopływ wody do złoża

-W

e

-W

e

B

w

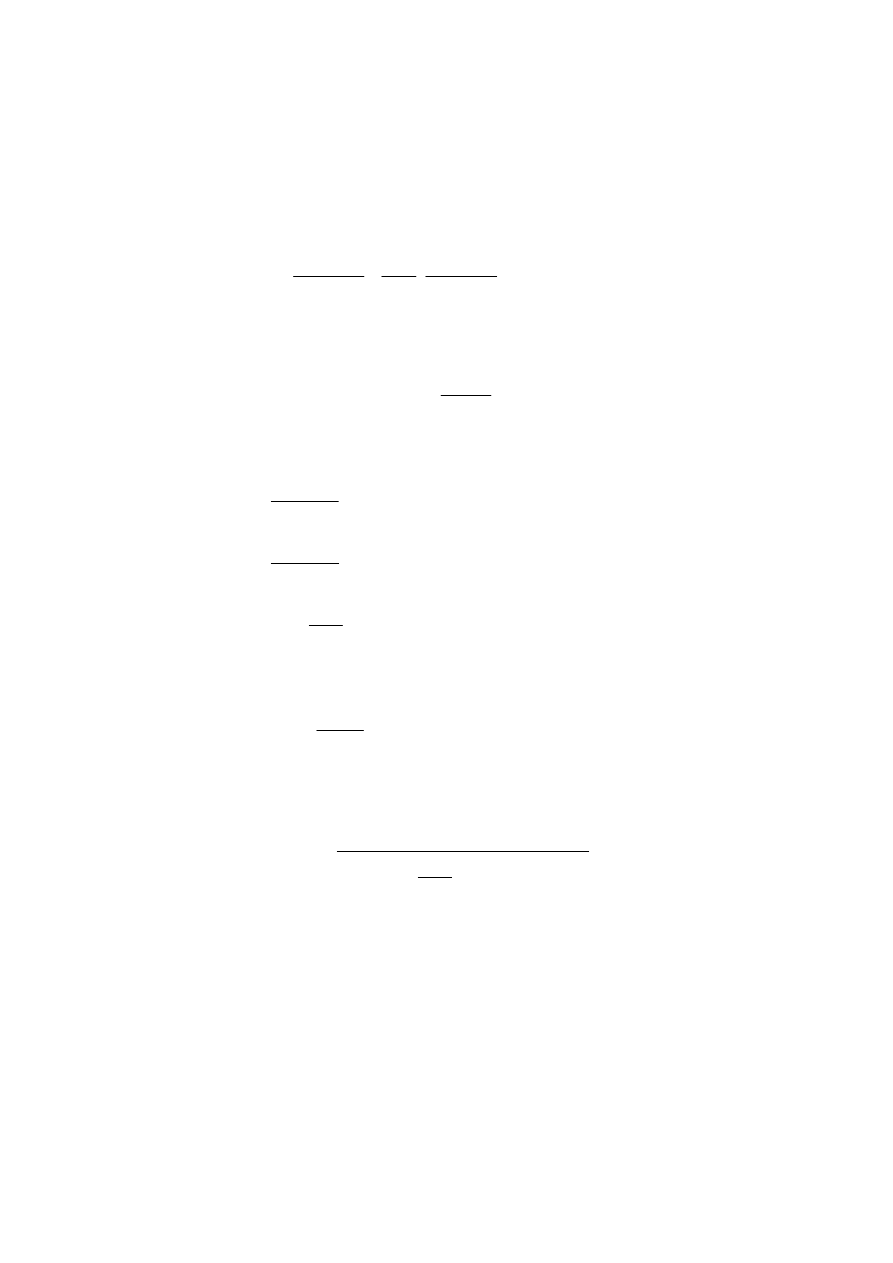
3

G

p

– ilość wydobytego gazu

Równanie

bilansu

masowego

dla

złoża

„czysto

gazowego”

z

uwzględnieniem ruchu wody, ściśliwości skały i ściśliwości wody oraz

dopływu wody spoza konturu przyjmuje postać:









w

m

wi

mi

g

p

w

p

g

w

p

e

gi

wi

mi

B

B

B

B

1

G B

B

V

S

G

B

B

W

W

B

B





























 



















(2)

Objętość porowa V

p

dla złoża gazu można zapisać jako:

gi

p

G B

V

1





 

(3)

Wykorzystując zależności

p

C

B

B

B

w

wi

wi

w









p

C

B

B

B

m

mi

mi

m









m

f

C

1

C











ostatecznie równanie bilansu masowego przyjmuje postać:













gi

g

gi

w

w

f

p

g

w

p

e

G B

G B

B

S

C

C

Δp

G

B

B

W

W

1

























 

(4)

lub









p

g

w

p

e

gi

g

w

w

gi

f

G

B

B

W

W

G

B

B

B

S C

C

Δp

1





















 

(5)

Metoda „p/z” w bilansie masowym

Metoda „p/z” interpretacji równania bilansu masowego jest oparta o

równanie 4. Przekształcając równanie (4) oraz dzieląc przez B

g

uzyskuje

się [Hagoort, 1993]]:

4









g

w

p

e

f

w

w

gi

gi

p

B

1

B

W

W

Δp

C

C

S

1

B

G

B

G

G

G







































(6)

wyciągając G przed nawias i dzieląc przez G uzyskuje się:









g

w

p

e

f

w

w

gi

gi

p

B

1

G

B

W

W

Δp

C

C

S

1

B

B

1

G

G



































(7)

wyciągając B

gi

przed nawias równanie (4.5) przyjmuje postać:











































gi

w

p

e

f

w

w

g

gi

p

B

G

B

W

W

Δp

C

C

S

1

1

1

B

B

1

G

G

(8)

Zazwyczaj ściśliwość skały i wody związanej w porównaniu ze ściśliwością

gazu jest niewielka i w rezultacie zaniedbywana, wówczas równanie (8)

przyjmuje postać:

























gi

w

p

e

g

gi

p

B

G

B

)

W

W

(

1

B

B

1

G

G

(9)

Przy założeniu izotermicznego charakteru procesu eksploatacji (T = const)

równanie (9) upraszcza się do postaci:

p

i

e

p

w

i

gi

G

1

G

p

p

(W

W )B

z

z

1

G B























(10)

Człon (W

e

–Wp)B

w

/(G/E

i

) oznacza część przestrzeni porowej zajętej przez

dopływającą do złoża wodę. W rezultacie, im więcej wody dopływa do

złoża, tym mniejszy spadek ciśnienia obserwuje się dla określonego

strumienia odbieranego gazu.

W przypadku braku dopływu wody przy zaniedbaniu ściśliwości wody i

skały złoże jest typu wolumetrycznego, wówczas równanie (10) upraszcza

się do postaci:

p

i

i

G

p

p

1

z

z

G

















(11)

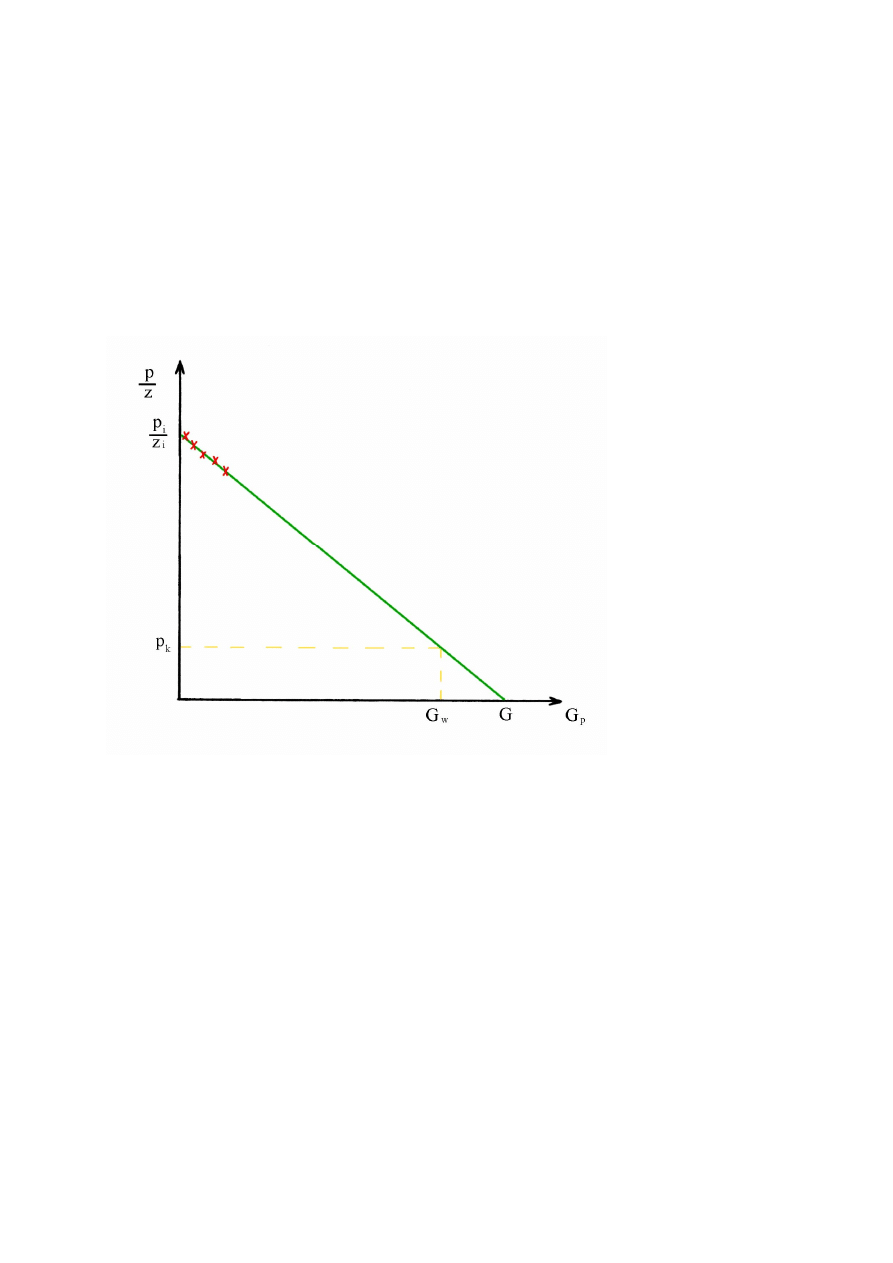
5

Równanie (11) wyraża zależność pomiędzy średnim ciśnieniem złożowym

a ilością wydobytego gazu. W przypadku braku wydobycia gazu Gp = 0

ciśnienie złożowe jest równe ciśnieniu początkowemu p = p

i

. Z kolei przy

całkowitym sczerpaniu zasobów złoża Gp = G ciśnienie jest równe zeru.

Zależność zmian ciśnienia złożowego w funkcji skumulowanego wydobycia

dla złoża wolumetrycznego w układzie p/z vs Gp jest liniową zależnością,

co pokazano na rys. 1.1.

Rys. 1.1 Graficzna postać równania bilansu masowego dla złoża

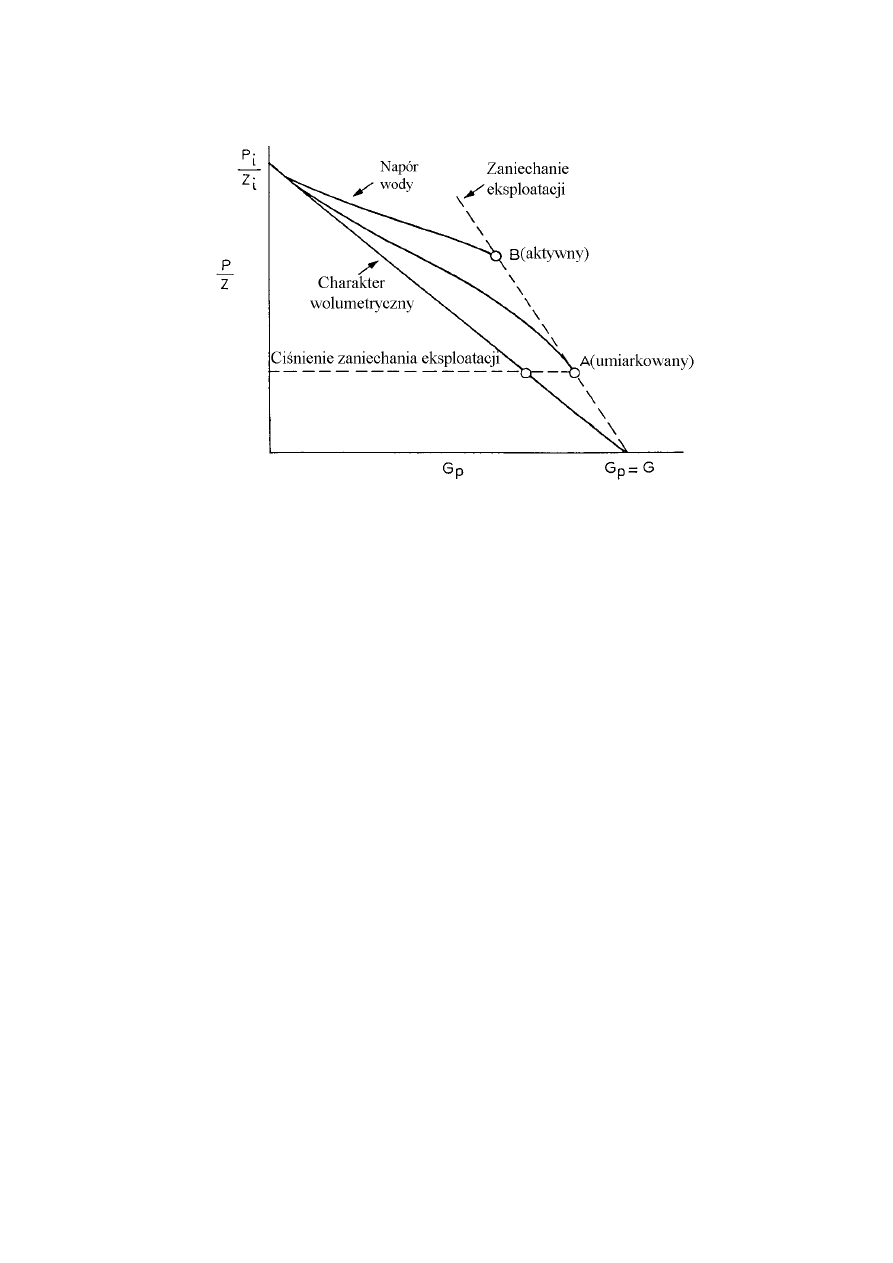
W przypadku dopływu wody do złoża, wykres p/z vs Gp będzie przebiegać

nieliniowo. Im większa aktywność „aquifera”, tym większe odchylenie

krzywej ku górze. Pokazano to na rys. 1.2.

6

Rys. 1.2. Graficzna postać równania bilansu masowego dla złóż gazu

ziemnego o charakterze wolumetrycznym i wodnonaporowym

[Dake, 2000]].

Technika interpretacji p/z wydaje się być prostą metodą, ale główne

niebezpieczeństwo leży w interpretacji wykresu p/z vs Gp i rozstrzygnięciu

o jego liniowym lub nieliniowym charakterze. Często dla złóż gazu z

ruchomą wodą wykres p/z wydaje się być pozornie linią prostą, gdy w

rzeczywistości nią nie jest. Popełnia się wówczas podwójny błąd:

interpretuje się złoże jako wolumetryczne, wyniki ekstrapolacji dają

zawyżone

wartości

początkowych

zasobów

złożowych.

W

wielu

przypadkach można uniknąć tego błędu powiększając skalę wykresu. Na

podstawie takich wykresów można szacować początkowe zasoby złożowe

ekstrapolując tylko początkową część wykresu jeszcze przed rozpoczęciem

ruchu wody złożowej.

7

Metoda Havlen’a-Odeh’a w bilansie masowym

W metodzie Havlen’a–Odeh’a równanie bilansu masowego przyjmuje

następującą postać:





w

e

fw

g

B

W

E

E

G

F







(12)

gdzie:

w

p

g

p

B

W

B

G

F





– całkowita ilość gazu i wody wydobytej ze złoża,

gi

g

g

B

B

E





– współczynnik ekspansji gazu w złożu,

p

S

1

)

c

S

c

(

B

E

wc

f

wc

w

gi

fw









– współczynnik wyrażający ekspansje

wody i przestrzeń porowej złoża,

Dla większości złóż gazu ziemnego szczególnie, gdy skała jest słabo

sprężysta zachodzi warunek, że E

fw

<<E

g

i współczynnik ekspansji układu

woda-przestrzeń porowa może być pominięty, wówczas równanie bilansu

(12) przyjmie postać:

w

e

g

B

W

GE

F





(13)

dzieląc powyższe równanie przez E

g

otrzymuje się:

g

w

e

g

E

B

W

G

E

F





(14)

Równanie (14) stanowi podstawę do określenia mechanizmu pracy złoża.

Naniesienie na wykres wartości ilorazu F/E

g

w funkcji ilości wydobytego

gazu G

p

pozwala zaobserwować zmiany tegoż ilorazu w trakcie

eksploatacji złoża, a tym samym określić charakter jego pracy.

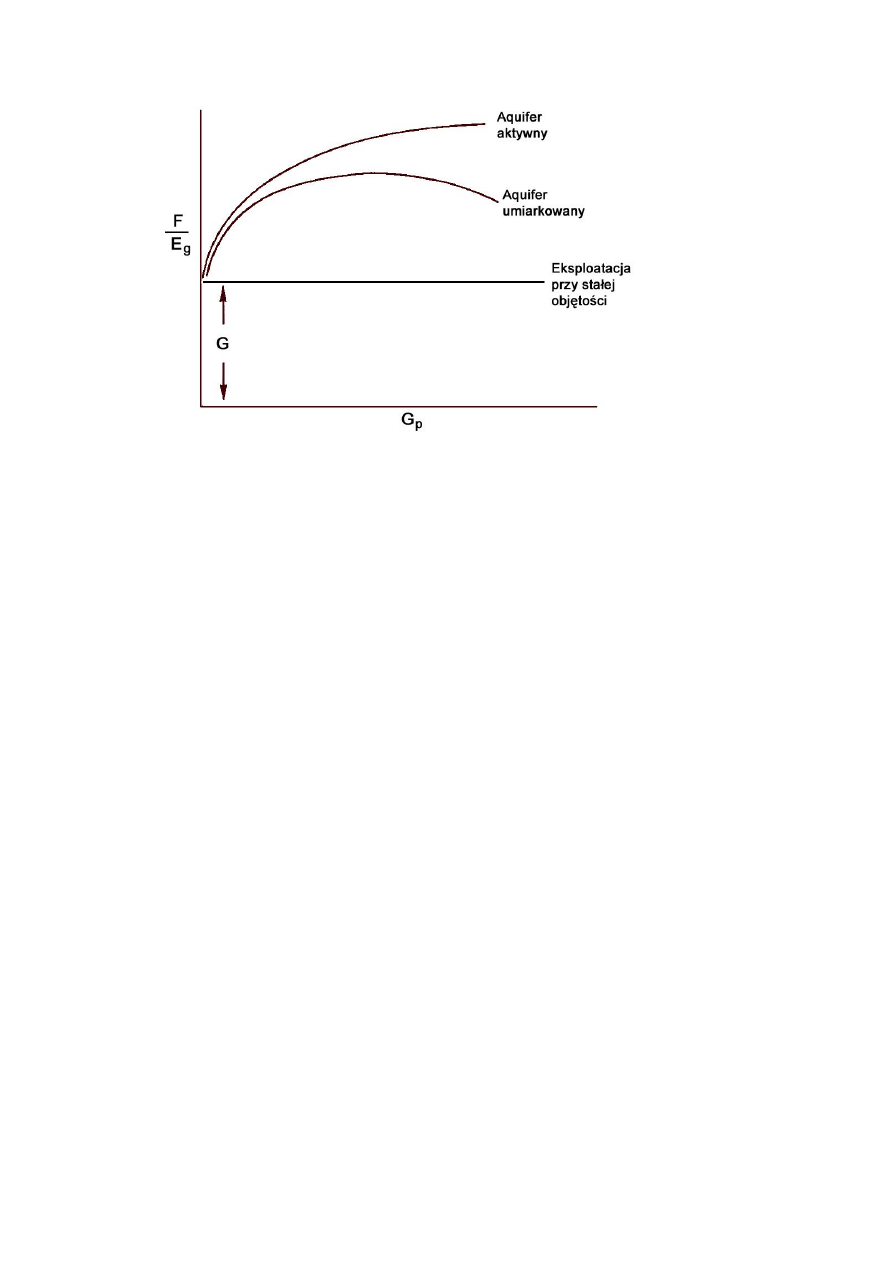
Sporządzony wykres może mieć jeden z trzech przebiegów pokazanych na

rys. 1.3.

8

Rys. 1.3. Wykres diagnostyczny bilansu masowego dla oceny mechanizmu

pracy złoża [Dake, 2000].

Jeżeli złoże jest typu wolumetrycznego (W

e

= 0), wówczas wartości ilorazu

F/E

g

vs Gp układają się wzdłuż linii prostej równoległej do osi odciętych. Z

kolei, gdy następuje dopływ wody do złoża, wtedy wykres przyjmuje

kształt łuku wypukłego ku górze. Jego charakter zależy od wielkości i

aktywności aquifera jak również od wielkości wydatku z jakim jest

odbierany gaz. Im większa aktywność aquifera, tym krzywa szybciej

narasta ku górze.

Główną zaletą metody Havlen’a-Odeh’a jest to, że jest ona znacznie

bardziej czuła na intensywność ruchu wody w złożu w stosunku do innych

metod i dzięki temu jest powszechnie stosowana do oceny warunków

energetycznych złoża.

Wskaźniki energii złożowej

Złoża węglowodorów mogą pracować z różnymi systemami

energetycznymi tj.: system ekspansyjny skały i cieczy, system

ekspansyjny gazu (warunki wolumetryczne), system wodnonaporowy.

Każdy z tych systemów może dominować w różnym stopniu w różnym

okresie eksploatacji złoża w zależności od uwarunkowań geologiczno-

złożowych. Udział poszczególnych systemów w całkowitej energii złoża

9

można określić na podstawie ogólnego równania bilansu masowego (14)

sprowadzając je do postaci bezwymiarowej jako:





e

p

w

gi

gi

w

w

f

p

g

p

g

w

p

g

W

W B

B

GB

(C S

C )

G

1

p

1

G

B

G B

1 S

G B













 

















(15)

Poszczególne człony równania (15) stanowią wskaźniki ich udziału w

całkowitej energii złożowej, odpowiednio:

gi

p

g

B

G

1

G

B



















- wskaźnik energii gazu,

gi

w

w

f

p

g

w

GB

(C S

C )

p

G B

1 S







- wskaźnik energii skał i wody związanej,





e

p

w

p

g

W

W B

G B



- wskaźnik energii wody z warstw okalających i

podścielających.

Suma poszczególnych wskaźników powinna być równa 1. W przypadku,

gdy suma nie jest równa jedności świadczy to o nie spełnieniu równania

bilansu masowego.

2. Metody określania dopływu wody do złoża

Wiele złóż gazowych połączonych jest z warstwami wodonośnymi

(aquifer), z których w miarę spadku ciśnienia złożowego spowodowanego

wydobyciem gazu następuje dopływ wody. Dopływająca woda wypiera

ekwiwalentną objętość gazu i jest źródłem podtrzymywania ciśnienia

złożowego, które musi być brane pod uwagę przy analizie bilansu

masowego. Efektywność procesu podtrzymywania ciśnienia złożowego i

wydatku dopływu wody do złoża zależy od charakterystyki aquifera,

głównie jego wielkości i kształtu oraz przepuszczalności i miąższości.

W literaturze opisano szereg metod obliczania dopływu wody do złoża, z

których najbardziej znane i najczęściej używane to metoda van

Everdingen’a Hurst’a (stosowana dla nieograniczonych aquiferów) oraz

metoda

Fetkovitch’a

(wykorzystywana

w

przypadku

aquiferów

ograniczonych).

10

W praktyce stosuje się również kombinację tych metod (zmodyfikowana

metoda Fetkovitch’a) w przypadkach dużych lecz ograniczonych auiferów.

W takim przypadku, w pierwszej fazie eksploatacji, w której aquifer

zachowuje się jak nieograniczony stosowana jest metodyka van

Everdingen’a Hurst’a. Od momentu zaobserwowania wpływu granic

aquifera na zmianę ciśnienia, wykorzystuje się metodykę Fetkovitch’a.

2.1. Metoda van Everdingen’a i Hurst’a

Metoda van Everdingen’a Hurst’a obliczania dopływu wody do złoża

ze strefy wodonośnej, opiera się na równaniu dopływu płynu

słabościśliwego

do

odwiertu,

które

wyrażone

przy

pomocy

bezwymiarowych zmiennych promienia, czasu i ciśnienia r

D

, t

D

, p

D

przyjmuje postać [Dake, 1978]:

D

D

D

D

D

D

D

t

p

r

p

r

r

r

1































(16)

gdzie:

b

a

D

r

r

r 

– bezwymiarowy promień,

2

b

t

D

r

c

t

k

t















– bezwymiarowy czas.

gdzie:

 – współczynnik lepkości wody,

k – współczynnik przepuszczalności,

 – współczynnik porowatości,

c

t

– całkowity współczynnik ściśliwości układu woda – skała,

r

a

– promień strefy wodonośnej

r

b

– promień strefy złoża.

Van Everdingen i Hurst przedstawili rozwiązanie równania (17) dla dwóch

przypadków:

 stałej wydajności „q”

 stałej różnicy ciśnień „p”

11

Rozwiązanie dla stałej wydajności „q” zakłada stałą wydajność dopływu

płynu słabościśliwego do odwiertu przez pewien okres czasu dla której jest

liczony

spadek

ciśnienia

w

odwiercie.

Rozwiązanie

to

znalazło

zastosowanie w eksploatacji złóż ropy i gazu.

W przypadku określenia ilości dopływu wody do złoża bardziej

interesującym jest rozwiązanie przy stałej różnicy ciśnień, gdzie zakłada

się stałą różnicę ciśnień na konturze złoże – strefa wodonośna przez

pewien okres czasu, wyznaczana jest natomiast ilość dopływającej wody

do złoża.

Rozwiązanie równania dopływu wody do złoża uzyskano dla warunków

początkowo-brzegowych w postaci:

1. Warunek początkowy

p = p

i

= const dla t = 0 i wszystkich wartości „r”

(17)

(stałe ciśnienie w całym obszarze)

2. Warunki brzegowe:

p = const dla r = r

0

i t > 0

(18)

(stała różnica ciśnień na konturze złoże – strefa wodonośna)

2a. Strefa wodonośna o nieograniczonym zasięgu

p = pi = const dla t > 0 i r = 

(19)

2b. Strefa wodonośna o ograniczonym zasięgu

0

r

p







dla t > 0 i r = ra

(20)

Rozwiązanie równania (16) przy warunkach początkowo-brzegowych (17)

– (20) jest następujące:

 

p

h

k

2

q

t

q

D

D



















(21)

gdzie:

q – wydajność dopływu wody,

h – miąższość złoża,

p – różnica ciśnień między ciśnieniem w aquiferze a ciśnieniem w

złożu,

12

q

D

(t

D

) – bezwymiarowa funkcja wydajności wyznaczona dla r

D

= 1

opisująca zmianę wydajności od zera do „q” spowodowanej

spadkiem ciśnienia p na granicy złoża „r

b

” w czasie t = 0.

Równanie (21) można wyrazić w postaci skumulowanego dopływu wody

poprzez obustronne jego scałkowanie.

 

D

D

D

t

0

D

t

0

dt

dt

dt

t

q

dt

q

Δp

h

k

π

2

μ

D























(22)

co daje:

 

k

r

c

μ

t

W

Δp

h

k

2π

μ

W

2

b

t

D

eD

e



















(23)

po przekształceniu uzyskuje się:

 

D

eD

t

2

b

e

t

W

Δp

c

h

r

π

2

W



















(24)

Równanie (24) zakłada radialny dopływ wody. W przypadku, gdy dopływ

wody do złoża nie jest radialny, wówczas w równaniu (24) wprowadza się

tzw. współczynnik niepełnej geometrii radialnej „f” definiowany jako:



360

f





, gdzie  - stanowi wycinek koła wyrażony w stopniach z którego

następuje dopływu wody do złoża, wówczas:

 

D

eD

t

2

b

e

t

W

Δp

f

c

h

r

π

2

W





















(25)

Równanie (25) pozwala wyznaczyć skumulowaną ilość wody dopływającej

do złoża przy stałej różnicy ciśnień p na konturze złoże - strefa

wodonośna. Jest ono często wyrażane w postaci:

 

D

eD

e

t

W

Δp

U

W







(26)

gdzie:

f

c

h

r

π

2

U

t

2

b

















jest stałą strefy wodonośnej,

W

eD

(t

D

) - bezwymiarowa funkcja dopływu wody.

Bezwymiarowa funkcja dopływu wody jest funkcją bezwymiarowego czasu

t

D

jak również stosunku wielkości strefy wodonośnej do wielkości złoża,

tzw. promienia zredukowanego r

eD

wyrażanego zależnością:

e

eD

b

r

r

r



(27)

gdzie:

13

r

e

- promień strefy wodonośnej,

r

o

- promień złoża.

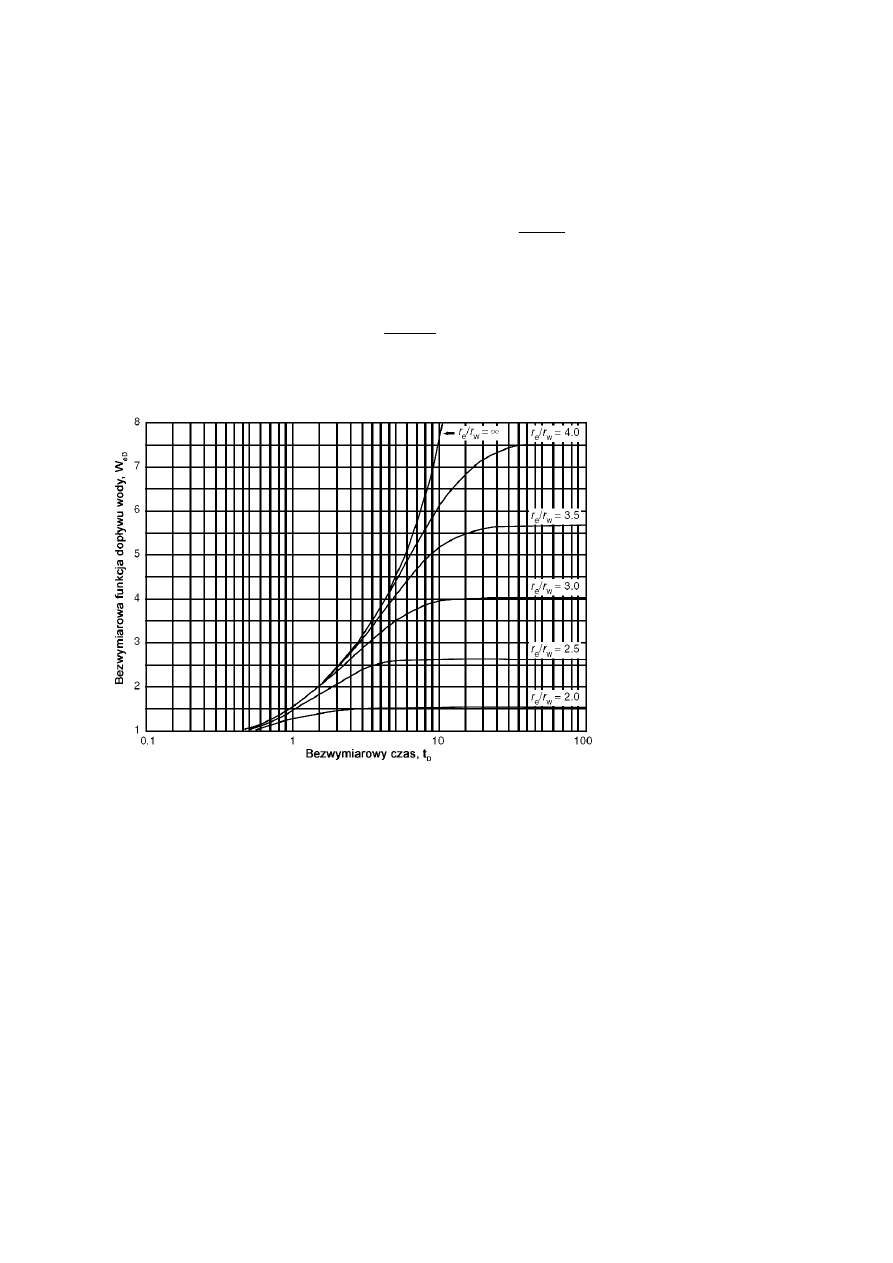
Zależność bezwymiarowej funkcji dopływu wody W

eD

(t

D

) w funkcji czasu

bezwymiarowego t

D

dla różnych wartości promienia bezwymiarowego r

eD

pokazano na rys. 2.1 i 2.2.

Wartości bezwymiarowej funkcji dopływu wody mogą być wyznaczone w

oparciu o formuły empiryczne dla różnych wartości bezwymiarowego

czasu t

D

, a zatem zarówno dla krótkich czasów gdy dopływ występuje w

stanie nieustalonym (nieskończony aquifer) jak również dla czasów

długich, gdzie mogą się ujawnić efekty oddziaływania granic aquifera

(aquifer ograniczony). Dla aquiferów nieograniczonych nie istnieje

oczywiście maksymalna wartość bezwymiarowej funkcji dopływu wody

gdyż pracują one w stanie nieustalonym.

W

przypadku

stref

wodonośnych

o

nieograniczonym

zasięgu

bezwymiarowa funkcja dopływu wody zależy jedynie od wartości

bezwymiarowego czasu t

D

i można ją wyznaczyć wg następujących

zależności wielomianowych [Ahmed, 2001]:

dla t

D

< 0.01

 

0.5

D

eD

D

t

W

t

2





  









(28)

dla 0.01< t

D

< 200

 

3/ 2

2

D

D

D

D

eD

D

D

D

1.2838

t

1.19328 t

0.269872 t

0.00855294 t

W

t

1 0.616599

t

0.0413008 t

























(29)

dla t

D

> 200

 

 

D

eD

D

D

4 29881+2 02566 t

W

t

ln t







(30)

Dla aquiferów ograniczonych w zależności od wielkości bezwymiarowego

promienia r

D

istnieje pewna wartość czasu bezwymiarowego t

Dkr

dla której

bezwymiarowa funkcja dopływu wody osiąga stałą maksymalną wartość.

Wartość czasu t

Dkr

wyznacza się wg zależności

2

Dkr

eD

t

0.4 (r

1)







(31)

14

Bezwymiarową funkcję dopływu wody dla czasów bezwymiarowych t

D

<

t

Dkr

wyznacza się wówczas tak jak dla stref o nieograniczonym zasięgu,

zaś dla czasów t

D

> t

Dkr

wg wzoru [Hagoort, 1988]:





2

D

eD

eD

*

2 t

W

0.5 r

1

1 exp

J



 

































(32)

gdzie:









eD

*

4

2

eD

eD

2

eD

ln r

J

r

0.25 1 3 r

r

1









 



(33)

Rys. 2.1. Bezwymiarowa funkcja dopływu wody W

eD

(t

D

), [1].

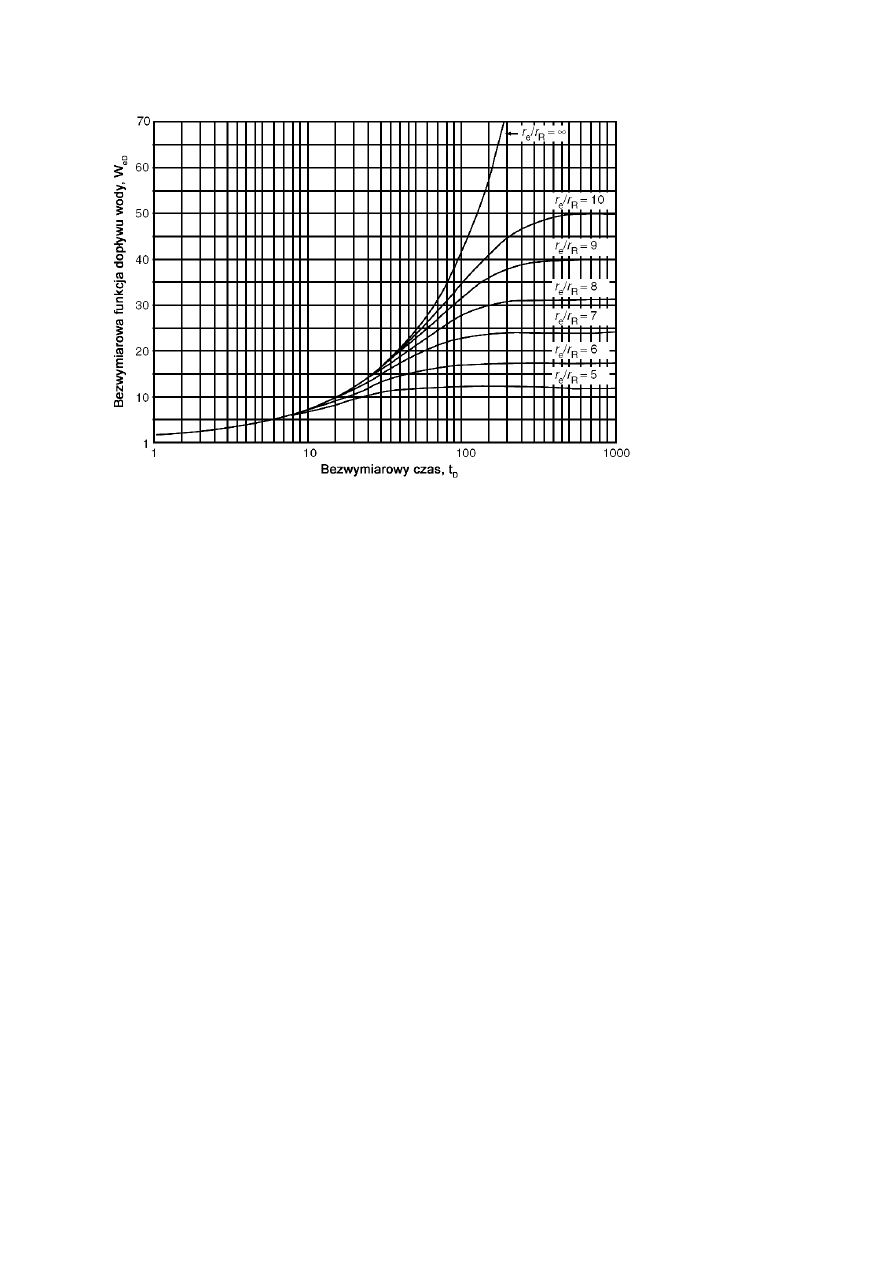
15

Rys. 2.2. Bezwymiarowa funkcja dopływu wody W

eD

(t

D

), [1].

Równanie (26) jest słuszne dla stałej różnicy ciśnień. W

rzeczywistym przypadku spełnienie tego warunku wobec obniżającego się

ciśnienia w eksploatowanym złożu nie jest możliwe w dłuższym okresie

czasu.

W celu zastosowania metody van Everdingen’a-Hurst’a do wyznaczenia

ilości dopływającej wody krzywą zmian ciśnienia dzieli się na serię

przedziałów czasowych dla których przyjmuje się p = const. Zmiana

ciśnienia złożowego może być wówczas aproksymowana z dowolną

dokładnością poprzez serię spadków ciśnienia. Aproksymacja zmian

ciśnienia pokazana jest na rys. 2.3. Spadki ciśnienia w poszczególnych

przedziałach czasowych wyznaczane są jako połowa spadku ciśnienia w

poprzednim przedziale czasowym plus połowa spadku ciśnienia w

aktualnym przedziale czasowym.

Dla spadków ciśnień pomiędzy poszczególnymi przedziałami czasowymi

można wówczas wyznaczyć ilość dopływającej wody a następnie stosując

zasadę

superpozycji

dla

poszczególnych

dopływów

traktowanych

oddzielnie obliczyć skumulowaną ilość wody jak a dopłynęła do złoża.

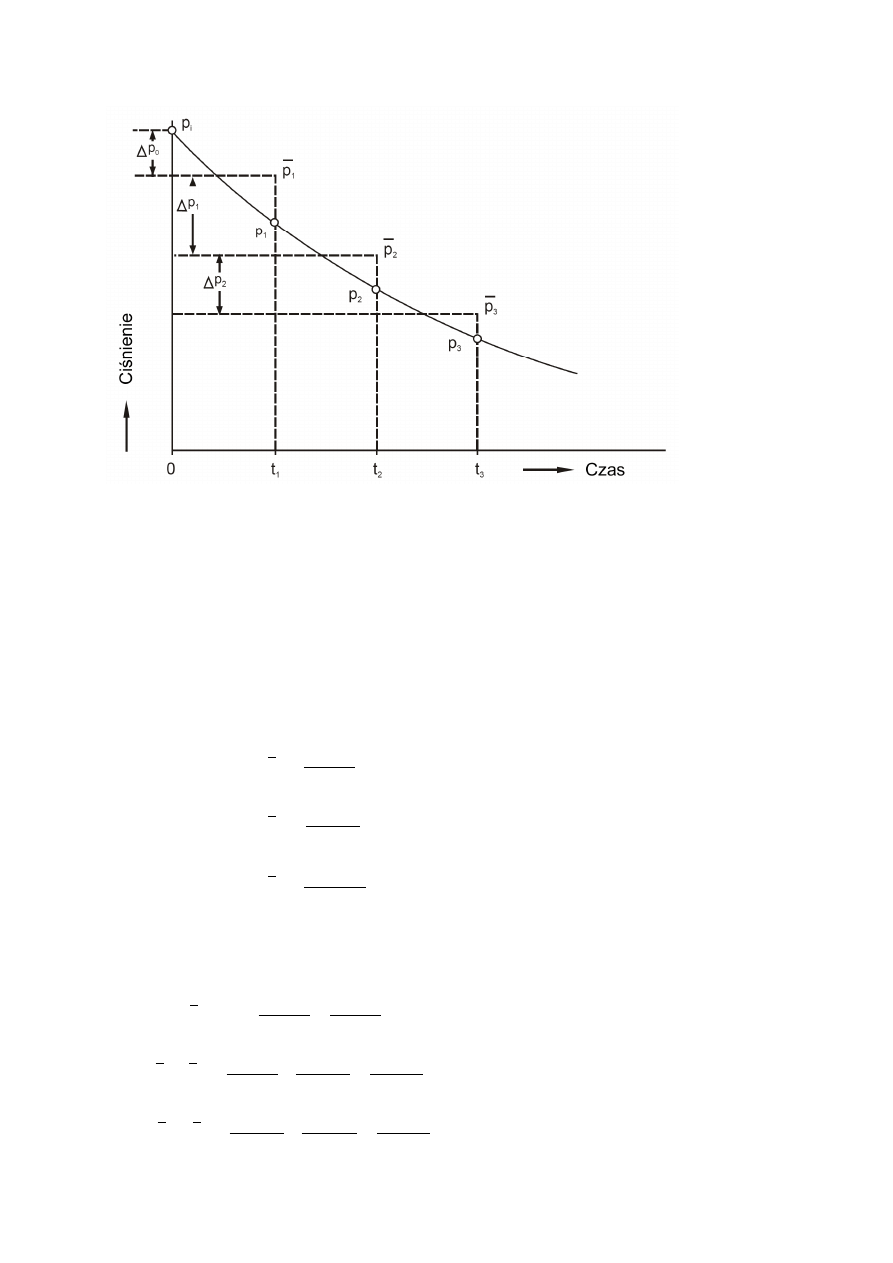
16

Rys. 2.3. Dyskretyzacja zmian ciśnienia złożowego na konturze złoże-

aquifer.

Zakładając, że kolejne ciśnienia złożowe są równe ciśnieniu na konturze

złoże-aquifer wówczas zmianę ciśnienia złożowego po czasie: 0, t1, t2, t3,

... można oznaczyć jako: p

i

, p

1

, p

2

, p

3

, .... . Następnie w każdym z

przedziałów czasowych wyznacza się wartości średniego ciśnienia wg

zależności:

2

p

p

p

1

i

1





2

p

p

p

2

1

2





.

2

p

p

p

j

1

j

j







(34)

Spadki ciśnień występujące po czasach 0, t

1

, t

2

.... wyznacza się wówczas

jako różnice ciśnień średnich w poszczególnych interwałach jako:

2

p

p

2

p

p

p

p

p

p

1

i

1

i

i

1

i

0

















2

p

p

2

p

p

2

p

p

p

p

p

2

i

2

1

1

i

2

1

1



















2

p

p

2

p

p

2

p

p

p

p

p

3

1

3

2

2

1

3

2

2



















17

.

.

.

2

p

p

2

p

p

2

p

p

p

p

p

1

j

1

j

1

j

j

j

1

j

1

j

j

j





























(35)

Zatem sumaryczny całkowity dopływ wody za cały okres eksploatacji t

c

będzie sumą ilości wody jaka dopłynęła do złoża pod wpływem kolejnych

spadków ciśnień zakładając, że spadki te trwają w złożu do końca

eksploatacji. W ten sposób całkowitą ilość wody wyznacza się metodą

superpozycji.





n 1

2

e

b

t

j

eD

D

D j

j 0

W

2

r

h

c f

p W

T

t





   

   

 









(36)

2.2. Metoda Fetkovich’a

Metoda van Everdingen’a i Hurst’a posiada wadę w postaci

złożoności i żmudności obliczeń, które wynikają z konieczności stosowania

metody superpozycji, co powoduje trudności w dopasowaniu parametrów

równania.

Metodą upraszczającą obliczenia stosowaną szeroko w inżynierii złożowej

jest metoda Fetkovitch’a w której przepływ wody do złoża został zapisany

formułą, przy założeniu ograniczonej strefy dopływu [Dake, 1978]:





e

w

a

r

dW

q

J p

p

dt







(37)

gdzie:

J – indeks wydajności aquifera,

p

a

– średnie ciśnienie w aquiferze,

p

r

– ciśnienie złożowe (ciśnienie na konturze ropa-woda lub

gaz-woda),

Drugim równaniem metody Fetkovich’a jest równanie bilansu masy dla

aquifera o stałej ściśliwości, z którego wynika, że spadek ciśnienia w

aquiferze jest wprost proporcjonalny do ilości wody wypływającej z

aquifera wg zależności:

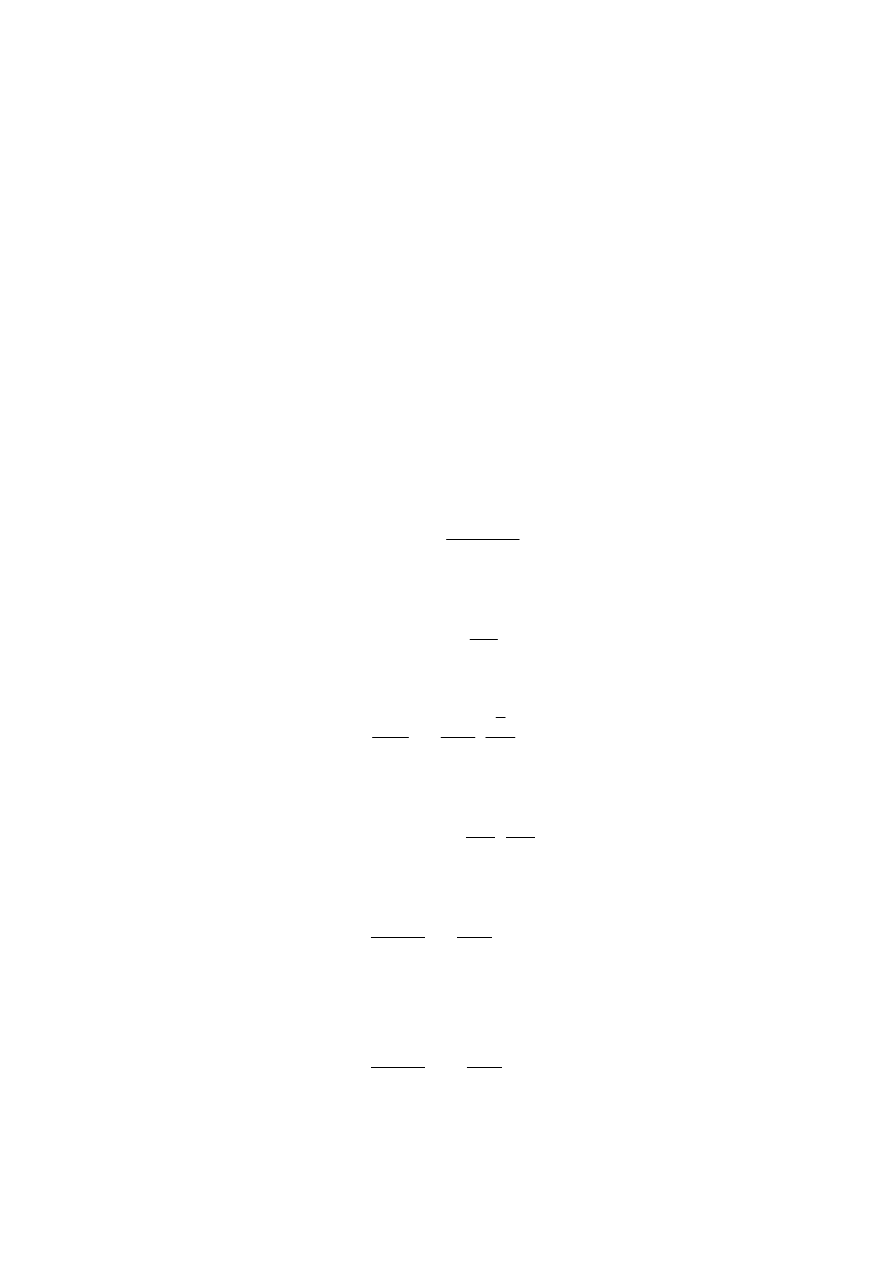
18

:

e

w

i

i

a

W

C

V (p

p )









(38)

gdzie:

C

w

– współczynnik ściśliwości wody [1/Pa],

V

i

– początkowa objętość wody w aquiferze [m

3

],

p

i

– ciśnienie początkowe w aquiferze [Pa].

Z równania (38) wynika, że maksymalny dopływ wody wystąpi, gdy p

a

=

0, zatem:

i

i

t

ei

p

W

c

W







(39)

Równanie (37) można przekształcić w celu określenia ciśnienia w aquiferze

po wypłynięciu z niego ilości wody W

e

jako:

e

a

i

w

i

i

W

p

p

1

C

V p























(40)

lub z wykorzystaniem zależności (39)

e

a

i

ei

W

p

p

1

W



















(41)

Różniczkując równanie (41) po czasie t uzyskuje się zależność:

dt

p

d

p

We

dt

dWe

a

i

i







(42)

Wstawiając równanie (37) do równania (42)





dt

dp

p

W

p

p

J

a

i

ei

r

a











(43)

rozdzielając zmienne uzyskuje się:

dt

W

p

J

p

p

dp

ei

i

r

a

a











(44)

Całkując obustronnie równanie (44)















dt

W

p

J

p

p

dp

ei

i

r

a

a

(45)

uzyskuje się:

19





C

t

W

p

J

p

p

ln

ei

i

r

a













(46)

Stałą całkowania wyznacza się na podstawie warunków początkowych, tj.

dla

t

=

0

(W

e

= 0, p

a

= p

i

), wówczas:





i

r

C

ln p

p





(47)

Wstawiając równanie (4.45) do równania (4.44) będzie:

t

W

p

J

p

p

p

p

ln

ei

i

r

i

r

a













(48)

Przekształcając powyższe równanie uzyskuje się:





ei

i

W

t

p

J

r

i

r

a

e

p

p

p

p















(49)

Wstawiając równanie (49) do równania (37) otrzymuje się:





ei

i

W

t

p

J

r

i

e

e

p

p

J

dt

dW















(49a)

Całkując równanie (49a) obustronnie w granicach 0 – W

e

oraz 0 – t:

























t

0

W

t

p

J

r

i

W

0

e

dt

e

p

p

J

dW

ei

i

e

(50)

otrzymuje się:









i

ei

J p t/W

ei

e

i

r

i

W

W

p

p

1 e

p

  











(51)

Jeżeli czas t w równaniu (51) zmierza do (∞) to można je zapisać w

postaci:









ei

e

i

r

t

i

i

r

i

W

W

p

p

c W

p

p

p















(52)

co wyraża maksymalny dopływ wody spowodowany spadkiem ciśnienia

między p

i

– p.

Uzyskane rozwiązanie jest słuszne dla stałej różnicy ciśnień. W praktyce

ciśnienie na konturze gaz-woda zmienia się w czasie, co powoduje

konieczność zastosowania zasady superpozycji. Fetkovitch natomiast

20

pokazał, że można uniknąć konieczności stosowania metody superpozycji

stosując następującą procedurę:

Dla pierwszego kroku czasowego

1

Δt









i

1

ei

J p Δt /W

ei

e1

i

r 1

i

W

ΔW

p

p

1 e

p

  











(53)

dla drugiego okresu czasu

2

t

 i

a1

p - średniego ciśnienia w strefie

wodonośnej pod koniec pierwszego interwału czasu dopływ wody wynosi:









i

2

ei

J p Δt /W

ei

e2

a1

r 2

i

W

ΔW

p

p

1 e

p

  











(54)

ogólnie dla n-tego okresu czasu:









i

n

ei

J p Δt /W

ei

en

r

an-1

n

i

W

ΔW

p

p

1 e

p

  











(55)

gdzie ciśnienie w strefie wodonośnej pod koniec okresu czasowego

„n-1” wyznacza się jako:

1

1

1

1

n

e j

j

a

i

n

ei

W

p

p

W

































 





























(56)

oraz ciśnienie średnie w złożu dla n-tego okresu czasowego:

2

p

p

p

n

r

1

n

r

n

r







(57)

Całkowity dopływ wody jest wówczas sumą dopływów w kolejnych

okresach czasowych

n

e

e j

j 1

W

W









(58)

Indeks wydajności zależy od przyjętej geometrii przepływu oraz stanu

hydrodynamicznego aquifera.

Dla stanu semiustalonego indeks wydajności jest identyczny jak w

przypadku dopływu płynu do odwiertu:

































4

3

r

r

ln

h

k

f

2

J

b

a

w

(59)

21

Dla stanu ustalonego:































b

a

w

r

r

ln

h

k

f

2

J

(60)

W przypadku złoża usytuowanego asymetrycznie względem aquifera

odbiegającego kształtem od radialnego, indeks wydajności może być

wyrażony za pomocą współczynnika kształtu Dietz’a jako:

2

b

A

r

C

γ

A

4

ln

2

μ

h

k

f

2

J





















(61)

gdzie:

C

A

– współczynnik kształtu Dietz’a,

 – stała Euler’a,

A – powierzchnia aquifera.

Metoda Fetkovitch’a może być także wykorzystywana dla opisu dopływu

wody z nieograniczonych stref wodonośnych lub stref skończonych ale

bardzo dużych rozmiarach. W takich przypadkach dla czasów krótkich

stosuje się metodę nieustalonego dopływu van Everdingen’a – Hurst’a, zaś

dla czasów długich prostszą metodę Fethkovich’a.

Obliczenia dopływu wody do złoża

Dopływ wody do złoża kontaktującego się ze strefą wodonośną

następuje w wyniku spadku ciśnienia złożowego spowodowanego

wydobyciem płynów złożowych. Wielkość i intensywność dopływu wody

jest funkcją zarówno tempa sczerpywania zasobów złożowych i

związanego z tym spadku ciśnienia w złożu jak też charakterystyki

aquifera, głównie jego wielkości i kształtu oraz własności petrofizycznych

ośrodka porowatego.

Równaniem pozwalającym określić zmianę ciśnienia w złożu w funkcji

wydobycia płynów złożowych jest równie bilansu masowego, które dla złóż

pracujących w warunkach ruchomej wody przyjmuje postać równania,

22

które dla dowolnego kroku czasowego „n” przy zaniedbaniu wydobycia

wody „W

p

” można zapisać jako:

n

n

p

i

e

w

n

i

gi

G

1

G

p

p

W

B

z

z

1

G B











 







 

 







(62)

Z kolei wielkość dopływu wody do złoża może być wyznaczona z

wykorzystaniem omówionych wcześniej metod van Everdingen’a-Hurst’a i

Fetkovich’a.

Obliczenia z użyciem metody van Everdingen’a-Hurst’a

W przypadku metody van Everdingen’a- Hurst’a dopływ wody opisywany

jest równaniem, które dla kroku czasowego „n” można zapisać wydzielając

ostatni człon jako:

















n

n 2

e

j

eD

n

j

n 1

eD

n

n 1

j 0

W

U

p W

u

t

t

p

W

u

t

t

























 

















(63)

gdzie:

n 2

n

n 1

p

p

p

2











oraz parametr „u” wynikający z definicji bezwymiarowego czasu t

D

2

t

b

k

u

c r



   



wówczas bezwymiarowy czas opisywany jest zależnością:

D

t

u t

 

Zachowanie się układu złoże-aquifer opisywane jest zatem układem

równań (62), (63). W równaniach tych nieznanymi parametrami są

ciśnienie „p

n

” i dopływ wody „W

en

” w bieżącym kroku czasowym „n”.

Ponieważ równania te są zależne od siebie muszą być zatem

rozwiązywane równolegle w sposób iteracyjny.

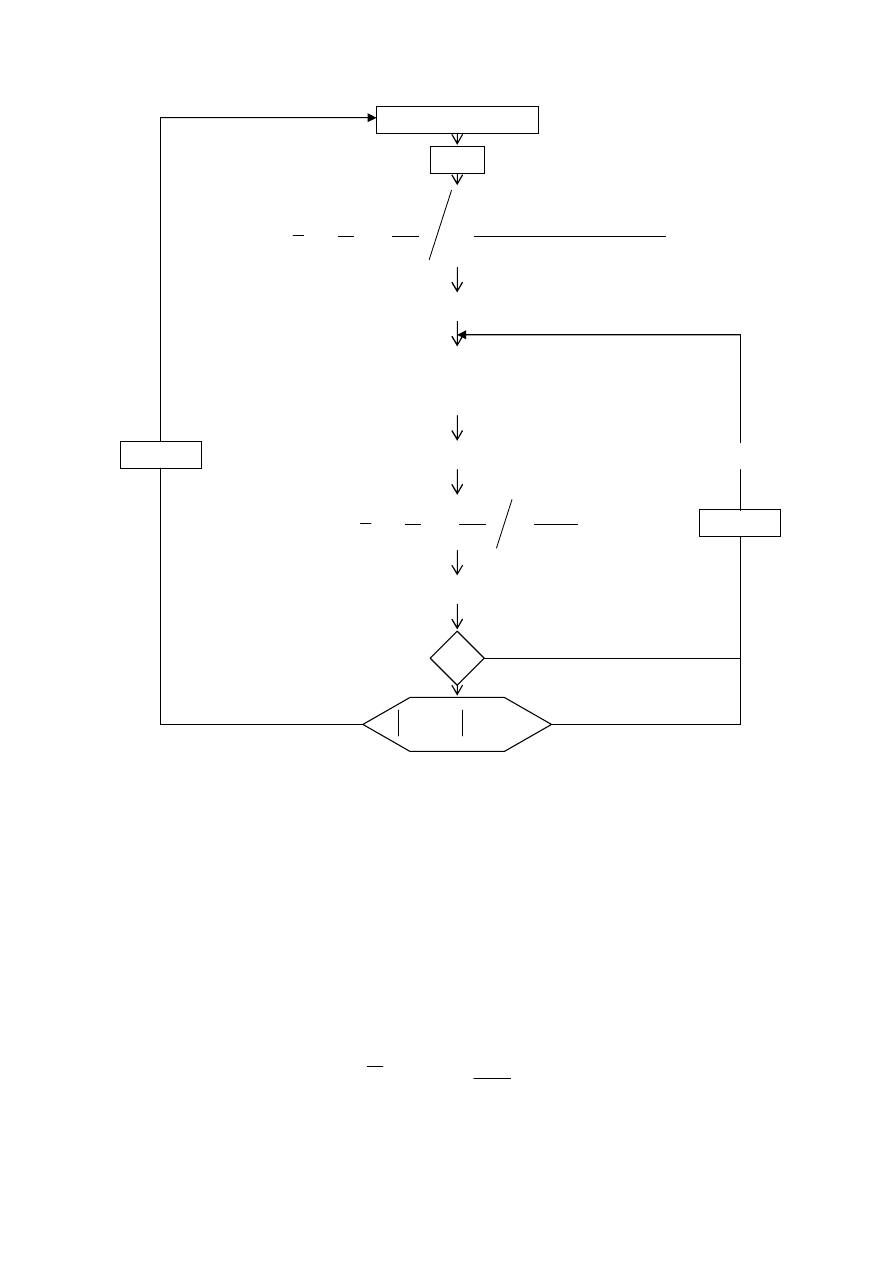
Sposób rozwiązania układu równań (62), (63) dla znanych parametrów

charakteryzujących strefę wodonośną i złoże przedstawiono na rys. 2.4.

23

k
n

p









n

n 2

j

eD

n

j

p

j 0

i

n

i

gi

U

p W

u

t

t

G

p

p

1

1

z

G

G B

z



















 













 



 







Krok czasowy = n

k = 1

















n

n 2

e

j

eD

n

j

n 1

eD

n

n 1

j 0

W

U

p W

u

t

t

p

W

u

t

t

























 

















n

k

e

W

n

n

k

p

e

i

n

i

gi

G

W

p

p

1

1

z

G

G B

z





 













 



 





k
n

p

k

k = k + 1

k

k 1

n

n

p

p





k

k 1

n

n

p

p

TOL







n = n + 1

k = 1

+

–

gdzie: k – krok iteracyjny, n – krok czasowy, TOL – błąd obliczeń

Rys. 2.4. Obliczenie ciśnienia złożowego oraz wielkości dopływu wody

(metoda van Everdingen’a - Hurst’a).[Dake, 1978]

Obliczenia z użyciem metody Fetkovich’a

Model Fetkovich’a stanowią równania:

 równanie bilansu masy dla strefy wodonośnej, pozwalające

wyznaczyć ciśnienie w strefie wodonośnej w kroku czasowym „n-1”.

n 1

e

a

i

n 1

ei

W

p

p

1

W























(64)

 równanie dopływu wody do złoża w kroku czasowym „n”.

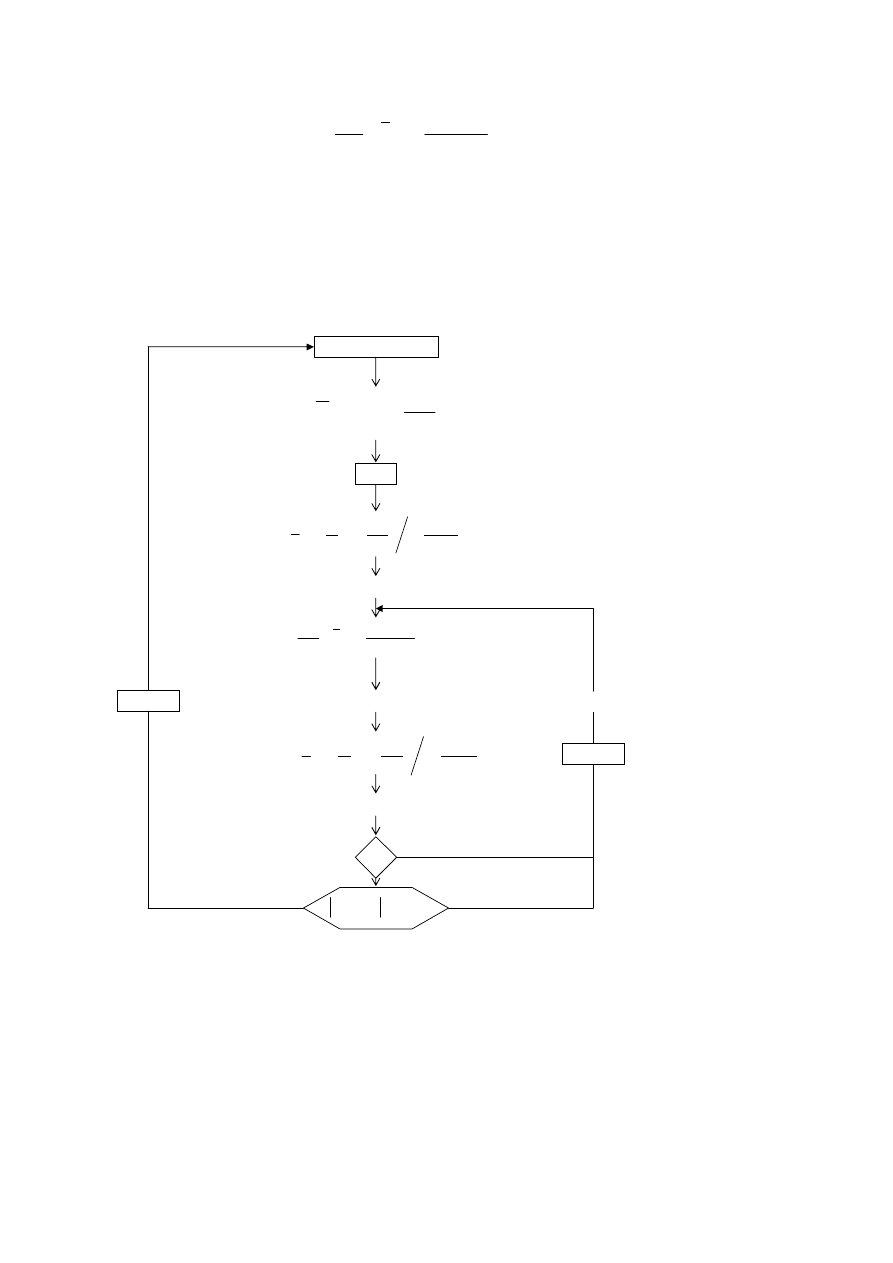
24





i

n

ei

n

n-1

k

J p Δt /W

k

ei

n 1

n

e

a

i

W

p

p

ΔW

p

1 e

p

2

  



























(65)

oraz całkowity dopływ wody

n

n

n 1

k

k

e

ej

e

j 0

W

W

W









 



(66)

Algorytm obliczania ciśnienia złożowego oraz dopływu wody dla

zdefiniowanej strefy wodonośnej pokazano na rys. 2.5.

k
n

p

k
n

p

n

n

k

k

p

e

i

n

i

gi

G

W

p

p

1

1

z

G

G B

z





 













 



 





k

k 1

n

n

p

p









i

n

ei

n

n-1

k

J p Δt /W

k

ei

n 1

n

e

a

i

W

p

p

ΔW

p

1 e

p

2

  



























k

k

k 1

n

n

p

p

TOL







k = 1

–

n

n 1

k

p

e

i

n

i

gi

G

W

p

p

1

1

z

G

G B

z





































Krok czasowy = n

k = 1

n

n 1

n

k

k

e

e

e

W

W

W





 

k = k + 1

n = n + 1

n 1

e

a

i

n 1

ei

W

p

p

1

W























+

Rys. 2.5. Obliczenie ciśnienia złożowego oraz

wielkości dopływu wody (metoda Fetkovich’a) [Dake, 1978]

25

Kalibracja modelu bilansowego – wyznaczanie parametrów strefy

wodonośnej.

Omówione

metody

rozwiązywania

bilansu

masowego

z

uwzględnieniem dopływu wody do złoża wymagają wcześniejszego

zdefiniowania parametrów charakteryzujących strefę wodonośną jak

również początkowych zasobów gazu w złożu. W praktyce parametry te

nie są znane i muszą być wyznaczone w oparciu o dane pomiarowe z

przebiegu eksploatacji tj. wydobycia płynów złożowych, pomiary ciśnień

złożowych jak też parametry PVT płynów złożowych. Jest to tzw.

rozwiązanie problemu odwrotnego polegające na dopasowaniu modelu

bilansowego do zmierzonych ciśnień złożowych (tzw. kalibracja modelu).

Dopasowywanymi parametrami są zasoby początkowe gazu w złożu „G”

oraz w zależności od przyjętej metody dopływu wody:

 dla metody van Everdingen’a – Hurst’a

 stała aquifera - U,

 promień zredukowany - r

eD

,

 paramter – u, opisany zależnością wynikającą z definicji

bezwymiarowego czasu t

D

 dla metody Fetkovich’a

 indeks wydajności aquifera - J,

 maksymalny dopływ wody ze strefy wodonośnej – W

ei

Kryterium dopasowania jest zbieżność średnich ciśnień złożowych

obliczonych i zmierzonych.

Poprawność kalibracji modelu bilansowego można zweryfikować

metodą Havlen’a – Odeh’a. Metoda ta pozwala na właściwy dobór

parametrów opisujących strefę wodonośną, a tym samym poprawne

oszacowanie ilości dopływającej wody zgodnie z równaniem (4.12). Jak

wynika z charteru równania (412) przy prawidłowo wyznaczonych

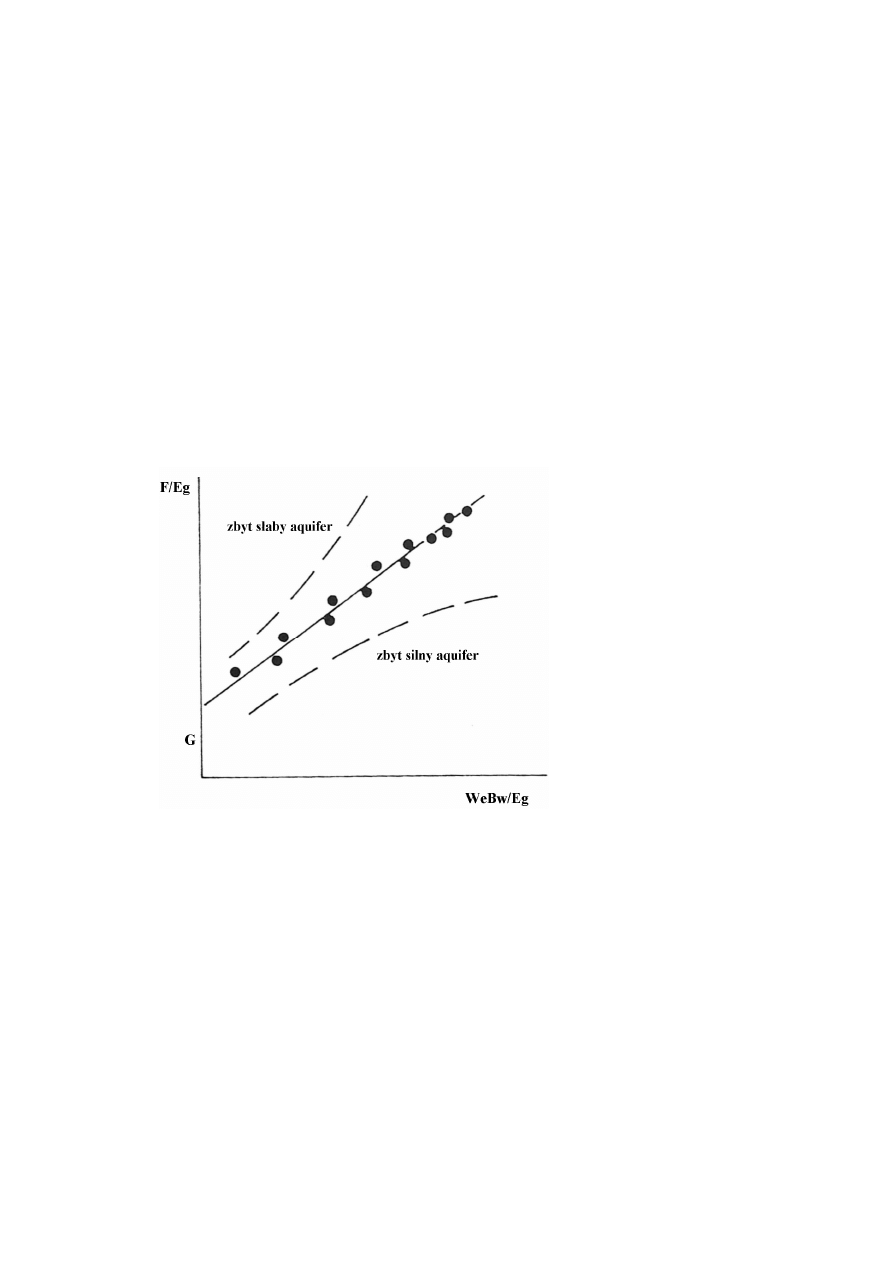
26

parametrach strefy wodonośnej punkty pomiarowe w układzie F/E

g

vs

W

e

B

w

/E

g

opisywane są zależnością liniową o nachyleniu 1, wówczas rzędna

początkowa określa wielkość zasobów początkowych, co pokazano na rys.

2.6. Alternatywnie jeśli punkty na wykresie w układzie F/E

g

vs W

e

B

w

/E

g

układają się nieliniowo wówczas świadczy to o błędnym doborze

parametrów strefy wodonośnej (rys. 4.6). Odchylanie się punktów do góry

ma miejsce dla zbyt słabej aktywności strefy wodonośnej (zbyt mały

dopływ wody), zaś gdy punkty układają się wzdłuż krzywej odchylającej

się ku dołowi wówczas aktywność strefy wodonośnej jest zbyt duża (za

duży dopływ wody do złoża).

Rys. 2.6. Wykres poprawnego dopasowania aktywności strefy wodonośnej

(metoda Havlena - Odeh), [Dake, 2000].

27

3. Analiza stożków i języków wodnych

Odwierty gazowe udostępniają strefę gazową złoża oddzieloną od

strefy zawodnionej, która może to być jako woda podścielająca lub woda

okalająca.

Z chwilą gdy odwiert rozpoczyna eksploatację, wokół niego

wytwarza się strefa obniżonego ciśnienia dzięki czemu następuje dopływ

płynów złożowych do odwiertu. Zaburzenie ciśnienia może osiągnąć strefę

zawodnioną złoża i powodować podciąganie wody w kierunku odwiertu.

Jest to zjawisko powstawania języka lub stożka wodnego.

Tworzenie się stożków wodnych ma duże znaczenie dla eksploatacji gazu

ze złoża. Są one głównym powodem wzrostu spadku ciśnienia w odwiercie

koniecznego do wyniesienia cięższej mieszaniny gazowo-wodnej. W

najgorszym przypadku woda dopływająca do odwiertu może nie być

wyeksploatowana wraz z gazem. Wówczas akumuluje się ona na dnie

odwiertu, zatrzymując dopływ gazu do odwiertu a co za tym idzie,

prowadzi do wyłączenia odwiertu z eksploatacji.

Prowadzone w referacie rozważania nad tworzeniem się stożków

wodnych, będą dokonane przy pewnych uproszczeniach tj: zakłada się

przepływ płynów w złożu z ostrą granicą między gazem a wodą. Oznacza

to, że siły kapilarne są zaniedbywalne i że wypieranie gazu przez wodę

jest tłokowe. Tłokowe wypieranie gazu przez wodę jest rozsądnym

przypuszczeniem ze względu na znacznie wyższą gęstość i lepkość wody

niż gazu.

3.1.

Wydatek krytyczny gazu wg Dupit’a.

Tworzenie się stożka wodnego można rozważać jako zależność

między siłami lepkości i ciężkości. Siły lepkości mają tendencje do

podnoszenia wody w kierunku odwiertu i są proporcjonalne do wydatku.

Siły grawitacyjne z kolei przeciwdziałają podnoszeniu się wody ze względu

na jej ciężar. Są one proporcjonalne do różnicy gęstości między wodą i

gazem. Dla określonego wydatku siły lepkości równoważą siły ciężkości.

28

Wydatek ten jest właśnie wydatkiem krytycznym, powyżej którego może

następować dopływ wody do odwiertu. Jest to zatem maksymalny

wydatek przy którym eksploatowany jest gaz bez wody.

Rozpatrujemy przepływ radialny wokół odwiertu całkowicie perforowanego

z występującą wodą podścielającą eksploatującego gaz z wydatkiem

krytycznym.

Zakładamy przepływ ustalony w złożu, jednorodność złoża, pomijając siły

kapilarne oraz zakładając stałą gęstość i lepkość płynów.

Siły kapilarne mogą być pominięte w warstwie o odpowiednio dużej

miąższości i przepuszczalności, gdzie przejściowa strefa występowania sił

kapilarnych pomiędzy gazem i wodą jest mała w porównaniu z grubością

strefy gazonośnej. Założenie stałości gęstości i lepkości gazu jest słuszne

tak długo jak spadek ciśnienia w strefie przyodwiertowej jest mały w

odniesieniu do średniego ciśnienia złożowego, co można zapisać

następująco:

1









p

h

g

ge



(67)

gdzie:  – różnica gęstości wody i gazu

h

ge

– miąższość strefy gazonośnej,

p – średnie ciśnienie złożowe

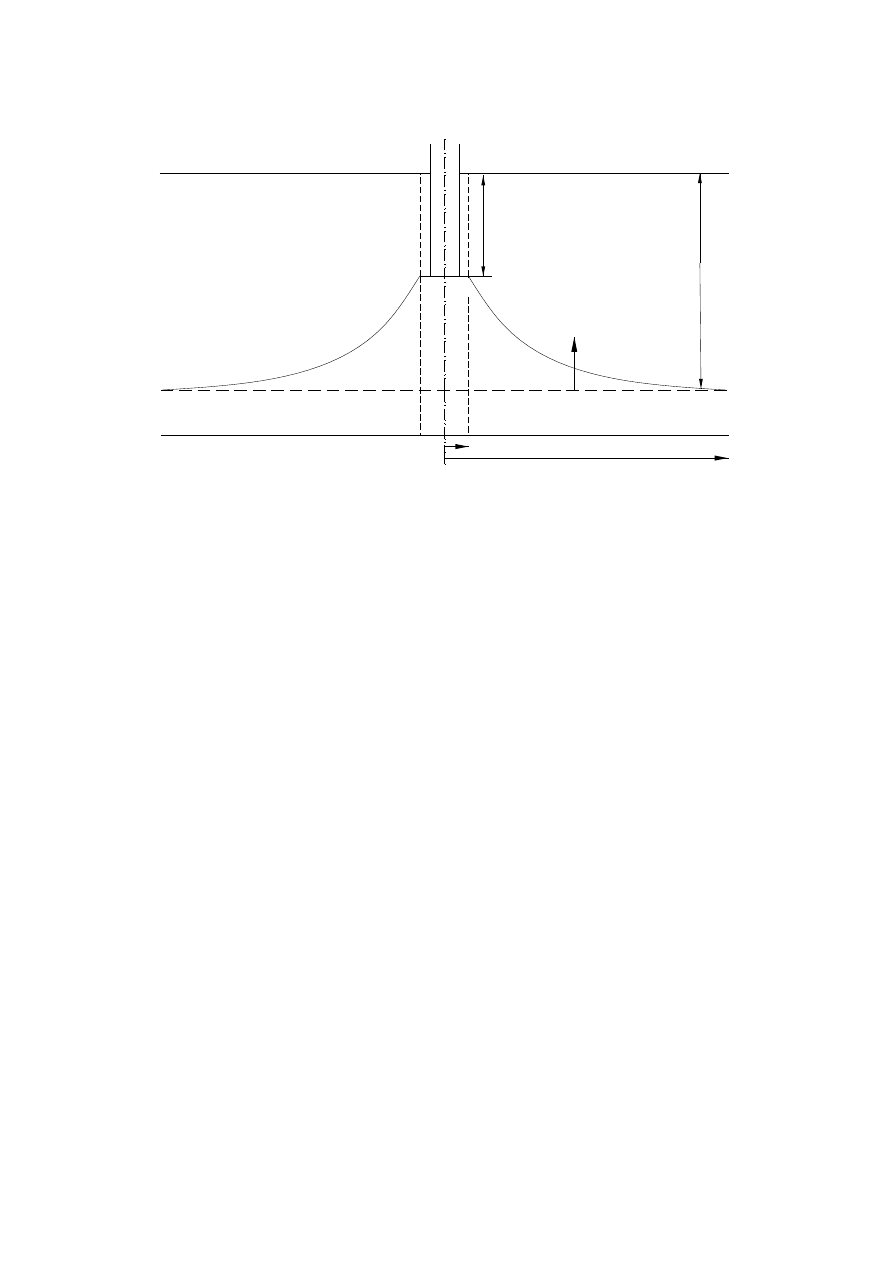
Maksymalny spadek ciśnienia przy którym stożek wodny sięga dna

odwiertu, lecz woda nie jest jeszcze eksploatowana (rys.3.1) stanowi

różnicę ciśnienia hydrostatycznego w strefie wodonośnej do miąższości

strefy gazonośnej.

Zakładając filtrację płynu o stałej gęstości wg prawa Darcy’ego możemy

napisać:









grad

k

u





(68)

gdzie:

u



– wektor prędkości filtracji,

k – przepuszczalność,

 – lepkość dynamiczna,

 – potencjał przepływu definiowany jako:

z

g

p













29

z

Gaz

Woda

A

B

C

D

h

h

gw

ge

r

e

r

w

Rys.3.1. Kształt stożka wodnego dla krytycznego wydatku Dupit’a

Przy założeniu stałej gęstości płynu równanie ciągłości przyjmie postać:

0



u

div



(69)

Z równań (68) i (69) przy założeniu stałej lepkości płynu otrzymujemy

potencjał przepływu:

0





grad

div

(70)

Jeśli eksploatacja gazu odbywa się z wydatkiem krytycznym, wówczas

ciśnienie w strefie wodonośnej jest ciśnieniem hydrostatycznym, zatem

potencjał przepływu dla wody 

w

możemy wyrazić:

z

g

p

w

w

w













(71)

Pomijając siły kapilarne możemy napisać, że ciśnienia po obu stronach

konturu woda-gaz muszą być sobie równe zatem:

z

g

z

p

z

p

w

w

i

w

i

g















)

(

)

(

(72)

gdzie: z

i

– położenie kontaktu gaz-woda

Potencjał przepływu dla gazu podobnie jak dla wody wyraża się poprzez:

i

g

i

g

i

g

z

g

z

p

z













)

(

)

(

(73)

Podstawiając do równania (73) zależność (72) otrzymamy:

i

w

i

g

i

w

w

i

g

z

g

z

g

z

g

z





































)

(

(74)

30

Dla odwiertu i zewnętrznej strefy złoża zakładamy, że gaz i woda znajdują

się w równowadze hydrostatycznej.

Dla gazu potencjał przepływu na ściance odwiertu dany jest

zależnościami:

dla

w

r

r 

,

gw

ge

i

h

h

z





)

(

gw

ge

w

g

h

h

g



















(75)

gdzie: r

w

– promień odwiertu,

h

ge

– miąższość strefy gazowej na granicy zasięgu odwiertu,

h

gw

– miąższość strefy gazowej na ściance odwiertu.

Na granicy zasięgu odwiertu mamy:

dla

e

r

r 

0



i

z

w

g







(76)

gdzie: r

e

– promień strefy zasięgu odwiertu.

Dla obliczenia wydatku krytycznego wg Dupit’a stosujemy twierdzenie

Ostrogradzkiego-Greena [ ] pozwalające wyznaczyć objętość zajmowaną

przez gaz. Twierdzenie to wyrażone jest zależnością:





dS

n

W

U

n

U

W

dV

W

U

U

W

V

S







































(77)

gdzie: S – powierzchnia ograniczająca objętość V,

n



– wektor jednostkowy normalny do powierzchni S.

W, U - zadane funkcje

W naszym przypadku za funkcje W i U podstawiamy odpowiednio:

















w

r

r

W

ln

(78)

g

U





(79)

Zakładamy, że powstały stożek nie zmienia swojej wysokości, zatem i

objętość gazu V pozostaje stała. Przy takim założeniu lewa strona

równania (77) będzie równa zeru.

Wykorzystując powyższe stwierdzenie i podstawiając (78) i (79) do

równania (77) otrzymamy:

















































S

w

g

g

w

dS

r

r

n

n

r

r

0

ln

ln













(80)

31

W rozpatrywanym modelu (rys.3.1.) powierzchnia S składa się z

elementów wyznaczonych przez powierzchnie obrotowe: BA, BC, CD i DA .

Dla powierzchni BA możemy napisać:































w

e

w

r

r

r

r

ln

ln

(81)

e

ge

rg

g

g

kr

g

r

h

kk

B

q

n









2







(82)

gdzie: q

kr

– krytyczny wydatek gazu w warunkach normalnych,



g

– lepkość gazu,

B

g

– współczynnik objętościowy gazu,

k

rg

– przepuszczalność względna dla gazu w strefie gazowej

nasyconej wodą związaną.

e

w

w

r

r

r

r

r

r

n

1

ln

ln











































(83)

dz

r

dS

e



2



(84)

Dla powierzchni BC (rys.3.2.):

Ponieważ potencjały obu płynów po obu stronach powierzchni rozdziału

woda-gaz są sobie równe więc:

0





n

g







(85)

r

r

r

grad

n

r

r

n

w

w







sin

ln

ln



















































(86)







sin

2

2

dz

r

rdl

dS





(87)

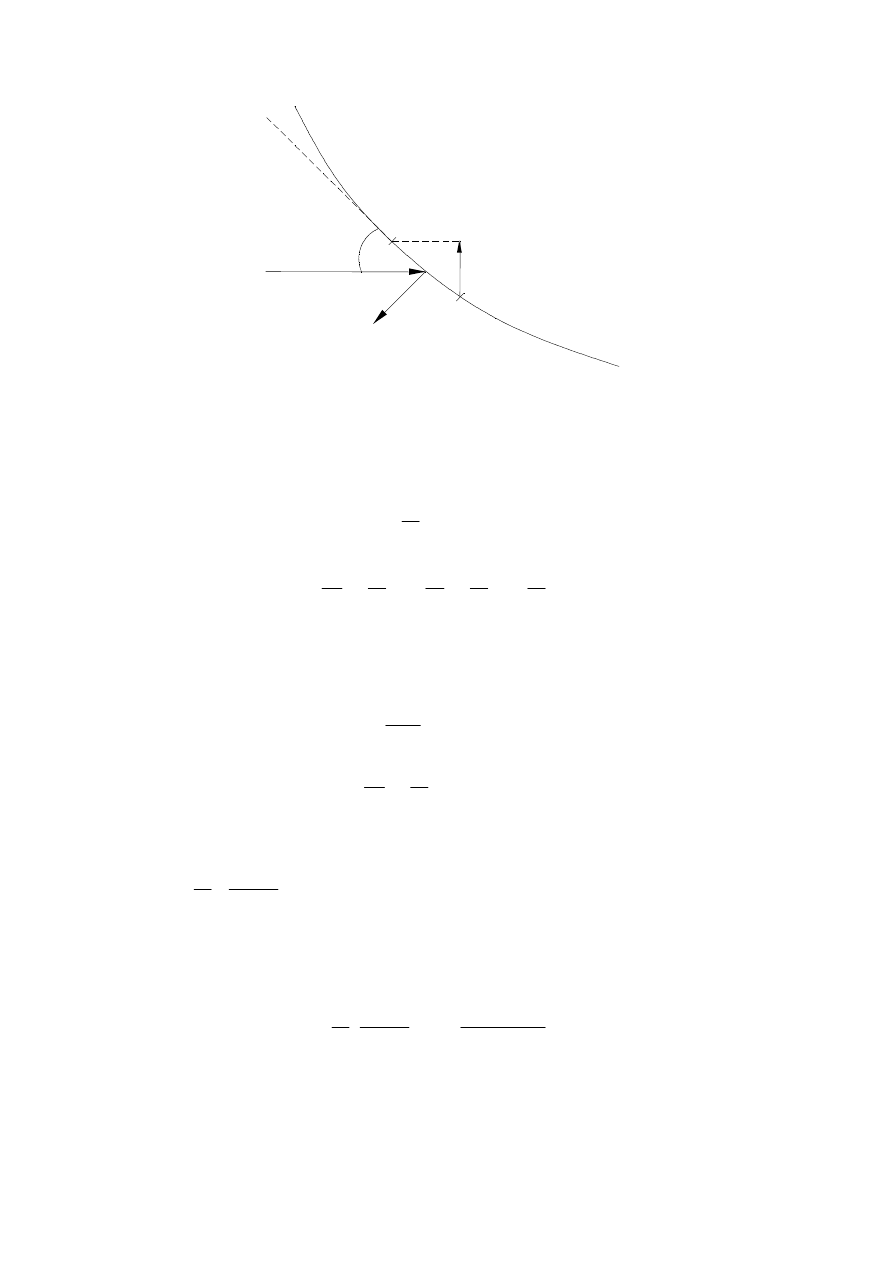
32

dz

dl

n



powierzchnia rozdziału

gaz-woda

Rys.3.2. Element powierzchni rozdziału gaz-woda.

Dla powierzchni CD:

0

ln



w

r

r

(88)

w

w

w

r

r

r

r

r

r

n

1

ln

ln















































(89)

dz

r

dS

w



2



(90)

Dla powierzchni DA:

0





n

g







(91)

0

ln

















w

r

r

n







(92)

Wstawiając zależności od (83) do (92) do równania (82) otrzymamy:









































ge

gw

ge

ge

gw

ge

h

h

h

h

h

h

w

g

i

g

e

g

rg

g

g

w

e

kr

dz

r

dz

z

dz

r

kk

r

r

q

0

0

)

(

)

(

)

(

2

ln



 B

(93)

Podstawiając warunki graniczne oraz wyrażenia na potencjał (równania

(75) - (79)) oraz całkując otrzymamy:





2

2

ln

2

2

gw

ge

rg

g

g

w

e

kr

h

h

g

kk

B

r

r

q





























(94)

po przekształceniu:

33





2

2

ln

gw

ge

w

e

g

g

rg

kr

h

h

r

r

B

gkk

q



























(95)

W powyższym wyprowadzeniu założono stałą przepuszczalność we

wszystkich kierunkach. W przypadku ośrodka anizotropowego wprowadza

się poprawkę mnożąc prawą stronę równania (29) przez

h

v

k

k /

oraz

wstawiając w miejsce „k” przepuszczalność poziomą „k

h

”. Zatem równanie

(95) przyjmie następującą postać:





h

v

gw

ge

w

e

g

g

rg

h

kr

k

k

h

h

r

r

B

k

gk

q























2

2

ln







(96)

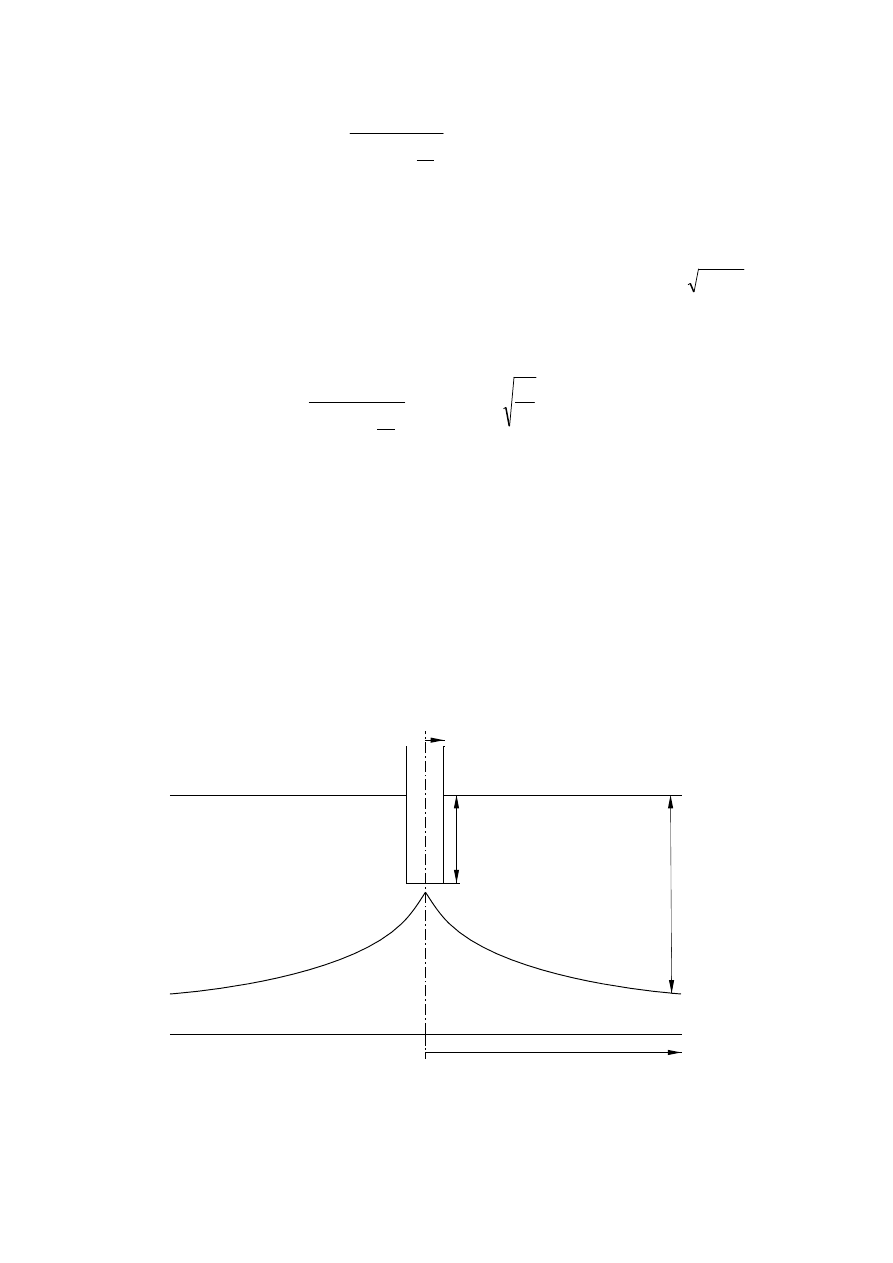
3.2. Wydatek krytyczny wg Schols’a.

Wydatek krytyczny określony przez Dupit’a odnosi się do całkowicie

perforowanych odwiertów, co jest nietypowe dla złóż gazowych z wodą

podścielającą. Aby zapobiec szybkiemu przebiciu się wody do odwiertu

zakańcza się je tak aby penetrowały tylko górną części złoża bądź

wykonuje się perforację odwiertu w jak największej odległości od poziomu

wody (rys.3).

Gas

Woda

b

r

r

e

w

h

ge

Rys. 3.3. Kształt stożka wodnego dla krytycznego wydatku Schols’a.

34

Empiryczna zależność na obliczanie wydatku krytycznego zaproponowana

przez Schols’a ma postać:





14

,

0

2

2

ln

432

,

0





































































e

ge

ge

w

e

g

g

rg

kr

r

h

b

h

r

r

B

gkk

q







(97)

Jak widać równanie na wydatek krytyczny wprowadzone przez Schols’a

jest podobne do równania Dupit’a. Jeśli zinterpretujemy poziom perforacji

rur w równaniu Dupit’a jako głębokość penetracji w równaniu Schols’a

wówczas stosunek obu wydatków będzie wynosił:

14

,

0

ln

432

,

0

1

)

(

)

(













































e

ge

w

e

kr

kr

r

h

r

r

Dupit

q

Schols

q



(98)

Z równania (98) można wywnioskować, iż wydatek krytyczny Dupit’a

jest mniejszy niż wydatek krytyczny Schols’a, jeśli r

e

/r

w

> 500 i h

ge

/r

e

>0,012 co pokrywa się z praktyką. Odwiert częściowo penetrujący może

eksploatować gaz wolny od wody z wyższym wydatkiem niż całkowicie

perforowany odwiert jak to jest w przypadku Dupit’a. Można to

wytłumaczyć przez fakt, że w przypadku Dupit’a stożek wodny sięga

spodu rur wydobywczych, stąd strefa wpływu stożka jest większa i w

konsekwencji spadek ciśnienia przy takim przepływie jest także większy.

Tak więc dla danego spadku ciśnienia wydatek gazu jest mniejszy.

W przypadku Schols’a wierzchołek stożka znajduje się w pewnej odległości

od spodu rur wydobywczych..

Zależność Schols’a można rozszerzyć uwzględniając anizotropowość

ośrodka. Wówczas należy wprowadzić poprawkę do równania (97):





07

,

0

14

,

0

2

2

ln

432

,

0





















































































v

h

e

ge

ge

w

e

g

g

rg

h

kr

k

k

r

h

b

h

r

r

B

k

gk

q







(99)

Jak widać z zależności (99) wydatek krytyczny dla danej przepuszczalności

poziomej wzrasta przy spadku przepuszczalności pionowej, jednakże

zależność ta jest słaba.

35

Stożki wodne i gazowe w odwiertach poziomych.

W przypadku odwiertów pionowych strefa zaburzenia ciśnienia jest

największa w pobliżu odwiertu. Zatem wokół odwiertu pionowego tworzy

się strefa wysokiej depresji. Dla odwiertów poziomych spadek ciśnienia

rozkłada się równomiernie wokół odwiertu, zaś w jego bezpośrednim

sąsiedztwie istnieje strefa wyższego spadku ciśnienia. Jednakże wielkość

tego spadku ciśnienia jest mniejsza w stosunku do tej jaka występuje

wokół odwiertu pionowego.

W związku z mniejszym spadkiem ciśnienia wokół odwiertów

poziomych uzyskuje się wyższe wydatki bez niebezpieczeństwa tworzenia

się stożków.

Wydatek krytyczny wg metody Efors’a.







































3

2

2

10

444

,

27

2

2

2

7

h

y

y

B

L

h

k

q

e

e

g

g

h

g





(100)

gdzie: q

g

– wydatek krytyczny gazu [tys. ft/day],

2y

e

– odległość miedzy odwiertami [ft],

h – odległość odcinka poziomego odwiertu od kontaktu gaz-woda

[ft],

k

h

– przepuszczalność pozioma [mD],

 – różnica gęstości [gm/cc],

L – długość odcinka poziomego odwiertu [ft],



g

– lepkość gazu [cP],

B

g

– współczynnik objętościowy gazu.

Wydatek krytyczny wg metody Giger’a i Karcher’a.

L

y

h

y

h

k

q

e

e

g

g

h

g















































 

























2

2

7

2

6

1

1

2

10

444

,

27





B

(101)

gdzie: oznaczenia podobnie jak we wzorze (34).

36

Przykład

Dla porównania krytycznej wydajności odwiertu poziomego w stosunku do

pionowego ze względu na niebezpieczeństwo powstania stożka wodnego

przyjęto następujące dane:

średnie ciśnienie złożowep = 6 MPa,

temperatura złoża

T = 320 K,

przepuszczalność pozioma

k

h

= 30 mD,

przepuszczalność pionowa

k

v

=10 mD,

gęstość gazu



g

= 47 kg/m

3

,

gęstość wody



w

=1020 kg/m

3

,

lepkość gazu



g

= 0.0144 cP,

współczynnik objętościowy gazu

B

g

= 0.019,

promień strefy zasięgu odwiertu

r

e

=200 m.,

promień odwiertu

r

w

=0.074 m.,

przepuszczalność względna gazu

k

rg

= 0.7,

miąższość strefy gazowej na granicy zasięgu odwiertu h

ge

= 30 m.,

miąższość strefy gazowej na ściance odwiertu

h

gw

= 5 m.,

głębokość perforacji odwiertu mierzona od stropu złożab = 5 m.,

odległość miedzy odwiertami

2y

e

= 1640.4 [ft],

długość odcinka poziomego odwiertu

L = 1312 [ft],

odległość odcinka poziomego odwiertu od kontaktu gaz-woda h = 82

[ft],

Wydatek krytyczny gazu dla odwiertu pionowego wg Dupit’a.





s

m

q

kr

3

15

15

2

2

3

15

147

.

0

10

30

10

10

5

30

074

.

0

200

ln

019

.

0

10

0144

.

0

7

.

0

10

30

807

.

9

974



































































d

m

q

kr

3

5

.

12722

Wydatek krytyczny gazu dla odwiertu pionowego wg Schols’a.

37





07

.

0

14

.

0

2

2

3

15

10

30

200

30

5

30

074

.

0

200

ln

432

.

0

019

.

0

10

0144

.

0

7

.

0

10

30

807

.

9

974





























































































kr

q

s

m

q

kr

3

447

















d

ft

tys

q

kr

3

.

1365

Wydatek krytyczny gazu dla odwiertu poziomego wg Efors’a.



















































d

ft

tys

q

kr

3

2

2

2

7

.

5

.

779

3

1312

4

.

1640

4

.

1640

019

.

0

014

.

0

1312

82

974

.

0

30

10

444

.

27















s

m

q

kr

3

262

.

0

Wydatek krytyczny gazu dla odwiertu poziomego wg Giger’a i Karcher’a.























































































d

ft

tys

q

kr

3

2

2

7

.

1600

1312

4

.

1640

82

6

1

1

4

.

1640

82

974

.

0

019

.

0

0144

.

0

30

10

444

.

27















s

m

q

kr

3

524

.

0

Analiza wyników

1.

Jednym z istotnych kryteriów określenia dopuszczalnego wydatku w

odwiercie jest warunek niedopuszczenia do powstania stożka wodnego.

Przedstawiona

metodyka

obliczenia

wydatków

krytycznych

dla

odwiertów

poziomych

i pionowych

bierze

pod

uwagę

efekty

grawitacyjne związane z przemieszczaniem się płynów złożowych.

2.

Wykonane obliczenia dopuszczalnych wydatków ze względu na

możliwość powstania stożka wodnego wskazują na zalety odwiertu

poziomego

w stosunku

do

odwiertu

pionowego.

Wykazano

w

obliczeniach szacunkowych, że dopuszczalna wydajność odwiertu

poziomego jest przeszło dwukrotnie większa niż dla odwiertu

pionowego. Wskazuje to na celowość rozwiercania złóż odwiertami

poziomymi uzyskując z nich znacznie większe wydajności przy tych

samych depresjach ciśnienia. Przy obecności odwiertu poziomego

38

niekorzystne przemieszczanie się wód odbywa się na większej

przestrzeni niż w przypadku odwiertu pionowego, co daje większą

pewność, że nie wystąpią niekorzystne dla procesu eksploatacji lokalne

odcięcia pewnych stref gazu przez wdzierającą się wodę. W świetle tego

wyjaśnienia widać, że w przypadku odwiertów poziomych występuje

konieczność przemieszczenia się większej ilości wody w kierunku

odwiertu, co jest przeszkodą w jej gwałtownym ruchu, mogącym

doprowadzić do rozmycia się konturu woda–gaz.

3.

W przypadku odwiertu pionowego powstały stożek wodny może być

trudny do likwidacji ze względu na hydrofilność większości skał

złożowych oraz siły kapilarne. W przypadku odwiertu poziomego

powstały stożek rozciąga się liniowo wzdłuż odwiertu tworząc

podniesiony wał wodny, co powinno sprzyjać łatwiejszego jego cofaniu

się jeżeli ustanie przyczyna jego tworzenia.