1.

Skutki działania sił zewnętrznych na ciało. Pojęcie sił wewnętrznych. Naprężenia.
Składowe naprężenia. Równania całkowe równowagi.

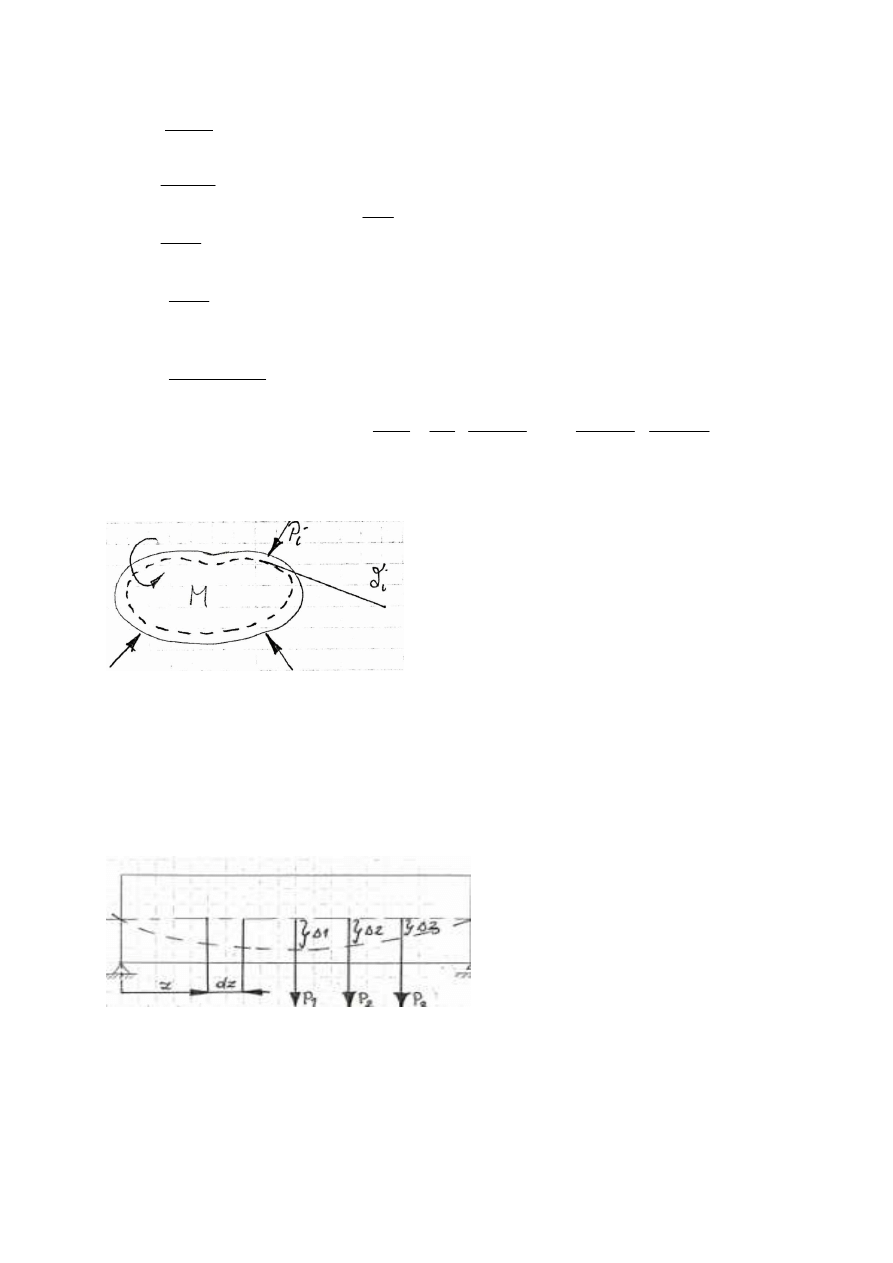
Siły jakie przykładamy do ciała z zewnątrz-zwane siłami zewnętrznymi możemy podzielić na
siły objętościowe (masowe) i siły powierzchniowe (obciążenia). Siły objętościowe (masowe)
są to siły wywołane przyspieszeniami i są związane z masą lub objętością ciała. Siły
powierzchniowe (obciążenia) są przyłożone do powierzchni danego ciała; przyczyną tych sił
jest zwykle oddziaływanie dwu ciał na siebie na zasadzie akcji i reakcji w miejscu ich
bezpośredniego kontaktu.
Skutek działania siły zewnętrznej na ciało będzie polegał na zmianie ruchu ciała bądź jego
odkształcenie przejawiające się zmianą objętości oraz kształtu a więc geometrii oraz zmianą
sił wewnętrznych wzajemnego oddziaływania międzycząsteczkowego.

Pojęcie siły wewnętrznej:
Siłą wewnętrzna nazywamy siłę występującą wewnątrz ciała wywołaną siłą zewnętrzną
działającą na to ciało.

Naprężenie:
Oddziaływanie lokalne (sprowadzone do punktu) w dowolnym punkcie ciała np. A.(x,y,z)
nazywamy naprężeniem. Pod pojęciem naprężenia rozumiemy granicę iloczynu przyrostu sił
wewnętrznych do przyrostu przekroju przy założeniu że przyrost przekroju zmierza do 0

Jednostką naprężenia jest [Pa]

Przez stan naprężenia – lub stan naprężeń - określonym punkcie ciała rozumiemy ogół
naprężeń otrzymanych dla wszystkich możliwych przekrojów przechodzących przez ten
punkt.
Rozróżniamy trzy charakterystyczne rodzaje stanu naprężenia w punkcie: jednoosiowy, płaski
i przestrzenny.
Jednoosiowy (czyli jednowymiarowy) stan naprężenia cechuje to, że dla każdego przekroju

przeprowadzonego przez dany punkt naprężenie

ma stały kierunek.

Płaski (dwuwymiarowy) stan naprężenia cechuje to, że naprężenia

odpowiadające

różnym przekrojom przeprowadzonym przez dany punkt-leżą w jednej płaszczyźnie, którą
nazywamy płaszczyzną stanu naprężenia.
Przestrzenny (trójwymiarowy) stan naprężenia cechuje to, że dla każdego z przekrojów

przeprowadzonych przez dany punkt naprężenia

posiada inny kierunek w przestrzeni.

Składowe stanu naprężenia.
W ogólnym przypadku naprężenie może posiadać dowolny kierunek względem określonej

płaszczyzny przekroju. Rzutujemy wówczas naprężenie

na kierunki osi układu

współrzędnych –x, y, z-którego początek znajduje się w punkcie B, otrzymamy trzy typowe
składowe zwane składowymi stanu naprężenia. Składowe te oznaczamy : składową normalną
symbolem σ a styczną symbolem τ, zaopatrując je odpowiednimi wskaźnikami. Wskaźnik

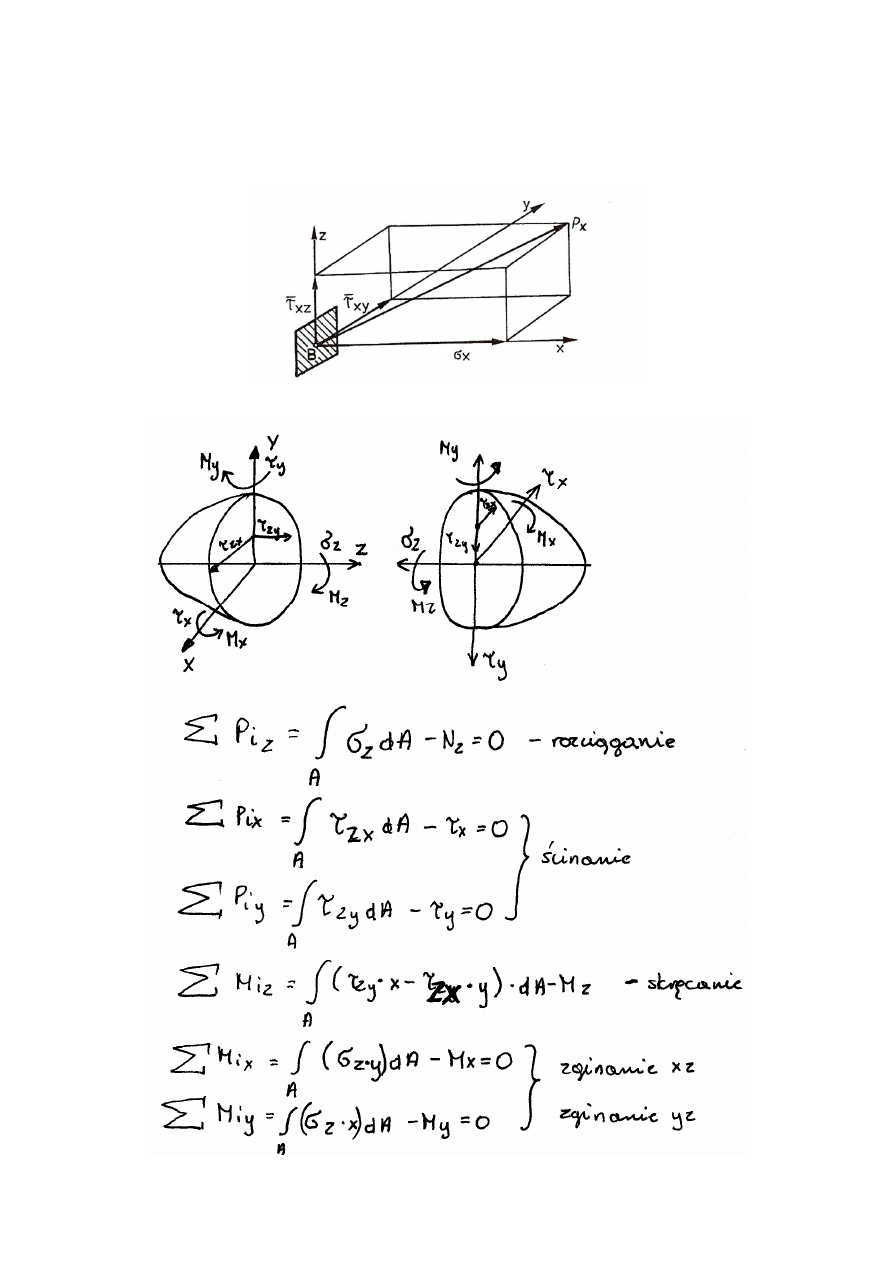
przy σ informuje, że jest to składowa normalna naprężenia, przynależna przekrojowi, którego
normalna zewnętrzna posiada kierunek tej osi. Pierwszy wskaźnik przy τ mówi to samo o
każdej z dwóch składowych stycznych naprężenia, wskaźnik drugi określa kierunek każdej z
tych osi.

Równania całkowe równowagi.

2. Rozciąganie i ściskanie. Naprężenia. Odkształcenia podłużne i poprzeczne. Prawo
Hooka dla jednoosiowego stanu naprężenia. Wykres rozciągania i ściskania.
Naprężenia dopuszczalne. Wymiarowanie przekrojów.

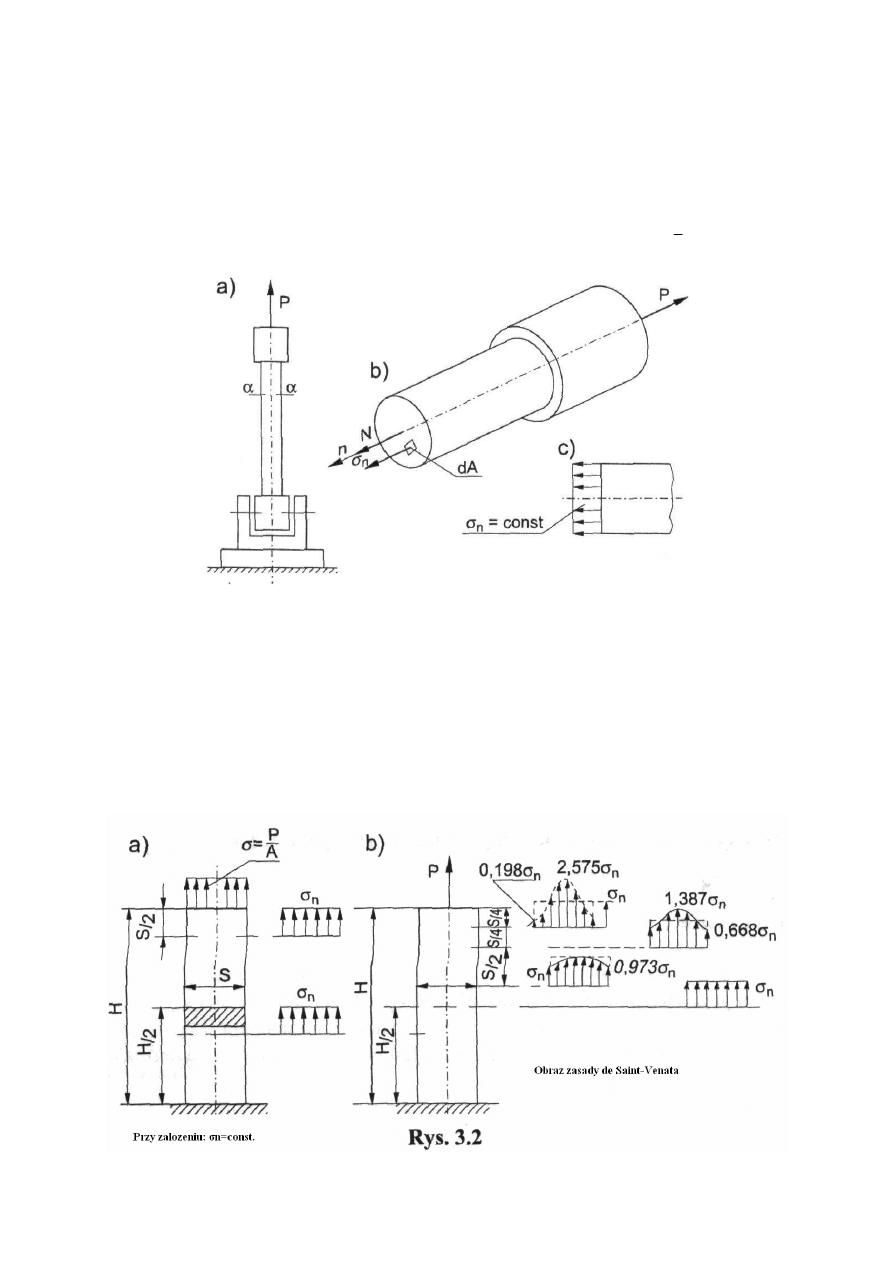
Rozciąganie: Przypadek rozciągania ma miejsce, kiedy siły wewnętrzne w przekroju
poprzecznym pręta zredukowane do środka ciężkości przekroju sprowadzają się do siły

wypadkowej N, działającej wzdłuż osi pręta, zgodnie z wektorem normalnym

n

do przekroju.

Ściskanie: Przy ściskaniu, siła wypadkowa ma zwrot przeciwny do wektora normalnego.

Siłe wewnętrzną N obliczyć można jako sumę elementarnych sił wewnętrznych:

dN=σ

n

dA na powierzchni A.

n

A

N

dA

σ

=

∫

Naprężenia: Przy założeniu jednorodności rozkładu naprężeń (σ

0

=const.), stałość przekroju

A na długości pręta oraz jednorodność materiału pręta, naprężenia można obliczyć jako:
σ

n

=N/A.

Jednak ten warunek zachodzi jedynie w przekroju oddalonym od punktu przyłożenia

siły o więcej niż maksymalny wymiar liniowy przekroju (rys. 3.2).

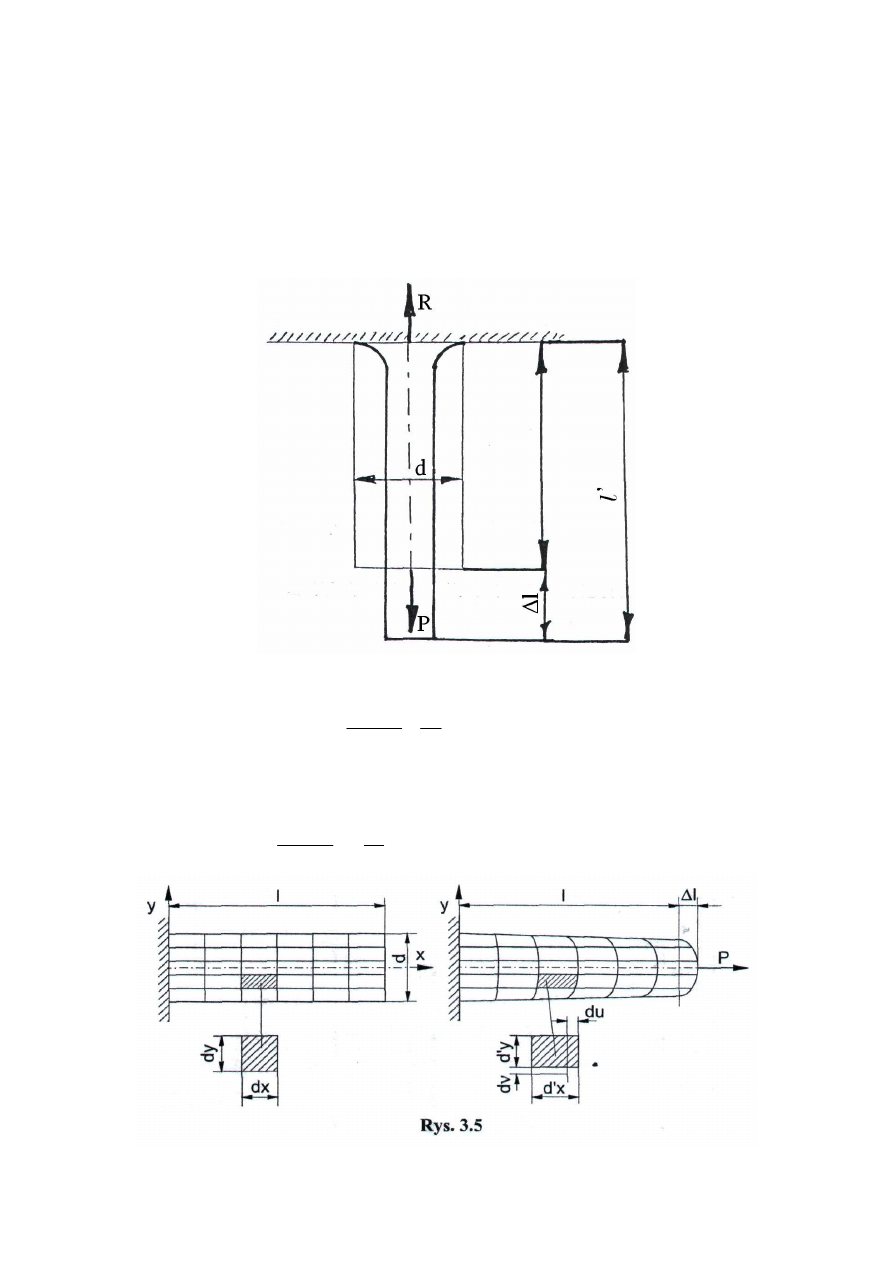
W przypadku obciążenia pręta pryzmatycznego różnymi układami obciążeń statycznie

równoważnych, w pobliżu powierzchni przyłożenia obciążenia rozkłady naprężeń na
przekroju pręta są niejednorodne, natomiast w odległości większej od największego wymiaru
przekroju poprzecznego , wpływ sposobu przyłożenia sił zewnętrznych staje się znikomy i
można go zaniedbać.

Odkształcenie – miara deformacji ciała poddanego siłom zewnętrznym.

Odkształcenia podłużne (względne jednostkowe): związane są ze zmianą długości pręta;

można je określić wzorami:

'

x

dx

dx

du

dx

dx

ε

−

=

=

;

0

l

x

x

l

dx

l

ε

ε

∆ =

= ⋅

∫

, gdzie ∆l to całkowite

wydłużenie pręta oraz ε

x

=const.

∆l = l’- l;

Odkształcenia poprzeczne: związane są ze zmianą szerokości pręta; można je

określić wzorami:

'

y

dy

dy

dv

dy

dy

ε

−

=

= −

;

/ 2

/ 2

d

y

y

d

d

dy

d

ε

ε

−

∆ = −

= − ⋅

∫

,

∆d = d’- d;

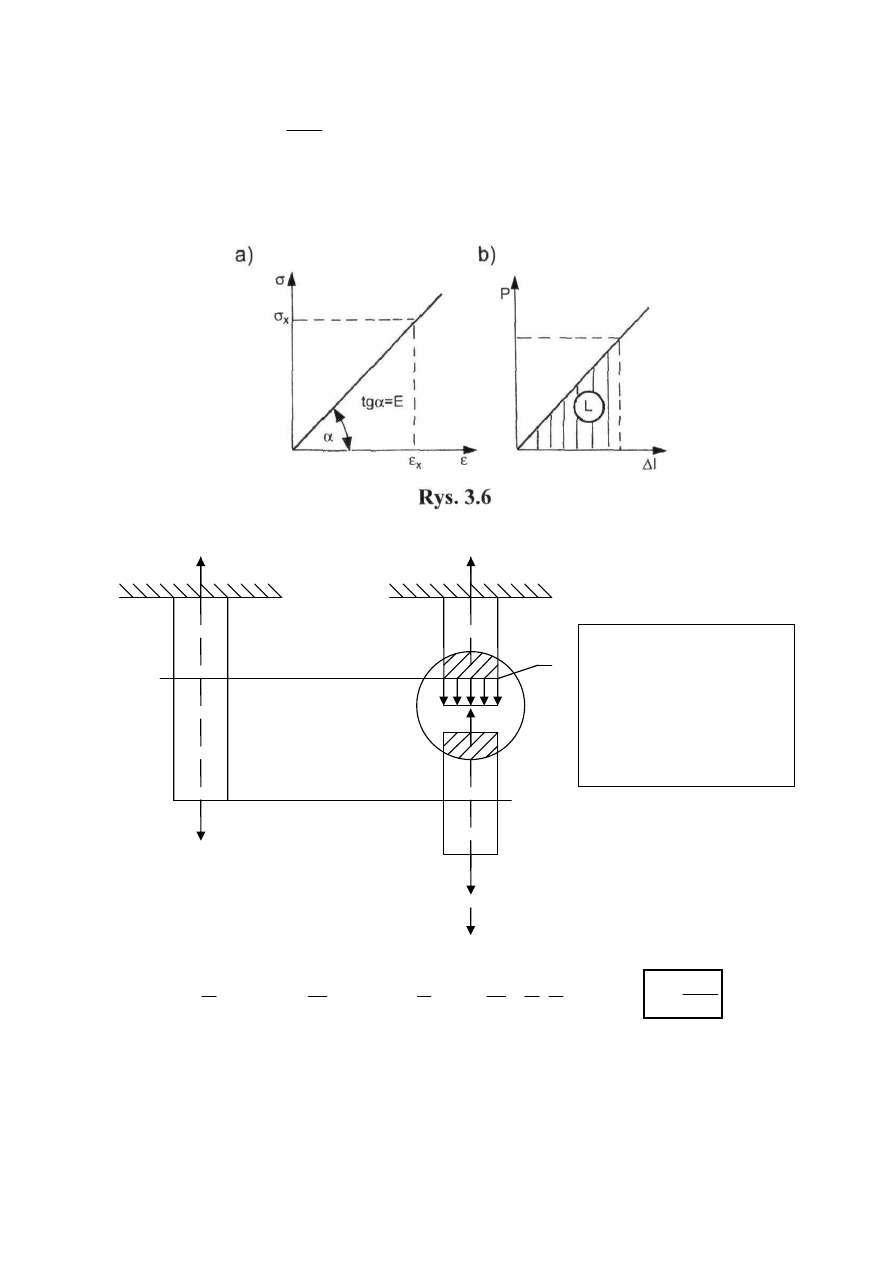
Prawo Hooke'a:

P l

l

E A

⋅

∆ =

⋅

„Ut tensio sie vis” -takie odkształcenie jaka siła.

Dla większości ciał stałych w pewnym zakresie naprężeń istnieje liniowa zależność pomiędzy
naprężeniami i odkształceniami tzn. odkształcenie jest wprost proporcjonalne do
odkształcenia, które je wywołało.
Dla jednorodnych naprężeń normalnych σ

n

wywołanych siłą P, prawdziwy jest wykres:

Wyprowadzenie prawa Hooke’a:

1

z

z

E

ε

σ

=

z

l

l

ε

∆

=

z

P

A

σ

=

1

l

P

l

E A

∆ = ⋅

P l

l

E A

⋅

∆ =

⋅

.

E - moduł sprężystości poprzecznej (moduł younga);
E

st

=2,1*10

5

MPa; E

Al

=0,15*10

5

MPa

EA - iloczyn modułu younga i pola przekroju nazywamy sztywnością na rozciąganie
i ściskanie;

A

R=P

P

P

N

σ

∑Piz=0 ∫σ

z

dA - N=0

σ

z

∫dA=N => σ

z

= N/A

∑Piz=P-N=0

P=N

z

R=P

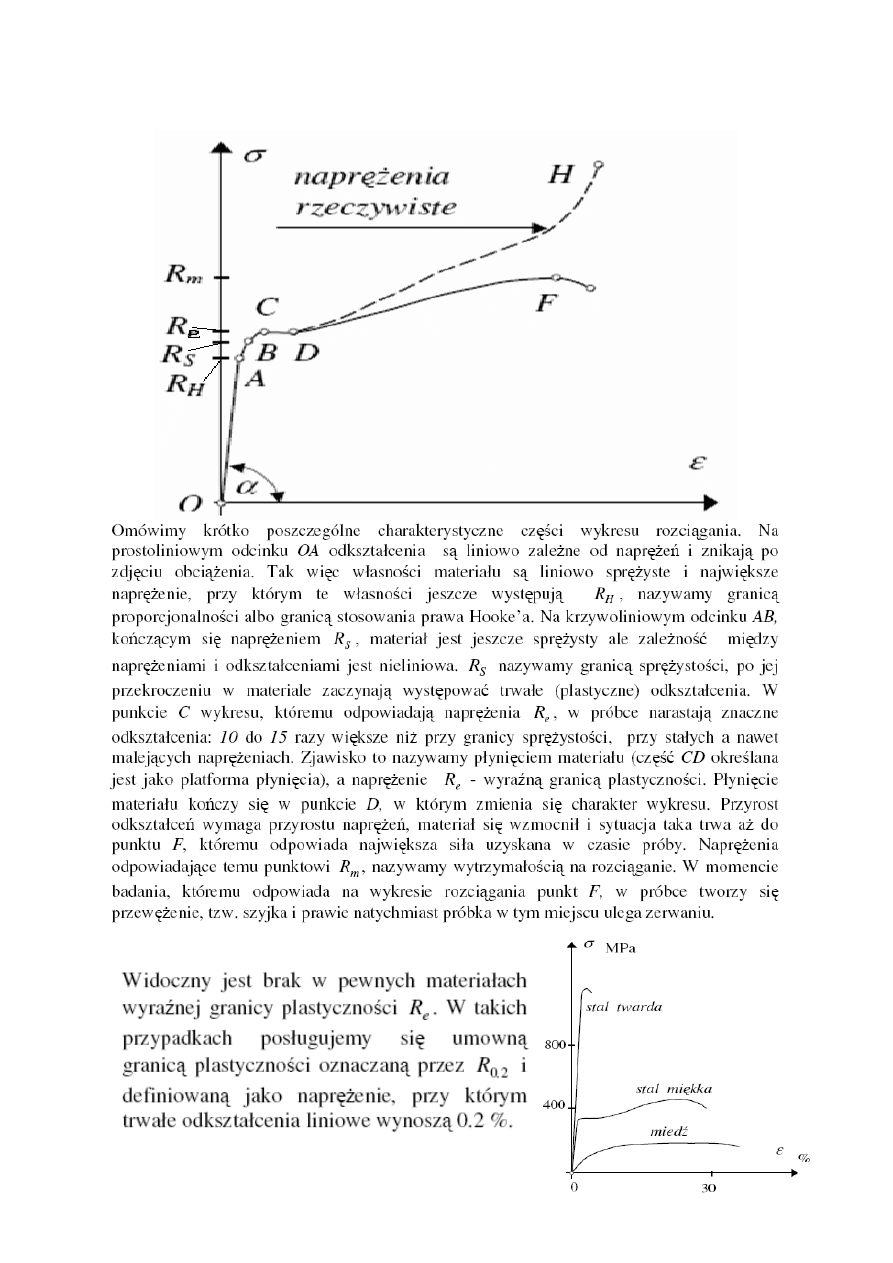
Wykres rozciągania dla stali miękkiej (niskowęglowej, 0,3%C):

Wykres rozciągania innych metali:

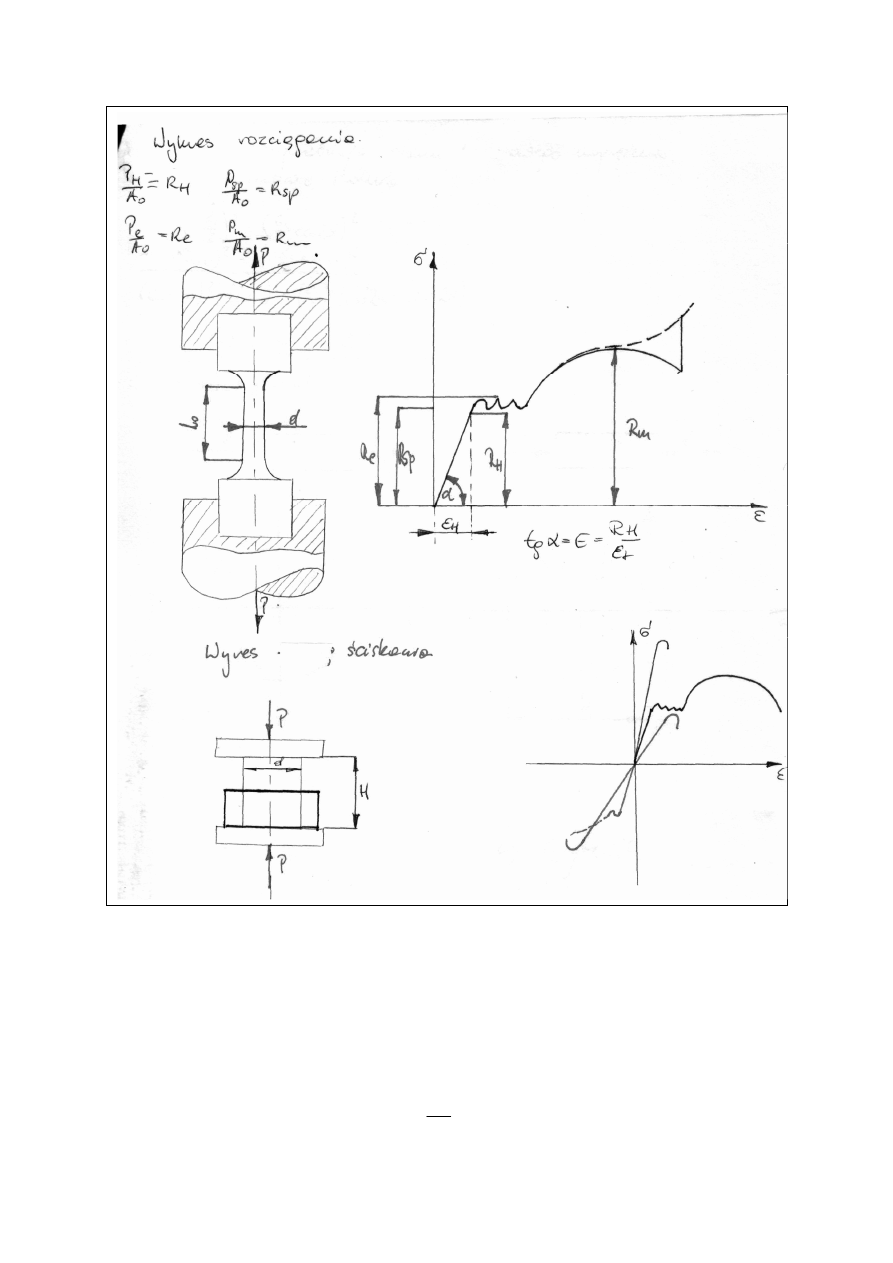
Warunki wytrzymałości kształtowania konstrukcji (wymiarowanie przekrojów):

Aby obliczyć wytrzymałość elementów konstrukcji, tzn. tak zaprojektować wymiary

tego elementu aby spełnić warunki:
-ekonomii; -lekkości
-sztywności; -związany jest z charakterem pracy oraz geometrią konkretnej konstrukcji,
sprawdzać należy w przypadku zadanych dopuszczalnych przemieszczeń ∆l

dop

.

Warunek ten dla pręta pryzmatycznego ściskanego lub rozciąganego zapisać można:

dop

Pl

l

l

EA

∆ =

≤ ∆

Rozciąganie

Ściskanie

-warunek bezpieczeństwa: wyraża postulat: aby naprężenia przekroju projektowanego
elementu były co najwyżej równe naprężeniom dopuszczalnym.

Naprężenia dopuszczalne jest to stosunek naprężenia krytycznego do założonego

współczynnika bezpieczeństwa.
σ≤k

k=K/n

K=R

e

-pojawienie się odkształceń plastycznych.

Pod pojęciem współczynnika bezpieczeństwa przyjmujemy liczbę niemianowaną „n”

wskazującą ile razy naprężenie dop. jest mniejsze od naprężenia krytycznego.

wg A. Bluma: n=1,5-1,7; n=2,3; n=8-10;

e

r

e

R

P

k

A

n

σ

= ≤ =

(lub kr=

m

m

R

n

dla materiałów elasto-kruchych) .

m

r

m

R

P

k

A

n

σ

= ≤ =

c

c

c

R

P

k

A

n

σ

= ≤ =

3 Zasada de ST. Venanta, zjawisko spiętrzania naprężeń, naprężenia wstępne zagadnia statycznie nie
wyznaczalne przy rozciaganiu i sciskaniu
Hipoteza de ST. Venanta (1837):
Miara wytężenia jest największe odkształcenie jednostkowe

Ε

Zgodnie z tą hipoteza wartość największego odkształcenia jednostkowego dla danego złożonego stanu
naprężenia nie może przekroczyc wartości dopuszczalnego odkształcenia jednostkowego. Określonego na
podstawie próby jednoosiowego rozciagania.

[

]

max

1

2

3

1

2

3

1

1

(

)

E

E

E

E

E

V

E

σ

σ σ

>

>

=

=

−

+

Zaś wartość dopuszczalnego odkształcenia jednostkowego dla jednoosiowego rozciagania będzie równe:

[

]

max

1

2

3

1

1

(

)

k

E

E

V

E

E

σ

σ σ

=

=

−

+

≤

Hip de ST. Venanta daje wyniki pokrywające się z doświdczeniem dla mat sprężysto – kruchych. Natomiast do
zastosowania dla mat sprężysto – kruchych daje duże niezgodności ponieważ mówi że próbka rozciagana w 2
lub 3 kierunkach była by bardziej wytrzymała niż próbka rozciagana w jednym kierunku.
Z przypadkami statycznie nie wyznaczalnymi mamy do czynienia wówczas gdy w danym układnie liczba
niewiadomych sił (zwykle reakcji wiezów) jest większa od liczby równań równowagi.
Stopień statycznej niewyznaczalności jest to liczba okreslajaca nadwyżke liczby niewiadomych ponad liczbe
pozostałych dysponowanych równań statyki. Dodatkowe równania zapiszemy reprezentując sprężyste
odkształcenia układu w formie tzw. Równań zgodności przemieszczeń.

Nz=r-1

dla układów liniowych

Nz=r-2

dla układu płaskiego

Nz=r-3

dla układu płaskiego dowolnego

Wtedy korzystamy z równań zgodności odkształceń
Zasada superpozycji skutku – skutek działania układu sił na ciała rzeczywiste w określonym punkcie i na
określonym kierunku równa się sumie algebraicznej skutków działania każdej z sił układu rozpatrywane osobno
w określonym punkcie i na określonym kierunku.

NAPREZENIA WSTEPNE – naprężenia wywołane bez udziału właściwych obciążeń nazywamy naprężeniami
wstępnymi. Jeżeli są one spowodowane zestawieniem części wykonanych z pewnymi niedokładnościami
wymiarowymi nazywamy je zestawieniowymi lub montażowymi. W konstrukcjach statycznie niewyznaczalnych
nieznaczne nawet odchyłki wymiarowe mogą spowodować znaczne naprężenia wstępne, często trudne do
przewidzenia. Ten stan może pogorszyć wytrzymałość konstrukcji . Stan te można jednak wywołać celowo, aby
pod obciążeniem wystąpił najodpowiedniejszy rozkład sił wewnętrznych i w rezultacie wzrosła efektywnie
wytrzymałość konstrukcji.

4

Geometryczne charakterystyki przekroju. Momenty statyczne. Momenty

bezwładności. Transformacja przez obrót i przesunięcie.

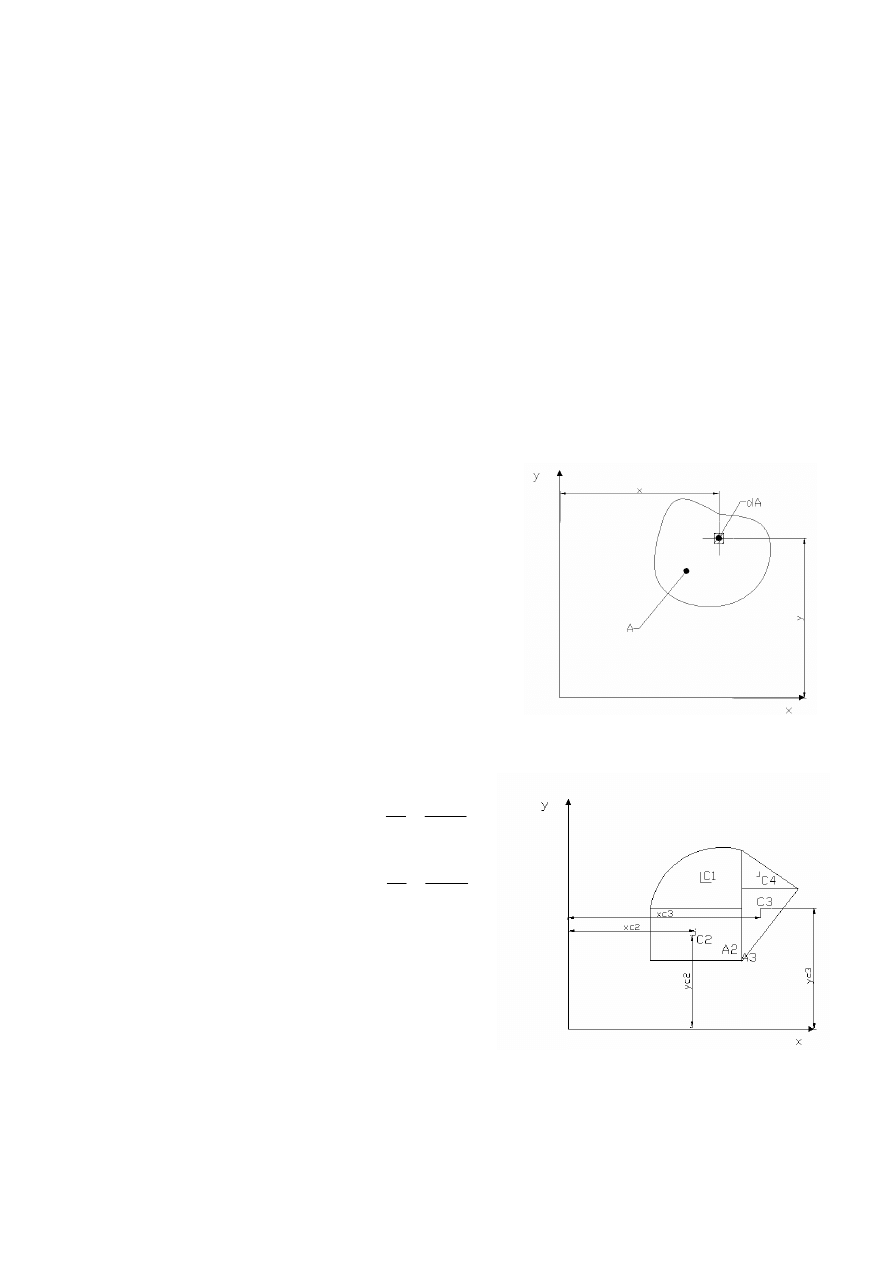
Geometryczne charakterystyki przekroju:

Momenty statyczne S [cm

3

m

3

] pole A figury płaskiej

względem osi x, y określić można z zależności:

x

A

y

A

S

ydA

S

xdA

=

=

∫

∫

Momenty statyczne mogą przyjmować wartości
dodatnie, ujemne lub równe zero. Momenty statyczne
obliczone względem osi symetrii lub względem
prostych przechodzących przez środek symetrii są
równe zero.


Środek ciężkości (X

c

, Y

c

)jest punktem przyłożenia wypadkowej ciężarów (geometrii)

wszystkich cząstek ciała bez względu na orientacje ciała przestrzeni.
Obliczamy go z wzoru:

śeby nie zamazywać rysunku nie
wpisałem wszystkich odległości. Robi
się to analogicznie jak na rysunku.

Osie centralne – osie przechodzące przez środek figury płaskiej.
Przy szukaniu środka ciężkości figury płaskiej korzystamy z twierdzeń:
-Jeżeli figura ma oś symetrii, to ta oś przechodzi przez środek ciężkości figury.
-Jeżeli figura posiada środek symetrii, to jest on równocześnie środkiem ciężkości tej figury.

1

1

*

*

*

*

y

A

c

x

A

c

x

c

y

c

n

x

ci

i

i

n

y

ci

i

i

xdA

S

x

A

A

ydA

S

y

A

A

S

y

A

S

x

A

S

y

A

S

x

A

=

=

=

=

=

=

=

=

=

=

∫

∫

∑

∑

Moment bezwładności[cm

4

, m

4

] I pole figury płaskiej A względem osi x, y prostopadłego

układu współrzędnych.
Moment bezwładności figury płaskiej (II rzędu)może być tylko dodatni.

2

2

2

2

2

0

2

2

2

(

)

x

A

y

A

x

y

A

A

I

y dA

I

x dA

I

dA

x

y dA

I

I

x

y

ρ

ρ

=

=

=

=

+

= +

=

+

∫

∫

∫

∫

Moment dewiacji – ośrodkowy moment bezwładności
względem prostokątnego układu osi xy

xy

A

D

xydA

=

∫

Promień bezwładności- i -pole A figury płaskiej
względem osi lub bieguna nazywamy odległość, w której umieszczona całkowita
powierzchnia A daje moment bezwładności względem tej prostej lub tego bieguna równy
momentowi samej figury.

0

0

2

2

2

0

x

x

y

y

x

y

I

i

A

I

i

A

I

i

A

i

i

i

=

=

=

=

+

Twierdzenie Steinera:
Moment bezwładności pola A figury płaskiej względem prostej równa się momentowi
bezwładności tej figury względem prostej do niej równoległej i przechodzącej przez środek
ciężkości pola, plus iloczyn pola A figury i kwadratu odległości obu prostych.
Wzory Steinera określają zależność między momentem bezwładności przy transformacji
układu przez równoległe przesunięcie osi ze środka ciężkości przekroju,

2

2

c

c

x

x

y

y

I

I

a A

I

I

b A

=

+

=

+

2

c c

w

c

xy

x y

I

I

r A

D

D

abA

= +

=

+

Transformacja układu przez obrót

2

2

2

2

cos

sin

sin 2

sin

cos

sin 2

1

cos 2

(

) sin 2

2

u

x

y

xy

v

x

y

xy

uv

xy

x

y

I

I

I

D

I

I

I

D

D

D

I

I

α

α

α

α

α

α

α

α

=

+

−

=

+

+

=

+

−

Główne osie bezwładności- są to osie
względem, których oblicza się główne
momenty bezwładności. Momenty
bezwładności obliczone względem

układu tych osi przyjmują wartość ekstremalną i nazywamy je głównymi momentami
bezwładności.

2

2

max,min

1,2

(

)

2

2

x

y

x

y

xy

I

I

I

I

I

I

D

+

−

=

=

±

+

Główne osie bezwładności przechodzące przez środek ciężkości figury nazywamy głównymi
centralnymi osiami bezwładności, a momenty względem ni obliczone głównymi centralnymi
momentami bezwładności.
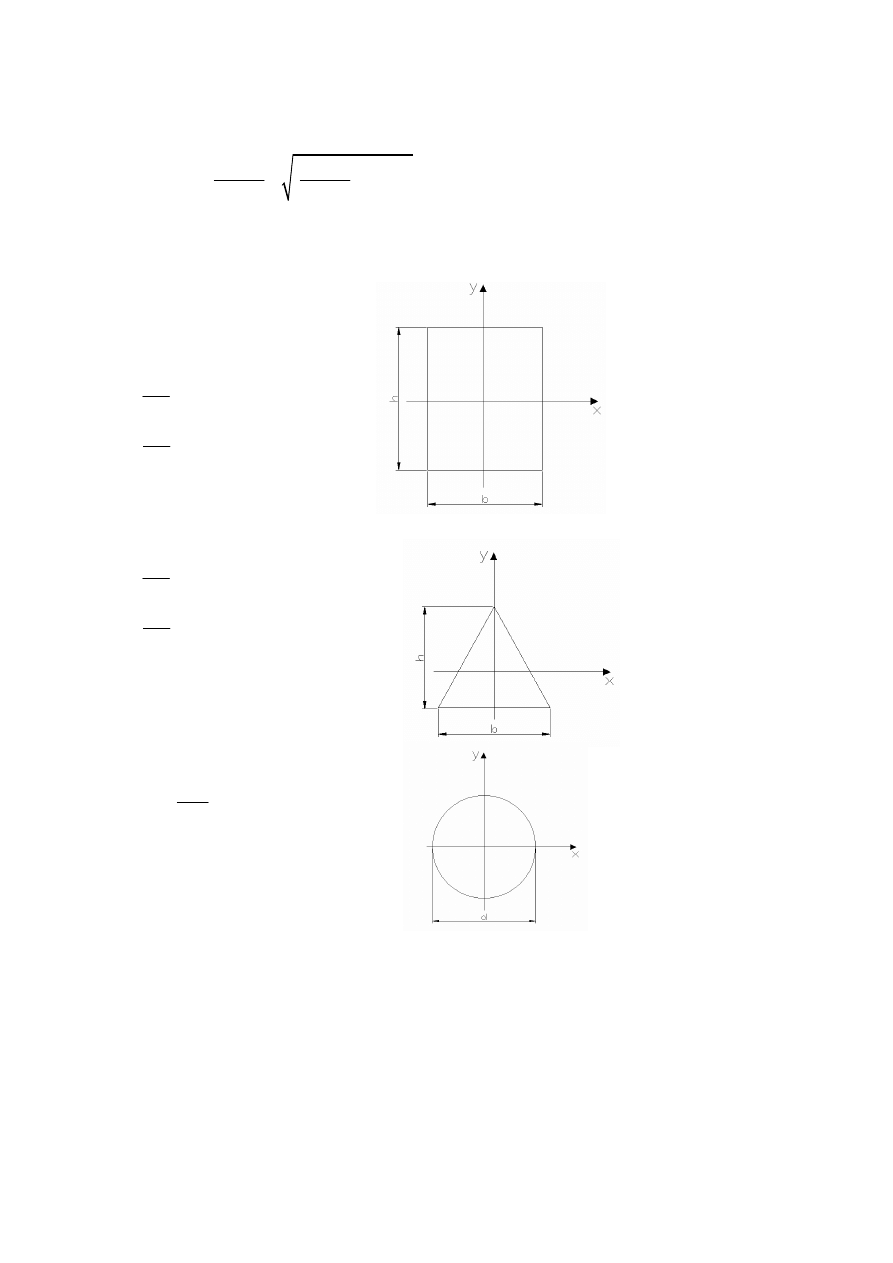
Momenty figur płaskich:



-prostokąt

3

3

12

12

x

y

bh

I

hb

I

=

=

-trójkąt równoramienny

3

3

36

48

x

y

bh

I

hb

I

=

=

-koło

4

64

x

y

d

I

I

π

=

=

5.

Stan naprężenia. Jedno, dwu i trójosiowy stan naprężenia. Naprężenie główne.
Transformacja z kierunków głównych. Transformacja na kierunki główne. Koło
Mohra.

Stanem naprężenia - ogół naprężę występujących w danym punkcie.

Stan naprężeń może być:
-jednorodny (rozkład naprężeń jest funkcją liniową)
-niejednorodny (rozkład naprężeń nie jest funkcją liniową)

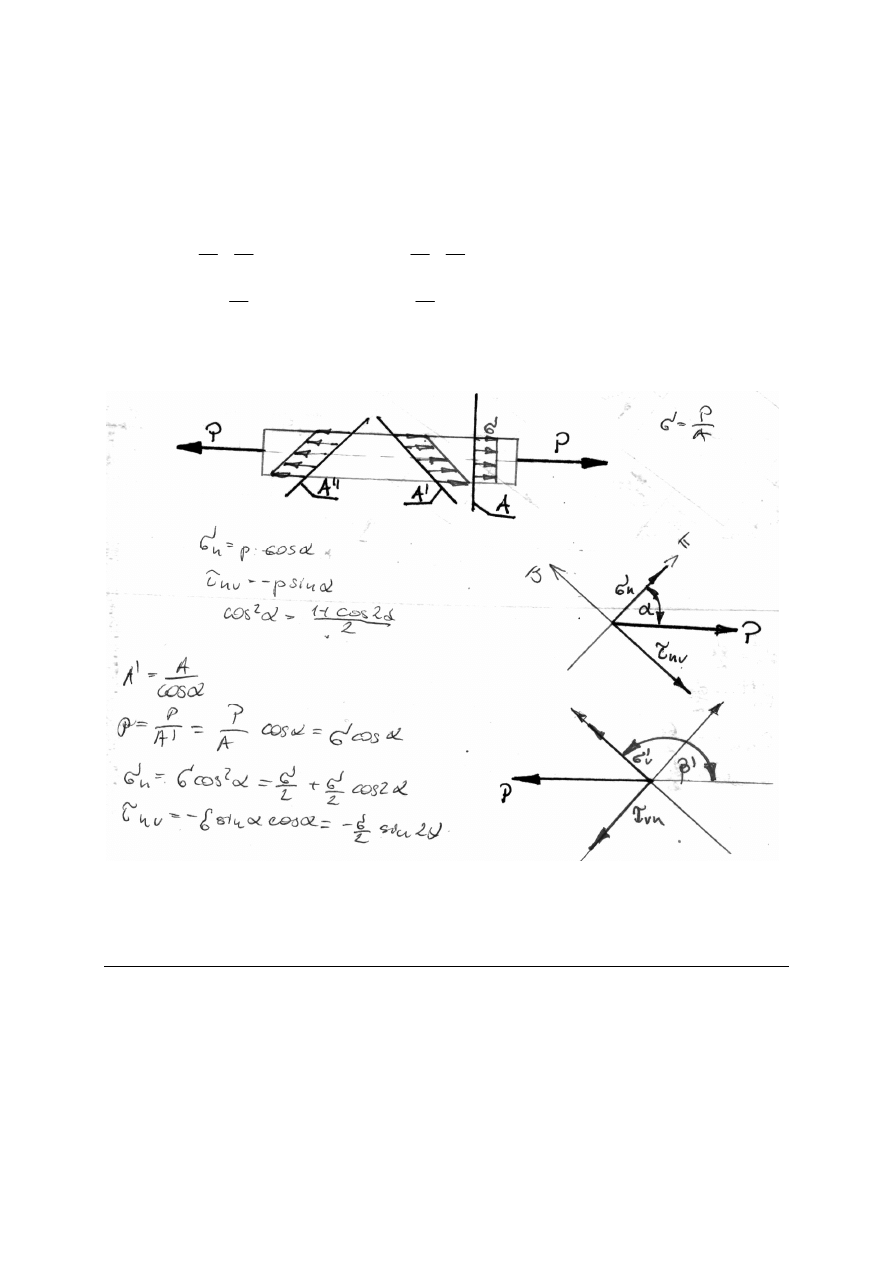
Pod pojęciem jednoosiowego stanu naprężenia rozumiemy taki stan, w którym

niezależnie od wykonanego myślowego przekroju, naprężenie posiada stały kierunek -zwany
kierunkiem głównym.

Przekrój, w którym naprężenie styczne przyjmuje wartość zero, a naprężenie normalne

przyjmuje wartość ekstremalną, nosi nazwę przekroju głównego, zaś naprężenie normalne
nazywamy głównym.

1

1

cos 2

2

2

n

σ σ

σ

α

=

+

⋅

;

1

1

cos 2

2

2

v

σ σ

σ

α

=

−

⋅

1

sin 2

2

nv

σ

σ

α

= −

⋅

;

1

sin 2

2

vn

σ

σ

α

=

⋅

Prawo Cauchy: |

| |

|

nv

vn

τ

τ

=

Dwuosiowy (płaski) stan naprężenia -stan naprężenia w którym, nie zależnie od
wykonanego przekroju naprężenia zawsze leżą w jednej płaszczyźnie zwanej płaszczyzną
stanu naprężenia.

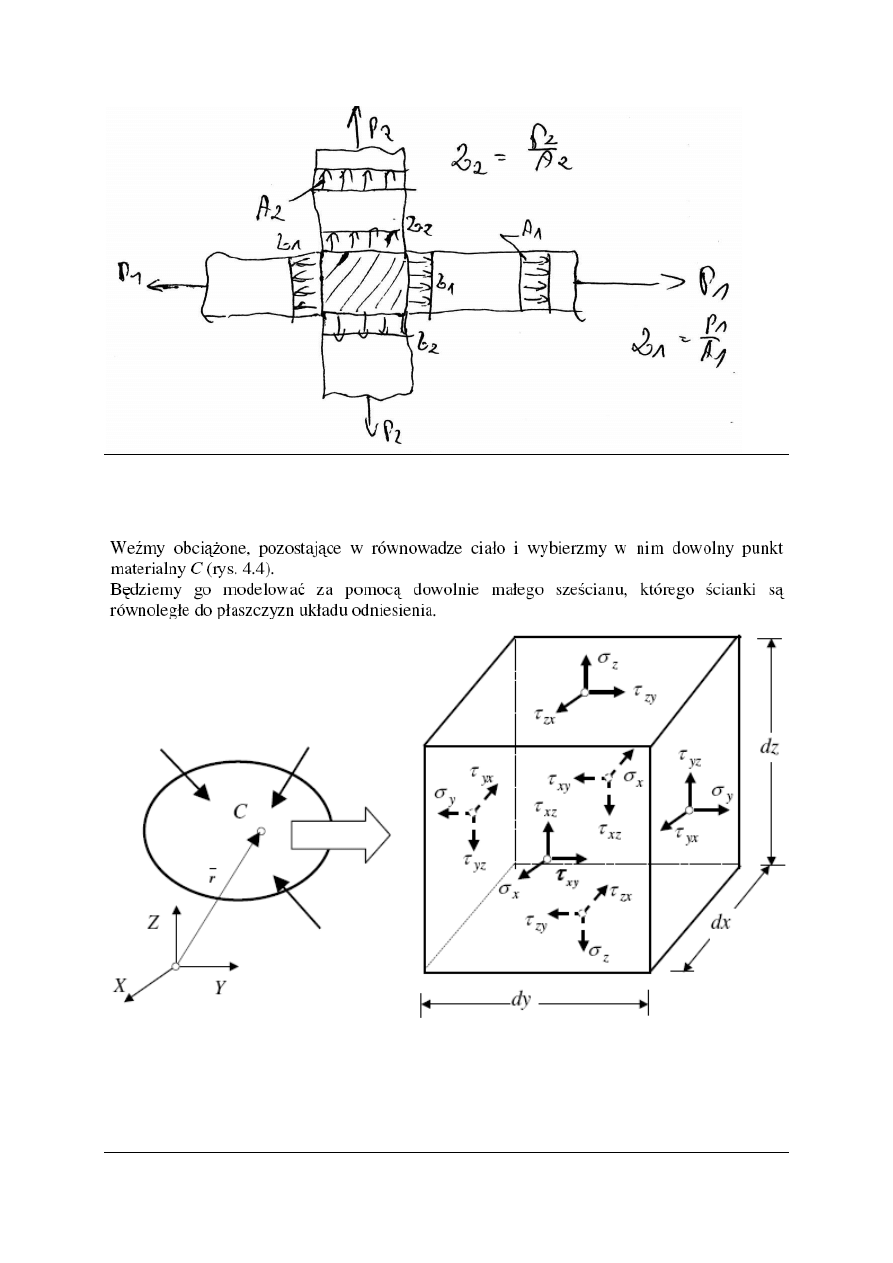
Trójosiowy (przestrzenny) stan naprężenia:

Jest to taki przypadek stanu naprężeń w którym w każdym przekroju myślowym

naprężenie posiada inny kierunek.

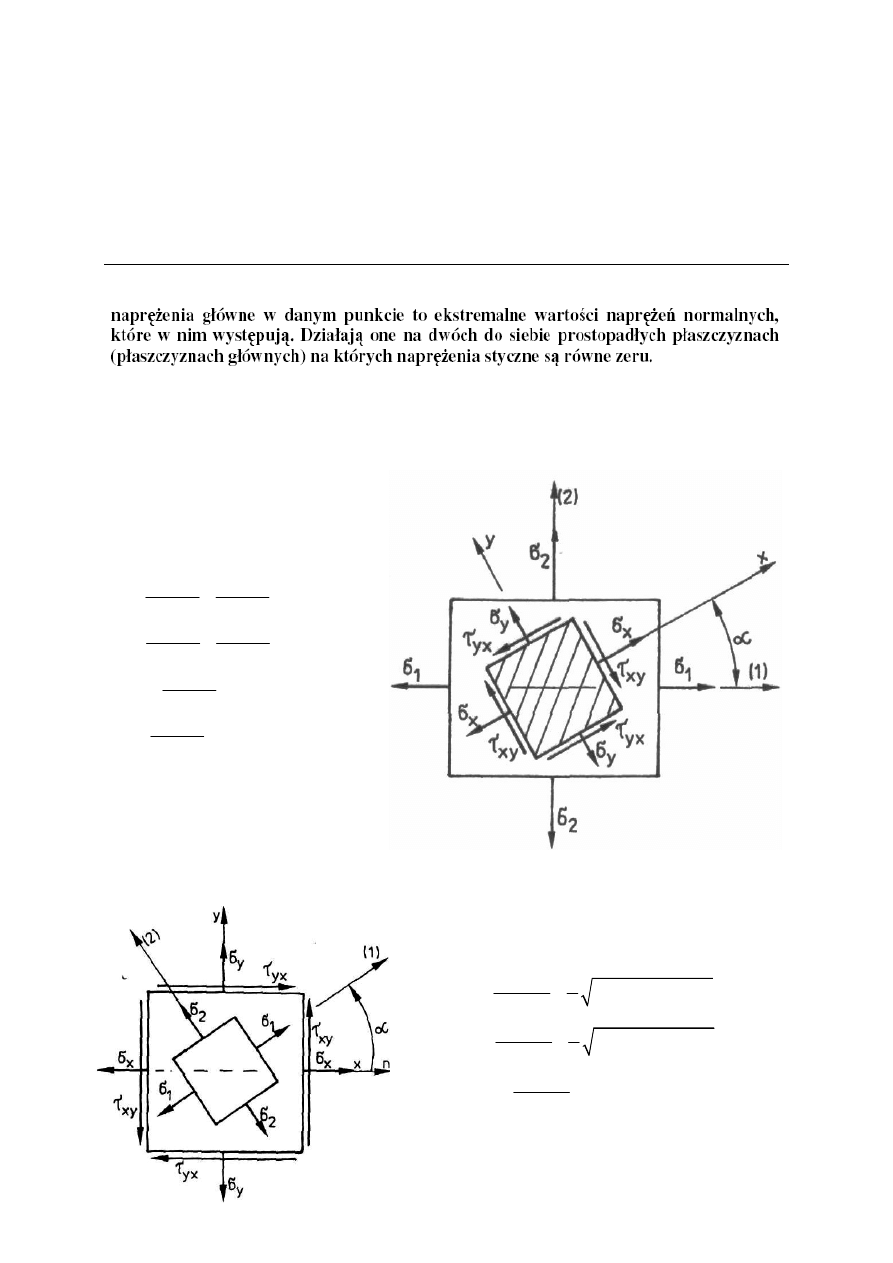
Tensor naprężeń:

T

=

σ

ij

=

x

xy

zx

yx

y

yz

zx

zy

z

σ

τ

τ

τ

σ

τ

τ

τ

σ





















Transformacja z kierunków głównych na dowolne:

1

2

1

2

cos 2

2

2

x

σ σ

σ σ

σ

α

+

−

=

+

⋅

1

2

1

2

cos 2

2

2

y

σ σ

σ σ

σ

α

+

−

=

−

⋅

1

2

sin 2

2

xy

σ σ

σ

α

−

= −

⋅

1

2

sin 2

2

yx

σ σ

σ

α

−

=

⋅

Transformacja z kierunków dowolnych na kierunki główne:

2

2

1

1

(

)

4

2

2

x

y

x

y

xy

σ σ

σ

σ σ

τ

+

=

+

−

+

2

2

2

1

(

)

4

2

2

x

y

x

y

xy

σ σ

σ

σ σ

τ

+

=

−

−

+

2

2

xy

x

y

tg

τ

α

σ σ

=

−

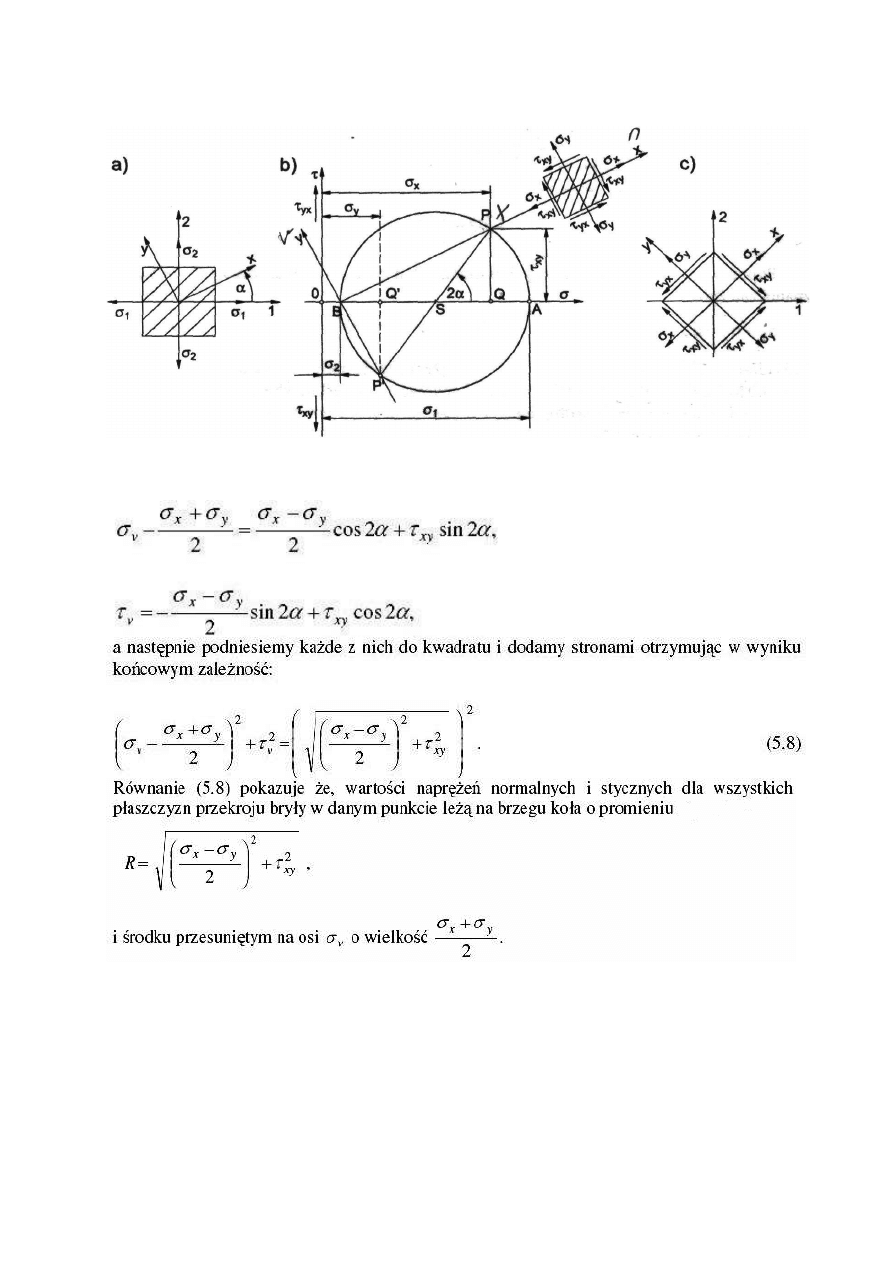
Koło Mohra - graficzna reprezentacja stanu naprężenia w danym punkcie!

Wyprowadzenie:

Kolo Mohra dla przestrzennego stanu naprężenia:

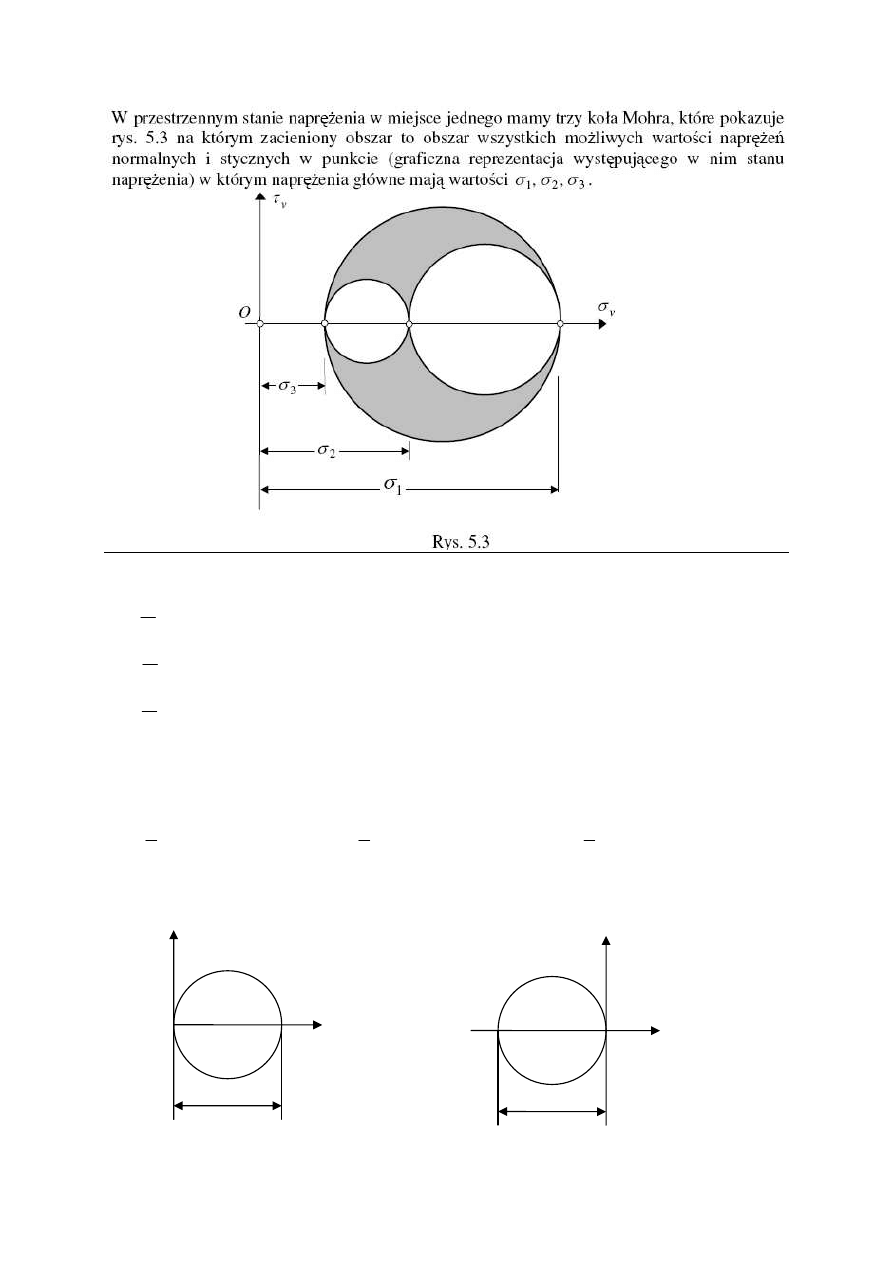
Uogólnione prawo Hooka dla kierunków głównych:

1

1

2

3

1

[

(

)]

E

ε

σ ν σ σ

=

−

+

2

2

1

3

1

[

(

)]

E

ε

σ ν σ σ

=

−

+

3

3

1

2

1

[

(

)]

E

ε

σ ν σ σ

=

−

+

Przykłady szczególnych stanów naprężeń (koła Mohra):

- Jednoosiowe rozciąganie i ściskanie:

1

(1 cos 2 )

2

x

σ

σ

α

=

+

;

1

(1 cos 2 )

2

y

σ

σ

α

=

−

;

1

sin 2

2

xy

τ

σ

α

= −

σ

1

σ

τ

Rozciąganie
(σ

1

> 0; σ

2

=0)

σ

2

σ

τ

Ściskanie
(σ

1

= 0; σ

2

<0)

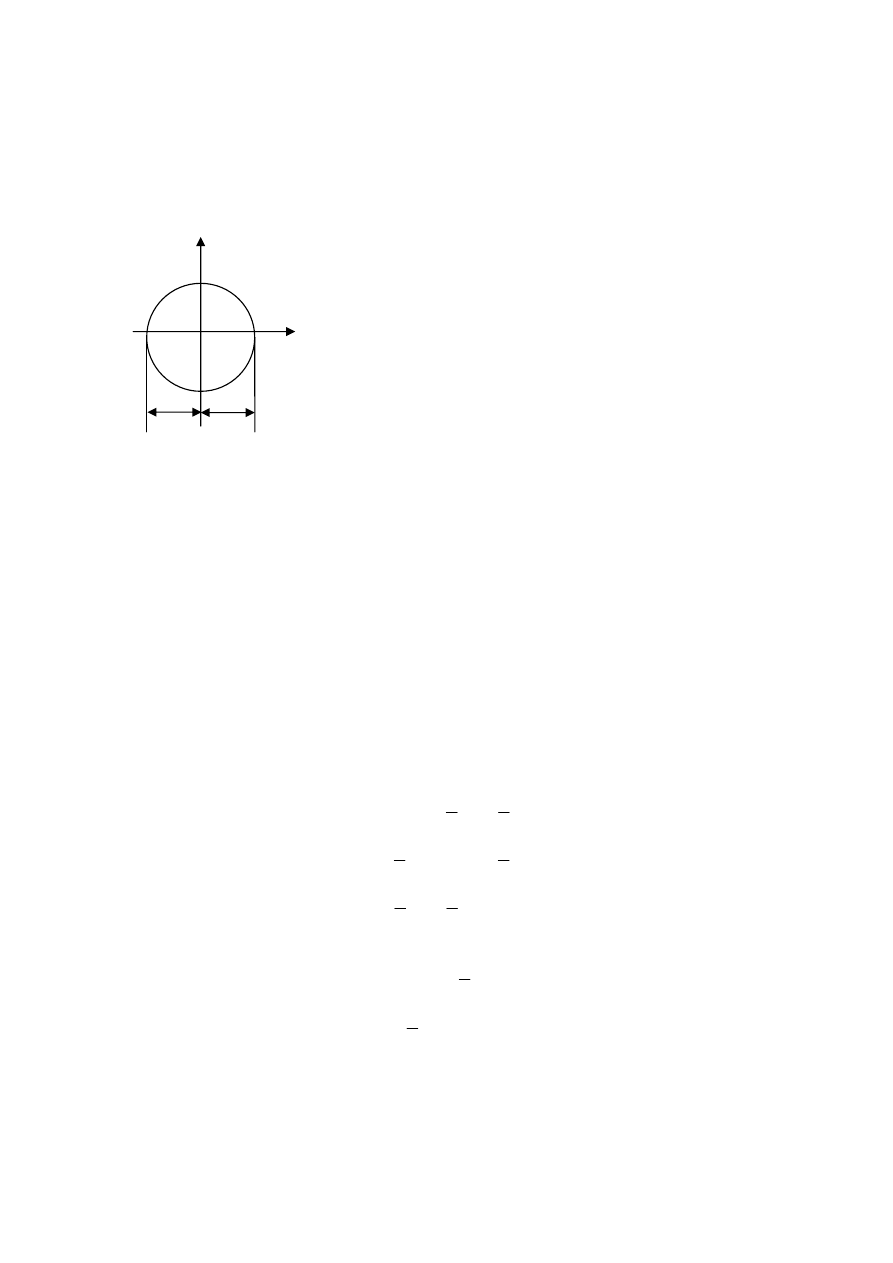
- Ścinanie:

cos 2

x

σ

σ

α

=

;

cos 2

y

σ

σ

α

= −

;

sin 2

xy

τ

σ

α

= −

6. Teoria stanu odkształcenia. Prawo Hooke’a dla ciał izotropowych. Odkształcenia
główne. Dylatacja.
Teoria stanu odkształcenia
Twierdzenie
W pewnych granicach własności danego materiału kąt odkształcenia postaciowego jest
wprost proporcjonalny do naprężenia stycznego, które je wywarło.

Stanem odkształcenia w punkcie nazywamy ogół odkształceń ( liniowych

,

,

x

y

z

ε ε ε

i

kątowych

,

,

xy

xz

yz

γ γ γ

) we wszystkich dowolnie zorientowanych elementach przekroju

zawierających ten punkt.

Elementarny prostopadłościan pod wpływem obciążenia ulega deformacji liniowej

,

,

x

y

z

ε ε ε

oraz deformacji kątowej ( postaciowej )

,

,

xy

yz

zx

γ γ γ

. Stan odkształcenia można zapisać w

postaci macierzowej, która jest reprezentacją tensora stanu odkształcenia:

1

1

2

2

1

1

2

2

1

1

2

2

x

xy

xz

ij

yx

y

yz

zx

zy

z

ε

γ

γ

ε

γ

ε

γ

γ

γ

ε

















=





















Dla płaskiego stanu odkształcenia:

1

0

2

1

0

2

0

0

0

x

xy

ij

yx

y

ε

γ

ε

γ

ε

















=





















Tensor odkształcenia jest analogiczny do tensora naprężeń i analizuje się go ?????????
Prawo Hooke’a dla ciał izotropowych

σ

1

σ

τ

(σ

1

= -σ

2

)

σ

2

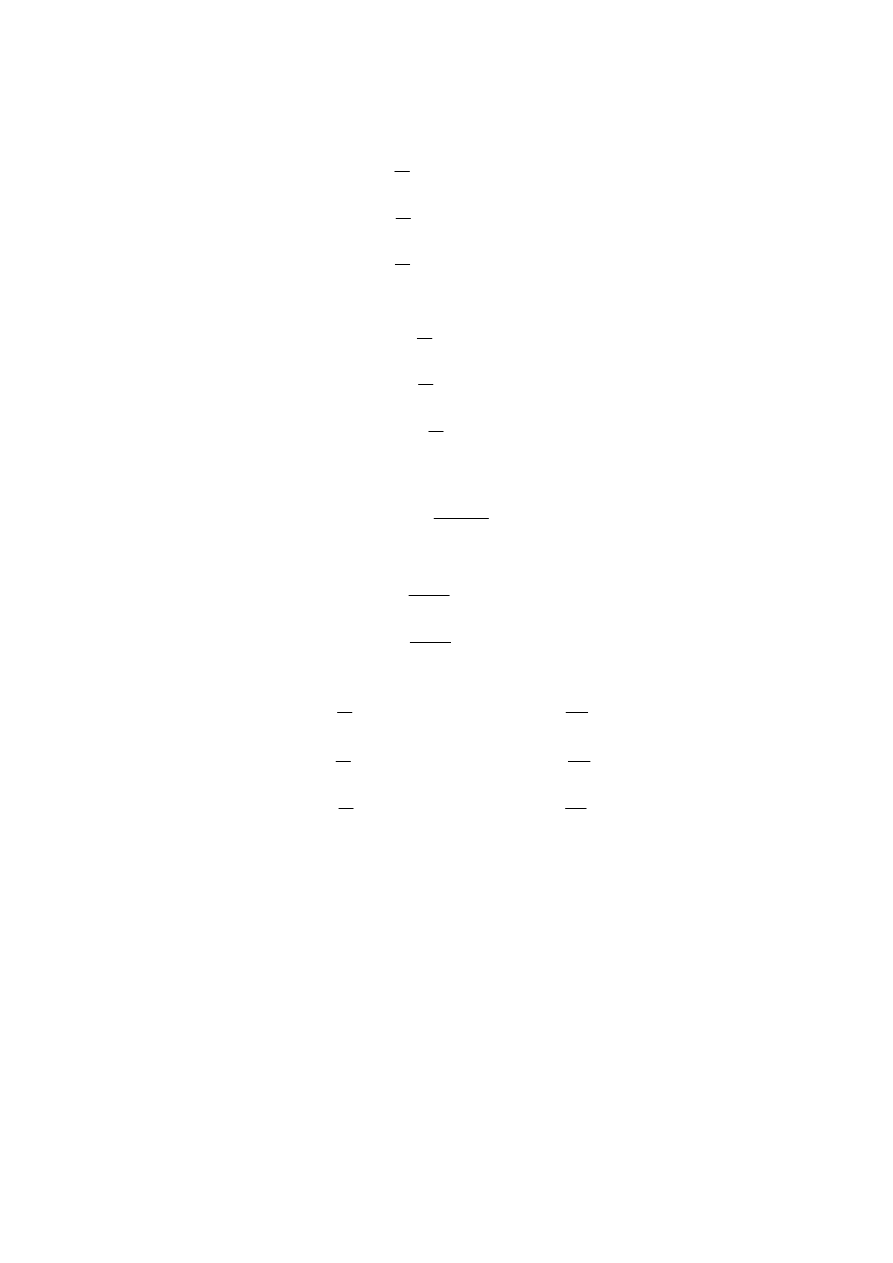
Określa związki między stanem naprężenia i stanu odkształcenia materiału jednorodnego i
izotropowego w najogólniejszym stanie naprężenia, czyli przestrzenny stan naprężenia.

1

1

2

3

1

[

(

)]

E

ε

σ ν σ σ

=

−

+

2

2

1

3

1

[

(

)]

E

ε

σ ν σ σ

=

−

+

3

3

1

2

1

[

(

)]

E

ε

σ ν σ σ

=

−

+

Płaski stan odkształcenia

3

0

σ

=

1

1

2

1

(

)

E

ε

σ νσ

=

−

2

2

1

1

(

)

E

ε

σ νσ

=

−

3

1

2

(

)

E

ν

ε

σ σ

= −

+

Zależność między modułem Young’a E ,modułem Kirchoffa G i współczynnikiem Poissona

ν

2(1

)

E

G

ν

=

+

Znając wartości odkształceń głównych

1

2

,

ε ε

można obliczyć naprężenia:

1

1

2

2

(

)

1

E

σ

ε νε

ν

=

+

−

2

2

1

2

(

)

1

E

σ

ε νε

ν

=

+

−

Dla kierunków dowolnych dowierzają zależności

1

[

(

)]

x

x

y

z

E

ε

σ ν σ σ

=

−

+

xy

xy

G

τ

γ

=

1

[

(

)]

y

y

z

x

E

ε

σ ν σ σ

=

−

+

yz

yz

G

τ

γ

=

1

[

(

)]

z

z

x

y

E

ε

σ ν σ σ

=

−

+

zx

zx

G

τ

γ

=

KURWA BRAKUJE ODKSZT GL I DYLATACJI , KURWA HUJ WIE CO TO JEST
W NECIE PISZE ZE ZWIAZANE Z PREDK KOSM, ALBO OTWOR W BUDOWN.

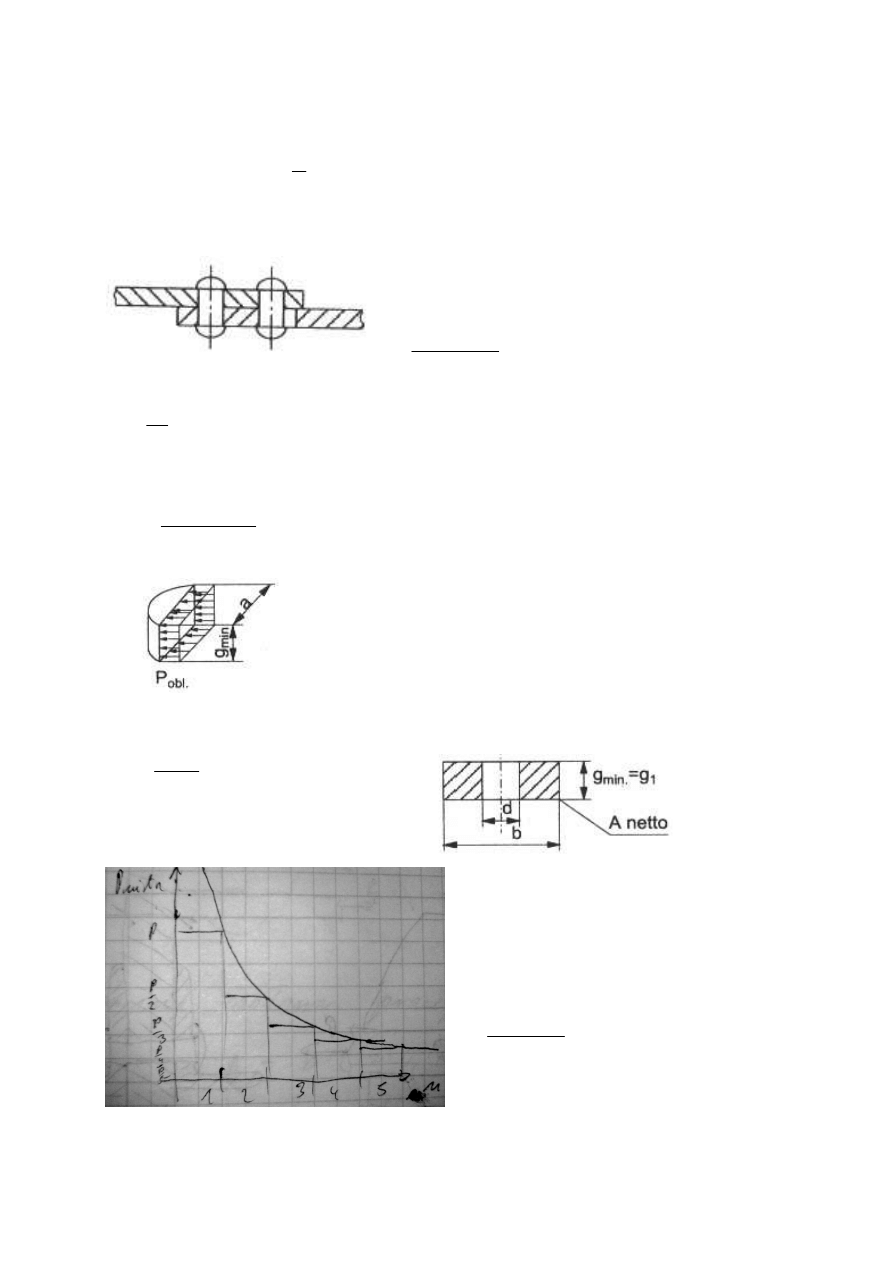
Ścinanie techniczne – przypadek wytrzymałościowy określany jako tzw. Ścinanie czyste, jest
to stan naprężenia, który scharakteryzować można wyłącznie poprzez naprężenia styczne.

warunek na ścinanie:

t

P

k

A

τ

= ≤

P – siła ścinająca
A – przekrój ścinany
k

t

– naprężenie dopuszczalne na ścinanie.

W przypadku połączeń nitowych zakłada się
równomierny rozkład sił ścinających na wszystkie nity
przy uwzględnieniu liczby płaszczyzn cięcia nita.

n – ilość nitów
i – liczba powierzchni ścinania

Naprężenia na docisk powierzchniowy obliczyć można z warunku:

d

dop

d

P

p

p

A

=

≤

A

d

– sumaryczna obliczeniowa powierzchnia na docisk

p

dop

– naprężenia dopuszczalne na docisk

Dla połączenia nitowego warunek na docisk:

n – obliczeniowa liczba nitów

p

dop

= (2-2,5)k

c

A

d

=d g

min

- rzut powierzchni docisku na płaszczyznę

średnicową nita dla blachy o minimalnej grubości w połączeniu.

Ponieważ wykonywanie otworów na nity osłabia elementy łączone, konieczne jest
sprawdzenie warunku bezpieczeństwa na rozciąganie.

r

r

netto

P

k

A

σ

=

≤

A

netto

= g

1

(b-d)

Widzimy że zastosowanie więcej niż 4 nity
mija się z celem gdyż kolejne nity nie
przenoszą obciążeń, tylko osłabiają przekrój.

2

4

t

P

n

d

k i

π

⋅

≥

⋅ ⋅ ⋅

2

4

t

P

k

n i

d

τ

π

⋅

=

≤

⋅ ⋅ ⋅

min

d

dop

P

p

p

n d g

=

≤

⋅ ⋅

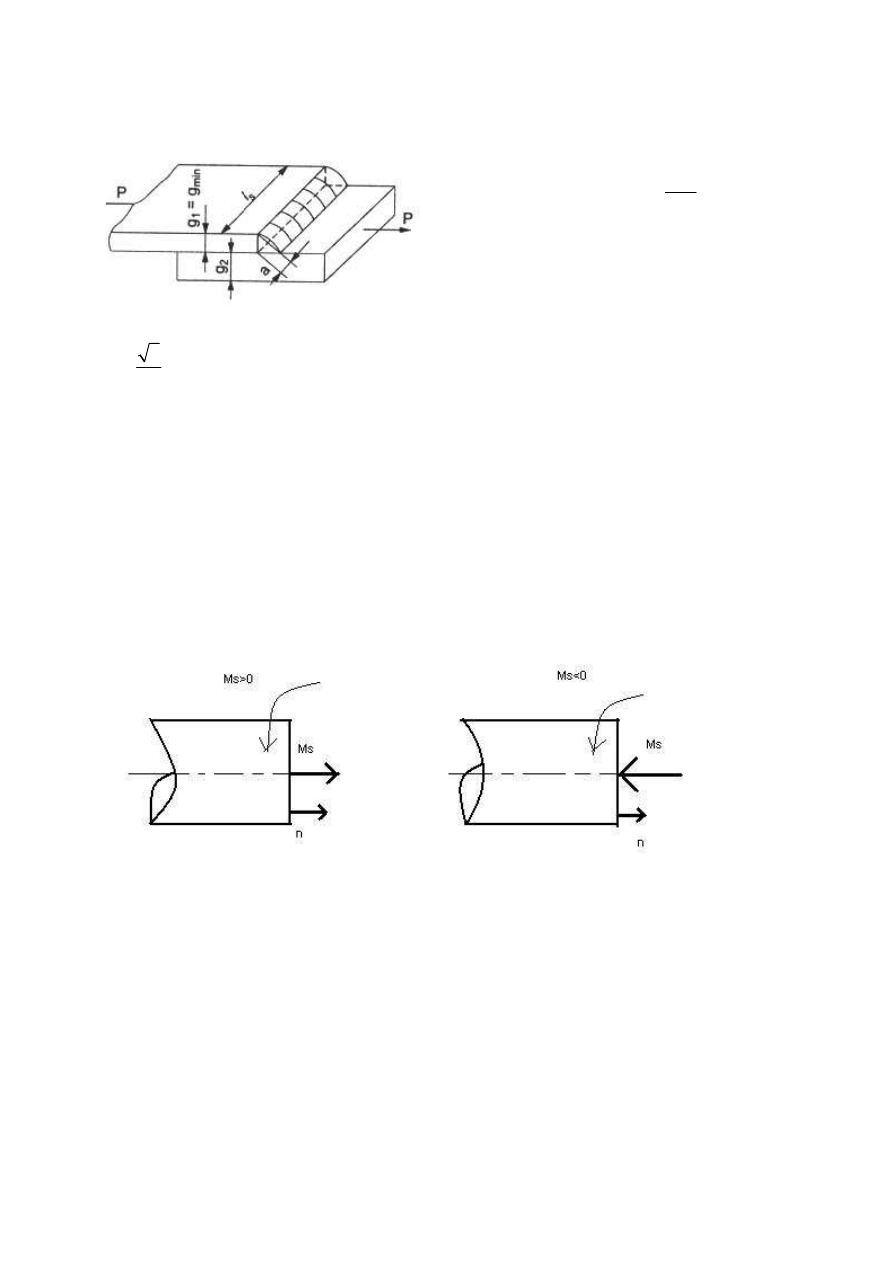
Dla połączeń spawanych ze spoinami pachwinowymi zakłada się, że zniszczenie następuje w
wyniku ścięcia w płaszczyźnie najsłabszego przekroju a

.

l

s

spoiny.

Warunek bezpieczeństwa:

ts

P

k

L a

τ

=

≤

⋅

L – obliczeniowa długość spoiny
a – obliczeniowa grubość spoiny
k

ts

– naprężenia dopuszczalne na ścinanie

Dla spoiny czołowej jako grubość obliczeniową
a spoiny przyjmuje się wysokość trójkąta

wpisanego w przekrój spoiny. Maksymalna wartość a można obliczyć jako:

min

min

2

0, 7

2

a

g

g

=

⋅

≅

⋅

, gdzie g

min

jest grubością cienkiego z łączonych elementów.

Spoiny pachwinowe: a=g

8 Skrecanie pretów o przekroju kołowym. Naprężenia i odkształcenia przy skrecaniu
Skręcanie – jest to taki przypadek wytrzymałości materiałów w którym na wynik redukcji wszystkich sił
zewnętrznych działających po jednej stronie myślowego przekroju otrzymamy w tym przekroju moment
skręcający.
Moment skręcający jest to algebraiczna suma momentów wszystkich sił zewnętrznych działających po jednej
stronie myślowego przekroju w płaszczyźnie prostopadłej do osi pręta.
Moment ten będziemy uważać za dodatni, jeżeli jego wektor posiada zwrot zgodny ze zwrotem normalnej
zewnętrznej do przekroju, w przypadku przeciwnym moment skręcający uważać będziemy za ujemny.

W przekroju poprzecznym prostopadłym do osi pręta podpartego i obciążonego występują tylko naprężenia
styczne do promienia.

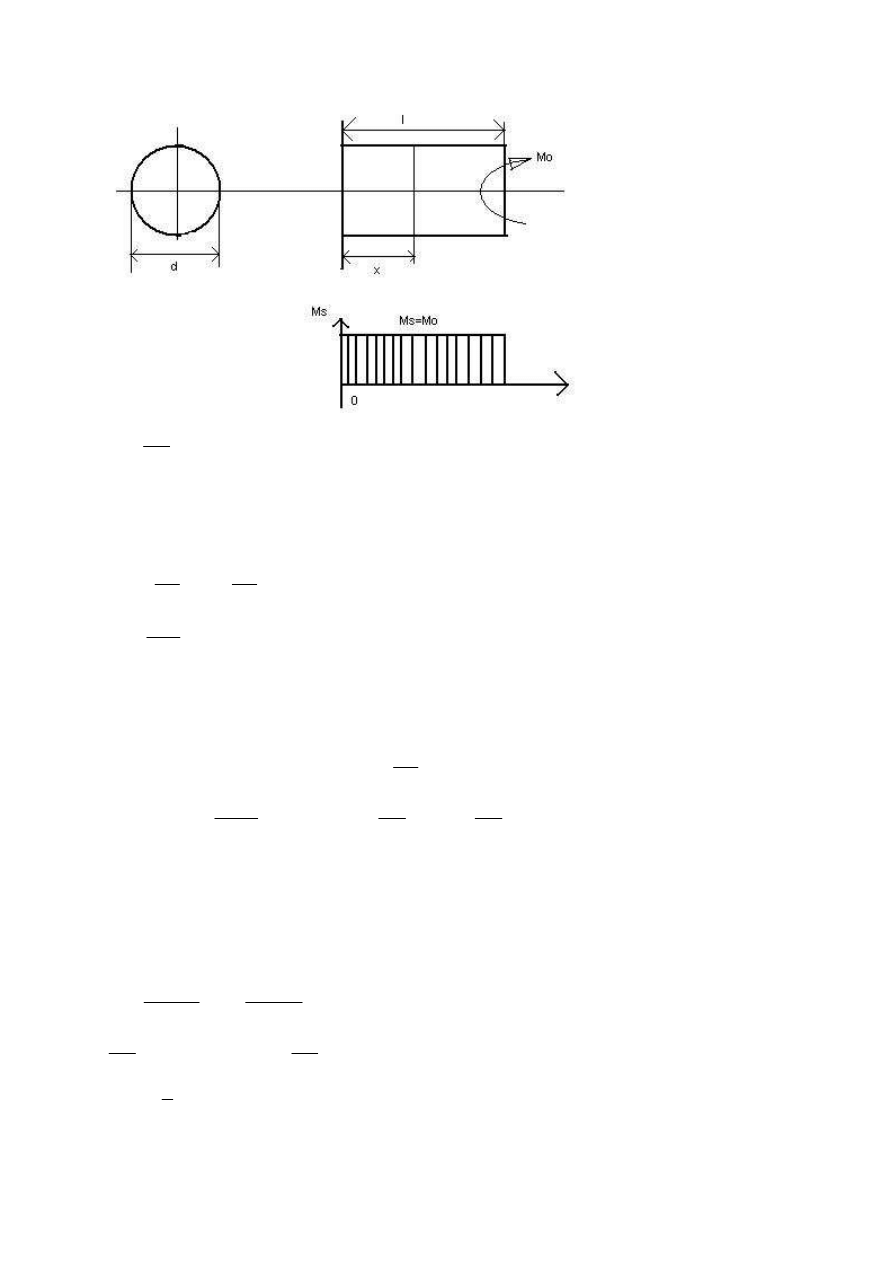
0

0

p

M

p

l

τ

=

Tp – naprężenia styczne w punktach odległych o „r” od środa przekroju
Ms – moment skręcający w danym przekroju
Io – biegunowy moment bezwładności pola przekroju względem środka koła

Największe naprężenia styczne w danym przekroju występują we włóknach skrajnych p=p

mac

max

max

0

0

0

0

max

Ms

Ms

p

I

W

I

W

p

τ

=

=

=

W

0

– wskaźnik wytrzymałości przekroju przy skręcaniu.

Diagram skręcający – jest to graficzna ilustracja przekroju momentu skręcającego w funkcji długości pręta.
Hipoteza płaskich przekrojów - stanowi ze przekrój przed odkształceniem pozostaje płaski po odkształceniu.

Naprężenia

1

2

,

σ τ σ

τ

=

= −

Warunek bezpieczeństwa na skręcanie

3

max

0

0

,

0, 2

Ms

kr W

d

W

τ

≤

≤

=

Sztywność :

0

*

180

,

,

*

180

o

rad

rad

dop

Ms l

G I

π

ϕ

ϕ ϕ

ϕ

ϕ

ϕ

π

=

≤

=

=

0

0

A

B

Miz

M

M

M

= −

+

−

=

∑

Równania statyki nie wystarczają, trzeba równania zgodności odkształceń (stosujemy zasade
superpozycji)

0

0

0

*

*

;

*

*

B

B

B

B

M

l

Mo Yz

G Io

G I

ϕ ϕ

ϕ

ϕ

+

=

−

=

=

- podstawiamy i redukujemy

0

2

2

B

A

B

M

Mo

M

M

M

=

→

−

=

0

2

l

z

≤ <

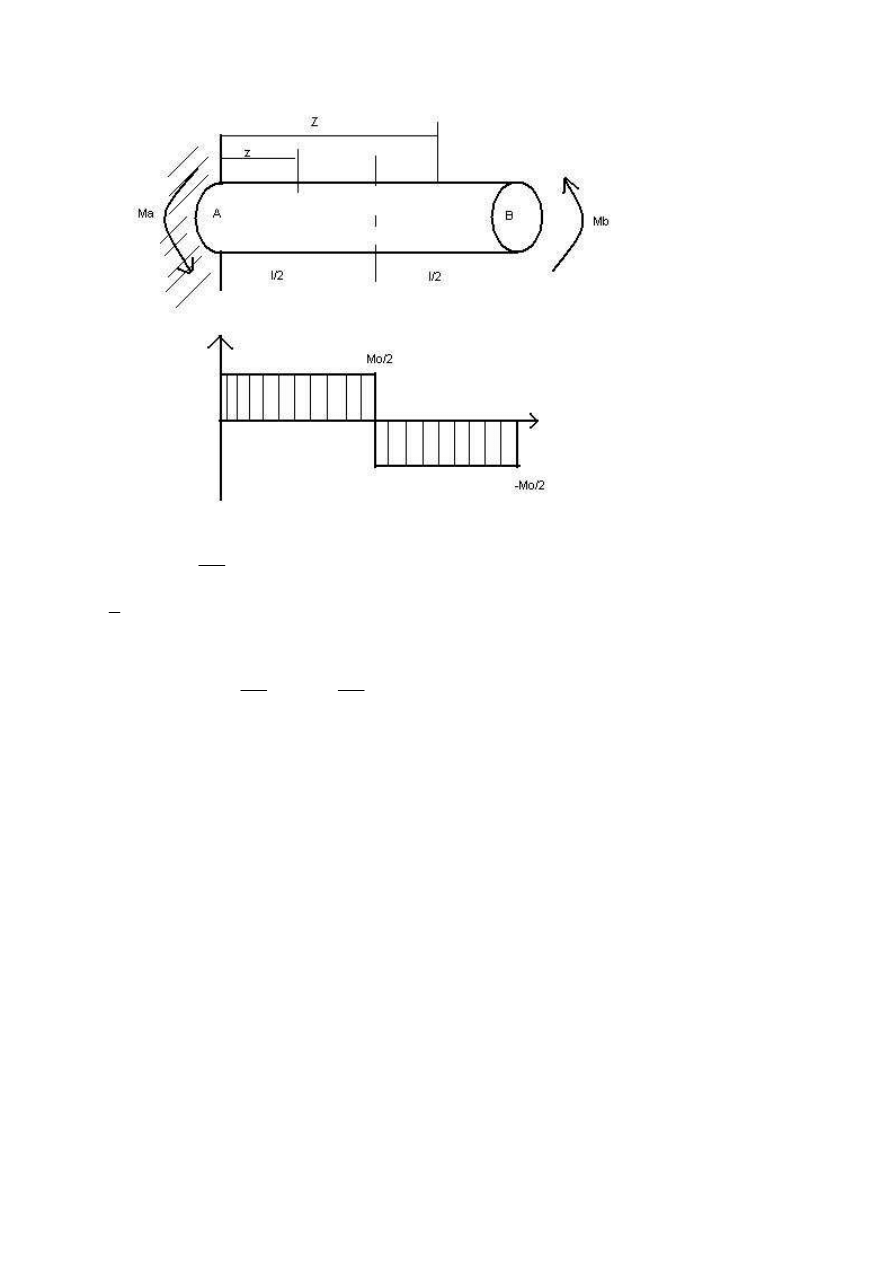
1

0

1

0

2

A

s

s

A

Miz

M

M

M

M

M

= −

+

=

=

=

∑

2

l

Z

l

≤ <

0

2

0

0

2

0

0

0

2

2

A

s

s

A

Miz

M

M

M

M

M

M

M

M

M

= −

+

+

=

=

−

=

−

= −

∑

9 Siły wewnętrzne w pretach zginanych. Def momentu zginającego o siły poprzecznej.
Wykresy sił poprzecznych i momentów zginających. Wzory Schwedlera – śurawskiego
Zginanie Tw Schwedlera – śurawskiego Obliczanie bedek
Zginanie jest to przypadek wytrzymałości materiałów w którym na wynik redukcji
wszystkich sił zawietrznych działających po jednej stronie myślowego przekroju wzgladem
srodka cieżkości tego przekroju otrzymamy moment gnacy.
Moment gnocy – algebraiczna suma momentu wszystkich sił zewnętrznych działających po
jednaj stronie myślowego przekroju w płaszczyźnie przechodzącej przez oś pręta
Belka – pręt prosty w którym za pośrednictwem odpowiednio pomyślanych (dobranych)
więzów odebrano odpowiednia ilsc stopnie swobody
Płaszczyzna główna zginania – płaszczyzna przechodzaca przez oś belki i przez jedną z
głównych centralnych osi bezwładności przekroju
Strefa martwa (obojetna) – znajduje się miedzy strefa rozciagana a sciskaną
Zginanie proste – jest to takie przypadek zginania w którym na wynik redukcji wszystkich
sił zewnętrznych działających po jednej stronie myślowego przekroju otrzymamy moment
gnacy i siłe poprzeczna; zaś płaszczyzną obciazonia zewnętrznego belki będzie się pokrywałą
z jedną z płaszczyzn głównych ścinania belki.

Siła poprzeczna – algebraiczna suma wszystkich sił zewnętrznych działających po jednej
stronie myślowego przekroju prostopadłych do osi belki.

Tw. Schwedlera – śurawskiego
Jest to związek miedzy momentem gnącym, siła poprzeczna i natężeniem obciążenia ciągłego

( )

( )

dT z

q z

dz

= −

- pochodna siły poprzecznej po zmiennej długości belki równa się

natężeniu obciążenia ciągłego ze znakiem ujemnym.

( )

( )

dM z

T z

dz

=

- pochodna momentu gnącego po zmiennej długości belki równa się sile

poprzecznej w myślowym przekroju belki

Algorytm rozwiązywania belek prostych statycznie wyznaczalnych metoda myślowych

przekrojów :

1.

Przyjąć schemat obliczeniowy belki

2.

wyznaczyc reakcje podporowe belki

3.

sprawdzic poprawność wyznaczonych reakcji podporowych belki

4.

ustalić równania przebiegu siły poprzecznej w przedziałach określoności belki

5.

naryskować wykres siły poprzecznej w funkcji długości belki

6.

ustalić równanie przebiegu momentu gnącego w przedziałach określoności belki

7.

wykonać wykres przebiegu momentu gnącego w Dunki długości belki i zaznaczyć
wartości ekstremalne w przedziałach określoności belki

DEFINICJA WYTRZYMALOSCI MATERIAŁÓW

Wytrzymałość materiałów jest to nauka zajmujaca się badaniem materiału konstrukcji
rzeczywistych określająca ich zdolność przenoszenia obciążeń zewnętrznych przez ta
konstrukcje przy jej odporności (tej konstrukcji) na odkształcenie i zniszczenie.


10.Zginanie czyste w zgięciu prostym. Odkształcenia i naprężenia. Wymiarowanie
zginanych belek.

Zginanie czyste w zginaniu prostym jest to taki przypadek zginania, w którym płaszczyzna
obciążenia pokrywa się z płaszczyzna główna belki, a na wynik redukcji wszystkich sił
zewnętrznych działających po jednej stronie myślowego przekroju belki otrzymamy moment
gnący zaś siła poprzeczna będzie równa zero.

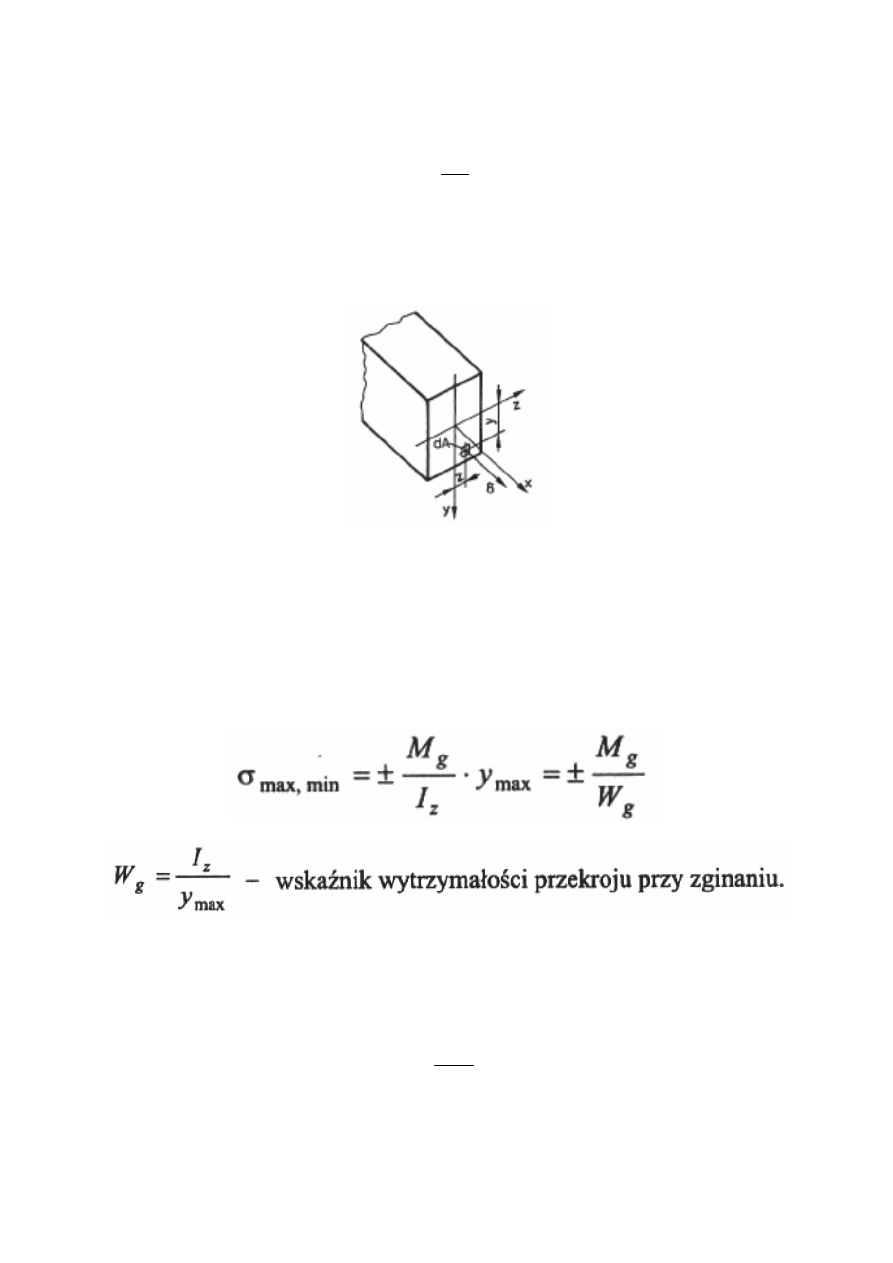
Naprężenia
Naprężenia w przekroju poprzecznym belki wyznaczamy ze wzoru:

g

z

M

y

I

σ

=

Gdzie:
M

g

– moment zginający w danym przekroju,

I

z

– moment bezwładności pola przekroju względem osi obojętnej z,

y – odległość rozpatrywanego punktu przekroju do osi obojętnej z,

Zależność ta została wyprowadzona po uwzględnieniu następujących założeń:
- przekrój płaski pozostaje po odkształceniu belki – płaski
- istnieje warstwa obojętna prostopadła do płaszczyzny działania pary sił momentu gnącego
- wystąpią wyłącznie naprężenia normalne w przekrojach poprzecznych belki, w przekrojach
podłużnych nie wystąpią żadne naprężenia.

Dla przekrojów poprzecznych, symetrycznych względem osi obojętnej największe naprężenia
rozciągające we włóknach skrajnych belki równe są największym naprężeniom ściskającym i
wynoszą:

Wymiarowanie zginanych belek
Dla tego przypadku, wymiarowania przekrojów belki dokonujemy z warunku
wytrzymałościowego:

max

max

g

g

M

k

W

σ

=

≤

Gdzie:
M

max

– największy moment zginający występujący w belce,

K

g

– naprężenie dopuszczalne na zginanie.

Wzór można stosować, gdy na danego materiału belki możemy przyjąć k

g

=k

c

=k

r

. W innych

przypadkach należy oddzielnie sprawdzić maksymalne naprężenia rozciągające i ściskające.

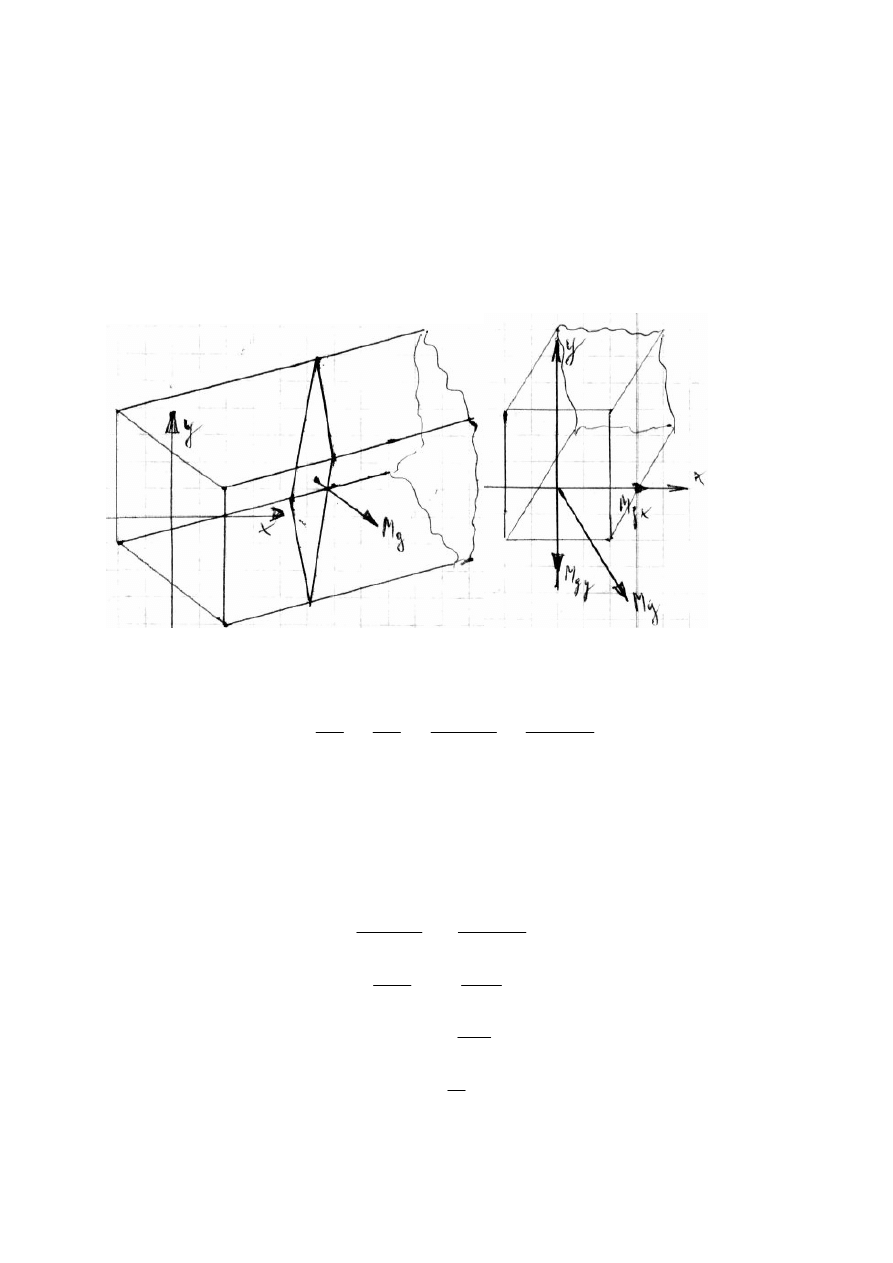
11. Zginanie ukośne. Jednoczesne zginanie i rozciąganie ( ściskanie ). Oś obojętna.
Rdzeń przekroju.
Zginanie ukośne jest to taki przypadek zginania, w którym płaszczyzna obciążenia przechodzi
przez oś belki, lecz nie pokrywa się z żadną z głównych płaszczyzn zginania belki.
Podczas określania naprężeń i odkształceń zginanie ukośne zastępujemy dwoma zginaniami
prostymi.

sin

x

g

M

M

α

=

cos

y

g

M

M

α

=

sin

cos

g

g

g

g

x

y

x

y

M

M

M

M

y

x

y

x

I

I

I

I

α

α

σ

=

+

=

+

Oś obojętna - krawędź przecięcia się płaszczyzny obojętnej z płaszczyzną przekroju nosi
nazwę osi obojętnej.

Równanie płaszczyzny obojętnej:

0

0

0

sin

cos

0

g

g

x

y

M

M

y

x

I

I

α

α

σ

=

+

=

0

0

sin

cos

x

y

y

x

I

I

α

α

= −

0

0

x

y

I x

tg

I y

α

= −

x

y

I

tg

ctg

I

α

ϕ

= −

x

y

I

tg

ctg

I

ϕ

α

= −

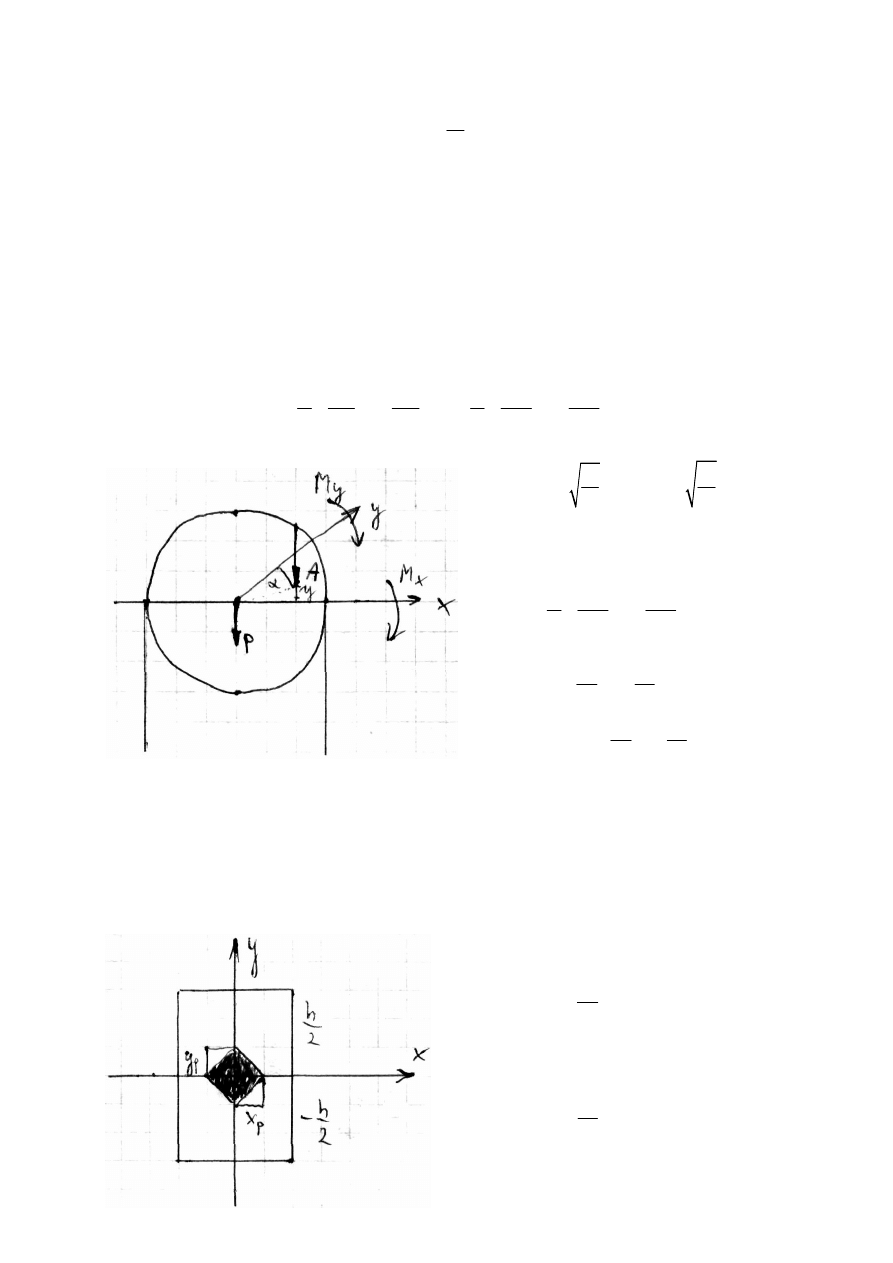
Ś

ciskanie mimośrodowe

W przypadku redukcji otrzymamy siłę ściskającą N=P oraz dwa momenty zginające:

x

x

p

M

P y

=

y

y

p

M

P x

=

Z czego widać, że naprężenie w dowolnym punkcie przekroju będzie zależało od
współrzędnych x i y.

0

y

p

p

x

A

A

A

A

A

x

Y

x

y

M

Py

Px

M

P

P

y

x

y

x

A

I

I

A

I

I

σ

= − −

−

= − −

−

=

x

x

I

i

A

=

,

y

y

I

i

A

=

2

x

x

I

i A

=

,

2

y

y

I

i A

=

2

2

0

p

p

A

A

x

x

Py

Px

P

y

x

A

i A

i A

− −

−

=

2

2

1

0

p

p

A

A

x

y

y

x

y

x

i

i

+

+

=

0

0

0

2

2

0 1

0

p

p

x

y

y

x

y

x

i

i

σ

= = +

+

=

Równanie osi obojętnej pozwala nam na wyznaczenie tzw. rdzenia przekroju.

Rdzeń przekroju
Jest to obszar wokół środka ciężkości przekroju, wewnątrz którego można umieścić punkt
przyłożenia siły, bez wywołania naprężeń o różnych znakach w całym przekroju

0

2

1

p

x

y

y

i

= −

0

2

1

p

y

x

x

i

= −

12.Linia ugięcia belki. Ugięcie i kąt ugięcia.

Pod pojęciem ugięcia rozumiemy przemieszczenie się środka ciężkości
przekroju poprzecznego belki pod wpływem obciążenia zewnętrznego na
kierunku prostopadłym do nieodkształconej części belki.
Linia ugięcia, miejsce geometryczne przekrojów poprzecznych belki na
kierunku prostopadłym do nieodkształconej części belki.
Maksymalne ugięcie oznaczamy f i nazywamy strzałką ugięcia.
Kąt obrotu przekroju poprzecznego belki jest to kąt o jaki obróci się przekrój
poprzeczny belki pod wpływem obciążenia zewnętrznego w stosunku do
położenia tego przekroju przed obciążeniem.

Metoda analityczna

- równanie różniczkowe ugięcia belki

Metoda grafoanalityczna
Metoda obciążeń wtórnych obliczenia przemieszczeń belki. W praktyce przy
obliczaniu konstrukcji najczęściej wystarczy wyznaczyć ugięcie lub kąt obrotu
przekroju w ściśle określonych miejscach belki bez wyprowadzania równań
ogólnych. W tych przypadkach stosujemy metodę obciążeń wtórnych opartą
na podobieństwie równań różniczkowych zachodzących pomiędzy ugięciem,
momentem gnącym natężeniem obciążenia ciągłego.

[

]

−

−

=

−

=

≈

=

=

+

−

+

=

=

=

)

(

''

1

'

'

)

(

'

)

'

(

1

''

1

''

)

(

1

3

2

2

2

z

M

EJy

y

EJ

z

M

tg

dz

dy

y

y

y

dz

y

d

y

EJ

z

M

ϕ

ϕ

ρ

ρ

)

(

)

(

)

(

)

(

''

2

2

2

2

z

dz

z

M

d

z

M

dz

y

d

EJ

z

M

EJy

ω

−

=

−

=

−

=

Wyobraźmy sobie inną belkę o takiej samej rozpiętości na które działa pewne
obciążenie pionowe ciągłe o natężeniu

)

(z

ω

i o zwrocie ku dołowi i to

obciążenie będzie równe polu wykresu M(z).
Jeżeli przyjmiemy że

)

(z

ω

=M(z) czyli że na belkę wtórną działa obciążenie

ciągłe zmieniające się według tej samej zależności analitycznej co M(z) belki

rzeczywistej to

2

2

2

2

)

(

dz

z

M

d

dz

y

d

EJ

=

Jeżeli będziemy całkowali to równanie i przyjmując że C

L

=C

P

i D

L

=D

P

to

otrzymujemy

_____

)

(

)

(

z

T

dz

z

M

d

EJ

dz

dy

EJ

=

=

=

=====

ϕ

Całkując po raz drugi otrzymamy

EJ

z

M

y

______

)

(

=

Wnioski:
1)Jeżeli ugięcie w danym przekroju belki rzeczywistej będzie równe 0 to
moment fikcyjny lub wtórny będzie zero.
2)Jeżeli kąt obrotu

ϕ

belki rzeczywistej będzie równy zero to w tym przekroju belki

siła fikcyjna też musi być równa zero.
3)Jeżeli w którym kolwiek przekroju belki rzeczywiste ugięcie jest

≠

0 i kąt obrotu

≠

0

to moment

≠

0 i siła fikcyjna T

≠

0

13.Zjawisko utraty stateczności. Wyboczenie. Wyznaczanie sił i naprężeń krytycznych
przy wyboczeniu. Kryteria normowe.

WYBOCZENIE jest to utrata stateczności ściskanego pręta objawiająca się zakrzywieniem
prostoliniowej osi pręta pod wpływem nacisku osiowej siły ściskającej pręt.

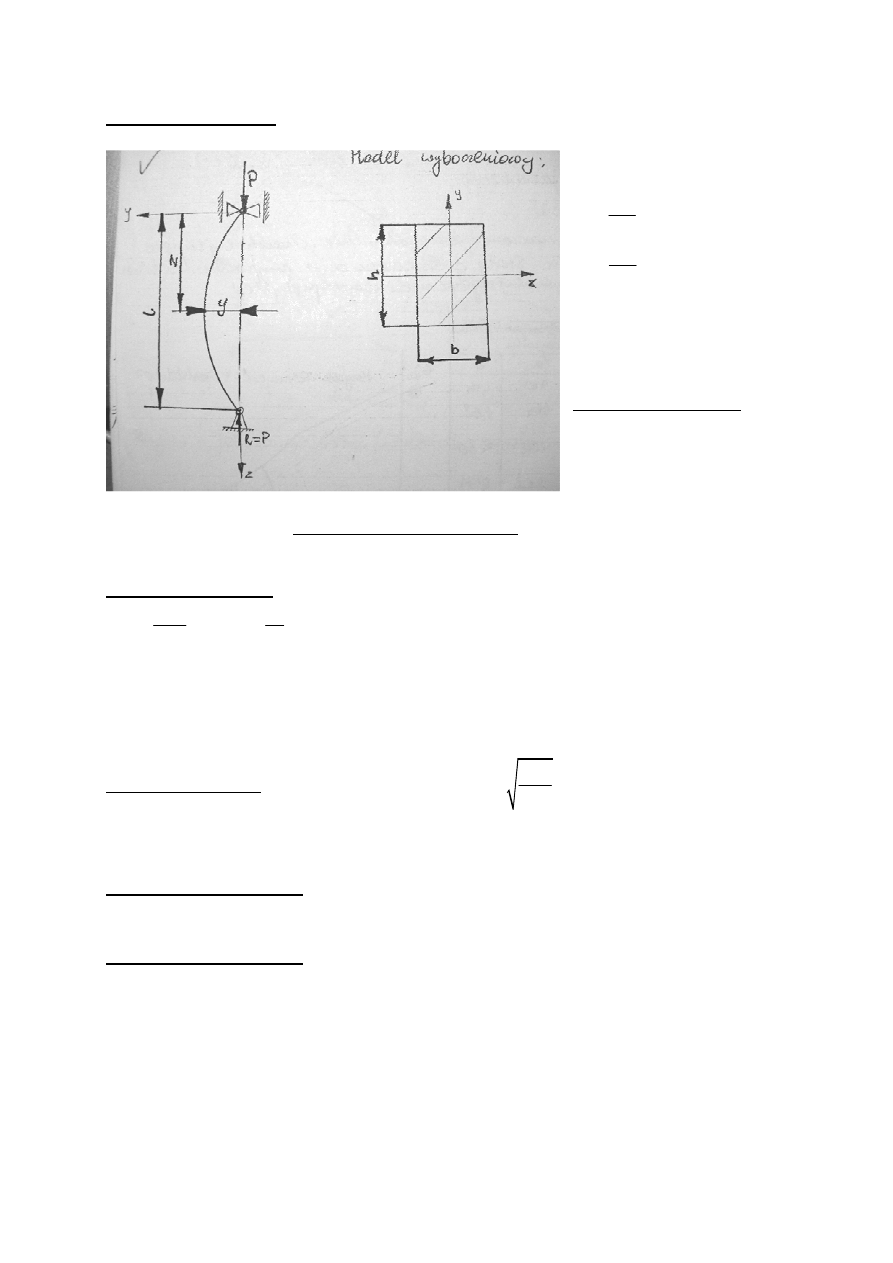
Model wyboczeniowy:

3

3

12

I min

12

bh

Ix

hb

Iy

=

=

=

Wybór największego
momentu bezwładności



Wyboczenie sprężyste:
DEF. BLUMA: to znaczy
takie, gdy po odciążeniu
pręta wraca on do
pierwotnego kształtu.

Wyboczenie sprężyste – wprowadzone przez EULERA: jest to utrata stateczności ściskanego
pręta w zakresie działania prawa Hook’a.

Naprężenie krytyczne dla wyboczenia sprężystego określone jest wzorem Eulera:

2

2

E

kr

π

δ

λ

=

gdzie

lw

li

λ

=

- smukłość pręta

lw – długość wyboczeniowa

i – promień bezwładności

Wyboczenie (sprężyste) zachodzi w zakresie Eulerowskim, kiedy smukłość pręta jest
większa od smukłości granicznej gr

λ

λ

<

Smukłość graniczną oblicza się wg zależności:

2

H

E

gr

R

π

λ

=

R

H

- granica proporcjonalności

Wyboczenie niesprężyste: przypadek kiedy smukłość pręta jest mniejsza od gr

λ

DEF BLUMA: to znaczy takie, gdy po odciążeniu pręta utrzymuje się jego wyboczony
kształt

gr

λ λ

<

Wyboczenie niesprężyste: jest to utrata stateczności pręta w zakresie przekraczającym
zakres Hook’a, gdy napężenia ściskające przekroczą granicę proporcjonalności. W tym
zakresie pojawiają się odkształcenia (niesprężyste), a ich związki z naprężeniami tracą
charakter liniowy. Dla tego zakresu naprężenia krytyczne wyznacza się na podstawie wzorów
empirycznych:

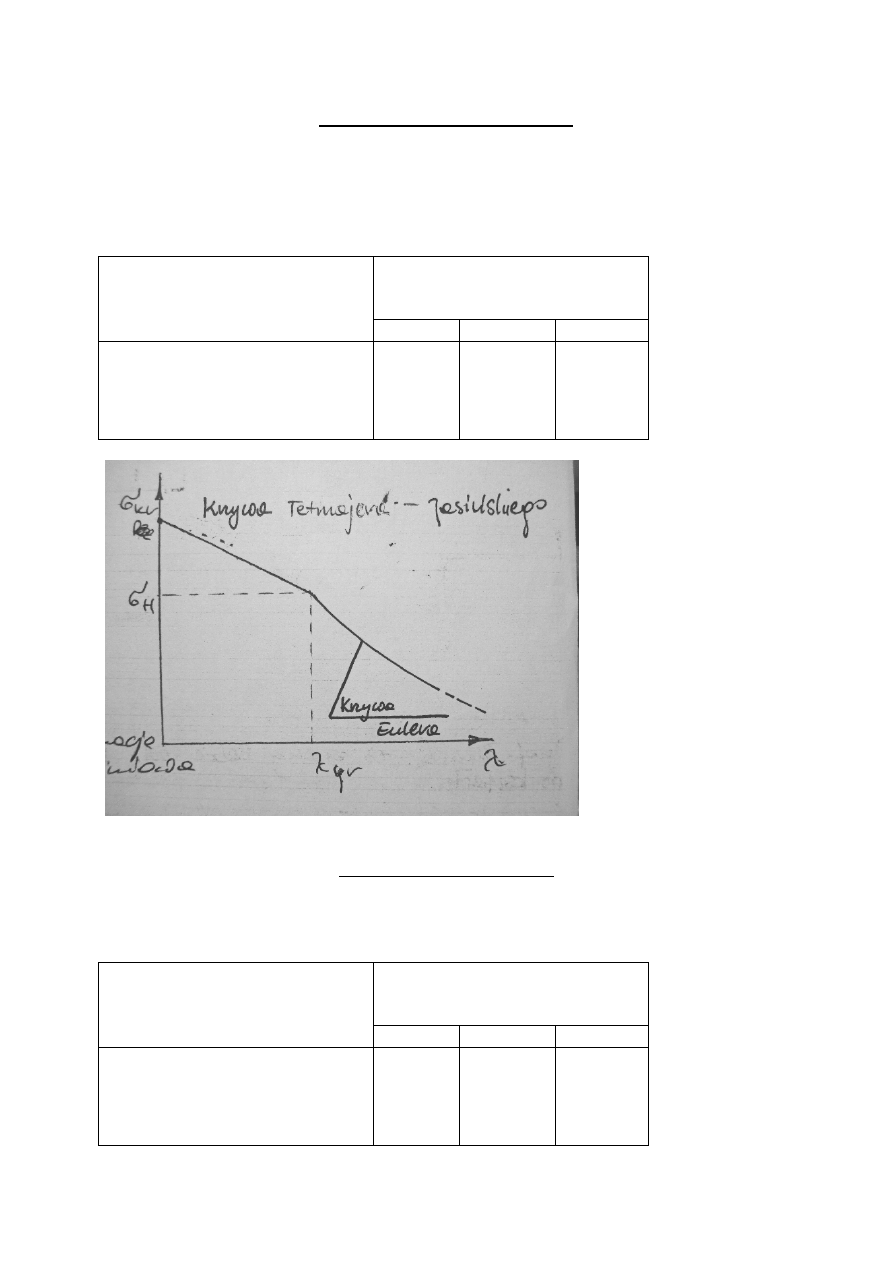
* Wzór Tetmajera – Jasińskiego:

2

kr

a b

c

δ

λ

λ

= −

+

Gdzie: a,b,c – stałe wyznaczane doświadczalnie, charakteryzujące właściwości materiału.
Stałą c stosowano w przypadku żeliwa jako materiału o charakterystyce nieliniowosprężystej.

Wzór Tetmajera – Jasińskiego
współczynniki

Materiał

λgr

a

b

Stal niskowęglowa
Stal (o zawartości 0, 28 037

÷

%C)

Stal niklowa (do 5% Ni)
Drewno miękkie (świerk)

105
100
86
100

310
464
470
29,3

1,14
3,62
2,30
0,194

Po przekroczeniu zakresu Eulerowskiego następuje aproksymacja liniowa.

Wzór Johnsona-Ostenfelda:

2

kr

A

B

δ

λ

= −

A,B – współczynniki materiałowe

Wzór Johnsona-Ostenfelda
współczynniki

Materiał

λgr

a

b

Stal niskowęglowa
Stal (o zawartości 0, 28 037

÷

%C)

Stal niklowa (do 5% Ni)
Drewno miękkie (świerk)

116
84
94
90

310
464
470
29,3

0,0116
0,0260
0,0266
0,002

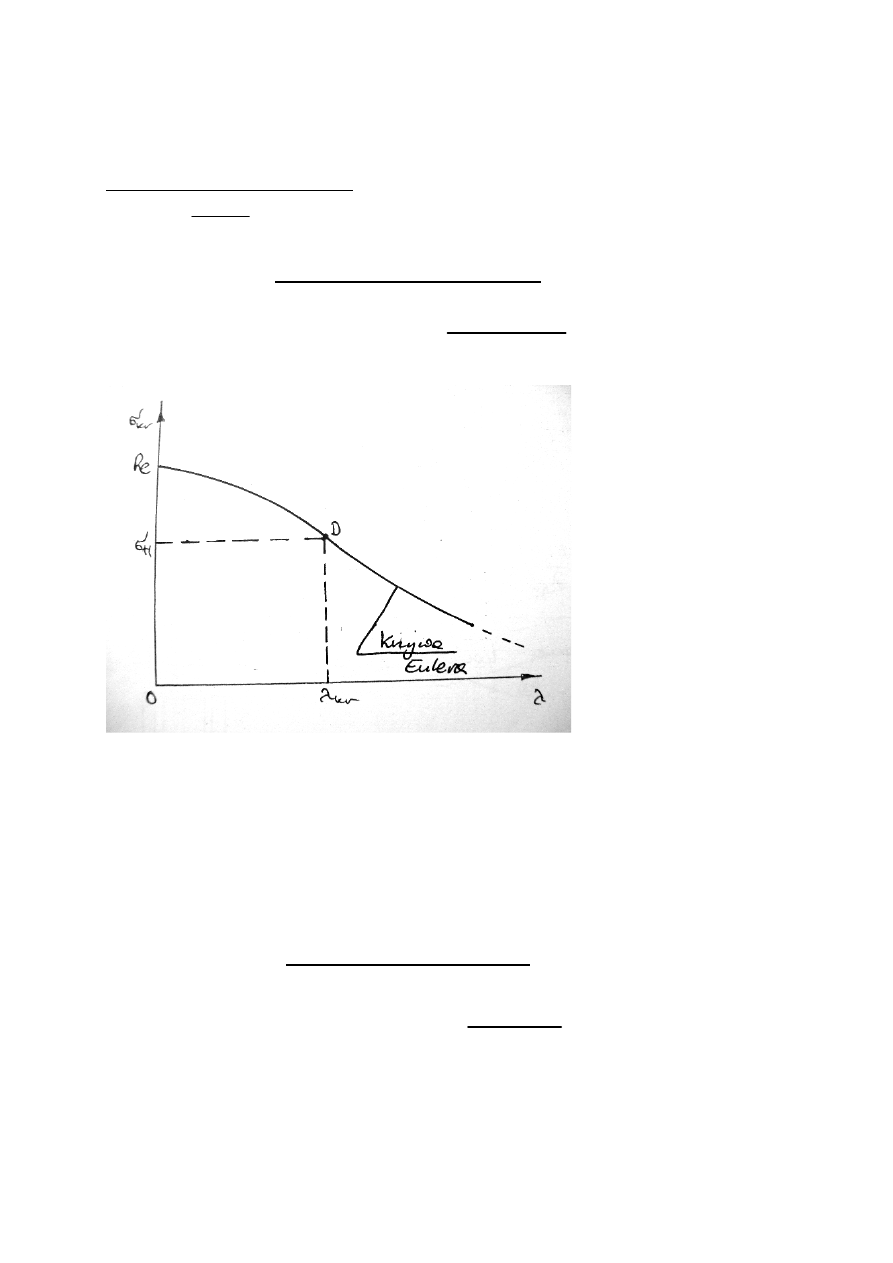
W przypadku znajomości wartości naprężeń przyjmujemy, że krzywa wykresu przechodzi
prez punkt o współrzędnych: λ=0,

Re

kr

δ

=

,

gr

λ λ

=

Stąd otrzymujemy współczynniki:

A=Re;

2

R

e

H

R

B

gr

λ

−

=

KRZYWA Johnsona – Ostenfelda wg wzoru:

2

2

Re

Re

H

R

kr

gr

δ

λ

λ

−

=

−

Dla

H

kr

δ

δ

=

Krzywa Johnsona – Ostenfelda wg wzoru:

2

2

2

Re

Re(1

)

4

kr

E

σ

λ

π

=

−

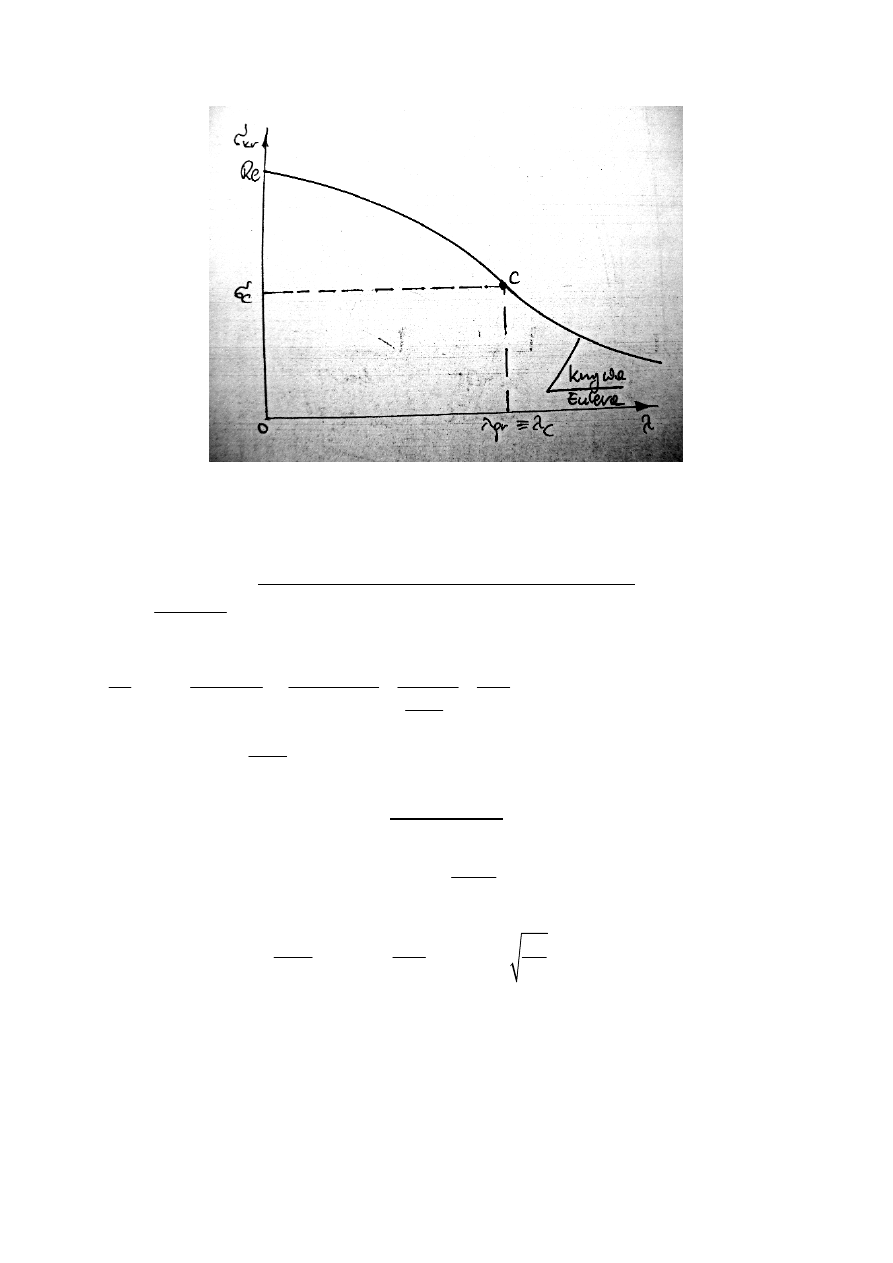
Po przekroczeniu zakresu Eulerowskiego następuje aproksymacja kwadratowa

>>> WYPROWADZENIE wzoru EULERA: <<<

2

2

I min

/ :

(

)

zr

E

Pkr

A

I

π

=

Pkr – siła krytyczna

l

zr

– długość zredukowana

2

2

2

2

2

2

2

2

2

I min

min

( )

( )

(

)

min

kr

kr

kr

zr

zr

zr

P

E

Ei

A

E

E

l

A

l

A

l

A

i

π

π

π

π

σ

σ

λ

=

=

→

=

=

=

λ – smukłość pręta

min

zr

l

i

WZÓR Eulera:

2

2

kr

E

π

σ

λ

=

Jeśli

2

2

2

2

kr

H

H

H

H

E

E

E

R

R

gr

gr

gr

R

R

π

π

σ

λ

λ

π

λ

=

→

=

⇒

=

→

=

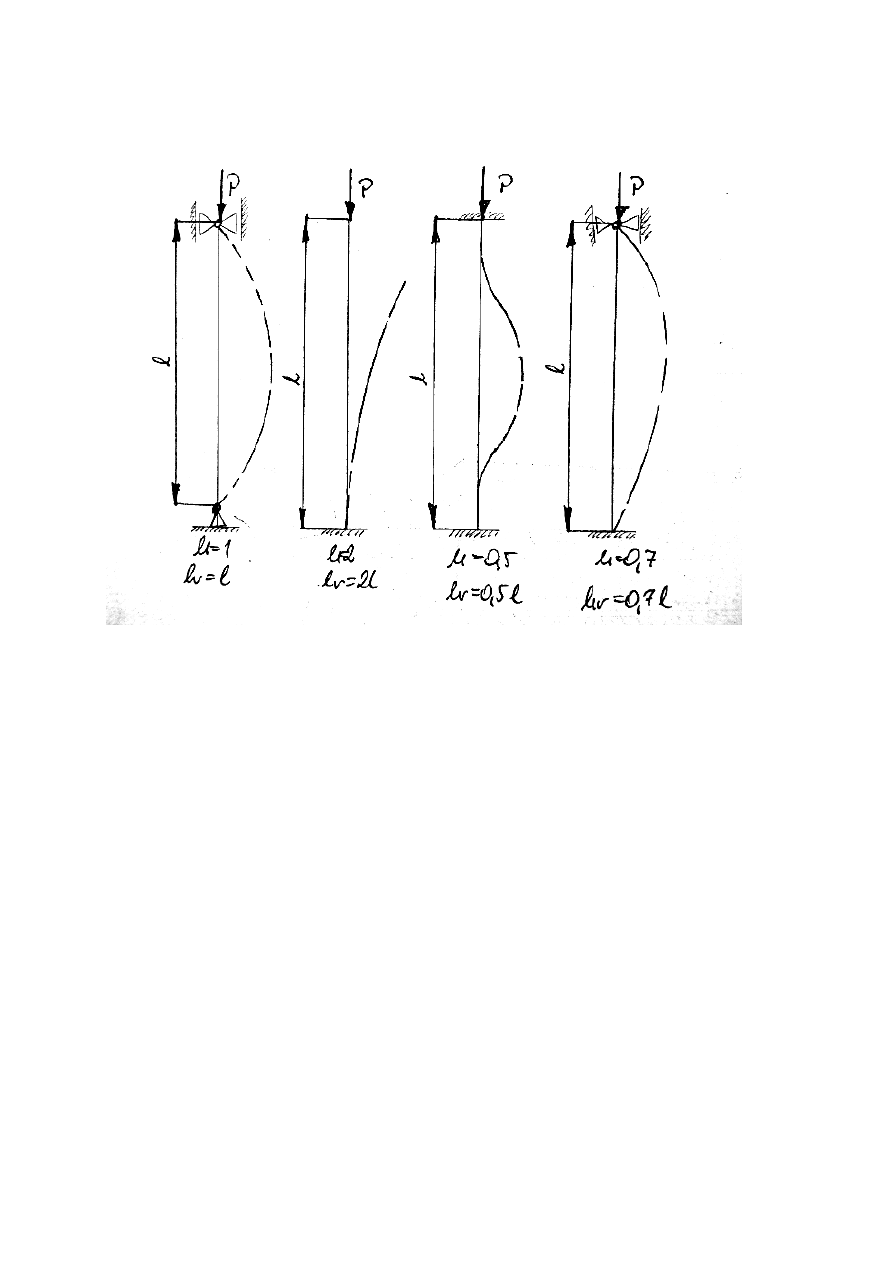
Możliwości zamocowania końców pręta i ich długość zredukowana

Norma PN-90/B-03200 stateczność prętów i płyt.
Stateczność- określeniem tym nazywa się równowagę zachodzącą w przypadku dowolnie
małych początkowych wychyleń z położenia równowagi, w wyniku którego ruch ciała jest
taki że wychylenia jakiegokolwiek z nich nie są większe od początkowych. Niespełnienie
tego warunku prowadzi nas do pojęcia równowagi niestatecznej.

Model równowagi:

Norma PN-90/B-03200 jest normą budowlaną której przedmiotem jest obliczanie i
projektowanie konstrukcji stalowych. Podaje ona podstawowe wartości naprężeń
dopuszczalnych zwanych naprężeniami dopuszczalnymi R. Norma dzieli przekroje wedlug 4
klas:
Przekrój klas I - wartości sił wewnętrznych można wyznaczyć z uwzględnieniem
plastycznego wyrównania momentów, nośność przekroju przy jego uplastycznieniu. W stanie
pełnego uplastycznienia przy zginaniu przekroje klasy I wykazują zdolność do obrotu,
niezbędną do plastycznej redystrybucji momentów zginających.
Przekrój klasy II- wartość sił wewnętrznej należy wyznaczyć w stanie sprężystym, a
nośność przekroju można określić przy jego uplastycznieniu. Przekroje klasy 2 mogą
osiągnąć nośność uogólnionego przegubu plastycznego, lecz w skutek miejscowej
niestateczności plastycznej wykazują ograniczoną zdolność do obrotu, uniemożliwiając
redystrybucję momentów zginających
Przekrój klasy III- wartości sił wewnętrznych oraz nośność przekroju należy wyznaczyć w
stanie sprężystym. Ich nośność jest uwarunkowana początkiem uplastycznienia strefy
ściskowej

max

c

d

f

σ

≤

Przekrój klasy IV- wartości sił wewnętrznych należy wyznaczyć w stanie sprężystym, a
nośność przekroju należy określić z uwzględnieniem utraty stateczności ścianek lub jego
nośność nadkrytyczną. Przekroje klasy 4 tracą nośność przy największych naprężeniach
ściskających( lub średnic ścinających) mniejszych od granicy plastyczności.

Z Wolnego
Podstawy znormalizowanych obliczeń wytrzymałościowych w konstrukcjach prętowych
stalowych podaje norma PN-80/B-03200. W normie tej podano dla stosowanych w kraju
gatunków stali podstawowe wartości naprężeń dopuszczalnych zwanych naprężeniami
obliczeniowymi R (w jednoosiowym stanie naprężenia, rozciąganie, ściskanie, zginanie), R,
(ścinanie), R

d

(docisk). Pierwszą operacją w obliczeniach wytrzymałościowych na

wyboczenie jest określenie długości wyboczeniowęj l

w

, przy czym norma rozszerza

zalecenie

2

2

I min

(

)

zr

E

Pkr

I

π

=

, podając pewne szacunkowe możliwości uwzględnienia

sprężystości umocnień obu końców pręta. Obliczoną smukłość pręta X należy przyrównać do
smukłości X

p

(porównawczej) zależnej od naprężeń obliczeniowych R (dla danego gatunku

stali). Można ją. obliczyć z zależności

1675

p

R

λ

=

gdzie R - wytrzymałość obliczeniowa,

[MPa] lub wyznaczyć z umieszczonej w normie tablicy. Dla danej wartości Xi X

p

obliczonej z

dokładnością 0,01 wyznacza się z tabeli 8.2 wartość współczynnika wyboczeniowego m

w

.

Pręty proste o stałym przekroju, o smukłości X> 0,2 X

p

należy sprawdzić na wyboczenie

według wzoru

w

P

m

R

A

⋅

≤

gdzie: P –sila, A - całkowite pole przekroju pręta.
Pręty osłabione otworami do połączeń śrubowych należy dodatkowo sprawdzić wg wzoru

nt

P

R

A

≤

gdzie

A

nt

- pole przekroju pręta w miejscu osłabionym otworem (tzw. netto).

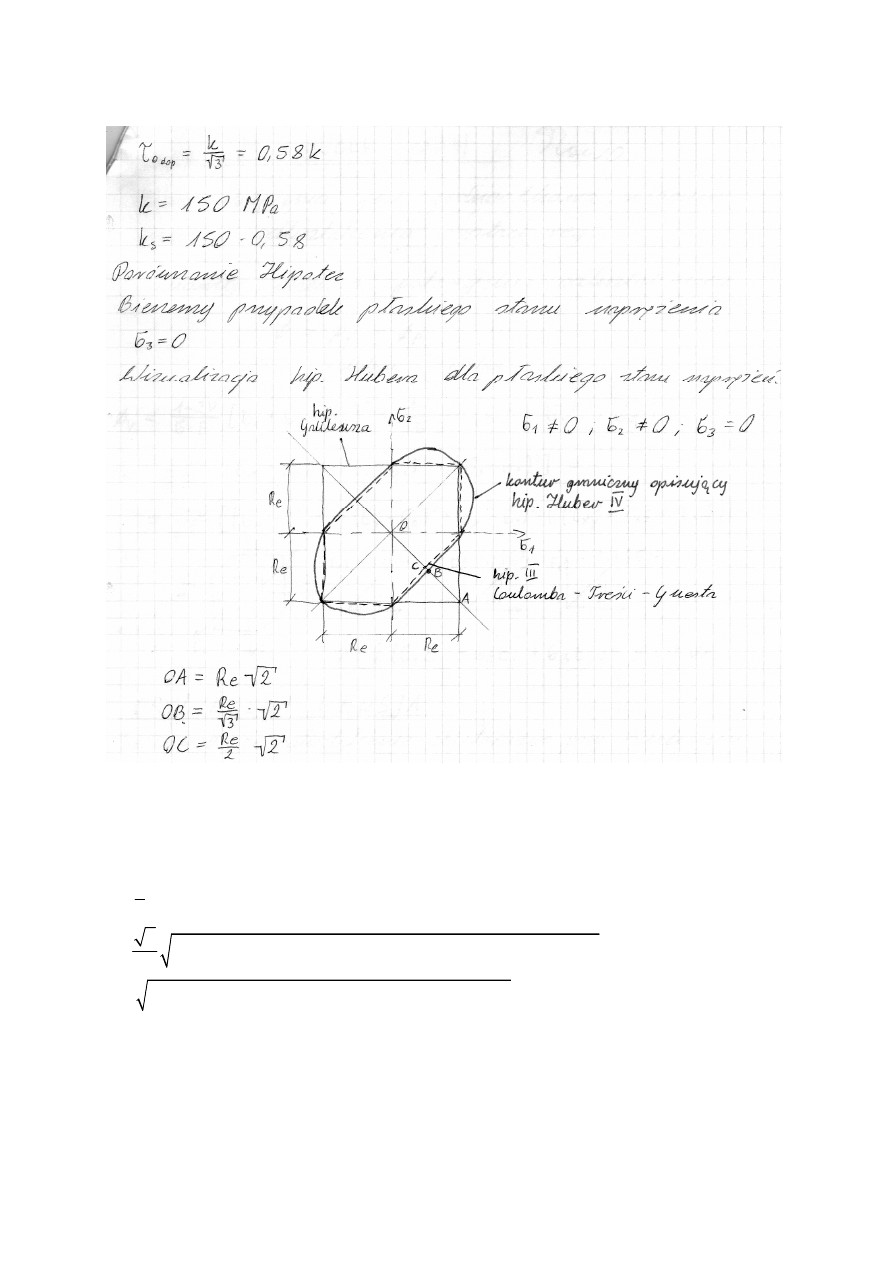
14.Wytężenie. hipotezy wytężeniowe. Zastosowanie hipotez w przypadku jednoczesnego
zginania i skręcania. Obliczenia. Obliczenia wałów.

Przez wytężenie materiału w punktach elementu konstrukcyjnego rozumiemy stan fizyczny
materiału wywołany obciążeniem określającym stopień narażenia go na pojawienie się stanu
niebezpiecznego. Przez stan niebezpieczny dla materiału rozumiemy utratę jego spójności lub
pojawienie się w nim odkształceń trwałych. Wytężenie zależy więc z jednej strony od
własności materiału, a z drugiej strony od składowych stanu naprężeń w danym punkcie
elementu konstrukcji. W ujęciu matematycznym wytężenie określa się jako funkcję
składowych stanów naprężenia W=f(σ

x

, σ

y,

σ

z,

τ

xy

, τ

xz,

τ

yz

). Postać tej funkcji zależy od

odpowiednio postawionej hipotezy wytężeniowej tzw. Hipotezy wytężenia.

Aby określić warunki pojawiania się stanu niebezpiecznego materiału w danym punkcie
elementu poddanego złożonemu stanowi naprężenia należy porównać wartości funkcji
wytężenia dla tego stanu z wartości tej samej funkcji dla stanu wytężenia przyjmującego w
próbce poddanej próbie statycznego rozciągania.

φ(σ

x

, σ

y,

σ

z,

τ

xy

, τ

xz,

τ

yz

)=φ

1

(σ

1

, σ

2,

σ

3

) = f(σ

o

)

jeżeli wartość naprężenia w elemencie będzie równa wartości naprężenia niebezpiecznego Re
to kryterium pojawienia się stanu niebezpiecznego:

φ(σ

x

, σ

y,

σ

z,

τ

xy

, τ

xz,

τ

yz

)=Re

W praktyce nie można dopuścić do powstania stanu niebezpiecznego dlatego wprowadza się
do obliczeń współczynnik bezpieczeństwa n przez który dzielimy granice plastyczności Re i
otrzymujemy naprężenia dopuszczalne: k=Re/n
Porównując naprężenia zastępcze z wartością naprężenia dopuszczalnego k=Re/n otrzymano
warunek wytrzymałościowy:

σ

zr

=(σ

x

, σ

y,

σ

z,

τ

xy

, τ

xz,

τ

yz

)= φ

1

(σ

1

, σ

2,

σ

3

)≤k

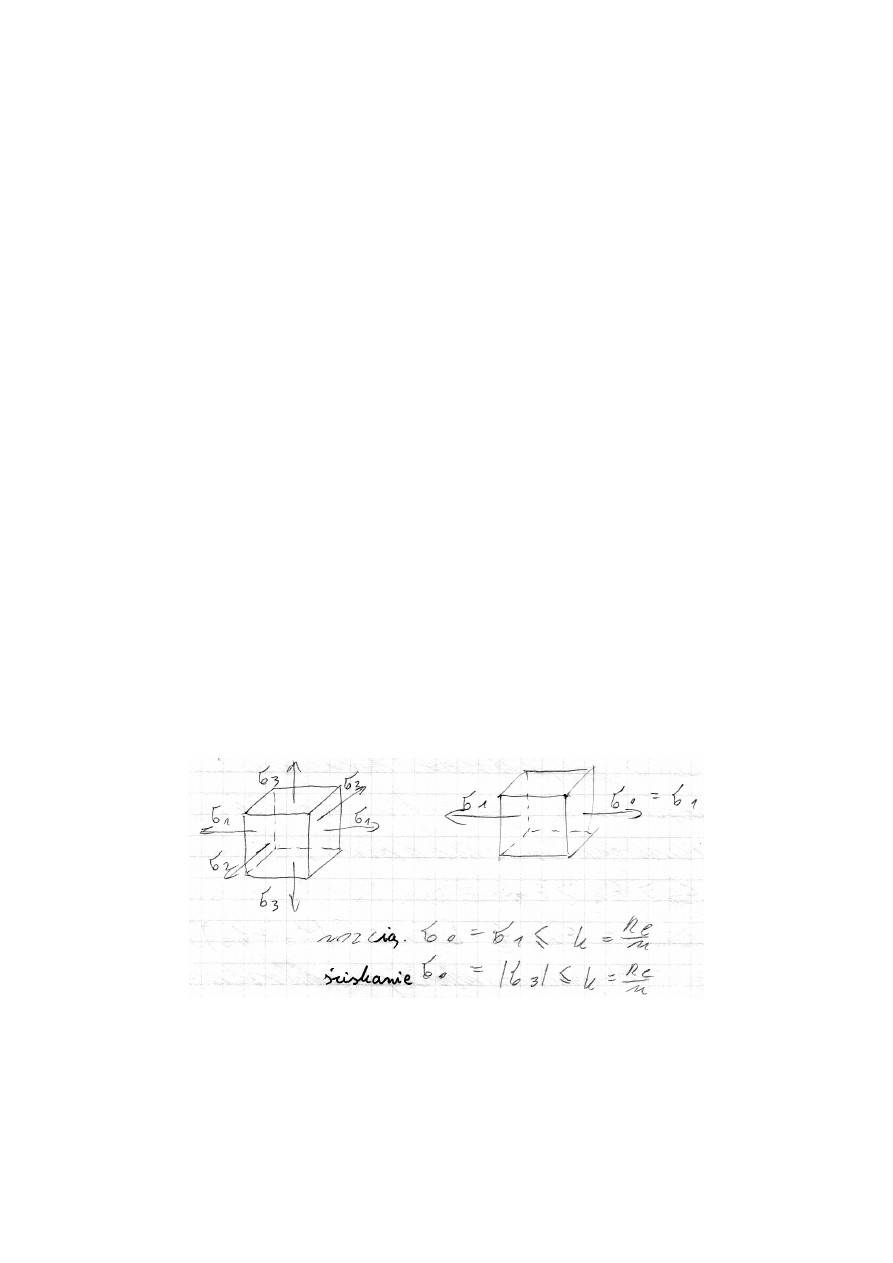
I.

Hipoteza największego naprężenia normalnego; postawili ją Galileusz (1638),
Leibniz (1684).

Miarą wytężenia jest największe naprężenie normalne.

Jak widać dla przestrzennego stanu naprężenia określanego składowymi głównymi σ

1

, σ

2,

σ

3

,

wytężenie zależy tylko od największego naprężenia σ

1

. Natomiast nie zależy od dwóch

pozostałych. Warunek ten pozostaje w sprzeczności z wynikami doświadczenia dotyczącego
złożonego stanu naprężeń.

II.

Hipoteza de ST. Venanta

III.

Hipoteza największych naprężeń stycznych. Coulomb (1776); potwierdzili Guest
(1900) i Tregca (1872).

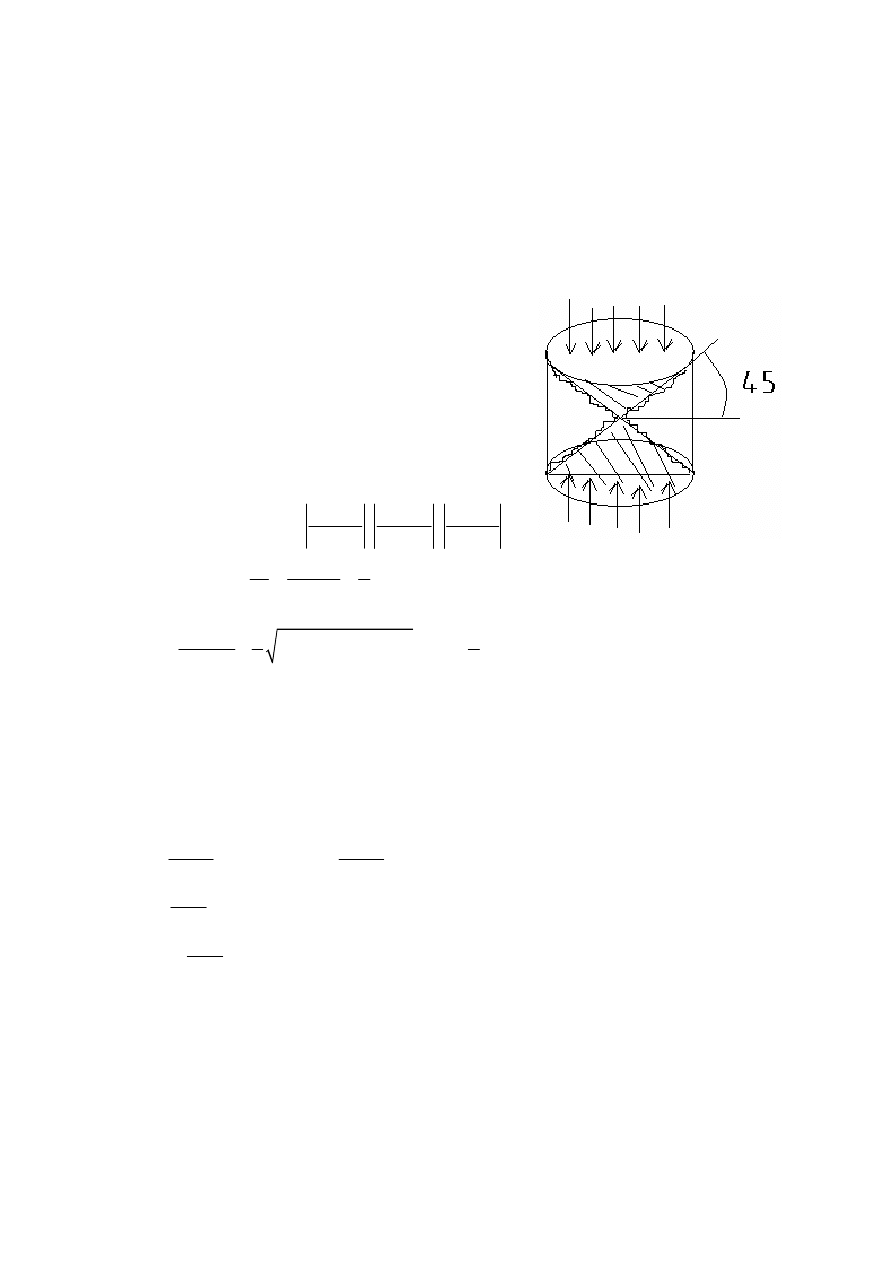
U podstawy tej hipotezy leżą dwa doświadczenia: Próbka betonowa w kształcie walca
poddana równomiernemu ściskaniu. Na ściankach czołowych niszczy się w sposób
charakterystyczny, a mianowicie w momencie zniszczenia tworzą się dwa stożki których
tworzące nachylają się do płaszczyzny pod określonym kątem 45

0

. W których występują

maksymalne naprężenia styczne.
Jeżeli stalowy płaskownik poddamy rozciąganiu
powyżej granicy plastyczności pojawią się matowe
prążki zwane liniami Ludersa, nachylone pod kątem
45

0

, co świadczy że tam pojawią się maksymalne

naprężenia styczne czyli największe wytężenie
materiału w przekrojach maksymalnych naprężeń
stycznych. Hipoteza ta przyjmuje za miary wytężenia
maksymalne naprężenia styczne.

2

3

3

1

1

2

max

1

3

1

1

max

(

)

max

;

;

2

2

2

0

2

2

2

C T

G

k

σ σ σ σ

σ σ

τ

σ σ

σ

σ

τ



−

−



−

− −

=









−

≠

=

=

≤

W ujęciu składowych dowolnych:

(

)

2

2

1,3

0

1

4

2

2

2

x

y

x

y

k

xy

σ σ

σ

σ σ

τ

σ

+

=

±

+

+

=

≤

Tą hipotezę można stosować dla materiałów których R

er

=R

ec

(rozciąganie = ściskanie).

IV.

Hipoteza M.T. Huber (1904).

Miarą wytężenia jest jednostkowa, właściwa energia odkształcenia postaciowego.
Całkowita energia potencjalna odkształcenia:

v

p

φ φ φ

= +

v – objętości; p – postaci

[

]

(

)

(

) (

) (

)

(

) (

)

(

)

(

)

2

2

2

2

1

2

3

x

y

z

2

2

2

1

2

2

3

3

1

2

2

2

2

2

2

x

y

y

z

x

z

xy

xz

yz

1 2

1 2

1

1

v

p

V

V

E

E

V

E

V

E

φ

σ σ σ

σ

σ

σ

σ

σ

φ

σ σ

σ σ

σ σ

σ

σ σ

σ σ

σ σ

σ σ

σ

σ

σ

−

−

=

+

+

=

+

+

⋅

⋅

+





=

−

+

−

+

−

=





⋅

+





=

−

+

−

+

−

+

+

+









⋅

Oryginalna wersja: Zważywszy że odkształcenie objętościowe przy ściskaniu nie wpływa
na niebezpieczeństwa pęknięcia, można z wielkim prawdopodobieństwem uważać energię
potencjalną za miarę wytężenia. Wniosek ten wysunął się Huberowi przy rozważaniu
wytężenia materiału w przypadku trójosiowego równomiernego ściskania.

Współcześnie hipoteza Hubera: Miarą wytężenia materiału jest ilość nagromadzonych w
nim energii odkształcenia postaciowego niezależnie od tego czy wartość energii powstała
w przypadku jednoosiowego czy przestrzennego stanu naprężeń.

V.

Hipoteza prof. Burzyńskiego (1928).

Wytężenie materiału jest wyrażone jako funkcja 3 niezmienników stanu naprężeń.

(

)

, ,

W

F s t u

=

(

)

(

)

(

)

(

)

x

y

z

2

2

2

2

2

2

x

y

z

y

z

z

x

x

y

2

2

2

x

y

z

x

y

z

1

3

2

3

3

2

xy

xz

yz

xy

xz

yz

yz

xz

xy

s

t

u

σ σ σ

σ

σ

σ

σ σ σ σ σ σ

τ

τ

τ

σ σ σ

τ

τ

τ

σ τ

σ τ

σ τ

=

+

+

=

+

+

−

−

−

+

+

+

=

+

+

+

−

−

−

Wytężenie to:

( )

,

W

F s t

=

u – ma bardzo małe znaczenie dla wytężenia materiałów.

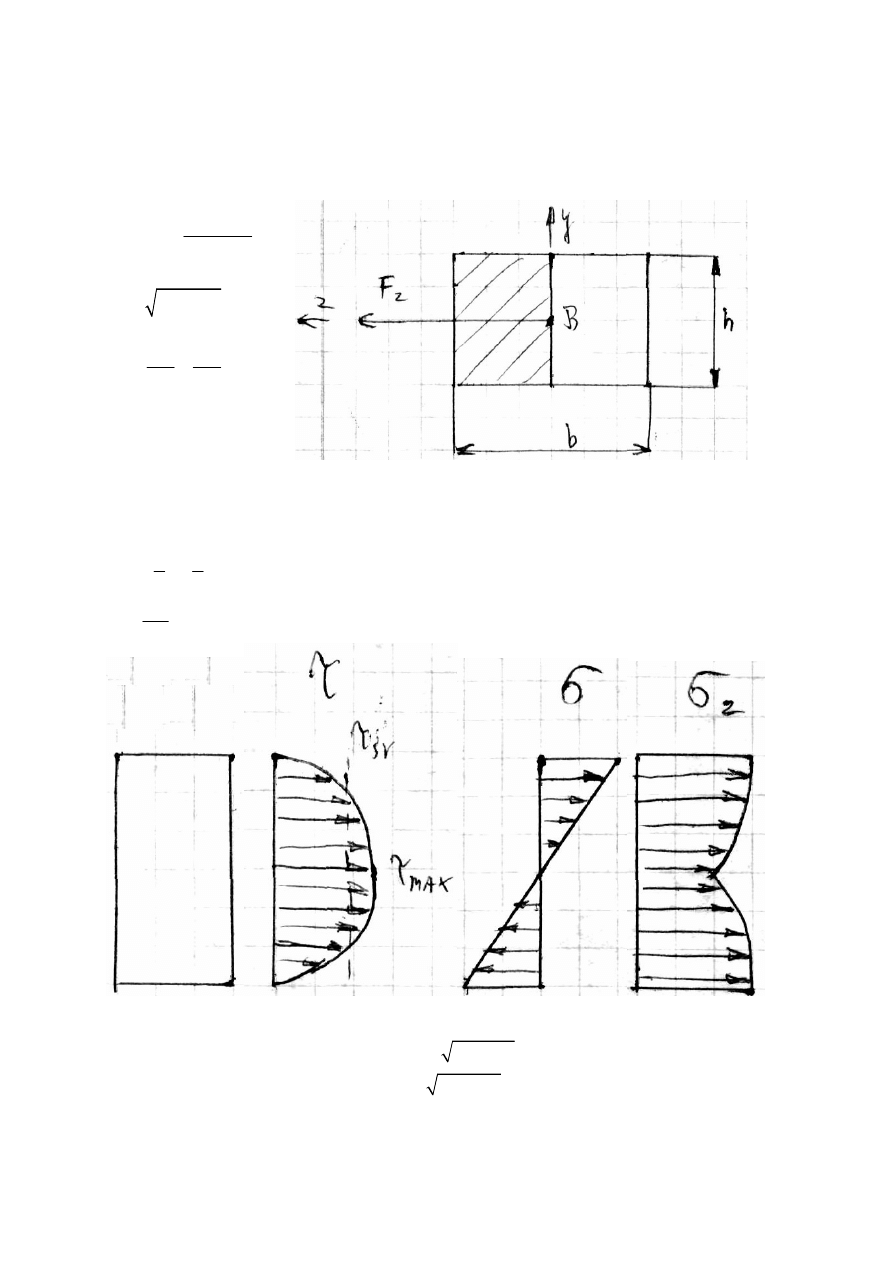
15. Zginanie ze ścinaniem. Obliczanie belek o przekrojach złożonych.
Jest to taki przypadek wytrzymałości złożonej gdzie po zredukowaniu sił zewnętrznych
działających po jednej stronie myślowo przekroju względem środka ciężkości otrzymamy
moment zginający i siłę tnącą.

( )

( )

od

x

yz

sc

x

T z S

I

b z

τ

τ

⋅

=

=

⋅

2

2

3

z

g

sc

σ

σ

τ

=

+

g

g

g

g

z

M

M

y

W

I

σ

=

=

odc

S

A

=

A - powierzchnia ścinania od środka ciężkości od punktu
S

odc

– moment styczny części przekroju belki ograniczonej rzędną y i konturem przekroju

względem osi obojętnej z.

2

4

odc

b

b

S

h

= ⋅ ⋅

3

12

y

b h

I

=

Naprężenia zastępcze można liczyć według dwóch hipotez:

H-M-H

2

2

3

z

z

k

σ

σ

τ

=

+

≤

T-G

2

2

4

z

z

k

σ

σ

τ

=

+

≤

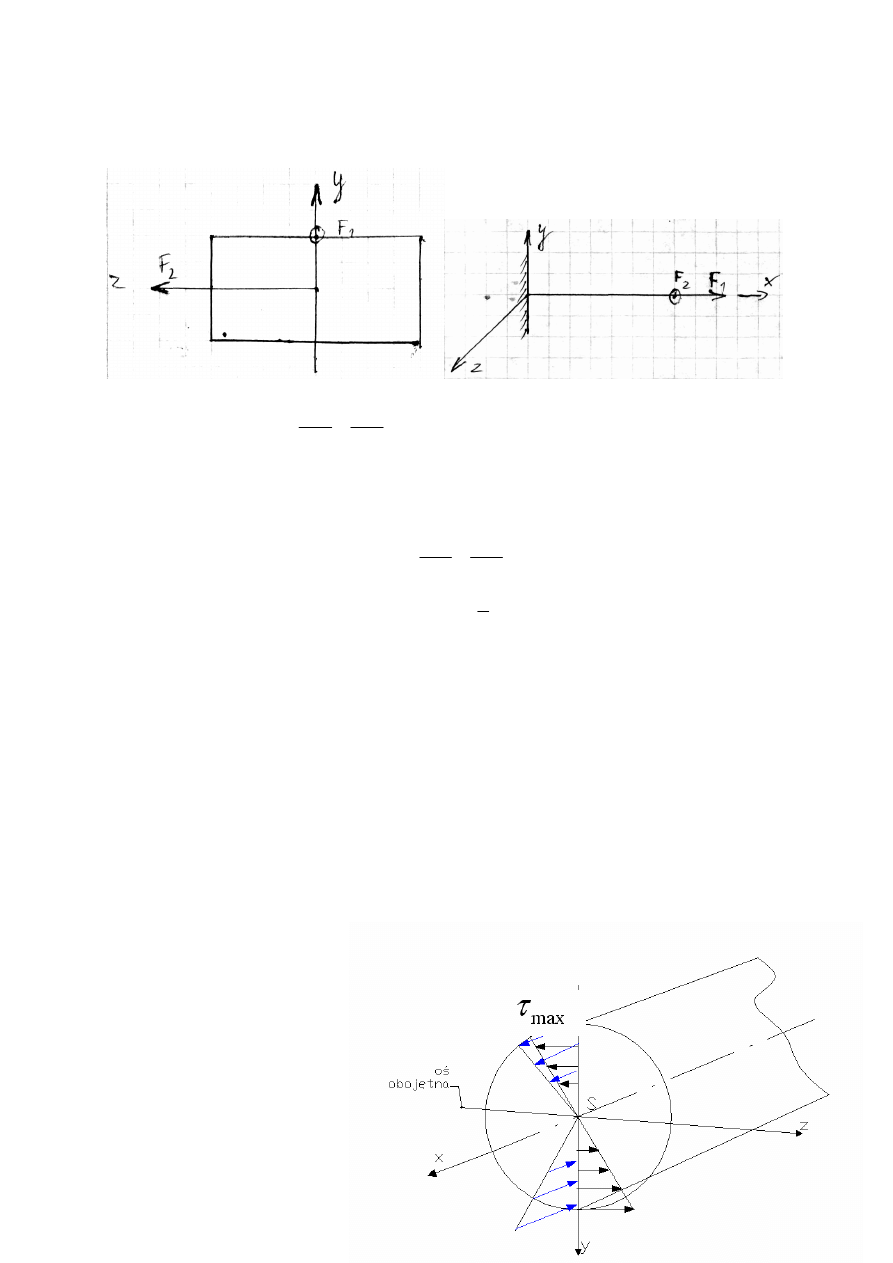
Zginanie na oś y:

y

y

y

y

g

g

g

g

y

M

M

z

W

I

σ

=

=

- naprężenie w punkcie przekroju

2

y

g

M

F I

=

⋅

Zginanie na oś z:

z

z

z

z

g

g

g

g

z

M

M

y

W

I

σ

=

=

2

2

z

g

h

M

F

=

⋅

Zginanie mimośrodowe
Jest to taki przypadek zginania, w którym na wynik redukcji sił zewnętrznych działających po
jednej stronie myślowego przekroju względem środka ciężkości otrzymamy siłę ściskającą (
rozciągającą) i 2 momenty gnące

x

p

M

P y

= ⋅

y

p

M

P x

= ⋅

16

Zginanie i skręcanie wałów o przekroju kołowym. Pojęcie momentu zastępczego

zredukowanego. Wyprowadź wzory na moment zastępczy w przypadku hipotezy
największych naprężeń statycznych i energii właściwej odkształcenia postaciowego.

Aby wyznaczyć naprężenia w
dowolnym punkcie przekroju
wału, należy określić wartości
momentu zginającego M

g

i

skręcającego M

s.

Dla wału

okrągłego o średnicy d
największe wartości naprężeń
składowych oblicza się ze
wzorów:
-normalne

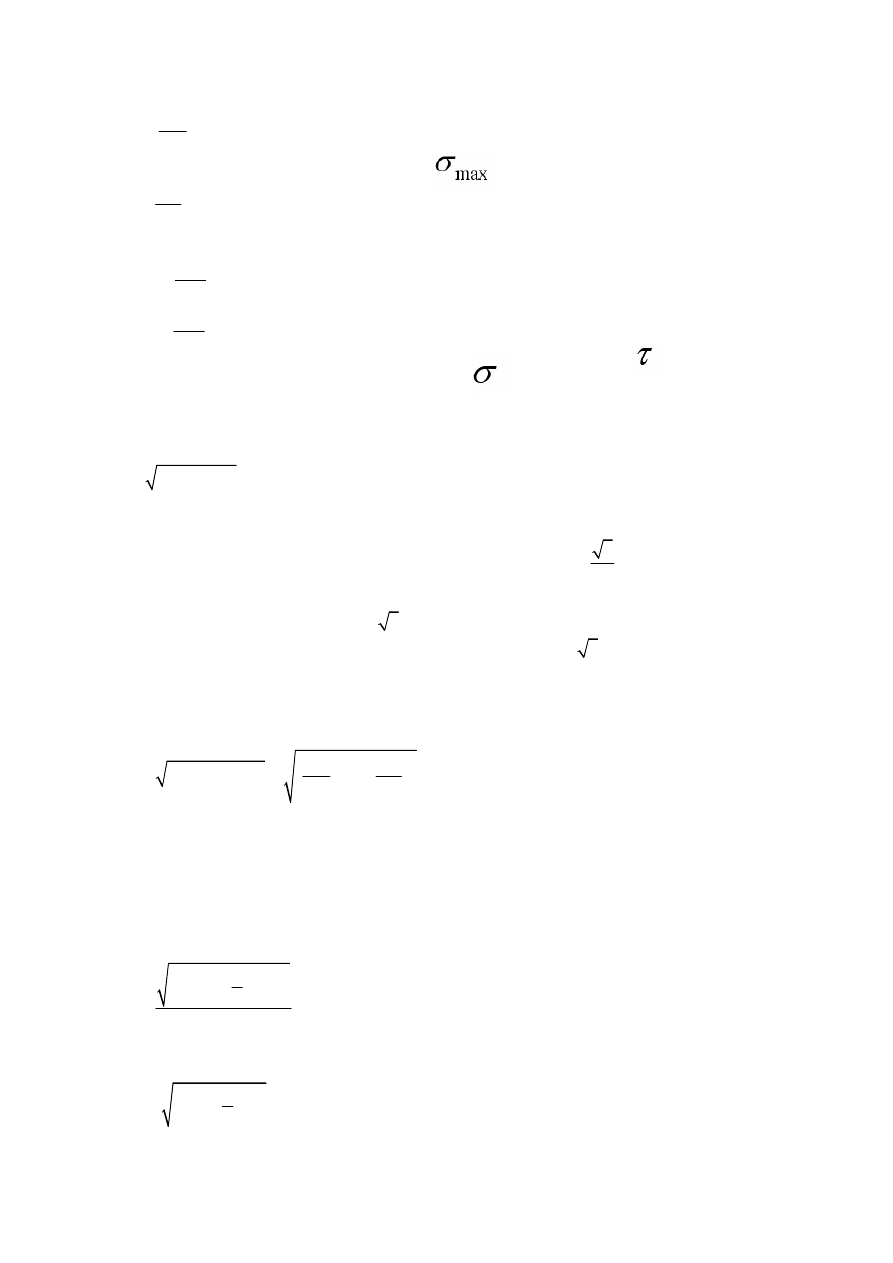
max

g

g

M

W

σ

=

-styczne

max

0

s

M

W

τ

=

Rozkład naprężeń jest proporcjonalny do

odległości

od osi

obojętnej dla naprężeń normalnych

σ

i

proporcjonalny do odległości od

środka ciężkości przekroju dla naprężenia stycznego

τ

.

Wartość naprężenia zredukowanego przy uwzględnieniu zmienności obciążeń:

2

2

(

)

z

m

σ

σ

τ

=

+

m- współczynnik redukujący naprężenia styczne do normalnych

•

Dla obustronnego zginania i jednostronnego skręcania

3

2

m

=

•

Dla obustronnego zginania i obustronnego skręcania lub jednostronnego zginania i

jednostronnego skręcania

3

m

=

•

Dla jednostronnego zginania i obustronne skręcanie

2 3

m

=

•

Uważając, że dla materiałów sprężysto-plastycznych (stal) najstosowniejsza jest hipoteza
energii odkształcenia postaciowego:

2

2

2

2

max

max

0

3

(

)

3(

)

g

s

red

dop

g

M

M

W

W

σ

σ

τ

σ

=

+

=

+

≤

Dla przekrojów kołowych:

0

2

g

W

W

=

Zatem:

2

2

3

(

)

(

)

4

g

s

red

g

M

M

W

σ

+

=

Moment zastępczy (zredukowany):

2

2

3

4

red

g

s

M

M

M

=

+

3

3

0

32

16

g

d

W

d

W

π

π

=

=

17. Metoda energetyczna wyznaczania przemieszczeń w układach prętowych.
Przemieszczenie uogólnione. Siła uogólniona. Energia sprężysta w typowych układach
wytrzymałościowych. Twierdzenie Castigliano, Maxwella Mohra, Wereszczagina.

Uogólnione tw. Castigliano:
Pochodna energii uzupełniającej względem wartości uogólnionej siły P, równa jest
odpowiadającej tej sile przemieszczeniu uogólnionemu u. Twierdzenie to wyraża równanie:

i

i

i

P

V

u

∂

∂

=

Twierdzenie Castigliano znalazło swoje zastosowanie w układach liniowo sprężystych.
Pochodna cząstkowa energii sprężystej całego układu liniowo sprężystego względem jednej z
niezależnie działających sil obciążających jest równa odpowiadającemu tej sile
przemieszczeniu.

i

i

i

P

V

u

∂

∂

=

W układach linowo sprężystych energia U układu, równa pracy sił wewnętrznych, na

odpowiadających im przemieszczeniach określa się wzorem :

∑

=

i

i

P

U

δ

2

1

a po podstawieniu do wzoru

∑

−

=

V

P

U

i

i

i

δ

o otrzymuje się U

i

=U

Czyli nasza praca

EA

l

P

L

P

L

2

1

2

1

=

∆

=

EA

Pl

l

=

∆

Wykres linowo sprężystej siły P i przemieszczenia δ

i

dz

EJ

N

U

dz

EJ

M

U

dz

ksEJ

M

U

dz

EA

k

T

U

s

RC

s

g

s

s

t

ii

∫

∫

∫

∫

=

=

=

=

2

2

2

2

2

2

2

δ

δ

δ

U

c

=100%=U

g

dz

EI

M

g

∫

=

2

2

dz

sztywnosc

W

U

RC

∫

=

)

(

2

2

A więc przemieszczenie

∫

∫

∂

∂

=

∂

∂

=

∂

∂

=

l

i

l

i

i

g

i

dz

P

z

Mg

EI

z

Mg

dz

EI

z

Mg

P

P

U

P

i

0

(

*

2

)

(

2

2

)

(

)

(lub

2

δ

Rys. do Castigliano

Metoda obliczeniowa z tw. Castigliano .
Jeżeli w zagadnieniu poszukiwane przemieszczenie odpowiada sile rzeczywiści działającej, to
zastosowanie tw. Castigliano nie nastręcz żadnych trudności. Jeżeli natomiast poszukuje się
przemieszczenia , dla którego kierunku brak rzeczywistej siły, należy po prostu założyć w
schemacie obciążeń siłę odpowiadającą poszukiwanemu przemieszczeniu, aby po
zróżniczkowaniu podstawić jej rzeczywistą wartość równą zero.

Metoda Maxwella-Mohra

Układ sił obciążenia zewnętrznego powoduje pojawienie się na włóknach belki
elementarnych sił wewnętrznych:
- siły podłużnej N

i

- siły poprzecznej T

i

-momenty gnące Mg

i

Metoda Maxwella-Mohra wyrażana jest zależnością

∑ ∫

=

=

h

i

l

i

dl

MgMg

EI

1

0

1

1

δ

Mg-moment pochodnej od siły rzeczywistej
Mg

1

-moment pochodzący od siły jednostkowej

Podobnie z siłami podłużnymi i poprzecznymi.

Ogólne wyrażenie na przemieszczenie w metodzie Maxwella-Mohra.

∑

∑

∑

+

+

=

li

si

i

i

i

i

i

li

si

i

i

i

i

i

li

si

i

i

i

i

d

I

E

Mg

Mg

d

A

G

T

T

d

A

E

N

N

f

'

'

'

β

β

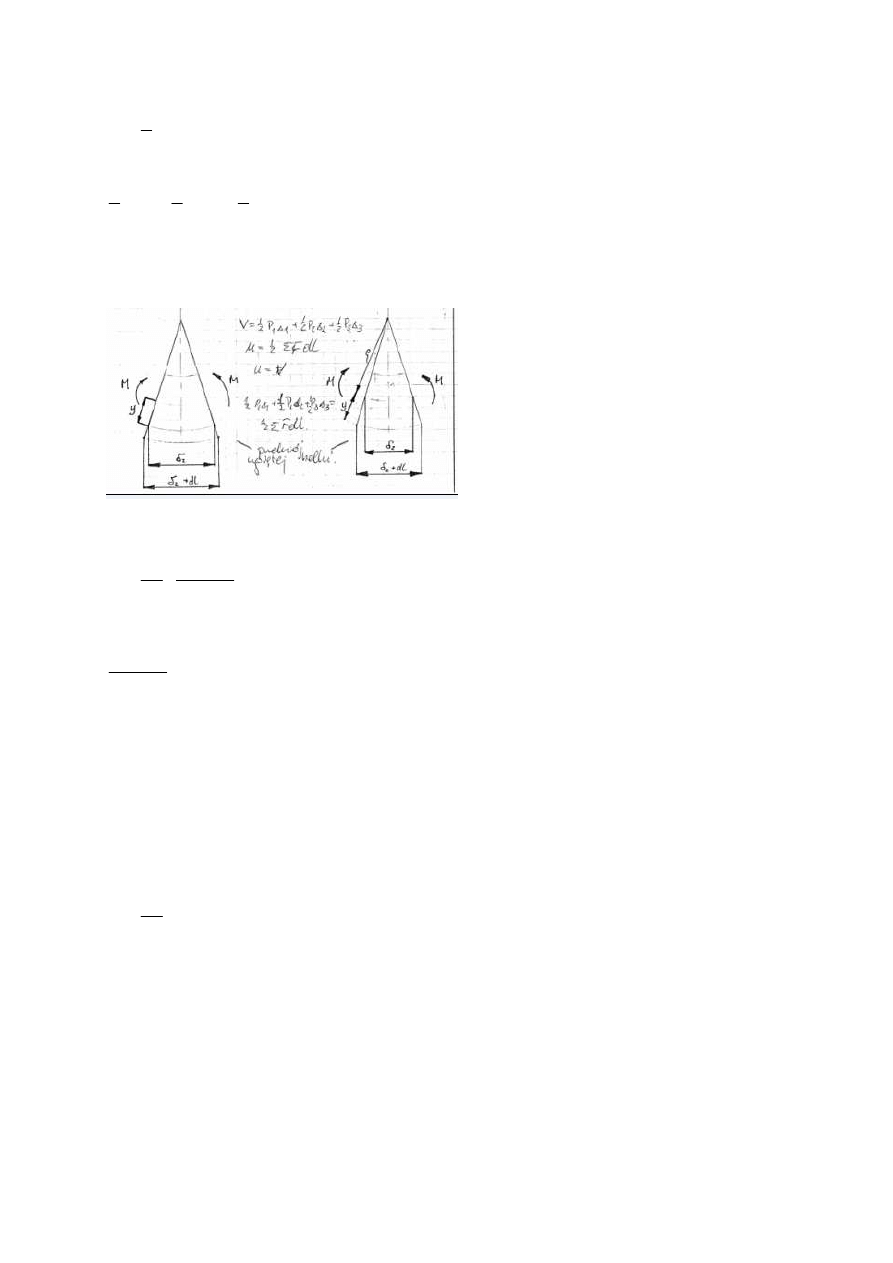
Metoda Maxwella-Mohra polega na obciążeniu belki siłą jednostkową w pkt. c rzędnego
przemieszczenia i na jego kierunku, które spowoduje pionowe przemieszczenie tego pkt.
równe odpowiednio w pkt. 1,2,3 przemieszczeni ∆1, ∆2, ∆3. Następnie rozpatrzymy belkę z
obciążeniem zewnętrznym. Wówczas całkowite przemieszczenie będzie równe

1

;

1

∆

=

∆

+

i

c

c

δ

δ

Zakładając stopniowe obciążenie jednostkowe przyłożone jako pierwsze związek między

pracą a energią wewnętrzną w postaci

∑

=

ndl

c

2

1

)

0

,

1

(

2

1

δ

n= osiowa siła rozciągająca
dl= całkowite wydłużenie
Przyjmując stopniowe obciążenie belki siłami P

1,

P

2,

P

3

praca sił zewnętrznych wynosi

c

P

P

P

V

∆

+

∆

+

∆

+

∆

=

)

0

,

1

(

2

1

2

1

2

1

3

3

2

2

1

1

'

Człon (1,0)δ

c

- praca przygotowana przez układ P

1,

P

2,

P

3

w pkt C

∑

∑

+

=

udl

Fdl

U

2

1

'

Z zasady równoważności energii i pracy mamy:

∑

∑

∑

∑

=

∆

+

∆

+

∆

+

∆

+

∆

+

∆

+

udl

c

udl

c

udl

c

P

P

P

c

)

0

,

1

(

2

1

2

1

)

0

,

1

(

2

1

2

1

2

1

)

0

,

1

(

2

1

3

3

2

2

1

1

δ

Dla przygotowanej belki mamy:

∫

∫

∫

∫

∑

∫ ∫

∑

=

∆

⇒

=

=

⇒

=

∆

l

l

A

l

l

A

dz

EI

Mm

dz

EI

Mm

c

dA

y

dz

EI

Mm

EJ

dAdz

mMg

dA

E

Mg

dA

J

mJ

udl

c

0

0

0

2

0

0 0

2

2

0

,

1

)

)(

(

)

0

,

1

(

∆

+

∆

+

∆

=

3

2

2

1

1

'

2

1

2

1

2

1

P

P

P

V

y

P

P

P

V

U

Fdl

U

=

∆

+

∆

+

∆

=

=

∑

3

2

2

1

1

2

1

2

1

2

1

2

1

Schemat i wzór obliczeniowy na przemieszczenie metodą Castigliano:

dx

P

x

Mg

EI

f

∫

∂

∂

=

)

(

1

(b)

P

x

Mg

∂

∂

)

(

-różniczka cząstkowa z momentu podług siły P

1)

Siła działa w kierunku szukanego przemieszczenia wtedy działa wzór(b) i w pkt
szukanego przemieszczenia

2)

Jeżeli siła nie działa w kierunku szukanego przemieszczenia i w jego pkt na belce
(ramie) należy przyłożyć siłę o wartości rzeczywistej 0. Po wykonaniu obliczeń
podstawić wartość zerowej siły

Metoda Maxwella- Mohra

dx

x

Mg

x

Mg

EI

f

∫

=

)

(

)

(

1

'

(c)

Mg(x)-moment od siły jednostkowej

W metodzie Maxwella-Mohra zamiast poszukiwania różniczki momentu podług siły, dany
element obciąża się siłą jednostkową (dla kąta momentem) i oblicza się przemieszczenie ze
wzoru(c). Siłę należy przyłożyć w pkt poszukiwanego przemieszczenia

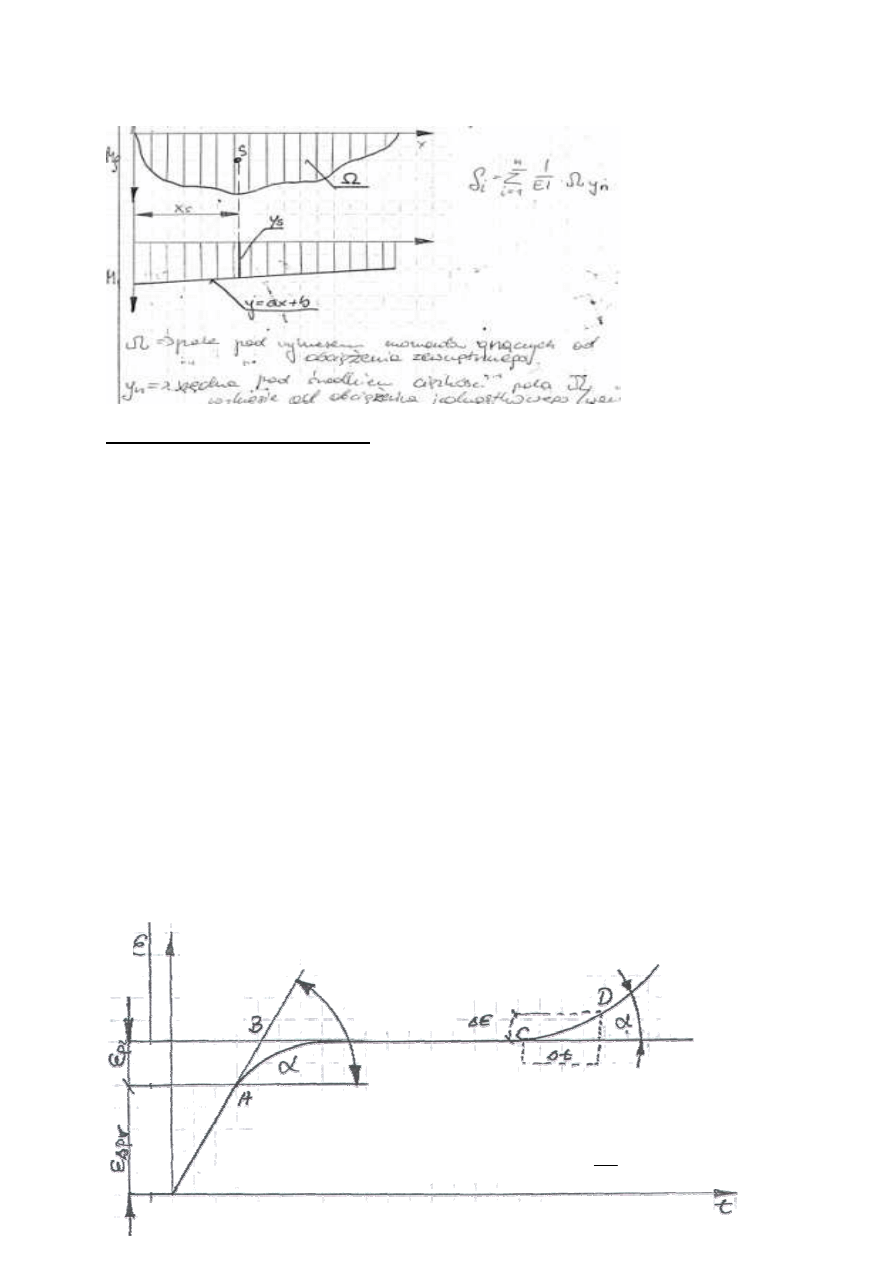
Sposób Wereszczagina- graficzny sposób wyznaczania przemieszczenia

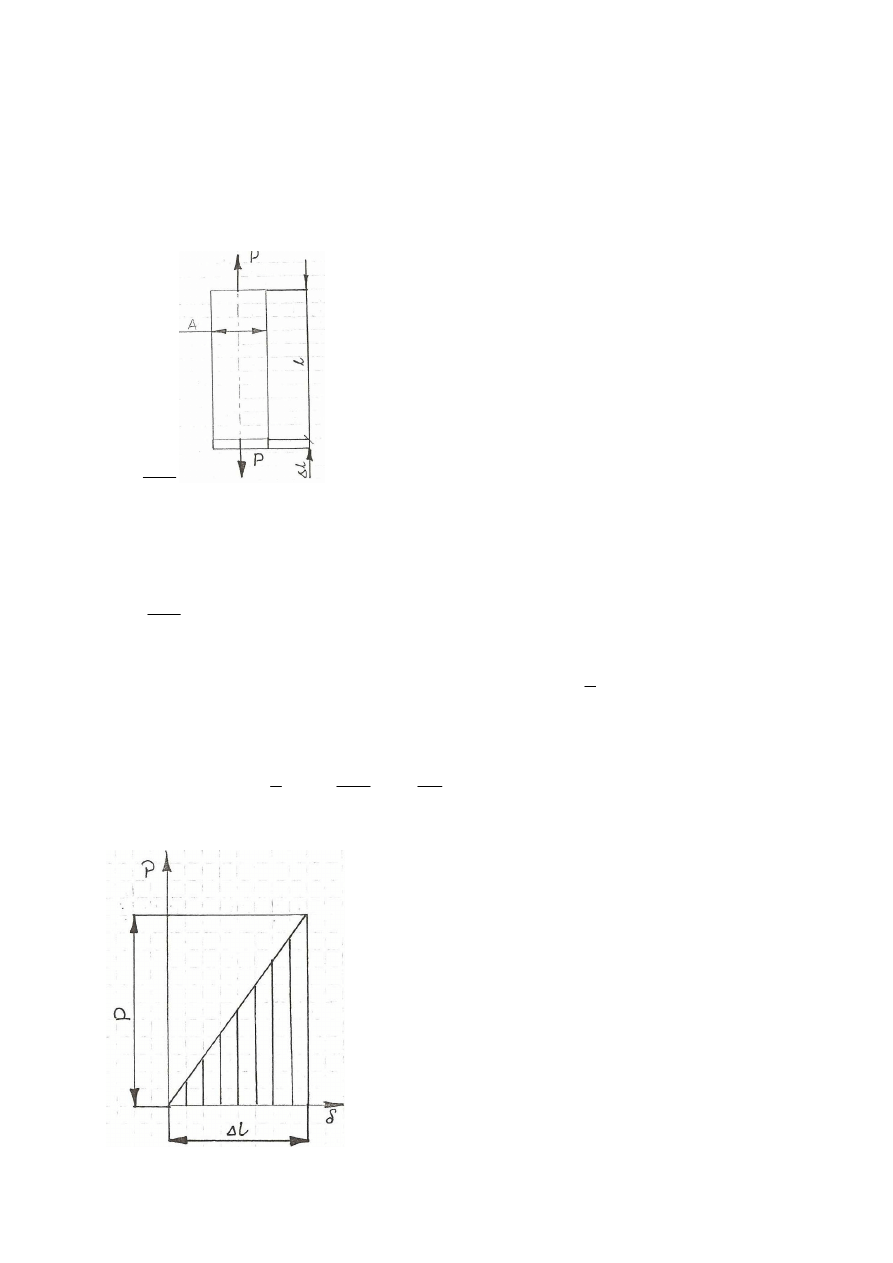
19. Pełzanie i relaksacja naprężeń.

Reologia- nauka zajmująca się badaniem odkształceń zmieniających swoją wartość w czasie.
Podstawowymi procesami reologicznymi są pełzanie i relaksacja. Pełzanie- jest to zjawisko
powolnego odkształcenia się ciala pod wpływem długotrwałych obciążeń. Zjawisko to
występuje w elementach konstrukcji poddanych obciążeniom o ustalonych wartościach.
Elementy te ulegają odkształceniom niesprężystym. Zjawisko pełzania w przypadku stali
najlepiej widoczne jest w podwyższonych temp. Stopy lekkie czy tworzywa sztuczne ulegają
już w temp. pokojowej. Według Bluma: pełzanie jest to ciągły wzrost z czasem odkształceń
materiału poddanego działaniu stałych co do wartości naprężeń przy podwyższonej temp.
Działanie temp. będzie powodować odkształcenie wzrastające w miarę wpływu czasu.
Elementy podlegające pełzaniu: rury ciśnieniowe pracujące w podwyższonych temp., łopaty
turbin. Relaksacja naprężeń- jest to charakterystyczne zjawisko towarzyszące pełzaniu,
polega na zmniejszeniu się naprężeń w elementach poddanych długotrwałemu obciążeniu o
stałej wartości. Występuje w śrubach kołnierzowych pracujących w wyższych temp.
Naciągnięte śruby ulegają z biegiem czasu zwiększającym się odkształceniom niesprężystym
co prowadzi do zmniejszenia się wartości naprężenia, w konsekwencji do zmniejszenia
szczelności połączenia, przez co należy okresowo dokręcać śruby. Granica pełzania- iloraz
stałego obciążenia i przekroju początkowego próbki, które to obciążenie po upływie
określonego czasu działania w danej temp. spowoduje trwałe wydłużenie próbki o określoną
wartość. Wytrzymałością na pełzanie nazywa się iloraz stałego obciążenia i przekroju
początkowego próbki, które to obciążenie po upływie określonego czasu działania w danej
temp spowoduje rozerwanie próbki. Najczęściej stosując się w badaniach nad relaksacją

p

p

T

const

V

prędkosc

pelzania

V

tg

t

ε

α

=

−

∆

=

=

∆

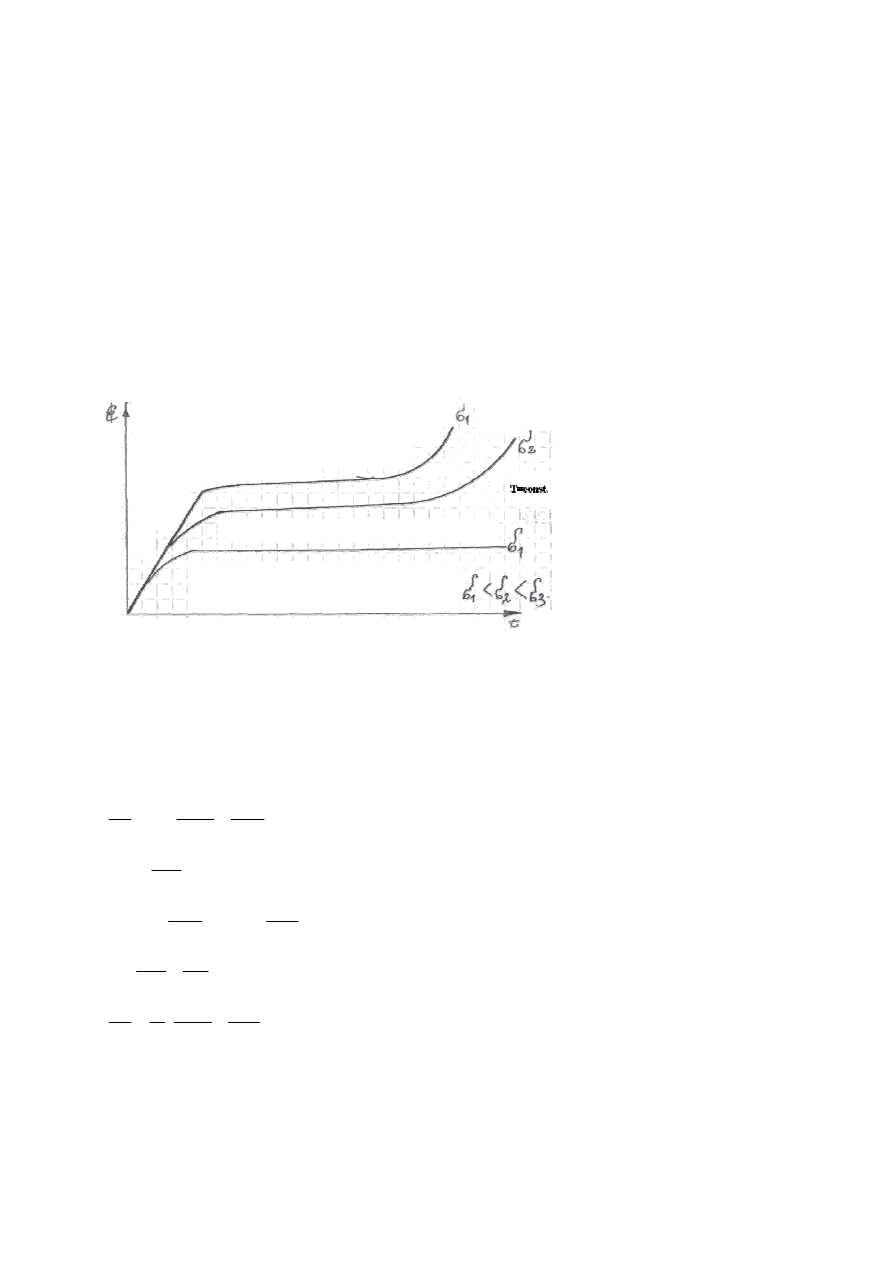
Krzywa pełzania

Przy obciążeniu próbki do podgrzanej temp. T odkształcenie wzrasta dość szybko(

ε

sprężysty) do punktu A. Zakłada się że w punkcie A kończy się obciążenie próbki.
Odkształcenie próbki z biegiem czasu wzrasta-materiał pełza.
Odcinek B-C- pełzanie ustalone- prędkość pełzania jest stała, pełzanie odbywa się w 3
stadiach:
A-B- zależy do materiału, temperatury i obciążenia
B-C- prędkość jest mała w stosunku do A-B
C-D- następuje lokalne przewężenie przekroju poprzecznego wywołane wzrostem naprężeń
co powoduje wzrost prędkości pełzania. W punkcie D następuje zerwanie próbki- złom
rozdzielczy.

Stopniowe zmniejszenie naprężeń w obciążonym elemencie, którego całkowite odkształcenie
pozostaje stałe, to zmniejszenie zachodzi na skutek stopniowego zmniejszenia się odkształceń
sprężystych i wzrastanie o tą wartość odkształcenia plastycznego.

Relaksacja- pełzanie przy stałym

ε

=const.

'

0

:

/

(

)

1

0

spr

spr

pl

pl

spr

pl

spr

spr

pl

pl

pl

spr

pl

spr

odksztalcenia

sprężyste

odksztalcenia

plastyczne

d

d

d

gdzie

dt

dt

dt

E

d

pl

n

t

dt

n

t

f

E

n

d

d

pl

dt

E

dt

n

ε

ε ε

ε

ε

ε

ε

ε

σ

ε

ε

σ

σ

ε

σ

σ

ε

ε

ε

σ

−

=

+

−

= =

+

=

= ⋅

→

=

⋅

=

+

⋅ ⋅

= ⋅

+

=

σ

A-B- w tym zakresie następuje zmniejszenie

….

w elemencie przy towarzyszącym

zmniejszeniu prędkości relaksacji. Ten okres zależy od materiału, temperatury, itp.
B-C- prędkość jest mniejsza niż w A-B

20. Prętowe ustroje statycznie niewyznaczalne. Metoda sił. Obliczanie statycznie
niewyznaczalnych ustrojów prętowych.

Do układów prętowych zaliczamy układy belkowe i ramowe. Ramą nazywamy strukturę
węzłową połączoną węzłami sztywnymi. Wyróżniamy układy statycznie niewyznaczalne
wewnętrznie lub zewnętrznie.

3

z

N

n

= −

- niewyznaczalność zewnętrzna

n- ilość niewiadomych reakcji

3

3(

1)

w

N

t

p

w

= ⋅ −

+ −

- niewyznaczalność wewnętrzna

t- ilość wycięć węzłów sztywnych
p- ilość prętów
w- ilość węzłów sztywnych

5 3

2

3 4 3(3 2 1)

0

z

w

N

N

= − =

= ⋅ −

+ − =

Metoda sił:

Równanie kanoniczne metody sił:

2

z

N

n

= −

- bo nie ma reakcji poziomej

n- ilość reakcji

4 2

2

z

N

= − =

2 podpory zastępuje myślowo reakcjami o wartości =1 i z zasady superpozycji. Skutek
działania sił na ciało rzeczywiste w określonym punkcie na określonym kierunku jest równy
sumie algebraicznej skutków działania każdej z sił układów rozpatrywanego z osobna na
określonym punkcie w określonym kierunku.

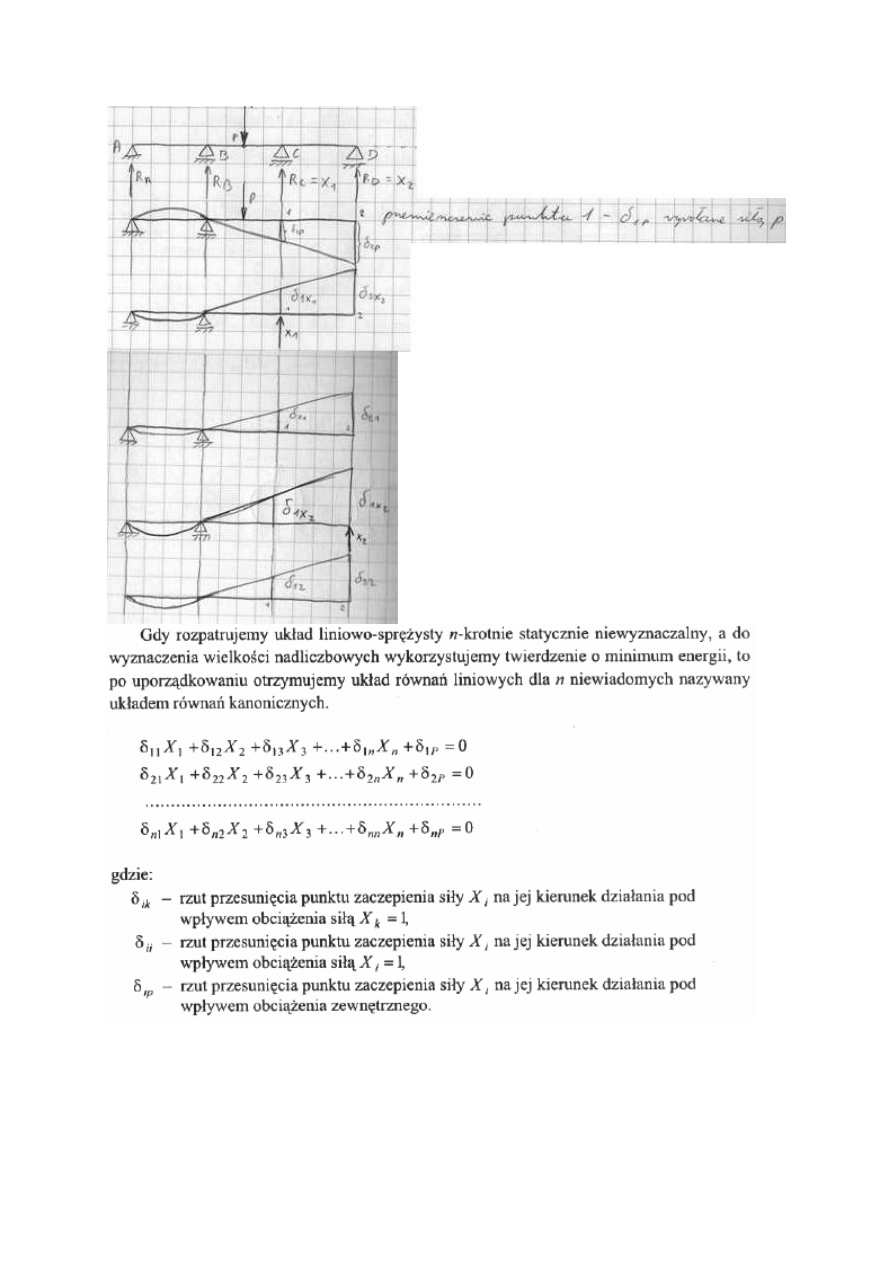
Twierdzenie Menabrea jest to szczególny przypadek tw. Castigliano i jest ono stosowane do
wyznaczenia reakcji hiperstatycznych udziałów- w zależności od tego ile mamy nadmiaru
reakcji tyle potrzeba równań.

Ogólny tok postępowania przy rozwiązywaniu układów statycznie niewyznaczalnych przy
zastosowaniu zasady minimum enegii.