1
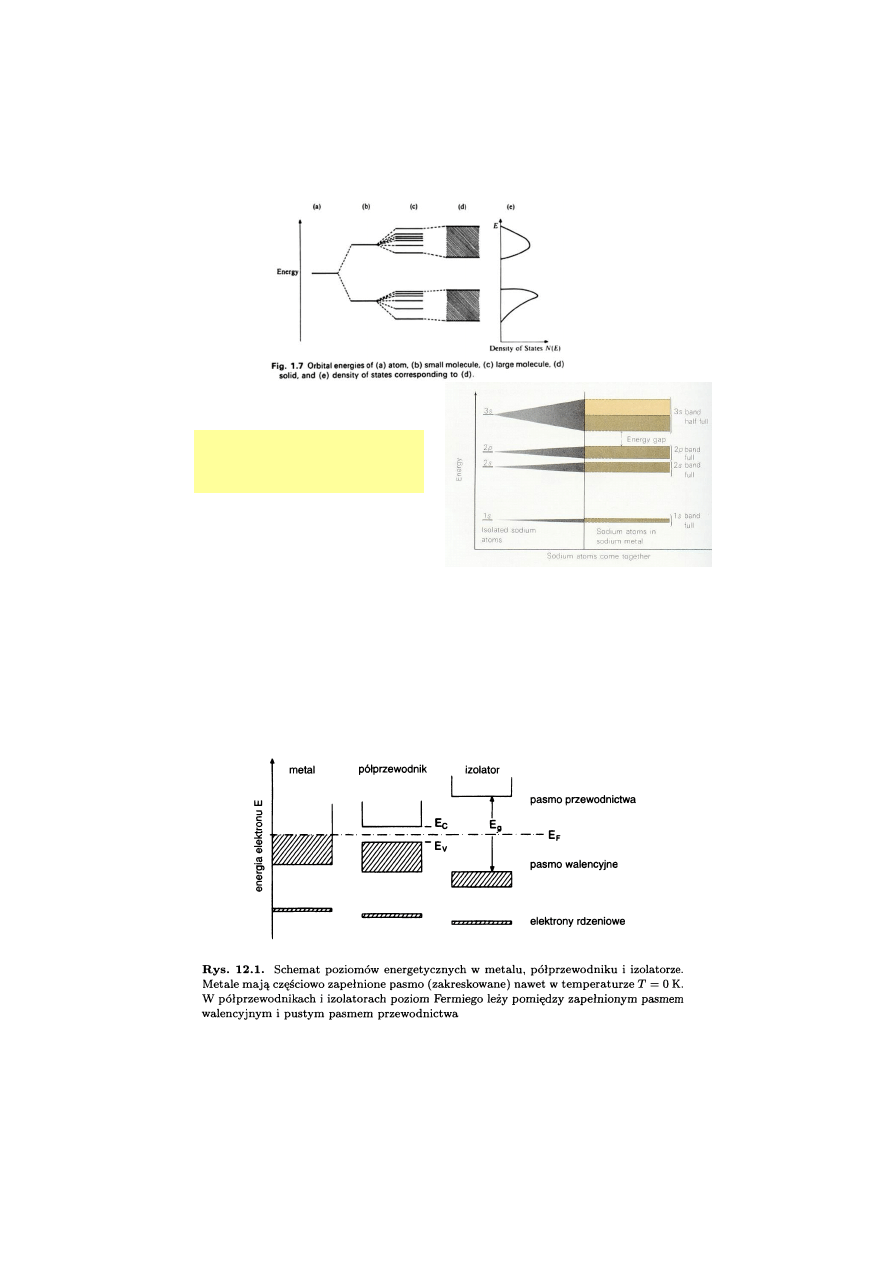
Teoria pasmowa ciał stałych
Poziomy elektronowe atomów w
cząsteczkach ulegają rozszczepieniu.
W kryształach zjawisko to prowadzi do
wytworzenia się pasm.
2
Metale, izolatory, półprzewodniki
Energia elektronu
swobodnego
Energia elektronu
w krysztale
jednowymiarowym
o stałej sieci a
Energia potencjalna
elektronu w liniowej sieci
rdzeni jonowych
Fale stojące:
ψ
(+)
∝ cos(πx/a)
ψ
(-)
∝ sin(πx/a)
ψ(+)
– elektrony skupione w pobliżu rdzeni jonów – obniżenie energii potencjalnej
ψ(-)
– elektrony skupione pomiędzy jonami – zwiększenie energii potencjalnej
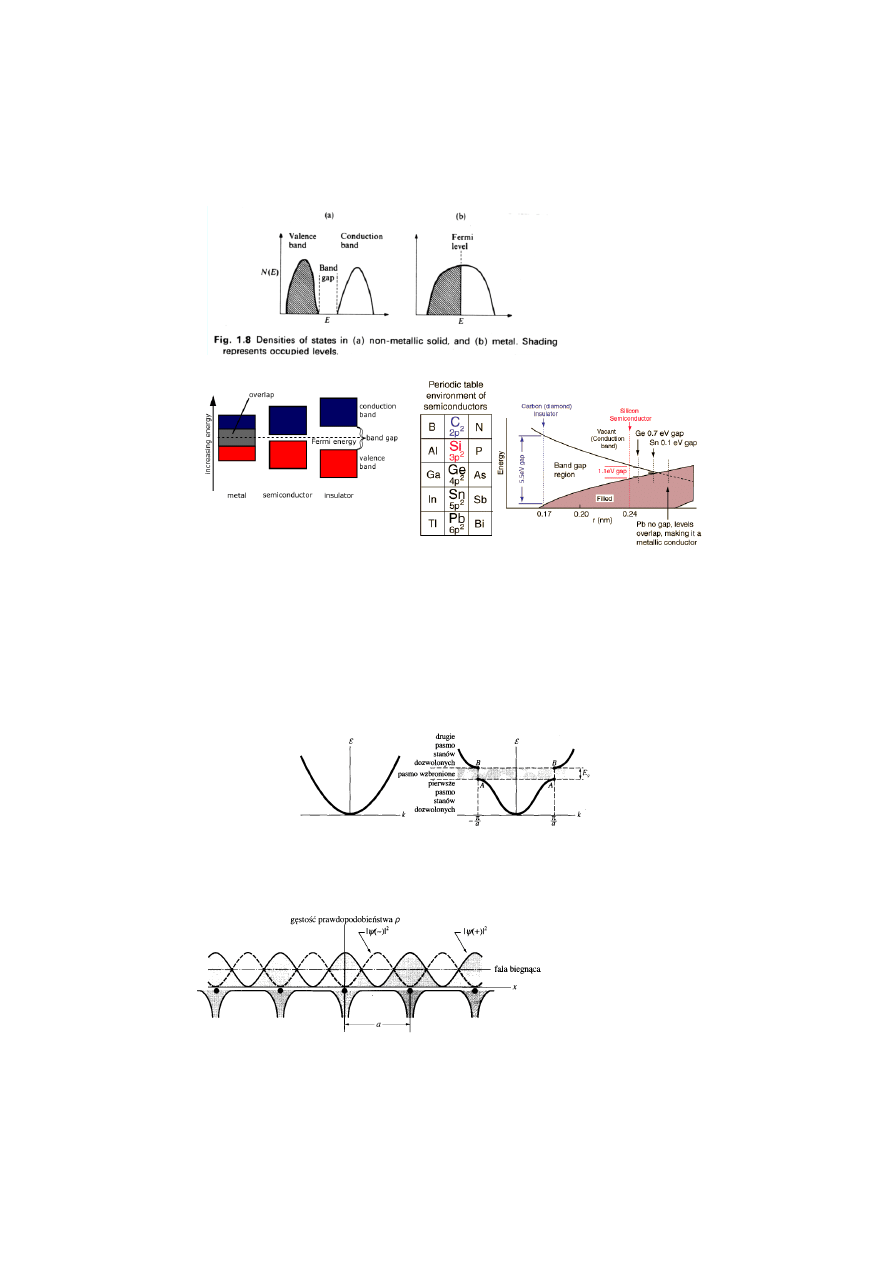
Model prawie swobodnych elektronów
Powstawanie fal stojących, gdy spełniony jest warunek Bragga odbicia
funkcji falowej elektronu od struktury periodycznej kryształu.
3
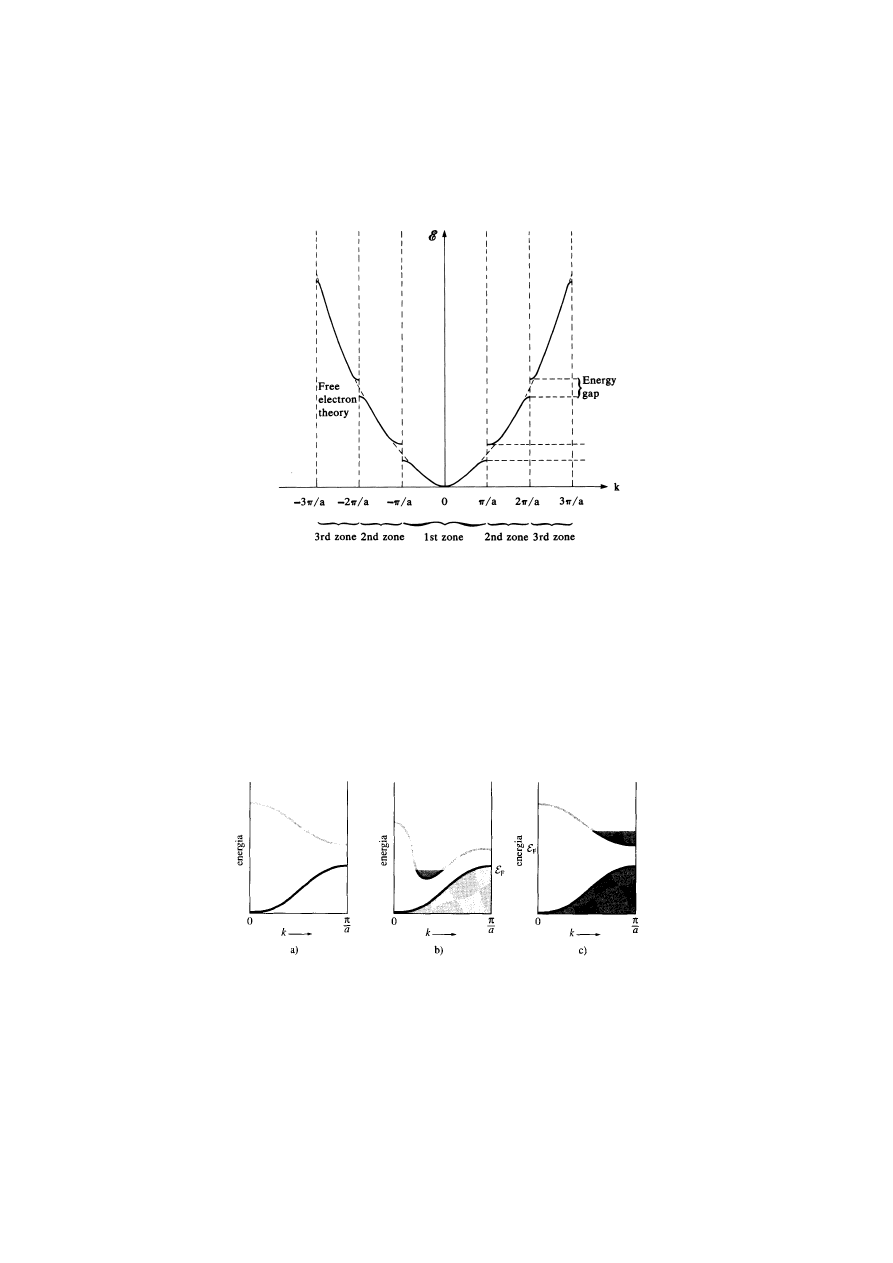
Energia w funkcji wektora falowego dla elektronów swobodnych (parabola) i dla
elektronów prawie swobodnych, przerwy energetyczne przy k=p
π/a, |p|=1,2,3..
Struktura pasmowa i stany obsadzone
Izolator
pasmo walencyjne
całkowicie zapełnione
Metal (półmetal)
przekrywanie się
pasm
Metal
pasmo walencyjne
częściowo zapełnione
4
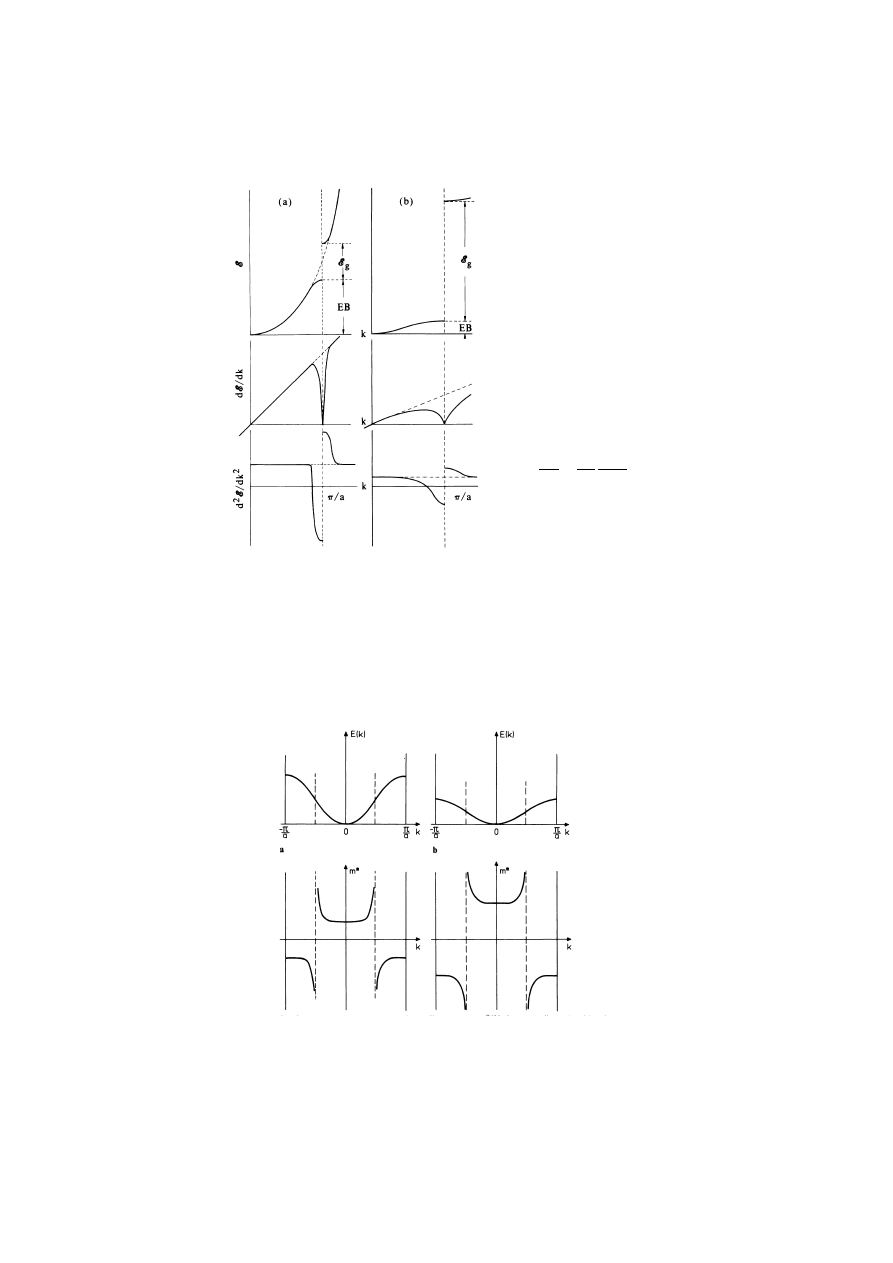
a) Szerokie pasma,
wąska lub szeroka przerwa,
mała masa efektywna.
b) Wąskie pasma,
szeroka przerwa energetyczna,
duża masa efektywna.
Masa efektywna
m
*
Energia w zależności od wektora
falowego
E(k)
i pochodne tej
funkcji – zachowanie w pobliżu
granicy strefy Brillouina
k=
π
/a
.
2
2
2
*
d
d
1
1
k
E
m
h
=
Masa efektywna elektronów m*(k) dla jednowymiarowej struktury pasmowej
Silne zakrzywienie pasm Mała krzywizna pasm
mała masa efektywna duża masa efektywna
W punktach przegięcia zależności E(k) masa efektywna jest nieokreślona
5
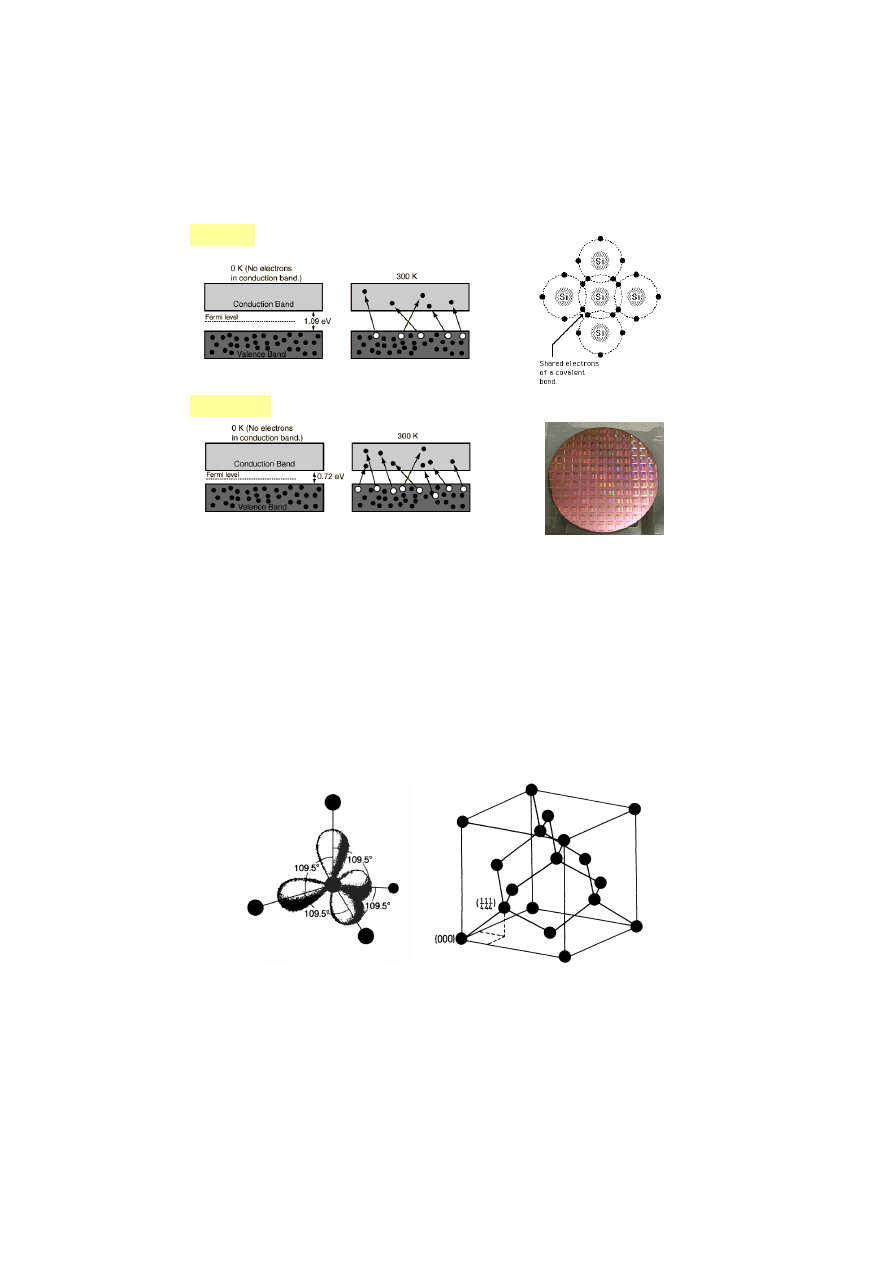
Krzem Si
German Ge
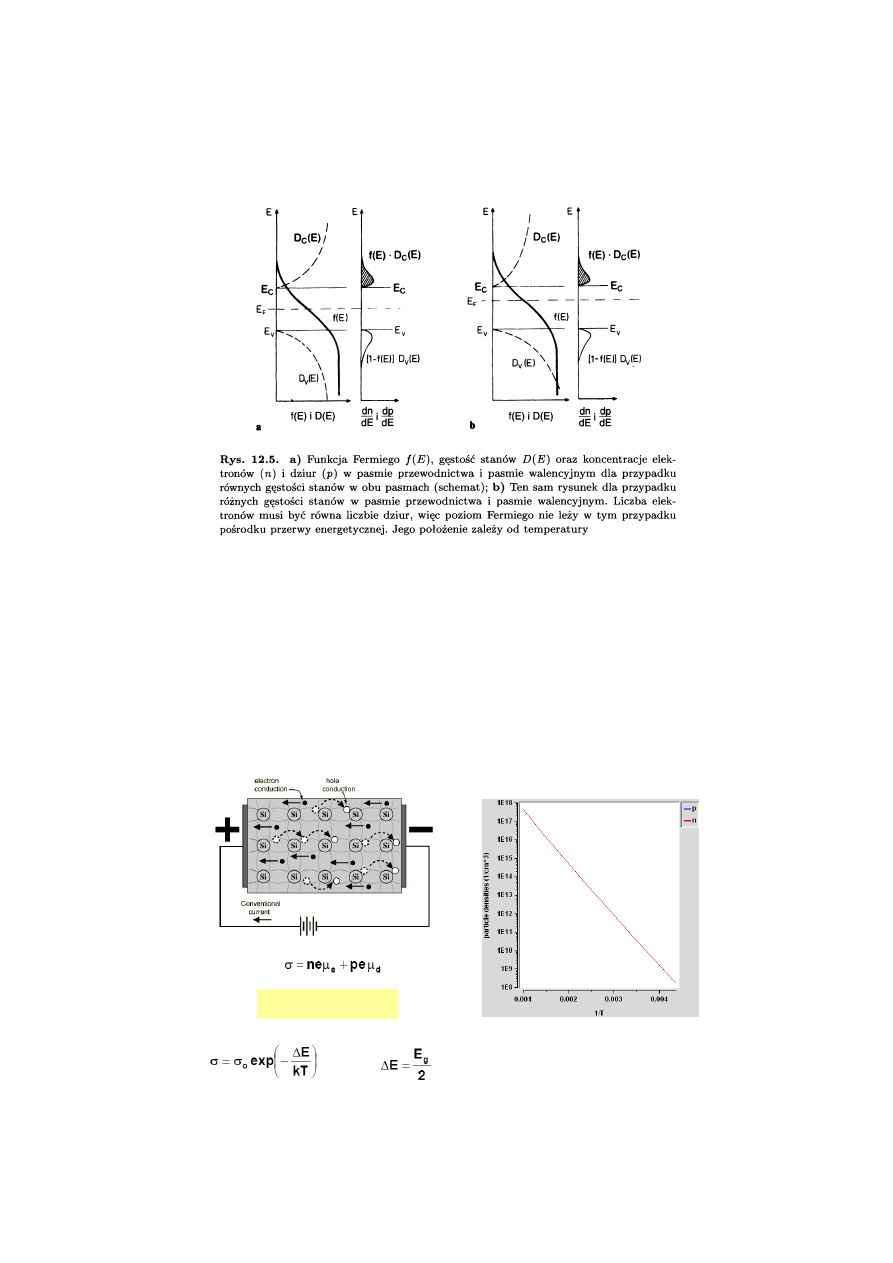
Półprzewodniki samoistne
Tetraedryczna konfiguracja najbliższych sąsiadów w sieci krystalicznej
diamentu, krzemu, germanu i cyny (odmiana
α
-Sn).
Występuje hybrydyzacja orbitali sp
3
ze stanów s, p
x
, p
y
, p
z
.
6
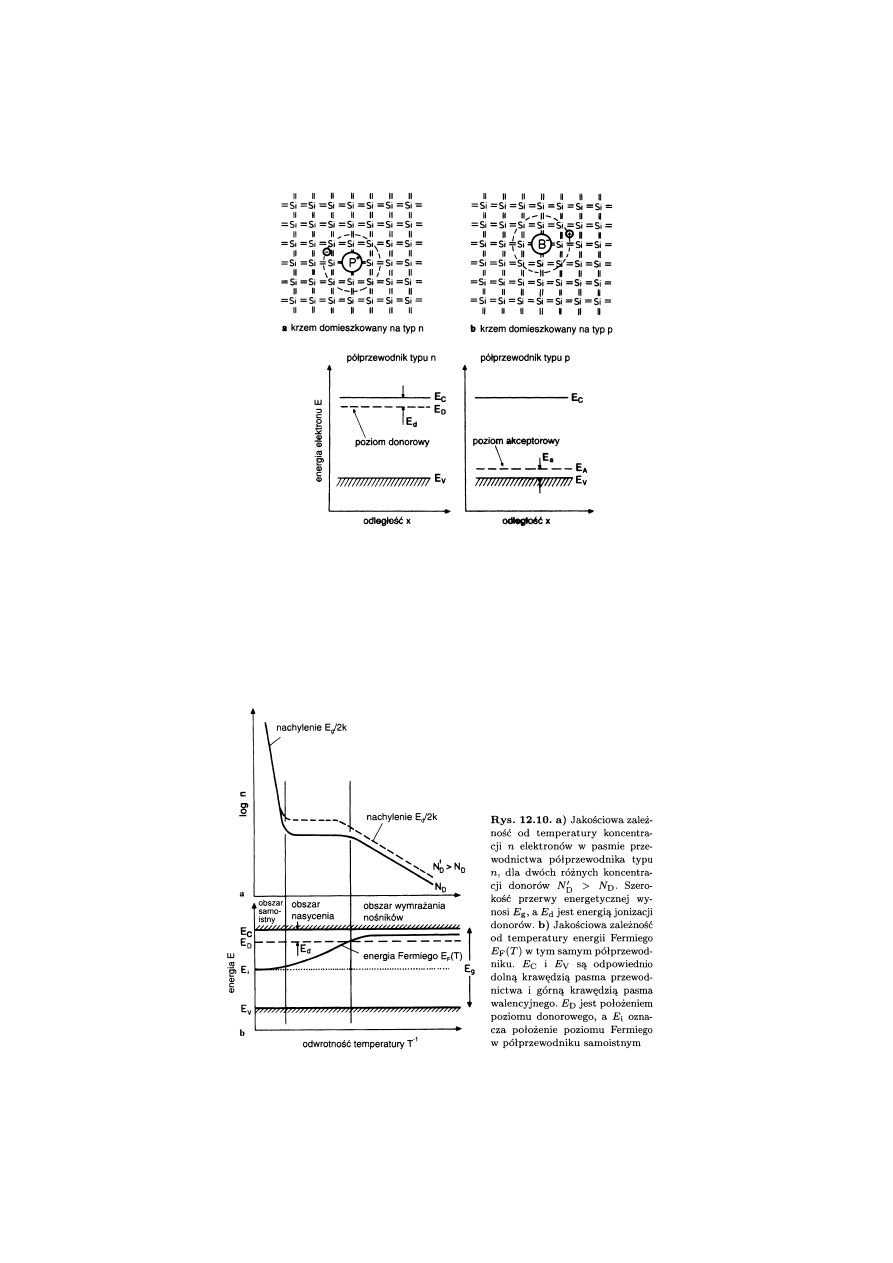
Przewodność elektryczna półprzewodników
p – koncentracja dziur
n – koncentracja elektronów
7
8
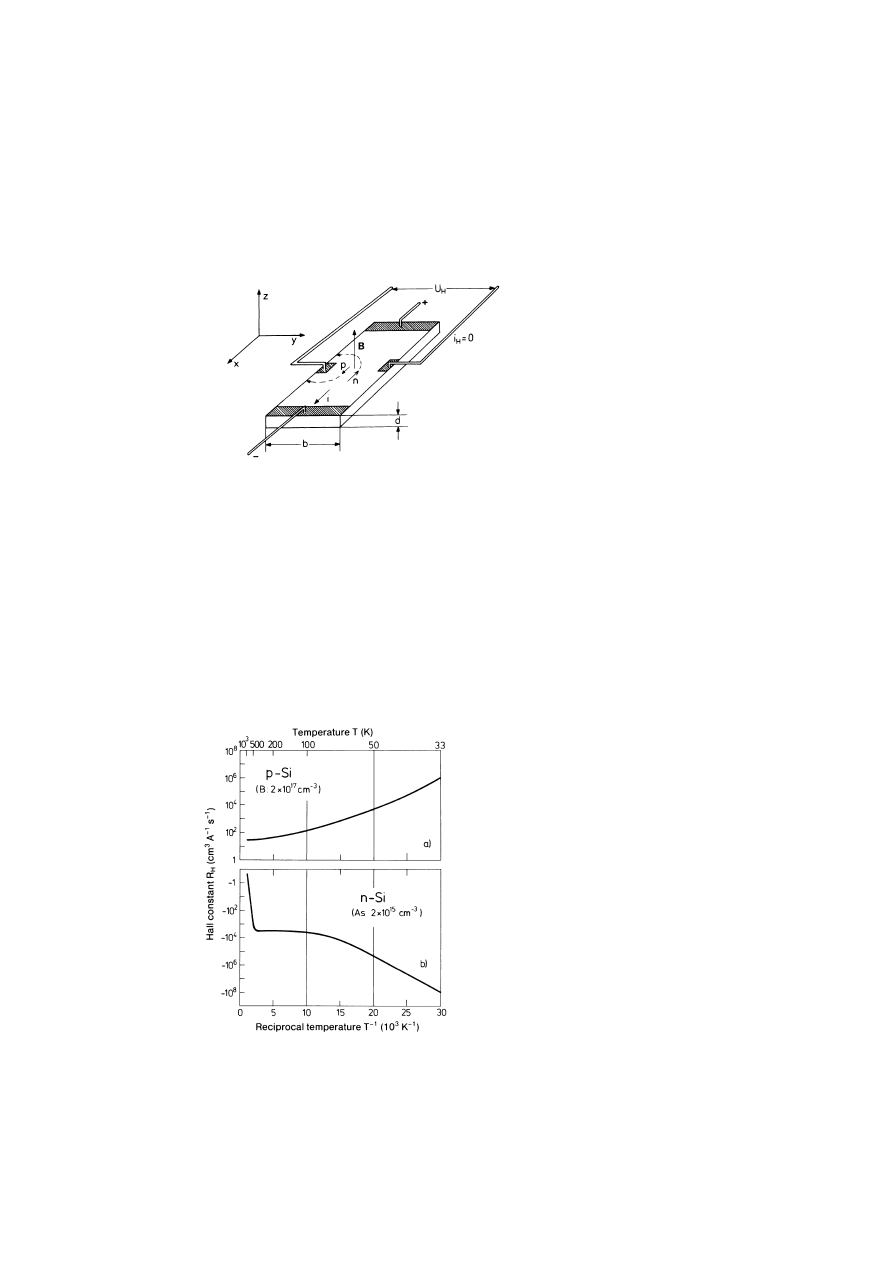
Schemat układu doświadczalnego do pomiaru efektu Halla.
Linie przerywane oznaczają tory, po których poruszałyby się elektrony i dziury,
gdyby nie pojawiło się napięcie Halla U
H
.
Stałą Halla wyznacza się na
podstawie pomiaru napięcia
Halla
U
H
, natężenia prądu
I
w warstwie o grubości
d
oraz
indukcji magnetycznej
B
:
R
H
=U
H
d/(IB)
Zależność stałej Halla
od temperatury dla krzemu
a) typ p, koncentracja boru
(akceptora) 2
×10
17
cm
-3
b) typ n, koncentracja arsenu
(donora) 2
×10
15
cm
-3
Gdy występuje jeden typ nośnika,
stała Halla
R
H
jest odwrotnie
proporcjonalna do koncentracji
nośników
n
R
H
=-(ne)
-1
Przy mniejszej koncentracji
domieszki (b) widoczny jest
obszar nasycenia i obszar
samoistny.
9
Wyszukiwarka
Podobne podstrony:
F3 polprzewodniki
F3 zlacza polprz
3b Właściwości optyczne półprzewodników
ZO NST 14 ĆW1CZ 1, 2 STUD F F3
3 Podstawy fizyki polprzewodnik Nieznany (2)
F 11 Półprzewodnik akceptorowy
otrzymywanie polprzewodnikow
Korbutowicz,optoelektronika,Technologia wytwarzania półprzewodnikowych struktur optoelektronicznych
2 Materiały półprzewodnikowe
f3, policja
cw8?danie właściwości optycznych półprzewodników
pamieci polprzew
3 Materiały półprzewodnikowe, własności, wytwarzanie i ich obróbka mechaniczna [tryb zgodności]
3 Diody półprzewodnikowe +
F3 Glikozydy nasercowe
c03 2012 el polprzewodnikowe
111-4, materiały studia, 111. WYZNACZANIE SZEROKOŚCI PRZERWY ENERGETYCZNEJ W PÓŁPRZEWODNIKU METODĄ T
więcej podobnych podstron