1
WYKŁAD 11+12
Przestrzeń R
2
Przestrzenią R
2
nazywamy zbiór punktów
{(x, y) : x, y ∈ R}
Jeśli punkty P (x, y) , P
0
(x
0
, y
0
) ∈ R
2
, to ich
odległość
(ozn.d(P, P
0
) ) określamy wzorem
d(P, P
0
)
df
=
q
(x − x
0
)
2
+ (y − y
0
)
2
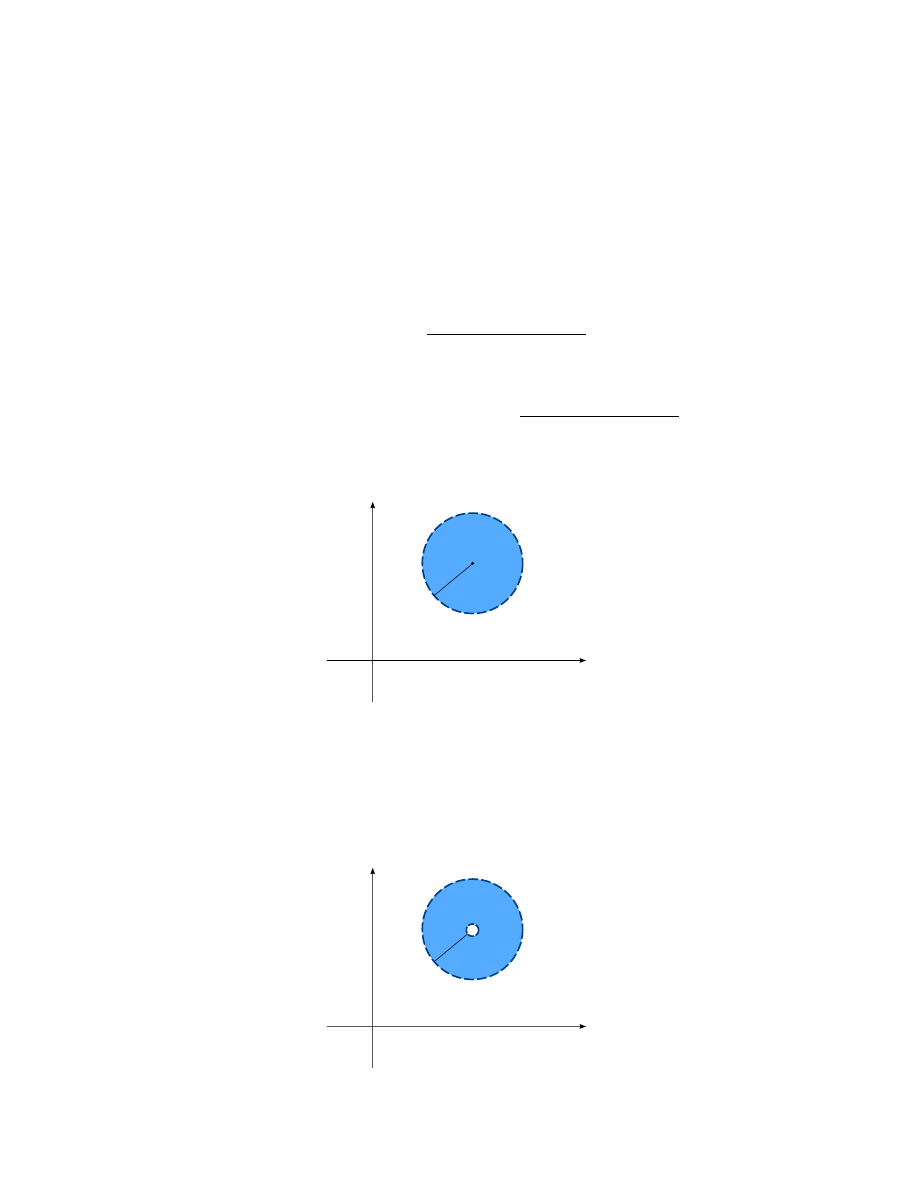
Definicja 1.
Otoczeniem o promieniu
r punktu P
0
(ozn.Q(P
0
; r)) nazywamy zbiór
{P ∈ R
2
: d(P, P
0
) < r} = {(x, y) ∈ R
2
:
q
(x − x
0
)
2
+ (y − y
0
)
2
< r}.
X
Y
0
(x ,y )
0
0
r
Definicja 2.
Sąsiedztwem o promieniu
r punktu P
0
(ozn.S(P
0
; r)) nazywamy zbiór
{P ∈ R
2
: 0 < d(P, P
0
) < r}.
X
Y
0
(x ,y )
0
0
r
2
Definicja 3. Punkt P
0
∈ D ⊂ R
2
jest
punktem wewnętrznym
zbioru D, jeżeli zbiór D
zawiera pewne otoczenie punktu P
0
.
X
Y
0
(x ,y )
0
0
D
Definicja 4. Zbiór D ⊂ R
2
nazywamy zbiorem
otwartym
, jeśli każdy jego punkt jest punk-
tem wewnętrznym zbioru D.
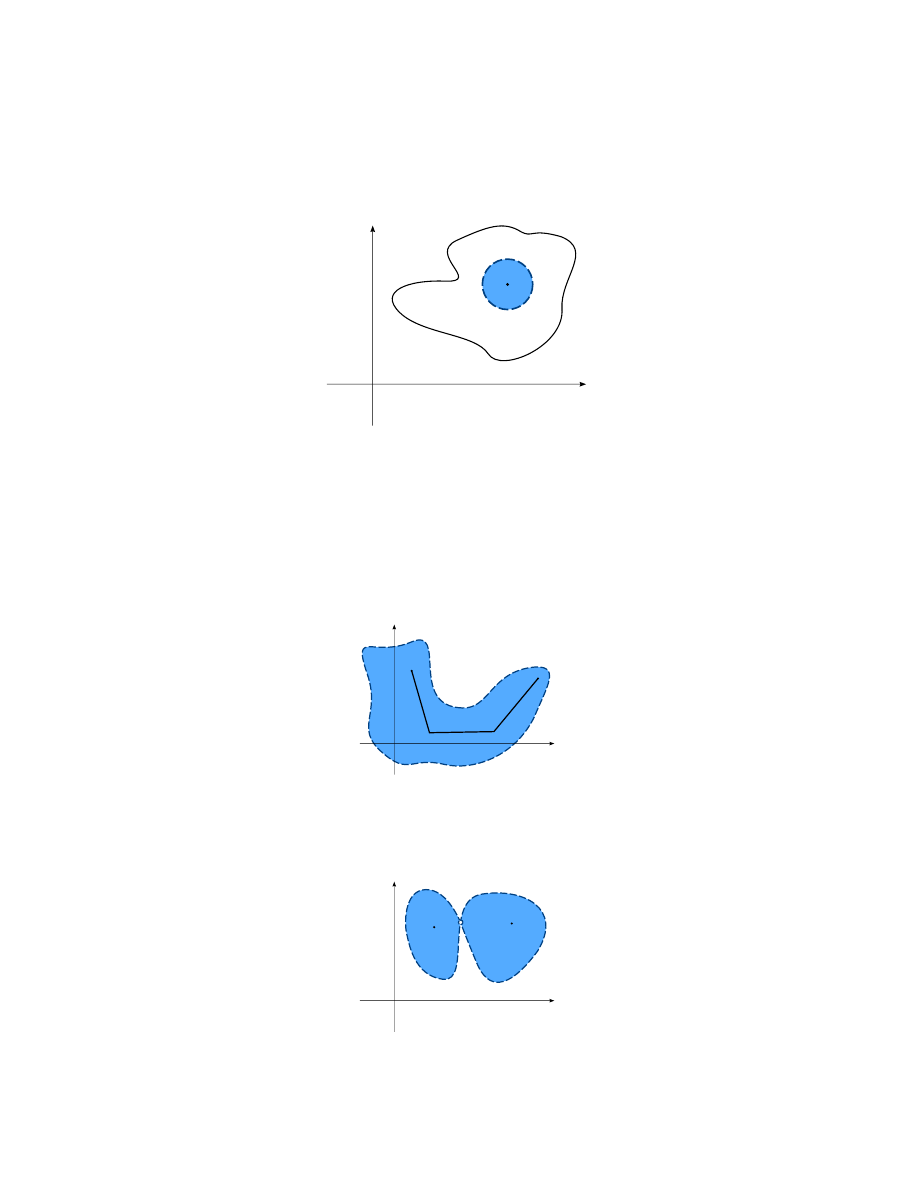
Definicja 5.
Obszar
w R
2
jest to taki zbiór otwarty, którego każde dwa punkty można
połączyć łamaną zawartą w tym zbiorze.
X
Y
0
Rysunek 1: Zbiór jest obszarem
X
Y
0
Rysunek 2: Zbiór nie jest obszarem
3
Funkcje dwóch zmiennych
Definicja 6. Funkcję f : D → R, gdzie D ⊂ R
2
, nazywamy funkcją dwóch zmiennych x , y.
Wartość funkcji f w punkcie P (x, y) oznaczamy przez f (x, y) lub f (P ).
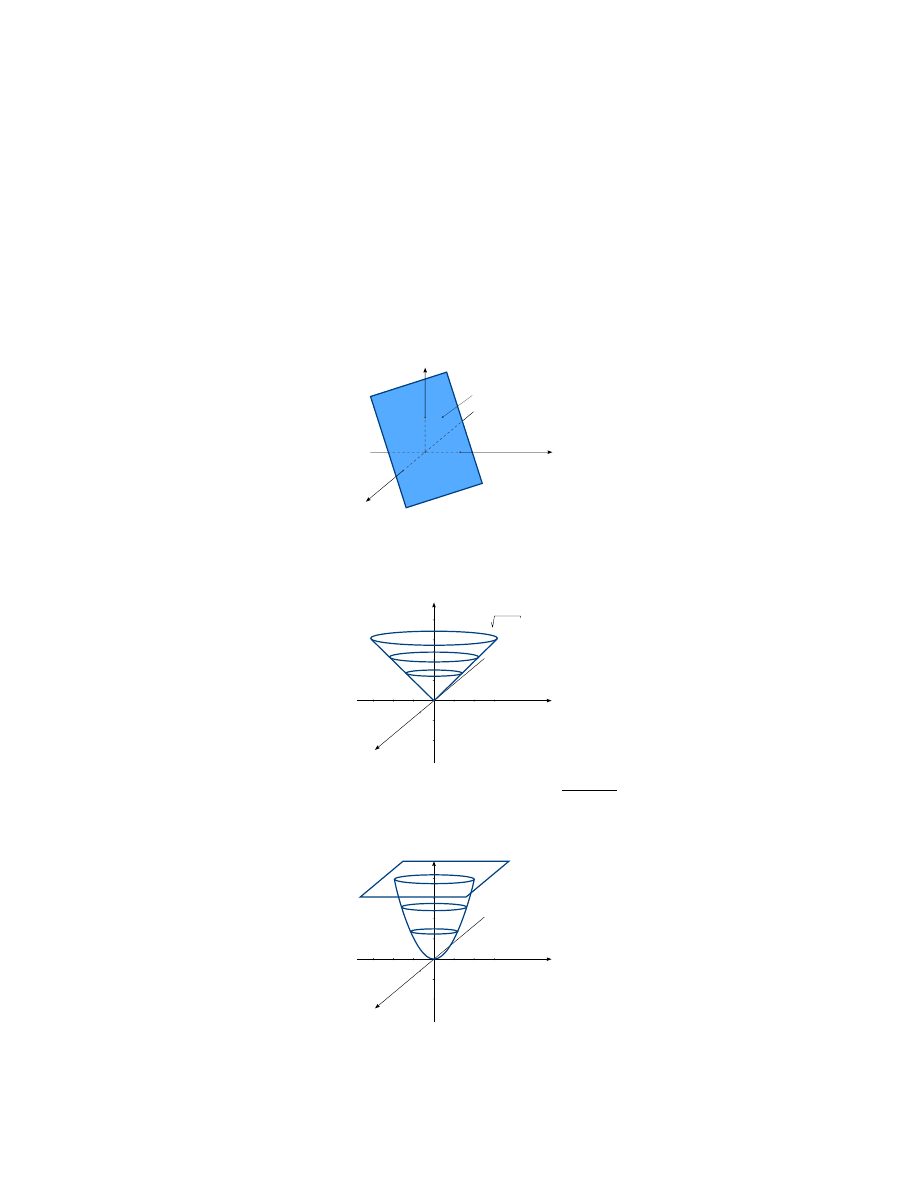
Definicja 7.
Wykresem funkcji
f : D → R, gdzie D ⊂ R
2
, nazywamy zbiór
{(x, y, z) ∈ R
3
: z = f (x, y) ∧ (x, y) ∈ D}
Przykłady wykresów funkcji dwóch zmiennych
Y
X
Z
x + y + z = 1
1
1
1
0
Rysunek 3: Wykres funkcji z = 1 − x − y
X
Z
1
1
0
z = x + y
Y
1
2
2
Rysunek 4: Wykres funkcji z =
√
x
2
+ y
2
X
Z
1
1
0
z = x + y
Y
1
2
2
z = 4
4
Rysunek 5: Wykres funkcji z = x
2
+ y
2

4
X
Z
1
1
0
z = 4 - x - y
Y
1
2
2
2
2
2
Rysunek 6: Wykres funkcji z =
√
4 − x
2
− y
2
Granica funkcji dwóch zmiennych
Niech (P
n
(x
n
, y
n
)) – ciąg punktów w R
2
i P
0
(x
0
, y
0
) ∈ R
2
.
Definicja 8. Ciąg punktów (P
n
) jest
zbieżny
do punktu P
0
(ozn. P
n
→ P
0
lub lim
n→∞
P
n
= P
0
lub lim
n→∞
(x
n
, y
n
) = (x
0
, y
0
)), jeśli
lim
n→∞
d(P
n
, P
0
) = 0
Uwaga 1. lim
n→∞
P
n
= P
0
⇔ lim
n→∞
x
n
= x
0
i lim
n→∞
y
n
= y
0
.
Załóżmy, że funkcja f : D → R, D ⊂ R
2
, jest określona w pewnym sąsiedztwie S punktu
(x
0
, y
0
).
Definicja 9. Liczba g jest
granicą podwójną
funkcji f w punkcie (x
0
, y
0
) (ozn. lim
x→x0
y→y0
f (x, y) = g
lub
lim
(x,y)→(x
0
, y
0
)
f (x, y) = g ), jeśli spełniony jest warunek:
∀((x
n
, y
n
)) ⊂ S
lim
n→∞
(x
n
, y
n
) = (x
0
, y
0
) ⇒ lim
n→∞
f (x
n
, y
n
) = g
Załóżmy, że funkcja f : D → R, D ⊂ R
2
, jest określona w pewnym otoczeniu punktu (x
0
, y
0
).
Definicja 10. Funkcja f jest
ciągła w punkcie
(x
0
, y
0
), jeśli
lim
(x,y)→(x
0
, y
0
)
f (x, y) = f (x
0
, y
0
)
Funkcja f jest
ciągła w zbiorze
, jeśli jest ciągła w każdym punkcie tego zbioru.

5
Pochodne cząstkowe
Zał. f : D → R , D ⊂ R
2
. Wybieramy i ustalamy punkt P
0
(x
0
, y
0
) ∈ D oraz dowolny punkt
P ∈ D taki, że P różni się od P
0
tylko na jednej współrzędnej.
Definicja 11.
Pochodną cząstkową
funkcji f względem zmiennej x w punkcie P
0
(ozn.
∂f
∂x
(P
0
)
lub
∂f
∂x
(x
0
, y
0
) ) nazywamy wartość granicy właściwej
∂f
∂x
(x
0
, y
0
)
df
= lim
∆x→0
f (x
0
+ ∆x, y
0
) − f (x
0
, y
0
)
∆x
;
Definicja 12.
Pochodną cząstkową
funkcji f względem zmiennej y w punkcie P
0
(ozn.
∂f
∂y
(P
0
)
lub
∂f
∂y
(x
0
, y
0
)) nazywamy wartość granicy właściwej
∂f
∂y
(x
0
, y
0
)
df
= lim
∆y→0
f (x
0
, y
0
+ ∆y) − f (x
0
, y
0
)
∆y
;
Jeżeli pochodne cząstkowe funkcji f istnieją w każdym punkcie zbioru D, to można mówić o
funkcjach pochodnych cząstkowych
:
∂f
∂x
,
∂f
∂y
– są to funkcje dwóch zmiennych.
Obliczanie pochodnych cząstkowych funkcji dwóch zmiennych polega na tym, że jedną
zmienną traktujemy jako stałą i obliczamy pochodną funkcji ze względu na drugą zmien-
ną; wówczas możemy korzystać ze wzorów i reguł obliczania pochodnych dla funkcji jednej
zmiennej.
Uwaga 2. Pochodne cząstkowe funkcji względem różnych zmiennych istnieją niezależnie od
siebie.
Uwaga 3. Ciągłość funkcji nie jest warunkiem koniecznym istnienia pochodnych cząstko-
wych.
Uwaga 4. Ciągłość funkcji nie jest warunkiem wystarczającym istnienia pochodnych cząst-
kowych.
Definicja 13.
Pochodne cząstkowe rzędu drugiego
funkcji f są to pochodne cząstkowe po-
chodnych cząstkowych
∂f
∂x
i
∂f
∂y
Oznaczamy je następująco
∂
∂x
∂f
∂x
!
ozn
=
∂
2
f
∂x
2
,
∂
∂y
∂f
∂y
!
ozn
=
∂
2
f
∂y
2
, ,
∂
∂x
∂f
∂y
!
ozn
=
∂
2
f
∂x∂y
,
∂
∂y
∂f
∂x
!
ozn
=
∂
2
f
∂y∂x
Dwie ostatnie pochodne cząstkowe drugiego rzędu nazywamy pochodnymi mieszanymi, róż-
nią się kolejnością obliczania pochodnych.
Podobnie określamy pochodne cząstkowe wyższych rzędów.
6
Twierdzenie 1. (Schwarza) Jeżeli funkcja f ma w pewnym obszarze D ⊂ R
2
ciągłe pochod-
ne mieszane drugiego rzędu
∂
2
f
∂x∂y
i
∂
2
f
∂y∂x
, to są one równe w tym obszarze.
C
m
(D) oznacza zbiór wszystkich funkcji, które w obszarze D mają ciągłe pochodne cząstko-
we do m – tego rzędu włącznie.
Niech f : D → R , D ⊂ R
2
; P
0
∈ D – punkt wewnętrzny zbioru D.
Definicja 14. Funkcja f ma w punkcie P
0
minimum lokalne
(odp.
maksimum lokalne
), jeśli
istnieje sąsiedztwo S punktu P
0
takie, że
∀P ∈ S [f (P
0
) ¬ f (P )]
(odp.∀P ∈ S [f (P
0
) f (P )])
Funkcja f ma w punkcie P
0
ekstremum
, jeśli ma w tym punkcie minimum lub maksimum.
Uwaga 5. Funkcja f ma w punkcie P
0
ekstremum, jeśli w pewnym sąsiedztwie tego punktu
przyrost ∆f = f (P ) − f (P
0
) ma stały znak.
Twierdzenie 2. (WK istnienia ekstremum) Jeżeli funkcja f ma w punkcie P
0
ekstremum
i istnieją pochodne cząstkowe pierwszego rzędu
∂f
∂x
(P
0
) i
∂f
∂y
(P
0
), to są one równe zero.
Uwaga 6. Ekstremum funkcji f poszukujemy wśród takich punktów P
0
, że
∂f
∂x
(P
0
) =
=
∂f
∂y
(P
0
) = 0 lub co najmniej jedna z pochodnych cząstkowych
∂f
∂x
(P
0
),
∂f
∂y
(P
0
) nie istnieje.
Punkt P
0
taki, że
∂f
∂x
(P
0
) =
∂f
∂y
(P
0
) = 0 nazywamy
punktem stacjonarnym
funkcji f .
Twierdzenie 3. (WW istnienia ekstremum) Jeżeli funkcja f jest klasy C
2
(Q((x
0
, y
0
); r))
oraz
1.
∂f
∂x
(x
0
, y
0
) =
∂f
∂y
(x
0
, y
0
) = 0,
2. W (x
0
, y
0
) =
∂
2
f
∂x
2
(x
0
, y
0
)
∂
2
f
∂y∂x
(x
0
, y
0
)
∂
2
f
∂x∂y
(x
0
, y
0
)
∂
2
f
∂y
2
(x
0
, y
0
)
> 0
to funkcja f ma w punkcie (x
0
, y
0
) ekstremum właściwe:
– maksimum, jeśli
∂
2
f
∂x
2
(x
0
, y
0
) < 0;
– minimum, jeśli
∂
2
f
∂x
2
(x
0
, y
0
) > 0.
Uwaga 7. Jeśli spełnione są dwa pierwsze założenia twierdzenia 3. i W (x
0
, y
0
) < 0, to w
punkcie (x
0
, y
0
) funkcja f nie ma ekstremum.

7
Dodatek
Pochodna przekształcenia
Niech g : D → R
2
, gdzie D ⊂ R
2
, tzn. dla t = (t
1
, t
2
) i g = (g
1
, g
2
):
g(t) = (g
1
(t
1
, t
2
), g
2
(t
1
, t
2
))
Określamy pochodną przekształcenia g(t) jako macierz (ozn.g
0
(t)):
g
0
(t)
df
=
∂g
1
∂t
1
∂g
1
∂t
2
∂g
2
∂t
1
∂g
2
∂t
2
.
Podobnie:
Dla g : P → R
2
, gdzie P ⊂ R, g
0
(t)
df
=
"
g
0
1
(t)
g
0
2
(t)
#
, g = (g
1
, g
2
).
Dla g : D → R, gdzie D ⊂ R
2
, g
0
(t)
df
=
"
∂g
∂t
1
∂g
∂t
2
#
, t = (t
1
, t
2
).
We wszystkich wzorach zakłada się, że odpowiednie pochodne istnieją.
Twierdzenia o pochodnej funkcji złożonej
P ⊂ R , D
2
⊂ R
2
. Dane są funkcje: (x, y) : P → D
2
oraz f : D
2
→ R;
Twierdzenie 4. Jeżeli funkcja f (x, y) jest klasy C
1
(D
2
) i funkcje x(t), y(t) posiadają po-
chodne x
0
(t), y
0
(t), to funkcja złożona z(t)
df
= f (x(t), y(t)) posiada pochodną z
0
(t) i prawdziwy
jest wzór
z
0
(t) =
"
∂f
∂x
∂f
∂y
#
·
"
x
0
(t)
y
0
(t)
#
D
1
⊂ R
2
, D
2
⊂ R
2
. Dane są funkcje: (x, y) : D
1
→ D
2
oraz f : D
2
→ R;
Twierdzenie 5. Jeżeli funkcja f (x, y) jest klasy C
1
(D
2
) i funkcje x(t
1
, t
2
), y(t
1
, t
2
) posia-
dają pochodne cząstkowe I rzędu, to funkcja złożona z(t
1
, t
2
)
df
= f (x(t
1
, t
2
), y(t
1
, t
2
)) posiada
pochodne cząstkowe I rzędu i prawdziwy jest wzór
z
0
(t) =
"
∂z
∂t
1
∂z
∂t
2
#
=
"
∂f
∂x
∂f
∂y
#
·
∂x
∂t
1
∂x
∂t
2
∂y
∂t
1
∂y
∂t
2
Zatem
∂z
∂t
1
=
∂f
∂x
·
∂x
∂t
1
+
∂f
∂y
·
∂y
∂t
1
∂z
∂t
2
=
∂f
∂x
·
∂x
∂t
2
+
∂f
∂y
·
∂y
∂t
2
Wyszukiwarka
Podobne podstrony:
anl1 w11 lato2009
anl1 w02 zima2012 id 65272 Nieznany (2)
anl1 w01 zima2012 id 65270 Nieznany (2)
anl1 w04 zima2012 id 65275 Nieznany (2)
anl1 w05 zima2012 id 65276 Nieznany (2)
anl1 w03 zima2012 id 65273 Nieznany (2)
anl1 w11 lato2009
anl1 w13 zima2013
anl1 w10 zima2013
anl1 z11 zima2013
W11 Scinanie czyste i techniczne
W11 mod
W11 analiza ekonomiczna
W11 Starzenie komórkowe (asus Komputer's conflicted copy 2012 05 26)
więcej podobnych podstron