Wybór zadań z algebry liniowej i geometrii, A.Lenarcik (eko.11,energ.11)

Macierze

m7. Oblicz wyznaczniki

a)

−1

−1

−1

1

,

b)

cos φ

− sin φ

sin φ

cos φ

,

c)

−1

2

−3

−2

1

4

1

0

1

,

d)

−i

1

2 + i

0

i

1

−2

i

1

,

e)

2 + 3i

2 − 2i

1 − i

2 + i

7 − 3i

3 − i

1 + i

4 − 6i

2 − 3i

,

f)

x

y

x + y

y

x + y

x

x + y

x

y

,

g)

1

0

2

−3

1

2

−1

1

−1

−1

−2

0

−3

2

4

1

.

m8. Dla jakich wartości λ wyznacznik zeruje się?

a)

3 − λ

−2

2

−2 − λ

,

b)

2 − λ

−2

0

−2

1 − λ

−2

0

−2

−λ

.

m9. Rozwiąż nierówności:

a)

3x − 5

x − 2

x − 3

2x + 1

x − 1

x + 2

3x + 2

x − 1

2x + 3

> 0,

b)

x

1

1

1

x

1

1

1

x

¬ 0.

m10. Rozwiąż układ równań: a)

2x − 3y

=

4

3x + 2y

=

−7

, b)







2x − y + z

=

0

−x − 3y + 2z

=

−5

3x − 4y − z

=

5

,

c)







ix + y − iz

=

3 − i

x + y − z

=

−2i

2ix − y + z

=

2 + i

, d)















−x + 2y − 3z + t

=

0

x + y − z + t

=

2

−x + 2y − 3z + 2t

=

2

2x − 2y + z − t

=

3

.

m11. Dla jakich wartości parametru a podany układ równań ma jednoznaczne rozwiązanie?

a)

ax + y

=

1

ax + a

2

y

=

−1

, b)







ax + 2y + 3z

=

1

−x + ay

=

0

ax + y + 2z

=

−1

.

m12. Zauważ, że podany układ równań ma zawsze rozwiązanie zerowe. Dla jakich wartości parametru b możliwe jest
istnienie rozwiązań niezerowych?

a)

bx − 2by

=

0

3x + by

=

0

, b)







2x + 2y + bz

=

0

−x + by − z

=

0

x + y + bz

=

0

.

m13. Dla jakich wartości parametru a macierz A jest odwracalna?

a) A =

a

4

a

a

, b) A =





a

2

a

−1

1

−2

1

3

1





.

m14. Znajdź macierz odwrotną do danej macierzy A. a) A =

−1

4

−3

2

, b) A =

a

b

c

d

,

c) A =

1

1 − i

1 + i

i

, d) A =





−1

0

1

1

2

2

−2

1

1





, e) A =







1

0

−1

0

1

2

1

−1

−1

0

1

1

−1

2

0

1







.

m15. Wylicz symbolicznie X z równania macierzowego: a) AX = B, b) XA + B = C,
c) A

−1

(X − B) = C, d) AXB + C = D, e) A(X − B) = CX.

m16. Wyznacz macierz X z równania macierzowego:

a) 3AX + B

T

= C, gdzie A =

3

2

−1

1

, B =

0

−1

2

1

, C =

−3

5

5

−5

,

b) A

−1

XB = D, gdzie A =





−1

1

2

2

−1

1

0

1

2





, B =





3

−1

1

−1

2

1

1

0

1





, D =





−6

3

0

−5

0

−1

4

0

2





,

c) (X + B)A = D, gdzie A =





1

2

0

−1

1

2

1

3

2





, B =





0

1

−1

2

1

0

−1

−2

1





, D =





0

3

2

0

6

4

4

4

0





.

m17. Metodą macierzową rozwiąż układ równań: a)

2x + 5y

=

3

−7x + 3y

=

10

, b)







x − 2y + 3z

=

9

x + z

=

3

2x − y

=

3

.

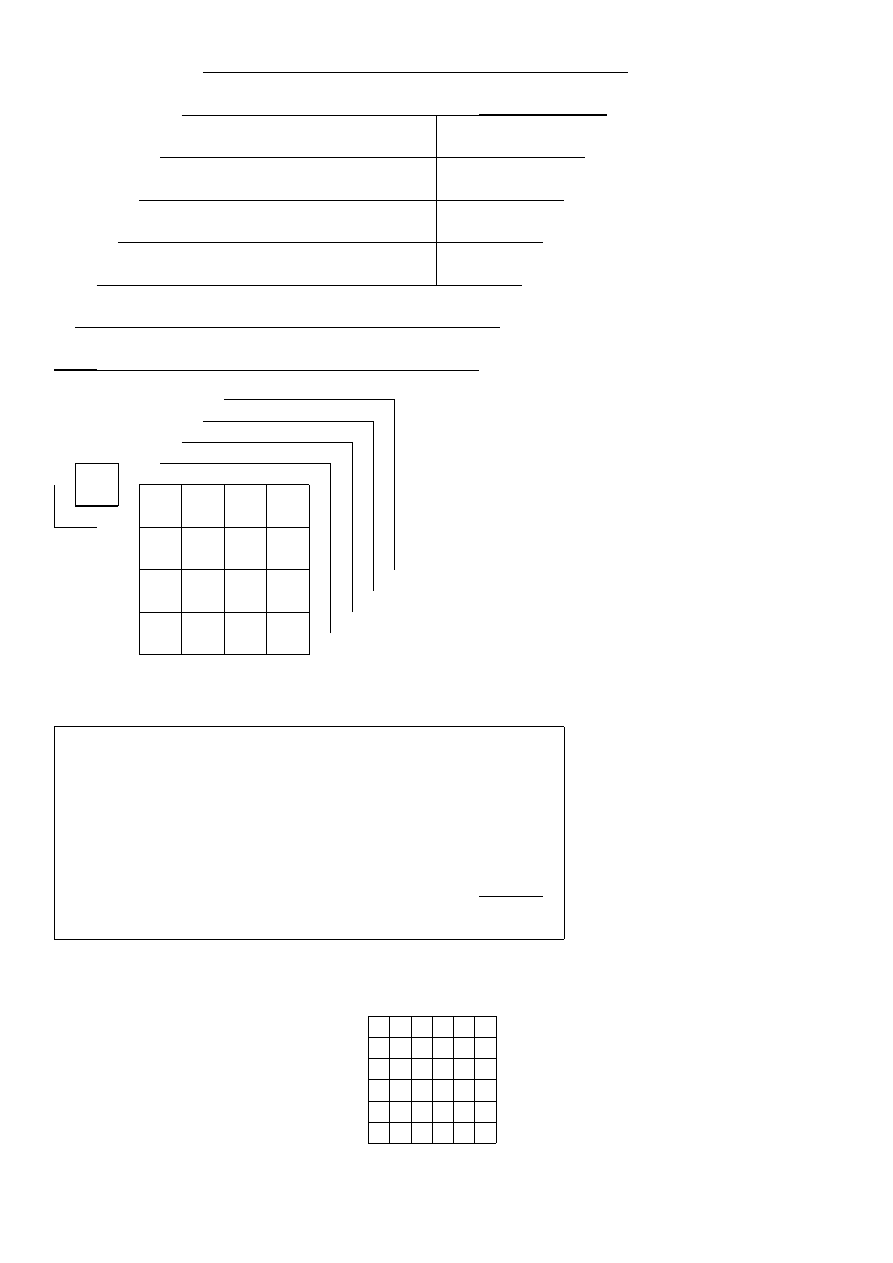
WEKTORY

w4. Przedstaw wektory ~a, ~b, ~

c, ~

d, ~

e, ~

f , ~

g, ~h, ~i jako kombinacje wektorów bazy (~

u, ~

v).

~

a

~b

~b

~

c

@

@

@

@

@

@

R

~

d

~

e

~

f

?

~

g

C

C

C

C

C

C

C

C

C

C

C

CO

~

h

-

~i

-

~

u

~

v

w5. Wyraź wektory ~

AB, ~

BC, ~

CD, ~

DA, ~

AC, ~

DB jako kombinacje liniowe wektorów bazy (~i,~j, ~

k).

s

A

s

B

s

C

s

D

~i

-

~j

6

~

k

układy współrzędnych

u3. Określ graficznie współrzędne x, y punktu P w układzie repera (O, ~

u, ~

v) oraz współrzędne x

0

, y

0

tego samego

punktu w układzie (O

0

, ~

u

0

, ~

v

0

).

*

~

u

~

v

O

·

-

~

u

0

A

A

A

K

~

v

0

·

O’

·

P

u4. Znajdź równanie krzywej x

2

+ 2xy + y

2

− 8x − 4y + 3 = 0 we współrzędnych x

0

, y

0

oraz równanie krzywej

3x

0

+ y

0

− 3 = 0 we współrzędnych x, y.

-

~i

6

~

j

@

@

R

~i

0

~

j

0

O

O’

iloczyn skalarny

s1. Dane są wektory ~

u, ~

v na płaszczyźnie takie, że ~

u ◦ ~

v = −1, oraz długości wektorów ~

u, ~

v są odpowiednio równe

√

3 oraz

√

2.

(a) Oblicz ~

p ◦ ~

q, gdzie ~

p = 2~

u − 3~

v, ~

q = −~

u + 2~

v.

(b) Oblicz długości wektorów ~

p i ~

q.

(c) Wyznacz

stałą α tak aby wektory ~

p i ~

q − α~

p były prostopadłe.

s3. Oblicz kąt pomiędzy wektorami ~

u i ~

v których współrzędne określone są w bazie ortonormalnej:

(a) ~

u = [2, 1],

~

v = [−3, 1],

(b) ~

u = [−2, 3], ~

v = [1, 5],

(c) ~

u = [6, 7, −1], ~

v = [13, 8, 5],

(d) ~

u = [10, 1, 7], ~

v = [1, −2, 1],

(e) ~

u =

[4, 1, −1], ~

v = [−2, 1, 2],

(f) ~

u = [−3, 2, −5], ~

v = [−2, −5, 3],

(g) ~

u = [−10, −7, −1], ~

v = [5, 3, 4],

(h) ~

u = [2, 8, 7],

~

v = [4, 3, 1]. Odp. a) 135

o

, b) 45

o

, c) 30

o

, d) 60

o

, e) 135

o

, f) 120

o

, g) 150

o

, h) 45

o

. Ciekawostka: Wektory o

współrzędnych całkowitoliczbowych na płaszczyźnie nigdy nie utworzą kąta 30

o

ani 60

o

!

s8. Wyznacz wektor równoległy do wektora ~

v 6= ~0 o długości 1:

(a) ~

v = [3, 4],

(b) ~

v = [2, 1, 2].

Wsk. Podziel

wektor przez jego długość. Czynność tę nazywamy normowaniem wektora.

s9. Dane są wektory ~a = [3, 4], ~b = [12, 5]. Znajdź wektor ~

c wyznaczający dwusieczną kąta pomiędzy danymi

wektorami. Wsk. Wystarczy unormować dane wektory i dodać.

prosta i płaszczyzna

p16. Znajdź równanie parametryczne prostej przechodzącej przez dwa dane punkty:

(a) A(−1, 4), B(3, −2);

(b) A(5, −1, 3),

B(1, −4, −3).

p17. Znajdź równanie parametryczne płaszczyzny przechodzącej przez trzy dane punkty:

(a) A(1, −1, 1), B(3, −4, 5),

C(−4, 6, 8);

(b) A(−2, −3, 1), B(−1, −1, 4), C(0, 1, 7);

(c) A(−2, −5, 0), B(−1, −3, 3), C(0, −1, 6).

Sprawdź, czy

punkty nie leżą na jednej prostej.

p18. Znajdź na płaszczyźnie równanie ogólne prostej przechodzącej przez punkt A(2, −3) i prostopadłej do wektora

~

v = [3, 4].

p19. Znajdź w przestrzeni równanie ogólne płaszczyzny przechodzącej przez punkt A(1, −2, 4) prostopadłej do wek-
tora ~

v = [5, −3, −2].

p20. Wyznacz wektor ~

n prostopadły jednocześnie do wektora ~

u = [−1, 3, 2] i do wektora ~

v = [3, −2, 1]. Wsk. Sko-

rzystaj z iloczynu wektorowego.

p21. Znajdź równanie ogólne płaszczyzny o równaniu parametrycznym:







x

=

2 + 3s − t

y

=

s + t

z

=

4 + 2t

.

p22. Znajdź równanie ogólne płaszczyzny przechodzącej przez trzy punkty: A(2, 4, −1), B(0, −3, 4), C(7, 5, 2).

p23. Znajdź równanie ogólne płaszczyzny przechodzącej punkt A(0, −4, 5) oraz prostą

x−2

3

=

y+3

−4

=

z

−1

.

p24. Prostą na płaszczyźnie opisaną równaniem 3x − 7y + 3 = 0 zapisz parametrycznie.

p25. Prostą na płaszczyźnie opisaną równaniem

x−1

3

=

y+2

−4

zapisz w postaci ogólnej.

p26. Płaszczyznę w przestrzeni opisaną równaniem x − 2y + 3z + 7 = 0 zapisz parametrycznie.

p27. Wyznacz punkt wspólny płaszczyzny 3x + y − z + 5 = 0 i prostej

x

2

=

y−3

−4

=

z+1

−2

.

p28. Prostą będącą krawędzią przecięcia płaszczyzn 2x − 3y + z + 1 = 0, −x + 5y + 3z − 2 = 0 opisz parametrycznie.

p29. Wyznacz kąt pomiędzy wektorem ~

x = [3, 4, 5], a płaszczyzną rozpiętą na wektorach ~

u = [−1, 2, 1] i ~

v =

[3, −2, 11]. Wsk. Wyznacz najpierw kąt pomiędzy wektorem ~

x i wektorem ~

n prostopadłym do płaszczyzny.

p32. Wyznacz rzut prostopadły punktu A(2, 3, −6) na płaszczyznę x + 2y + z + 4 = 0. Wsk. Napisz równanie
parametryczne prostej prostopadłej do płaszczyzny.

p33. Wyznacz punkt symetryczny do punktu A względem płaszczyzny z poprzedniego zadania.

p34. Wyznacz rzut prostopadły punktu A(−2, 9) na prostą 2x + 5y = 38, następnie wyznacz punkt symetryczny do
A względem prostej.

p35. Znajdź rzut punktu A(1, −2, 1) na prostą x + 1 =

y+8

−1

=

z−2

2

.

Wsk. Poprowadź płaszczyznę przechodzącą przez punkt A i prostopadłą do prostej.

p36. Wyznacz rzut prostopadły prostej

x

4

=

y−1

3

=

z−2

2

na płaszczyznę x − y + 3z + 8 = 0.

p37. Wyznacz kąt pomiędzy prostymi x + y + 1 = 0,

2x − y = 0.

p38. Wyznacz kąt pomiędzy płaszczyznami x − y + 2z = 0,

−2x + y + z = 0. Wsk. Jest to kąt pomiędzy wektorami

normalnymi.

p39. Wyznacz kąt pomiędzy płaszczyzną −x + 2y − 3z = 0 i prostą

x

2

=

y+1

1

=

z−1

3

.

p40. Wyznacz równania dwusiecznych kątów utworzonch przez proste y = x ,

y = 7x. Wsk. Zad. 9.

p41. Oblicz obwód i pole trójkąta ABC dla A(1, 2, −1), B(3, 0, 4), C(3, 5, 3).

p42. Oblicz odległość punktu A(5, 6) od prostej 2x + 3y − 1 = 0.

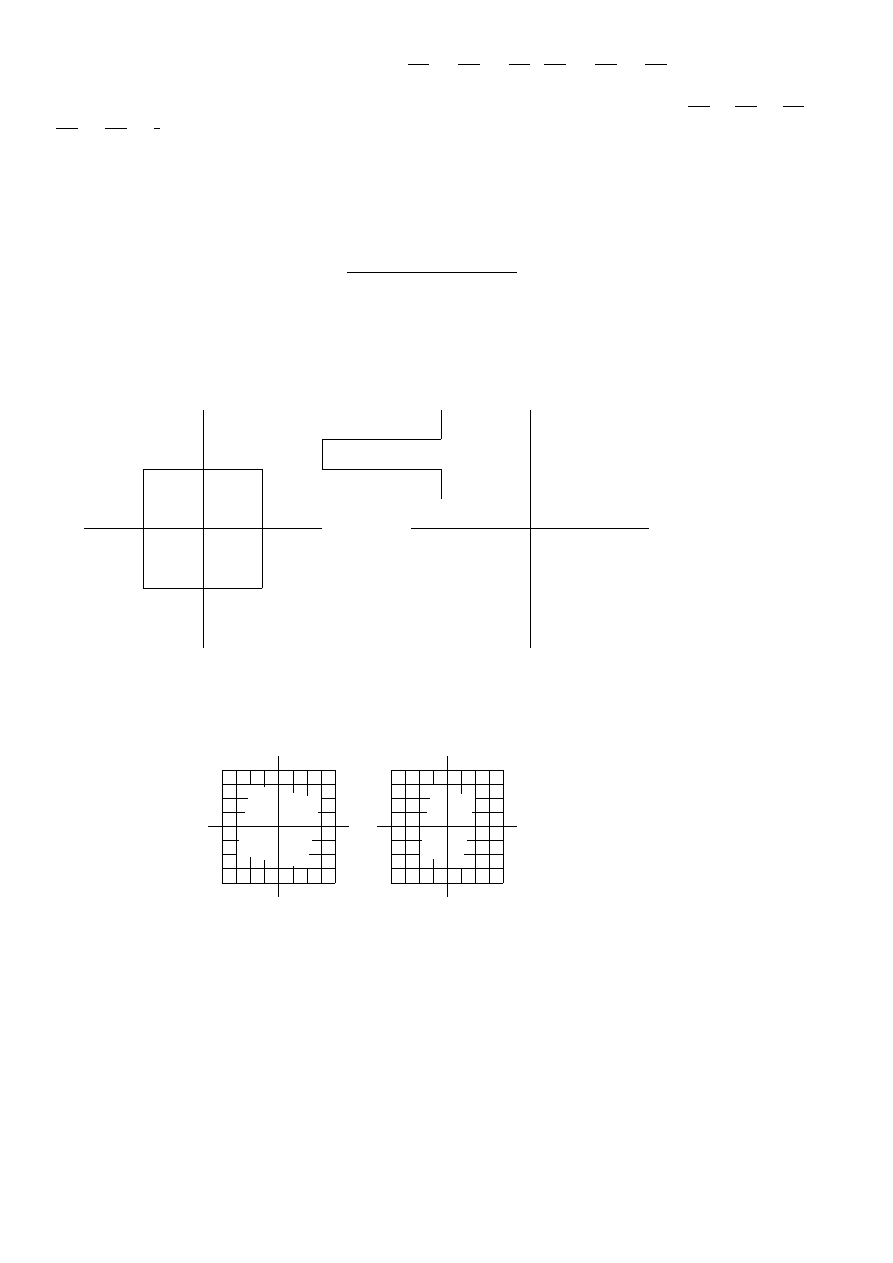
p43. Oblicz odległość punktu A(3, 4, 3) od płaszczyzny x + 2y − z + 2 = 0.

p44. Wyznacz odległość między prostymi skośnymi

x+3

4

=

y−6

−3

=

z−3

2

,

x−4

8

=

y+1

−3

=

z+7

3

. Wsk. Przez jedną z

prostych przeprowadź płaszczyznę równoległą do drugiej prostej.

p45. Znajdź równanie prostej przechodzącej przez punkt A(1, 2, 1) i przecinającej dwie proste:

x−1

1

=

y+3

−2

=

z−3

2

,

x−2

2

=

y−2

1

=

z
3

. Wsk. Przez jedną z prostych i punkt A przeprowadź płaszczyznę która przetnie drugą prostą w

punkcie B. AB jest szukaną prostą.

Operatory

o50. Za pomocą operatora ~

f : R

2

→ R

2

, opisanego macierzą A, przekształć kwadrat dany na rysunku poniżej. Znajdź

obrazy punktów P, Q, R, S, O i zaznacz je jako punkty P

0

, Q

0

, R

0

, S

0

, O

0

w układzie obok. Współrzędne punktów

odczytaj z rysunku wiedząc, że P = (1, 1). Porównaj iloraz

pole czworokąta P

0

Q

0

R

0

S

0

pole czworokąta P QRS

z wyznacznikiem macierzy A. Rozważ następujące warianty:

a) A =

3

1

1

2

,

b) A =

−1

0

0

1

,

c) A =

1

0

0

1

,

d) A =

1

−2

2

1

,

e) A =

2

4

1

2

.

-

x

6

y

·

P

·

Q

·

R

·

S

·

O

Z

Z

Z

Z

-

x

6

y

o54. Wyznacz macierz A operatora ~

f : R

2

→ R

2

w bazie naturalnej, który przekształca figurę F na F

0

zgodnie z

podanym rysunkiem.

`

`

`

`

`

`

``

`

`

-

x

6

y

·

P

·

Q

·

R

·

S

F

P

P

P

P

P

P

-

x

6

y

·

S’

·

P’

·

Q’

·

R’

F’

o55. Znajdź wartości i wektory własne operatora określonego daną macierzą. W przykładach (g) i (h) wyznacz
dodatkowo płaszczyzny niezmiennicze.

(a)

−2

−4

1

3

,

(b)

−3

4

2

−1

,

(c)





0

3

1

3

0

−1

1

−1

−4





,

(d)





2

5

−1

5

−2

−5

−1

−5

2





,

(e)





4

−2

2

−2

3

0

2

0

0





,

(f)





4

−2

2

−2

3

0

2

0

0





,

(g)





1

2

−1

−5

−3

−3

−2

−1

−2





,

(h)





2

0

1

5

1

5

2

−3

−2





.