
INWESTYCJE KAPITAŁOWE
•finansowym maj
ątkiem trwałym (np. obligacje, weksle długoterminowe, akcje lub
udzia
ły spółek kapitałowych, certyfikaty inwestycyjne)
Są to nakłady o charakterze długoterminowym, które w
przyszłości przyniosą korzyści jednostce gospodarującej.
•warto
ściami niematerialnymi i prawnymi (np. badanie i rozwój, kształcenie oraz
inwestycje socjalne)
Poj
ęcie inwestycje kapitałowe obejmuje zatem nakłady długoterminowe związane z:
•rzeczowym maj
ątkiem trwałym (np. budynki, budowle, urządzenia, maszyny,
środki transportowe)
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro

Technik
ą wspomagającą podejmowanie decyzji
d
ługookresowych jest
BUD
ŻETOWANIE KAPITAŁOWE
(Rachunek inwestycyjny),
wymagaj
ące zastosowania
w
łaściwych metod oceny efektywności projektów
inwestycyjnych, tzn. przeprowadzenia przez podejmuj
ących
decyzje rachunku op
łacalności inwestycji na podstawie
w
łaściwych kryteriów wyboru.
CELE I ETAPY BUDŻETOWANIA KAPITAŁOWEGO
Wszystkie d
ługookresowe decyzje, a zwłaszcza dotyczące
inwestycji produkcyjnych, musz
ą być wynikiem przemyślanego,
świadomego wyboru określonego projektu spośród różnych
wariantów inwestycyjnych.
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro

4) Etapy wdrożenia projektu i kontroli jego wykonania poprzez porównanie
przewidywanych danych z aktualnymi wynikami, co zapewnia efektywne sprzężenie
zwrotne.
Budżetowanie kapitałowe
- polega na podejmowaniu
długookresowych decyzji w zakresie inwestowania
i jest procesem kilkuetapowym. W procesie tym wyróżnia się:
1)
Etap planowania obejmujący
:
Identyfikację projektu tj. ustalenie typu przedsięwzięcia inwestycyjnego umożliwiającego
osiągnięcie wymaganych celów,
Przedstawienie różnych wariantów projektu inwestycyjnego,
Przygotowanie danych wartościowych, ilościowych oraz jakościowych, charakteryzujących
poszczególne warianty projektu,
2) Etap oceny wariantów projektu inwestycyjnego oraz podjęcia decyzji inwestycyjnej;
3) Etap gromadzenia środków dla sfinansowania przedsięwzięcia inwestycyjnego,
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro

Podział inwestycji wg kryterium rodzajowego:
• inwestycje odtworzeniowe
• inwestycje modernizacyjne
• inwestycje rozwojowe
• inwestycje innowacyjne
• inwestycje strategiczne
• inwestycje interesu publicznego
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro

Rachunek inwestycyjny
Aby rachunek inwestycyjny był podstawą trafnych decyzji długookresowych musi:
1.
Uwzgl
ędnić taką kategorię ekonomiczną, będącą wynikiem zastosowania
projektu, w której optymalizacja umo
żliwiałaby wzrost wartości
przedsi
ębiorstwa w długim okresie, a zatem jego rozwój w przyszłości.
2. Zosta
ć przeprowadzany na podstawie metod, które uwzględniają wartość
pieni
ądza w czasie, tzn. fakt, że na wartość pieniądza ma wpływ moment jego
uzyskania lub wydatkowania.
3. W rachunku op
łacalności inwestycji wielkością podlegającą optymalizacji jest
nadwy
żka pieniężna (przepływy pieniężne netto tj. cash flow), czyli różnica
mi
ędzy wpływami a wydatkami związanymi z wdrożeniem i użytkowaniem
przedsi
ęwzięcia inwestycyjnego w poszczególnych latach.
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro

METODY OCENY EFEKTYWNOŚCI
INWESTYCJI KAPITAŁOWYCH
Metody dyskontowe oceny efektywności obejmują:
•Aktualną wartość netto (net present value - NPV)
•Wewnętrzną stopę zwrotu (internal rate of return - IRR)
•Wskaźnik efektywności (E)
Metody pozwalaj
ących na ocenę efektywności inwestycji można podzielić na:
metody niedyskontowe (proste) i dyskontowe.
Metody niedyskontowe oceny efektywności obejmują:
•Księgową stopę zwrotu (accounting rate of return - ARR)
•Stopa zwrotu kapitału własnego (Zn/Kwł)
•Okres zwrotu nakładów inwestycyjnych (Tz)
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro

KSIĘGOWA STOPA ZWROTU
Jedn
ą z najczęściej stosowanych metod służących do oceny
efektywno
ści inwestycji jest KSIĘGOWA STOPA ZWROTU
(
Accouting Rate of Return
), czyli stosunek przeci
ętnego zysku do
nak
ładów inwestycyjnych związanych z realizacją projektu.
Podstawową wadą księgowej stopy zwrotu jako metody szacowania
opłacalności inwestycji (niezależnie od sposobu obliczania) jest to, że nie
uwzględnia ona wartości pieniądza w czasie - w rezultacie rentowność projektu
jest zwykle zawyżana.
Drugą znaczącą wadą księgowej stopy zwrotu jest to, że opiera się ona na
koncepcji zysku ksi
ę
gowego, a nie przep
ł
ywach pieni
ęż
nych.
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro
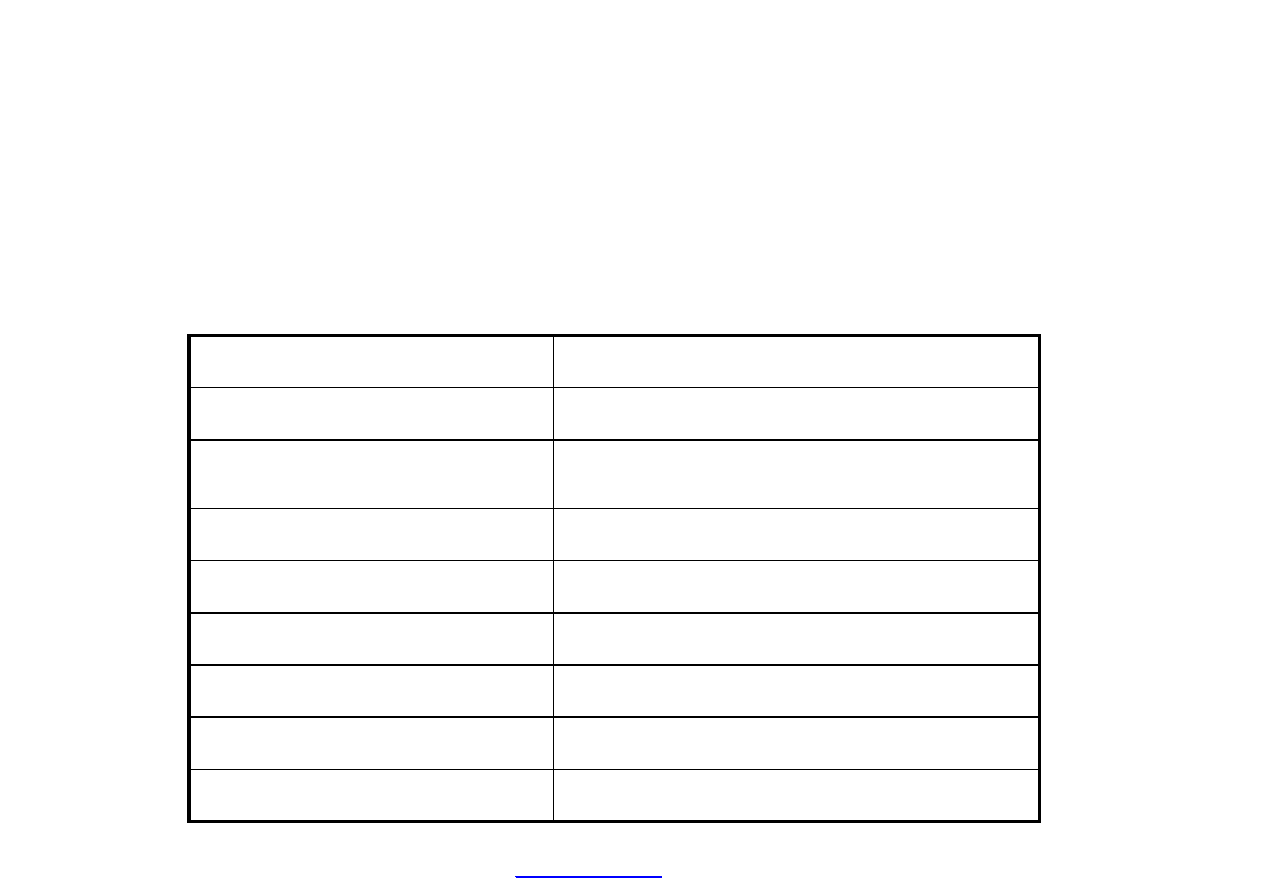
Zadanie 1
Załóżmy, że wymagana przez przedsiębiorstwo X minimalna księgowa stopa
zwrotu wynosi 9 %. Przedsiębiorstwo zamierza podjąć projekt, którego
charakterystyka jest następująca:
20 000
Roczna amortyzacja prosta
30 000
Rok 5
35 000
Rok 4
30 000
Rok 3
27 000
Rok 2
20 000
Rok 1
Przepływy pieniężne netto (zysk
+ amortyzacja):
5 lat
Czas trwania projektu
100 000
Nakłady inwestycyjne
ARR = przeciętny zysk/nakłady inwestycyjne
ARR – księgowa stopa zwrotu
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro
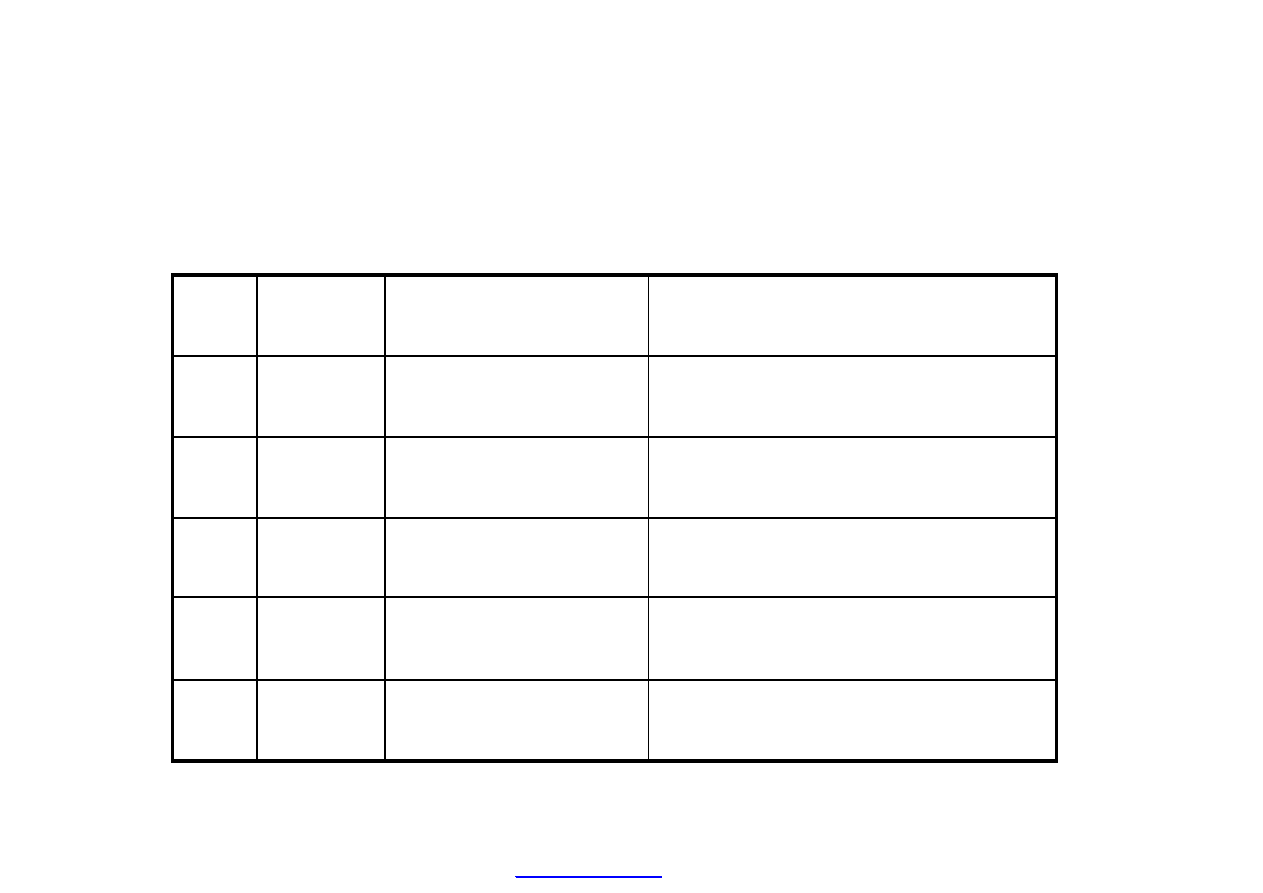
Rozwiązanie powyższego problemu dla kolejnych lat „życia projektu” można
przedstawić następująco:
10%
100 000
10 000
5
15%
100 000
15 000
4
10%
100 000
10 000
3
7%
100 000
7 000
2
0%
100 000
0
1
Księgowa stopa zwrotu w roku
Środki trwałe
brutto (zł)
Zysk (zł)
Rok
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro

Ksi
ęgowa stopa zwrotu w pierwszych dwóch latach projektu jest niska. W roku trzecim,
czwartym i piątym wartość księgowej stopy zwrotu rośnie. Ponieważ w pierwszych latach
realizacji projektu księgowa stopa zwrotu jest niższa od wymaganej, a w latach następnych
wyższa, niemożliwe jest więc podjęcie dotychczas otrzymanych wyników jednoznacznej decyzji
o realizacji bądź zaniechaniu projektu. Konieczne jest zatem obliczenie przeciętnej stopy
zwrotu z projektu na przestrzeni 5 lat.
100 000
Nakłady inwestycyjne
8 400
Średni zysk w roku
42 000
Zysk za okres pięciu lat
142 000
Przepływy pieniężne netto (zysk + amortyzacja za okres 5 lat)
Dane pomocnicze do wylicze
ń
przedstawione s
ą
poni
ż
ej:
Należy podkreślić, że ksi
ęgowa stopa zwrotu jest liczona w oparciu o
zysk, a nie przepływy pieniężne, stąd też przepływy pieniężne
z treści przykładu są korygowane w dół o amortyzację
(100 000 zł/5 lat = 20 000 zł).
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro

Ponieważ obliczona powyżej przeciętna księgowa stopa zwrotu (8,4 %) jest niższa od stopy minimalnej
wymaganej w przedsiębiorstwie dla projektów o porównywalnym ryzyku, to analizowany projekt nie
powinien być zrealizowany.
Podstawową wadą księgowej stopy zwrotu jako metody szacowania opłacalności
inwestycji (niezależnie od sposobu obliczania) jest to, że nie uwzględnia ona
wartości pieniądza w czasie - w rezultacie rentowność projektu jest zwykle
zawyżana.
Drugą znaczącą wadą księgowej stopy zwrotu jest to, że opiera się ona na
koncepcji zysku księgowego a nie przepływach pieniężnych.
Księgowa stopa zwrotu może być obliczona w następujący sposób:
średni zysk w roku
8400
nakłady inwestycyjne
100 000
=
=
8,4 %
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro
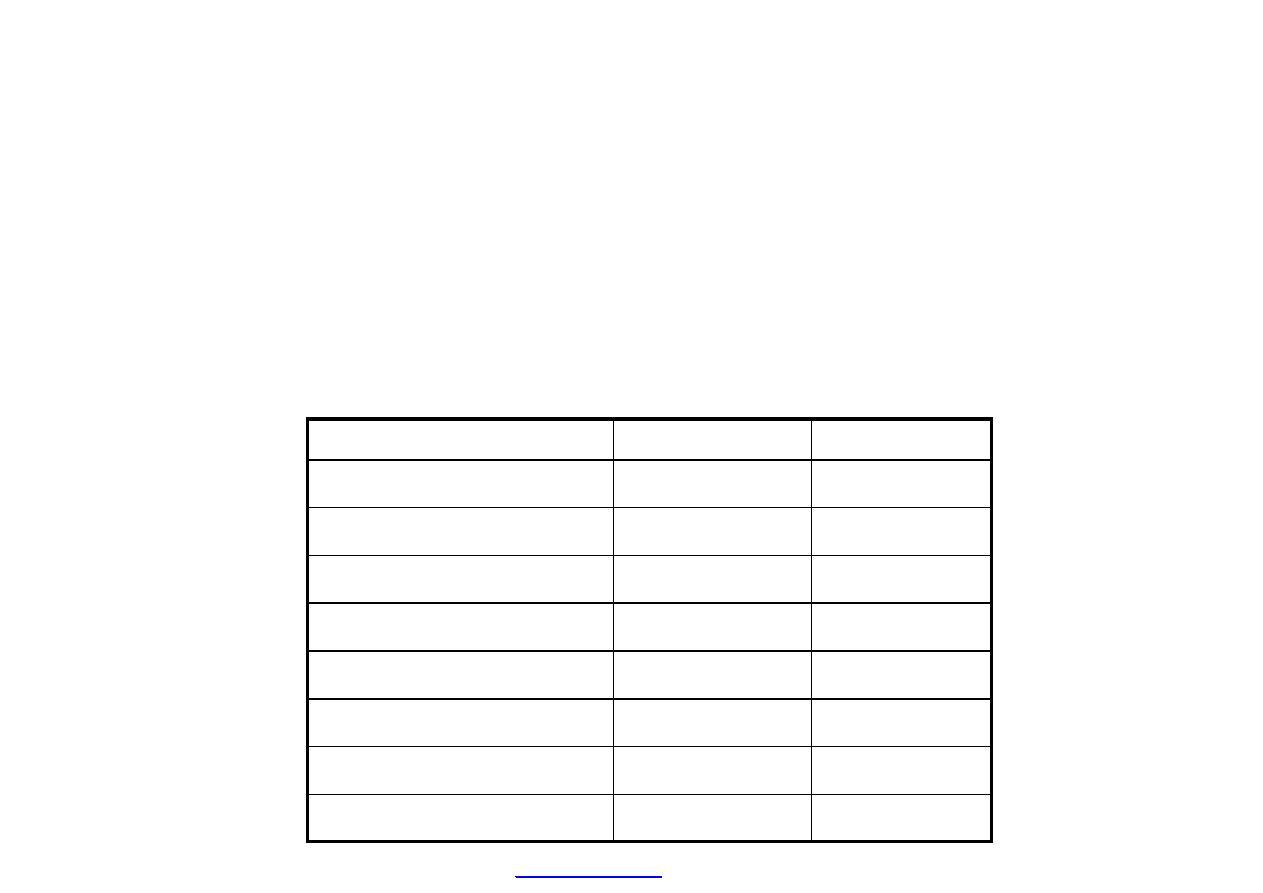
DŁUGOŚĆ OKRESU ZWROTU -
Jest to okres po którym wydatki środków pieniężnych związane z realizacją i eksploatacją
projektu zostaną pokryte przez wpływy z tytułu eksploatacji inwestycji, czyli inaczej mówiąc
okres zwrotu definiujemy jako liczbę lat, po których wpływy wynikające z realizacji danego
projektu zrównają się z nakładami. Najprostszym sposobem obliczania okresu, po którym
nastąpi zwrot nakładów, jest kumulowanie przepływów pieniężnych netto projektu do momentu,
w którym wyniosą one zero.
Zadanie 2
Dla zilustrowania tej metody przyjmijmy, że przedsiębiorstwo ABC zamierza podjąć jeden z dwóch
projektów, których charakterystyki są następujące:
1 500
500
Rok 5
2 000
500
Rok 4
500
500
Rok 3
500
1 000
Rok 2
500
1 000
Rok 1
Przepływy pieniężne netto:
5 lat
5 lat
Czas trwania projektu
2 000
2 000
Nakłady inwestycyjne
Projekt 2
Projekt 1
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro
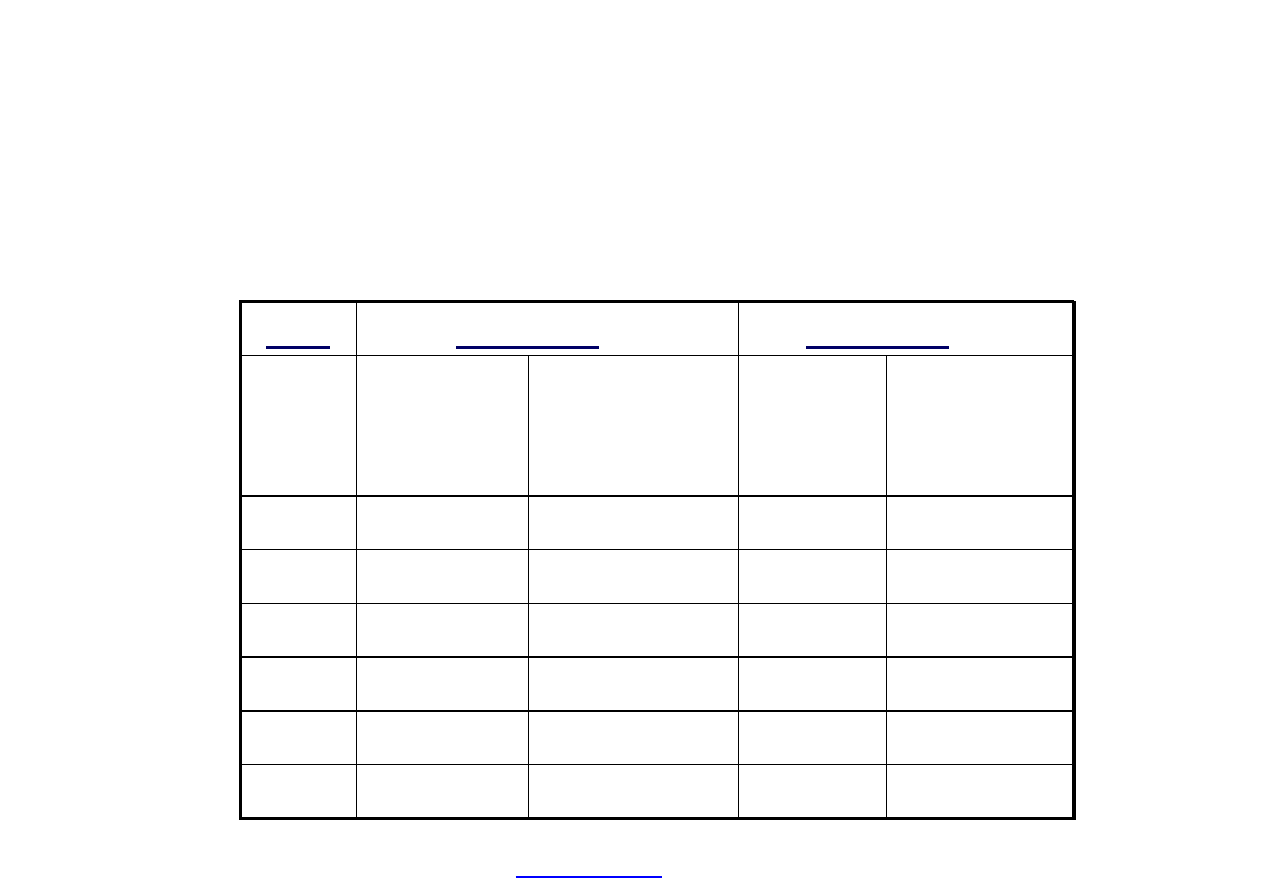
Należy zaznaczyć, że do szacowania opłacalności inwestycji przy zastosowaniu okresu
zwrotu wyliczenia należy oprzeć na wielkości zysku przed odliczeniem amortyzacji
(zysk + amortyzacja), który odpowiadać może w przybliżeniu wielkości przepływów
pieniężnych netto z projektu.
W celu obliczenia okresu zwrotu poniesionych nakładów tworzymy tabelę skumulowanych
przepływów pieniężnych netto projektu w okresie od t = 0 do t =5
3 000
1 500
1 500
500
5
1 500
2 000
1 000
500
4
(500)
500
500
500
3
(1 000)
500
0
1 000
2
(1 500)
500
(1 000)
1 000
1
(2 000)
(2 000)
(2 000)
(2 000)
0
Skumulowane
przepływy
pieniężne
netto (zł)
Przepływy
pieniężne
netto (zł)
Skumulowane
przepływy
pieniężne netto
(zł)
Przepływy
pieniężne
netto (zł)
Projekt 2
Projekt 1
Rok
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro

Jak wida
ć
z tabeli, w przypadku projektu pierwszego, nak
ł
ady inwestycyjne zwróc
ą
si
ę
ju
ż
w
ko
ń
cu drugiego roku realizacji.
W przypadku projektu drugiego nakłady inwestycyjne zwrócą się w roku czwartym. Przy
założeniu, że przepływy pieniężne są w ciągu danego roku rozłożone równomiernie, możemy
jeszcze dokładniej oszacować okres zwrotu projektu drugiego.
Ponieważ w końcu trzeciego roku inwestycji do „pokrycia” zostało jeszcze 500 zł nakładów,
a w roku czwartym nastąpił wpływ środków pieniężnych netto w wysokości 2 000 zł, to
pełne pokrycie koszów projektu drugiego będzie miało miejsce w jednej czwartej roku
czwartego (500 zł: 2 000 zł = 0,25). Stąd okres zwrotu tego projektu wynosi 3,25 roku.
Im krótszy jest okres, po którym następuje zwrot poniesionych nakładów, tym
projekt jest lepszy. Jeżeli firma ma problemy z płynnością lub też pragnie
zaangażować środki w inne przedsięwzięcia, wówczas menedżer może wybrać
projekt pierwszy, ponieważ jego okres zwrotu jest krótszy.
Okres zwrotu projektu jest stosunkowo prostą metodą oceny efektywności i z tego
powodu często bywa wykorzystywany jako wstępna miara opłacalności inwestycji.
Projekty inwestycyjne nie powinny być jednak oceniane wyłącznie na podstawie
tego kryterium. Należy zwrócić uwagę na to, że okres zwrotu jako kryterium
decyzyjne ma dwie zasadnicze wady - po pierwsze nie uwzględnia wartości
pieniądza w czasie, po drugie bierze pod uwagę tylko przepływy pieniężne do
wysokości nakładów inwestycyjnych.
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro

WARTOŚĆ BIEŻĄCA NETTO
(NPV)
Aktualna wartość netto projektu inwestycyjnego
to
aktualna wartość wszystkich wpływów i wydatków
związanych z realizacją i eksploatacją projektu
inwestycyjnego
Kiedy uświadomiono sobie braki metody okresu zwrotu, rozpoczęły się poszukiwania nowych
procedur prowadzących do lepszej oceny efektywności inwestycji. Owocem tych prac były
techniki DCF (discounted cash flow), czyli zdyskontowanych strumieni pieniężnych. Jedną z
nich jest określanie wartości bieżącej netto (NPV).
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro

Każda typowa inwestycja generuje serię przepływów pieniężnych CFt, gdzie t jest rokiem wystąpienia danego przepływu.
Dla t=1,.....n ciąg przybiera postać CF1, CF2,CF3....CFn. Obecnie wartość tego strumienia jest następująca:
PV = ΣCF1t (1+r) -t
Wzór ten przedstawia wpływy pieniężne netto z projektu. Jeżeli początkowe nakłady inwestycyjne przedstawimy jako K, to
odejmując od wartości bieżącej (PV) wpływów pieniężnych, wartość bieżącą (PV) nakładów inwestycyjnych otrzymamy
wartość bieżącą netto
inwestycji
NPV = PV – K NPV = ΣCFt (1+r) –1-t – K
Decyzja o podjęciu projektu zapada na podstawie NPV w następujący sposób:
NPV projektu > 0 realizacja NPV projektu < 0 zaniechanie NPV projektu = 0 nie ma znaczenia
Jeżeli mamy do czynienia z dwoma wykluczającymi się projektami, to akceptujemy ten o wyższej wartości bieżącej netto.
Zadanie 3. Ocenę opłacalności projektu według kryterium NPV można przeanalizować na
przykładzie firmy XYZ, która rozważa zainwestowanie 20 000 zł w urządzenia do pakowania
żywności. Koszt kapitału wynosi 24 %, a okres eksploatacji aktywów 4 lata, po którym to okresie
będzie miała miejsce sprzedaż – możliwa do uzyskania cena wynosi 4 000 zł (cena ta będzie równa
wartości księgowej środka trwałego.)
Należy obliczyć opłacalność inwestycji, wiedząc, że szacowane zyski są następujące:
2 000
4
3 000
3
7 000
2
5 000
1
Zysk
Rok
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro
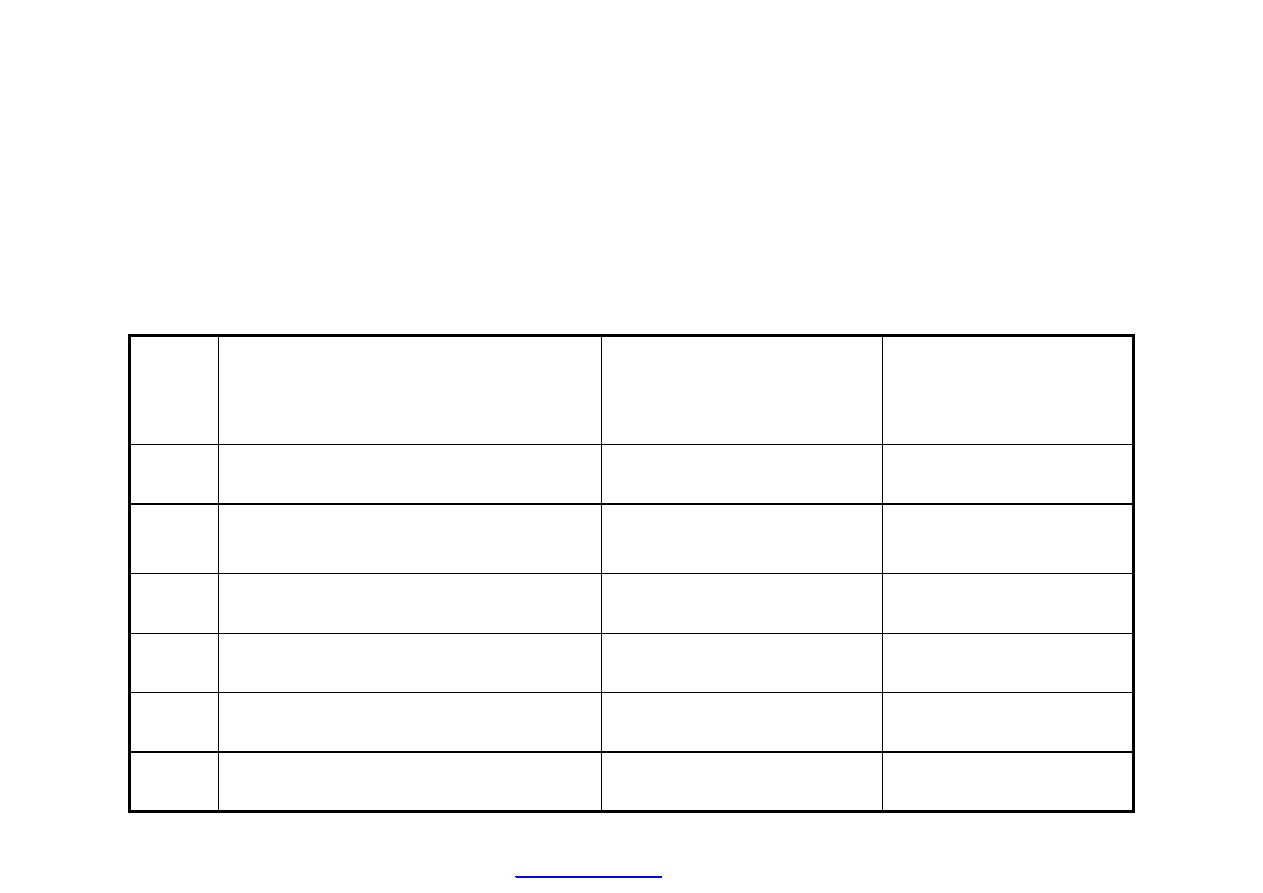
Przy za
łożeniu amortyzacji liniowej, roczny odpis amortyzacyjny wyniesie:
koszt – warto
ść końcowa = 20 000 zł – 4 000 zł = 16 000 zł
Aby obliczy
ć przepływy pieniężne w poszczególnych latach, musimy skorygować
zyski z poprzedniej tabeli wielko
ścią amortyzacji (amortyzacja jest kosztem, nie jest
jednak wydatkiem).
Dodatkowo przep
ływy pieniężne w roku czwartym powiększamy o cenę sprzedanych
urz
ądzeń (4 000 zł).
NPV = 2315
4 230
0,4230
2 000 + 4 000 + 4 000
4
3 672
0,5245
3 000 + 4 000
3
7 154
0,6504
7 000 + 4 000
2
7 259
0,8065
5 000 + 4 000
1
(20 000)
1,000
(20 000)
0
Zdyskontowane
przepływy pieniężne
netto (zł)
Czynnik dyskontujący
(24 %)
Przepływy pieniężne netto (zł)
Rok
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro
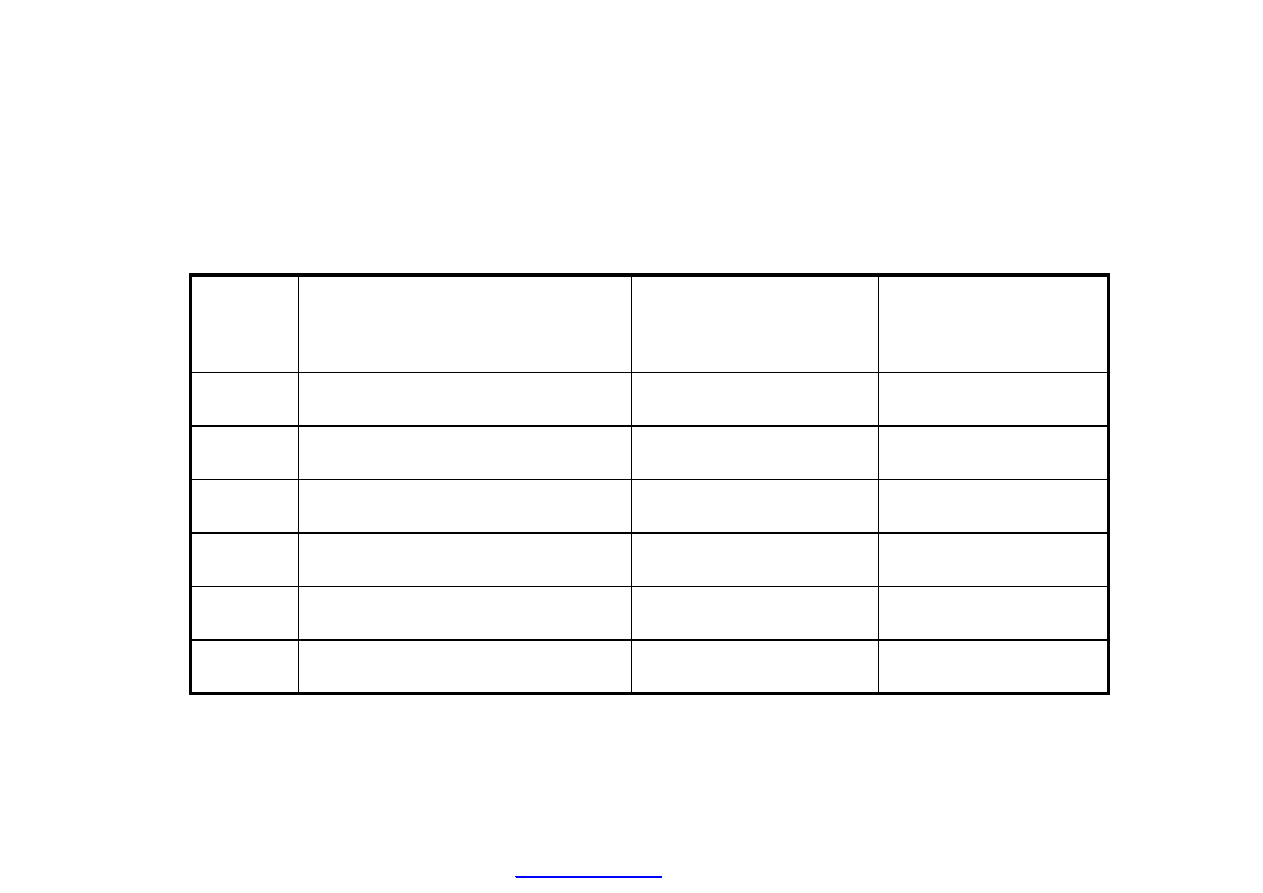
Przy r = 24 % projekt należy zaakceptować.
Można zbadać również, co stałoby się z projektem, gdyby koszt
wynosił nie 24 %, ale 36 %.
NPV = - 1 728
2 923
0,2923
2 000 + 4 000 + 4 000
4
2 783
0,3975
3 000 + 4 000
3
7 154
0,6504
7 000 + 4 000
2
7 259
0,8065
5 000 + 4 000
1
(20 000)
1,000
(20 000)
0
Zdyskontowane
przepływy
pieniężne netto (zł)
Czynnik
dyskontujący (36 %)
Przepływy pieniężne netto (zł)
Rok
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro

Przy wzroście kosztu kapitału do 36 % inwestycja w nową linię
technologiczną staje się nieopłacalna, gdyż generuje ujemną NPV, równą
NPV = - 1 728 zł.
W ramach podsumowania nale
ż
y stwierdzi
ć
,
ż
e jako
ść
oceny
op
ł
acalno
ś
ci inwestycji metod
ą
NPV zale
ż
y od:
1)
Poprawnego określenia kosztu kapitału (kredytu czy kapitału
własnego)
2)
Prawidłowego szacunku przepływów pieniężnych w przyszłości
3)
Wpływu inflacji, która generalnie komplikuje analizę
W zależności od czynnika dyskontującego (r), NPV projektu może
przyjmować różne wartości: ujemne i wówczas inwestycja jest nieopłacalna,
bądź dodatnie i wówczas projekt powinien być zrealizowany.
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro

WEWNĘTRZNA STOPA ZWROTU (IRR) -
Przy podejmowaniu decyzji o inwestycjach kapitałowych jednostki stosujące wewnętrzną stopę zwrotu
wybierają projekty charakteryzujące się wyższą wewnętrzną stopą zwrotu, pod warunkiem, że ta stopa jest
wyższa od rynkowej stopy zwrotu.
Wewnętrzna stopa zwrotu więc jest definiowana jako taka, przy której obecna wartość (PV)
oczekiwanych przyszłych wpływów gotówkowych równa się z obecną wartością oczekiwanych
nakładów
PV wpływów = PV nakładów
PV wydatków - PV nakładów = 0
Lewa strona równania jest określona wzorem na NPV, w którym niewiadomą jest r.
Przyjmijmy, że r = IRR:
CF0 + CF1 + CF2 + .....+ CFn = 0
ΣCFt = 0
Wewn
ę
trzna stopa zwrotu projektu (IRR) jest zwykle porównywana z kosztem kapita
ł
u (k), a decyzja
odno
ś
nie inwestowania zapada wed
ł
ug schematu:
• IRR> k, wówczas inwestowa
ć
•IRR<k, wówczas zaniecha
ć
inwestycji
•IRR = k, wówczas decyzja nie ma znaczenia
stopa procentowa, przy użyciu której aktualna wartość netto wszystkich wpływów i wydatków
związanych z realizacją i eksploatacją projektu inwestycyjnego jest równa zeru.
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro
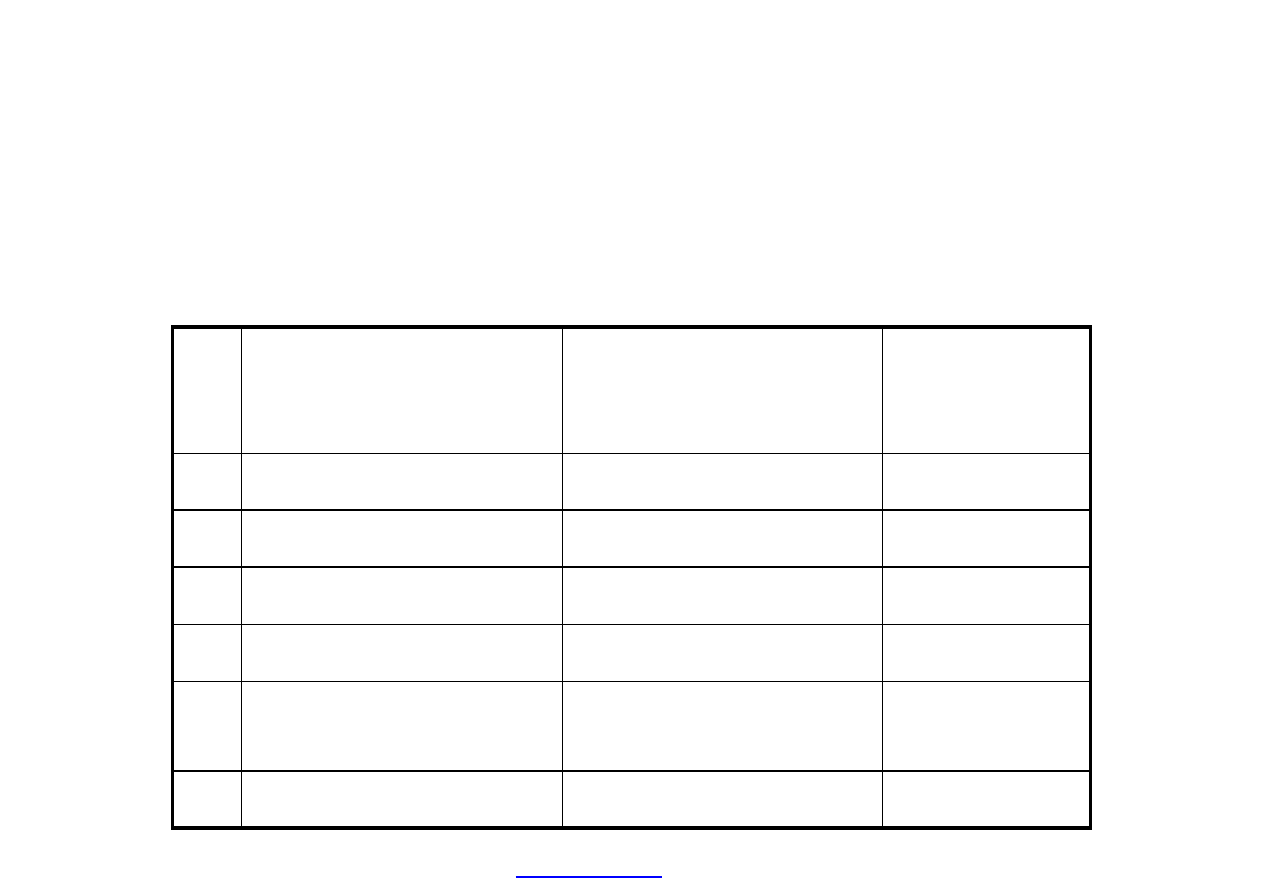
Chcąc uzyskać lepsze oszacowanie wewnętrznej stopy zwrotu, najpierw
poprzez proces prób i błędów, możemy określić dwie wartości NPV
charakteryzujące się tym, że jedna z nich jest nieznacznie większa, a druga
nieznacznie mniejsza od zera. Następnie stosując interpolację szacujemy
wartość IRR (szacujemy r, przy którym NPV = 0). Określamy NPV dla r =
30 % i r = 32 %.
3 501
0,3501
10 000
4
NPV = 119
3 186
0,4552
7 000
3
6 509
0,5917
11 000
2
6 923
0,7692
9 000
1
(20 000)
1
(20 000)
0
Zdyskontowane
przepływy
pieniężne netto
(zł)
Czynnik dyskontujący (30
%)
Przepływy pieniężne netto
(zł)
Rok
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro

NPV = - 531
3 294
0,3294
10 000
4
3 044
0,4348
7 000
3
6 313
0,5739
11 000
2
6 818
0,7576
9 000
1
(20 000)
1
(20 000)
0
Zdyskontowane
przepływy pieniężne
netto (zł)
Czynnik dyskontujący (32
%)
Przepływy pieniężne
netto
Rok
Można więc stwierdzić, że IRR znajduje się między 30 % a 32 %, z tym, że jest bliższe
30 %. Wewnętrzna stopa zwrotu analizowanego projektu wynosi więc IRR = 30,37 %
Oznacza to, że projekt jest opłacalny tak długo jak długo koszt kapitału, którym
będzie finansowany jest mniejszy od 30,37 %.
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro

ZMODYFIKOWANA WEWNĘTRZNA STOPA
ZWROTU - MIRR
W celu obliczenia wskaźnika procentowego MIRR należy:
•
ustalić tzw. końcową wartość projektu jako iloczyn przewidywanych przepływów pieniężnych
do końca okresu objętego rachunkiem efektywności i czynników pomnażających na poziomie
kosztu kapitału.
•
określić stopę zwrotu, która zrównuje zdyskontowaną końcową wartość projektu z
początkowymi wydatkami inwestycyjnymi.
MIRR stanowi stopę dyskontową, przy której zaktualizowana wartość (PV) jest równa
zaktualizowanej wartości sumy przyszłych przepływów pieniężnych, pomnożonych
zgodnie z czynnikami procentu składanego odpowiadającego kosztowi kapitału.
W metodzie MIRR (Modified Internal Rate of Return) przyjmuje się założenie, że
środki pieniężne uzyskiwane z danej inwestycji są reinwestowane po stopie równej
kosztowi kapitału.
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro

MIRR jest więc wyprowadzana z następującego równania:
PV wydatków inwestycyjnych = PV wartości końcowej projektu
Stopa zwrotu uzyskiwana z tytułu reinwestycji jest zazwyczaj różna
od wewnętrznej stopy zwrotu projektu, stąd jej nazwa:
zmodyfikowana wewnętrzna stopa zwrotu. Innymi słowy jest to
taka wartość stopy dyskontowej, która zrównuje zaktualizowaną
wartość końcową dodatnich przepływów pieniężnych z wartością
ujemnych przepływów pieniężnych,
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro
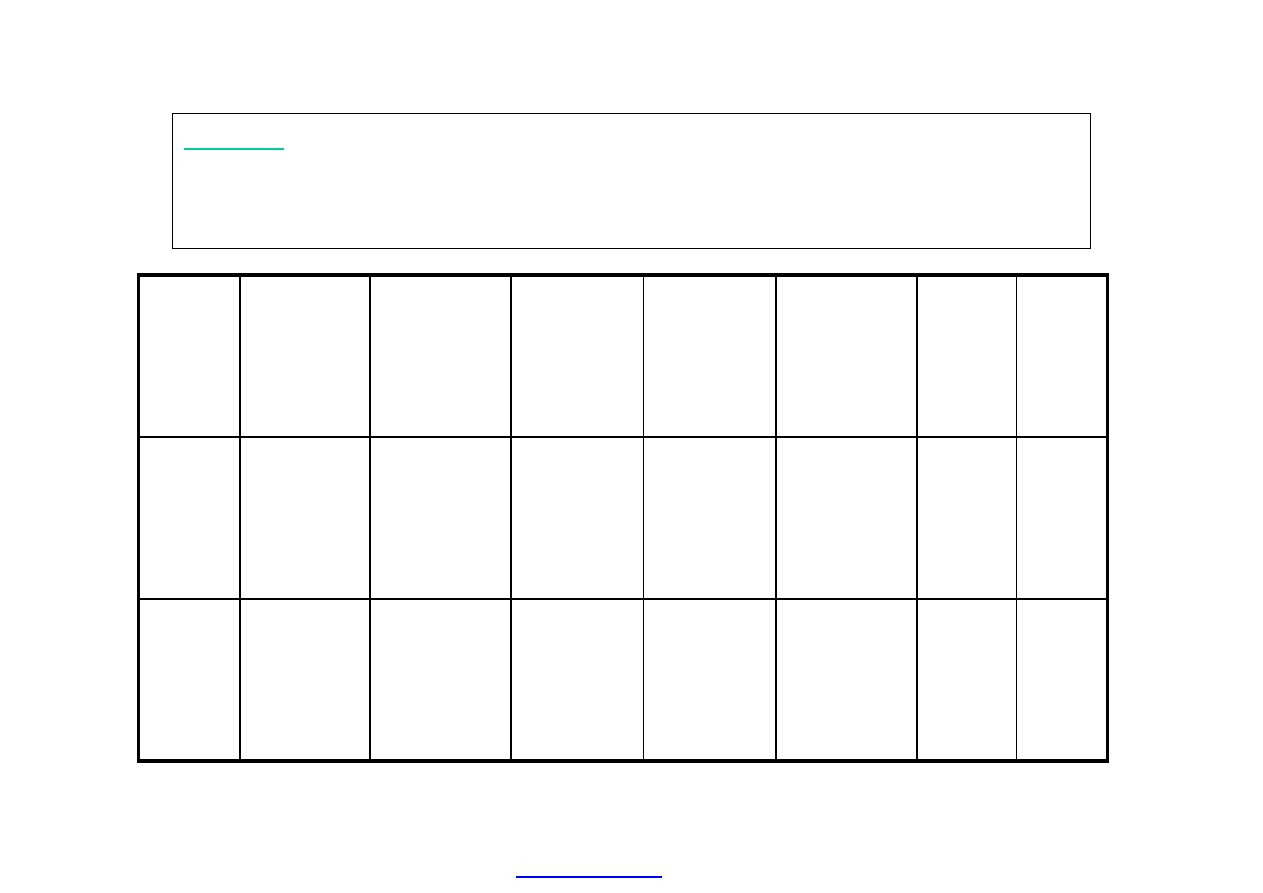
Zadanie 5
Spółka „Gama” wybrała spośród różnych propozycji do ostatecznej oceny dwa wzajemnie
wykluczające się projekty inwestycyjne: A i B, dane do tych projektów przedstawia
poniższa tabela:
28,5
%
17 085
27 000
27 000
27 000
27 000
-60 000
A
27 %
16 335
10 000
20 000
30 000
40 000
-60 000
B
IRR
NPV w
zł dla
R=15
%
Przepływy
środków
pieniężnych
4
Przepływy
środków
pieniężnyc
h 3
Przepływy
środków
pieniężnyc
h 2
Przepływy
środków
pieniężnych
1
Początkow
e nakłady
inwestycyj
ne
Projekt
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro
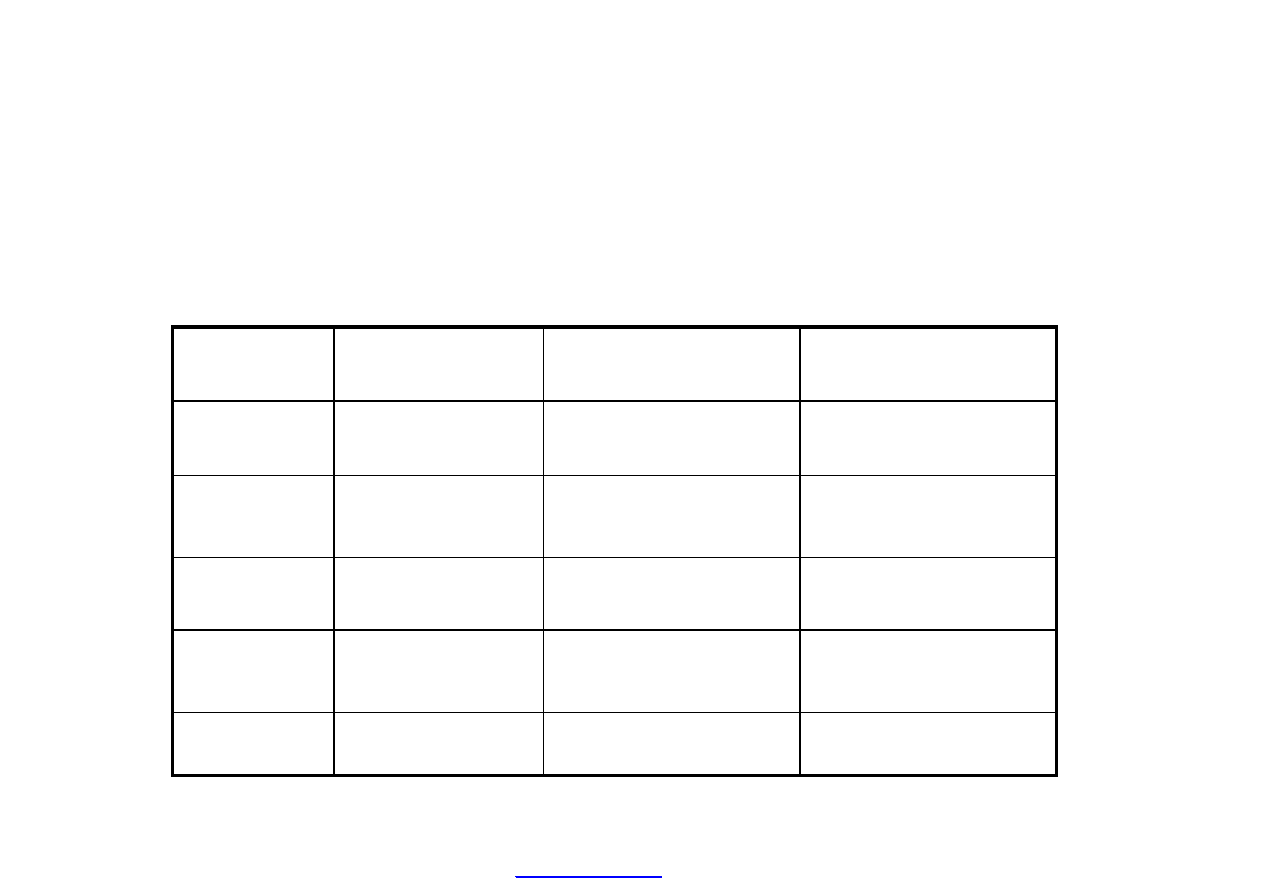
Zak
ładając, że koszt kapitału (k) spółki wynosi 15 % należy obliczyć
zmodyfikowan
ą wewnętrzną stopę zwrotu.
Który projekt powinna wybra
ć spółka na podstawie tego kryterium ?
Wartość końcowa (TV) projektu A jest sumą przepływów środków
pieniężnych przewidywanych po jego wdrożeniu, które uprzednio
sprowadzono do porównywalnej wartości przyjmując stopę procentową
równą kosztowi kapitału.
134.822
X
X
Razem
27.000
1,15
0
=1
27 000
4
31.050
1,15
1
=1,15
27 000
3
35.708
1,15
2
= 1.3225
27 000
2
41.064
1,153
3
= 1.5209
27 000
1
Wartość końcowa
(TV) w zł
Procent składany
dla k=15 %
Przepływy
pieniężne w zł
Rok
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro

W celu ustalenia MIRR projektu A:
1) należy podzielić końcową projektu przez kwotę początkowych wydatków inwestycyjnych, co
pozwoli ustalić wskaźnik procentu składanego oznaczony umownie jako W tj.:
W =134.822:60.000 = 2,247
2) następnie trzeba odszukać w tabeli zawierającej liczby procentu składanego, w wierszu
odpowiadającym liczbie lat n =4, takie dwie wielkości W1 i W2, między którymi znajduje się
liczba W =2,247; odczytanym W1 i W2 odpowiadają stopy procentowe r1 i r2, czyli;
W1= 2,0736 -> r1=20%
W2 = 2,3642 -> r2 = 24 %
3) na podstawie odczytanych danych i przy zastosowaniu formuły interpolacji liniowej należy
obliczyć procentowy wskaźnik oznaczający MIRR, tzn;
MIRR = r
1
+ (W-W1)(r2-r1)
czyli
MIRR A = 20% +(2,247- 2,0376) x (24% -20 %) =
Sprawdzenie oblicze
ń
dla projektu A:
a) na podstawie formuły wartości zaktualizowanej
134.822 (1+MIRR)
-4
= 60 000
134.822 (1+0,224
)-4=
134.822:1,224
4
=134,822:2,246 = 60 000
b) na podstawie formuły wartości przyszłej
60 000 (1 +MIRR)
4
= 134.822
60 000 (1+0,224)
4
= 60 000 x 1,224
4
= 60 000 x 2,246 = 134,822
Zmodyfikowana wewnętrzna stopa zwrotu projektu b wynosi 22,08 %,
odpowiada jej wielkość procentu składanego W=2,225 (W=133,511 :60
000 = 2,225)
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro
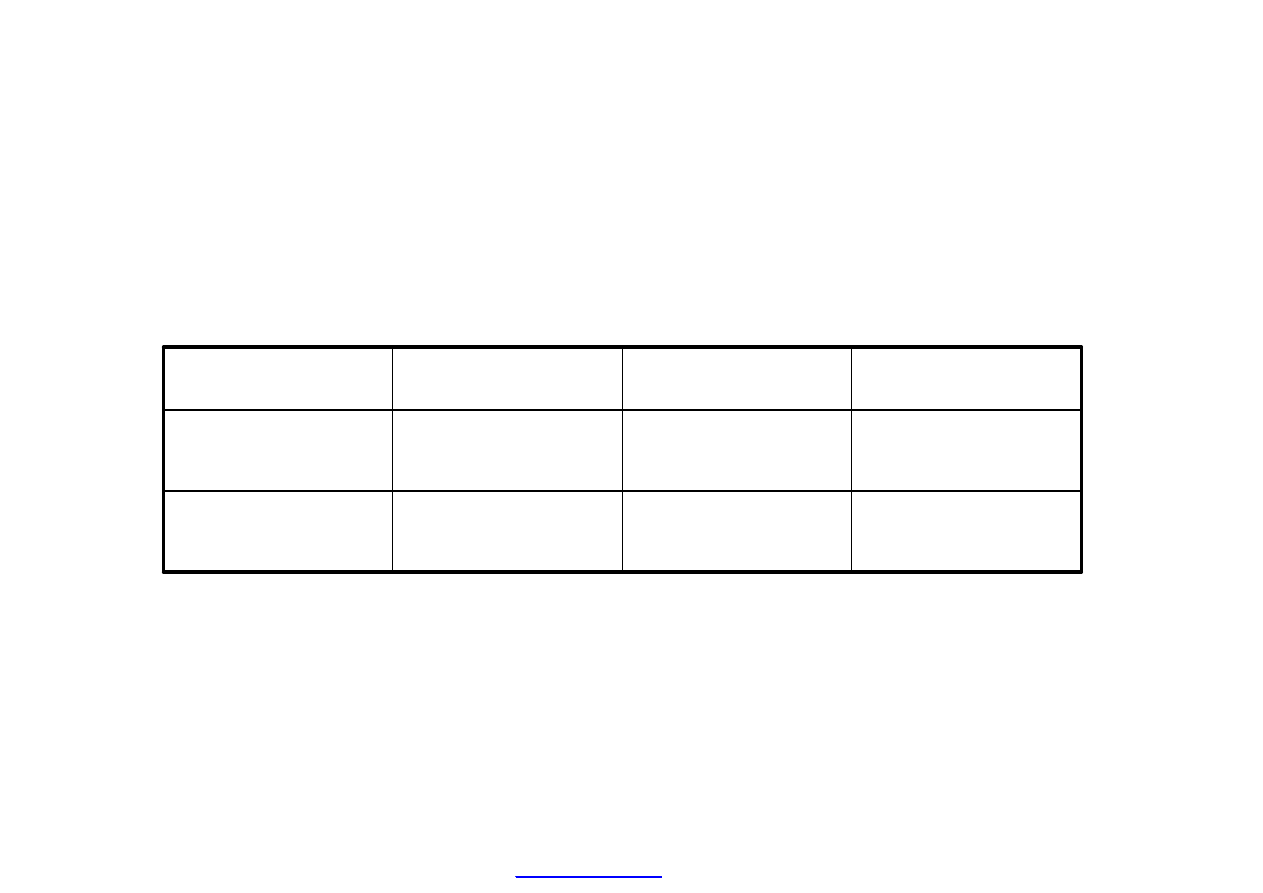
Oceniane projekty inwestycyjne charakteryzują następujące
wielkości trzech podstawowych wskaźników dyskontowych:
22,08 %
27,5 %
16 335
B
22,40 %
28,5 %
17 085
A
MIRR
IRR
NPV w zł
Projekt
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro

Zmodyfikowane stopy zwrotu projektów A i B są niższe od ich IRR,
ponieważ przyjmuje się przy kalkulacji MIRR, że przepływy środków
pieniężnych każdego projektu są powtórnie inwestowane po stopie
dyskontowej równej kosztowi kapitału, który w przypadku spółki „GAMA”
wynosi 15 %.i jest niższy od IRR obu projektów.
MIRR projektu A jest wyższy od MIRR projektu B jedynie o 0,32 %.
Zarówno ten wskaźnik, jak i i NPV oraz IRR, wykazują nieznaczną
przewagę przedsięwzięcia A nad B, toteż projekt A należy przyjąć do
realizacji.
Metody NPV i MIRR prowadzą do takiej samej decyzji o wyborze projektu
inwestycyjnego, jeśli różne projekty mają takie same nakłady i taki sam
przewidywany okres działalności przedsięwzięcia.
W przypadku wyboru projektu spośród istotnie różniących się skalą,
wzajemnie wykluczających się projektów, wskaźnik MIRR może
prowadzić do odmiennej decyzji niż NPV. Metoda NPV jest wtedy
podstawą wyboru bardziej efektywnego przedsięwzięcia. Mimo przewagi
metody MIRR nad IRR metoda NPV jest nadal uznawana z najlepsze
kryterium oceny efektywności przedsięwzięć inwestycyjnych, ponieważ
daje możliwość wyboru przedsięwzięć zwiększających wartość
przedsiębiorstwa.
PDF stworzony przez wersj
ę demonstracyjną pdfFactory Pro
Wyszukiwarka
Podobne podstrony:
Metody oceny?ektywności inwestycji
Szkol Metody Oceny Ryzyka wykład
Metody oceny projektów inwestycyjnych
8. METODY OCENY EFEKTYWNOŚCI PROJEKTÓW INWESTYCYJNYCH, 1 Wstęp
Metody ilościowej i jakościowej oceny ryzyka wykład
zad 2 - metody oceny projektów inwestycyjnych, ćwiczenia
3d proste i dyskontowe metody oceny efektywnosci inwestycj suez4
Pediatria. Metody oceny rozwoju fizycznego dzieci, Wykłady, PEDIATRIA
zadanie dodatkowe, af metody oceny projektow inwestycyjnych, WSTĘP
METODY OCENY PROJEKTÓW GOSPODARCZYCH 11.10.2014, V rok, Wykłady, Metody oceny projektów gospodarczyc
Wyk. 03 Metody oceny rozwoju fizycznego, Lekarski, Propedeutyka pediatrii, Wykłady
Metody oceny projektów inwestycyjnych
MOPG-wykłady, METODY OCENY PROJEKTÓW GOSPODARCZYCH
metody oceny projektow inwestycyjnych, Elektrotechnika-materiały do szkoły, Gospodarka Sowiński
więcej podobnych podstron

