Adam Paweł Zaborski

Project “The development of the didactic potential of Cracow University of Technology in the range of

modern construction” is co-financed by the European Union within the confines of the European Social Fund

and realized under surveillance of Ministry of Science and Higher Education.

13. Cross-section characteristics

Introduction

Definitions

cross-section area

∫∫

=

A

A

A

d

, [m

2

]

static moments of area (first moments of area, first moments of inertia)

∫∫

∫∫

=

=

A

z

A

y

A

y

S

A

z

S

d

d ,

, [m

3

]

gravity centre (when the calculation concerns a geometrical shape only the term centroid is used)

A

S

z

A

S

y

z

y

C

y

c

z

c

c

c

=

=

,

:

)

,

(

centroidal axis, central axis – an axis passing through the centroid (the gravity centre)
(second moments of area), inertia moments (about y and z axes and product moment)

∫∫

∫∫

∫∫

=

=

=

A

yz

A

z

A

y

A

yz

J

A

y

J

A

z

J

d

d

d

,

,

2

2

, [m

4

]

central inertia moment – inertia moments about central axis
matrix of inertia moments















−

−

z

yz

yz

y

J

J

J

J

principal central inertia moments – inertia moments resulting from the eigenvalue problem

yz

y

yz

z

y

z

y

yz

z

y

z

y

J

J

J

J

J

J

J

J

J

J

J

J

J

J

J

−

−

=

α

+















−

−

+

=

+















−

+

+

=

1

2

2

2

2

2

1

tan

,

2

2

,

2

2

,

principal central axes – such axes

2

1

, x

x

that:













→















−

−

2

1

0

0

J

J

J

J

J

J

z

yz

yz

y

principal central inertia radii

A

J

i

A

J

i

2

2

1

1

,

=

=

, [m]

ellipse of inertia – an ellipse in which half-axes are equal to principal inertia radii
polar inertia moment

∫∫

=

A

O

A

r

J

d

2

, [m

4

]

Superposition principle

Due to additivity of the double integrals, every integral may be calculated over subareas. It means that a
cross-section may be divided into simpler geometric figures and the total results are the sum of the partial
results.

Parallel axes theorem (Steiner’s formulae)

Let’s suppose the first and second inertia moments about the central axis c are known. Their values about
any parallel axis l, at distance d from central axis c, read:

d

A

S

S

c

l

⋅

+

=

,

2

d

A

J

J

c

l

⋅

+

=

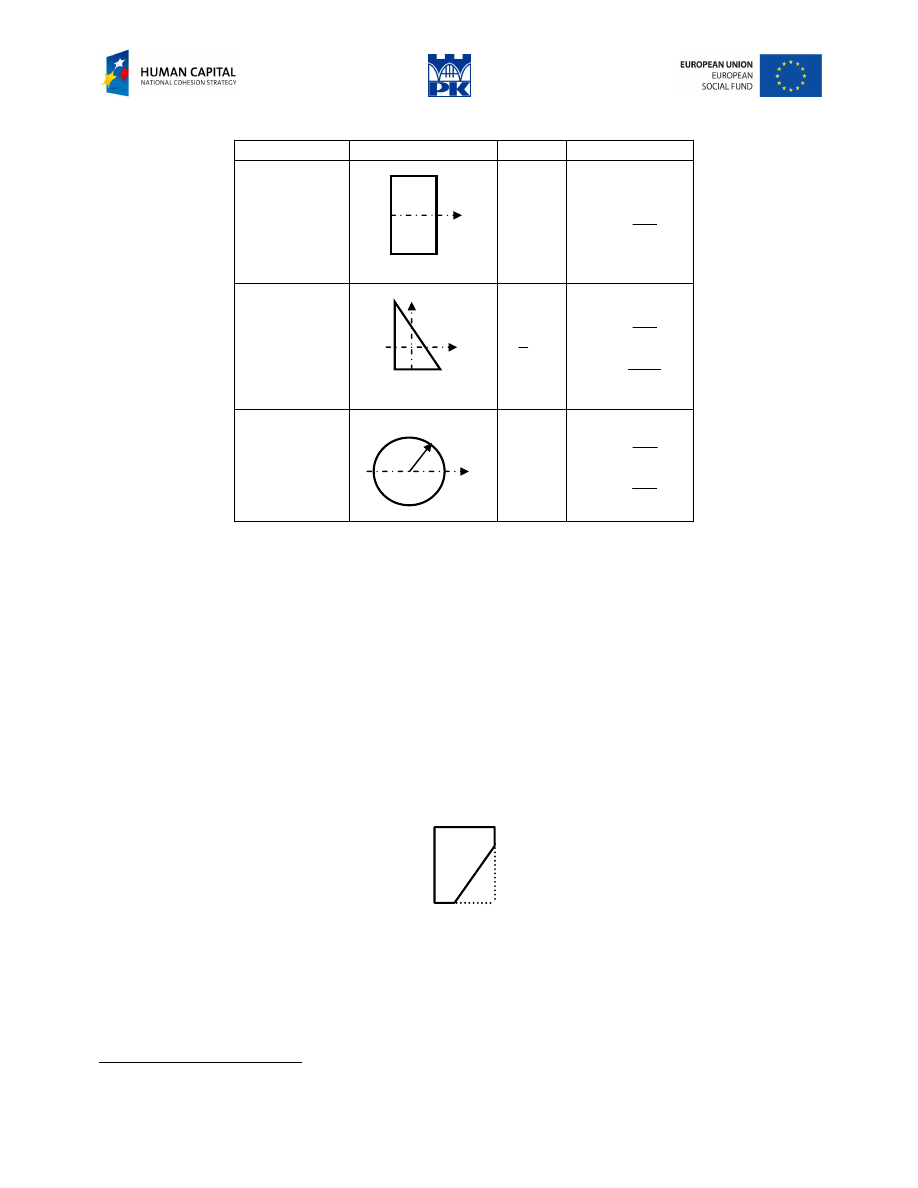
Adam Paweł Zaborski

Project “The development of the didactic potential of Cracow University of Technology in the range of

modern construction” is co-financed by the European Union within the confines of the European Social Fund

and realized under surveillance of Ministry of Science and Higher Education.

Formulae to memorize

figure

drawing

area

inertia moment

rectangle

y

h

b

bh

12

3

bh

J

y

=

right triangle

z

h

y

b

bh

2

1

36

3

bh

J

y

=

72

2

2

h

b

J

yz

−

=

1

circle

r

y

2

r

π

4

4

r

J

y

π

=

2

4

0

r

J

π

=

Table 13.1 Characteristics of basic figures – formulae to memorize

Tensor calculus conclusions

The principal inertia moments are extreme (maximal and minimal).
Every symmetry axis is the principal central axis. Second axis is perpendicular to the symmetry axis and
passes through the gravity centre.
Tip: The characteristics calculations for symmetric cross-section are simpler because we can compute
principal moments directly.
If a cross-section has more then two symmetry axes, every central axis is principal too. In that case every
central moment is also a principal one.

Example

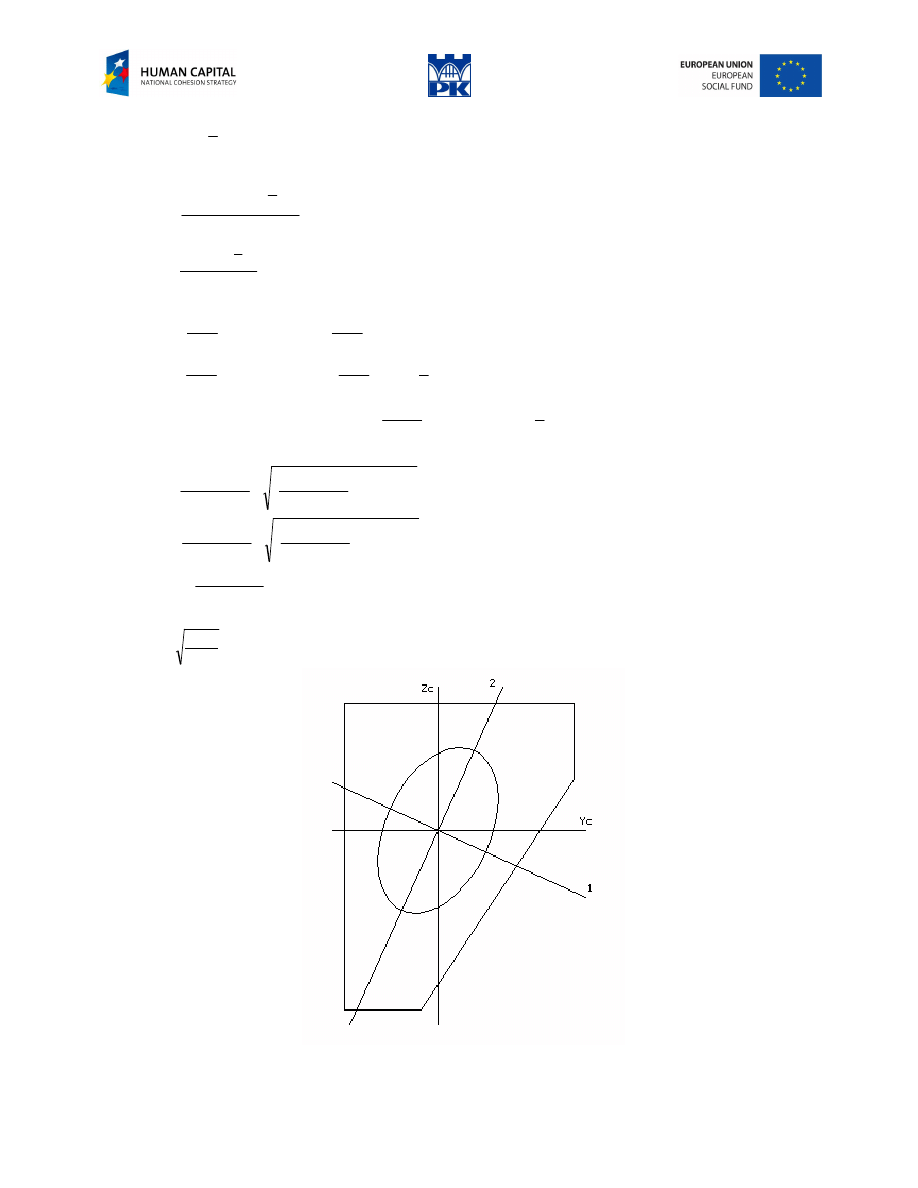
Determine the geometric characteristics for the section in Fig. 13.1.

4

3

1

1

Fig. 13.1 Cross-section

Solution
The calculation is made for the rectangle “minus” the triangle.
area:

1

the sign of the product moment changes each time a reflection is made

Adam Paweł Zaborski

Project “The development of the didactic potential of Cracow University of Technology in the range of

modern construction” is co-financed by the European Union within the confines of the European Social Fund

and realized under surveillance of Ministry of Science and Higher Education.

3

2

2

1

4

3

⋅

⋅

−

⋅

=

A

gravity centre:

222

.

1

9

2

3

2

1

3

5

.

1

12

=













⋅

+

⋅

−

⋅

=

c

y

cm

333

.

2

9

3

3

1

3

2

12

=

⋅

⋅

−

⋅

=

c

z

cm

central inertia moments:

5

.

10

)

333

.

2

1

(

3

12

3

2

)

333

.

2

2

(

12

12

4

3

2

3

2

3

=

−

⋅

−

⋅

−

−

⋅

+

⋅

=

yc

J

cm

4

556

.

5

222

.

1

2

3

2

1

3

12

3

2

)

222

.

1

5

.

1

(

12

12

4

3

2

3

2

3

=













−

⋅

+

⋅

−

⋅

−

−

⋅

+

⋅

=

zc

J

cm

4

(

)

833

.

2

222

.

1

2

3

2

1

333

.

2

1

3

72

3

2

)

222

.

1

5

.

1

(

)

333

.

2

2

(

12

0

2

2

=













−

⋅

+

⋅

−

⋅

−

⋅

−

−

⋅

−

⋅

+

=

zycc

J

cm

4

principal central inertia moments and direction

79

.

11

833

.

2

2

556

.

5

5

.

10

2

556

.

5

5

.

10

2

2

1

=

+













−

+

+

=

J

cm

4

27

.

4

833

.

2

2

556

.

5

5

.

10

2

556

.

5

5

.

10

2

2

2

=

+













−

−

+

=

J

cm

4

(

)

°

−

−

==

α

→

−

=

−

−

=

α

48

.

24

4273

.

0

4553

.

0

833

.

2

5

.

10

79

.

11

tan

principal central inertia radii:

14

.

1

9

79

.

11

1

=

=

i

cm

Fig. 13.2 Inertia ellipse of the cross-section

Adam Paweł Zaborski

Project “The development of the didactic potential of Cracow University of Technology in the range of

modern construction” is co-financed by the European Union within the confines of the European Social Fund

and realized under surveillance of Ministry of Science and Higher Education.

69

.

0

9

27

.

4

2

=

=

i

cm

The inertia ellipse is shown in Fig. 13.2.

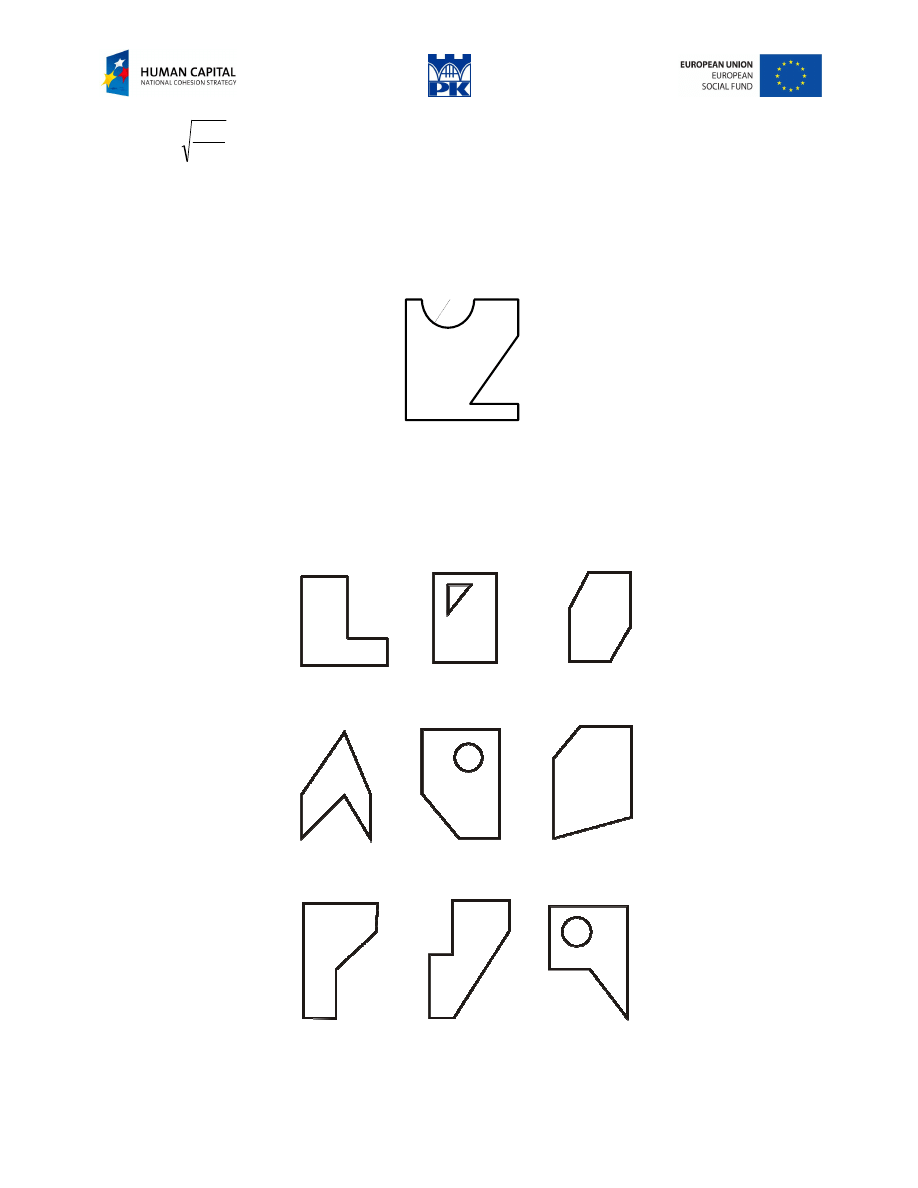
Workshop theme

Adopt numerical input data for the cross-section in Fig. 13. 3 and determine principal central inertia
moments. Draw the inertia ellipse.

r

e

e

d

c

b

a

Fig. 13.3 Cross-section to compute

Review problems

Adopt numerical input data and determine principal central inertia moments.

Fig. 13.4 Review problems

Adam Paweł Zaborski

Project “The development of the didactic potential of Cracow University of Technology in the range of

modern construction” is co-financed by the European Union within the confines of the European Social Fund

and realized under surveillance of Ministry of Science and Higher Education.

Addendum

Hints

Tip: Inertia moment about the central axis is minimal in reference to other parallel axes.

Tip: The gravity centre is always inside a circumscribed polygon.

Except for a few cases, all calculations in strength of materials are carried on with respect to the principal
central axes.

Glossary

first moment of area, static moment – moment statyczny
second moment of area, inertia moment – moment bezwładności
centroidal inertia moment, central inertia moment – centralny moment bezwładności
inertia product moment – moment dewiacji
centroid, gravity centre – środek ciężkości
centroidal axis, central axis – oś centralna
principal central axis – oś główna centralna
principal central inertia moment – główny centralny moment bezwładności
inertia radius – promień bezwładności
ellipse of inertia – elipsa bezwładności