większość pytań się powtórzyło się z tego, co było na gmailu. Z pytań "niespodziewanych"
pojawiło się:
- 3 reaktory do narysowania (a nie tylko do podpisania)
- jakie są rodzaje filtrów i filtracji do izolowania biomasy. Od czego zależy szybkość izolacji
biomasy.
- jedno zadanie brzmiało mniej więcej tak: "Zawiesina o objętości 75m3 zawierała biomasę o
stężeniu 12 kg suchej masy. Po od wirowaniu z odpłukaniem, stężenie biomasy wyniosło 36
kg suchej masy. Do jakiej objętości zagęszczono zawiesinę i ile wody odpłukano?"
- jedno zadanie jak na ostatnim kole u Wojczukowej (to ze stała Henry'ego)
- też zadanie z ostatniego koła: zadanie na policzenie liczby obrotów mieszadła dla przebiegu
burzliwego, przy podanej gęstości, siły lepkości i średnicy mieszadła

WYKŁAD 1, 16.02.2012

Wykład organizacyjny

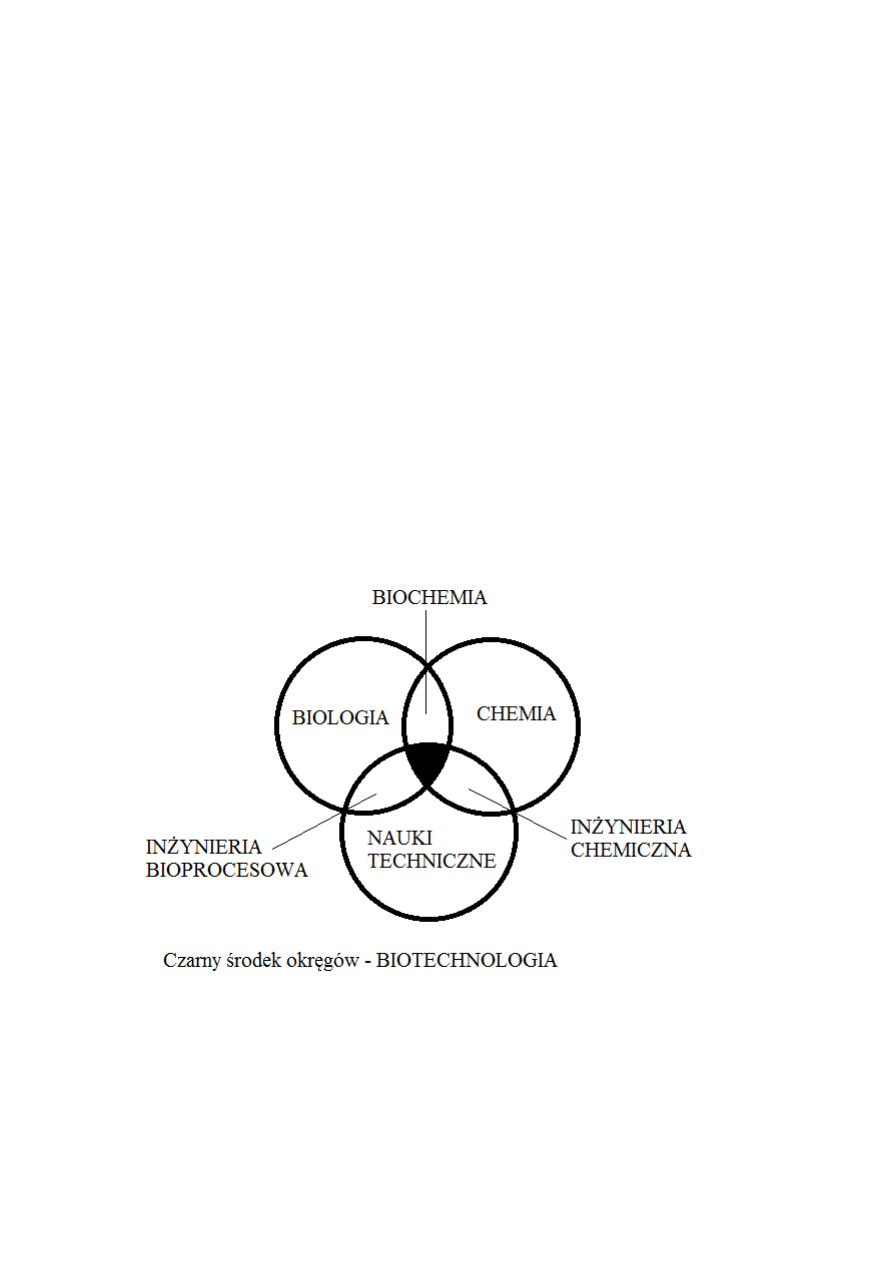
Biotechnologia jest interdyscyplinarną dziedziną nauki, obejmującą różne kierunki

technicznego wykorzystania materiałów i procesów biologicznych.

Zgodnie z definicją UE, biotechnologia jest dziedziną integrującą biochemię, mikrobiologię,

biologię molekularną, genetykę i chemię w celu praktycznego, użytkowego wykorzystania

kultur mikroorganizmów, tkanek lub elementów ich struktury.

IUPAC określa biotechnologię jako zastosowanie biochemii, biologii molekularnej,

mikrobiologii i inżynierii chemicznej w procesach przemysłowych i ochronie środowiska.

Wspólną cechą tych definicji jest:



interdyscyplinarny charakter biotechnologii



przemysłowe zastosowanie mikroorganizmów, enzymów lub kultur tkankowych

Interdyscyplinarny charakter biotechnologii powoduje, że może ona być opisywana z różnych

punktów widzenia – najczęściej z punktu widzenia biochemika lub mikrobiologa. W takich

przypadkach główny nacisk położony jest na wyjaśnienie przemian biochemicznych

zachodzących w komórkach i fizjologicznych uwarunkowań procesów technologicznych.

Termin „technologia” ma dwojakie znaczenie:



oznacza metodę wytwarzania określonego produktu



oznacza naukę o metodach wytwarzania określonego produktu

EKOLOGIA, BIOLOGIA KOMÓRKI, MIKROBIOLOGIA, GENETYKA, BIOCHEMIA,

BIOLOGIA MOLEKULARNA, CHEMIA, INŻYNIERIA, MATEMATYKA,

INFORMATYKA, FIZYKA, EKONOMIA

↓

BIOTECHNOLOGIA

↓

OCHRONA ZDROWIA, OCHRONA ŚRODOWISKA, ROLNICTWO, PRZEMYSŁ

SPOŻYWCZY, PRZEMYSŁ CHEMICZNY, SUROWCE, NOŚNIKI ENERGII,

ANALITYKA, INNE ZASTOSOWANA

Biotechnologia zielona → rolnictwo, produkcja żywności

Biotechnologia czerwona → medycyna, farmacja

Biotechnologia szara → ochrona środowiska, bioremediacja

Biotechnologia biała → zastosowania przemysłowe, wykorzystanie enzymów

Biotechnologia niebieska → technologie wodne, wykorzystanie organizmów wodnych

Biotechnologia fioletowa → ustawodawstwo związanie z biotechnologią

Główne zalety biotechnologii:



przetwarzanie surowców odnawialnych – cukrowce (skrobia, sacharoza, celuloza)

stanowią około 1% biomasy (10

14

-10

15

kg); obecnie cukrowce i ich pochodne (np.

melasa) są głównymi surowcami w procesach biotechnologicznych; szacuje się, że w

niedalekiej przyszłości można liczyć na przynajmniej 10-krotne zwiększenie

biotechnologicznego

wykorzystania

surowców roślinnych, pod warunkiem

opracowania efektywnej metody przetwarzania celulozy, lignin i hemiceluloz

(biopolimery ulegają bardzo powolnej biodegradacji)



duża różnorodność bioprocesów i otrzymywanych bioproduktów



selektywne otrzymywanie enancjomerów biologicznie czynnych



łagodne warunki przebiegu bioprocesów



niska energochłonność bioprocesów



duży stopień bezpieczeństwa



mniejsze niż w przypadku procesów chemicznych zanieczyszczenia środowiska;

łatwiejsze do neutralizacji ewentualne skażenia

Biotechnologia dzieli się na:



biotechnologię tradycyjną – wykorzystuje do procesów chemicznych naturalne

enzymy, szczepy drobnoustrojów i komórki organizmów wyższych nie zawierające

obcego materiału genetycznego



biotechnologię nowoczesną – stosowane są szczepy drobnoustrojów lub linie

komórkowe skonstruowane metodami inżynierii genetycznej, względnie enzymy

zmodyfikowane technikami inżynierii białka; nowoczesne metody i rozwiązania

biotechnologiczne obejmują również:

o rekombinacje genetyczne in vitro i klonowanie genów

o

fuzje komórek (protoplastów)

o

inżynierię białka

o techniki hodowli in vitro komórek organizmów wyższych

o

technologie immobilizacji enzymów

o

biokatalizę w układach niewodnych

o komputerowe modelowanie i sterowanie bioprocesami

o

technikę ciągłych procesów biotechnologicznych

o

nowoczesne techniki izolacji i oczyszczania bioproduktów

Najważniejsze wydarzenia w historii biotechnologii:

1. Wyjaśnienie przez Ludwika Pasteura (1857) roli drożdży w fermentacji alkoholowej.

2. Wprowadzenie do praktyk przemysłowych i medycznych czystych kultur

bakteryjnych, grzybów mikroskopijnych (pleśni) i drożdży.

3. Uruchomienie produkcji drożdży piekarniczych w warunkach napowietrzonych

hodowli wgłębnych (1880), wprowadzenie czystych kultur drożdży do piwowarstwa

(1883).

4. Wykorzystanie wyciągu z pleśni Aspergillu oryzae do scukrzania zacierów

skrobiowych.

5. Uruchomienie przemysłowej produkcji amylazy pleśniowej TAKA-DIASTAZA w

USA (1894).

6. Opracowanie techniki złoża zraszanego z mikroflorą degradującą składniki wód

ściekowych.

7. Wykorzystanie bakterii do oczyszczania ścieków w Manchesterze (1914).

8. Opracowanie mikrobiologicznych metod syntezy butanolu i acetonu na drodze

fermentacji acetonowo-butanolowej przez Clostridium (1918).

9. Opracowanie metod beztlenowej degradacji zanieczyszczeń ściekowych.

10. Uruchomienie przemysłowej produkcji etanolu z hydrolizatów drewna.

11. Uruchomienie wielkoprzemysłowej produkcji penicyliny pod koniec II Wojny

Światowej, co przyczyniło się do opracowania w następnych latach wielu procesów

produkcji innych antybiotyków.

12. Opracowanie metod biotransformacji mikrobiologicznej różnych steroidów.

13. Wprowadzenie do praktyki przemysłowej technologii immobilizowanych enzymów.

14. Konstruowanie nowych genotypów metodami inżynierii genetycznej.

15. Dalszy postęp w konstruowaniu bioreaktorów i prowadzeniu bioprocesów.

WYKŁAD 2, 23/02/2012

Prawie każdy proces biotechnologiczny można przedstawić w ogólnym zarysie jako

kombinację kolejnych operacji:



wybór mikroorganizmów do danego procesu



przygotowanie pożywki



hodowla mikroorganizmów, wytwarzanie produktu



wydzielanie i oczyszczanie produktu

Realizacja każdego procesu biotechnologicznego wymaga harmonijnego zgrania wszystkich

tych elementów składowych – należy przy tym pamiętać, że głównym kryterium efektywnego

prowadzenia procesu biotechnologicznego jest ekonomika produkcji. Oznacza to, że nie

wystarczy otrzymać wymagany produkt, lecz że należy wytwarzać go w taki sposób, aby

produkcja przynosiła zysk.

Udział różnych dyscyplin w rozwoju procesów biotechnologicznych

Operacje

Dyscypliny

Wybór mikroorganizmów

Systematyka
Genetyka
Fizjologia
Biochemia

Przygotowanie podłoża

Fizjologia
Chemia
Inżynieria bioprocesowa

Hodowla mikroorganizmów

Fizjologia
Inżynieria bioprocesowa

Wydzielanie produktów

Chemia
Inżynieria bioprocesowa

Praktyka przemysłowa pokazuje, że wiedza z zakresu chemii, biochemii i mikrobiologii jest

niewystarczająca do rozwiązania problemów przemysłu fermentacyjnego, spożywczego i

farmaceutycznego. Reakcja biochemiczna stanowi zasadniczy, ale tylko jeden etap procesu

produkcyjnego. Znacznie więcej problemów stwarza przygotowanie surowców, prowadzenie

procesu oraz izolacja produktu.

Generalnie, przemysł biotechnologiczny uszeregowany jest w sposób branżowy, np.



produkcja etanolu



produkcja kwasu cytrynowego



produkcja lizyny lub metioniny



produkcja penicylin (i ogólnie antybiotyków)



produkcja drożdży paszowych i piekarniczych

W różnych nitkach technologicznych występują takie same operacje jednostkowe oraz

procesy podstawowe, np.



fermentacja tlenowa lub beztlenowa



sedymentacja, wirowanie



odparowywanie, zatężanie



filtracja, krystalizacja, suszenie

Pomimo, że liczba bioprocesów i otrzymywanych produktów jest bardzo duża, liczba

procesów podstawowych jest niewielka.

Celem inżynierii bioprocesowej jest stworzenie matematycznego opisu procesów

podstawowych i operacji jednostkowych:



aby można było przewidzieć ich przebieg



w dowolnej skali



bez konieczności wykonywania doświadczeń pomocniczych

Umożliwia to budowę instalacji przemysłowej bez konieczności prowadzenia kosztownych

prób w skali półtechnicznej i technicznej.

Obszar tematyczny inżynierii bioprocesowej:



przenoszenie pędu – operacje dynamiczne, zachodzące pod działaniem siły



przenoszenie masy – operacje dyfuzyjne, zachodzące pod wpływem różnicy stężeń

jako siły napędowej



inżynieria reakcji chemicznych i biochemicznych



bioreaktory

Oczekiwania biotechnologii wobec inżynierii bioprocesowej:



tworzenie modeli matematycznych oddziaływań biologicznych



procesy rozdzielania (izolacji) złożonych i wrażliwych produktów



projektowanie bioreaktorów

Ogólny schemat pełnego procesu biotechnologicznego:

PRZYGOTOWANIE SUROWCÓW

(SUBSTRATÓW)

up-stream processing

↓

BIOPRZEMIANA

bioreaktor

↓

IZOLACJA ORAZ OCZYSZCZANIE

PRODUKTU

down-stream processing

1929r – Fleming uzyskał penicylinę G w postaci rozcieńczonego, zanieczyszczonego,

niestabilnego preparatu.

1940-1943r – produkcja i oczyszczanie penicyliny metodą wymrażania pary wodnej ze

stratą >60% produktu w kolejnych etapach

1943r – firma SHELL opracowała technologię zbliżoną do obecnej – zwiększona wydajność

do 85%

Podstawy logistyczne procesu biotechnologicznego:

DOSTAWY

↓

dostarczenie i magazynowanie surowców

UP-STREAM PROCESSING

↓

dejonizacja, pasteryzacja, mieszanie

FERMENTACJA

↓

DOWN-STREAM PROCESSING

↓

wytrącanie, dejonizacja, chromatografia,

odparowywanie, filtracja, krystalizacja,

suszenie

pakowanie, magazynowanie, dostawa

KLIENT

Surowce

Materiały używane w procesach fermentacyjnych:



woda, powietrze



cukry (jako główne źródło węgla)



źródła azotu (głównie amoniak)



sole mineralne



czynniki wzrostowe (witaminy, aminokwasy)

Źródła węgla i energii stosowane w procesach fermentacji mogą być sklasyfikowane jako:



nieoczyszczone (surowe)



częściowo oczyszczone



oczyszczone (rafinowane)

Surowe substraty są tańsze niż substraty oczyszczone lub częściowo oczyszczone, lecz

zawierają różne zanieczyszczenia, które będą musiały być usunięte na dalszych etapach

obróbki (down-stream lub up-stream). Występujące zanieczyszczenia mogą nawet

powodować zahamowanie procesu fermentacji. Surówka może także charakteryzować się

zmienną jakością, co może wpływać na jakość końcowego produktu.

Przykłady stosowanych substratów:

Surówka

Olej palmowy
Mączka rybna, mączka sojowa
Melasa
Namok kukurydziany
Woda odpadowa

Substraty częściowo oczyszczone

Syropy glukozowe, syropy fruktozowe
Oleje roślinne
Skrobia

Substraty oczyszczone (rafinowane)

Media do hodowli komórek
Hydrolizaty białkowe
Glukoza (proszek)
Sacharoza (krystaliczna)

Pepton – hydrolizat białkowy powstały przez trawienie białka pepsyną.

Trypton – hydrolizat białkowy powstały przez trawienie białka trypsyną.

Niektóre różnice pomiędzy procesem chemicznym i biochemicznym (różnice odnoszą się do

procesu biochemicznego):



bardziej złożone mieszaniny reagujące (skład, fazy)



przyrost stężenia biomasy reagenta jako wynik reakcji biochemicznej



zdolność mikroorganizmów do syntezy katalizatorów (enzymów) swoich własnych

reakcji



łagodne warunki temperaturowe reakcji



zasadniczo reakcje przebiegają w fazie wodnej



stosowane jest niskie stężenie substratu i produktu w mieszaninie reakcyjnej

Kluczowe składniki w projektowaniu bioreakcji:



termodynamika – zmiany równowagi reakcji, ciepło dostarczane lub wyzwalane,

równowaga fazowa



kinetyka – szybkości reakcji biochemicznych, kinetyka wymiany masy



stechiometria – ilościowe przekształcenia biochemiczne



równowaga – bilans masowy i energetyczny



parametry fizyczne – przepływ materiału, mieszanie w reaktorze

Skala laboratoryjna

Eksperymenty na małą skalę
Badanie kinetyki i wydajności
Hodowle wytrząsane lub małe bioreaktory
Wstępny szacunek kosztów

Skala półtechniczna (pilotowa)

Bioreaktor 100-1000L
Badanie kinetyki i wymiany mas
Ocena kosztów i zysków (ocena ekonomiczna)
Badania nad zwiększeniem skali
Badania nad izolacją produktu

Skala przemysłowa

Produkcja komercyjna
Bioreaktor 1000-1000000L
Rozwiązywanie problemów technicznych
Wprowadzanie ulepszeń
Optymalizacja procesu
Zapewnienie jakości

WYKŁAD 3, 1/03/2012

Główne typy komórek stosowanych w procesach fermentacyjnych

Typy komórek

Przykład

Komórki zwierzęce

CHO – komórki jajnika chomika chińskiego
komórki HYBRIDOMA (do produkcji
przeciwciał monoklonalnych
komórki owadzie

Grzyby

Penicillum sp.
Aspergillus sp.

Drożdże

Saccharomyces sp.
Saccharomycopsis sp.
Kluyveromyces sp.
Pichia sp.
Candida sp.

Bakterie

Escherichia coli
Bacillus sp.
Pseudomonas sp.
Streptomyces sp.

Porównanie niektórych właściwości organizmów/komórek stosowanych w procesie

biokatalizy

BAKTERIE

DROŻDŻE

GRZYBY

KOMÓRKI

ZWIERZĘCE

szybkość

wzrostu

+++++

+++

++

+

łatwość

manipulacji

genetycznych

+++++

+++

++

++

fałdowanie

białek

-

++

++

++++

glikozylacja

białek

-

?

?

++++

odporność

mechaniczna

++++

++++

++++

+

Chociaż przedstawione porównanie jest bardzo dużym uogólnieniem, to z tabeli tej wynika,

że komórki bakteryjne pomimo szybkiego wzrostu i łatwości manipulacji genetycznej, nie

posiadają dwóch bardzo ważnych cech: właściwego fałdowania obcych białek

(rekombinowanych) oraz ich glikozylacji (generalnie zdolności do modyfikacji

potranslacyjnych). Z tych powodów szereg firm farmaceutycznych coraz powszechniej

wykorzystuje komórki zwierzęce do produkcji białek zwierzęcych (ludzkich) dla celów

terapeutycznych (w tym np. enzymów do leczenia niektórych genetycznie uwarunkowanych

schorzeń genetycznych).

Główne produkty procesu biochemicznego

TYP PRODUKTU

TYPOWY STOSOWANY

MIKROORGANIZM

WIELKOŚĆ RYNKU

ŚWIATOWEGO

(ton/rok)

związki organiczne

Saccharomyces cerevisiae

2 x 10

7

biomasa

drożdże

5 x 10

5

kwasy organiczne

Aspergillus niger

3 x 10

5

aminokwasy

Brevibacterium flavum

3 x 10

5

transformacje
mikrobiologiczne

Rhizopus arrhizus

4 x 10

4

antybiotyki

Penicillum chrysogenum

4 x 10

4

enzymy

Aspergillus niger

1,4 x 10

3

Transformacje mikrobiologiczne – np. transformacje steroidów (zmiana podstawników,

stereoizomeria).

Rodzaje procesów przemysłowych

PROCES

CZYNNIK KATALITYCZNY

PRZYKŁADY

BIOSYNTEZY

drobnoustroje

biosynteza aminokwasów,
antybiotyków, polisacharydów
produkcja preparatów paszowych

komórki zwierzęce

produkcja szczepionek i przeciwciał
monoklonalnych

komórki roślinne

biosynteza terpenów, estrów i
alkaloidów

enzymy

biosynteza makrolidów, dekstranu,
akrylamidu

BIOTRANS-

FORMACJE

drobnoustroje

biotransformacje steroidów
otrzymywanie kwasu octowego i
innych kwasów, sorbozy

enzymy

konwersja glukozy do fruktozy,
fumaranu do jabłczanu
transformacje steroidów

HYDROLIZA

enzymy

hydroliza białek, oligosacharydów i
polisacharydów
hydroliza enancjomerów

Bilansowanie wzrostu mikroorganizmów

Ilościowe ujęcie procesu technologicznego jest podstawowym narzędziem w każdej

dyscyplinie inżynierskiej. Modele matematyczne są szeroko stosowane w projektowaniu,

optymalizacji i sterowaniu procesami inżynierii chemicznej. Opisy ilościowe obejmują

bilanse masowe i energetyczne oraz opisy kinetyki danego procesu. Zestawienie bilansów

masowego i energetycznego jest podstawową czynnością przy projektowaniu procesu

technologicznego. Zasady bilansowania procesów (przemian) chemicznych są znane

(stechiometria reakcji) i zasadniczo nie sprawiają trudności.

Przemiany biochemiczne różnią się od przemian chemicznych tym, że główny składnik

przemian biochemicznych – mikroorganizmy – cechuje zmienność typowa dla organizmów

żywych, zaś reakcje przebiegające wewnątrz komórek są bardziej złożone. Z tych powodów

bezpośrednie zastosowanie reguł stechiometrycznych do przemian biochemicznych nie jest

możliwe.

Trudności, jakie stwarza ilościowe ujęcie przemian biochemicznych ilustruje podany niżej

przykład.

Reakcję utleniania węgla można opisać prostym równaniem:

C + O

2

→ CO

2

+ Q (Δ

h

0

= -397,7kJ/mol)

Zgodnie z powyższym równaniem stechiometrycznym, podczas spalania 1kg węgla

powinniśmy otrzymać 3,67kg CO

2

oraz 32,8MJ energii.

W rzeczywistości bezpośrednie wykorzystanie tego równania nie jest możliwe, gdyż węgiel

kamienny, obok pierwiastka węgla (około 60%), zawiera również inne składniki, zarówno

palne (siarka), jak i niepalne. Skład węgla kamiennego jest zmienny. Spalanie węgla

kamiennego można przedstawić w sposób ogólny na schemacie:

WĘGIEL

KAMIENNY

+

POWIETRZE

→

GAZY

SPALINOWE

+

ŻUŻEL

+

Q

Ilość wydzielanego ciepła zależy od rodzaju spalanego węgla. Wynosi przeciętnie

16-22MJ/kg węgla. Ilość i skład gazów spalinowych zależą również od składu spalanego

węgla.

Zatem do sporządzenia bilansu spalania węgla kamiennego niezbędne są dane o jego składzie

i stopniu przekształcenia składników węgla w gazy spalinowe. Bilans taki będzie prawdziwy

dla konkretnego surowca oraz warunków spalania. Z praktycznego punktu widzenia możliwe

jest sporządzenie takiego bilansu dla pewnych przeciętnych danych dotyczących składu węgla

i stopnia konwersji. Przy takim podejściu nie uwzględnia się wszystkich przemian

zachodzących podczas spalania, nie przeprowadza się również bilansowania wszystkich

pierwiastków występujących w węglu kamiennym.

W przypadku bilansowaniu procesów biochemicznych stopień napotykanych trudności jest

znacznie większy, ponieważ:



skład elementarny mikroorganizmów jest zmienny



zmienny jest stopień przetworzenia substratów w produkty

Wzrost mikroorganizmów jest zjawiskiem bardzo złożonym. Komórki do wzrostu potrzebują

szeregu substancji. Wewnątrz komórki zachodzi szereg przemian biochemicznych, w wyniku

których powstają produkty i wytwarzana jest niezbędna energia.

Typowe substraty w układach biologicznych (źródła pierwiastków):

źródła węgla

glukoza, aminokwasy

źródła azotu

NH

4

Cl, (NH

4

)

2

SO

4

, aminokwasy, białka

źródła tlenu

powietrze

źródła wodoru

związki organiczne

źródła fosforu

fosforan nieorganiczny PO

4

3-

Typowe produkty w systemach biologicznych to biomasa, produkty reakcji i metabolity.

Ustalenie struktury chemicznej i podanie wzoru produktu i metabolitu jest proste. Lecz jaki

wzór chemiczny przypisać można komórce (biomasie)? Z uwagi na złożoność i różnorodność

procesów biochemicznych zachodzących w komórce, nie jest możliwe uwzględnienie

wszystkich relacji stechiometrycznych i kinetycznych tych przemian.

Generalnie, punktem wyjścia jest oparcie się o znane szlaki metaboliczne. Można zauważyć,

że makroskopowe przedstawienie procesu nie uwzględnia wszystkich elementów danej

przemiany. Dobrym przykładem może być produkcja etanolu przez drożdże S. cerevisiae oraz

X. mobilis.

W przypadku drożdży, makroskopowo równanie wygląda w ten sposób:

C

6

H

12

O

6

→ 2C

2

H

5

OH + 2CO

2

Biochemicznie, reakcja netto:

C

6

H

12

O

6

+ 2ADP + 2P

i

→ 2C

2

H

5

OH + 2CO

2

+ 2ATP + 4H

2

O +Q

W przypadku X. mobilis zapis makroskopowy jest identyczny, jak u drożdży, ale zapis

biochemiczny netto jest inny:

C

6

H

12

O

6

+ ADP + P

i

→ 2C

2

H

5

OH + 2CO

2

+ ATP + 2H

2

O +Q

Z uwagi na wspomnianą złożoność procesu wzrostu mikroorganizmów, wszelkie opisy

ilościowe muszą ograniczać się do wybrania istotnych zależności występujących podczas

rozwoju populacji mikroorganizmów. Modelowanie procesów biologicznych jest zatem

trudniejsze od modelowania procesów chemicznych. Podstawowa metoda ilościowego ujęcia

procesu wzrostu mikroorganizmów polega na poszukiwaniu takich wielkości

charakteryzujących mikroorganizmy oraz procesy ich namnażania, których wartości są

względnie stałe. Umożliwia to konstruowanie modeli uogólniających. Zależności takie,

średnie wartości parametrów, służyć mogą do obliczeń szacunkowych procesu wzrostu

mikroorganizmów.

Skład biomasy mikroorganizmów

Podanie zawartości wszystkich pierwiastków tworzących biomasę jest trudne – w praktyce

ogranicza się do czterech podstawowych pierwiastków: C, H, O, N. Ponieważ stanowią one

około 95% całości suchej masy, zatem sporządzenie bilansu dla tych pierwiastków jest

wystarczająco dobrym przybliżeniem. Jedynie w wyjątkowych przypadkach uwzględnia się

siarkę i fosfor.

Dla celów bilansu elementarnego, skład biomasy mikroorganizmów można przedstawić w

postaci analogicznej do wzoru stechiometrycznego związku chemicznego:

C

δ

H

a

O

b

N

c

δ = 0 lub 1 (węgla nie ma w związku lub w nim jest)

Dla E. coli:

C: 50% suchej masy

H: 8% suchej masy

O: 20% suchej masy

N: 14% suchej masy

Na tej podstawie wyliczono średni wzór dla biomasy:

CH

1,8

O

0,5

N

0,2

Ilość substancji odpowiadająca temu wzorowi nazywana jest węglomolem (C-mol), a zatem

węglomol to taka ilość substancji, która zawiera 1 mol węgla.

Zgodnie z tą definicją wzory i masy węglomola podanych substancji są następujące:

etanol → C

2

H

5

OH → CH

3

O

0,5

→ 23g/C-mol

glukoza → C

6

H

12

O

6

→ CH

2

O → 30g/C-mol

Dla związków nie zawierających węgla (δ=0) wzór nie ulegnie zmianie, a węglomol jest

równy molowi tego związku.

W przypadku biomasy należy ustalić strukturę węglomola w oparciu o dane analizy

elementarnej. Doświadczalnie wykazano, że współczynniki stechiometryczne zmieniają się w

podanych niżej przedziałach:

H: 1,5-2,0

O: 0,43-0,56

N: 0,10-0,25

Jako średnią wartość przyjmujemy wzór:

CH

1,8

O

0,5

N

0,2

Skład elementarny wybranych mikroorganizmów

MIKROORGANIZM

WĘGLOMOL

Saccharomyces cerevisiae

CH

1,83

O

0,54

N

0,1

Candida utilis

CH

1,83

O

0,50

N

0,17

Klebsiella aerogenes

CH

1,87

O

0,56

N

0,20

Aerobacter aerogenes

CH

1,83

O

0,55

N

0,25

Znając wzór węglomola biomasy można wyliczyć zapotrzebowanie na substraty podczas jej

produkcji.

Stechiometria pewnej reakcji:

C

6

H

12

O

6

+ aO

2

+ bNH

3

→ cCH

1,66

O

0,5

N

0,18

+ dCO

2

+ eH

2

O

Bilans pierwiastkowy:

węgiel

6 = c + d

wodór

12 + 3b = 1,66c + 2e

tlen

6 + 2a = 0,5c + 2d + e

azot

b = 0,18c

Mamy układ czterech równań z pięcioma niewiadomymi. Konieczna jest znajomość

parametru, który pozwoli na wyeliminowanie jednej niewiadomej (aby rozwiązać układ

równań). Często do tego celu używa się tzw. iloraz oddechowy RQ, określający stosunek

uwalnianego CO

2

do ilości wykorzystywanego O

2

.

W omawianym przypadku:

RQ =

d

/

a

= 1,02

RQ pozwala na wyeliminowanie jednej wartości (d lub a) i rozwiązanie układu równań

opisującego bilans pierwiastków. Znając współczynniki stechiometryczne i masę węglomola

biomasy można łatwo obliczyć wydajność tworzenia biomasy w przeliczeniu na zużycie

substratu i tlenu.

WYKŁAD 4, 8/03/2012

Oznaczanie zawartości biomasy jest jedną z podstawowych czynności analitycznych podczas

bioprocesu. Znajomość zmian stężeń biomasy jest niezbędne do wyznaczenia kinetyki

wzrostu mikroorganizmów i przyrostu produktu podczas hodowli i obliczania wydajności.

Biomasa – masa mikroorganizmów rosnących na pożywce; może odnosić się do dwóch pojęć:



mokra biomasa – masa mikroorganizmów oddzielonych od pożywki poprzez

wirowanie lub filtrację; jest to zatem łączna masa mikroorganizmów i wody zawartej

w przestrzeni pomiędzy komórkami



sucha biomasa – masa mikroorganizmów oddzielonych od pożywki i wysuszonych w

temperaturze 105ºC do stałej wagi

105ºC – temperatura, w której pozbywa się wody krystalizacyjnej. Wyższa temperatura

mogłaby zniszczyć związki organiczne.

Metody oznaczania biomasy mikroorganizmów hodowanych w ciekłych podłożach:



bezpośrednie, polegające na wagowym oznaczeniu masy drobnoustrojów

oddzielonych od pożywki – dające wartość mokrej biomasy



pośrednie:

o metoda turbidymetryczna – polega na pomiarze zmętnienia zawartości

komórek w pożywce; metoda ta może być wykorzystywana tylko w

określonym zakresie stężeń; dokładność pomiaru zależy również od

właściwego przygotowania próby (konieczne jest wyeliminowanie składników

pożywki, które wpływają na pomiar)

o metody chemiczne – polegają na oznaczeniu stężenia określonego składnika

komórki; przyjmując, że jego zawartość jest wartością stałą; najczęściej

oznacza się zawartość ATP (np. metody luminescencyjne z lucyferazą)

W ciągu doby organizm ludzki jest w stanie wyprodukować około 45kg ATP.

Technika filtracji membranowej obejmuje:



zawiesina fermentacyjna jest filtrowana przez wysuszony, wytarowany filtr

membranowy (standardowo sączek z octanu celulozy)



filtr jest przemywany celem usunięcia rozpuszczalnych składników medium



filtr jest suszony i ważony

sucha masa (g/dm

3

) =

(masa membrany po filtracji – masa membrany przed filtracją)

/

objętość próby

Technika wirowania obejmuje:



wirowanie zawiesiny fermentacyjnej w wysuszonych, zważonych probówkach przy

najwyższych obrotach



usunięcie supernatantu, przemycie osadu i ponowne wirowanie



wysuszenie osadu w probówce i jej zważenie

sucha masa (g/dm

3

) =

(masa probówki po filtracji – masa probówki przed filtracją)

/

objętość próby

Wzrost mikroorganizmów jest wysoce złożoną przemianą, w której z surowców podłoża

hodowlanego wytwarzana jest biomasa oraz produkty metabolizmu.

Bilans ogranicza się w zasadzie do czterech podstawowych pierwiastków (C, H, O, N). W

rzeczywistości w pożywce może występować kilka substancji pełniących identyczne funkcje

(np. stanowiących źródło węgla). Do celów bilansowych można je zastąpić jednym

substratem o odpowiednio dobranym składzie (w sensie chemicznym). W takim ujęciu ogólny

schemat rozpatrywanego procesu można przedstawić następująco:

S

S

+ S

N

+ O

2

→ X + P + CO

2

+ H

2

O + Q

S

S

– źródło węgla

S

N

– źródło azotu

X – biomasa

P – produktu metabolizmu

Q – ciepło

ν

S

CH

aS

O

bS

N

cS

+ ν

N

C

δN

H

aN

O

bN

N

cN

+ ν

O

O

2

→ ν

X

CH

aX

O

bX

N

cX

+ ν

P

CH

aP

O

bP

N

cP

+ ν

C

CO

2

+ ν

w

H

2

O

C:

ν

S

+ ν

N

δ

N

= ν

X

+ ν

P

+ ν

C

H:

ν

S

a

S

+ ν

N

a

N

= ν

X

a

X

+ ν

P

a

P

+ 2ν

W

O:

ν

S

b

S

+ ν

N

b

N

+ 2ν

O

= ν

X

b

X

+ ν

P

b

P

+ 2ν

C

+ ν

W

N:

ν

S

c

S

+ ν

N

c

N

= ν

X

c

X

+ ν

P

c

P

W tym układzie równań występuje 7 niewiadomych współczynników bilansowych, układ nie

ma zatem rozwiązania. Niezbędne więc są 3 równania dodatkowe, wiążące ze sobą

współczynniki bilansowe.

Przemianę ogólną można opisać równaniem:

CH

i

O

j

+ a NH

3

+ b O

2

→ c CH

k

O

l

N

m

+ d CH

n

O

o

N

p

+ e H

2

O + f CO

2

+ Q

c, d, f – ułamki ilości węgla przekształconego w biomasę, produkty metabolizmu i CO

2

Bilans pierwiastków prowadzi do następującego układu równań:

C:

1 = c + d + f

H:

i + 3a = c

k

+ d

n

+ 2e

O:

j + 2b = c

l

+ d

o

+ e + 2f

N:

a = c

m

+ d

p

Otrzymano 4 równania i znacznie więcej niewiadomych, co uniemożliwia rozwiązanie

równania. Problem jest znacznie prostszy, jeżeli znamy wartości poszczególnych

współczynników.

Rozważmy wzrost drożdży Saccharomyces cerevisiae. Przyjmując, że skład biomasy drożdży

jest następujący C

6

H

10

O

3

N i rosną one na glukozie, wykorzystując ją jako źródło węgla,

można napisać następujące równanie:

C

6

H

12

O

6

+ b O

2

+ c

NH

3

→ d C

6

H

10

O

3

N + e H

2

O + f CO

2

C

6

H

12

O

6

→ 2 C

2

H

5

OH + 2 CO

2

Uwzględniając tu fakt, że glukoza jest również przekształcana w etanol. Jeżeli oznaczymy

przez ‘E’ ułamek ilości glukozy przekształconej w etanol, to w biomasę przekształcone będzie

‘1-E’ glukozy. Jeśli zatem pierwsze równanie pomnożymy przez ‘1-E’, a drugie przez ‘E’ i

dodamy je stronami, otrzymamy równanie:

C

6

H

12

O

6

+ (1-E) b O

2

+ (1-E) c NH

3

→ (1-E) d C

6

H

10

O

3

N + [(1-E) + 2E] CO

2

+ (1-E) e H

2

O + 2E C

2

H

6

O

C:

6 = 6(1-E)d + (1-E)f + 2E + 4E

H:

12 + 3(1-E)c = 10(1-E)d + 2(1-E)e + 12E

O:

6 + 2(1-E)b = 3(1-E)d + 2(1-E)f + 4E + (1-E)e + 2E

N:

(1-E)c = (1-E)d

Doświadczalnie można wyznaczyć kilka wartości i pozbyć się współczynników b, f i c lub d.

Współczynniki wydajności określają ilość powstającej biomasy lub produktu z określonej

ilości substratu.

1. wyrażone w węglomolach



współczynnik wydajności biomasy względem substratu (c-mol/c-mol)

y

X/S

= ν

X

/ν

S



współczynnik wydajności produktu względem substratu (c-mol/c-mol)

y

P/S

= ν

P

/ν

S

2. współczynniki masowe (g

X

/g

S

, g

P

/g

S

)

Y

X/S

= Δm

X

/-Δm

S

= y

X/S

∙ (M

C, X

/M

C, S

)

Współczynnik wydajności wzrostu drożdży na glukozie

Wydajność masowa: Y

X/S

= 0,5g/g

c-mol glukozy: 30g/c-mol

c-mol biomasy: 25,9g/c-mol

y

X/S

= Y

X/S

∙ (M

C,S

/M

C,X

) = 0,5 ∙ 30/25,9 = 0,58 c-mol/c-mol

W przedstawionej metodzie bilansowania wzrostu podstawową rolę odgrywa założenie, że

skład biomasy mikroorganizmów jest stały w warunkach wzrostu ustalonego.

Można zatem przyjąć, że relacje pomiędzy ilością zużywanego substratu i ilością powstającej

biomasy są również stałe. Relacje te opisuje współczynnik wydajności biomasy względem

substratu. W praktyce stosuje się masowy współczynnik wydajności:

Y

X/S

= y

X/S ∙

(σ

S

/σ

X

)

gdzie σ oznacza zawartość węgla w danym związku.

σ

glukoza

= 6C/C

6

H

12

O

6

= 72/180 = 0,40

σ

biomasa

= 12/24,6 = 0,49

WYKŁAD 5, 15/03/2012

Współczynnik wydajności biomasy jest zależny od:



rodzaju substratu



rodzaju medium (pożywki) i warunków wzrostu (wydajność jest wyższa w

optymalnych warunkach pH, składu pożywki i natlenienia)

Zasada Finka

Podczas wzrostu drożdży około 1/3 węgla z substratu wydzielana jest w postaci CO

2

,

natomiast 2/3 jest wbudowywane w biomasę. Zgodnie z tą zasadą wartość współczynnika

y

X/S

= 0,67. Wartość ta jest zbliżona do średnich wartości tego współczynnika wydajności w

przypadku wzrostu na węglowodanach. Nie jest to jednak reguła ogólna i obserwuje się

różnice w wartości tego współczynnika w odniesieniu do różnych substratów

metabolizowanych przez ten sam mikroorganizm.

Współczynnik wydajności biomasy:



wyznaczony eksperymentalnie



wielkość tego współczynnika różni się w zależności od organizmu, warunków wzrostu

lub substratu

Teoretyczna wydajność produktu

Znajomość teoretycznej maksymalnej wydajności, z jaką surowiec jest przekształcany w

produkt jest ważnym parametrem w projektowaniu bioprocesu i jego doskonaleniu. Zwrot

zainwestowanych środków w udoskonalenie produkcji jest wyższy, jeśli wyjściowa

wydajność była znacząco niższa od teoretycznego maksimum niż wtedy, gdy wydajność jest

bliska maksimum.

Przykład

Obliczyć teoretyczną maksymalną wydajność produkcji fenyloalaniny z glukozy dla E. coli

rosnącej na pożywce z glukozą i amoniakiem.

Przebieg szlaku metabolicznego:

GLUKOZA → → → → → FENYLOALANINA

W uproszczeniu przebieg reakcji jest następujący:

1 GLUKOZA → 2 PEP (fosfoenolopirogronian)

1 GLUKOZA → 1 E4P (erytrozo-4-fosforan)

1 PEP + 1 E4P → „INTERMEDIAT A“

INTERMEDIAT A + 1 PEP → FENYLOALANINA

Sumarycznie:

2 GLUKOZA → FENYLOALANINA

2 ∙ 180g

165g

Y

P/S

= 165/360 = 0,458g Phe/ g glukozy

Można wyróżnić następujące sytuacje:

1. Produkty są wytwarzane bezpośrednio z substratów w sposób energetycznie

uprzywilejowany, tzn. następuje wytworzenie energii chemicznej netto.

1 mol glukozy → 2 mole etanolu + 2 mole ATP

Teoretyczna maksymalna wydajność wynosi:

Y

P/S

= 96/180 = 0,51 kg etanolu/kg glukozy

Rzeczywista wydajność jest niższa, gdyż część glukozy jest przekształcana w biomasę i na

pokrycie energetycznego zapotrzebowania komórek. Podstawą obliczeń jest sumaryczne

równanie glikolizy.

2. Produkcja glutaminianu z glukozy przez Corynebacterium glutamicum przebiegające w

następującym szlaku metabolicznym:

GLUKOZA + 2 ADP + 2 P

i

→ 2 PIROGRONIAN + 2 ATP

PIROGRONIAN + NAD

+

→ ACETYLO-CoA + CO

2

+ NADH/H

+

PIROGRONIAN + CO

2

+ ATP + H

2

O → SZCZAWIOOCTAN + ADP + P

i

ACETYLO-CoA + SZCZAWIOOCTAN + NAD

+

→ α-KETOGLUTARAN + CO

2

+ NADH/H

+

α-KETOGLUTARAN + NADPH/H

+

+ NH

3

→ GLUTAMINIAN + NADP

+

+ H

2

O

Sumarycznie:

GLUKOZA + NH

3

+ ADP + P

i

+ NADPH/H

+

+ 2 NAD

+

→

→ GLUTAMINIAN + CO

2

+ ATP + 2 NADH/H

+

+ NADP

+

Zatem reakcja jest energetycznie możliwa (powstaje 1 mol ATP i 2 mole NADH/H

+

);

maksymalna teoretyczna konwersja (w odniesieniu do węgla) wynosi:

5 c-moli Glu/6 c-moli glukozy

Y

P/S

= 143/180 = 0,79g Glu/g glukozy

3. Wytwarzanie produktu wymaga nakładu energii (pochodzącej z katabolizmu substratu) i

można proces ten opisać równaniem ogólnym:

a C

α

H

β

O

γ

N

δ

+ b C

α

H

β

O

γ

N

δ

+ c ATP → C

α

H

β

O

γ

N

δ

+ c ADP + c P

i

Energia jest generowana w wyniku katabolizmu substratu.

C

α

H

β

O

γ

N

δ

+ b O

2

+ d ADP + d P

i

→ c CO

2

+ d ATP

Maksymalna wydajność jest kombinacją dwóch reakcji, w których produkcja/zużycie ATP

wynosi 0. W obliczeniach, dla uproszczenia, przyjmuje się, że NADH/H

+

jest

równoważnikiem 3 ATP. We wszystkich obliczeniach zakłada się również, że ΔG

0

dla każdej

reakcji jest ujemna.

Przykład obliczania wydajności biomasy

Komórki zarodka sosny Douglasa hodowano w bioreaktorze. Po okresie wstępnego wzrostu

komórki potraktowano regulatorami wzrostu, powodując powstanie zarodków (identycznych

klonów), które tworzyły następnie „syntetyczne nasiona”.

Medium wyjściowe zawierało 200kg glukozy i 25kg amoniaku na 1m

3

.

Do 0,95m

3

medium dodano 0,05m

3

komórek, inicjując hodowlę. Po dwóch tygodniach

nastąpiło całkowite zużycie glukozy.

Otrzymano 0,35m

3

biomasy.

Stężenie amoniaku obniżyło się do 0,001kg/m

3

.

Specyficzna gęstość mokrej biomasy była równa 1020kg/m

3

, a zawartość H

2

O wynosiła 90%.

Obliczyć Y

X/glukoza

i Y

X/amoniak

. Wyrazić biomasę jako suchą masę.

1. Obliczyć suchą masę biomasy.

X

wstępna

: 0,05m

3

∙ 1020kg/m

3

∙ 10% = 5,1kg

X

końcowa

: 0,35m

3

∙ 1020kg/m

3

∙ 10% = 35,7kg

Przyrost biomasy: 35,7kg – 5,1kg = 32,6kg

2. Obliczyć wydajność biomasy.

Y

X/glukoza

=

[przyrost biomasy]

/

[ilość przekształconej glukozy]

= 32,6/(0,95∙200) = 0,16kg biomasy/kg glukozy

Y

X/amoniak

= 32,6/(0,95∙25) = 1,29kg biomasy/kg amoniaku

Masę końcową amoniaku można pominąć, ze względu na bardzo niskie stężenie.

Bilanse pierwiastków można uogólniać, wprowadzając pojęcie stopnia redukcji. Jest to

liczba moli wolnych elektronów w przeliczeniu na 1 mol węgla. Elektrony te mogą być

przekazywane na tlen w procesie utlenienia.

Liczba elektronów obliczana jest addytywnie.

C – dawca 4 elektronów (+4)

H – dawca 1 elektronu (+1)

O – akceptor 2 elektronów (-2)

N – akceptor 3 elektronów (-3)

Bilans tlenu

W przypadku bilansu tlenu w procesie wzrostu mikroorganizmów korzystamy ze stopnia

redukcji.

Rozważmy całkowite utlenienie substratu o wzorze ogólnym:

C

δ

H

a

O

b

N

c

Jak obliczyć ilość tlenu niezbędną do utlenienia tego substratu?

Równanie reakcji jest następujące:

C

δ

H

a

O

b

N

c

+ n O

2

→ δ CO

2

+ ½ a H

2

O + ½ c N

2

Bilans elementarny dla tlenu jest następujący:

b + 2n = 2δ + ½ a

n = ¼ (4δ + a – 2b)

Γ = 4δ + a – 2b

Γ (bezwzględny stopień redukcji) – liczba elektronów przeniesionych na tlen przy jego

całkowitej redukcji.

γ

i

= Γ

i

– c

i

/c

N

∙ Γ

N

γ

i

(względny stopień redukcji) – zależny od związku, który jest źródłem azotu; dla soli

amonowych Γ

N

= 3, zatem:

γ

i

= 4 + a

i

– 2b

i

– 3c

i

Przyjmując za punkt wyjścia równanie stechiometryczne reakcji:

ν

S

CH

aS

O

bS

N

cS

+ ν

N

C

δN

H

aN

O

bN

N

cN

+ ν

O

O

2

→ ν

X

CH

aX

O

bX

N

cX

+ ν

P

CH

aP

O

bP

N

cP

+ ν

C

CO

2

+ ν

w

H

2

O

Można w oparciu o współczynnik bilansowy rozwinąć równanie bilansowe względem ν

O

:

ν

O

= ¼ (ν

S

Γ

S

+ ν

N

Γ

N

– ν

X

Γ

X

– ν

P

Γ

P

)

Znajomość współczynników wydajnośći biomasy z substratu i współczynnika wydajności

produktu umożliwia wyznaczenie ilości zużywanego azotu:

ν

N

/ν

X

= 1/c

N

∙ (c

X

– c

S

/y

X/S

– c

P

∙ y

P/X

)

Pozwala to wyeliminować z równania ν

N

. Równanie przyjmuje postać:

ν

O

= ¼ (ν

S

γ

S

– ν

X

γ

X

– ν

P

γ

P

)

Wprowadzenie pojęcia względnego stopnia redukcji oznacza przyjęcie za stan odniesienia

stopień redukcji związku stanowiącego źródło azotu. Jeżeli uwzględnimy definicję względnej

wydajności biomasy y

X/S

, to można wyznaczyć współczynnik zużycia tlenu.

Dla glutaminianu C

5

H

9

O

4

N:

Γ

X

= 4 + 1,8 – 2 ∙ 0,5 – 3 ∙ 0,2 = 4,2

Γ

N

= 4 ∙ 5 + 9 – 2 ∙ 4 – 3 = 18

γ

X

= Γ

X

– c

X

/c

N

∙ Γ

N

= 4,2 – 1/5 ∙ 18 = 0,6

y

O/X

= ν

O

/ν

X

= ¼ (γ

S

/y

X/S

– γ

X

– y

P/S

γ

P

)

Jeżeli ν

P

= 0 (czyli nie powstaje produkt metabolizmu):

y

O/X

= ¼ (γ

S

/y

X/S

– γ

X

)

W przypadku wzrostu drożdży na glukozie:

y

O/X

= ¼ (4/0,52 – 4,2) = 0,87 mola tlenu/g suchej masy = 1,07g tlenu/g s.m.

Wartość współczynnika y

O/X

jest wartością nieujemną, zatem:

y

X/S

< γ

S

/γ

X

– y

P/S

∙ γ

P

/γ

X

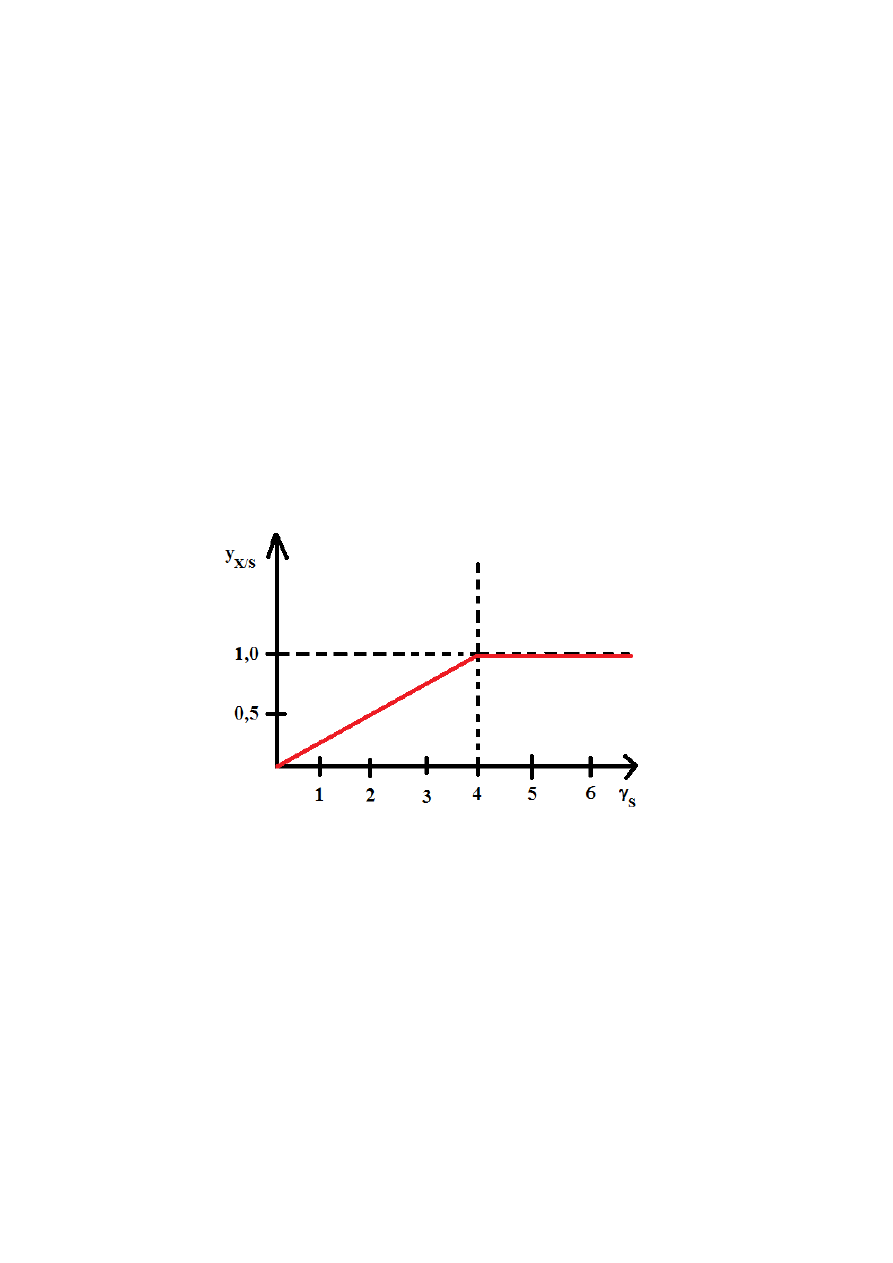
To równanie podaje ograniczenie bilansowe, wynikające z bilansu tlenu. Z bilansu węgla

wynika kolejne ograniczenie:

y

X/S

< 1 – y

P/S

Zatem dla prostego wzrostu (y

P/S

= 0) będą występowały dwa zakresy limitowania

współczynnika wydajności biomasy z substratu:



dla γ

S

< γ

X

ograniczenie wynika z bilansu tlenu



dla γ

S

> γ

X

ograniczenie wynika z bilansu węgla

WYKŁAD 6, 22/03/2012

Zależności między współczynnikiem wydajności biomasy z substratu y

X/S

i stopniem redukcji

substratu γ

S

wyznaczono doświadczalnie, otrzymując wartości:

γ

S

< 4,67 → y

X/S

= 0,13γ

S

γ

S

> 4,67 → y

X/S

= 0,60

Wykres zależności teoretycznej, przy założeniu, że z substratu powstaje wyłącznie biomasa.

Wartości te umożliwiają przybliżone obliczenie asymilacji tlenu. Na podstawie tych wartości,

dla przeciętnego składu biomasy:

dla γ

S

≤ 4,67

y

O/X

= ν

O

/ν

X

= 0,87 mola tlenu/c-mol biomasy

dla γ

S

≥ 4,67

Y

O/X

= 0,417γ

S

- 1,05 mola tlenu/kg biomasy

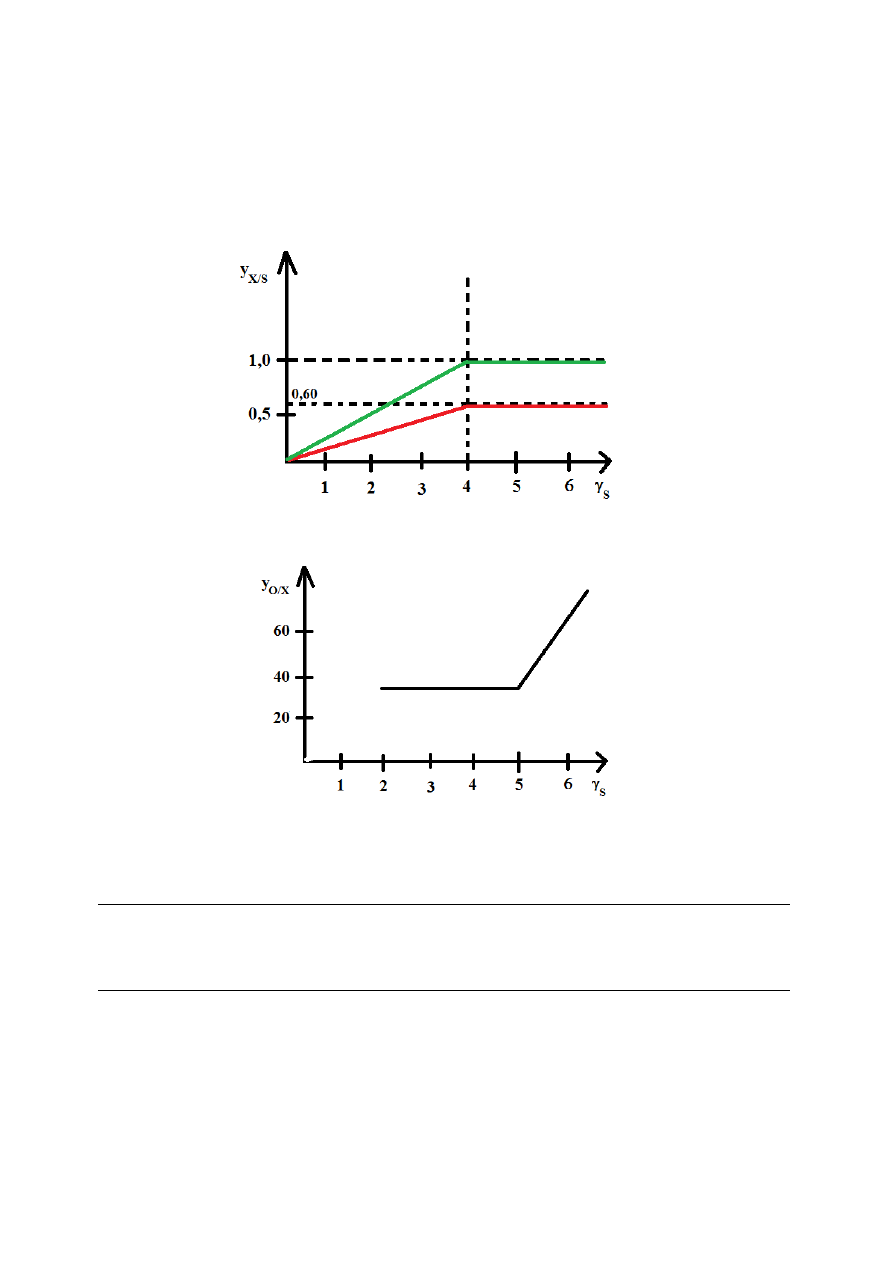
Należy pamiętać, że współczynniki wydajności dla tego samego substratu mogą być różne dla

różnych mikroorganizmów. Znajomość ograniczeń pozwala na optymalny dobór składu

pożywki.

Zależność współczynnika wydajności biomasy od stopnia redukcji substratu:

Zależność współczynnika zużycia tlenu od stopnia redukcji substratu:

Przeciętne

wartości

współczynnika

wydajności

(uśrednione

dla

wszystkich

mikroorganizmów):

y

X/S

(c-mol/c-mol)

Y

O/X

(mol/kg)

Y

O/X

(MJ/kg)

GLUKOZA

0,54

32,0

14,7

GLICEROL

0,61

34,5

15,9

METAN

0,59

93,6

43,1

ETANOL

0,57

63,3

29,1

Współczynniki wydajności wzrostu różnych mikroorganizmów na glukozie w warunkach

tlenowych:

y

X/S

(c-mol/c-mol)

Y

O/X

(mol/kg)

Y

O/X

(MJ/kg)

Candida utilis

0,60-0,66

18,2-23,8

8,7-11,4

Saccharomyces
cerevisiae

0,65

19,1

9,0

Trichoderma viridae

0,62-0,71

9,2-21,8

4,8-10,5

Eschericha coli

0,52-0,62

21,8-25,9

10,5-12,5

Pseudomonas
fluorescens

0,45

45,7

21,5

Rozważmy proste równanie stechiometryczne:

CH

i

O

j

+ a NH

3

+ b O

2

→ y CH

r

O

s

N

t

+ z CH

u

O

v

N

w

+ c H

2

O + d CO

2

(S)

(X)

(P)

Stopień redukcji (γ) można zdefiniować następująco:

S:

γ

S

= 4 + i – 2j

X:

γ

X

= 4 + r – 2s – 3t

P:

γ

P

= 4 + u – 2v – 3w

γ

H2O

= γ

CO2

= γ

NH3

= 0

Wyprowadzamy zależność:

γ

S

– 4b = yγ

X

+ 2γ

P

b = ¼ (γ

S

– yγ

X

– 2γ

P

)

Warunkiem wyprowadzenia tej zależności jest znajomość:



wartości stopnia redukcji (γ

i

) związków – a więc ich struktura



ilości wyprodukowanej biomasy (y)



ilości powstałego produktu (z)

Przykład

Obliczyć ilość butanolu wyprodukowanego ze 100 moli glukozy, zgodnie z równaniem

stechiometrycznym

100 C

6

H

12

O

6

+ a NH

3

→ 13 C

4,46

H

16,01

O

3,88

N

0,86

+ x CH

3

(CH

2

)

3

OH + 22 C

3

H

6

O +

0,4 CH

3

(CH

2

)

2

COOH + 14 CH

3

COOH + y CO

2

+ 135 H

2

+ 0,7 C

2

H

5

OH

Wartości niezbędne do obliczeń zebrano w tabeli:

ZWIĄZEK

γ

i

γ

i

∙ ν

i

SUBSTRATY

C

6

H

12

O

6

24

24 ∙ 100 = 2400

NH

3

0

a ∙ 0 = 0

PRODUKTY

X (biomasa)

23,51

23,51 ∙ 13 = 305,63

CH

3

(CH

2

)

3

OH

24

x ∙ 24

C

3

H

6

O

16

16 ∙ 22 = 352

CH

3

(CH

2

)

2

COOH

20

20 ∙ 0,4 = 5

CH

3

COOH

8

8 ∙ 14 = 112

CO

2

0

y ∙ 0 = 0

H

2

2

2 ∙ 135 = 270

C

2

H

5

OH

12

12 ∙ 0,7 = 8,4

SUBSTRATY: γ

i

∙ ν

i

= 2400

PRODUKTY: γ

i

∙ ν

i

= 1053,03 + 24x

2400 = 1053,03 + 24x

x = 56,12

Oznacza to, że ze 100 moli glukozy (18 000g) otrzymujemy 56,12 moli butanolu (4152,88g).

Wynik ten otrzymano bez potrzeby wyznaczana współczynników a oraz y.

Jeśli równanie:

γ

S

– 4b = yγ

X

+ zγ

P

podzielimy przez γ

S

, otrzymamy:

4b/γ

S

+ y γ

X

/γ

S

+ z γ

P

/γ

S

= 1

↑

↑

↑

ε + η + ξ

P

= 1

ε – ułamek ilości elektronów przekazanych na tlen

η – ułamek ilości elektronów przekazanych do biomasy

ξ – ułamek ilości elektronów przekazanych do produktu

Często skład substratu jest nieznany. W takim przypadku metodę obliczania stopnia redukcji

można uzupełnić następującymi, prostymi regułami.

Q

O

= 112,968 kJ/mol

Jest to równoważnik energetyczny 1 mola elektronów przekazanych na tlen.

γ

X

= 4,29 (w przeliczeniu na 1 gramoatom w biomasie)

σ

X

= 0,462g węgla/g suchej biomasy

Dla biomasy o standardowym składzie:

σ

X

= 12/24,6 = 0,488g węgla/g suchej masy

Bilans tlenu – iloraz oddechowy RQ

RQ = ν

C

/ν

O

= [4(1 – y

X/S

– y

P/S

)] / [γ

S

– y

X/S

γ

X

– y

P/S

γ

P

]

Jeśli nie tworzy się produkt: y

P/S

= 0

RQ = [4(1 – y

X/S

)] / [γ

S

– y

X/S

γ

X

]

Iloraz oddechowy dla wzrostu drożdży na:

1. glukozie

C

6

H

12

O

6

+ 6O

2

→ 6CO

2

+ 6H

2

O

RQ = [4(1 – 0,6)] / [4 – 0,6 ∙ 4,2] = 1,08

2. etanolu

C

2

H

5

OH + 3O

2

→ 2CO

2

+ 3H

2

O

RQ = [4(1 – 0,6)] / [6 – 0,6 ∙ 4,2] = 0,49

Przykład

Obliczyć współczynnik wydajności biomasy y

X/S

dla drożdży Pichia sp. hodowanych na a)

glukozie i b) etanolu, wiedząc, że z 1g substratu powstało odpowiednio a) 0,56g suchej masy i

b) 0,61g suchej masy tych drożdży.

c-mol glukozy – 30g

c-mol etanolu – 23g

c-mol biomasy – 25,9g

y

X/S

= Y

X/S

∙ M

S

/M

X

y

X/glukoza

= 0,56 ∙ (30/25,9) = 0,65

y

X/etanol

= 0,61 ∙ (23/25,9) = 0,54

Obliczyć współczynnik zużycia tlenu

a. dla drożdży rosnących na glukozie:

y

O/X

= ¼ (4/0,65 – 4,2) = 0,488 mola tlenu/c-mol biomasy

Y

O/X

= 0,488/25,9 = 0,019 mola tlenu/g suchej masy

b. dla drożdży rosnących na etanolu:

y

O/X

= ¼ (6/0,54 – 4,2) = 1,728 mola tlenu/c-mol biomasy

Y

O/X

= 1,728/25,9 = 0,067 mola tlenu/g suchej masy

Wzrost mikroorganizmów a generowanie ciepła (termodynamika)

Wzrost mikroorganizmów jest wynikiem szeregu powiązanych ze sobą procesów

metabolicznych. Reakcje kataboliczne i anaboliczne są ze sobą sprzężone tak, że energia

wyzwalana w tych pierwszych jest wykorzystywana jako siła napędowa w tych drugich.

Należy pamiętać, że część energii jest tracona (rozpraszana) w postaci ciepła.

W procesach na dużą skalę konieczne jest odprowadzanie (usuwanie) tego ciepła tak, aby

prowadzić hodowlę w temperaturze fizjologicznej.

W małych bioreaktorach ciepło metaboliczne jest łatwo usunąć; w dużych reaktorach

(> 10 000dm

3

), w których zachodzi szybki wzrost mikroorganizmów, konieczne jest

zaprojektowanie efektywnego systemu wymiany ciepła (jego odprowadzania). Temperatura

zawartości bioreaktora musi być utrzymywana z dokładnością do 0,5ºC dla zapewnienia

fizjologicznych warunków wzrostu.

W warunkach wzrostu, gdy powstaje praktycznie wyłącznie biomasa, a ilość powstającego

produktu jest znikoma, reakcję można zapisać równaniem:

C

6

H

12

O

6

+ a NH

3

+ b O

2

→ c CH

1,8

O

0,5

N

0,2

+ e CO

2

+ f H

2

O

Ponieważ zużycie azotu w porównaniu ze zużyciem węgla jest niewielkie, a ponadto azot nie

ulega utlenieniu tak, jak węgiel, równanie uprości się do postaci:

C

6

H

12

O

6

+ b O

2

→ c CH

1,8

O

0,5

N

0,2

+ e CO

2

+ f H

2

O

Bilans cieplny ten reakcji będzie następujący (w przeliczeniu na mole zużywanej glukozy):

Q

(uwalniane ciepło)

= c [(M.cz.

X

) ∙ (-ΔH

X

)] – [(-ΔH

S

) ∙ (M.cz.

S

)]

gdzie (-ΔH

X

) i (-ΔH

S

) to ciepło spalania 1g biomasy lub substratu.

Q/M.cz.

S

= c ∙ M.cz.

X

/M.cz.

S

∙ (-ΔH

X

) – (-ΔH

S

)

Wyrażenie po lewej stronie równania jest ilością ciepła uwalnianego w przeliczeniu na 1g

zużywanego substratu. Natomiast stosunek przyrostu biomasy na jednostkę zużywanego

substratu (pierwszy człon wyrażenia po prawej stronie równania) jest wydajnością biomasy z

substratu.

Równanie przyjmie postać:

Y

Δ/S

= (Y

X/S

)(-ΔH

X

) – (-ΔH

S

)

Po podzieleniu równania przez Y

X/S

:

Y

Δ/X

= (-ΔH

X

) – (-ΔH

S

)/(Y

X/S

)

Podane równania są przydatne do oznaczenia ciepła związanego ze wzrostem biomasy oraz ze

zużywanym substratem. Dane eksperymentalne z szeregu doświadczeń wykazują liniową

zależność pomiędzy ilością uwalnianego ciepła i ilością zużywanego tlenu.

Ciepło spalania biomasy (przykłady):

(-ΔH

S

), kJ/g

Escherichia coli

23,03

Candida lipolytica

21,34

Candida boidinii

20,14

Kluyveromyces fragilis

21,66

Bacillus thuringiensis

22,08

WYKŁAD 7, 29/03/2012

Ustalona doświadczalnie zależność ilości uwalnianego ciepła od ilości zużytego tlenu wynosi

(na 1 mol tlenu):

Y

Δ/O2

= 16,21 kJ/g O

2

Zależność ta pozwala wyliczyć ilości generowanego ciepła na podstawie ilości zużytego tlenu.

W przypadku, gdy oprócz biomasy powstaje dodatkowy produkt, równanie ulegnie

modyfikacji:

Q

(uwalniane ciepło)

= c [(M.cz.

X

) ∙ (-ΔH

X

)] + d [(M.cz.

P

) · (-ΔH

P

)] – [(-ΔH

S

) ∙ (M.cz.

S

)]

gdzie (-ΔH

P

) to ciepło spalania 1 g produktu.

Dzieląc równanie stronami przez M.cz.

S

otrzymamy:

Y

Δ/S

= (Y

X/S

)(-ΔH

X

) + (Y

P/S

)(-ΔH

P

) - (-ΔH

S

)

Dzieląc z kolei przez Y

S/X

, otrzymamy:

Y

Δ/X

= - (ΔH

X

) + (Y

P/X

)( -ΔH

P

) - (-ΔH

S

)/( Y

S/X

)

Y

Δ/S

– wydajność cieplna z substratu

Y

Δ/X

– wydajność cieplna z biomasy

Generowanie ciepła reakcji – przykłady obliczeń

Wartości ciepła reakcji można wyliczyć z dobrym przybliżeniem, znając:



stechiometrię reakcji



wydajność procesu



ciepło spalania biomasy i substratu

Przykład

Należy obliczyć ciepło reakcji hodowli drożdży na glukozie, jako źródle węgla. Równanie

reakcji:

7 CH

2

O + 2,33 O

2

→ C

4

H

6,67

O

2

+ 3 CO

2

+ 3,66 H

2

O

M.cz.

X

= 86,67 g/mol

-ΔH

X

= 1,52·10

3

kJ/100 g

-ΔH

S

= 2,82·10

3

kJ/mol

Zużycie glukozy na węglomol drożdży wynosi:

7 · 30 g = 210 g/c-mol glukozy,

co stanowi:

(210 g)/(180 g) = 1,167 mola glukozy/c-mol drożdży

Wydajność produkcji biomasy:

Y

X/S

= (ΔX)/(ΔS) = (86,67 g)/(210 g) = 0,41

Zatem masa wyprodukowanych komórek drożdży wynosi:

0,41 · 210 g = 86,1 g

Efekt cieplny obliczamy z zależności:

ΔH

reakcji

= 2,82·10

3

kJ/mol · (7 M

CH2O

)/(M

C6H12O6

) - 1,52·10

3

kJ/mol · (86,1 g/100 g) =

= 1,98·10

3

kJ/210 g glukozy = 1,98·10

3

kJ/86,1 g komórek =

= 0,23·10

2

kJ/g komórek

Jeśli skład substratu jest nieznany, to do obliczania efektu cieplnego reakcji można się

posłużyć znajomością stopnia redukcji oraz, wspomnianymi już, prostymi regułami:

Q

O

= 112,97 kJ/mol (równowartość energetyczna 1 mola elektronów przekazanych na O

2

)

γ

X

= 4,29 (w przeliczeniu na gramoatom węgla w biomasie)

σ

X

= 0,462 g C/g suchej masy

Przykład

Ze 100 moli glukozy w obecności tlenu i amoniaku otrzymano 2000 g lizyny i 4000 g

biomasy. Oblicz efekt cieplny reakcji, wiedząc, że stopień redukcji glukozy wynosi w tym

wypadku:

100 · 24 = 2400

Oblicz, jaka część ze stopnia redukcji została przekazana do produktu.

ilość moli lizyny: n

P

= 2000/182,65 = 10,96 mola Lys

γ

P

= 24+14-4-6+1-1 = 28

n

P

· γ

P

= 306,88 moli (część elektronów przekazana do produktu)

Oblicz, jaka część ze stopnia redukcji została przekazana do biomasy.

n

X

· γ

X

= (4000 g · σ

X

· γ

X

)/12 = 660,7 moli

W rezultacie, stopień redukcji zużyty na efekt cieplny X

Q

obliczamy z bilansu:

2400 = X

Q

+ n

P

· γ

P

+ n

X

· γ

X

X

Q

= 1432,42 moli

Pozwala to obliczyć efekt cieplny reakcji:

Q = 112,97 kJ/mol · 1432,42 moli = 161820,5 kJ

Kinetyka wzrostu mikroorganizmów

Z punktu widzenia praktyki – podstawowe znaczenie ma obliczenie:



szybkości namnażania się biomasy drobnoustrojów



szybkości asymilacji składników odżywczych



szybkości wydzielania produktów metabolizmu

W obliczeniu tych parametrów korzystamy z bilansów procesów biochemicznych oraz

równań kinetycznych opisujących przyrost biomasy. We wszystkich ujęciach kinetycznych

rzeczywiste, złożone procesy życiowe komórek oraz rozmnażanie mikroorganizmów

ujmowane są w uproszczeniu i generalnie sprowadzają się do przyrostu biomasy.

Biomasa – ogólnie substancje organiczne komórek mikroorganizmów, roślin lub zwierząt. W

przypadku inżynierii bioprocesowej termin ten odnosi się najczęściej do masy

mikroorganizmów.

Zastosowanie biomasy – jako źródło białka (w postaci paszy lub jako surowiec dla przemysłu

spożywczego). Biomasa często określana jest jako „białko jednokomórkowców” – SCP.

Początki takiego zastosowania – okres I wojny światowej, lata 30 XX wieku, okres II wojny

światowej.

Obecnie przyczyną dużego zainteresowania SCP jest światowy deficyt białka. Na jego

pokrycie nie wystarcza już źródeł tradycyjnych (mączka rybna, sojowa). Uruchomienie

produkcji SCP dla celów paszowych pozwala na zmniejszenie uzależnienia hodowli zwierząt

od importu pasz.

Zalety przemysłu produkcji białek:



szybszy przyrost biomasy mikroorganizmów w porównaniu z roślinami i zwierzętami



wyższa zawartość białka w suchej masie biomasy



szeroki wachlarz utylizowanych surowców, najczęściej odpadowych



wysoka wydajność, niewielka przestrzeń zajmowana przez instalacje produkcyjne



niezależność od zmian pogody, klimatu i sezonowości



możliwość wzbogacania produktu żywnościowego w niezbędne składniki, np.

aminokwasy egzogenne (Val, Leu, Ile, Phe, Tyr, Trp, Lys, Met, Thr), które występują

w niedomiarze w produktach roślinnych



biomasa jest nie tylko źródłem białka, lecz także związków biologicznie czynnych, np.

witamin

Porównanie szybkości przyrostu biomasy różnych organizmów:

ORGANIZM

Czas podwojenia biomasy

Bakterie

1 – 7 godzin

Glony

6 – 50 godzin

Trawy

1 – 2 tygodnie

Kura

3 – 4 tygodnie

świnia

4 – 6 tygodni

Zawartość białek w różnych produktach naturalnych:

SUROWIEC

ZAWARTOŚĆ BIAŁKA

Grzyby mikroskopowe

31 – 50%

Mikroalgi

47 – 63%

Drożdże

47 – 53%

Bakterie

72 – 78%

Mleko

22 – 25%

Wołowina

81 – 90%

Jaja

31 – 38%

Ryż

8 – 9%

Surowce do produkcji biomasy:

SUROWIEC

ŹRÓDŁO

C-1 metan

Gaz naturalny, węgiel kamienny, gazyfikacja
drewna, proces dygestii

C-1 metanol

Gaz syntezowy

C-2 etanol, kwas octowy

Fermentacja alkoholowa, etylen

Modele wzrostu mikroorganizmów

Wyróżnia się następujące grupy modeli:



model wzrostu ustalonego oraz model wzrostu nieustalonego; podział ten wynika z

uwzględnieniem lub nie warunków ustalonych w przemianach metabolicznych;

najczęściej przyjmuje się założenia o ustalonych warunkach wzrostu



modele ciągłe lub korpuskularne; kryterium podziału jest w tym wypadku

uwzględnienie lub nie „ziarnistej struktury biomasy”, tzn. występowanie wydzielania

żywych komórek; w ujęciu ciągłym zamiast populacji mikroorganizmów rozpatruje

się pewną jednorodność (homogenność), „biofazę”, co pozwala na uniknięcie opisu

zjawisk związanych z istnieniem indywidualnych mikroorganizmów



model strukturalny i niestrukturalny; w tym podziale rozpatrywany jest sposób ujęcia

przemian

metabolicznych;

w

modelu

niestrukturalnym

mikroorganizmy

reprezentowane są jednym parametrem – biomasą; wzrost jest rozpatrywany jako

przemiana substratu bezpośrednio w biomasę

Najpowszechniej używa się modelu najprostszego – niestrukturalnych, ciągłych modeli

wzrostu ustalonego.

Drożdże Saccharomyces cerevisiae:



dobrze poznany genom



dobrze zaprojektowane metody genetyczne



model dla innych eukariontów



nie produkuje toksyn; organizm GRAS



około 6000 genów



zdolność do wydzielania białek



możliwość modyfikacji potranslacyjnych

Wzrost wykładniczy mikroorganizmów

X – liczba komórek

n – liczba podziałów komórkowych

X = 2

n

dX/dt = αX = μX

α – współczynnik proporcjonalności

μ – szybkość właściwa wzrostu

Można wyznaczyć stosunek stężenia biomasy do czasu poprzez scałkowanie równania w

przedziale czasu od t

0

do t

1

1/X dX = μ dt

Jeśli w czasie t

0

stężenie biomasy w reaktorze wyrazimy jako X

0

, a w czasie t

1

stężenie

biomasy wyrazimy jako X

1

, to równanie przyjmie postać:

∫ 1/X dX = μ ∫ dt

Całkując obie strony otrzymujemy:

lnX

1

– lnX

0

= μ (t

1

– t

0

)

ln(X

1

/X

0

) = μ (t

1

– t

0

)

Zatem stężenie biomasy po określonym czasie hodowli opisuje równanie:

X

1

= X

0

· e

μ(t1-t0)

Czas podwojenia (okres generacji) a szybkość właściwa wzrostu

Czas podwojenia (t

d

, t

g

, τ

d

) jest wyrażeniem stosowanym powszechnie przez mikrobiologów

do opisu szybkości wzrostu komórek. Jest to czas potrzebny do podwojenia się liczby

komórek; w fazie wykładniczej jest to wartość w przybliżeniu stała. Stosunek między

szybkością właściwą wzrostu (μ) i czasem podwojenia (t

d

) jest następujący:

X

1

→ 2X

1

w czasie t

d

= t

2

– t

1

t

d

= ln2/μ

Przykład

X

0

= 2 g/dm

3

X

1

= 15,96 g/dm

3

t = 90 min

μ = (lnX

1

– lnX

0

)/Δt

μ = 0,023/min = 1,3847/h

t

d

= ln2/μ = 0,69/1,38 = 0,5 h

Zgodnie z modelem wzrostu wykładniczego biomasa będzie ciągle rosła. W rzeczywistości,

dostępność pokarmu nie jest nieograniczona i w chwili, gdy następuje jego ograniczenie,

szybkość wzrostu komórek obniży się lub nawet wzrost ustanie. Powstające produkty

metabolizmu również mogą hamować wzrost. Wzrost wykładniczy nie będzie miał miejsca

także w przypadku niedoboru tlenu lub w przypadku nieodpowiedniego mieszania. W tych

przypadkach wzrost będzie bardziej ograniczony wymianą mas niż limitowany kinetyką.

Ograniczenia w wymianie mas są głównym czynnikiem limitującym wzrost

mikroorganizmów w dużych bioreaktorach.

Nie-wykładniczy wzrost ma miejsce również w przypadku, gdy podziały komórkowe nie

zachodzą ze stałą szybkością. Takie zjawisko jest powszechne w przypadku grzybów

pleśniowych, organizmów wielokomórkowych, niektórych organizmów rozmnażających się

przez pączkowanie oraz wielu typów komórek zwierzęcych.

Powszechnie popełnianych błędem przy analizie procesów fermentacyjnych jest przyjęcie

zależności logarytmicznych, podczas gdy nie występują one w rzeczywistości.

Przemiana podstawowa

SUBSTRAT → WZROST BIOMASY + PODTRZYMYWANIE FUNKCJI ŻYCIOWYCH

Podtrzymywanie funkcji życiowych

MODEL HERBERTA

MODEL PIRTA

Na przemiany podstawowe zużywana jest

część biomasy

Na przemiany podstawowe zużywana jest

część substratu

r

e

= μ

e

· C

X

r

e

= m

s

· C

S

μ

e

– właściwa szybkość przemian

egzogennych

m

s

– współczynnik przemian podstawowych

r

X

= Y

X/S

· r

S

- μ

e

· C

X

r

S

= (1/Y

X/S

) · r

X

+ m

s

· C

S

r

e

– szybkość przemiany podstawowej

r

S

– szybkość asymilacji substratu

WYKŁAD 8, 5/04/2012

Wzrost komórek/przyrost biomasy:



pojęcie przemiany podstawowej



modele Herberta i Pirta



model Herberta – część biomasy jest zużywana na przemianę podstawową

(utrzymanie metabolizmu endogennego); szybkość takiego zużywania biomasy w

procesie endogennym jest proporcjonalna do stężenia biomasy

Ponieważ dla opisu procesów zachodzących w bioreaktorze podstawową miarą jest określenie

przyrostu biomasy; w tym celu istotny jest opis wzrostu pojedynczych komórek. Analiza taka

ma na celu sprawdzenie:



czy nie występują ograniczenia wzrostu



czy nie można przewidzieć ogólnego charakteru zależności dla wzrostu populacji

mikrobów

Zakładamy, że szybkość asymilacji substratu jest zależna od:



stężenia tego substratu



powierzchni komórki



substratem limitującym jest źródło węgla; należy uwzględnić zużycie części substratu

na przemianę podstawową.

dm

K

/dt = a

K

J

S

- μ

e

m

K

m

K

– masa komórki

a

K

– powierzchnia właściwa komórki

J

S

– strumień asymilowanego substratu

μ

e

– właściwa szybkość metabolizmu endogennego

Zależność pomiędzy masą a powierzchnią komórki wynika z kształtu komórki i sposobu jej

wzrostu. W praktyce wyróżniamy dwa przypadki: komórki kuliste i komórki pałeczkowate

(walcowate).

Komórki pałeczkowate – średnica jest stała, wzrost następuje przez wydłużanie się

powierzchni (a

K

). Dla stałego strumienia asymilowanego substratu, właściwa szybkość

wzrostu (μ) jest stała w warunkach ustalonych. Nie będą występowały ograniczenia wzrostu

pojedynczych komórek, ale też np. grzybni.

μ = 4J

S

/d

X

ρ

X

– μ

e

Komórki kuliste – wzrost poprzez powiększanie średnicy. Właściwa szybkość wzrostu

wynosi w tym przypadku:

μ = J

S

[(4Π)

1/3

· (3/ρ

X

)

2/3

] m

K

-1/3

– μ

e

Dla komórek kulistych właściwa szybkość wzrostu maleje wraz ze wzrostem średnicy,

graniczną szybkość wzrostu określa równanie:

m

K,gr

= (36 · Π · J

S

3

)/(ρ

X

· μ

e

3

)

co oznacza taką wielkość, dla której strumień substratu asymilowanego przez jej

powierzchnię jest zużywany wyłącznie na przemianę podstawową (geometryczne

ograniczenie wzrostu).

Czynniki wpływające na wydajność wzrostu mikroorganizmów:



temperatura



pH



dostępność substratu (źródło węgla i azotu)



zapotrzebowanie na tlen i jego dostarczanie



szybkość mieszania zawiesiny komórek



sposób mieszania

Model Monoda – niestrukturalny, ciągły model ustalonego wzrostu w fazie wzrostu

wykładniczego.

μ = (μ

max

· S)/(K

S

+ S)

K

S

– stała nasycenia (mg/dm

3

)

μ

max

– maksymalna właściwa szybkość wzrostu

Podobieństwa między równaniem Monoda i równaniem Michaelisa-Menten dotyczą kształtu

krzywej, postaci funkcji i sposobu wyznaczania parametrów.

Hodowla okresowa



system zamknięty, dobrze mieszany, o stałej objętości



dostępność substratu jest czynnikiem limitującym



wzrost pod koniec fermentacji



po wejściu komórek w fazę stacjonarną wzrostu należy pamiętać, że także inhibicja

przez powstający produkt końcowy prowadzi do zahamowania wzrostu



w typowych warunkach w fazie logarytmicznej stężenie substratu limitującego jest

znacznie wyższe niż K

S

Wyznaczanie K

S



w hodowlach okresowych jest trudne i obarczone błędem, zwłaszcza, jeśli stosuje się

metody bezpośrednie



teoretycznie lepiej zastosować metodę wyznaczania K

S

podobną do wyznaczania

wartości K

m

(Lineweavera-Burka, Eadie-Hofstee); metody te dają również wynik

obciążony błędem w przypadku hodowli okresowych



wiarygodne wyniki uzyskuje się w przypadku hodowli ciągłych (w chemostacie).

Model Monoda – może służyć do opisu (z pewnym przybliżeniem) większości procesów

zachodzących w hodowlach komórkowych. Model ten może być łatwo zmodyfikowany celem

opisu bardziej złożonych zjawisk, m.in. do opisu inhibicji (przez produkt końcowy lub nawet

przez powstającą biomasę). Należy pamiętać, że szereg substratów w wyższych stężeniach

może być toksyczny dla mikrobów (metanol, fenol, aminy).

WYKŁAD 9, 12/04/2012

Równanie Andrewsa:

Równanie Levenspiela:

Pod K

I

można podstawić S (jeśli substrat hamuje wzrost biomasy) lub X (jeśli biomasa

hamuje wzrost biomasy).

Równanie Monoda:

Istnieją mikroorganizmy, których zapotrzebowanie na substrat jest niskie (rosną lepiej przy

niskim stężeniu substratu w pożywce) oraz mikroorganizmy, których zapotrzebowanie na

substrat jest wysokie.

Z powodów ekonomicznych dąży się do zwiększenia współczynnika wydajności fermentacji,

gdyż prowadzi to do obniżenia zużycia surowców przy zwiększeniu ilości produktów, lecz:



nie zawsze prowadzi to do zwiększenia zysków



nie zawsze prowadzi to do zwiększenia produktywności (szybkości tworzenia danego

produktu)

W dużych fermentatorach, podczas procesów aerobowych, tlen jest czynnikiem limitującym

wzrost. Zwiększenie napowietrzania może zwiększyć współczynnik wydajności. W pewnych

sytuacjach zwiększenie napowietrzenia powoduje znaczny wzrost zużycia mocy i wzrost

kosztów może przeważać nad zyskami.

Jeśli w zmodyfikowanym procesie zwiększono współczynnik wydajności, lecz szybkość

powstawania produktów obniżyła się (wydłużył się czas), produktywność obniżyła się.

Jedynie w wypadku, gdy zwiększeniu współczynnika wydajności Y

X/S

lub Y

P/S

towarzyszy

zwiększenie szybkości tworzenia produktu – całkowita produktywność będzie większa.

Rodzaje współczynników wydajności

W procesach fermentacyjnych używa się zasadniczo dwóch podstawowych współczynników

wydajności: Y

X/S

i Y

P/S

(biomasy z substratu i produktu z substratu).

Współczynnik wydajności biomasy jest stosunkiem średniej masy biomasy do masy

wykorzystanego substratu. W hodowli okresowej Y

X/S

oblicza się z wyrażenia:

Y

X/S

= ΔX/ΔS

Analogicznie wyznacza się współczynnik wydajności produktu Y

P/S

:

Y

P/S

= ΔP/ΔS

Niekiedy wydajność produktu podaje się w stosunku do biomasy:

Y

P/X

= ΔP/ΔX

Ten sposób jest przydatny do oceny ilościowej produkcji wtórnych metabolitów.

Proste matematyczne modele procesów fermentacji

Poznaliśmy już model opisujący tworzenie biomasy równaniem:

dX/dt = (μ

max

· S)/(K

S

+ S) · X

Aby model opisywał cały proces fermentacyjny należy w równaniach uwzględnić

wykorzystanie substratu i tworzenie produktu.

Przy założeniu, że powstawanie produktu i biomasy jest bezpośrednio powiązane z

wykorzystaniem substratu (jego ubytkiem) poprzez współczynniki wydajności, można

napisać:

dX/dt = -Y

X/S

· dS/dt

dP/dt = -Y

P/S

· dS/dt

Cały proces fermentacyjny/wzrost mikroorganizmów można opisać trzema równaniami:

dX/dt = (μ

max

· S)/(K

S

+ S) · X

dS/dt = -1/Y

X/S

· (μ

max

· S)/(K

S

+ S) · X

dP/dt = Y

P/S

/Y

X/S

· (μ

max

· S)/(K

S

+ S) · X

Ostatnie równanie jest prawdziwe tylko wtedy, gdy przyrost produktu jest proporcjonalny do

przyrostu biomasy, czyli przyrost produktu jest powiązany ze wzrostem. W procesie

fermentacji często taka zależności nie występuje.

Opisane równania rozwiązuje się zasadniczo metodami numerycznymi, rozwiązując równania

różniczkowe.

Znajomość stałych pozwala na wyznaczenie znormalizowanej kinetyki τ(S). Zmienność X, S

i P jest opisana układem następujących równań różniczkowych.

τ(S) = S/(K

S

+ S)

dX/dt = μ

max

· τ(S) · X

dS/dt = -1/Y

X/S

· μ

max

· τ(S) · X

dP/dt = Y

P/S

· μ

max

· τ(S) · X

W oparciu o model kinetyczny można uzyskać ważną informację – mianowicie określić

długość czasu fermentacji (informacji takiej nie uzyska się w oparciu o wyznaczenie

współczynnika wydajności). Dzięki temu możliwe jest obliczenie ilości cykli produkcyjnych

na jednostkę czasu, a tym samym oszacowanie zysków.

Zalety i wady hodowli okresowych:



proste, dobrze przetestowane rozwiązania



łatwość prowadzenia procesu



względna łatwość zapobiegania zakażeniom



cykl wzrostu jest mało wydajny (faza zwłoki – lag)



jeśli pożądany produkt powstaje tylko w określonej fazie wzrostu, pozostałe fazy

powodują stratę czasu



wymagane jest przygotowanie stosunkowo dużej ilości materiału do zaszczepienia

(inokulum)



konieczność mycia i sterylizacji bioreaktora i urządzeń towarzyszących po każdym

cyklu produkcyjnym (szarży)

Hodowle ciągłe – chemostat Monoda

Reaktory do hodowli ciągłych na dużą skalę mają największe zastosowanie w oczyszczaniu

ścieków:



nie ma konieczności stosowania czystych kultur, nie ma więc zagrożenia zakażeniem



wieloletnia praktyka wykazała, że stosowanie takich oczyszczalni nie stwarza

zagrożenia dla ludzi ani środowiska



z ekonomicznego punktu widzenia, biorąc pod uwagę wielkie objętości utylizowanych

ścieków jest to jedyne sensowne rozwiązanie

Poza oczyszczaniem ścieków, reaktory do hodowli ciągłych na bardzo dużą skalę są używane

do produkcji białka jednokomórkowców (SCP) do celów paszowych. Przykładem może być

wielki bioreaktor koncernu ICI (USA) o objętości 1 000 000 dm

3

, w którym metanol

przekształcany jest przez Methylophilus methylotropus w biomasę.

Charakterystyczne parametry:



szybkość rozcieńczania (D)



czas przebywania (τ)

D = (szybkość przepływu, dm

3

/h) / (objętość reaktora, dm

3

) = F/V (h

-1

)

τ = (objętość reaktora, dm

3

) / (szybkość przepływu, dm

3

/h) = V/F (h)

Szybkość przepływu:



objętościowa

F = V/t



masowa (szybkość przepływu masy)

m = (ρ · F)/t

Produkcja biomasy oraz produktu reakcji:



tworzenie tych składników



usuwanie tych składników

dX/dt = μX – DX

dP/dt = Y

P/S

/Y

X/S

· μX – DP

Wyrażenia określające akumulację substratu zawierają trzy składniki:



wykorzystanie substratu przez mikroorganizmy



dopływ substratu (zasilanie)



usuwanie substratu w odpływie

dS/dt = -1/Y

X/S

· μX + DS

0

– DS

Model matematyczny chemostatu:



dla biomasy:

dX/dt = [(μ

max

· S)/(K

S

+ S)] · X – DX



dla substratu limitującego:

dS/dt = -1/Y

X/S

· [(μ

max

· S)/(K

S

+ S)] · X + D(S

0

– S)



dla produktu:

dP/dt = Y

P/X

· [(μ

max

· S)/(K

S

+ S)] · X – DP

WYKŁAD 10, 19/04/2012

W stanie równowagi:

dX/dt = 0

dS/dt = 0

dP/dt = 0

Zatem:

μX = DX → μ = D

W chemostacie, w stanie równowagi, szybkość właściwa wzrostu może być kontrolowana

przez szybkość rozcieńczania.

Relacje pomiaru szybkości rozcieńczania (D) i stężenia substratu (S): jeżeli μ = D, równanie

Monoda przyjmie postać:

S = (DK

S

)/(μ

max

– D)

Stan równowagi w chemostacie a stężenie biomasy:

dS/dt = -1/Y

X/S

· μX + D(S

0

– S) = 0

X = Y

X/S

(S

0

– S)

X = Y

X/S

[S

0

– (DK

S

)/(μ

max

– D)]

Stan równowagi w chemostacie a stężenie produktu:

dP/dt = 0 = Y

P/X

· μX – DP

P = Y

P/S

(S

0

– S)

P = Y

P/S

[S

0

– (DK

S

)/(μ

max

– D)]

Wszystkie przedstawione równania stosuje się tylko do sytuacji, gdy powstawanie produktu

powiązane jest ze wzrostem.

Powstawanie produktu jest związane

ze wzrostem

Powstawanie produktu nie jest związane

ze wzrostem

Wpływ szybkości rozcieńczania:



wymywanie komórek mikroorganizmów

dX/dt = μX – DX

μX – przyrost biomasy

DX – ubytek biomasy

Równanie równowagowe mas biomasy posiada dwa składniki:



składnik tworzenia (wzrostu) biomasy: μX



składnik usuwania biomasy: DX

Jeżeli szybkość usuwania biomasy przewyższa szybkość jej powstawania (D>μ):

Przy zwiększaniu szybkości rozcieńczania (D) wzrost biomasy spada, przez co

wykorzystywane jest mniej substratu (będzie go więcej w reaktorze). Jeżeli D>μ, nastąpi

wymycie mikroorganizmów. Hodowle ciągłe rozpatrywane były w stanie osiągniętej

równowagi dynamicznej, w której D = μ.

Komórki nie mogą rosnąć szybciej niż wynosi ich maksymalna szybkość wzrostu (lub nie

może być ona określana jako maksymalna). Rozważając równanie dla chemostatu, nie można

mieć ani nieograniczonego, ani ujemnego stężenia substratu.

μ

max

– D ≠ 0 ^ μ

max

– D > 0

Gdy szybkość rozcieńczania jest wyższa niż szybkość właściwa wzrostu, stężenie biomasy w

reaktorze będzie spadać, aż do całkowitego wymycia mikroorganizmów. Szybkość

rozcieńczania, przy której następuje wymywanie mikroorganizmów określamy jako szybkość

krytyczną rozcieńczania (D

kryt

), równą μ

max

.

WNIOSKI:

1. Szybkość rozcieńczania w chemostacie musi być mniejsza od krytycznej wartości

rozcieńczania (D < D

kryt

).

2. Równania stosowane do obliczenia stężeń w stanie równowagi dynamicznej nie mają

zastosowania w przypadku warunków wymywania.

3. W przypadku wymywania komórek z bioreaktora, zmienne przyjmą wartości:

S = S

0

X = 0

P=0

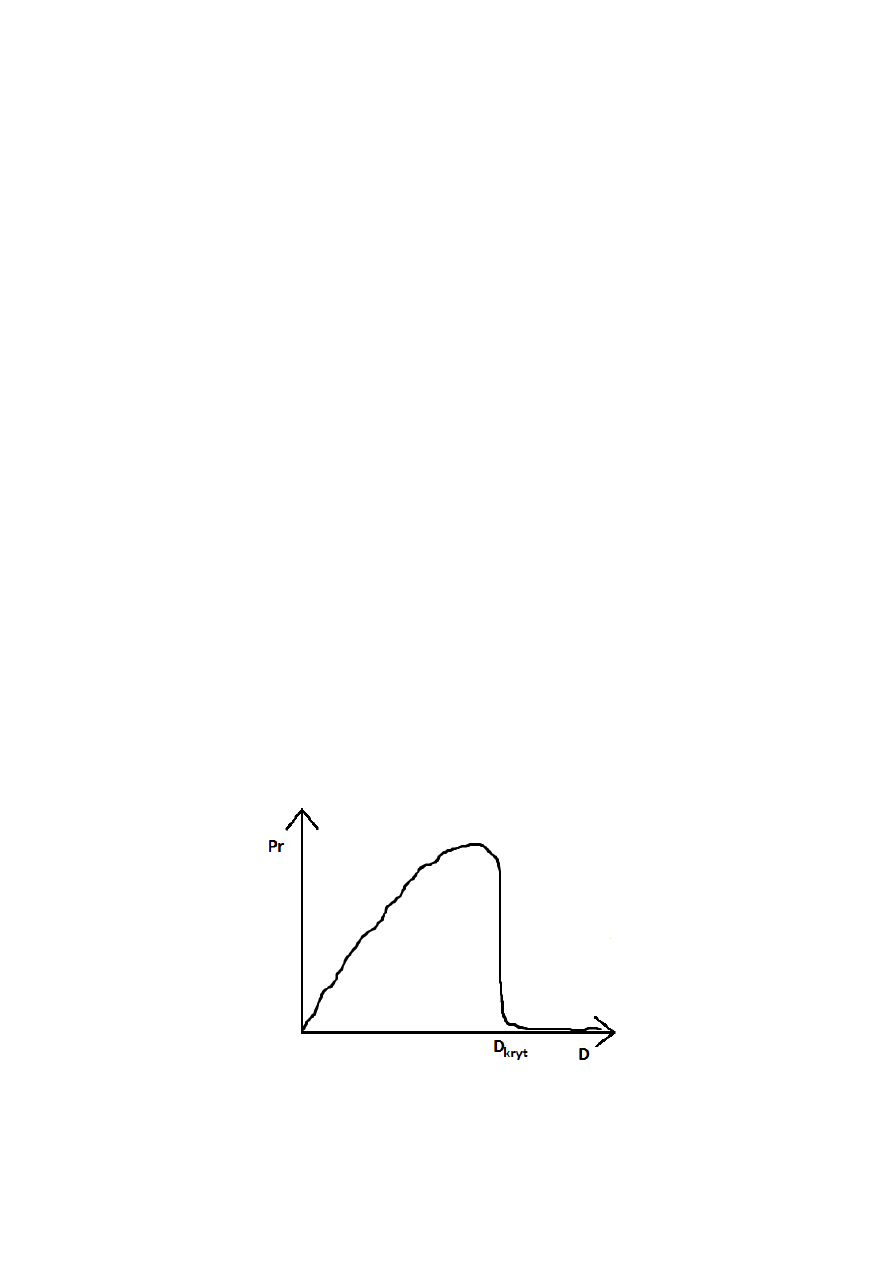
Produktywność w hodowlach ciągłych

Produktywność definiowana jest jako ilość wytworzonego danego składnika na jednostkę

czasu. W przypadku reaktora przepływowego, produktywność (Pr) będzie równa szybkości

przepływu masy składnika.

Dla biomasy:

Pr

X

= m

X

= F · X

Dla produktu:

Pr

P

= m

P

= F · P

W oparciu o model Monoda, produktywność tworzenia biomasy można wyliczyć z równania:

Pr

X

= FY

X/S

[S

0

– (DK

S

)/(μ

max

– D)]

Wybór optymalnej szybkości rozcieńczania

Jeśli wydajność produkcji biomasy jest stała przy różnych szybkościach rozcieńczenia, to

produktywność (Pr) biomasy będzie rosła wraz ze zwiększaniem szybkości rozcieńczania aż

do osiągnięcia wartości D

kryt

, to jest aż do momentu wymycia mikroorganizmów.

W rzeczywistości ani wydajność produkcji biomasy, ani produktu nie jest stała. Stwierdzono

ponadto, że często wydajność tworzenia szeregu ważnych komercyjnie produktów jest

największa wtedy, gdy wzrost jest najwolniejszy. Zatem stosowanie wysokim wartości

szybkości rozcieńczania nie zawsze jest najkorzystniejszą opcją dla tworzenia produktu

(często jest to opcja najmniej korzystna). Należy również wziąć pod uwagę, że zwiększenie

szybkości rozcieńczania (D) prowadzi do zwiększenia stężenia substratu w wypływie.

Zależność produktywności od szybkości rozcieńczania w hodowlach ciągłych:

Równania modelu Monoda można przekształcić tak, aby otrzymać współczynniki wydajności.

Wyznaczanie stałych kinetycznych dla modelu Monoda (transformacja Lineweavera-Burka

dla modelu Monoda):

Szybkość rozcieńczania, dla której produktywność wynosi swoją maksymalną wartość,

nazywamy D

max

. D

max

można obliczyć ze wzoru:

Przy D

max

(lub D

m

) następuje częściowa utrata substratu. D

max

jest bardzo blisko D

kryt

.

Współzawodnictwo mikroorganizmów w chemostacie

Jeśli dwa mikroorganizmy współzawodniczą o ten sam substrat limitujący wzrost w

chemostacie, przeżyje ten, mikroorganizm, który będzie utrzymywał niższe stężenie substratu

w mieszaninie fermentacyjnej.

Jest tak, ponieważ w reaktorze nie może być dwóch różnych stężeń tego samego substratu. W

przypadku współzawodnictwa dwóch mikroorganizmów utrzymywane jest niższe stężenie

substratu (tzn. wygrywa ten mikroorganizm utrzymujący to niższe stężenie). Można obliczyć

właściwą szybkość wzrostu obu mikroorganizmów przy niższym stężeniu substratu.

WYKŁAD 11 → nie mam, bardzo mi przykro…

WYKŁAD 12, 10/05/2012

METABOLIZM

PIERWOTNY

WTÓRNY

TROPOFAZA

podczas zrównoważonego wzrostu (w

sytuacji nadmiaru pożywienia)

IDIOFAZA

przy braku dostatecznej ilości pożywienia

Metabolity wytwarzane podczas idiofazy z acetylo-CoA:



cytrynian



kwasy tłuszczowe



chinony



terpeny



poliketydy (makrolidy)



sterole (steroidy) i inne

Kolorem czarnym zaznaczona biomasa, kolorem czerwonym – metabolit pierwotny, zaś kolorem zielonym

metabolit wtórny.

Tworzenie biomasy i produktu – zależności metaboliczne:



wytwarzanie energii w postaci ATP



wytwarzanie materiału budulcowego

Produkcja biomasy jest efektem skierowania części ATP do syntezy materiału komórkowego.

ATP jest również niezbędny do zapewnienia innych funkcji: homeostazy i ruchu.

Homeostaza jest utrzymywaniem wewnątrzkomórkowej integralności. Obejmuje m.in.

aktywny transport na zewnątrz komórki końcowych produktów metabolizmu, jonów wodoru,

toksycznych składników.

Przełączanie szlaków katabolicznych organizmu powoduje również zmiany wydajności

produkcji biomasy. Szereg organizmów (komórek) ma zdolność fermentacji (proces

beztlenowy), jak i potrafi oddychać (proces tlenowy):



fermentacja (glikoliza beztlenowa):

GLUKOZA → 2 ATP



oddychanie (glikoliza, cykl kwasów trójkarboksylowych, łańcuch oddechowy):

GLUKOZA → CO

2

+ H

2

O + 30-38 ATP

Z równań tych wynika, że fermentacja prowadzi do niższej wydajności produkcji biomasy,

niż oddychanie.

Dwa główne czynniki mogą wymuszać na fakultatywnych beztlenowcach fermentację:



ograniczony dostęp tlenu (efekt Pasteura)



wysokie stężenie rzeczywiście degradowanych substratów (efekt Crabtree lub efekt

glukozy)

W warunkach braku tlenu lub innych związków nieorganicznych podlegających redukcji,

fakultatywne beztlenowce przełączają się na fermentację.

Z porównania schematów fermentacji i oddychania widać, że odtwarzanie NAD

+

w

przypadku fermentacji jest prostsze i szybsze niż w przypadku oddychania. Zdolność

przełączania się z oddychania na fermentację daje przewagę fakultatywnym beztlenowcom

nad bezwzględnymi tlenowcami w kulturach mieszanych, np. w ekosystemach.

Efekt Crabtree:



wiele bakterii prowadzących procesy beztlenowe podlega temu efektowi bardzo

wyraźnie



przy wysokim stężeniu substratu organizmy te produkują mleczan z dużą wydajnością;

bakterie fermentacji homomleczanowej przekształcają glukozę w mleczan prawie

stechiometrycznie w warunkach glikolizy beztlenowej



pierwszorzędnym celem komórek jest wykorzystanie substratu możliwie jak

najszybciej; jeżeli komórka oddycha, szybkość utlenienia NADH może być niższa niż

aktualnie potrzebna – następują wówczas zaburzenia szlaku glikolizy, zaczynają

gromadzić się metabolity, zwłaszcza fruktozo-1,6-bisfosforan i pirogronian



metabolity te są równocześnie aktywatorami kluczowych enzymów uczestniczących w

glikolizie beztlenowej, jak również inhibitorami enzymów odpowiadających za

przekształcenie pirogronianu w acetylo-CoA (inhibitory kompleksu dehydrogenazy

pirogronianowej)

Metabolity wtórne:



szereg enzymów (najczęściej rekombinowanych)



przeciwciała monoklonalne



pigmenty



toksyny



alkaloidy



antybiotyki (wiele spośród nich produkowanych jest tylko w fazie stacjonarnego

wzrostu)

Końcowe produkty fermentacji – mleczan, etanol, cytrynian, octan.

Rozprzężenia metaboliczne

Nagromadzenie się końcowych produktów metabolizmu prowadzi do tzw. rozprzężenia

metabolizmu. Zwiększa się gradient stężeń i komórka jest zmuszona do usuwania produktów

metabolizmu na zewnątrz. W tej sytuacji znacznie więcej ATP jest potrzebne do utrzymania

homeostazy – tym samym mniej może być zużyte do syntez. W tym czasie komórka będzie

produkowała więcej końcowych metabolitów w procesie syntezy ATP. Na koniec produkcja

biomasy ustanie całkowicie, a będą powstawać tylko końcowe metabolity.

Przenoszenie masy – wpływ na wzrost

Dotychczasowe rozważania dotyczące wzrostu mikroorganizmów w różnych systemach

fermentacyjnych (hodowle okresowe, półokresowe, ciągłe) charakteryzowały się szeregiem

uproszczeń. Generalnie założono, że:



szybkość wzrostu komórek w reaktorze jest zależna od charakterystyki kinetycznej



wymieszanie jest idealne (zakłada się, że w takim modelu chemostatu skład odpływu

jest identyczny, jak skład zawartości reaktora; składniki w dopływie, wchodzące do

reaktora są natychmiast równomiernie rozpraszane w całej objętości cieczy w

reaktorze)



wszystkie składniki są roztworami wodnymi

Przedstawione uproszczenia pomijają jeden ważny fakt – przenoszenie masy pomiędzy oraz

wewnątrz faz nie jest natychmiastowe!!! W praktyce wykazano wielokrotnie, że:



kinetyka charakteryzująca biokatalizator nie zawsze jest czynnikiem ograniczającym

całkowitą szybkość reakcji



mieszanie nie zawsze jest bliskie wymieszaniu idealnemu, jak również substrat lub

biokatalizator nie zawsze są w postaci wodnej



transfer cząsteczek zachodzi pomiędzy różnymi fazami

Dobrym przykładem jest transfer tlenu. Tlen atmosferyczny jest dostarczany w postaci

gazowej – w pęcherzykach powietrza. Gazowy tlen musi zostać przetransportowany do fazy

ciekłej, w której ulega rozpuszczeniu – i tylko w takiej postaci jest dostarczany do komórek.

Całkowita szybkość reakcji jest często determinowana nie przez kinetykę katalizy, lecz przez

szybkość przenoszenia mas. W każdej reakcji musi występować ruch mas – jeśli ruch ten

będzie wolny, to i szybkość reakcji będzie niska. Każda reakcja katalizowana obejmuje:



etap przenoszenia mas



etap katalizy

Etap przenoszenia mas może być wolny, jeśli ruch cząsteczek katalizatora/substratu jest

ograniczony lub jeśli stężenie katalizatora/substratu jest niskie. Etap katalizy zależy w dużym

stopniu od czynników środowiska: temperatury, pH i innych.

Rozważając oba etapy:



jeśli szybkość przenoszenia mas jest tak niska, że ogranicza szybkość całkowitą

reakcji – mówimy, że reakcja jest ograniczana przenoszeniem mas



jeśli szybkość przenoszenia mas jest wyższa od szybkości katalizy – reakcja jest

ograniczana katalitycznie

Przenoszenie mas w roztworach

Bez mieszania wymuszonego ruch rozpuszczonych związków w roztworze zachodzi dzięki

spontanicznej dyfuzji lub naturalnej konwekcji. Procesy te są zbyt wolne, aby osiągnąć

wystarczającą szybkość przenoszenia mas dla większości reakcji. Wymuszona konwekcja

(mieszanie) jest zatem powszechnym sposobem na zwiększenie szybkości przenoszenia mas,

przy zastosowaniu różnego typu mieszadeł, pomp lub kompresorów.

Szybkość przenoszenie mas w roztworze zależy od:



intensywności mieszania



lepkości (μ) i gęstości (ρ) cieczy

Z kolei intensywność mieszania zależy od:



kształtu mieszadeł i reaktora



mocy mieszadła

Lepkość i gęstość cieczy zależą od składu roztworu i jego temperatury.

Wraz ze wzrostem intensywności mieszania rosną koszty spowodowane rosnącym zużyciem

energii oraz pojawiają się problemy z destrukcją komórek, enzymów, a niekiedy produktów.

Zatem te czynniki mogą ograniczać stosowanie optymalnych szybkości mieszania.

Odpowiednie zaprojektowanie systemu mieszania oraz reaktora może przyczynić się do

sukcesu lub niepowodzenia całego bioprocesu. Należy pamiętać, że w dużych bioreaktorach

mogą występować martwe strefy, które znacząco wpłyną na obniżenie wydajności.

Szybkość reakcji rośnie wraz ze wzrostem stężenia substratu. W przypadku, gdy substrat

dostarczany jest w postaci niewodnej, musi najpierw ulec rozpuszczeniu. W tym przypadku

stężenie rozpuszczonego w wodzie substratu (a nie jego stężenie całkowite) będzie określało

kinetykę katalizy.

Przenoszenie mas gaz-ciecz jest ważne w procesach biotechnologicznych i dotyczy głównie

transportu tlenu. Obejmuje również procesy usuwania CO

2

oraz procesy destylacji produktów

lotnych.

Przenoszenie mas ciecz-ciecz ma znaczenie w przypadku reakcji w układach dwufazowych,

konwersji związków hydrofobowych (oleje, alkany) oraz w procesach ekstrakcji.

Przenoszenie mas ciało stałe-ciecz ma miejsce w przypadku stosowania osadu komórek

bakterii, komórek immobilizowanych i immobilizowanych enzymów. Transfer taki jest

istotnym czynnikiem w procesach adsorpcji, wymiany jonowej czy też krystalizacji.

Ponieważ ruch cieczy w warstwie granicznej jest wolny, ruch rozpuszczonych związków

poprzez tę warstwę będzie determinowany raczej przez siły dyfuzji, a nie konwekcji, zatem

szybkość tej dyfuzji będzie czynnikiem limitującym.

Etapy transferu rozpuszczonego związku między fazami:

1. rozpuszczony związek wędruje przez pęcherzyk i osiąga granicę faz

2. rozpuszczony związek wędruje przez granicę faz

3. związek wędruje przez warstwę międzyfazową do cieczy otaczającej

Ponieważ szybkość ruchu rozpuszczonego związku przez warstwę międzyfazową jest

określana tylko przez dyfuzję, etap trzeci uważany jest powszechnie za etap ograniczający

szybkość reakcji.

Czynniki wpływające na proces przenoszenia mas między fazami

Ruch cząsteczek poprzez warstwę międzyfazową jest determinowany przez dyfuzję i

zachodzi od wysokiego do niskiego stężenia. Szybkość dyfuzji jest determinowana

gradientem stężeń w warstwie międzyfazowej.

Szybkość można zwiększyć poprzez:



zwiększenie powierzchni międzyfazowej



zwiększenie gradientu stężeń w poprzek warstwy międzyfazowej



obniżenie grubości warstwy międzyfazowej



zwiększenie szybkości ruchu cząsteczek w poprzek warstwy międzyfazowej

Mieszanie a przenoszenie mas między fazami:



intensywne mieszanie wytwarza silne siły ścinające, które rozdrabniają pęcherzyki

gazu i krople



następuje szybsze usuwanie rozpuszczonego związku z warstwy międzyfazowej i

utrzymanie gradientu stężeń



następuje spadek grubości warstwy międzyfazowej

WYKŁAD 13, 17/05/2012

Szybkość przenoszenia mas jest determinowana przez dwa czynniki:



mieszanie



dyfuzję

Opisy matematyczne, dotyczące tego procesu w bioreaktorach z wymuszonym mechanizmem

muszą zatem uwzględniać:



szybkość mieszania



sposób zaprojektowania reaktora



średnicę turbiny



gęstość i lepkość medium



gęstość pęcherzyków



szybkość dyfuzji

W obliczeniach inżynierskich korelacje te charakteryzują różna wartości bezwymiarowe, np.

liczba Reynoldsa, liczba mocy (Newtona).

Wychodząc z założenia, że etapem ograniczającym przenoszenie mas między fazami jest

szybkość dyfuzji związku przez warstwę międzyfazową, możemy opisać to równaniem:

dC

S

/dt = kA(C

S

*

- C

S

)

C

S

– stężenie rozpuszczonego związku w medium otaczającym

C

S

*

- stężenie tego związku w warstwie międzyfazowej

A – całkowita powierzchnia międzyfazowa

k – współczynnik przenoszenia mas

Zwiększenie wartości współczynników k i A będzie prowadziło do zwiększenia szybkości

przenoszenia mas. Współczynniki te są zależne od:



k → temperatury, lepkości medium, wielkości rozpuszczonego związku,

intensywności mieszania, obecności związków interferujących



A → intensywności mieszania, działania sił ścinających, obecności czynników

powodujących zlepianie

Napowietrzanie

Fermentacje tlenowe są podstawowymi procesami biotechnologicznymi, prowadzącymi do

otrzymania ważnych komercyjnie produktów. Dostarczanie tlenu, niezbędnego w tych

procesach, jest dla technologów jednym z największych problemów do rozwiązania. Wynika

to z wspomnianego już faktu, że tlen jest słabo rozpuszczalny w wodzie. Tak więc dostępność

tlenu jest bardzo często czynnikiem limitującym szybkość procesu fermentacji tlenowej.

Często koszty związane z napowietrzaniem hodowli w skali przemysłowej są bardzo

poważnym składnikiem kosztów całkowitych hodowli.

Jeśli mamy do czynienia z prostym układem – zawiesiną pojedynczych komórek, to etapem

limitującym przenoszenie tlenu będzie przenikanie cząsteczek tlenu poprzez warstwę

międzyfazową.

W przypadku dobrego mieszania zawartości bioreaktora, etapem limitującym przenoszenie

tlenu będzie szybkość jego dyfuzji poprzez warstwę międzyfazową.

OTR = dC

O

/dt = k

L

a(C

O

*

- C

O

)

Ponieważ nie jest możliwe dokładne zmierzenie całkowitej powierzchni międzyfazowej, w

praktyce stosuje się łączny termin k

L

a, określający szybkość transferu tlenu na jednostkę

objętości.

Ponieważ nie ma również możliwości technicznej pomiaru stężenia tlenu w warstwie

międzyfazowej, dane te uzyskuje się metodą pośrednią: napowietrzając sterylną zawartość

fermentora, osiągniemy stan równowagi przy maksymalnym (w danej temperaturze) stężeniu

tlenu w roztworze. W tym przypadku stężenie tlenu zarówno w warstwie międzyfazowej, jak i

w roztworze będzie równe, co wynika z równania:

dC

O

/dt = k

L

a(C

O

*

- C

O

)

dC

O

/dt = 0 → C

O

*

= C

O

Maksymalna rozpuszczalność tlenu w cieczy może być wyznaczona w oparciu o równanie

Henry’ego:

C

O

*

= P

O

/H

O

Czynniki wpływające na współczynnik transferu tlenu (k

L

) przez warstwę międzyfazową:



wartość k

L

możemy zwiększyć poprzez zmniejszenie warstwy międzyfazowej



zwiększenie szybkości przenikania tlenu przez tę warstwę

Grubość warstwy międzyfazowej zależy od intensywności mieszania. Szybkość dyfuzji tlenu

przez tę warstwę zależy od lepkości środowiska i temperatury. Wzrost temperatury powoduje

spadek lepkości, ale równocześnie zmniejsza się rozpuszczalność tlenu w roztworze. Jeśli

mieszanie jest zbyt wolne lub przepływ powietrza zbyt duży, zbiera się ono pod turbiną,

pęcherzyki łączą się w duże bąble i spada wydajność natleniania.

Na stopień wykorzystania tlenu zawartego w powietrzu wprowadzanym do ścieków mają

wpływ:



wielkość

pęcherzyków

powietrza,

zależna

od

konstrukcji

elementów

napowietrzających



głębokość założenia elementów napowietrzających



kształt napowietrzanej komory



sposób ułożenia elementów napowietrzających w stosunku do rzuty poziomego

komory

Zatrzymanie gazu (G

H

) określa objętość gazu w stosunku do objętości cieczy w reaktorze.

Wartość G

H

podnosi się wraz ze wzrostem przepływu powietrza, a wartości G

H

i czasu

przebywania (τ) rosną wraz z:



wzrostem lepkości cieczy



spadkiem wielkości pęcherzyków



wysokością reaktora

Należy pamiętać, że dłuższy czas przebywania czy też wyższa wartość współczynnika G

H

nie

zawsze muszą zwiększać wymianę tlenu – ponieważ im dłużej pęcherzyk przebywa w

reaktorze, tym mniej tlenu może zawierać. Małe pęcherzyki szybciej oddają tlen; w praktyce

tak dobiera się warunki napowietrzania, aby pęcherzyki miały średnicę około 3mm.

Stała Henry’ego (H

O

) zależy od temperatury i zawartości soli w roztworze. Przy ciśnieniu

1 atm. ciśnienie parcjalne tlenu wynosi 0,21 atm. Dla czystego tlenu ciśnienie parcjalne w

normalnych warunkach ciśnienia atmosferycznego wynosiłoby 1 atm. A zatem, teoretycznie,

zwiększenie wymiany tlenu można osiągnąć przez natlenianie reaktora czystym tlenem,

zamiast powietrzem.

OUR – szybkość pobieranego tlenu

Stężenie rozpuszczonego tlenu w medium w bioreaktorze jest określane równowagą

pomiędzy szybkością przenoszenia tlenu (OTR) i jego pobieraniem (OUR).

dC

O

/dt = OTR – OUR

W ruchu laminarnym tory cząsteczek mało różnią się od siebie. Pozostające w ruchu medium

można traktować jako zbiór oddzielnych warstw, poruszających się względem siebie z różną

prędkością i nie mieszających się ze sobą. W ruchu turbulentnym ruch cząsteczek płynu

powoduje mieszanie się różnych warstw.

Lepkość cieczy

Lepkość (μ) najogólniej jest definiowana jako miara tarcia wewnętrznego cieczy (siły

międzycząsteczkowego przyciągania cieczy). Na charakterystykę lepkościową cieczy

składają się:



lepkość w zależności od temperatury



wskaźnik lepkości

W technice wyróżnia się:



lepkość dynamiczną – μ



lepkość kinematyczną – ν

Lepkość dynamiczną wyrażamy w jednostkach układu SI:

1 Pa · s = 1 N · s/m

2

= 1 kg/m · s

Lepkość dynamiczna jest często wyrażana w systemie CGS w puazach:

1 P = 1 dyna · s/cm

2

= g/cm · s =

1

/

10

Pa · s

Lepkość kinematyczna to stosunek lepkości dynamicznej danej cieczy do jej gęstości.

Zarówno lepkość kinematyczna, jak i lepkość dynamiczna muszą być wyznaczane w tej samej

temperaturze.

WYKŁAD 14, WYKŁAD 15 → również nie było mnie na nich, więc nie mam notatek…