1

Ruch ogólny bryły

Wykład - kinematyka

2

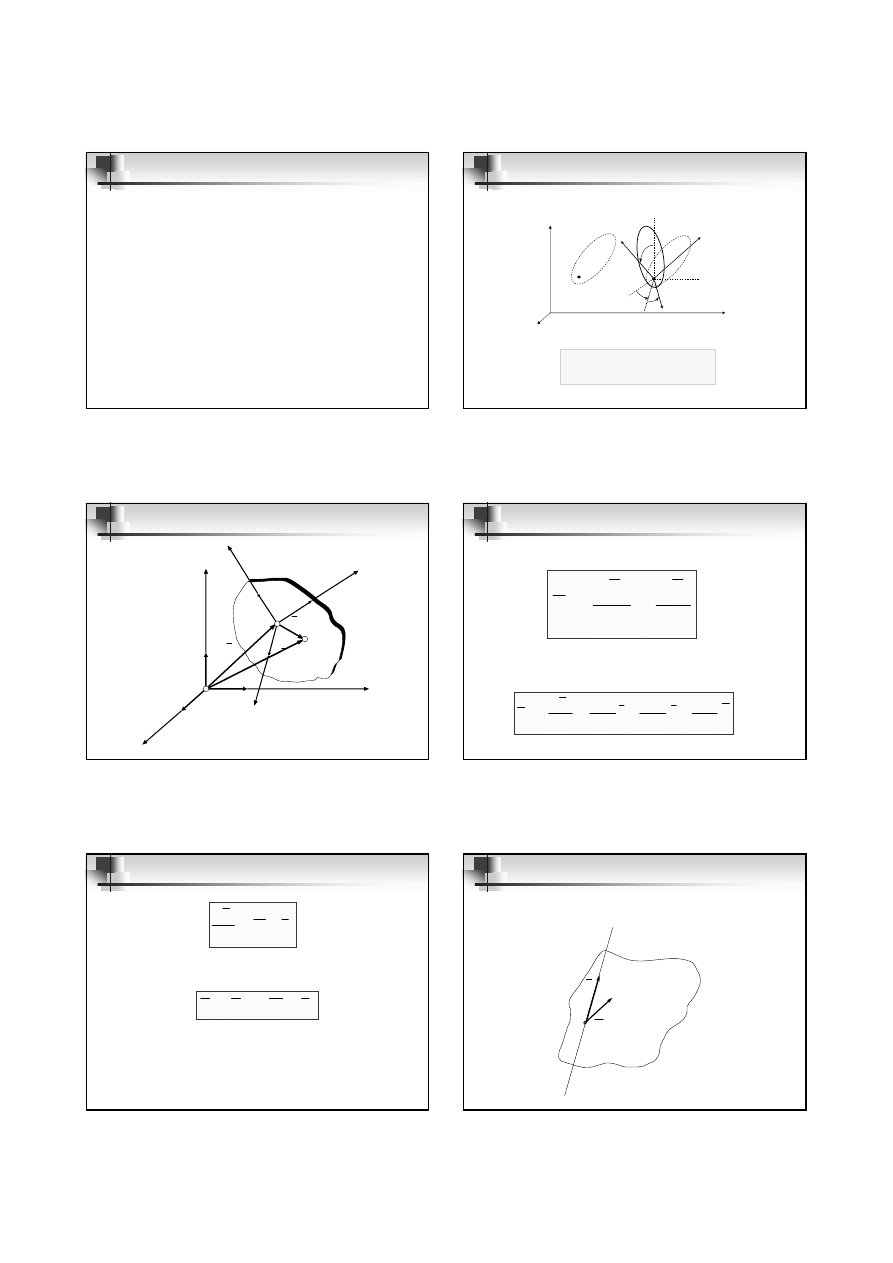
Przemieszczenia bryły w ruchu ogólnym

0

x

y

z

I

II

A

A

N

ψ ϕ

υ

Ruch ogólny jest więc złożony z ruchu postępowego i kulistego

Współrzędne bieguna A i kąty Eulera są pewnymi funkcjami czasu, a więc:

( )

( )

( )

( )

( )

( )







=

=

=

=

=

=

.

,

,

,

,

,

6

5

4

3

2

1

t

f

t

f

t

f

t

f

z

t

f

y

t

f

x

A

A

A

υ

ϕ

ψ

Powyższe równania będziemy nazywać równaniami ruchu ogólnego.

3

Prędkość dowolnego punktu bryły w ruchu ogólnym

y

y’

x

z

O

P

i

k

j

k’

j’

i’

A

z’

x’

r

r’

r

A

4

Prędkość punktu P wyraża zależność:

Pochodna wektora r

A

względem czasu jest prędkością

punktu A:

Prędkość dowolnego punktu bryły w ruchu ogólnym

dt

'

r

d

dt

r

d

v

A

+

=

k

dt

dz

j

dt

dy

i

dt

dx

dt

r

d

v

A

A

A

A

A

+

+

=

=

5

Prędkość dowolnego punktu bryły w ruchu ogólnym

Pochodna wektora r’:

Zatem prędkość dowolnego punktu P bryły w ruchu ogólnym
określa zależność:

Prędkość dowolnego punktu P bryły jest równa sumie prędkości
v

A

dowolnie obranego bieguna A, przyjętego za początek

ruchomego układu współrzędnych, oraz iloczynu wektorowego

ω

ωω

ω

×r’ prędkości kątowej

ω

ωω

ω

i promienia wodzącego r’ punktu P w

ruchomym układzie współrzędnych.

'

r

dt

'

r

d

×

=

ω

'

r

v

v

A

×

+

=

ω

7

V

A

ω

A

Chwilowa oś obrotu

Niech chwilowy ruch bryły określony będzie wektorami

ω

ωω

ω

i V

A

.

Prędkość dowolnego punktu bryły w ruchu ogólnym

2

8

V

A

V

ω

A

V

1

Chwilowa oś obrotu

Rozłożymy prędkość bieguna V

A

na dwie składowe, z których

jedna ma kierunek chwilowej osi obrotu, a druga jest do niej prostopadła.
Składowe te na rysunku oznaczymy przez V i V

1

.

Prędkość dowolnego punktu bryły w ruchu ogólnym

9

V

A

V

ω

A

V

1

Chwilowa oś obrotu

Na kierunku prostopadłym do płaszczyzny, w której leżą obie składowe,
odmierzamy odcinek AP:

ω

1

V

AP

=

Wyznaczony punkt P ma prędkość
równą

sumie

geometrycznej

prędkości ruchu postępowego V

A

i

prędkości obrotu V

P0

.

1

0

P

0

P

V

V

czyli

,

AP

V

=

⋅

=

ω

Kierunek

tych

prędkości

jest

jednakowy,

a

ich

zwroty

są

przeciwne. Punkt P

ma więc

prędkość równa:

V

V

V

V

0

P

A

P

=

+

=

V

A

.

P

V

P0

V

P

=V

Oś centralna

Oś centralna ruchu ogólnego

10

Punkt P i wszystkie punkty
leżące na osi równoległej do

ω

,

przechodzącej przez punkt P,
mają prędkość równoległą do
chwilowej osi obrotu. Oś tę
nazywamy

osią

centralną

ruchu ogólnego.

Oś centralna ruchu ogólnego

.

.

A

V

A

ω

P

V

A

V

P0

Oś centralna

V

P

12

Punkt P i wszystkie punkty leżące na
osi równoległej do

ω

, przechodzącej

przez punkt P, mają

prędkość

równoległą do chwilowej osi obrotu.
Oś tę nazywamy osią centralną
ruchu ogólnego.

Oś centralna ruchu ogólnego

.

.

A

V

A

ω

P

V

A

V

P0

Oś centralna

V

P

14

Przyspieszenie dowolnego punktu bryły w ruchu ogólnym

'

r

)

'

r

(

'

r

a

a

2

A

ω

ω

ω

ε

−

⋅

+

×

+

=

Wzór na przyspieszenie punktu można przedstawić w nieco innej postaci po

rozpisaniu występującego w nim podwójnego iloczynu wektorowego zgodnie
z zależnością: