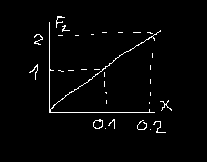Fizyka I - Egzamin

1. Na wykresie przedstawiono zależność siły Fz rozciągającej sprężynę od wydłużenie sprężyny (dla sprężyny nie-rozciągniętej x=0). Jaką pracę trzeba wykonać, Aby rozciągnąć sprężynę od położenia 0.1 m do położenia 0.2 m ?

Odp.

Praca:

W = F ⋅ s

1

W =

⋅1⋅ 1,

0 = 1

,

0

2

2. Wektory położenia mas m1 = 2kg, m2 = 1kg to odpowiednio r1 = [4,-4,1]m, r2=[4,1,-4]m.

Wyznacz położenie środka masy układu.

Odp.

Środek ciężkości, punkt ciała lub układu ciał, w którym przyłożona jest wypadkowa siła ciężkości działająca na ciało. W jednorodnym polu grawitacyjnym położenie środka ciężkości pokrywa się z położeniem środka masy.

n

n

n

∑ m x

∑ m y

∑ m z

n

n

n

n

n

n

n=

x

1

n=

y

1

n=

z

1

c =

c =

c =

n

n

n

∑ m

∑ m

∑ m

n

n

n

n=1

n=1

n=1

3. Walec o masie m i promieniu r wiruje wokół osi będącej osią symetrii walca pod wpływem siły F przyłożonej do jego powierzchni bocznej. Moment bezwładności walca wynosi mr2/2.

Ile wynosi przyśpieszenie kątowe walca?

Odp.

M = I ⋅ ε

M = F ⋅ r

F ⋅ r = I ⋅ ε

F ⋅ r

ε = I

4. Cząstka o masie m porusza się po okręgu o promieniu R z prędkością kątową ω. W wyniku działania sił wewnętrznych układu jej promień wzrósł do wartości równej 2R. Ile wynosi nowa prędkość kątowa tej cząstki.

Odp.

J = ω ⋅ I

2

I = mr

ω ⋅ m 2 r = ω ⋅ mr

2

( )2

2

1

2

ω ⋅ mr

1

ω =

2

2

4 mr

5. Jakie warunki muszą być spełnione, aby ciało (bryła sztywna) pozostawało w równowadze?

Odp.

Bryła sztywna jest w równowadze jeśli spełnione są warunki:

- wypadkowa siła zewnętrzna jest równa zeru

- moment wypadkowy sił zewnętrznych jest równy zeru.

6. Masa księżyca jest 81 razy mniejsza od masy Ziemi, a stosunek promieni Księżyca i Ziemi wynosi 3/11. Oblicz przyśpieszenie ciała na Księżycu.

Odp.

GM m

Siła działająca na dane ciało na Ziemi:

z

F =

z

2

Rz

GM m

GM m

121 GM m

121

Siła działająca na dane ciało na Księżycu:

k

z

z

F =

=

=

⋅

=

F

k

2

2

2

z

R

 3



729

R

729

k

z

81

R 

z

11



121

F =

F

k

729 z

121

ma =

mg

729

121

a =

g

729

m

a ≈ .

1 63 2

s

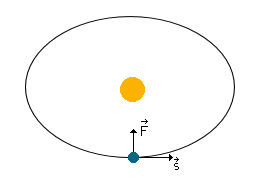
7. Jakie wielkości fizyczne nie zmieniają się w ruchu orbitalnym Ziemi wokół Słońca ?

Nie zmienia się :

- moment pędu

Zmienia się :

- pęd

- odległość Ziemi od słońca

- przyśpieszenie

8. Zdefiniuj współczynnik napięcia powierzchniowego cieczy.

Odp.

Zjawisko fizyczne występujące na styku powierzchni cieczy z ciałem stałym, gazowym lub inną cieczą.

Zjawisko to polega na powstawaniu dodatkowych sił działających na powierzchnię cieczy w sposób kurczący ją tak, że zachowuje się ona jak sprężysta błona. Napięciem powierzchniowym nazywa się również wielkość fizyczną ujmującą to zjawisko ilościowo. Zjawisko to ma swoje źródło w siłach przyciągania pomiędzy molekułami cieczy. Występuje ono zawsze na granicy faz termodynamicznych, dlatego zwane jest też napięciem międzyfazowym. Napięcie powierzchniowe silnie zależy od temperatury cieczy. Zmniejsza się wraz ze wzrostem temperatury i spada aż do zera w temperaturze krytycznej.

Miarą napięcia powierzchniowego jest praca, jaką trzeba wykonać, by utworzyć jednostkową powierzchnię cieczy, co można wyrazić wzorem:

W

∆

σ =

jednostką w SI J/m2

S

∆

gdzie:

σ (uż ywa się też oznaczenia γ ) – napię cie powierzchniowe,

∆ W – praca potrzebna do utworzenia powierzchni ∆ S,

∆ S – pole powierzchni.

Powyższy wzór jest równoważny:

F

σ =

l

gdzie:

F – siła napię cia powierzchniowego działają ca równolegle do powierzchni cieczy, dążą ca do zmniejszenia powierzchni cieczy,

l – długość odcinka na którym działa siła.

9. W ruchu harmonicznym położenie ciała o masie m = 0.5 kg jest opisane równaniem x(t) =0.02cos(π t/4 + π /3) w SI. Ile wynosi okres drgań i całkowita energia mechaniczna tego ciała ?

Odp.

x( t) = A co (

s ω t

0

+ ϕ′)

Okres drgań T:

2π

T = ω

0

Natomiast częstotliwość drgań v wynosi:

ω0

v = π

2

Całkowita energia mechaniczna jest sumą energii potencjalnej i kinetycznej: 2

kA

E = E + E =

p

k

2

10. Do probówki napełnionej wodą (gęstość ρ i objętość V) wrzucono ciało o masie m. Po pewnym czasie zaczęło spadać ruchem jednostajnym. Ile wynosi siła oporu działająca na ciało?

Odp.

Oznacz to, że siła ciężkości Q = mg działająca na ciało zrównoważyła siłę Archimedesa oraz siłę oporu, dlatego ciało porusza się ruchem jednostajnym.

mg = F + F

o

A

F = mg − F

o

A

11. Pierścień z drutu o promieniu R i masie m zawieszono na gwoździu (patrz rysunek) i wprawiono w drgania o niewielkiej amplitudzie. Ile wynosi okres małych drgań harmonicznych pierścienia ?

Odp.

Drganiem harmonicznym nazywamy ruch, w którym siła działająca na drgający obiekt jest wprost proporcjonalna do wychylenia z położenia równowagi i zwrócona w stronę położenia równowagi. Każdy ruch powtarzający się w regularnych odstępach czasu nazywany jest ruchem okresowym. Jeżeli ruch ten opisywany jest sinusoidalną funkcją czasu to jest to ruch harmoniczny. Ciało porusza się ruchem harmonicznym prostym, jeżeli znajduje się pod wpływem siły o wartości proporcjonalnej do wychylenia z położenia równowagi i skierowanej w stronę położenia równowagi:

F = − kx

gdzie:

k - współczynnik proporcjonalnoś ci,

x - wychylenie z położ enia równowagi.

Wartość przyśpieszenia w ruchu harmonicznym:

a

2

= ω

− x

Okres małych drgań harmonicznych pierścienia obliczymy z wzoru:

I

T = 2π mRg

2 R

T = 2π

g

12. Interferencją nazywamy dodawanie fal. Jaką wielkość dodaje się podczas interferencji ?

Odp.

Interferencja to zjawisko nakładania się fal prowadzące do zwiększania lub zmniejszania amplitudy fali wypadkowej. Interferencja zachodzi dla wszystkich rodzajów fal, we wszystkich ośrodkach, w których mogą rozchodzić się dane fale. W ośrodkach nieliniowych oprócz interferencji zachodzą też inne zjawiska wywołane nakładaniem się fal, w ośrodkach liniowych fale ulegając interferencji spełniają zasadę superpozycji.

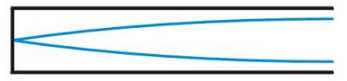
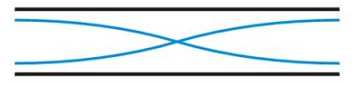
13. O jakich długościach mogą powstać fale stojące w otwartej z obu stron rurach o długości równe L=6m

Odp.

Długość max= L·2

Rodzaje rur i rozkład w fal:

14. Z dwóch źródeł fal S1 i S2 docierają do detektora w punkcie P, odległego od źródeł

odpowiednio o l1 i l2 dwie fale o jednakowych długościach λ. Jeśli wiemy, że źródła pracują w zgodnych fazach to jaki jest warunek na interferencje wzmocnienia fal w punkcie P ?

Odp.

- dla faz zgodnych : S1P-S2P=kλ

- dla faz przeciwnych: S1P-S2P=1/2λ w ogólnym przypadku S1P-S2P=(2k+1)*1/2λ

15. Rozpędzone ciało o cieple właściwym c, uderza w twardą przeszkodę. W wyniku zderzenia połowa energii uległa rozproszeniu, a druga połowa spowodowało wzrost temperatury ciała o ∆ t. Ile wynosiła prędkość tego ciała przed uderzeniem w przeszkodę ?

Odp.

mv 2 = 1 E = Q

∆ = mc t

∆

k

w

4

2

16. Jeżeli pęd układu ciał nie ulega zmianie to, oznacza to, że: Odp.

Jeżeli na ciało nie działają żadne siły lub siły działające na ciało się równoważą to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.

17. Praca siły niezachowawczej:

Siłą niezachowawczą nazywamy siłę, która wzdłuż dowolnego zamkniętego toru wykonuje pracę różną od zera. Siła niezachowawcza działająca na ciało wykonuje pracę zależną od długości toru ruchu ciała.

Siłami niezachowawczymi są np. siła tarcia i wszelkie siły oporu.

- zależy od toru po którym porusza się ciało

- zależy od początkowego i końcowego punktu toru

- zależy od kształtu toru i sposobu ruchu

- zależy od drogi jaką obierzemy

18. Punkt materialny rozpoczyna ruch po okręgu o promieniu R ze stałym przyśpieszeniem stycznym a. Jego przyspieszenie dośrodkowe jest pięciokrotne większe od przyśpieszenia stycznego po czasie:

Odp.

Przyśpieszenie dośrodkowe jest określane wzorem:

v 2

a =

R

czyli:

v 2

5 a = R

5 R

v =

a

19. Częstość rezonansowa drgań samochodu na resorach wynosi ω. Samochód ten jadąc po drodze ułożonej z płyt o długości l każda będzie drgał najsilniej jadąc z prędkością równą: Odp.

Częstotliwość rezonansowa jest określana wzorem:

ω

f = π

2

Zatem, odpowiedź:

ω l

v = π

2

20. Dwie kulki o masach m1 = m i m2 = 3m mają takie same pędy. Energie kinetyczne E1 i E2 tych kulek spieniają zależność:

Odp.

2

2

m v

3 m v

1

1

=

2

2

3 E = E

1

2

21. Stacjonarny satelita Ziemi (promień Ziemi wynosi 6,4•103km) znajduje się na orbicie o promieniu równym 4,2•104 km. Ile wynosi prędkość liniowa v satelity na orbicie?

Odp.

F = F

g

odś

GMm

mV 2

=

R 2

2

GM

V =

R

22. Co mówi zasada zachowania pędu układu ciał?

Odp.

Zasada zachowania pę du:

Jeżeli na ciało lub układ ciał nie działa żadna siła zewnętrzna (pochodząca od innego ciała), to całkowity pęd układy jest stały.

Zasada zachowania momentu pę du:

Jeżeli na ciało lub układ ciał wypadkowy układ działających sił jest równy 0, to b = const.

23. Dwa ciała, A oraz B, mają jednakowe energie kinetyczne. Masa ciała A jest 9 razy większa od masy ciała B. Ile wynosi stosunek pędów ciał? Odpowiedź uzasadnij.

Odp.

p

r

= p r

A

B

ponieważ:

2

m v

9

2

m v

B 1

B

2

=

2

2

24. Ciało porusza się po okręgu o promieniu R z prędkością v. Ile wynosi praca siły dośrodkowej? Odpowiedź uzasadnij.

Odp.

W = F ⋅ s

Siła dośrodkowa - grawitacji w ruchu kołowym nie wykonuje pracy ponieważ w każdym punkcie wektor siły skierowany jest prostopadle do wektora przesunięcia. A ponieważ cos 90o = 0, to W = 0.

25. Kula lecąca poziomo z prędkością v1 przebija przeszkodę i dalej porusza się poziomo. W

wyniku tego zderzenia kula zmniejsza swoją energię mechaniczną o połowę. Ile wynosi prędkość v2 kuli po przejściu przez przeszkodę?

Odp.

2

mv 1

E

=

1

m

2

2

mv 2

E

=

m 2

2

E 1

m

= 2

Em 2

2

v 1 = 2

2

v 2

2

v

2

1

v =

2

2

v 1

v =

2

2