



Analiza wariancji w układzie BLOKÓW LOSOWANYCH
Arkusz do wprowadzania danych: Plik
Nowy
Dane
Wybór analizy:
Analizuj
ANOVA
Modele liniowe
Ustawiamy:
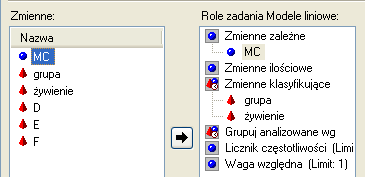
Wybieramy analizę wariancji w układzie bloków losowanych (model): Odznaczamy w opcjach modelu sumę kwadratów (Typ I) Wyniki bloków losowanych:
Source
DF Sum of Squares Mean Square F Value Pr > F
Model
7
302.2265000 43.1752143
18.83 <.0001
Error
12
27.5190000
2.2932500
Corrected Total
19
329.7455000
R-Square
Coeff Var
Root MSE
MC Mean
Źródła zmienności:
Error (Błąd) – resztowa
Corrected total (Razem
0.916545 3.950301 1.514348 38.33500
skorygowana) - ogólna
Source
DF
Type III SS
Mean Square F Value
Pr > F
grupa
4 202.7530000 50.6882500
22.10 <.0001
żywienie
3
99.4735000 33.1578333
14.46 0.0003
Źródła zmienności:
grupa – blok
Wartość statystyki i prawdopodobieństwo dla obiektów żywienie – obiekt
Analiza wariancji – KWADRAT ŁACIŃSKI Analiza wykonywana analogicznie jak analiza wariancji w układzie bloków losowanych. Ustawiamy 3 zmienne klasyfikujące.
Wyniki kwadratu łacińskiego: Source
DF Sum of Squares Mean Square F Value Pr > F
Model
6
1.03333333 0.17222222
51.67 0.0191
Error
2
0.00666667 0.00333333
Corrected Total
8
1.04000000
Źródła zmienności:
Error (Błąd) – resztowa
corrected total (Razem
R-Square
Coeff Var
Root MSE tłuszcz Mean
skorygowana) - ogólna
0.993590 1.506131 0.057735
3.833333
Source DF
Type III SS
Mean Square F Value
Pr > F
krowa
2 0.68666667 0.34333333 103.00 0.0096
okres
2 0.08666667 0.04333333
13.00 0.0714
oliwa
2 0.26000000 0.13000000
39.00 0.0250
Źródła zmienności:
Krowa – kolumna
Okres – wiersz
Wartość statystyki i prawdopodobieństwo dla obiektów Oliwa – obiekt
Wyszukiwarka
Podobne podstrony:
Nierówności kwadratowe
Postać kanoniczna funkcji kwadratowej
Test HI kwadrat
Kwadrans przed Przenajświętszym
miała baba koguta, Prezentacje, Bloki tematyczne do zajęć
kwadrat,nazwy
kwadrat przepływu pieniędzy
Funkcja kwadratowa
ZOZNAM RASTLÍN PRAKTICKÁ ČASŤ SKÚŠKY Z BOTANIKY II
1 Plan całkowicie losowy, blok losowy, kwadrat łaciński
09 pfsc sas gido3vwa6mgy2a3eiib Nieznany (2)
funkcja kwadratowa praca klasowa
Prawa+kwadratu+logicznego, [ POZOSTAŁE ], [ Logika ]
5 wnioski z metody najmniejszych kwadratów
Konspekt; Obwody prostokątów i kwadratów 2 lekcja
więcej podobnych podstron
