Wstawka matematyczna 1. Rachunek wektorowy

wielkości fizyczne

wielkości wektorowe

wielkości skalarne

wektor – uporządkowana

para punktów (początek i koniec).

skalary – do określenia

wielkości skalarnej wystarczy

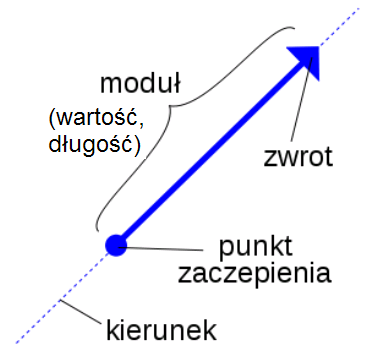
Cechy wektora:

jedna liczba

* moduł (wartość, długość)

* kierunek

* zwrot

* punkt przyłożenia

masa m

czas t

siła F

energia E

prędkość v

temperatura T

przyspieszenie a

pęd p

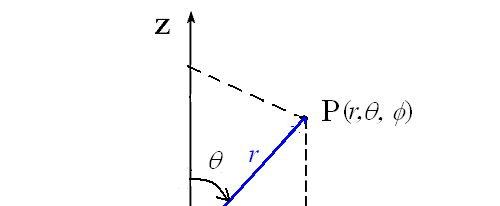
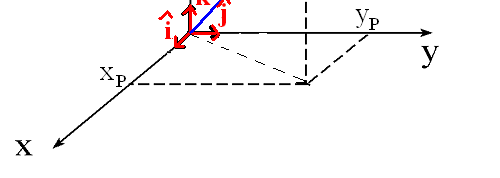
układy współrzędnych

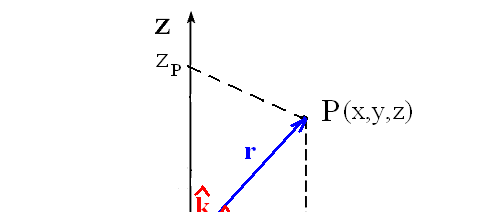
układ kartezjański

układ sferyczny

r = x iˆ + y jˆ + z kˆ

x = r sinθ cosφ

y = r sinθ sinφ

iˆ - wersor to wektor jednostkowy z = r cosθ

r - wektor położenia

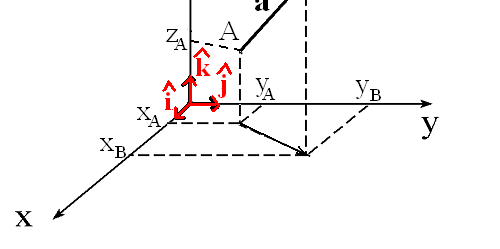
położenie r

prędkość v

wektory przyspieszenie a pęd p

współrzędne wektorów:

AB = a = [ a , a , a ]

x

y

z

a =x -x , a =y -y , a =z -z

x

B

A

y

B

A

z

B

A

a = a iˆ + a + a x

+ a jˆ

y

+ kˆ

z

równość wektorów:

a =b , a =b , a =b .

x

x

y

y

z

z

długość wektora:

2

2

2

a = a + a + a x

y

z

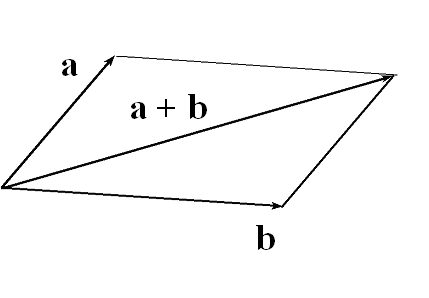
dodawanie wektorów:

a + b = c

c =a +b , c =a +b , c =a +b

x

x

x

y

y

y

z

z

z

mnożenie wektora

przez liczbę:

c = k a

c = k a , c = k a , c = k a

x

x

y

y

z

z

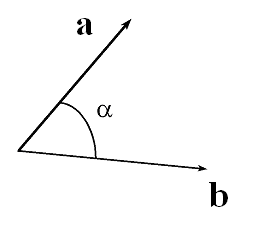
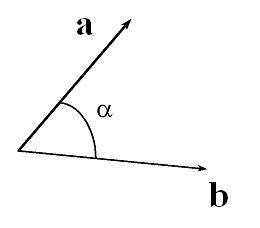
iloczyn skalarny wektorów:

a—b = a b cosα

a—b = a b + a b + a b x x

y y

z z

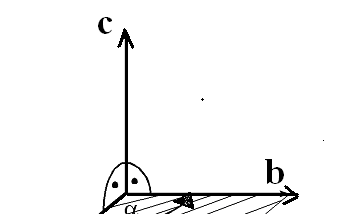
iloczyn wektorowy :

a x

x b = c

c=a b sin α

iˆ

jˆ

kˆ

c = c iˆ + c jˆ + c kˆ

c = a

a

a

x

y

z

x

y

z

b

b

b

x

y

z

Wstawka matematyczna 2. Pochodne i całki

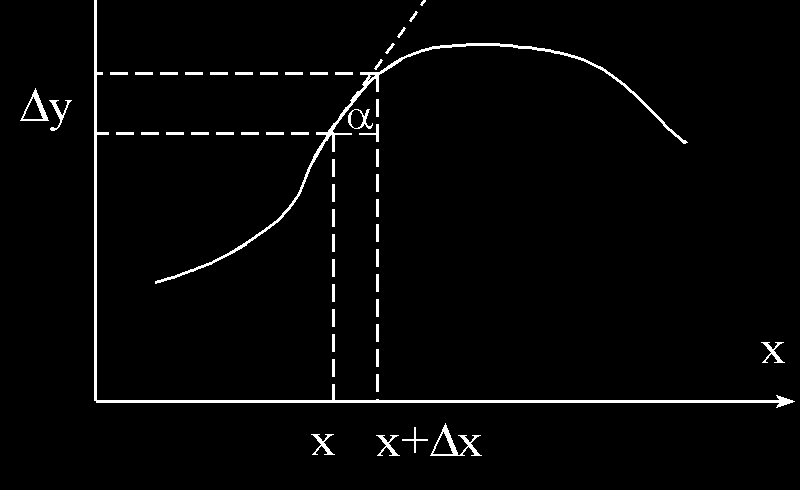
Pochodna funkcji f(x)

df

f ( x + ∆ x) − f ( x) f '( x) =

= lim∆ →

dx

x

0

∆ x

Pochodna funkcji Podstawowe własności pochodnej : df

dg

d

df

dg

⋅ g − f ⋅

( f + g) =

+

d ( f / g) dx dx

=

dx

dx

dx

2

dx

g

d

df

dg

d

df ( u) dg ( x ( f ⋅ g ) =

⋅ g + f ⋅

[ f ( g( x)]

)

]=

⋅

dx

dx

dx

dx

du

dx

gdzie : u = g ( x) Przykłady:

d

n

1

( x )

−

=

n

nx

d

d

dx

(sin x) = cos x

(cos x) = − sin x

dx

dx

d

x

x

d

1

( e ) = e

(ln x) =

( x > 0)

dx

dx

x

Pochodna wektora

W

W prze

z d

e zi

z a

i l

a e

l

e cz

c a

z s

a u

s ∆ t

∆ p

rzy

z rost

s w

e

w k

e to

t ra

r

a r(

r t

( ) w

y

w nosi

s

i ∆r

∆ :

r

:

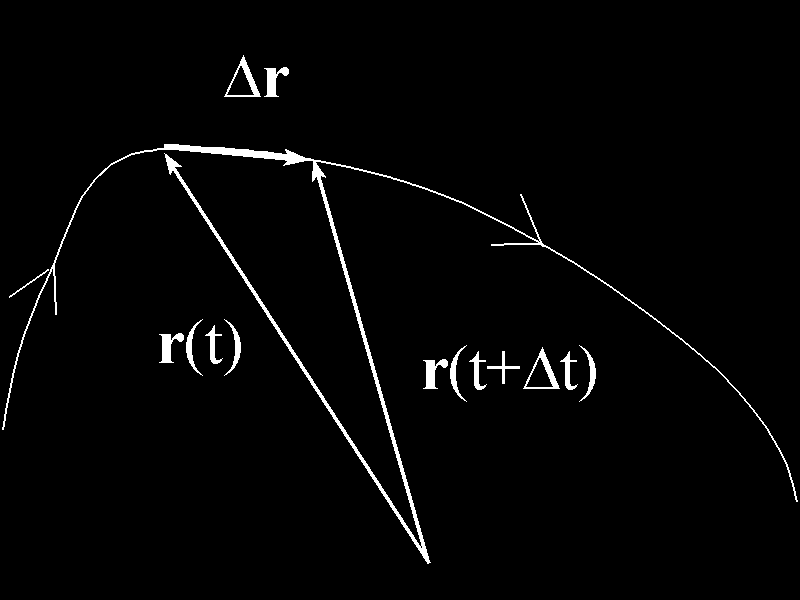
∆r = r( t+∆ t) – r( t), to stosunek:

∆r r t( + t

∆ ) − r t()

dr

r t

( + t

∆ ) − r t

=

→

=

( )

lim∆ →

t

∆

t

∆

dt

t

0

t

∆

dr

 dx dy dz 

=  , , 

dt

 dt dt dt 

Całka nieoznaczona

∫ g( x) dx = f ( x) ściślej:

∫ g( x) dx = f ( x) + C

Wynik operacji całkowania:

znaleziona funkcja pierwotna f(x) ma taką własność, że po zróżniczkowaniu jej otrzymujemy funkcję podcałkową g(x): [f (x)+C]' = g(x) Przykłady:

n

1

x dx =

x n 1

+

∫

+ C

n + 1

∫ ex dx = ex + C

∫ (1/x) dx = ln x + C

∫ cos x dx = sin x + C

∫ sin x dx = - cos x + C

Całka oznaczona: Niech :

∫ g( x) dx = f ( x) + C

przyrost funkcji pierwotnej na przedziale [a,b]: b

f b

( ) − f ( a) = [ f b ( ) + C]− [ f ( a) + C] = ∫

b

g( x) dx

= g( x) dx

a

∫

a

nazywamy całką oznaczoną.

CZYLI CAŁKA OZNACZONA TO:

b

∫ g( x) dx = f ( b) − f ( a) gdzie:

∫ g( x) dx = f ( x) + C

a

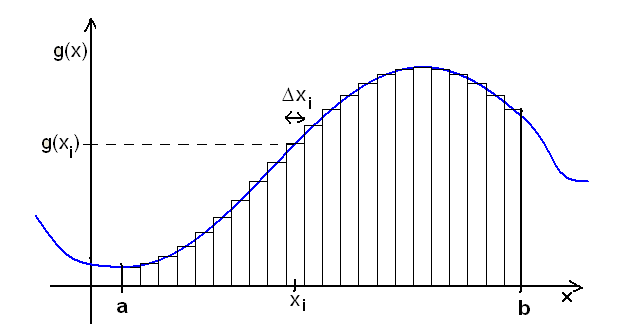
Znaczenie całki oznaczonej:

f

∆ ( xi

g( x ) =

)

f '( x ) =

lim

∆ ( ) = ( )∆

i

i

∆

f x

g x

x

x

i

i

i

i

x

∆ → 0

i

b

N

N

∫ g( x) dx = f b ( ) − f ( a) =

lim

∑ f

∆ ( x ) = lim ∑ g( x ) x

∆ = S

i

i

i

a

x

i

∆ → 0

x

i

∆ → 0

i

i

b

S = ∫ g( x) dx a