1

Wstawka matematyczna

1. Rachunek wektorowy

Wszystkie prawa fizyki mają taka samą
postać w dowolnym inercjalnym

.

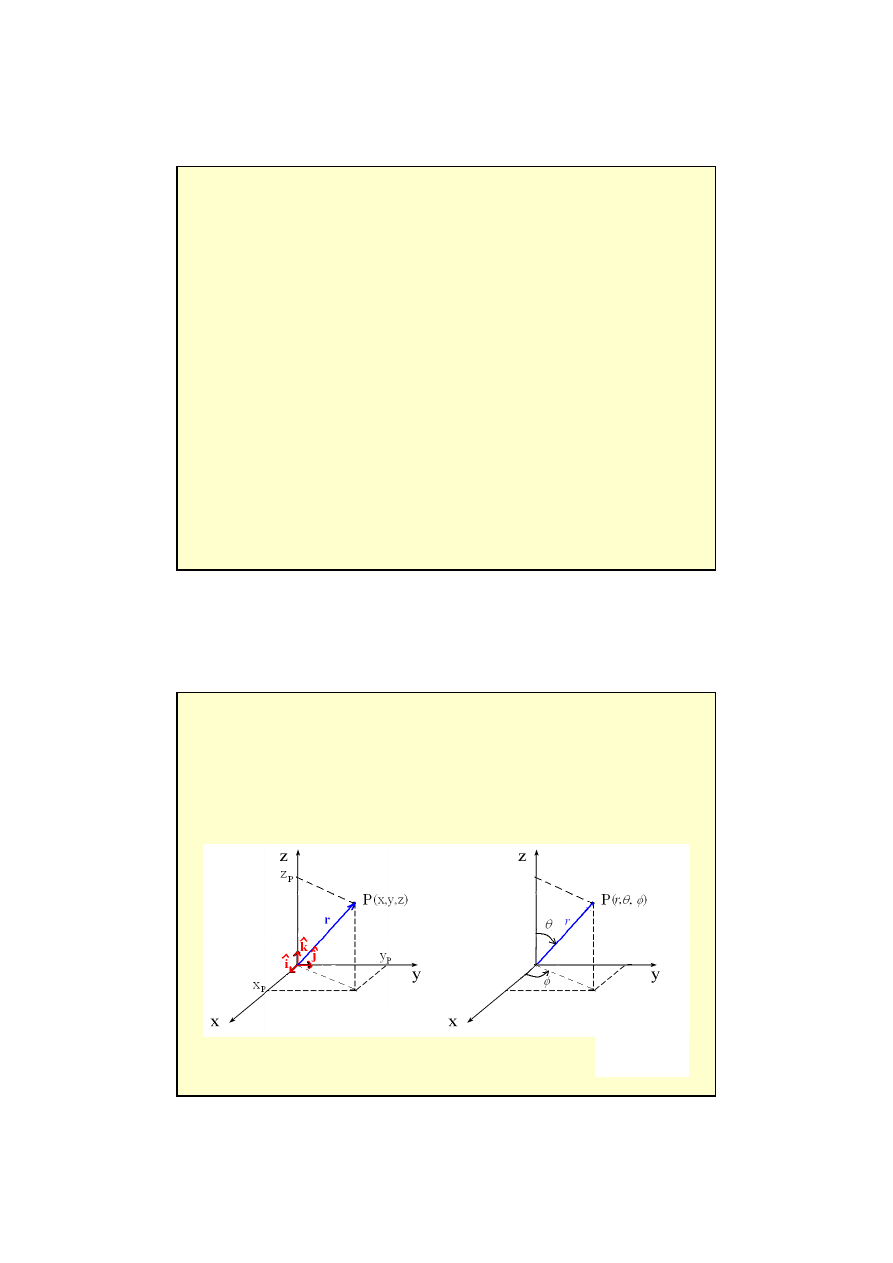
układ kartezjański

układ sferyczny

k

j

i

r

ˆ

ˆ

ˆ

z

y

x

+

+

=

θ

φ

θ

φ

θ

cos

sin

sin

cos

sin

r

z

r

y

r

x

=

=

=

2

położenie r

prędkość v

przyspieszenie a

pęd p

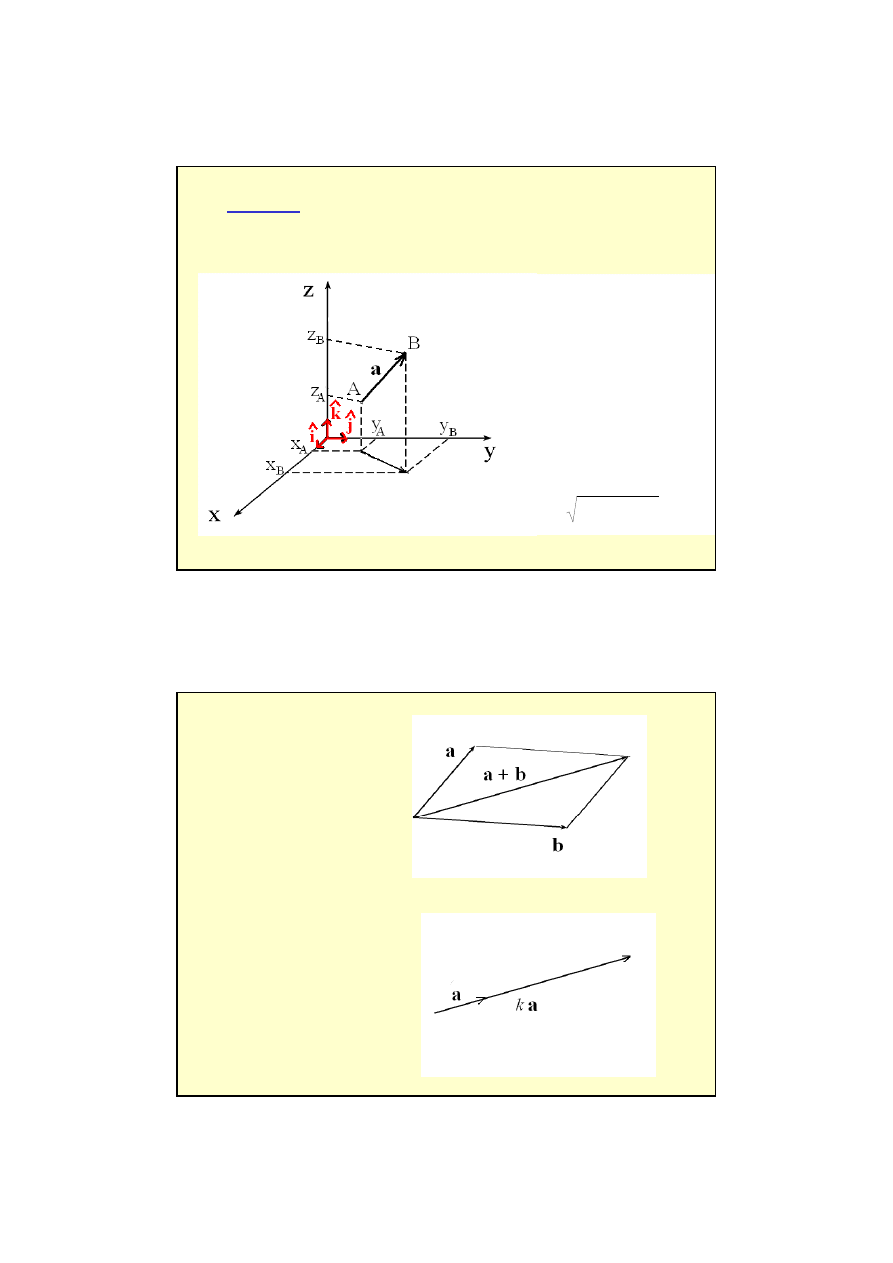
a

x

=x

B

-x

A

, a

y

=y

B

-y

A

, a

z

=z

B

-z

A

AB = a = [ a

x

, a

y

, a

z

]

k

j

i

a

ˆ

ˆ

ˆ

z

y

x

a

a

a

+

+

=

wektory

długo

ść

wektora:

a

x

=b

x

, a

y

=b

y

, a

z

=b

z

.

współrz

ę

dne wektorów:

równo

ść

wektorów:

2

2

2

z

y

x

a

a

a

a

+

+

=

dodawanie wektorów:

mno

ż

enie wektora

przez liczb

ę

:

a + b = c

c

x

=a

x

+b

x

, c

y

=a

y

+b

y

, c

z

=a

z

+b

z

c

x

= k a

x

, c

y

= k a

y

, c

z

= k a

z

c = k a

3

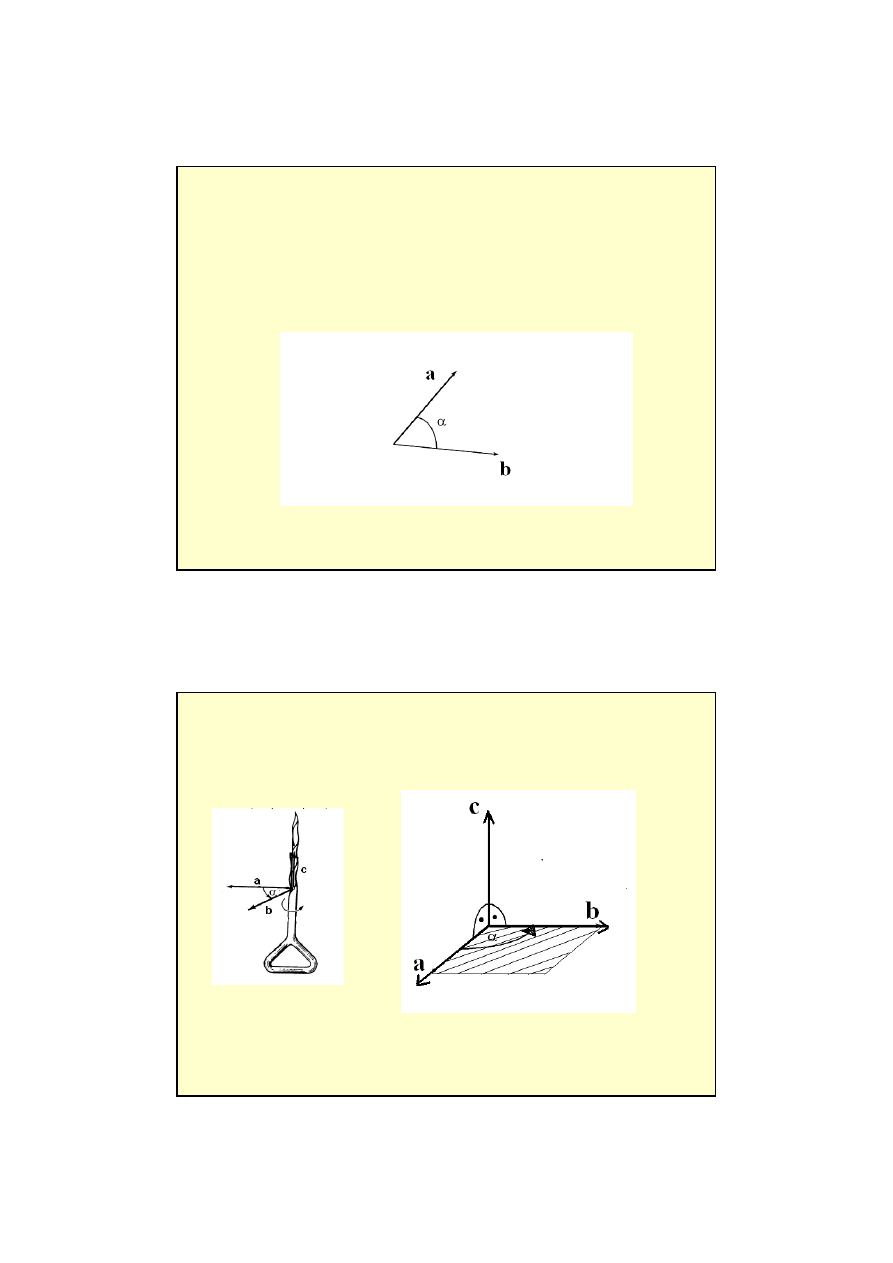
iloczyn skalarny wektorów:

a—

—

—

—b = a b cos

α

a—

—

—

—b =a

x

b

x

+ a

y

b

y

+ a

z

b

z

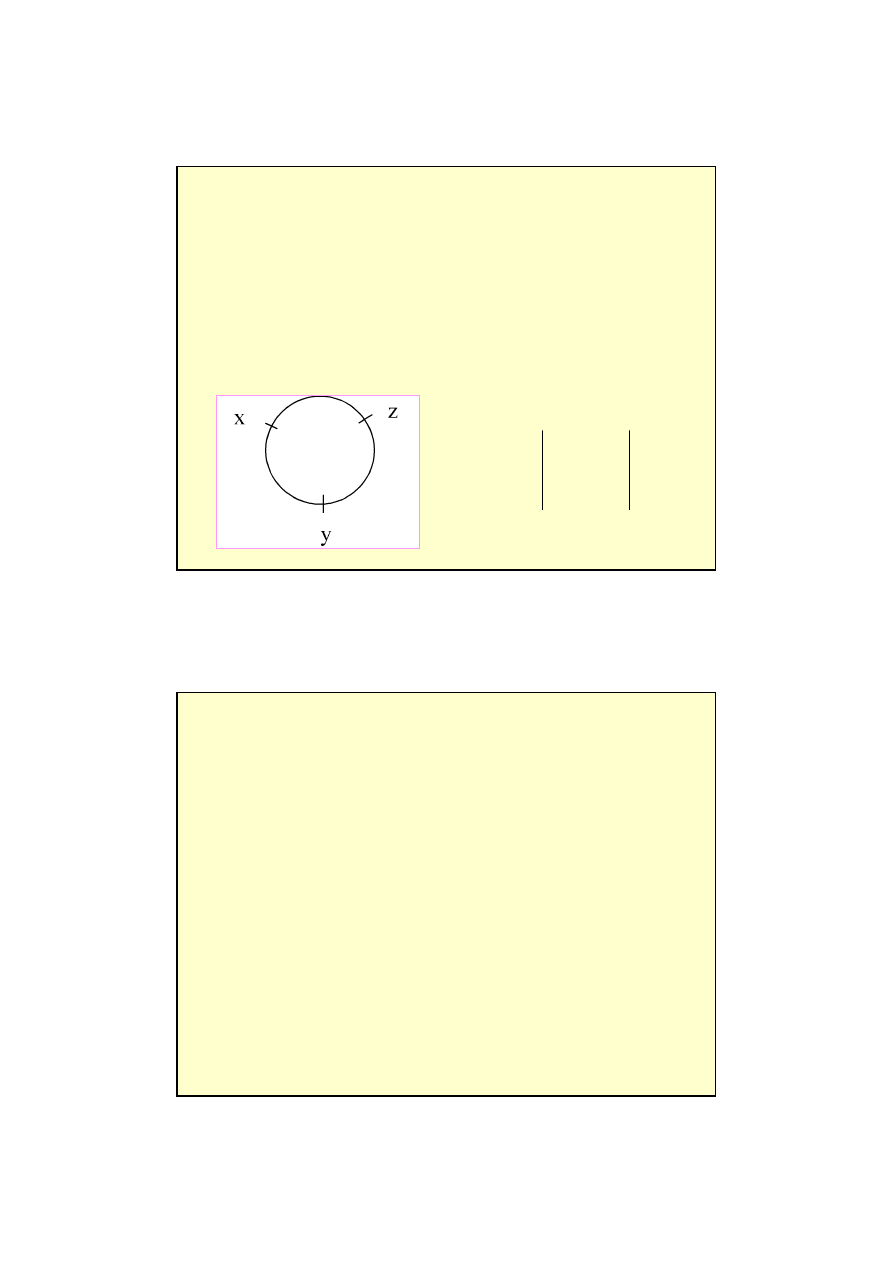
iloczyn wektorowy :

a x

x

x

x b = c

c=a b sin

α

4

c

x

=a

y

b

z

- a

z

b

y

c

y

=a

z

b

x

– a

x

b

z

c

z

=a

x

b

y

– a

y

b

x

Konwencja:

z

y

x

z

y

x

b

b

b

a

a

a

k

j

i

c

ˆ

ˆ

ˆ

=

a x

x

x

x b = c

iloczyn wektorowy (współrz

ę

dne):

k

j

i

c

ˆ

ˆ

ˆ

z

y

x

c

c

c

+

+

=

Wstawka matematyczna

2. Pochodne i całki

5

x

x

f

x

x

f

dx

df

x

f

x

∆

−

∆

+

=

=

→

∆

)

(

)

(

lim

)

(

'

0

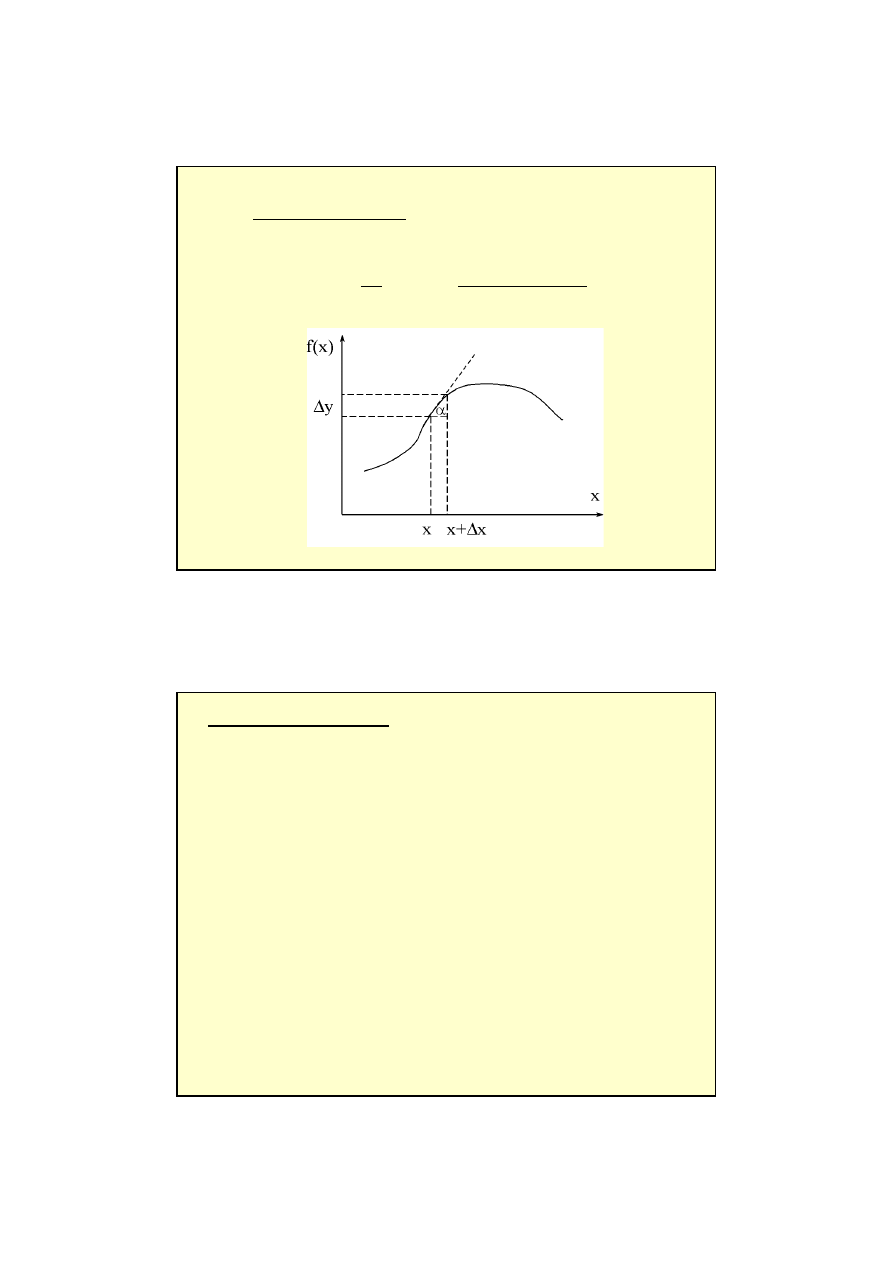
Pochodna funkcji f(x)

Pochodna funkcji f(x)

Podstawowe własności pochodnej :
(g + f)' = g ' + f '
(g f)' = gf ' + fg '
(g/f)' = (g ' f – f ' g) / f

2

[ f (g(x)) ] ' = f '(u) g '(x) = f ' [g(x)] g'(x)

( gdzie: u=g(x) )

Przykłady:
(x

n

)' = n x

n-1

(ln x)' = 1/x (x>0)
(sin x)' = cos x
(cos x)’= - sin x
(e

x

)' = e

x

6

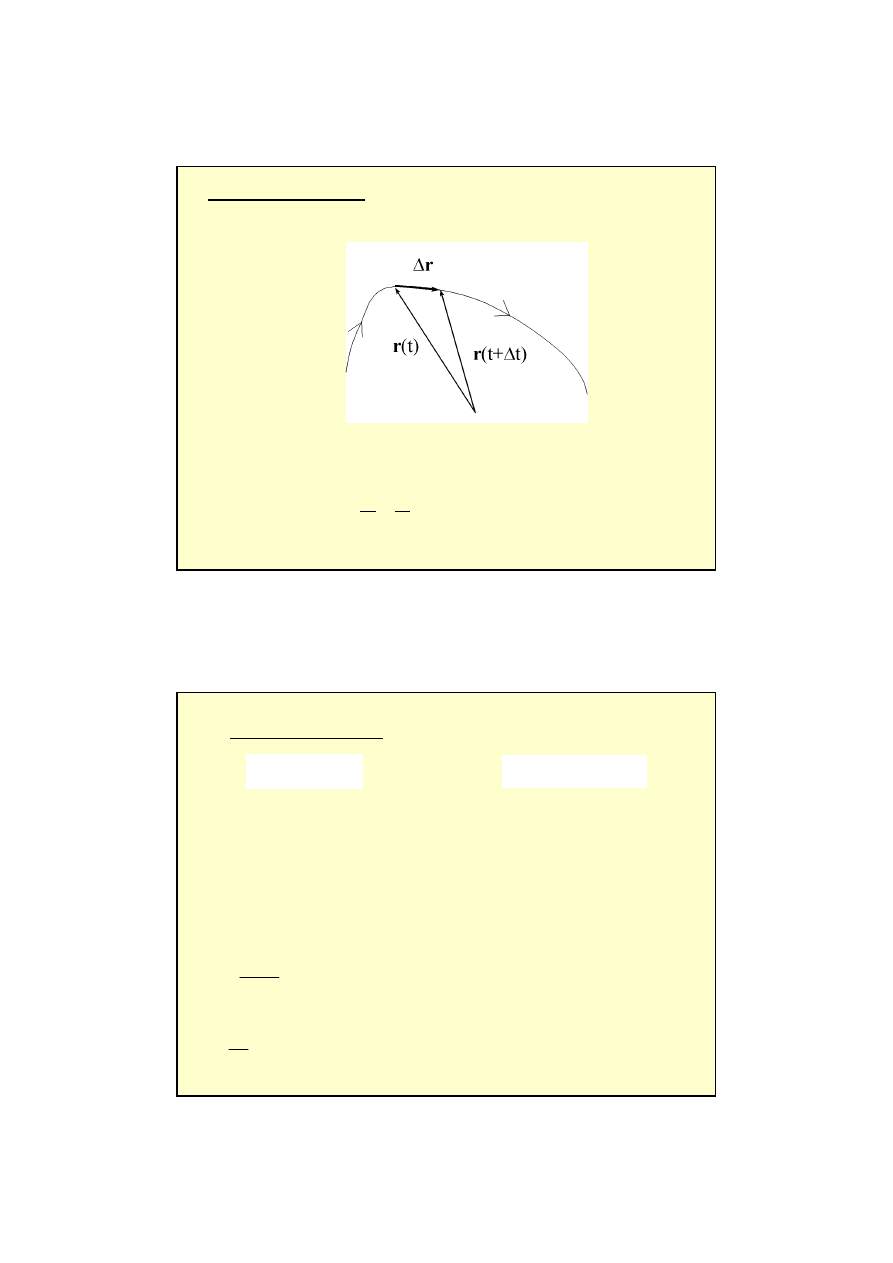
W przedziale czasu

∆

t przyrost wektora r(t) wynosi

∆

r:

∆

r = r(t+

∆

t) – r(t),

to stosunek:

dt

d

t

r

r

→

∆

∆

(gdy

∆

t

→

0)

Pochodna wektora

Całka nieoznaczona

∫

=

)

(

)

(

x

f

dx

x

g

Wynik operacji całkowania:
znaleziona funkcja f(x) ma taką własność, że po zróżniczkowaniu jej
otrzymujemy funkcję podcałkową g(x):

[f (x)+C]' = g(x)

C

x

f

dx

x

g

+

=

∫

)

(

)

(

ściślej:

C

x

f

dx

dx

x

df

+

=

∫

)

(

)

(

inaczej:

oraz:

∫

=

)

(

)

(

x

g

dx

x

g

dx

d

7

∫ e

x

dx = e

x

+ C

∫ (1/x) dx = ln x + C

∫ cos x dx = sin x + C

∫ sin x dx = - cos x + C

Przykłady:

C

x

1

n

1

dx

x

1

n

n

+

+

=

+

∫

Całka oznaczona:

[

] [

]

∫

∫

=

=

+

−

+

=

−

b

a

b

a

dx

x

g

dx

x

g

C

a

f

C

b

f

a

f

b

f

)

(

)

(

)

(

)

(

)

(

)

(

C

x

f

dx

x

g

+

=

∫

)

(

)

(

Niech :

przyrost funkcji pierwotnej na przedziale [a,b]:

nazywamy całką oznaczoną.

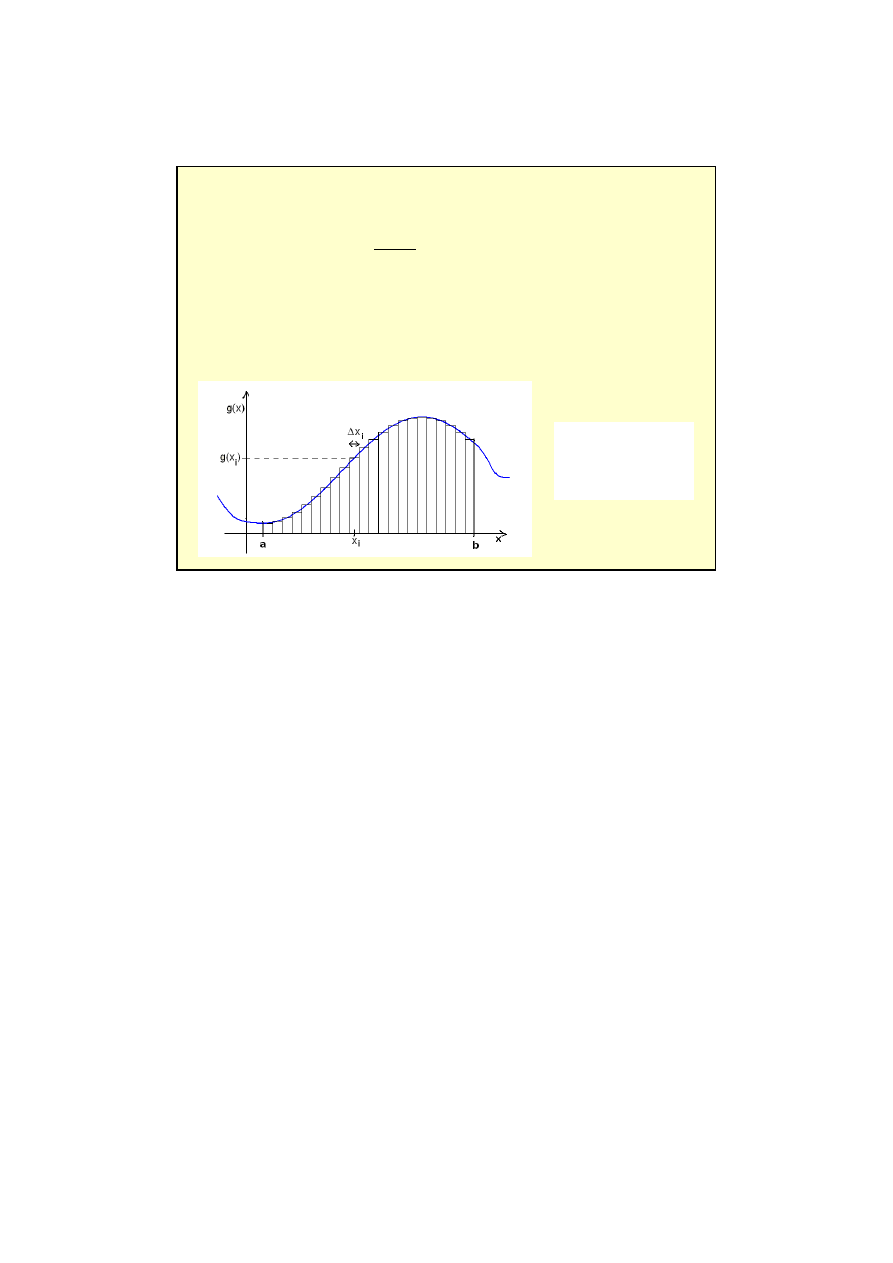
8

S

x

x

g

x

x

f

x

a

f

b

f

dx

x

g

i

N

i

i

i

N

i

i

i

b

a

=

∆

→

∆

=

∆

→

∆

=

−

=

∑

∑

∫

)

(

0

lim

)

(

0

lim

)

(

)

(

)

(

Znaczenie całki oznaczonej:

i

i

i

i

i

x

x

f

x

x

f

x

g

∆

∆

→

∆

=

=

)

(

0

lim

)

(

'

)

(

i

i

i

x

x

g

x

f

∆

=

∆

)

(

)

(

∫

=

b

a

dx

x

g

S

)

(