Filia Jelenia Góra, Technika Analogowa (Teoria Obwodów), Zestaw Zadań nr 4

4.1 Narysuj następujące funkcje oraz wyznacz ich transformaty Laplace’a:

−

−

−

−

−

−

a)

2 t

e 1( t)

b)

2( t 1)

e

1( t)

c)

2 t

e 1( t −1) d)

2( t 1)

e

1( t −1) .

4.2 Wyznacz transformaty Laplace’a następujących funkcji: a)

b)

f( t)

f( t)

 π 

1

5 c o s 

t 

 2 

5

t

t

0

1

3

5

0

1

2

3

4

5

−

−

c) ( + )

1

t

t

e 1( t)

d) ( t + )2

2 1( t −1)

e) sin(ω t + ϕ )1( t) f)

3 t

te

sin(2 t)1( t) .

0

4.3 Wyznacz odwrotne transformaty Laplace’a następujących funkcji: 2

2 s + 3

s + 2

3

s

1

( s + )1

a)

d)

e)

2

s + s +

b)

2

3

s +

c)

s

(

2

2

3

s + )2

2

1

3 s ( s + 4) ( s + 2)

2

s − 2 s + 2

− s

−2 s

e

+ e

s + 2

s +1

f)

h)

3

2

s + s + 4 s +

g)

4

(

4

3

2

s + )( s + )2

1

2

s + 5 s + 7 s +

i)

3 s

( s + 2)( 2 s + s + )1

1

( s + 2)( s + 4) 2

s − s +1

−2 s

e

−1

j) (

k)

.

2

s + )3

1 ( s + 2)

( s + )1( s +3)( s +

l)

5)

s + 2 s +

m)

4

s ( s + )

1

4.4 Wyznacz składowe przejściową i ustaloną. Klucz K zwarto w chwili t = 0. Warunki początkowe są zerowe.

t = 0

R 1

K

R 2

E

L u( t) = ?

C

E = 2 , R 1 = R 2 = 1, C = 1, L = 1

4.5 W obwodzie panował stan ustalony. W chwili t = 0 klucz K zwarto. Wyznacz napięcie u C( t) dla t ≥ 0. Dane: Iz = 3 A = const, R 1 = 2 Ω, R 2 = 1 Ω, L = 2 H, C = ½ F.

K

R1

I

R

z

2

uc( t)

C

L

4.6 Klucz K znajdował się nieskończenie długo w położeniu 1. W chwili t = 0 klucz K przełączono w położenie 2.

Wyznacz napięcie u( t) dla t ≥ 0.

R2

E = 4 = const. ,

e (t) = 5e-t 1(t), R

L

1 = 1, R2 = 2/3,

R1

t=0

L =1, C = 1/3.

K

C

u( t) = ?

1

2

E

e(t)

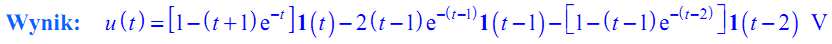
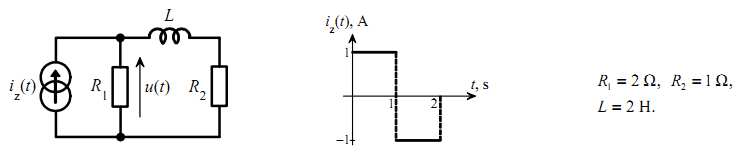
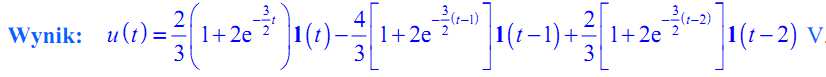
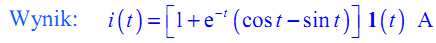
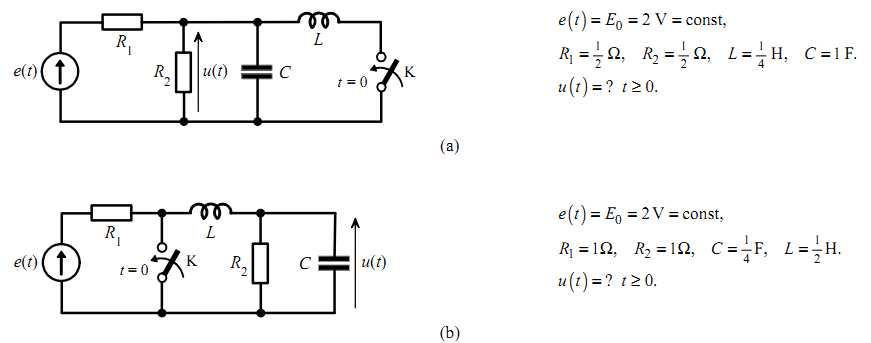
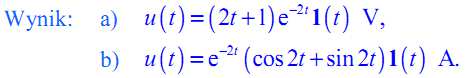
4.7 Wyznacz napięcie u( t), warunki początkowe są równe zero.

4.8 Wyznacz napięcie u( t), warunki początkowe są równe zero.

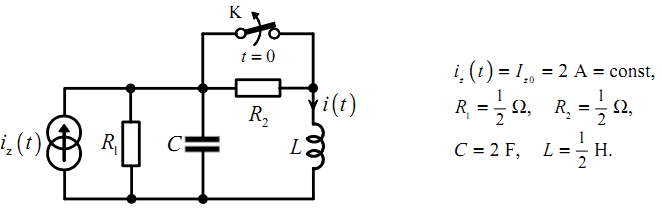
4.9 Klucz K był nieskończenie długo zwarty. W chwili t = 0 klucz K rozwarto. Wyznacz prąd i( t) dla t ≥ 0.

4.10 Klucz K był nieskończenie długo rozwarty. W chwili t = 0 klucz K zwarto. Wyznacz napięcie u( t) dla t ≥ 0.