LOGISTYKA

Sterowanie zapasami w

warunkach braku ci

ą

gło

ś

ci

(Technika WAGNERA-WITHINA)

Sterowanie zapasami w

warunkach braku ci

ą

gło

ś

ci

W sytuacjach gdy obserwuje si

ę

brak ci

ą

gło

ś

ci

popytu (potrzeb) lub du

ż

e jego wahania, wła

ś

ciwymi

metodami

dokonywania

zakupów

s

ą

metody

zaprojektowane przez autorów H.M. Wagnera i T.M.
Withina

Optymalne partie zakupów – wg wskazania metody
- s

ą

wielko

ś

ciami zmiennymi obejmuj

ą

cymi ró

ż

ne

horyzonty zakupu

Horyzonty

te

s

ą

wyznaczane

odpowiednio

do

kształtowania

si

ę

prognozowanego

popytu

lub

planowanych

potrzeb

w

ustalonych

krótszych

odcinakach (np. miesi

ą

cach) i kosztów zwi

ą

zanych z

tworzeniem i utrzymaniem zapasów

Metoda Wagnera - Withina

Metoda

ta

obejmuje

procedur

ę

optymalizacyjn

ą

opart

ą

na

modelu

programowania dynamicznego.

Celem

metody

jest

znalezienie

optymalnej

strategii

zamawiania

dla

całego planu

potrzeb

netto

poprzez

zminimalizowanie

ł

ą

cznych

kosztów

zaopatrzenia i utrzymania zapasu.

Wprowadzamy nast

ę

puj

ą

ce

zało

ż

enia i oznaczenia

1.

Przez y

t

oznaczamy potrzeby (popyt) w okresie „t” (t= 1, 2,

…, N), gdzie N jest horyzontem planu

2.

Dostawa zamówionych partii nast

ę

puje na pocz

ą

tku

ustalonych krótszych okresów

3.

Cena zakupu nie zale

ż

y od wielko

ś

ci dostawy

4.

Oszacowane koszty tworzenia i utrzymywania zapasów nie
ulegaj

ą

zmianie na przestrzeni danego roku planowanego,

5.

Rozpatrywany materiał jest zamawiany indywidualnie

6.

Okres realizacji zamówie

ń

jest znany i stały

7.

Polityka zakupów jest prowadzona w sposób nie
dopuszczaj

ą

cy zaistnienia sytuacji wyczerpania zapasów

8.

Dostawy nast

ę

puj

ą

jednorazowo na cała zamówiona ilo

ść

9.

Koszt utrzymania zapasów odnosi si

ę

tylko do tej ilo

ś

ci,

która przechodzi na nast

ę

pny okres

Dodatkowe zało

ż

enia

A.

Zamówienie

jest

wystawiane

jedynie

wówczas gdy poziom zapasu na koniec
danego przedziału sterowania ma osi

ą

gn

ąć

stan zerowy

B.

Istnieje pewna granica opłacalno

ś

ci wł

ą

czania

do

opracowanego

zamówienia

potrzeb

materiałowych, które wyst

ę

puj

ą

w dalszych

okresach. Granica ta wyznacza horyzont
zakupu poza który nie nale

ż

y ”wychodzi

ć

”.

Przykład -

Dla i-tego miesi

ą

ca nale

ż

y

znale

źć

minimum kosztów i-wariantów

Niech F (t) oznacza ł

ą

czne koszty najlepszej

polityki zakupów, zaspokajaj

ą

cej potrzeby w

okresach l, 2, ..., t. Potrzeby produkcyjne na
pewn

ą

odkuwk

ę

w okresie: stycze

ń

– grudzie

ń

2008 wykazane w tabeli. Odpowiednie koszty
tworzenia i utrzymania zapasu wynosz

ą

:

koszt tworzenia zapasu (zakupu) K

z

= 54 zł,

jednostkowa cena zakupu C

z

= 20 zł,

stopa

rocznego

jednostkowego

kosztu

utrzymania zapasu r = 24%, => zatem
roczny koszt

utrzymania

zapasu

jednej

odkuwki jest równy: K

u

= r • C

z

= 0,24 • 20zł

= 4,8 zł,

jednostkowy miesi

ę

czny koszt utrzymania

zapasu:

4

,

0

12

8

,

4

12

.

,

=

=

=

u

mies

u

K

K

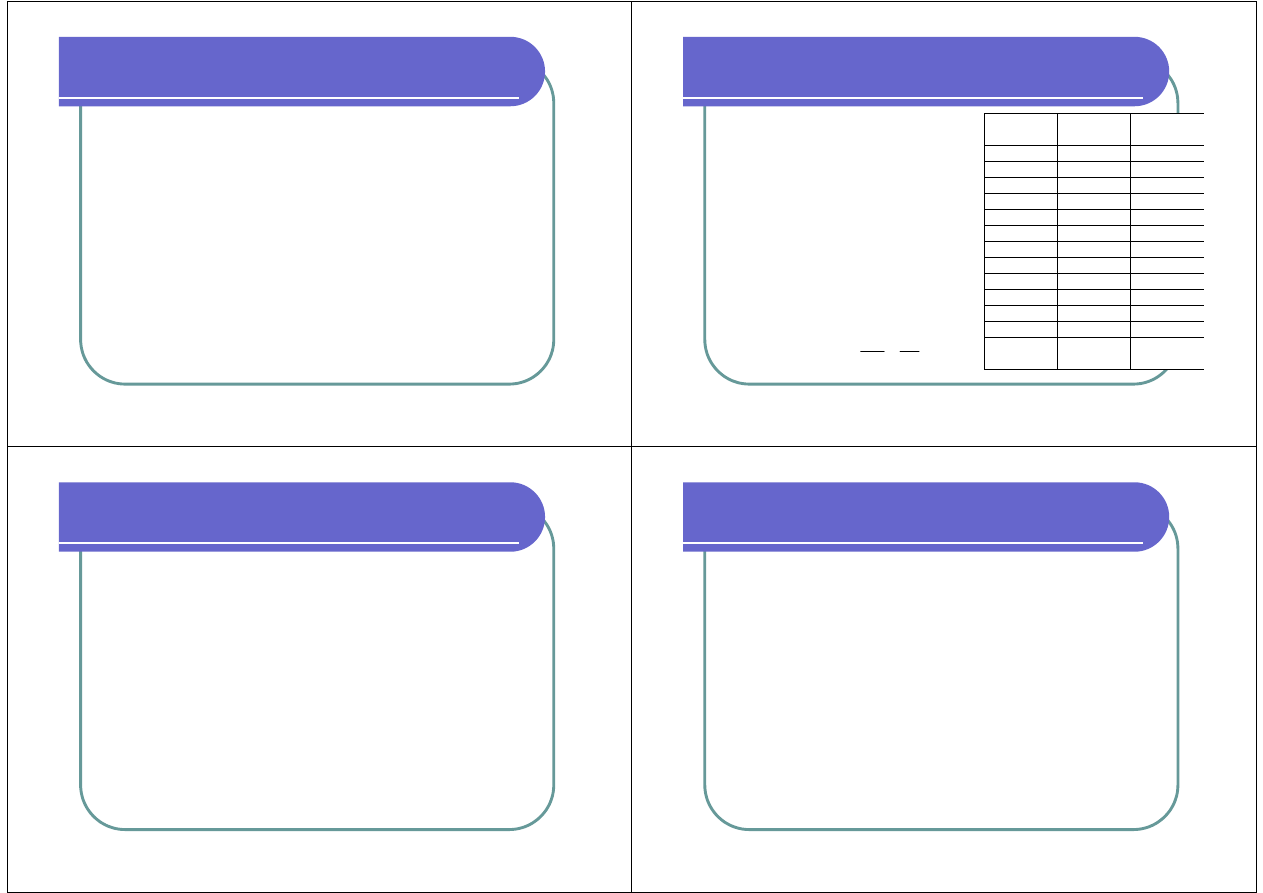
Miesiąc

Kolejny numer

(t)

Potrzeby (y

t

)

Styczeń

1

10

Luty

2

62

Marzec

3

12

Kwiecień

4

130

Maj

5

154

Czerwiec

6

129

Lipiec

7

88

Sierpień

8

52

Wrzesień

9

124

Październik

10

160

Listopad

11

238

Grudzień

12

41

Razem 921

szt.

Ł

ą

czne koszty polityki zakupów dla t=1

t=1 => F(1) = K

z

= 54 zł

Ł

ą

czne koszty optymalnej polityki zakupów

(ŁKZ) dla t = 1 s

ą

równe, oczywi

ś

cie,

tylko kosztowi zakupu styczniowej partii,

(koszt utrzymania zapasu jest liczony

dopiero wówczas, gdy zapas przechodzi

na nast

ę

pny miesi

ą

c - por. zało

ż

enie 9).

Ł

ą

czne koszty polityki zakupów dla t=2

Wariant I

Zakup w dwóch partiach

o wielko

ś

ciach

odpowiadaj

ą

cych

potrzebom stycznia

(Q=10) i lutego (Q=62)

ŁKZ

wI

= F(1)+K

z

=

=54+54=104

Wariant II

Jednorazowy zakup

obejmuj

ą

cy ł

ą

czne potrzeby

stycznia i lutego (Q=72)

ŁKZ

wII

=K

z

+1•Ku,mies.•y

2

=

= 54+1•0,4•62= 78,8

√

Ł

ą

czne koszty polityki zakupów dla t=3

Wariant I

Optymaln

ą

ustalon

ą

wcze

ś

niej polityk

ę

zakupu

dla horyzontu t=2 oraz

oddzielnie zakup marcowy

=> dokonanie dwóch

zakupów dla Q

1

=72 oraz

Q

2

=12

ŁKZ

wI

= F(2)+K

z

=

78,8+54=132,8

Wariant II

Ł

ą

czny zakup dla trzech

pierwszych miesi

ę

cy(Q=84)

ŁKZ

wII

=K

z

+1•Ku,mies.•y

2

+2•Ku,mies.•y

3

=

=54+1•0,4•62+2•0,4•12= 88,4

√

Uproszczenie

Dla potrzeb bardzo zróżnicowanych w czasie, ale

ciągłych (tzn. charakteryzujących się tym, że y

t

> O dla

każdego „t" ), Wagner i Within formułują następującą,
oczywistą zresztą, zasadę:

Jeżeli potrzeby w okresie „t" są tak duże, iż:

y

t

K

u,mies.

> K

z

czyli

wielkość graniczna (WG)

wówczas rozwiązaniem optymalnym będzie zakup

(dostawa) tej ilości (y

t

) na początku danego okresu

planowego „t".

=

>

.

,mis

u

z

t

K

K

y

135

4

,

0

54

.

,

=

=

=

mies

u

z

K

K

WGU

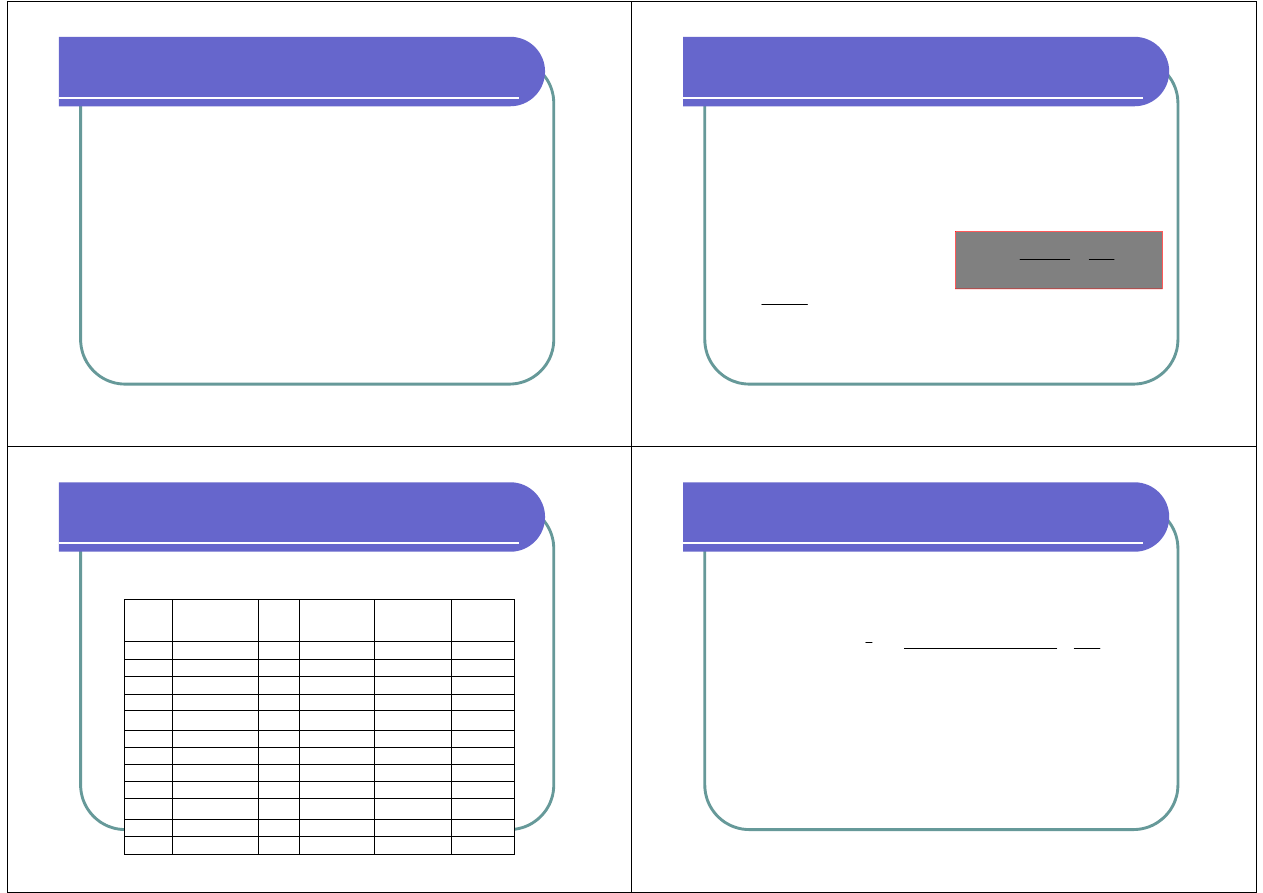
Przykład C.D.

Zestawienie optymalnej polityki zakupów (sterowania zapasami)
dla rozpatrywanego przykładu przedstawia poni

ż

sza tabela

Miesiąc

Zapas

początkowy

Zakup

Potrzeby (y

t

) Zapas końcowy

Dokonano

zakupu

1

0

84

10

74

√

2

74

0

62

12

3

12

0

12

0

4

0

130

130

0

√

5

0

283

154

129

√

6

129

0

129

0

7

0

140

88

52

√

8

52

0

52

0

9

0

124

124

0

√

10

0

160

160

0

√

11

0

279

238

41

√

12

41

0

41

0

Przykład C.D.

Rezultaty takiej polityki zakupów s

ą

nast

ę

puj

ą

ce:

ś

redni zapas w okresie 12 miesi

ę

cy:

liczba zakupów: n

opt

=7,

ł

ą

czne koszty zakupów: ŁK

Z

=K

z

• n

opt

=54 • 4=378 zł,

ł

ą

czne koszty utrzymania zapasów:

ŁK

U

= 4,8 • 25,57= 123,20 zł,

tak wice ł

ą

czne koszty zapasów wynosz

ą

:

ŁKZ = 378 + 123,20 =501,20 zł

67

,

25

12

308

12

41

52

129

12

74

,

≈

=

+

+

+

+

=

k

s

Wady i zalety

Algorytm

Wagnera-Whitina

uwzgl

ę

dnia

zmiany

kosztów zakupu materiałów w rozpatrywanym okresie,
a tak

ż

e zmiany kosztów utrzymania zapasów.

Wad

ą

algorytmu jest jednak zało

ż

enie, dotycz

ą

ce

zerowych warto

ś

ci pozycji zapasów w okresie t = 0

oraz t = T+1, czyli w okresach poprzedzaj

ą

cym i

nast

ę

puj

ą

cym

po

rozpatrywanym

przedziale

czasowym. Uwzgl

ę

dnienie zmiennych warto

ś

ci

w

okresie nast

ę

puj

ą

cym t = T+1 wymaga wł

ą

czenia tego

okresu

do

przedziału

czasowego,

w

którym

dokonujemy ustalenia wielko

ś

ci partii dostawy. Zapas

z okresu poprzedzaj

ą

cego pierwszy z rozpatrywanych,

tj. okresu t = 0, musi zosta

ć

uwzgl

ę

dniony w postaci

obni

ż

enia wielko

ś

ci zapotrzebowania na pierwsze

okresy rozpatrywanego przedziału czasowego.