1

00531 Fale mechaniczne, part 2 D

TEORIA

00531

Fale mechaniczne, część 2 D

Podstawowe cechy dźwięków.

Efekt Dopplera.

Zjawisko interferencji i dyfrakcji fali.

Zasada Huygensa.

Energia fal dźwiękowych.

Instrukcja dla zdającego
1.

Proszę sprawdzić, czy arkusz teoretyczny zawiera 10
stron. Ewentualny brak należy zgłosić.

2.

Do arkusza może być dołączona karta wzorów i sta-
łych fizycznych. Jeśli jest, należy ją dołączyć do od-
dawanej pracy.

3.

Proszę uważnie i ze zrozumieniem przeczytać zawar-
tość arkusza.

4.

Proszę precyzyjnie wykonywać polecenia zawarte w
arkuszu: rozwiązać przykładowe zadania, wyprowa-
dzić wzory, gdy jest takie polecenie.

5.

Proszę analizować wszelkie wykresy i rysunki pod
kątem ich zrozumienia.

6.

W trakcie obliczeń można korzystać z kalkulatora.

7.

Wszelkie fragmenty trudniejsze proszę zaznaczyć w
celu ich późniejszego przedyskutowania.

8.

Uzupełniaj wiadomości zawarte w arkuszu o informa-
cje zawarte w Internecie i dostępnej ci literaturze.

ś

yczymy powodzenia!

(Wpisuje zdający przed rozpoczęciem pracy)

PESEL ZDAJĄCEGO

Aktualizacja

Styczeń

ROK 2009

Dane osobowe właściciela arkusza

2

00531 Fale mechaniczne, part 2 D

TEORIA

Temat 148

Podstawowe cechy dźwięków.

1.

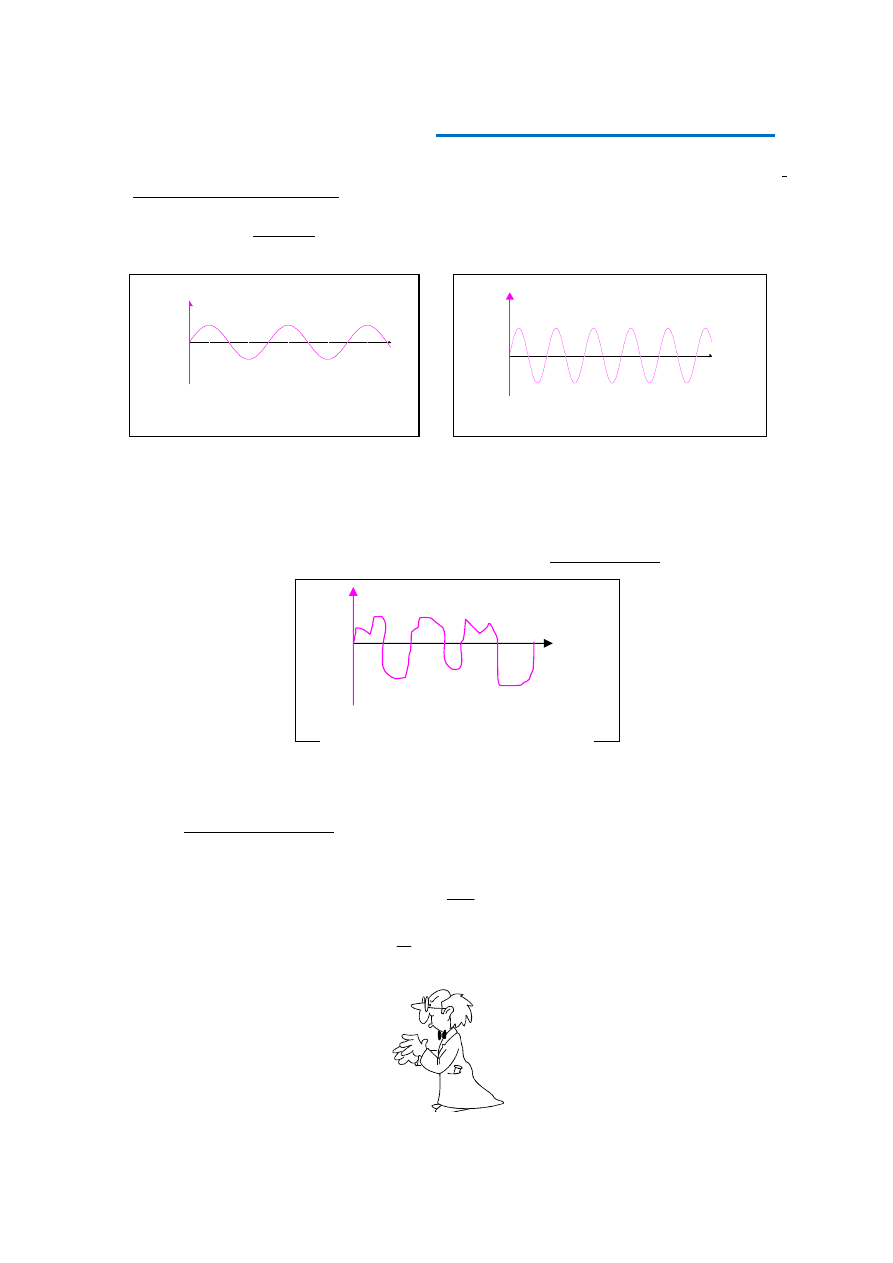
Na podstawie subiektywnych wrażeń słuchowych przypisujemy dźwiękom trzy cechy:,
wysokość, barwa i głośność:

a)

fizyczną miarą wysokości dźwięku jest częstotliwość fali dźwiękowej, przy czym dźwięk jest tym wyższy
im większa jest jego częstotliwość: (rys. 1a i 1b).

b)

dźwięki o jednakowej wysokości wydawane przez różne źródła wywołują odmienne
wrażenia słuchowe. Różnice spowodowane są charakterystycznym dla danego źródła
dźwięku nakładaniem się na podstawowe drgania harmoniczne drgań harmonicznych
o większych częstotliwościach i określone są mianem barwy dźwięku (rys. 2).

c)

d)

miarą intensywności dźwięku, tj. cechą odróżniającą dźwięki silne od słabych, jest je-
go natężenie (głośność), czyli ilość energii E przenoszonej przez falę dźwiękową w
jednostce czasu t przez jednostkę powierzchni fali S. Gdy powierzchnia jest prostopa-
dła do promienia fali, wtedy:

(1)

t

S

E

I

⋅

=

lub

(2)

S

P

I

=

, gdzie P – moc fali

x

0.5 π

1π

1 .5π

2π

2 .5 π

3 π

3 .5 π

4 π

4.5π

5π

- 1

0

1

y

t

Rys. 1a Ton „niski”.

x

1π

2π

3π

4π

5π

6π

7π

8π

9π

10π

-1

0

1

t

y

Rys. 1b Ton „wysoki”

Rys. 2 Dźwięk o złożonej barwie.

3

00531 Fale mechaniczne, part 2 D

TEORIA

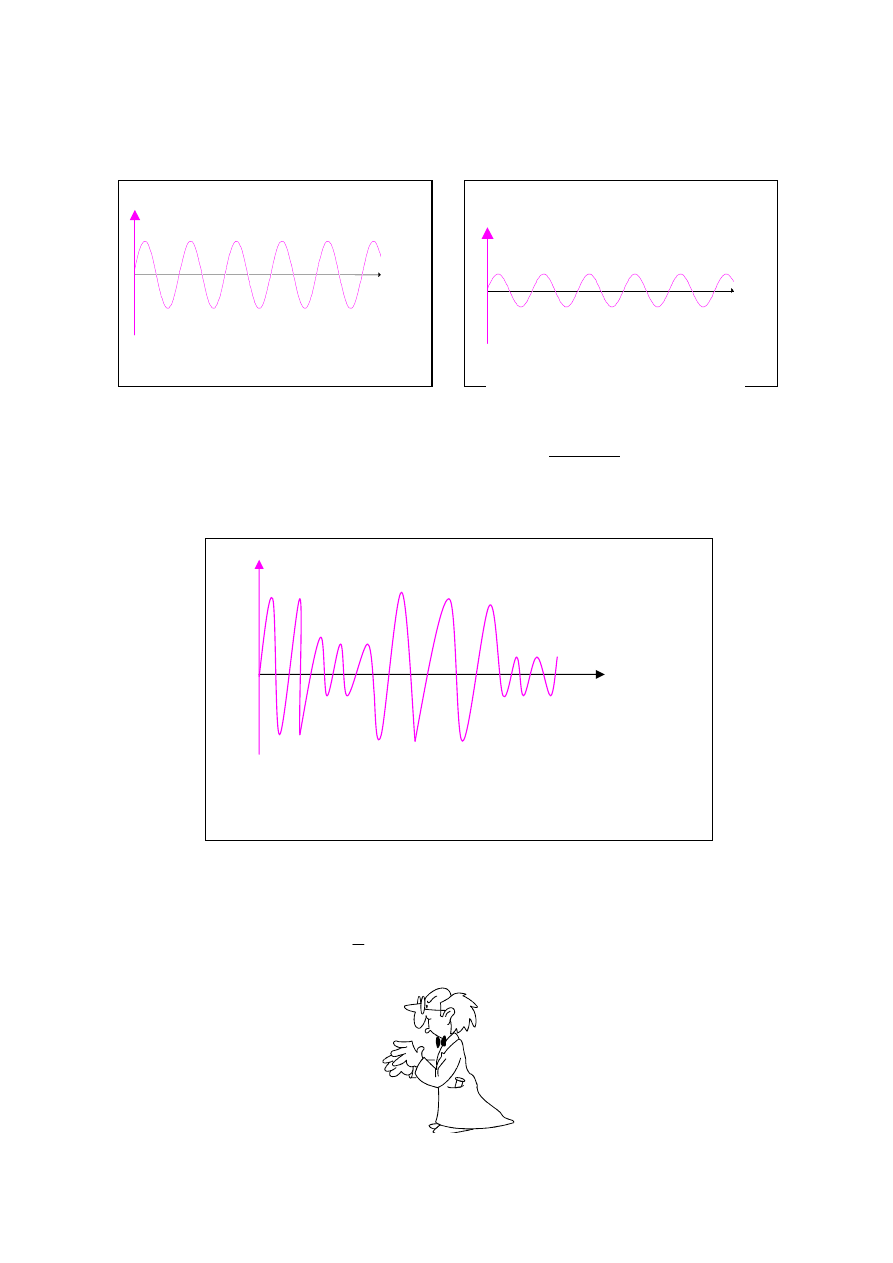
Badania wykazały, że natężenie dźwięku jest proporcjonalne do kwadratu amplitudy fali,
dlatego dźwięki słabe różnią się od silnych przede wszystkim amplitudą fali (rys. 3a i b).

2.

W wyniku nakładania się dwóch fal dźwiękowych o zbliżonych, lecz nie jednakowych
częstotliwościach występuje charakterystyczne zjawisko dudnienia, które polega na okre-
sowym osłabianiu i wzmacnianiu natężenia dźwięku. Przyczyną tego zjawiska jest okre-
sowy wzrost i spadek amplitudy fali wypadkowej (rys. 4) spowodowany nakładaniem się
wychyleń interferujących fal.

3.

Stosunek prędkości źródła dźwięku v (np. pocisku) do prędkości u wytworzonej fali
dźwiękowej nosi nazwę liczby Macha mającej zastosowanie m.in. w lotnictwie.

(3)

u

v

M

=

Określenie liczby Macha

x

1π

2π

3π

4π

5π

6π

7π

8π

9π

10π

-1

0

1

Rys. 3a Dźwięk „silny”.

x

1π

2π

3π

4π

5π

6π

7π

8π

9π

10π

-2

0

2

Rys. 3a Dźwięk „słaby”.

Rys. 4 Zjawisko dudnienia, czyli okresowe wzmacnianie się i
osłabianie wypadkowej dwóch fal o zbliżonych częstotliwo-
ś

ciach.

4

00531 Fale mechaniczne, part 2 D

TEORIA

Temat 149

Efekt (zjawisko) Dopplera.

1.

Ani zjawisko odbicia, ani zjawisko załamania nie mają wpływu na częstotliwość odbiera-
nego tonu. Zmiana częstotliwości tonu odbieranego w stosunku do częstotliwości tonu
nadawanego występuje w przypadku ruchu źródła, ruchu obserwatora lub też obu naraz
względem ośrodka, w którym rozchodzi się fala dźwiękowa. Mimo, że zjawisko to, znane
pod nazwą efektu Dopplera, występuje we wszystkich rodzajach ruchu falowego, omó-
wimy je dokładnie w odniesieniu do fal głosowych, gdyż w tej dziedzinie znamy je ogól-
nie z naszych codziennych obserwacji.

Każdy z nas niejednokrotnie miał okazję stwierdzić dość gwałtowną zamianę wysokości
odbieranego tonu w momencie, gdy poruszające się źródło dźwięku nas wymija. Zmienia
się wysokość tonu gwizdka przejeżdżającego obok nas parowozu, zmienia się wysokość
tonu syreny mijającego nas samochodu itp.
Następujące rozumowanie pozwoli ustalić zależność między częstotliwością f tonu wysy-
łanego, częstotliwością f’ tonu odbieranego oraz prędkościami: źródła v

z

, obserwatora v

0

i

głosu v

g

.

Załóżmy początkowo, , że źródło głosu i obserwator (rys. 1) poruszają się wzdłuż tej sa-
mej prostej w tym samym kierunku. Niech punkt Z przedstawia położenia źródła w chwili
nadania pierwszego sygnału akustycznego. Punkt O niech wyobraża położenie obserwato-
ra w chwili odbioru sygnału. Odległość ZO jest drogą przebytą przez falę głosową w pew-
nym czasie t

1

, a zatem:

(Wyprowadzenie efektu Dopplera – poniższe – wykracza poza zakres
programu liceum i jest nadobowiązkowe!)

(1)

1

t

v

ZO

g

⋅

=

.

Drugi z kolei sygnał akustyczny jest wysyłany przez źródło po czasie T (okres fal nada-
wanych) z nowego położenia Z

1

. Odległość ZZ

1

jest drogą przebytą przez źródło w czasie

T, a więc:

(2)

T

v

ZZ

z

⋅

=

1

.

Ten drugi sygnał dogania obserwatora po czasie t

2

w nowym położeniu O

1

. Odległość

Z

1

O

1

równa jest zatem:

(3)

2

1

1

t

v

O

Z

g

⋅

=

.

Czas upływający między odbiorem pierwszego i drugiego sygnału jest okresem drgań od-
bieranych, który oznaczymy przez T’. W tym czasie obserwator przesunie się o odległość
OO

1

, przy czym:

(4)

'

1

T

v

OO

o

⋅

=

.

Spoglądając na rys.1 łatwo możesz sprawdzić, że odległość ZO

1

można wyrazić dwojako:

jako sumę ZZ

1

+Z

1

O

1

lub jako sumę ZO + OO

1

, czyli:

T

v

z

⋅

2

t

v

g

⋅

Z

Z

1

O

O

1

1

t

v

g

⋅

'

0

T

v

⋅

rys. 1

5

00531 Fale mechaniczne, part 2 D

TEORIA

(5a)

'

1

2

T

v

t

v

t

v

T

v

o

g

g

z

⋅

+

⋅

=

⋅

+

⋅

,

czyli

(5b)

(

)

T

v

T

v

t

t

v

z

g

⋅

−

⋅

=

−

'

0

1

2

,

Czas upływający między chwilą nadania pierwszego sygnału i chwilą odbioru drugiego
sygnału możemy wyrazić również dwojako: jako sumę t

1

+T’ lub jako sumę T+t

2

, a zatem:

(6a)

2

1

'

t

T

T

t

+

=

+

,

czyli

(6b)

T

T

t

t

−

=

−

'

1

2

.

Wstawiając wyrażenie (6b) do równania (5a) otrzymujemy:

(7)

(

)

T

v

T

v

T

T

v

z

g

⋅

−

⋅

=

−

'

'

0

,

skąd otrzymujemy okres drgań odbieranych :

(8)

0

'

v

v

v

v

T

T

g

z

g

−

−

=

.

Pamiętając, że okres jest odwrotnością częstotliwości drgań, znajdujemy:

z

g

g

v

v

v

v

f

f

−

−

=

0

'

)

9

(

Wzór (9) określa częstotliwość drgań odbieranych w zależności od częstotliwości drgań
nadawanych, prędkości rozchodzenia się głosu, prędkości źródła i prędkości obserwatora.
Przy interpretacji powyższej zależności przyjmij, że zwrot wektora prędkości głosu jest
dodatni (przy czym interesuje nas tu głos docierający do obserwatora, bowiem fala dźwię-
kowa w danej chwili czasu rozchodzi się we wszystkie strony !)

2.

Kończąc omawianie zjawiska Dopplera raz jeszcze podkreślam, że chodzi tu o zmianę
częstotliwości (wysokości) odbieranego tonu, wynikającą z ruchu źródła i obserwatora.
Należy to sobie wyraźnie uświadomić, aby nie kojarzyć błędnie efektu Dopplera ze zmia-
ną natężenia dźwięku, wynikającą ze zmiany odległości obserwatora od źródła. W ośrod-
ku jednorodnym i nie pochłaniającym energii natężenie dźwięku zmienia się odwrotnie
proporcjonalnie do kwadratu odległości od źródła fali kulistej (w przypadku źródła punk-
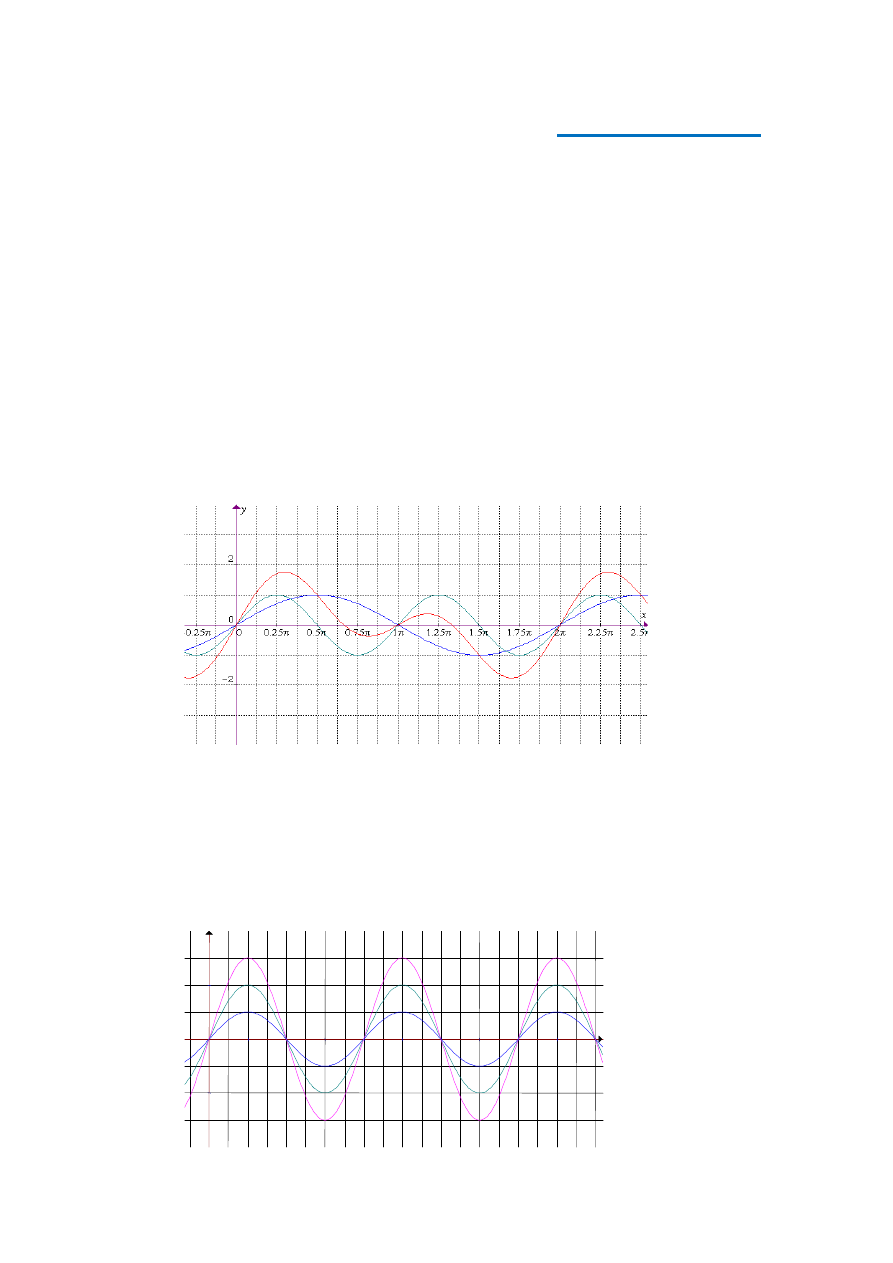
towego lub kulistego):

2

1

2

2

2

1

)

10

(

r

r

I

I

=

.

To prawo nie ma nic wspólnego ze zjawiskiem Dopplera !

6

00531 Fale mechaniczne, part 2 D

TEORIA

Temat 150

Interferencja fali.

1.

Wśród zjawisk związanych z ruchem falowym kilka jest właściwych tylko temu rodzajo-
wi ruchu. Do tych szczególnych zjawisk należą:

♦

interferencja (superpozycja), czyli nakładanie się fal,

♦

dyfrakcja, czyli ugięcie fal,

♦

polaryzacja, czyli porządkowanie drgań w danej płaszczyźnie.

2.

Do tej pory rozważaliśmy rozchodzenie się w ośrodku sprężystym pojedynczego zaburze-
nia tego ośrodka lub pojedynczego ciągu falowego. Możliwe są takie przypadki, kiedy w
danym ośrodku rozchodzi się równocześnie kilka ciągów falowych.

3.

Podobnie jak w ruchach punktu materialnego i ciała sztywnego, w ruchu falowym obo-
wiązuje zasada niezależności ruchów: jeżeli w ośrodku rozchodzi się kilka fal, wysyła-
nych równocześnie przez różne źródła, to wypadkowy ruch każdej cząstki ośrodka jest
złożeniem ruchów, jakie wykonywałaby ta cząstka przy rozchodzeniu się każdej fali z
osobna. Jest to tzw. zasada superpozycji.

4.

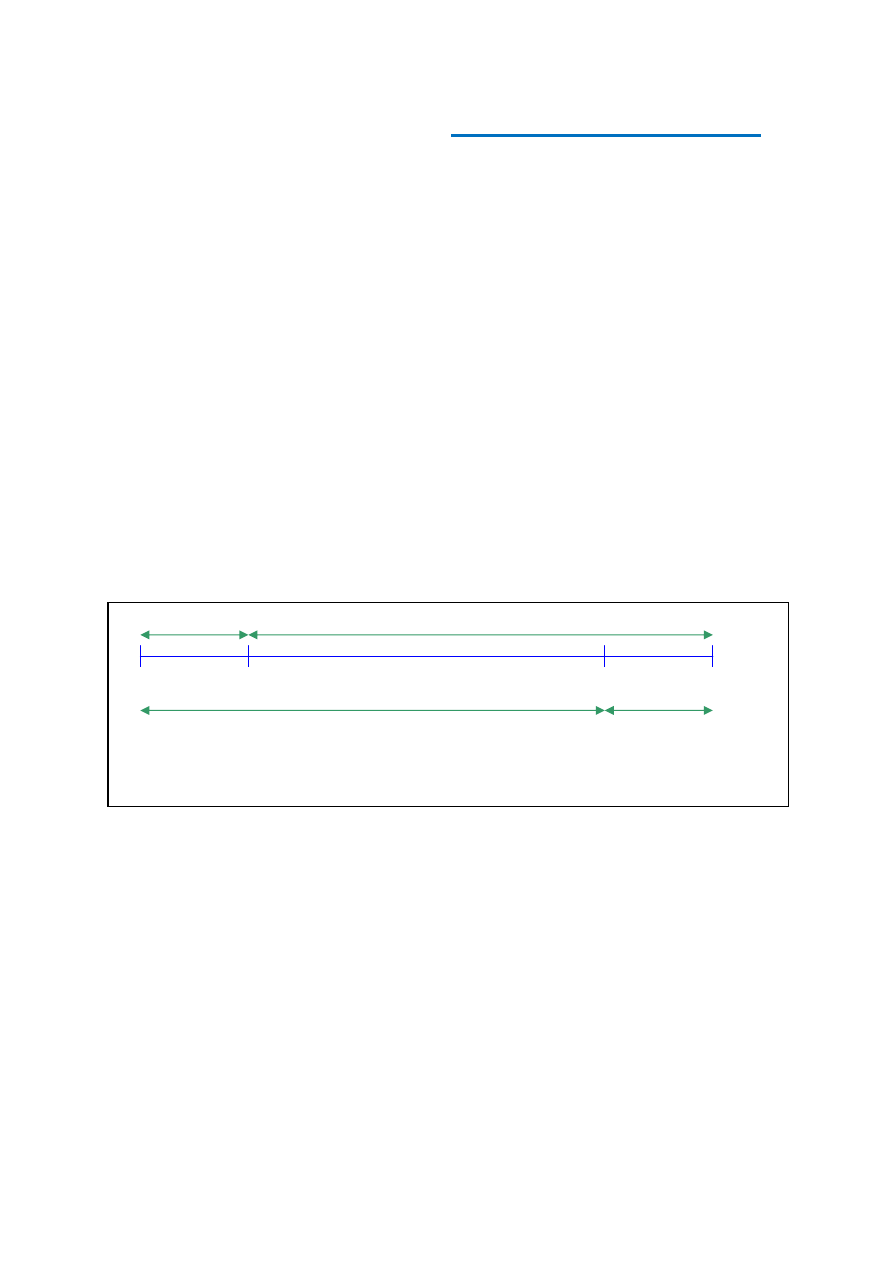
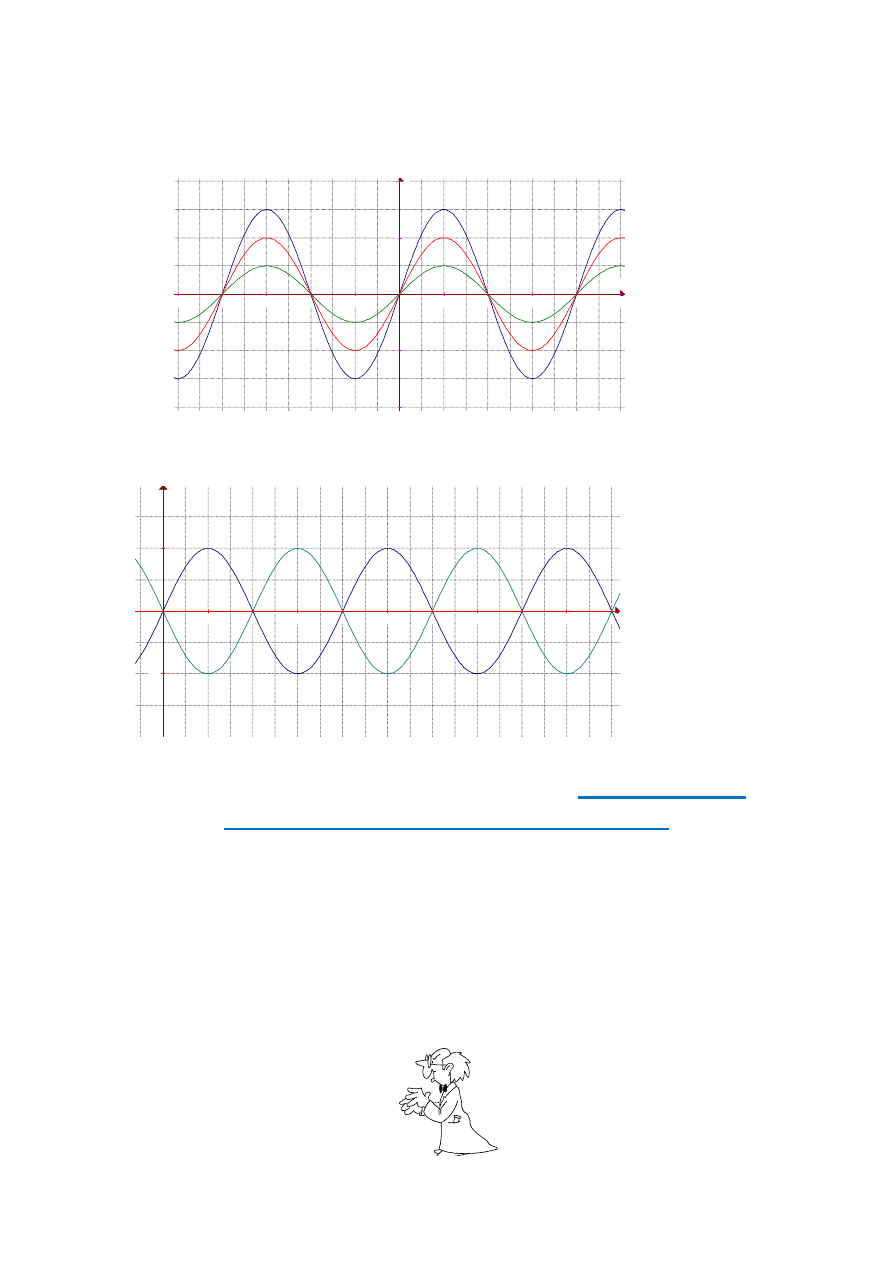
Aby określić wychylenie punktów ośrodka, w którym rozchodzi się fala lub kilka fal,
trzeba w każdym punkcie sumować (geometrycznie) wychylenie wszystkich fal (rys. 1).

Na rys. 1 zaznaczono linią niebieską i zieloną fale składowe, zaś czerwoną – falę wypadkową obliczoną
zgodnie z zasadą superpozycji.

5.

Rysunek 2 przedstawia interferencję dwóch fal sinusoidalnych „niebieskiej” i „zielonej” o
jednakowych długości

λ

, rozchodzących się w jednakowym kierunku. Fale te mają zgod-

ne fazy i w wyniku interferencji nastąpiło wzmocnienie drgań. Amplituda fali „czerwo-
nej” będącej wypadkową fal wymienionych wcześniej jest równa sumie amplitud fal skła-
dowych: A

cz

= A

z

+ A

n

.

x

y

0

0.5π

1π

1.5π

2π

2.5π

3π

3.5π

4π

4.5π

5π

-2

0

2

Rys. 1

Rys. 2

7

00531 Fale mechaniczne, part 2 D

TEORIA

6.

Jeżeli zaś interferująca fala ma fazę przeciwną do fali, z którą się nakłada (rys. 3), to
drgania osłabiają się, a amplituda fali wypadkowej jest równa nie sumie, lecz różnicy am-
plitud fal składowych.

7.

W przypadku, gdy omawiane fale miałyby jednakowe amplitudy i przeciwne fazy – na-
stąpiłoby całkowite wygaszenie drgań (rys. 4).

Temat 151

Dyfrakcja fali.

Zasada Huygensa rozchodzenia się fal.

1.

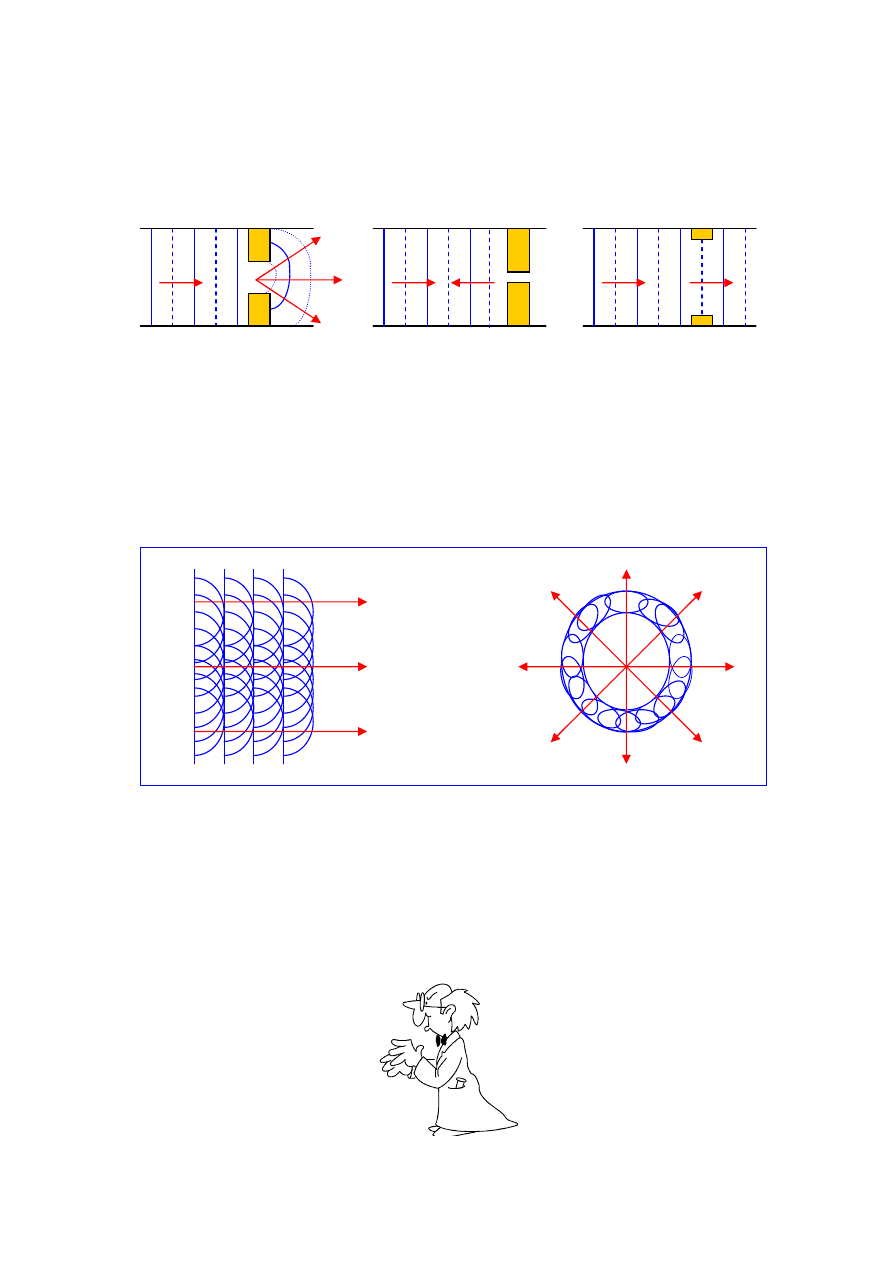
W ośrodku jednorodnym fale rozchodzą się po liniach prostych i zachowują kształt swych
powierzchni falowych. Gdy na drodze fali pojawi się jakaś niejednorodność ośrodka np.
jakaś przegroda lub otwór w przegrodzie, wtedy fala na ogół przestaje rozchodzić się
wzdłuż linii prostej, a ponadto zmieni ona kształt powierzchni falowej.

2.

Zjawisko zmiany kierunku rozchodzenia się fali przy napotkaniu niejednorodności ośrod-
ka z jednoczesną zmianą kształtu powierzchni falowej nazywamy dyfrakcją lub ugięciem
fali.

x

y

−2.5π

−2π

−1.5π

−1π

−0.5π

0

0.5π

1π

1.5π

2π

2.5π

-4

-2

0

2

4

Rys. 3

x

y

0

0.5π

1π

1.5π

2π

2.5π

3π

3.5π

4π

4.5π

5π

-1

0

1

Rys. 4

8

00531 Fale mechaniczne, part 2 D

TEORIA

3.

Zjawisko dyfrakcji jest szczególnie widoczne wtedy, gdy rozmiary niejednorodności są
porównywalne z długością fali. Gdy niejednorodności ośrodka są znacznie większe od
długości fali, wtedy występuje zjawisko przejścia fali bez zmiany jej parametrów. Jeśli
rozmiary niejednorodności są znacznie mniejsze od długości fali – następuje odbicie fali
(rys. 1, 2 i 3).

4.

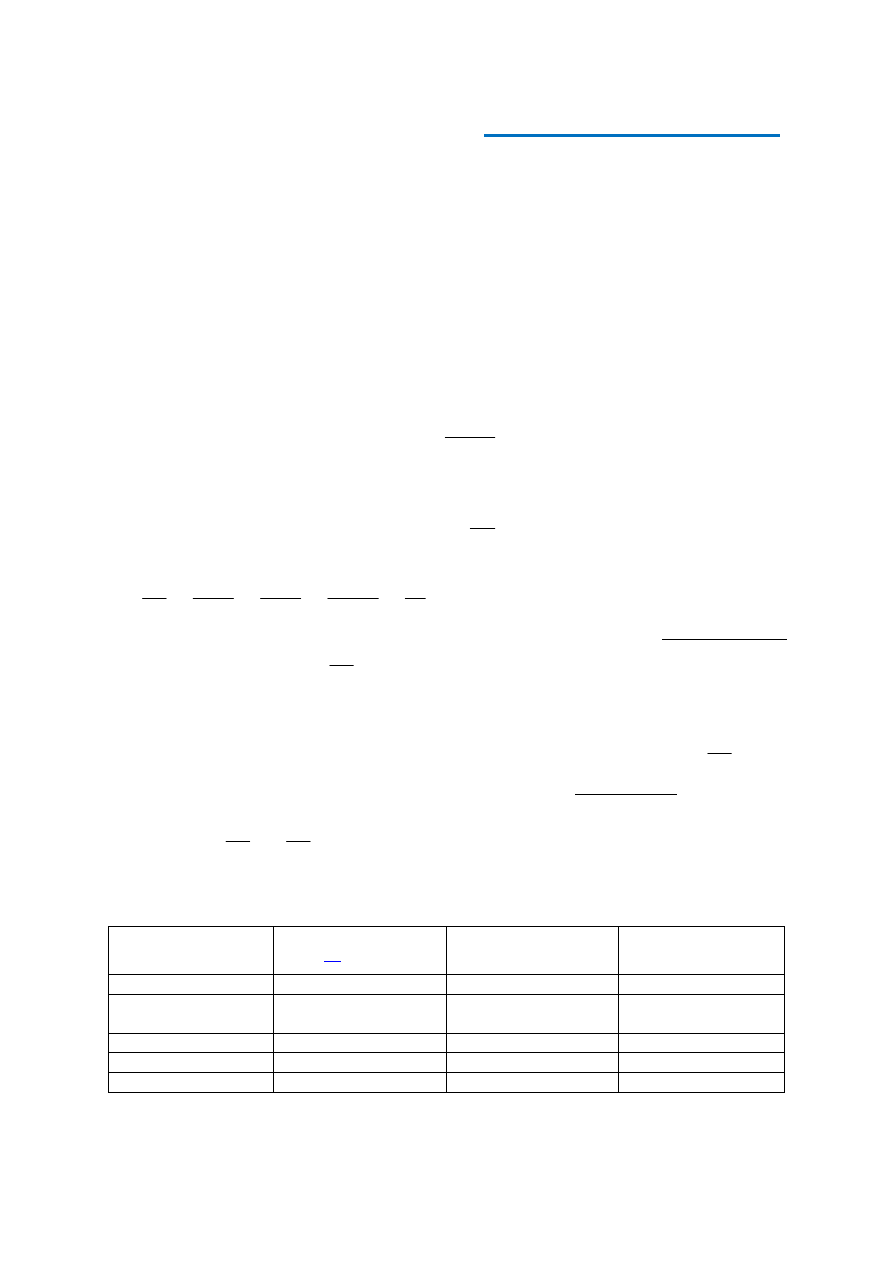
Wyjaśnienie zjawiska dyfrakcji ułatwia zasada Huygensa :
każdy punkt ośrodka, do którego dotarła jakaś fala, staje się źródłem nowej fali, która w
ś

rodowisku jednorodnym jest falą kulistą. Nowa powierzchnia falowa jest obwiednią

wszystkich cząstkowych fal kulistych, wytworzonych w sąsiadujących ze sobą punktach
ośrodka (rys. 4).

5.

Amplitudę drgań cząsteczek ośrodka leżących na nowej powierzchni falowej wyznaczamy
na podstawie zasady superpozycji jako wektorową sumę amplitud fal kolistych (kulistych)
cząstkowych. W przypadku fal rozchodzących się na wodzie fale cząstkowe wytworzone
w każdym punkcie powierzchni tej wody są falami kolistymi, gdyż właściwości sprężyste
powierzchni wody są inne niż objętości wody znajdującej się pod powierzchnią. Wodę
wraz z jej powierzchnią nie można zatem uważać za ośrodek jednorodny.

Rys. 1 Ugięcie fali

Rys. 2 Odbicie fali

Rys. 3 Przejście fali
bez ugięcia

Rys. 4

Mechanizm roz-
chodzenia się fali
płaskiej i kolistej
w oparciu o za-
sadę Huygensa.

9

00531 Fale mechaniczne, part 2 D

TEORIA

Temat 152

Energia fal dźwiękowych.

1.

Rozchodzenie się fal mechanicznych jest ściśle związane z transportem energii. Dotyczy
to także fal mechanicznych dźwiękowych. Wiemy o tym dobrze z życia codziennego: wy-
buchy wytwarzające fale dźwiękowe o dużych amplitudach, mogą doprowadzić do wybi-
cia szyb w budynkach albo innych podobnych zniszczeń.

2.

W fizyce nie wystarczy mówić, że dźwięk jest „cichy” lub „głośny”. Aby scharakteryzo-
wać ilość energii niesionej przez fale dźwiękowe, wprowadza się pojęcie natężenia
dźwięku.

Za miarę natężenia dźwięku przyjmuje się stosunek ilości energii

∆

E, która w ciągu czasu

∆

t przechodzi przez przekrój poprzecz-

ny

∆

S, prostopadły do kierunku rozchodzenia się fali dźwiękowej

do wielkości tego przekroju

∆

S i czasu

∆

t.

(1)

t

S

E

I

∆

⋅

∆

∆

=

.

Stosunek ilości energii

∆

E do czasu

∆

t jest chwilową mocą

∆

P, przenikającą przez ele-

ment powierzchni

∆

S:

(2)

S

P

I

∆

∆

=

.

Ze wzoru (2) wynika, że jednostką natężenia dźwięku (głośności) w układzie SI jest

3

3

2

2

2

2

2

1

1

1

1

1

s

kg

s

m

m

kg

s

m

m

N

s

m

J

m

W

=

⋅

⋅

=

⋅

⋅

=

⋅

=

. Oczywiście ze wzrostem natężenia dźwięku

słyszymy dźwięk coraz głośniejszy. Na przykład przy częstości 1000 Hz próg słyszalności

odpowiada mocy P = 10

-12

2

m

W

. Dźwięki o większym natężeniu słyszymy, o mniejszym –

nie słyszymy (jest to oczywiście umowna granica odpowiadająca przeciętnym zdolnością
słyszenia). Dla większej częstości fal dźwiękowych wartość progu słyszenia oczywiście

jest inna. Dla częstości 1000 Hz przy natężeniu dźwięku większym od około 1

2

m

W

zaczy-

namy odczuwać ból. Mówimy, że natężenie takie odpowiada progowi bólu.
A zatem normalne dźwięki przy częstości 1000 Hz odpowiadają zakresowi natężeń I po-

między 10

-12

2

m

W

, a 1

2

m

W

.

Poniższa tabela podaje typowe natężenie dźwięków pochodzących z różnych źródeł. Od-
czuwalna siła głosu nie jest liniową funkcją natężenia !

Źródło

Natężenie dźwięku

ሾ

ࢃ

࢓

૛

ሿ (około)

Natężenie dźwięku

[dB] (decybel)

Głośność

[fony]

Szelest liści

10

-11

10 – 15

10 – 15

Szept (z odległości 1

m)

10

-9

– 10

-8

30 – 40

30 – 40

Głośna rozmowa

10

-5

65 – 70

65 – 70

Hałaśliwa ulica

10

-4

– 10

-3

80 – 90

80 – 90

Silnik samolotu

więcej niż 10

0

więcej niż 120

więcej niż 120

10

00531 Fale mechaniczne, part 2 D

TEORIA

3.

Wrażenie jest proporcjonalne do logarytmu z podniety, o czym mówi tzw. prawo Webera – Fech-
nera:

Poziomem głośności, wyrażonym w decybelach, nazywamy wielkość
zdefiniowaną wzorem:

0

log

10

I

I

⋅

=

β

,

gdzie I jest natężeniem badanego głosu, a I

0

= 10

-12

2

m

W

jest tzw. pro-

giem słyszalności.

Przy wzroście natężenia od 10

-5













2

m

W

do wartości 10

-4













2

m

W

logarytm dziesiętny natężenia I

wzrasta o 1, od –5 do –4. Podobnie o jeden wzrasta logarytm dziesiętny natężenia I, jeżeli natęże-

nie wzrośnie od 10

-4













2

m

W

do 10

-3













2

m

W

(czyli logarytm wzrasta od –4 do –3). Wygodnie więc w

technice charakteryzować „siłę” głosu jako wielkość proporcjonalną do logarytmu dziesiętnego z
logarytmu natężenia. Aby nie używać liczb ujemnych umówiono się, że

natężeniu 10

-12

2

m

W

odpowiada o beli, natężeniu 10

-11













2

m

W

– 1 bel, natężeniu 10

-10













2

m

W

odpo-

wiadają 2 bele, ..., natężeniu 10

0













2

m

W

odpowiada 12 beli.

4.

Mówimy, że jeżeli natężenie wzrasta o 1 rząd (czyli 10 razy), to wzrasta o 1 bel. Inaczej mówiąc:
dwa natężenia I

1

i I

2

różnią się o 1 bel ( 1 B), jeżeli

1

log

1

2

=

I

I

.

Bel okazał się jednostką zbyt dużą, wprowadzono więc jednostkę 10 razy mniejszą: decybel (1 dB
= 0,1 B). Odpowiada on wzrostowi logarytmu o 0,1, czyli dla stosunku dwóch natężeń I

1

i I

2

za-

chodzi:

1

,

0

log

1

2

=

I

I

czyli

1

2

I

I

= 10

0,1

=1,2589. Zgodnie z tym, co mówiliśmy powyżej, dla częstości 1000 Hz próg sły-

szalności odpowiada zeru decybeli, próg bólu – 120 decybelom.

5.

Ucho ludzkie nie jest jednakowo wrażliwe na dźwięki o różnej wysokości. Wprowadza się więc
dodatkową jednostkę głośności: fon.

Przyjmujemy, że

dźwięk ma głośność n fonów, jeżeli wywołuje to samo wrażenie co dźwięk o
częstości 1000 Hz o natężeniu n decybeli. W szczególności zero fonów od-
powiada progowi słyszalności, a 120 fonów progowi bólu.