1

00532 Fale EM i optyka D, part 1

TEORIA

00532*

Fale EM i optyka, część 1 D

Pierwsze próby wyznaczania

prędkości światła.

Wyznaczanie prędkości światła metodą:

Römera, Bradleya, Fizeau,

Foucaulta, Michelsona.

Instrukcja dla zdającego
1.

Proszę sprawdzić, czy arkusz teoretyczny zawiera 12
stron. Ewentualny brak należy zgłosić.

2.

Do arkusza może być dołączona karta wzorów i sta-
łych fizycznych. Jeśli jest, należy ją dołączyć do od-
dawanej pracy.

3.

Proszę uważnie i ze zrozumieniem przeczytać zawar-
tość arkusza.

4.

Proszę precyzyjnie wykonywać polecenia zawarte w
arkuszu: rozwiązać przykładowe zadania, wyprowa-
dzić wzory, gdy jest takie polecenie.

5.

Proszę analizować wszelkie wykresy i rysunki pod
kątem ich zrozumienia.

6.

W trakcie obliczeń można korzystać z kalkulatora.

7.

Wszelkie fragmenty trudniejsze proszę zaznaczyć w
celu ich późniejszego przedyskutowania.

8.

Uzupełniaj wiadomości zawarte w arkuszu o informa-
cje zawarte w Internecie i dostępnej ci literaturze.

ś

yczymy powodzenia!

(Wpisuje zdający przed rozpoczęciem pracy)

PESEL ZDAJĄCEGO

Aktualizacja

Styczeń

ROK 2009

Dane osobowe właściciela arkusza

2

00532 Fale EM i optyka D, part 1

TEORIA

Temat 153 Pierwsze próby wyznaczania prędkości światła.

1.

Przystępujemy teraz do omówienia problemu, który pojawił się już w XVII wieku, a mia-
nowicie, czy światło jest falą (twórcą teorii falowej światła był Huygens), czy też ruchem
pewnych cząstek, które dzisiaj nazwalibyśmy fotonami (twórcą teorii korpuskularnej
ś

wiatła był Newton). Przez długi czas obie te hipotezy traktowano jako sprzeczne ze sobą

i wyszukiwano argumentów na potwierdzenie jednej lub drugiej. Początkowo teoria Huy-
gensa nie miała wielu zwolenników, być może wpływ na to miał wielki autorytet Newto-
na, który występował przeciwko tej teorii. Wiek XX przyniósł najbardziej niespodziewane
rozwiązanie: obie hipotezy okazała się jednocześnie prawdziwe! To pozornie absurdalne
stwierdzenie leży u podstaw całej fizyki współczesnej. Ale na razie zajmiemy się falową
naturą światła i pewnymi jej konsekwencjami.

2.

Jeżeli światło jest falą, to powinno:

♦

przenosić energię,

♦

rozchodzić się ze skończoną prędkością.

Pierwsze z tych stwierdzeń nie budzi wątpliwości. Z życia codziennego wiemy, że światło
przenosi energię ze Słońca na Ziemię. To dostarczanie energii wywołuje wiele znanych
zjawisk w atmosferze (np. pory roku), a także umożliwia życie na Ziemi (asymilacja ro-
ś

lin zielonych).

Wiemy, że światło rozchodzi się z bardzo dużą prędkością, równą w przybliżeniu
300 000[km/s], czyli z prędkością skończoną! Nie mówiliśmy jednak jak tę prędkość
można zmierzyć. Teraz zajmiemy się tym zagadnieniem.

3.

Ś

wiatło biegnie tak szybko, że nic z naszej codziennej praktyki nie sugeruje, iż jego pręd-

kość może być skończona. Damianus, syn Heliodora z Larissy uważał, że rozchodzenie
się światła jest natychmiastowe, gdyż „w tej samej chwili gdy Słońce przeziera się przez
chmury, jego światło dociera do nas”. Oczywiście nic z takiej argumentacji nie wynika, bo
przecież nie możemy zobaczyć, że Słońce przeziera się przez chmury, dopóki nie dotrze
wywołane przezeń światło. Kepler, w zgodzie z poglądem Damianusa, zastrzegał, że
„światło nie ma ani masy ani ciężaru”.
Galileusz jako jeden z pierwszych zasugerował, że światło może potrzebować na przeby-
cie drogi pomiędzy dwoma punktami pewnego skończonego czasu. W swojej książce „Di-
scorsi” przedstawił on teorię prędkości światła, wykładając ją w dialogu, jaki prowadzą
Sagredo i Simplicio. A dialog ten brzmi następująco:

Simplicio: Codzienne doświadczenie pokazuje, że rozchodzenie się światła jest
natychmiastowe: przecież gdy z daleka widzimy, jak strzela artyleria, to błysk do-
ciera do naszych oczu od razu, a dźwięk dociera do ucha dopiero po jakimś cza-
sie.
Sagredo: Tak Simplicio, ale jedyny wniosek jaki jestem w stanie z tego wyciągnąć
jest, że dźwięk w swej drodze do naszego ucha podróżuje znacznie wolniej niż
ś

wiatło; nie wiem natomiast, czy światło rozchodzi się natychmiast, czy też, cho-

ciaż niezwykle szybko, ale jednak potrzebuje na to czasu.

Sagredo, najwyraźniej sam Galileusz, sugeruje następnie sposób pomiaru prędkości światła. W nocy dwaj
mężczyźni, każdy z latarnią i odpowiednią maską do osłonięcia latarni, powinni stanąć naprzeciw siebie w
pewnej odległości. Jeden z mężczyzn szybko odkrywa swoją latarnię. Drugi mężczyzna w momencie, gdy
widzi światło, odkrywa również swoją latarnię. Pierwszy mężczyzna w momencie, gdy widzi światło z la-
tarni z naprzeciwka notuje czas, jaki upłynął od momentu, gdy odkrył on swoje światło do chwili, gdy zo-
baczył błysk latarni swojego partnera. Nie musimy wcale tłumaczyć, że dla większości wchodzących w grę
odległości na Ziemi czas reakcji człowieka jest dużo za długi, w porównaniu z czasem, jaki jest potrzebny
ś

wiatłu, aby mogło przebyć drogę w obie strony, tym samym taki eksperyment nie ma żadnych szans po-

wodzenia.

3

00532 Fale EM i optyka D, part 1

TEORIA

O nich warto wiedzieć...

Galilei, Galileo (Galileusz) (1564 – 1642) – fizyk, matematyk i astro-
nom włoski. W 1589 roku został profesorem uniwersytetu w Pizie, w
latach 1592 – 1610 był profesorem uniwersytetu w Padwie, od 1610
roku matematykiem i filozofem nadwornym księcia Cosimo II Medy-
ceusza. Stworzył podstawy mechaniki, w szczególności dynamiki, wy-
kazał względność ruchu, podał sposób transformacji współrzędnych z
jednego układu odniesienia do drugiego, znalazł prawa rządzące spad-
kiem swobodnym i ruchem wahadła, prowadził podstawowe badania w
dziedzinie akustyki i nauki o cieple. Skonstruował lunetę, przy pomocy
której prowadził obserwacje astronomiczne, odkrył księżyce Jowisza i

fazy planety Wenus. Był zwolennikiem poglądów Kopernika i przeciwstawił je w swoim
dziele Dialogo sopra i due massimi sistemi del mondo (1632) poglądom Ptolemeusza. Zo-
stał postawiony za to przed sąd Inkwizycji i zmuszony (1633) do odwołania twierdzenia,
ż

e Ziemia się porusza. Jak głosi legenda, wychodząc z sali sądu powiedział: „Eppur si

muove” (tłumaczenie: a jednak się porusza). Skazany został na zamieszkanie w Sienie, a
potem we własnym domu w Arcetri pod Florencją, gdzie do końca życia pozostawał
więźniem Inkwizycji. Mimo to udało mu się przesłać do Holandii rękopis swego dzieła o
mechanice Discorsi e dimonstrazioni matematiche intorno a due nuove scienze (1638).

Temat 154

Wyznaczanie prędkości światła

metodą Römera

1.

Ś

wiatło rozchodzi się w przestrzeni z prędkością niezwykle dużą. Ponieważ kilkakrotne

próby mierzenia prędkości światła czynione przez Galileusza i Descartesa nie dały żad-
nych wyników, jeszcze w początkach XVII wieku przypuszczano, że prędkość rozcho-
dzenia się światła jest nieskończenie wielka.

2.

Dopiero w 1676 roku Ole Römer (prowadząc badania w obserwatorium paryskim) roz-
strzygnął zagadnienie prędkości światła opierając się na swych obserwacjach zaćmień
księżyców Jowisza. Planeta Jowisz, największa planeta Układu Słonecznego, ma 12 Księ-
ż

yców. Cztery największe: Io, Europę, Ganimadesa i Callisto odkrył w 1610 roku Galile-

usz Pozostałe, znacznie mniejsze, nie były znane w czasach Römera.

3.

Księżyce Jowisza obiegają planetę w płaszczyźnie bardzo bliskiej płaszczyzny orbity Jo-
wisza w jego ruchu dokoła Słońca. Wskutek tego podczas każdego obiegu dokoła planety
księżyce wchodzą w cień Jowisza, ulegając tym samym regularnym zaćmieniom. Okres
obiegu najbliższego, czyli Io, wynosi około 42,5 godziny, najdalszego (Callisto) – prawie
17 dni.

4.

Römer zauważył, że obserwowane z Ziemi odstępy czasu między kolejnymi dwoma za-
ć

mieniami maleją, gdy Ziemia w swym ruchu dokoła po orbicie zbliża się do Jowisza, ro-

sną natomiast, gdy Ziemia oddala się (okres obiegu Jowisza dokoła Słońca wynosi prawie
12 lat, więc podczas jednego pełnego obiegu Ziemi dokoła Słońca, na co nasza planeta
potrzebuje około jednego roku, Jowisz przesunie się na swojej orbicie stosunkowo niewie-
le). Zaćmienia możemy uważać za sygnały świetlne wysyłane w równych odstępach cza-
su, a więc – jako wskazania swego rodzaju zegara.

5.

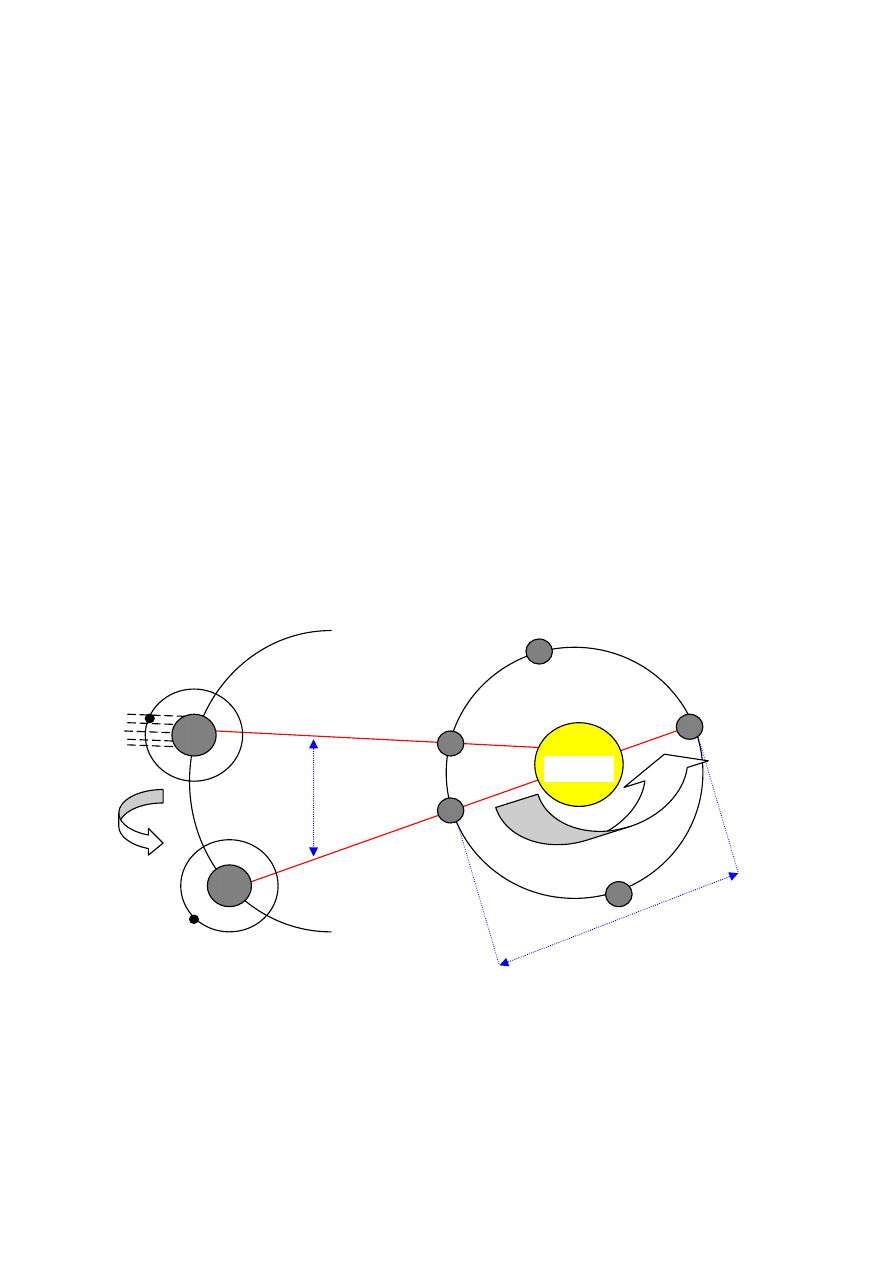
Będąc na Ziemi możemy stwierdzić, że zegar ten chodzi nieregularnie: spieszy się, gdy
Ziemia się od niego zbliża, a opóźnia – gdy Ziemia się od niego oddala. W sytuacji, gdy
Ziemia zbliża się prawie wzdłuż linii prostej łączącej ją z Jowiszem (położenie Z

4

rys. 1)

obserwowane z Ziemi przyspieszenie tego „zegara” wynosi niespełna 2 sekundy dla Io,
zaś prawie 15 sekund dla Callisto. Gdy Ziemia oddala się (pozycja Z

3

) tyleż wynoszą

4

00532 Fale EM i optyka D, part 1

TEORIA

opóźnienia naszego „zegara”. Są to wartości maksymalne, bowiem w sytuacjach pośred-
nich, gdy Ziemia biegnie ukośnie względem prostej łączącej ją z Jowiszem, różnice są
mniejsze.

6.

Obserwując ten specyficzny „zegar” w ciągu całego roku zarejestrować można globalne
skutki tych efektów. Na podstawie pierwszych wielomiesięcznych obserwacji Römer
oszacował w ten sposób sumaryczne opóźnienie (w położeniu Z

2

względem Z

1

) na około

22 minuty. Tyleż powinno wynosić sumaryczne przyspieszenie (w położeniu Z

2

wzglę-

dem Z

1

).

7.

Co z tego wynika? Gdyby światło biegło z nieskończoną prędkością, to żadnych opóź-
nień, ani przyspieszeń byśmy nie stwierdzili. Skoro bowiem regularnie wysyłane sygnały
docierają do nas raz nieco za późno (gdy oddalamy się od zegara), raz nieco za wcześnie
(gdy zbliżamy się doń), wobec tego muszą one stracić nieco czasu, by nas dogonić (lub
zyskać, jeśli wybiegamy im naprzeciw). Zatem sygnały biegną ze skończoną prędkością !

8.

Skoro wiemy już, że światło przemieszcza się ze skończoną prędkością, nasuwa się kolej-
ne pytanie: z jaką ? Aby na nie odpowiedzieć, trzeba dokładniej znać ów czas opóźnienia
(Römer oszacował go na 22 minuty, czyli 1320 sekund) i średnicę orbity okołosłonecznej
Ziemi. Aby obliczyć prędkość światła wystarczy podzielić średnicę orbity Ziemi przez
opóźnienie. Dokładność pomiaru zależy od dokładnej znajomości orbity Ziemi. Za cza-
sów Römera rozmiary te nie były jeszcze dokładnie znane. W każdym razie Römer wy-
znaczył wartość prędkości światła jako c = 215 000[km/s].

9.

Jak dzisiaj wiemy, maksymalne opóźnienie zaćmienia księżyca Jowisza wynosi około
1000 sekund, zaś średnica orbity okołosłonecznej Ziemi ma wartość około

8

10

3

⋅

[km].

Posługując się podanymi powyżej wartościami i dzieląc średnicę orbity Ziemi przez mak-
symalne opóźnienie otrzymujemy c = około 300 000[km/s]

Z

4

Z

3

Z

2

Z

1

Jowisz

K

ś

rednica orbity Ziemi

przebycie tej drogi trwa ½ roku

½ roku

Jowisz

Słońce

Rys. 1
Metoda Römera pomiaru prędkości światła. Z

1

– Z

4

– kolejne położenia Ziemi, K –

księżyc Jowisza.

5

00532 Fale EM i optyka D, part 1

TEORIA

Ziemi

v

r

α

p

v

r

c

r

Temat 155

Wyznaczanie prędkości światła

metodą Bradleya

1.

W roku 1735 James Bradley (1693 – 1762) zaproponował drugą po Römerze astrono-
miczną metodę wyznaczania prędkości światła. Początkowo za obiekt obserwacji wybrał
najjaśniejszą gwiazdę gwiazdozbioru Smoka (Ladona) – Etamin. Ladon jest rozległym
gwiazdozbiorem położonym blisko północnego bieguna świata. Głowa jego składa się z
czterech gwiazd o nazwach: Alwaid (niebieska), Etamin (zielona), Grumium (czerwona) i
Kuma (żółta).

2.

Odkryte przy okazji zjawisko aberracji światła było pierwszym dowodem fizycznym na
ruch Ziemi dokoła Słońca, czyli pierwszym dowodem słuszności teorii Kopernika.

3.

Ś

wiatło rozchodzi się w przestrzeni z bardzo dużą prędkością. Pierwszego historycznego

wyznaczenia prędkości światła dokonał Römer około 1675 roku, jednak nie wszyscy po-
godzili się od razu z koncepcją, że światło rozchodzi się ze skończoną szybkością, że nie
jest to zjawisko natychmiastowe. Pogląd ten został powszechnie przyjęty dopiero po roku
1735, a więc po wyznaczeniu przez Bradleya prędkości światła. Angielski astronom kró-
lewski James Bradley obliczył prędkość rozchodzenia się światła na podstawie badań
aberracji astronomicznej światła.

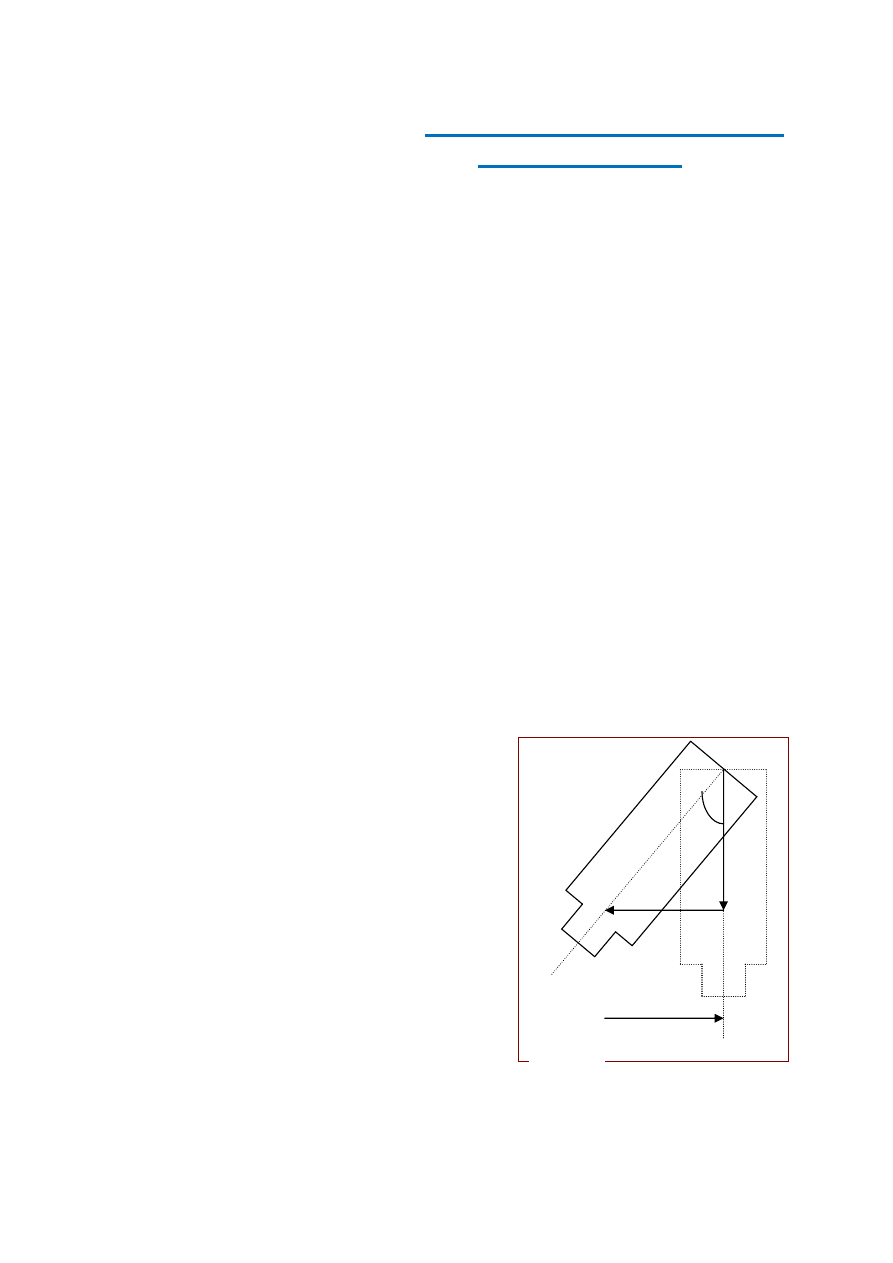
4.

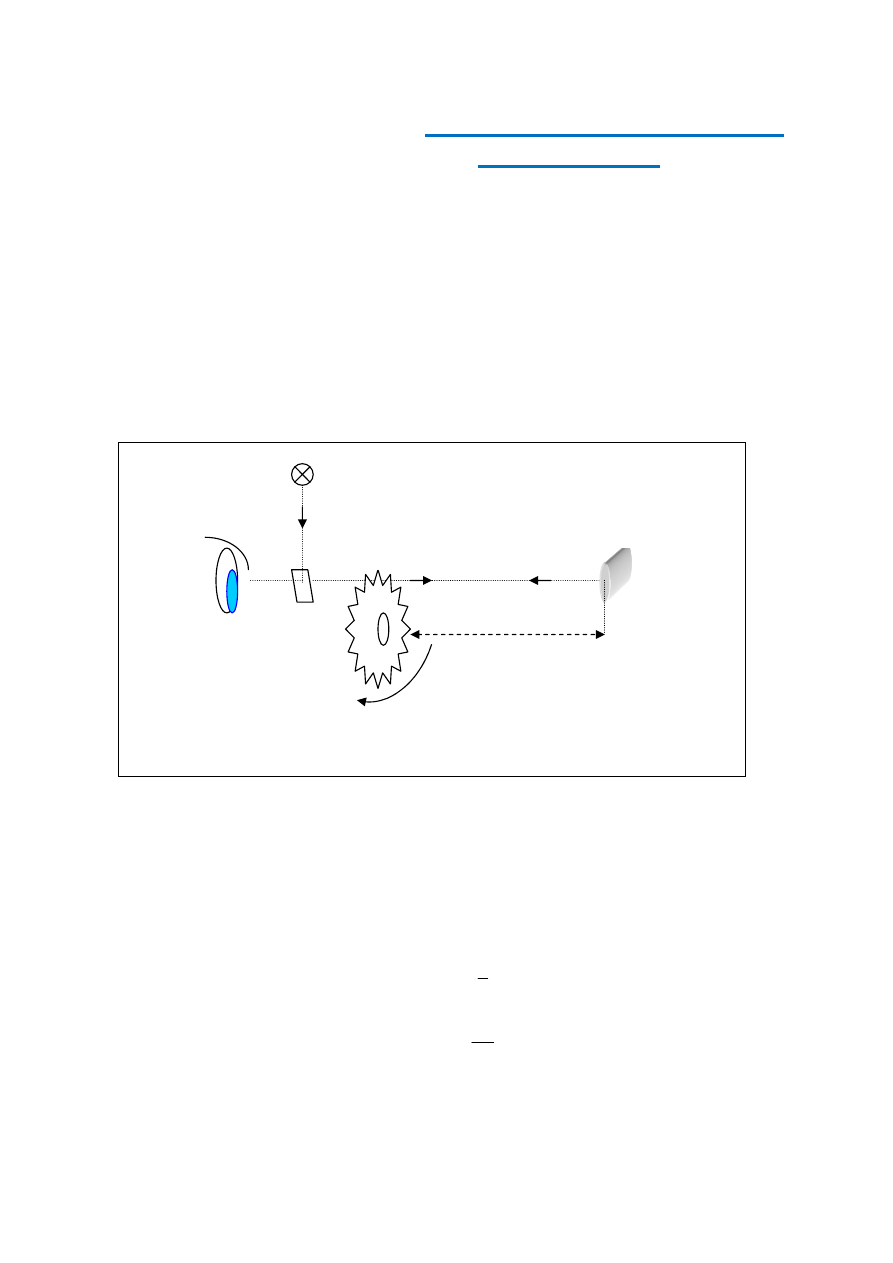
W czasie swoich obserwacji Bradley zauważył, że gwiazdy w ciągu roku zakreślają na
sferze niebieskiej elipsy (w szczególnych przypadkach – okręgi bądź odcinki prostej). Ten
pozorny ruch wyjaśnił on jako wynik wektorowego sumowania się prędkości światła c i
prędkości obserwatora v (czyli prędkości Ziemi w ruchu dokoła Słońca). Jeżeli Ziemia by-
łaby nieruchoma, to wyznaczony przez obserwację kierunek, w którym widzimy gwiazdę,
byłby rzeczywistym kierunkiem. Jednak nasza planeta porusza się z prędkością v, dlatego
też teleskop, przez który obserwujemy daną gwiazdę, jest odchylony od rzeczywistego
kierunku o kąt

α

(dzięki temu światło wchodzące do obiektywu trafia do okularu (rys. 1).

Na rysunku przez v

p

oznaczono pozorną skła-

dową wypadkowej prędkości światła (proporcje
między prędkościami nie zostały zachowane).
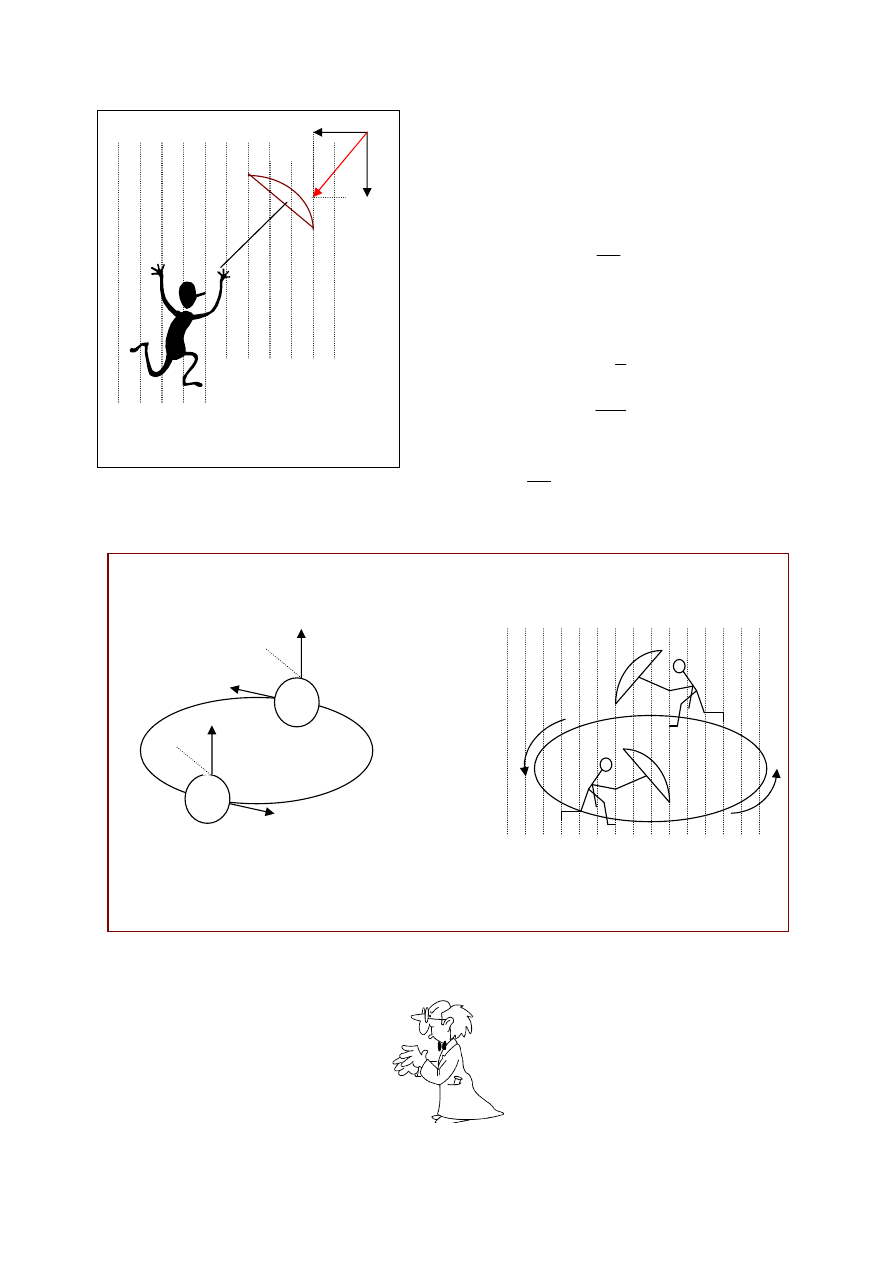
Aby łatwiej to zrozumieć posłużymy się przykła-
dem, z jakim możemy zetknąć się na co dzień.
Gdy stoimy w padającym pionowo deszczu, chro-
nimy się przed zmoknięciem, trzymając parasol
prosto nad głową. Natomiast gdy biegniemy, mu-
simy go nieco pochylić, aby osłonić głowę przed
deszczem (rys. 2).

5.

Powrócimy teraz do ruchu Ziemi wokół Słońca.
Gdy pół roku później od pierwszej obserwacji pla-
neta znajdzie się w przeciwnym punkcie orbity, jej
prędkość będzie miała przeciwny zwrot, więc po-
zorne położenie gwiazdy zmieni się o kąt 2

α

względem pierwszej obserwacji. Analogicznie będzie w przypadku człowieka biegnącego
po kołowym torze (rys. 3).

Rys. 1

6

00532 Fale EM i optyka D, part 1

TEORIA

Znajomość

nachylenia

teleskopu

względem

wybranego układu współrzędnych w czasie obu
obserwacji pozwoli nam znaleźć różnicę nachyleń
wynoszącą 2

α

, a tym samym i wartość kąta

α

.

Bradley stwierdził, że wynosi ona 20’48’’ =ok.
10

-4

rad. Wiedząc, że prędkość Ziemi w ruchu po

orbicie wynosi około 30

s

km

i korzystając z zależ-

ności przedstawionych na rys. 1, możemy następu-
jąco obliczyć prędkość światła:

c

v

=

α

tg

,

α

tg

v

c

=

.

Wartość, jaka w ten sposób otrzymał Bradley wy-

nosiła 303 000

s

km

.

k

v

r

p

v

r

v

p

– pozorna składowa

wypadkowej

prędkości

kropli względem człowie-
ka,
v

k

– prędkość kropli.

Rys. 2

kierunek
pozorny

do gwiazdy

do gwiazdy

Rys. 3

7

00532 Fale EM i optyka D, part 1

TEORIA

Temat 156

Wyznaczanie prędkości światła

metodą Fizeau.

1.

Po raz pierwszy fizyczną metodę pomiaru prędkości światła zastosował Armand Hippoly-
te Louis Fizeau (1819 – 1896)w połowie XIX wieku.

2.

Fizeau był wybitnym fizykiem, członkiem Paryskiej Akademii Nauk, od 1863 profesor
Ecole Politechnique w Paryżu. Wynalezioną przez siebie metodą koła zębatego dokonał w
roku 1849 pomiaru prędkości światła w warunkach ziemskich. Badał on wpływ ośrodka
na prędkość światła, zajmował się także rozszerzalnością cieplną ciał i promieniowaniem
podczerwonym. Wspólnie z Foucaultem odkrył prążki absorpcyjne w podczerwonej czę-
ś

ci widma słonecznego.

3.

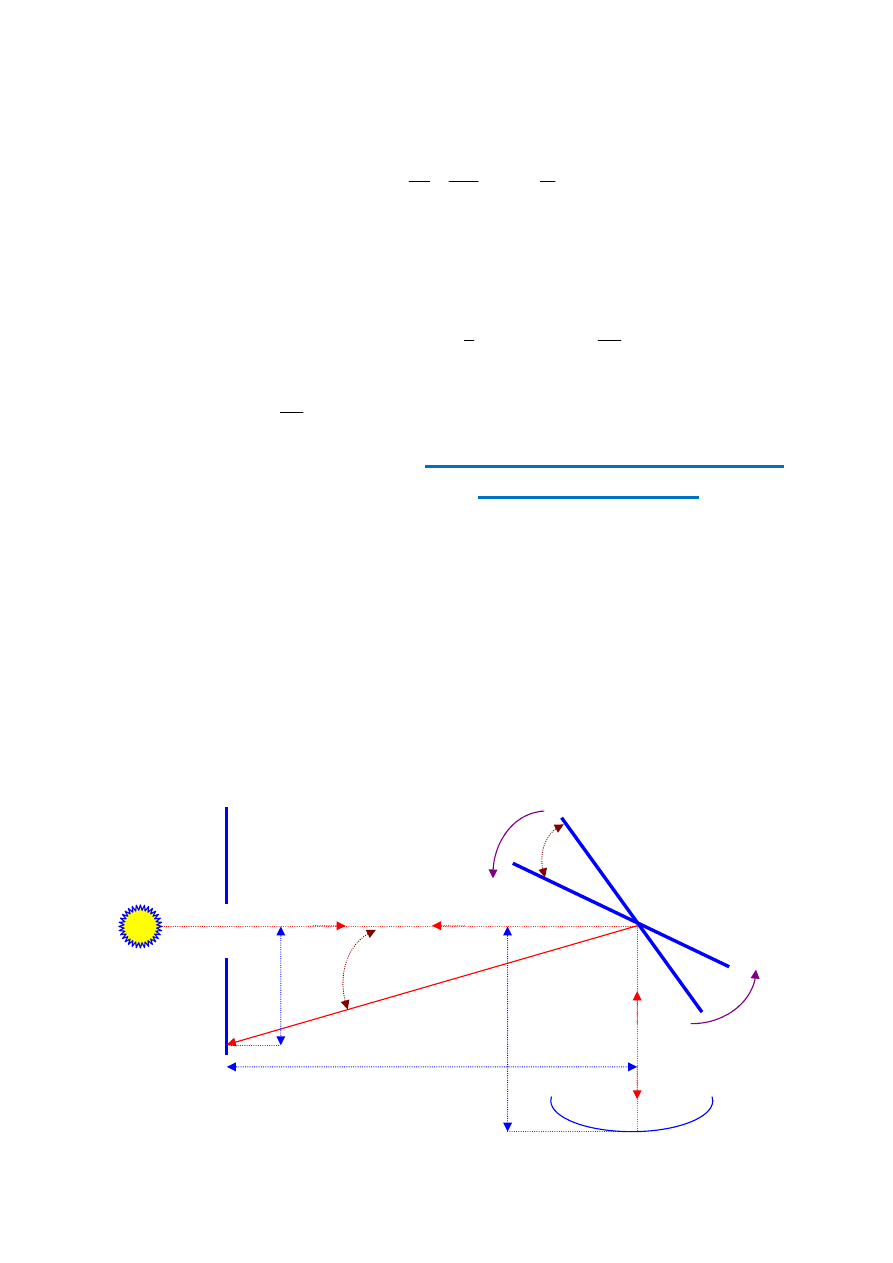
Doświadczenie Fizeau.

Ś

wiatło ze źródła S pada na płytkę szklaną P częściowo przezroczystą a częściowo odbijającą światło. Po

odbiciu promień kierowany jest w kierunku koła zębatego K służącego do okresowego formowania krót-
kich impulsów świetlnych. Światło przelatuje w przerwie między zębami koła i biegnie w kierunku lustra Z
ustawionego w odległości L od koła zębatego. Po odbiciu od zwierciadła promień wraca do obserwatora
(oko na rys. 1). Gdy koło zostanie wprawione w ruch obrotowy, wtedy przy pewnej częstości obrotów ob-
serwator przestaje widzieć światło odbite. Oznacza to, że w czasie, gdy światło przebywa odległość od koła
zębatego do zwierciadła i z powrotem, czyli 2L, koło obraca się o odcinek równy odległości przerwy od zę-
ba. Tak więc natrafia nie na przerwę między zębami, lecz na ząb i nie przedostaje się dalej. Znając często-
tliwość obrotów koła, liczbę zębów i odległość od koła do zwierciadła, można obliczyć prędkość światła:

(1)

t

s

v

=

,

wstawiamy teraz: v = c oraz s = 2L i otrzymujemy:

(2)

t

L

c

2

=

.

Rys. 1

S

oko

P

L

Z

K

8

00532 Fale EM i optyka D, part 1

TEORIA

Fizeau użył koła zębatego o 720 zębach i 720 odstępach i zaobserwował pierwszą ciemność, gdy koło wy-
konywało 12,6 obrotów na sekundę.. Wobec tego czas, jakiego potrzebuje koło, aby przesunąć się o szero-
kość jednego odstępu, wynosi:

(3)

f

T

bo

nf

n

T

t

1

,

2

1

2

=

=

=

,

Wstawiamy teraz ostateczną postać wzoru (3) do wzoru (2) i dostajemy:

(4)

n

f

L

c

⋅

⋅

=

4

.

We wzorze (4) użyto oznaczeń: c – prędkość światła, L – odległość od koła zębatego do
zwierciadła, f – minimalna częstotliwość drgań, n – ilość zębów na obwodzie koła.
Wstawiamy wartości liczbowe:

(5)













=

⋅













⋅

⋅

=

s

km

s

m

c

313274

720

1

6

,

12

]

[

8633

4

Dokładniejszy pomiar wykonany tą samą metodą wykonany Perrotina w 1901 roku dał

wynik 299860

±

80













s

km

.

Temat 157

Wyznaczanie prędkości światła

metodą Foucaulta.

1.

Jean Bernard Leon Foucault (1819 – 1868) to fizyk francuski, który pracował w paryskim
obserwatorium astronomicznym. Był członkiem paryskiej, berlińskiej oraz petersburskiej
Akademii Nauk oraz londyńskiego Royal Society. W 1851 za pomocą wahadła o długości
67 m, zawieszonego w paryskim Panteonie, przeprowadził obserwacje będące bezpośred-
nim dowodem ruchu obrotowego Ziemi. W 1852 roku wynalazł żyroskop, poza tym od-
krył zjawisko nagrzewania się przewodników obracających się z dużą prędkością w polu
magnetycznym, na skutek przepływu indukujących się w nich prądów wirowych; prądy te
nazwano prądami Foucaulta. Szereg jego prac jest poświęconych zagadnieniom optycz-
nym. Zbudował pryzmat polaryzacyjny i fotometr. W 1862 roku opracował nową metodę
pomiaru prędkości światła przy zastosowaniu wirującego zwierciadła.

2.

Idea doświadczenia Foucaulta jest przedstawiona na poniższym rysunku:

b

Z’

Z

1

Z

2

l

α

S

S

1

E

a

2

α

Rys. 1

9

00532 Fale EM i optyka D, part 1

TEORIA

Promień pada przez szczelinę S na zwierciadło płaskie Z

1

, następnie na zwierciadło wklę-

słe Z

2

, z kolei po odbiciu się od obydwu zwierciadeł powraca przez tę samą szczelinę S.

Jeżeli jednak zwierciadło Z

1

zostanie wprawione w szybki ruch wirowy, to promień odbity

od zwierciadła wklęsłego po przejściu drogi 2l napotyka zwierciadło Z

1

, odchylone o kąt

α

(położenie Z’) i odbijając się od niego padnie na ekran E w punkcie S

1

przesuniętym

względem szczeliny S o odcinek a. Gdyby światło miało nieskończoną prędkość również
przy obracającym się zwierciadle Z

1

powracałoby tą samą drogą do źródła światła.

Nowy promień odbity od odwróconego zwierciadła płaskiego Z’ odchylony jest od pier-
wotnego b o kąt 2

α

.

3.

Wyznaczanie prędkości światła metodą Foucaulta wyjaśnimy za pomocą poniższego
przykładu:

Zwierciadło płaskie w aparacie Foucaulta (rys. 1) osadzone w odległości l = 4[m] od
zwierciadła wklęsłego i w odległości b = 2,5[m] od szczeliny S, jest obracane z częstotli-
wością f = 48 000[obrotów na minutę]. Oblicz prędkość światła, jeżeli przesunięcie na
ekranie promienia odbitego względem szczeliny wynosi a = 0,67[mm].

Rozwiązanie przykładu:
Prędkość światła na drodze od zwierciadła Z

1

do zwierciadła Z

2

i z powrotem określa

wzór:

(1)

t

l

c

2

=

,

przy czym czas t, który odpowiada obrotowi zwierciadła o kąt

α

, można obliczyć z następującej zależności (uwzględniając, że w do-

ś

wiadczeniu Foucaulta kąt

α

jest niewielki):

(2)

b

a

=

≈

α

α

2

2

tg

, czyli

(3)

f

b

f

t

⋅

⋅

=

⋅

=

π

α

π

α

2

2

2

.

W zależności (3) wykorzystaliśmy znany wzór z kinematyki ruchu obrotowego:

t

f

t

t

⋅

⋅

=

⋅

=

⇒

=

π

ω

α

α

ω

2

.

Podstawiamy teraz zależność (3) do wzoru (1):

(4)

a

f

b

l

c

⋅

⋅

⋅

=

π

2

2

2

i ostatecznie dostajemy:

(5)

a

l

f

b

c

⋅

⋅

⋅

=

π

8

.

Wstawiamy wartości liczbowe:

(6)

s

km

s

m

s

m

m

m

c

000

299

000

800

299

00067

,

0

4

800

5

,

2

14

,

3

8

=

=

⋅

⋅

⋅

⋅

⋅

⋅

=

.

Za pomocą tej samej aparatury można określić prędkość światła w innych ośrodkach, wstawiając między ziwerciadła Z

1

i Z

2

rurkę wy-

pełnioną odpowiednią substancją. Na podstawie podobnych doświadczeń stwierdzono, że prędkość siwatła w różnych ośrodkach prze-
zroczystych jest mniejsza niż w próżni i zależy od barwy, czyli od długości fali badanego światła.

Stosując podaną powyżej metodę Foucault w 1862 roku znalazł prędkość światła i okreslił jako 298 000

s

km

.

10

00532 Fale EM i optyka D, part 1

TEORIA

Temat 158

Wyznaczanie prędkości światła

metodą Michelsona.

1.

Albert Abraham Michelson (1852 – 1931) urodził się w Polsce, w Strzelnie. W wieku
dwóch lat wyjechał z rodzicami do Stanów Zjednoczonych. Ukończył, a następnie nauczał
w U.S. Naval Academy. Pracował również w Szkole Nauki Stosowanej Case’a w Cleve-
land, w Clark University w Worchester i Uniwersytecie w Chicago. Za opracowanie inter-
ferometru, noszącego obecnie jego imię, otrzymał w 1907 roku nagrodę Nobla. Był
pierwszym uczonym z USA, którego spotkało to wyróżnienie. Nazwisko Michelsona roz-
sławiły nie tylko bardzo precyzyjne pomiary prędkości światła, ale również jego wkład do
metrologii i spektroskopii, a także badania nad sztywnością Ziemi, opracowanie i ulep-
szenie urządzenia do wykonywania siatek dyfrakcyjnych oraz badania nad unoszeniem
eteru, które stały się podstawą dla teorii względności. Michelson zajmował się także ana-
lizą linii widmowych i pomiarem średnic kątowych gwiazd.

2.

Opracowany przez Michelsona interferometr jest wyjątkowo wszechstronnym instrumen-
tem. Jego zastosowania są właściwie niezliczone. Jednym z nich jest pomiar współczyn-
nika załamania światła dla płytki szklanej, którą umieszcza się w jednym z ramion interfe-
rometru i odpowiednio pochyla. Zmiana efektywnej grubości, wskazywana przez przesu-
nięcie prążków, wiąże się bezpośrednio ze współczynnikiem załamania.

3.

Już w starożytności wiedziano, że światło rozchodzi się prostoliniowo, a kiedy odbija się
od płaskiego zwierciadła, równy jest kątowi odbicia, pod jakim to zwierciadło opuszcza.
Starożytni znali załamanie światła, wierzono jednak, że prędkość światła jest nieskończo-
na. Jak pamiętamy, pierwsze eksperymenty przeprowadzał Galileusz, ale ze względu na
brak odpowiednich przyrządów zakończyły się one niepowodzeniem. Dopiero w 1676 ro-
ku nastąpił przełom dzięki zakończonym powodzeniem eksperymentom Römera, który
dowiódł, że prędkość światła jest skończona. Potem nastąpiły badania Fizeau, Foucaulta i
Michelsona.

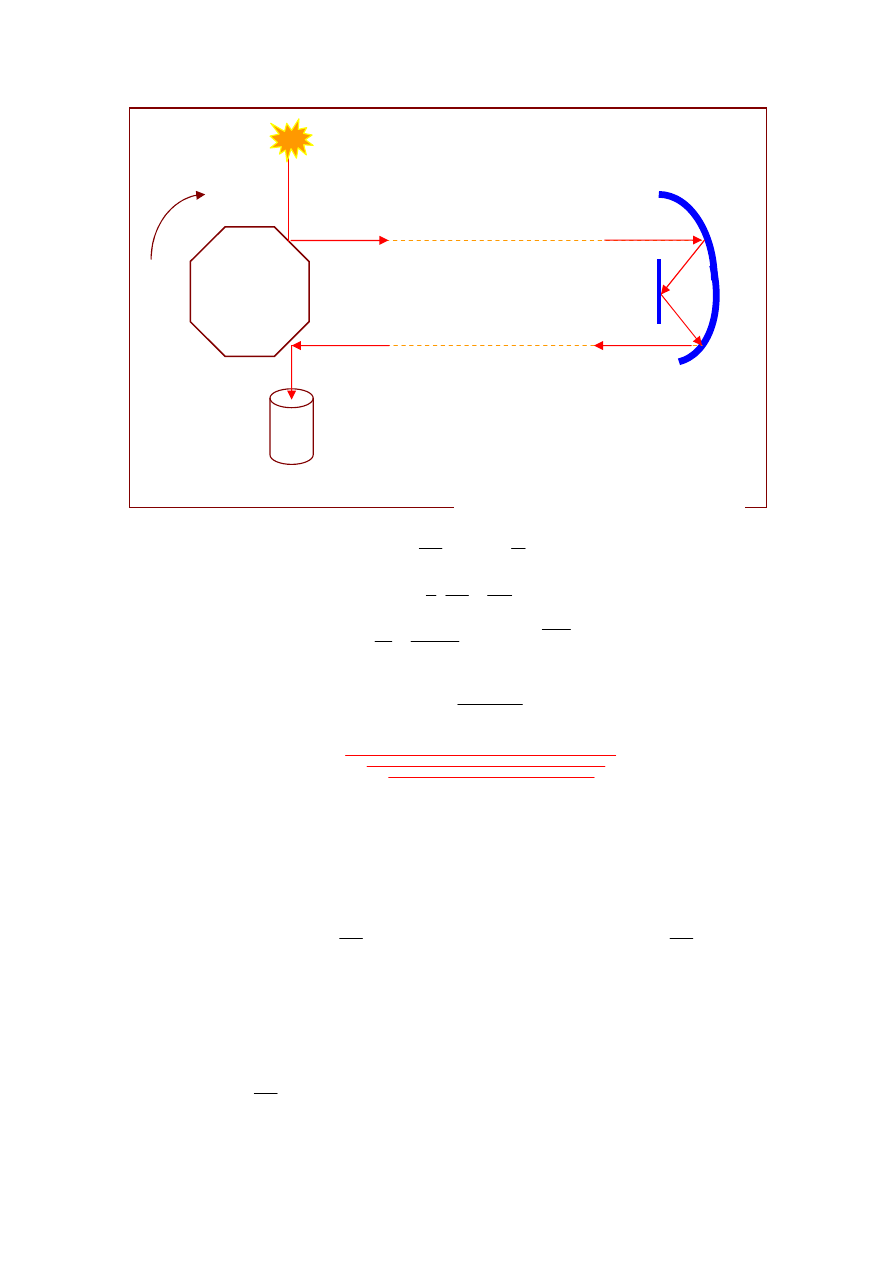
4.

Do pomiaru prędkości światła Michelson użył aparatury działającej na zasadzie idei opra-
cowanej przez Foucaulta. Liczba powierzchni odbijających wirującego zwierciadła,
wprawionego w ruch przez strumień powietrza została zwiększona do ośmiu, a odległość
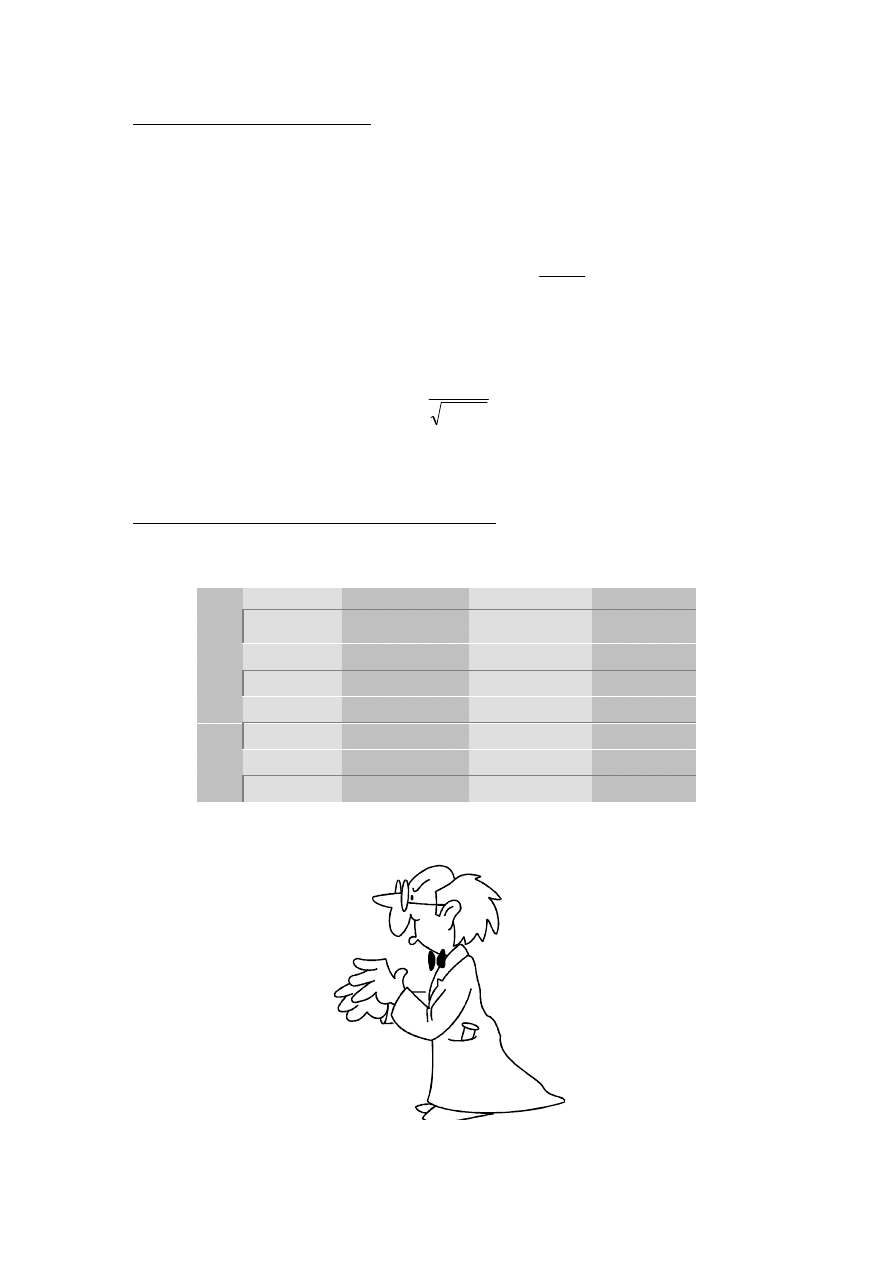
przebywana przez światło do ponad 35 km. Rysunek 1 przedstawia w nieco uproszczony
sposób ideę eksperymentu Michelsona. Światło ze źródła S pada na jedną ze ścian ośmio-
bocznego zwierciadła M i jest odbijane w kierunku odległego układu zwierciadeł D.
Stamtąd światło wraca do M i zostaje odbite w kierunku lunety T. Gdy zwierciadło M wi-
ruje, wówczas na ogół światło powracające z D nie pada na ściankę trzecią zwierciadła M
dokładnie pod kątem 45

0

i wobec tego nie trafia do lunety. Jeżeli jednak zwierciadło M

obraca się dostatecznie szybko tak, aby ścianka drugiego zwierciadła zdążyła zająć pozy-
cję uprzednio zajmowaną przez ściankę trzecią, to wówczas światło trafia do lunetki T. W
ten sposób, znając odległość MD i prędkość kątową obrotu zwierciadła M, możemy obli-
czyć prędkość światła:

11

00532 Fale EM i optyka D, part 1

TEORIA

(1)

ω

π

2

=

T

oraz

8

T

t

=

,

(2)

ω

π

ω

π

4

2

8

1

=

⋅

=

t

,

(3)

π

ω

4

2

2

⋅

=

=

l

t

l

c

, gdzie l =

MD

π

ω

l

c

⋅

=

8

)

4

(

5.

W oryginalnym eksperymencie wykonanym w 1924 roku wirujące zwierciadło znajdowa-
ło się w obserwatorium Mt. Wilson, a układ D na górze Mt. San Antonio, w odległości
35,4[km]. Odległość ta została wyznaczona z dokładnością przewyższającą 1 :

7

10

1

,

1

⋅

.

Ś

redni czas przebiegu światła tam i z powrotem, znaleziony w ponad tysiącu siedmiuset

wykonanych pomiarach wyniósł 0,00023[s]. Stąd obliczono, że prędkość światła w po-

wietrzu jest równa 299 728













s

km

, a po przeliczeniu dla próżni – 299 796













s

km

.

6.

Michelson podjął następnie próbę bezpośredniego pomiaru prędkości w próżni. W tym
celu zbudowano rurę o długości 1,6[km], z której można było odpompować powietrze aż
do ciśnienia 0,5[mm Hg]. Wirujące zwierciadło miało 32 ścianki i długość drogi światła w
rurze w wyniku wielokrotnych odbić wynosiła 16[km]. Michelson zmarł w 1931 roku,
przed rozpoczęciem eksperymentu. Wykonane doświadczenie, już po jego śmierci, dało

wynik 299 774













s

km

. Całe urządzenie zostało zniszczone przez trzęsienie Ziemi w 1933

roku.

S

T

7

1

5

3

2

6

4

8

D

Rys. 1

M

12

00532 Fale EM i optyka D, part 1

TEORIA

7.

Współczesne metody pomiarów. We wcześniejszych pomiarach prędkości światła wyko-
rzystywano migawki elektrooptyczne, takie jak komórka Kerra, ale podstawowe założenia
tych metod nie różniły się od ich poprzedniczek. Opracowano również szereg bardzo pre-
cyzyjnych metod, w których wykorzystano rezonatory wnękowe, interferencję mikrofal,
widma rotacyjne itd. Obecnie przyjmuje się, że prędkość światła wynosi

s

km

c

3

,

0

793

299

±

=

Prędkość światła można wyznaczyć pośrednio ze stosunku wielkości pewnych jednostek elektromagne-
tycznych i elektrostatycznych, które wyprowadza się z równań Maxwella:

0

0

1

ε

µ

⋅

=

c

Jednak dokładność osiągana w ten sposób jest niższa od dokładności bezpośrednich pomiarów, chociaż z
drugiej strony jest to niezaprzeczalnie wartościowa droga potwierdzenia teorii elektromagnetycznej.

8.

Wyniki ciekawszych pomiarów prędkości światła:

Lp. Nazwisko

Data pomiaru Wynik w m/s

Błąd w m/s

1.

Fizeau

1849

8

10

133

,

3

⋅

-

2.

Foucault

1862

8

10

98

,

2

⋅

500 000

3.

Michelson

1880

8

10

9991

,

2

⋅

50 000

4.

Michelson

1926

8

10

99796

,

2

⋅

4 000

5.

Anderson

1941

8

10

99776

,

2

⋅

14 000

6.

Bergstrand 1950

8

10

997927

,

2

⋅

250

7.

Edge

1956

8

10

997929

,

2

⋅

200