1

00536 Fale EM i optyka D – part 5

TEORIA

00536

Fale EM i optyka D, część 5

Przejście światła przez płaską płytkę.

Soczewki i zwierciadła.

Rozpraszanie światła.

Instrukcja dla zdającego
1.

Proszę sprawdzić, czy arkusz teoretyczny zawiera 12
stron. Ewentualny brak należy zgłosić.

2.

Do arkusza może być dołączona karta wzorów i sta-
łych fizycznych. Jeśli jest, należy ją dołączyć do od-
dawanej pracy.

3.

Proszę uważnie i ze zrozumieniem przeczytać zawar-
tość arkusza.

4.

Proszę precyzyjnie wykonywać polecenia zawarte w
arkuszu: rozwiązać przykładowe zadania, wyprowa-
dzić wzory, gdy jest takie polecenie.

5.

Proszę analizować wszelkie wykresy i rysunki pod
kątem ich zrozumienia.

6.

W trakcie obliczeń można korzystać z kalkulatora.

7.

Wszelkie fragmenty trudniejsze proszę zaznaczyć w
celu ich późniejszego przedyskutowania.

8.

Uzupełniaj wiadomości zawarte w arkuszu o informa-
cje zawarte w Internecie i dostępnej ci literaturze.

ś

yczymy powodzenia!

(Wpisuje zdający przed rozpoczęciem pracy)

PESEL ZDAJĄCEGO

Aktualizacja

Styczeń

ROK 2009

Dane osobowe właściciela arkusza

2

00536 Fale EM i optyka D – part 5

TEORIA

Temat 175

Przejście światła przez pryzmat i płytkę

płaską równoległościenną.

1.

Bryła ograniczona ścianami płaskimi przecinającymi się pod kątem

ϕ

stanowi pryzmat.

Kąt dwuścienny

ϕ

nosi nazwę

kąta łamiącego pryzmatu

. Prosta AB, wzdłuż której przeci-

nają się płaszczyzny ścian bocznych, nosi nazwę

krawędzi pryzmatu

(rys. 1). Ściana prze-

ciwległa kątowi

ϕ

może mieć kształt dowolny, gdyż nie ma ona wpływu na bieg promieni.

Często na schematycznych rysunkach pryzmatów trzecia ściana przecina ściany boczne w
równych odległościach od krawędzi. Wtedy pryzmat w przekroju prostopadłym do kra-
wędzi przedstawia się jako trójkąt równoramienny (rys. 2). Ściana przeciwległa do krawę-
dzi nosi nazwę

podstawy pryzmatu

.

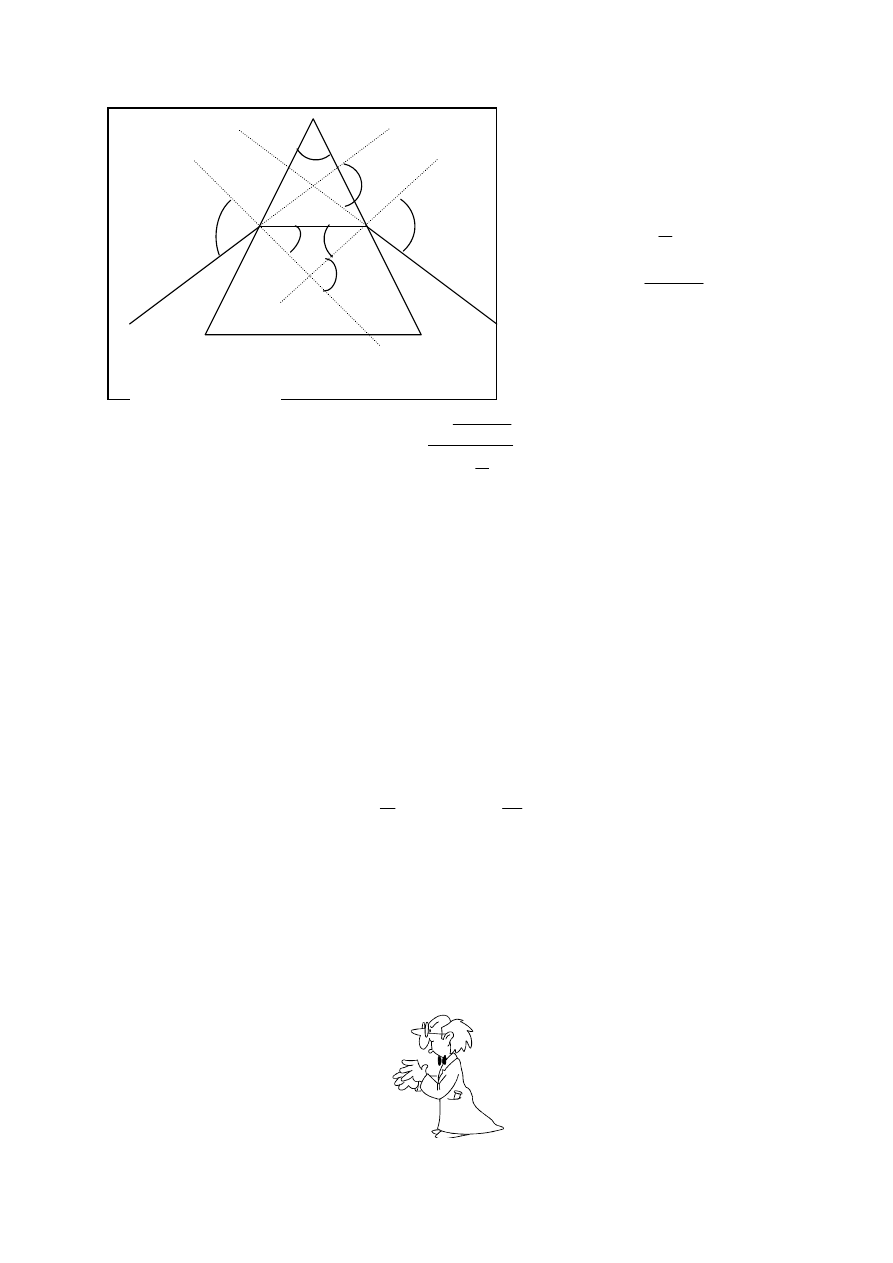
2.

Niech promień monochromatyczny pada na ścianę pryzmatu pod kątem

α

, załamuje się

pod kątem

β

(rys. 2), pada na drugą ścianę pod kątem

β

1

i wychodzi z niej pod kątem

α

1

.

Normalne do obu ścian bocznych pryzmatu tworzą ze sobą kąt równy kątowi łamiącemu
pryzmatu

ϕ

. Przedłużenie promieni padającego i wychodzącego z pryzmatu tworzą kąt

δ

,

zwany

kątem odchylenia pryzmatu

.

3.

Postaramy się wyrazić współczynnik załamania pryzmatu w zależności od kątów

ϕ

i

δ

. W

tym celu musimy znaleźć zależności między kątami

ϕ

,

δ

,

α

i

β

, aby móc podstawić odpo-

wiednie wartości na współczynnik załamania

(1)

β

α

sin

sin

=

n

.

Z twierdzenia o kącie zewnętrznym w trójkącie wynika, że

(2a)

1

β

β

ϕ

+

=

oraz (2b)

1

1

β

α

β

α

δ

−

+

−

=

.

We wzorach wystąpiły dodatkowo kąty

α

1

i

β

1

. Doświadczenie uczy, że zmiana kąta pa-

dania

α

pociąga za sobą zmianę kąta

α

1

i zmianę kąta

δ

. Początkowo przy zmniejszaniu

kąta padania

α

kąt odchylenia

δ

stopniowo się zmniejsza, przy pewnej wartości kąta

α

osiąga minimum, a następnie przy dalszym zmniejszaniu kąta

α

kąt odchylenia

δ

znów

rośnie. Tej najmniejszej wartości kąta odchylenia

δ

min

, zwanej kątem najmniejszego

odchylenia, odpowiada równość kątów

β

i

β

1

. Stąd wynika równość kątów

α

i

α

1

. Promień

załamany biegnie w tych warunkach równolegle do podstawy pryzmatu (rys. 3).

Rys. 2

ϕϕϕϕ

B

A

Rys. 1

β

1

δ

ϕ

α

1

α

N’

N

β

ϕ

3

00536 Fale EM i optyka D – part 5

TEORIA

Gdy spełnione są omówione powyżej
zależności, to równania (2a) i (2b)
przyjmą postać:

(3)

ϕ

= 2

β

oraz

(4)

δ

min

= 2

α

– 2

β

, a zatem

(5)

2

ϕ

β

=

i...

(6)

2

min

ϕ

δ

α

+

=

.

Po wstawieniu do wzoru (1)
otrzymamy:

(7)

2

sin

2

sin

min

ϕ

ϕ

δ

+

=

n

.

4.

Kąt

ϕ

zależy od kształtu pryzmatu i jest dla danego pryzmatu stały. Kat

δ

min

natomiast jest

różny dla promieni różnych barw. Gdy na pryzmat pada wiązka promieniowania
złożonego (niemonochromatycznego), to każdy ze składowych promieni załamuje się pod
innym kątem. Mówimy wówczas o zjawisku rozszczepienie (dyspersji) światła w
pryzmacie. Jeżeli na pryzmat szklany pada wąska wiązka światła białego, to na ekranie
ustawionym poza pryzmatem, otrzymamy smugę świetlną, w której barwy przechodzą
jedna w drugą w sposób ciągły. Smugę tę nazywamy widmem ciągłym. Najbardziej
odchylony od biegu pierwotnego jest promień fioletowy, najmniej odchylony – czerwony.

5.

Inna zależność między wartością współczynnika załamania, kątem odchylenia i kątem
łamiącym znajdziemy przy założeniu, że kąt łamiący pryzmatu i kąt padania promienia na
pryzmat są bardzo małe. Wtedy opierając się na przybliżonej równości sin

α

≈

α

, a także

sin

β

≈

β

piszemy:

(8)

β

α

=

n

oraz (9)

1

1

β

α

=

n

, czyli

(8a)

β

α

⋅

=

n

i (9a)

1

1

β

α

⋅

=

n

Podstawiając powyższe tożsamości do wzoru na kąt odchylenia pryzmatu

δ

otrzymujemy:

(10)

(

)

(

) (

)

1

1

1

1

β

β

δ

β

β

α

α

δ

+

⋅

−

=

⇒

−

−

+

=

n

.

Ostatecznie dostajemy:

(11)

(

)

ϕ

δ

⋅

−

=

1

n

β

δ

min

ϕ

α

α

N’

N

β

ϕ

Rys. 3

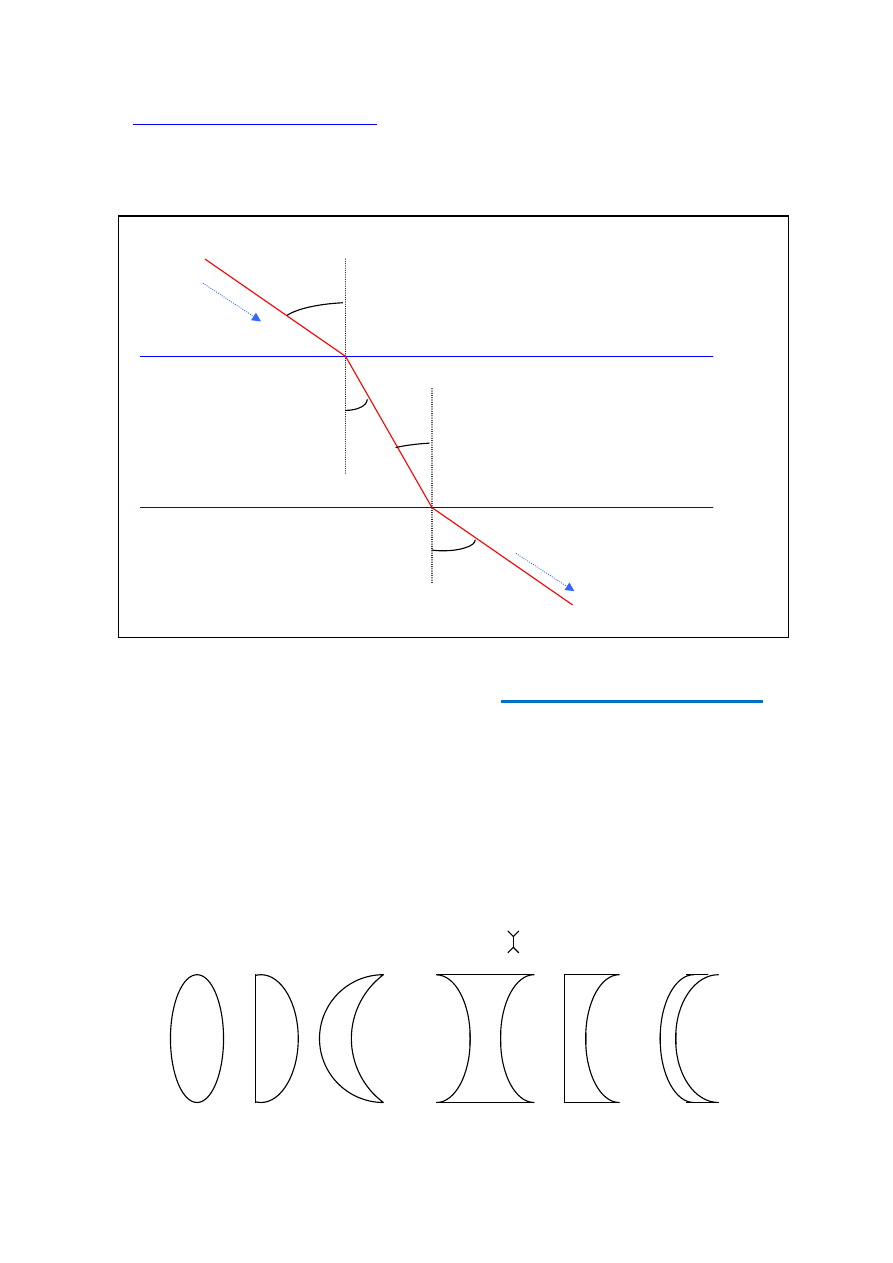
4

00536 Fale EM i optyka D – part 5

TEORIA

6.

Płytka płasko-równoległościenna

. Podczas przejścia przez płytkę o ścianch płaskich i

równoległych promień ulega dwukrotnemu załamaniu (rys. 4). Jeśli ośrodek, z którego
promień wchodzi do płytki i ośrodke, do którego on z płytki wychodzi jest ten sam,
promień ulega równoległemu przesunięciu.

Temat 176

Soczewki i ich rodzaje.

1.

Dotychczas analizowaliśmy załamanie światła na powierzchniach płaskich; obecnie
przejdziemy do badania załamania światła w soczewkach.

2.

Soczewkami nazywamy bryły przezroczyste, ograniczone powierzchniami regularnymi:
kulistymi, parabolicznymi, walcowymi itp. Zajmiemy się soczewkami sporządzonymi z
materiału posiadającego większą gęstość optyczną niż ośrodek. Tego rodzaju soczewki
działają skupiająco na wiązkę promieni, jeśli w środkowej części są grubsze niż na brze-
gach. Na rys. 1 przedstawione są trzy rodzaje soczewek kulistych skupiających i trzy ro-
dzaje soczewek kulistych rozpraszających. Są to soczewki dwuwypukłe, płasko-wypukłe,
wklęsło-wypukłe. Soczewki zbierające przyjęto oznaczać schematycznie na rysunkach
symbolem ↕, a soczewki rozpraszające – symbolem .

β

β

α

α

Rys. 4

5

00536 Fale EM i optyka D – part 5

TEORIA

3.

Soczewka wykonana jest z przezroczystego materiału i może skupiać przechodzące przez
nią promieniowanie i wytwarzać obraz. Soczewki wykonywane przez człowieka i stoso-
wane w przyrządach optycznych z reguły ze szkła lub plastyku, natomiast soczewkę oczną
tworzy przezroczysta błona wypełniona przejrzystą cieczą.

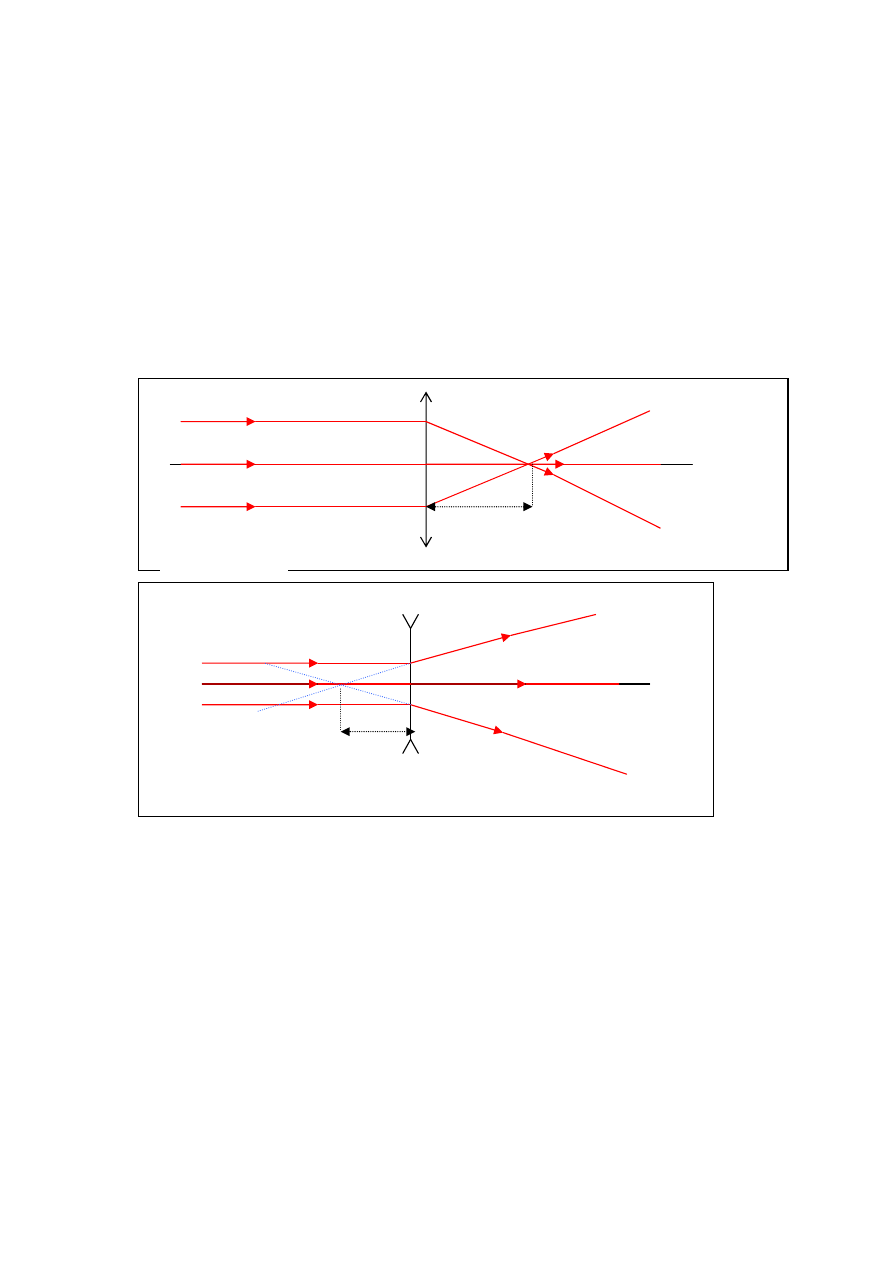
4.

Soczewka skupiająca załamuje promienie w kierunku swojej osi, która jest linią przecho-
dzącą przez środki krzywizn jej powierzchni ograniczających. W ten sposób równoległa
wiązka promieni jest przez soczewkę skupiana w jednym punkcie (rys. 2). Każdy wie, że
soczewka skupiająca może skupić promienie słoneczne w punkcie i że natężenie światła w
takim punkcie może być wystarczająco wysokie na to, żeby zapalić np. papier. W so-
czewkach rozpraszających promienie są odchylane od osi soczewki (rys. 3).

5.

Jeżeli do soczewki docierają promienie z odległego źródła, tworząc wiązkę promieni pra-
wie równoległych do osi soczewki, to zostają one załamane przez soczewkę i skupione w
jednym punkcie F, zwanym

ogniskiem, tworząc tam obraz źródła. W soczewce rozprasza-

jącej promienie równoległe po przejściu przez soczewkę rozchodzą się na zewnątrz osi
soczewki, tak że wydaje się, iż wyszły one z jednego punktu F’ znajdującego się po dru-
giej stronie soczewki – jest to ognisko soczewki rozpraszającej. Odległość od środka so-
czewki do ogniska nazywa się

ogniskową f. Zwyczajowo przyjmuje się, że ogniskowa dla

soczewki skupiającej jest dodatnia, a dla soczewki rozpraszającej ujemna.

6.

Ogniskowa soczewki zależy od współczynnika załamania światła n materiału, z którego
jest wykonana oraz od promieni krzywizn r

1

i r

2

powierzchni ograniczających soczewkę.

Związek pomiędzy tymi wielkościami można wyprowadzić korzystając z prawa Snelliusa,
przy założeniu, że kąty padania są małe. Wyprowadzenie tej zależności jest stosunkowo
długie i podamy tu tylko ostateczną postać wzoru, która dla materiału o współczynniku
załamania n, w ośrodku o współczynniku załamania 1 (próżnia), jest następująca:

F

f

główna oś optyczna soczewki

Rys. 2

Rys. 3

F’



f



6

00536 Fale EM i optyka D – part 5

TEORIA

(1)

( )













+

⋅

−

=

2

1

1

1

1

1

r

r

n

f

,

natomiast dla soczewki zanurzonej w cieczy o współczynniku załamania n

1

mamy:

(2)













+

⋅













−

=

2

1

1

1

1

1

1

r

r

n

n

f

Wzory (1) i (2) to

wzory szlifierzy soczewek

. Przy korzystaniu z tych równań warto pamię-

tać o przestrzeganiu kilku reguł:
⇒

powierzchnia płaska (np. przy analizie soczewek płasko-wypukłych) jest traktowana
jako wycinek powierzchni sferycznej o nieskończonym promieniu krzywizny,

⇒

w przypadku soczewek dwuwypukłych oba promienie krzywizny r

1

i r

2

uważamy za

dodatnie,

⇒

w przypadku soczewek dwuwklęsłych oba promienie krzywizny r

1

i r

2

uważamy za

ujemne,

⇒

jeśli stosując wzory (1) i (2) otrzymamy ujemną wartość ogniskowej, to oznacza, że
mamy do czynienia z soczewką rozpraszającą,

⇒

odwrotność ogniskowej zwana jest zdolnością skupiającą soczewki Z, którą mierzymy

w dioptriach:

f

1

= Z oraz [Z] = [m

-1

].

Temat 177

Wzór soczewkowy Gaussa.

1.

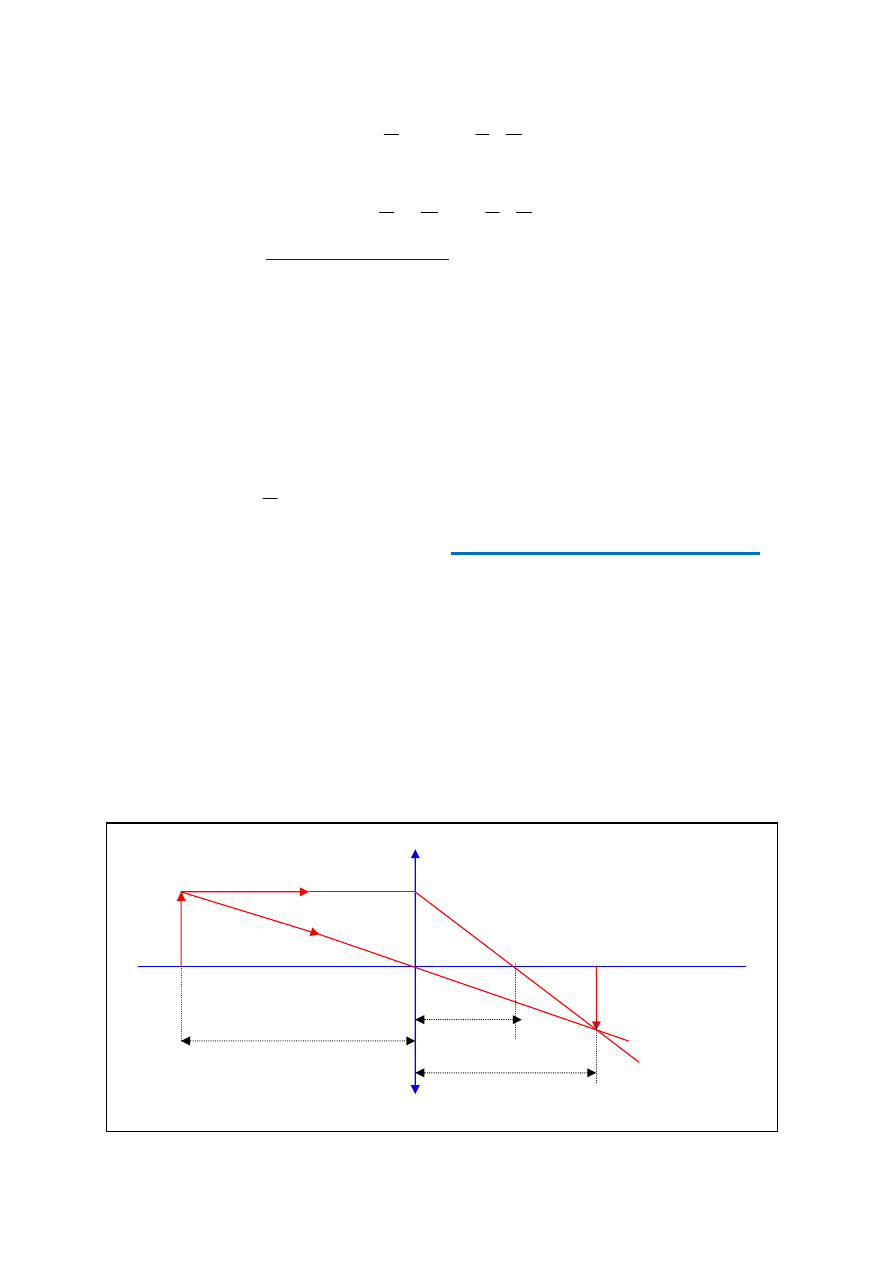
Na rys. 1 przedstawiono metodę graficznego wyznaczania położenia obrazu. Do kon-
strukcji jest przydatna znajomość biegu tzw. promieni głównych:
⇒

promień (1) wychodzący z ogniska po przejściu przez soczewkę staje się równoległy
do osi optycznej soczewki,

⇒

promień (2) biegnący równolegle do osi optycznej, po przejściu przez soczewkę, prze-
cina oś optyczną w punkcie zwanym ogniskiem soczewki,

⇒

promień (3) przechodzący przez środek geometryczny soczewki nie zmienia kierunku
swojego biegu.

2.

Wyposażenie w powyższe informacje najpierw rysujemy promień (2), a następnie pro-
mień (3):

f

y

x

F

P

0

A’

B’

B

A

7

00536 Fale EM i optyka D – part 5

TEORIA

W celu usystematyzowania symboli stosowanych przy opisie soczewek i obrazów za ich pomocą otrzymy-
wanych, podajemy poniżej ich zestawienie:

⇒

AB – strzałka przedstawiająca symbol świecącego przedmiotu, jego rozmiary najczę-
ściej oznaczamy przez X,

⇒

x – odległość przedmiotu od soczewki, zwana odległością przedmiotową,

⇒

A’B’ – strzałka przedstawiająca symbol otrzymanego za pomocą soczewki obrazu,
którego wielkość oznaczamy jako Y,

⇒

y – odległość obrazu od soczewki, zwana odległością obrazową,

⇒

f – odległość ogniska od soczewki, zwana ogniskową,

3.

Wyprowadzimy teraz ilościowy związek między odległością przedmiotową, odległością
obrazową i ogniskową soczewki. Trójkąty ABO i A’B’O są trójkątami podobnymi, a za-
tem spełniona jest równość:

(1)

x

y

AB

B

A

=

'

'

,

trójkąty POF oraz A’B’F są także trójkątami podobnymi, toteż:

(2)

f

f

y

PO

B

A

−

=

'

'

.

Ponieważ PO = AB, więc prawe strony równań (1) i (2) są sobie równe:

(3)

f

f

y

x

y

−

=

, czyli

(4)

y

x

f

1

1

1

+

=

Wzór (4) nazywamy wzorem dla cienkich soczewek lub wzorem soczewkowym Gaussa.

4.

Powiększenie liniowe soczewki określamy następująco:

(5)

x

y

X

Y

p

=

=

.

Im dalej od soczewki tworzy się obraz, tym jego rozmiary poprzeczne są wieksze.

Rys. 1

8

00536 Fale EM i optyka D – part 5

TEORIA

Temat 178 Obrazy otrzymywane za pomocą soczewek.

1.

W celu graficznego przedstawienia obrazów tworzących się w soczewkach cienkich, nale-
ży zaznaczyć schematycznie soczewkę, nakreślić jej oś główną i zaznaczyć po obu stro-
nach soczewki punkty F i 2F. Obraz punktu znajdujemy biorąc pod uwagę bieg dwóch w
zasadzie dowolnych promieni (wybieramy je z reguły z trzech tzw. głównych promieni).
Punkt S na poniższych rysunkach jest zwany środkiem optycznym soczewki cienkiej. Pa-
miętajmy jeszcze, że obrazy rzeczywiste tworzą się na przecięciach promieni rzeczywi-
stych, a obrazy pozorne – na przecięciach przedłużeń promieni rzeczywistych.

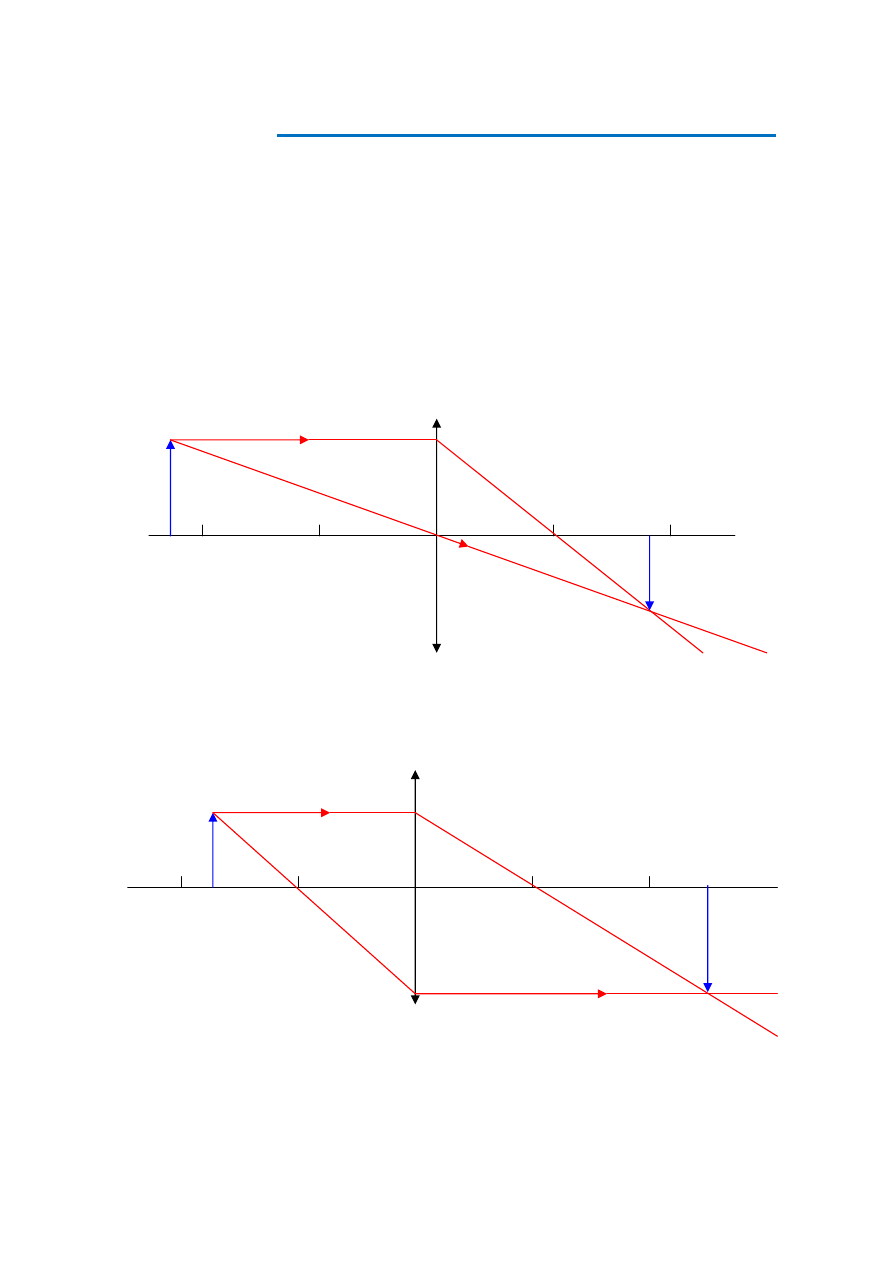
2.

Obrazy otrzymywane za pomocą soczewek skupiających.

a)

odległość przedmiotowa jest większa od podwójnej ogniskowej: x

>

2f. Powstaje ob-

raz rzeczywisty, odwrócony i pomniejszony.

b)

odległość przedmiotowa spełnia warunek: f

<

x

<

2f. Powstaje obraz rzeczywisty, od-

wrócony i powiększony.

2F

2F

F

S

F

2F

2F

F

S

F

9

00536 Fale EM i optyka D – part 5

TEORIA

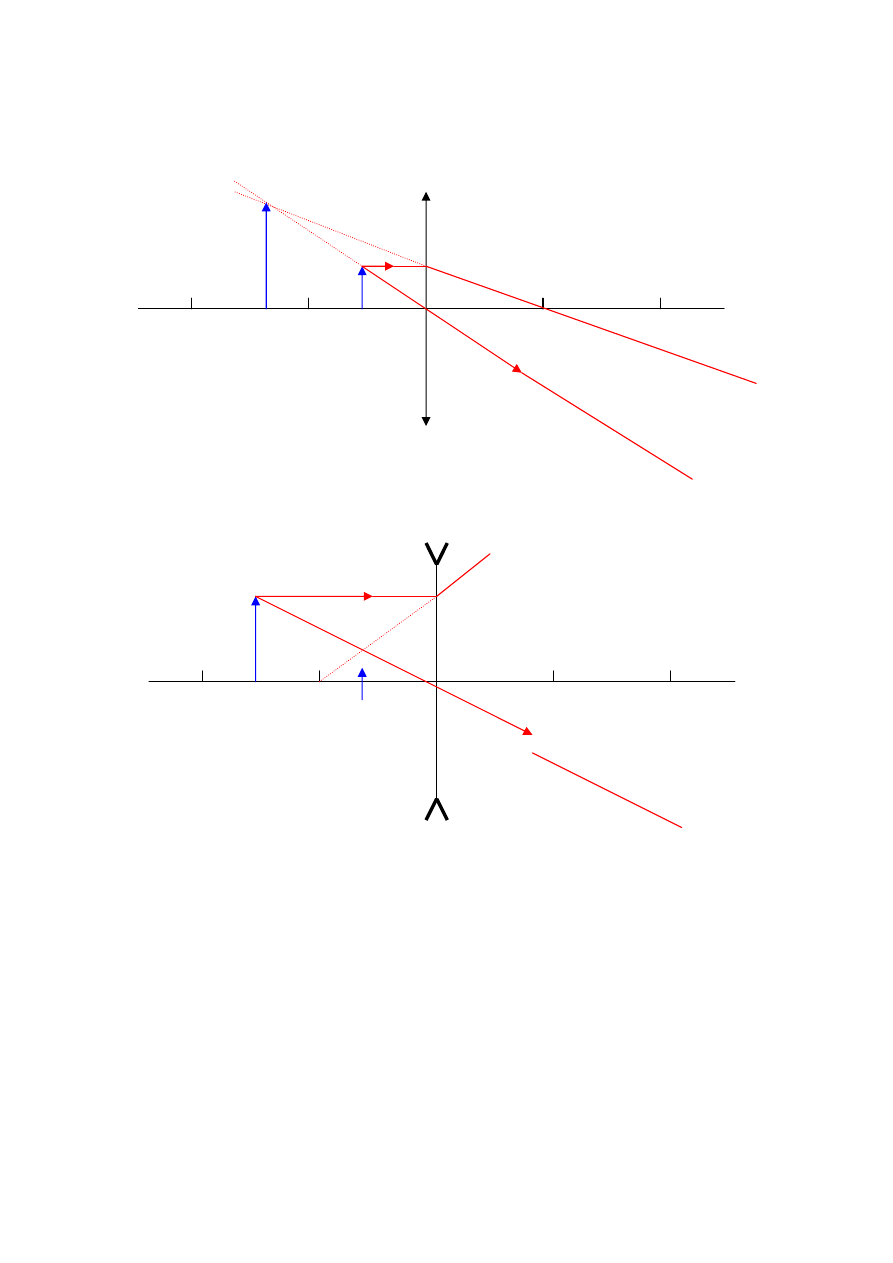
c)

przedmiot znajduje się w odległości mniejszej niż ogniskowa: x

<

f. Powstaje obraz

pozorny, prosty i powiększony.

3.

Obrazy otrzymywane za pomocą soczewek rozpraszających są pozorne, pomniejszone i
proste w każdym przypadku, dlatego zamiast trzech rysunków podamy tylko jeden:

4.

Po analizie powyższych rysunków spróbuj odpowiedzieć na dwa pytania:
⇒

jaki obraz wytworzy soczewka skupiająca, jeżeli przedmiot (świecącą strzałkę) umie-
ścimy w odległości x = 2f,

⇒

jaki obraz wytworzy soczewka skupiająca, jeżeli przedmiot (świecącą strzałkę) umie-
ścimy w odległości x = f.

2F

2F

F

S

F

2F

2F

F

S

F

10

00536 Fale EM i optyka D – part 5

TEORIA

Temat 179

Równanie zwierciadła sferycznego.

1.

Zwierciadłami nazywać będziemy powierzchnie, które odbijają (całkowicie lub prawie
całkowicie) padające na nie promieniowanie. Dobrymi zwierciadłami są np. wypolerowa-
ne powierzchnie metali lub szkła. Jeszcze lepszym zwierciadłem jest powierzchnia świeżo
nalanej do naczynia rtęci. Gdy światło przy przejściu z wody lub szkła do powietrza albo
ze szkła do wody pod odpowiednio dużym kątem na powierzchnię graniczną, zachodzi
całkowite odbicie promieni padających. Powierzchnie całkowicie odbijające stanowią naj-
lepsze zwierciadła, jakimi rozporządzamy.

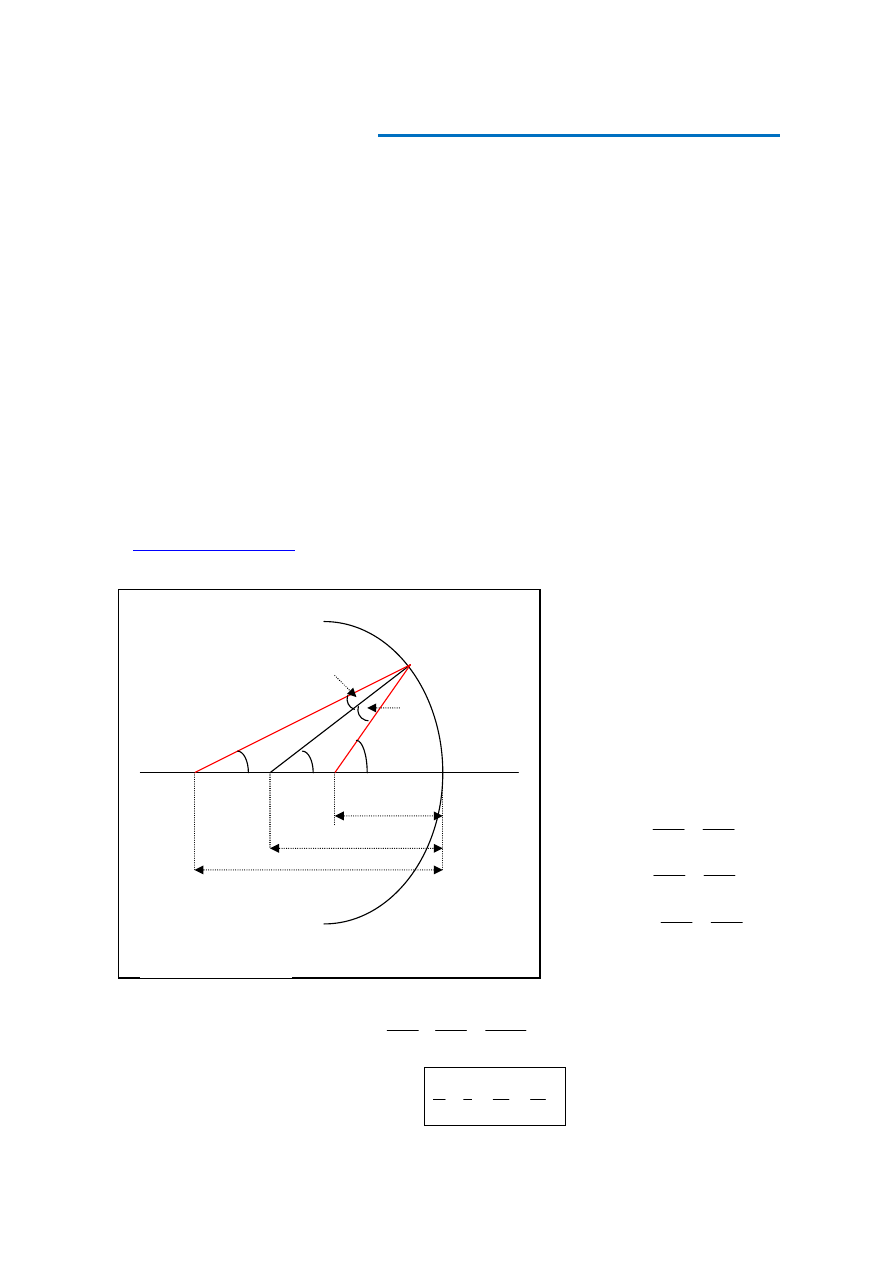
2.

Niech przedmiotem będzie punkt 0 na osi optycznej. Obrazem, w kierunku którego zbiega
się światło odbite przez zwierciadło, jest inny punkt I, także na osi optycznej. Aby spełnić
prawo odbicia światła

α

=

α

’, powierzchnia zwierciadła musi być zakrzywiona, jak ilu-

struje to rysunek 1. Normalna wystawiona w jakimkolwiek punkcie powierzchni, jeżeli
ma długość równą promieniowi krzywizny R zwierciadła, wyznacza środek krzywizny C.
Punkt, w którym oś przebija tę powierzchnię, nazywamy punktem wierzchołkowym W
zwierciadła. Odległość od przedmiotu do punktu wierzchołkowego nazywamy nazywana
jest odległością przedmiotową o, odległość zaś od punktu wierzchołkowego do obrazu –
odległością obrazową i.

3.

Równanie zwierciadła

można wyprowadzić z twierdzenia mówiącego, że kąt zewnętrzny

w trójkącie równy jest sumie dwu przeciwległych kątów wewnętrznych. Jak wynika z

konstrukcji:

(1)

α

+

β

=

γ

, oraz

(2)

β

+ 2

α

=

δ

.

Mnożąc równanie (1) przez 2 i
odejmując równanie (2) dosta-
jemy:

(3)

β

+

δ

= 2

γ

Jeżeli kąty są małe, to są równe
(lub w przybliżeniu równe)
wyrażeniom:

(4)

o

PW

W

PW

=

≈

0

β

,

(5)

R

PW

CW

PW

=

≈

γ

,

(6)

i

PW

IW

PW

=

≈

δ

.

Podstawiając wyrażenia (4), (5)
i (6) do równania (3) dostaje-

my:

(7)

R

PW

i

PW

o

PW

2

=

+

,

Ostatecznie mamy:

(8)

R

f

i

o

2

1

1

1

=

=

+

Jeżeli o

→

∞

, wówczas odległość obrazowa staje się równa ogniskowej, i = f.

P

i

R

o

W

I

C

0

α

’

α

γ

δ

β

Rys. 1

Równanie zwierciadła

sferycznego.

11

00536 Fale EM i optyka D – part 5

TEORIA

4.

Równanie zwierciadła sferycznego zawiera dwa parametry opisowe, ogniskową f i pro-
mień krzywizny R, oraz dwie wielkości funkcyjne, odległość przedmiotową o oraz odle-
głość obrazową i. Chociaż to równanie wyprowadzone zostało dla zwierciadła wklęsłego i
dla przedmiotów umieszczonych dalej od zwierciadła niż jego środek krzywizny, to samo
równanie obowiązuje również dla każdego położenia przedmiotu, a także dla zwierciadła
płaskiego i wypukłego.

5.

Reguła znaków

: Stosować będziemy następującą regułę znaków:

⇒

odległość przedmiotową przyjmuje się za dodatnią,

⇒

odległość obrazową przyjmuje się za dodatnią dla obrazu rzeczywistego i jako ujemną
dla obrazu pozornego (obraz leżący po tej samej stronie co przedmiot jest rzeczywisty,
po przeciwnej – pozorny),

⇒

ogniskowe są dodatnie dla układów skupiających, ujemne dla układów rozpraszają-
cych,

⇒

promień krzywizny zwierciadła, tak jak ogniskowa, jest dodatni dla zwierciadła wklę-
słego (skupiającego) i ujemny dla zwierciadła wypukłego (rozpraszającego).

6.

Zwierciadło płaskie

. Dla zwierciadła płaskiego R

→

∞

. Dlatego z równania zwierciadła

sferycznego otrzymujemy:

(9)

∞

=

+

2

1

1

i

o

, czyli o = – i. ,

co oznacza, że zwierciadła płaskie tworzą obrazy pozorne, symetryczne względem zwier-
ciadła.

Temat 180

Obrazy otrzymywane za pomocą

zwierciadeł sferycznych.

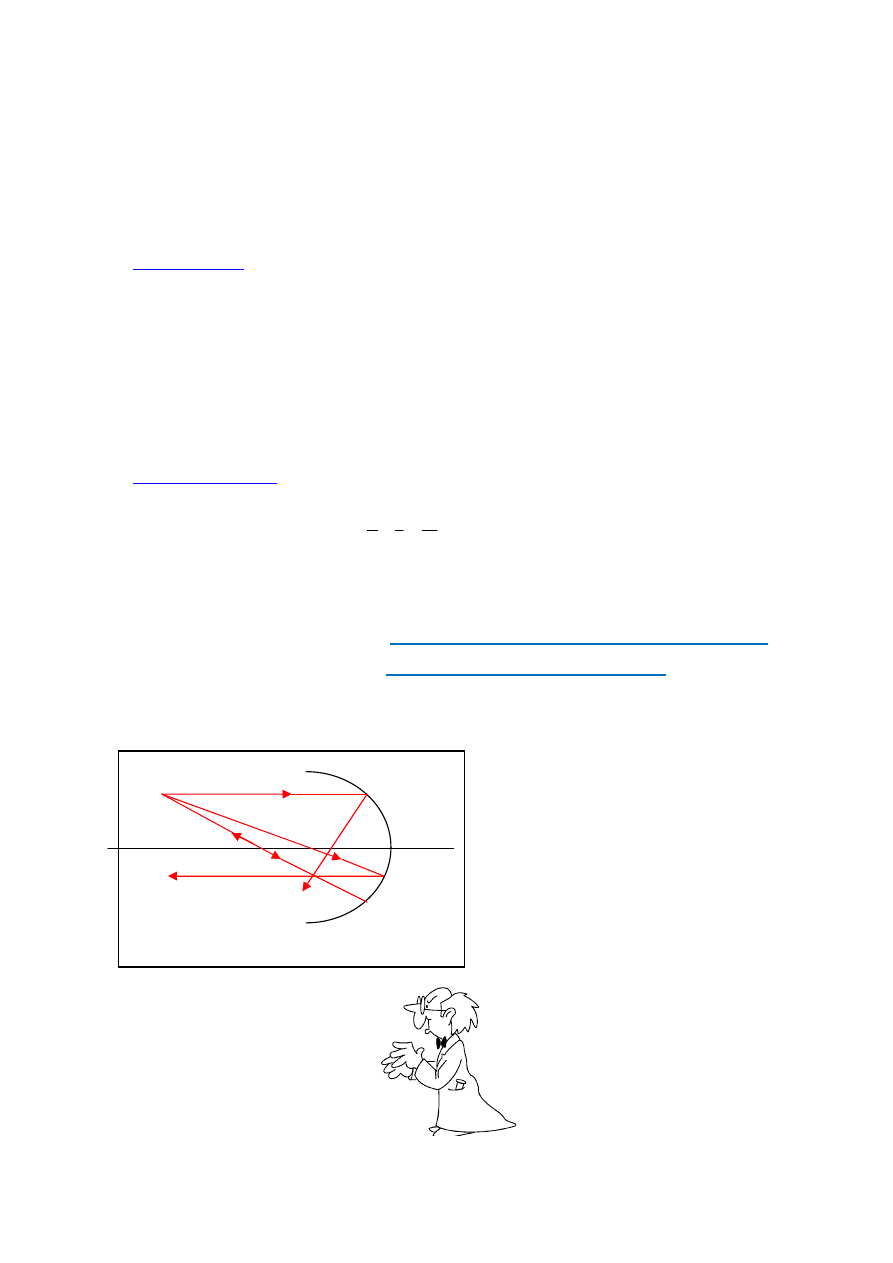
1.

Bieg promieni docierających i odbijających się od zwierciadeł przypomina analizy zwią-
zane z soczewkami cienkimi:

Promień (1) nazywamy promieniem
równoległym.
Promień (2) nazywamy promieniem
ogniskowym.
Promienień (3) nazywamy promieniem
głównym.

C

F

(3)

(2)

(1)

Rys. 1

12

00536 Fale EM i optyka D – part 5

TEORIA

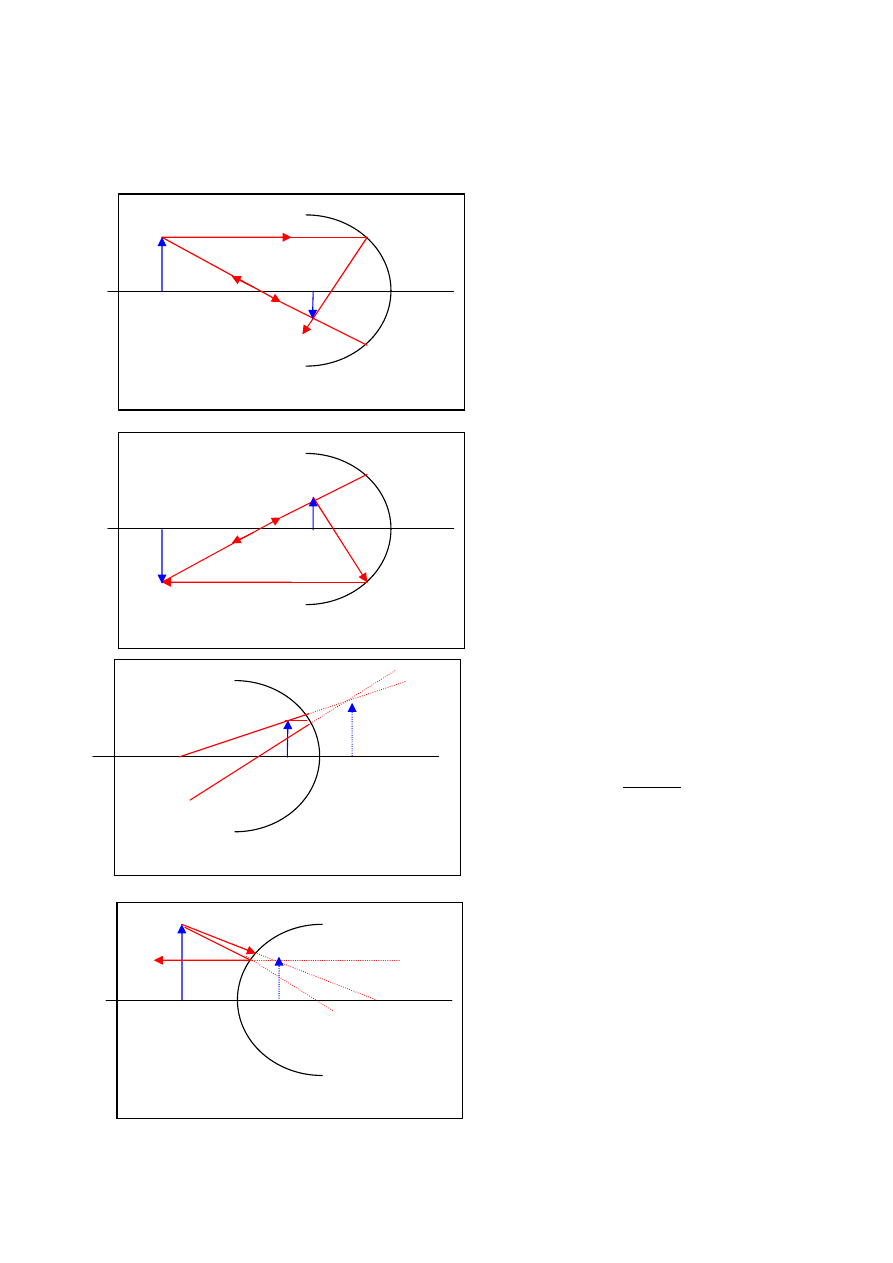
2.

Zwierciadła wklęsłe znali już starożytni Grecy. Archimedes miał podobno podpalić statek
atakujących Rzymian za pomocą ogromnego zwierciadła wklęsłego. Tworzenie obrazów
przedstawiają poniższe rysunki. Strzałka oznaczona jako X oznacza przedmiot, zaś Y –
obraz.

Odległość przedmiotowa jest większa od
podwójnej ogniskowej (rys. 2). Powstaje
obraz

rzeczywisty,

odwrócony

i

pomniejszony.







Odległość przedmiotowa jest większa od
ogniskowej, ale mniejsza od podwójnej
ogniskowej. Powstaje obraz rzeczywisty,
odwrócony i powiększony.

Przedmiot znajduje się w odległości mniej-
szej od ogniskowej zwierciadła. Powstaje
obraz powiększony, pozorny i prosty.

Obraz utworzony za pomocą zwierciadła
wypukłego

jest

zawsze

pozorny,

pomniejszony i prosty.

Y

X

C

F

Rys. 2

X

Y

C

F

Rys. 3

C

F

Rys. 4

C

F

Rys. 5