1

Ć

wiczenie 5

STATYCZNA PRÓBA SKRĘCANIA I WYZNACZANIE MODUŁU

SPRĘŻYSTOŚCI POSTACIOWEJ

Opracował: dr inż. Stefan Sawiak

1. Wprowadzenie

Próbę skręcania przeprowadza się na próbkach okrągłych o odpowiednio dobranych

częściach uchwytowych, które pozwalają na zamocowanie próbek w skręcarce. Próbkę
obciąża się na końcach dwoma, równoważącymi się momentami skręcającymi M

s

,

działającymi w płaszczyznach prostopadłych do osi próbki. Zakładamy, że próbka skręca się
równomiernie, czyli kąt obrotu poprzecznego przekroju jest proporcjonalny do odległości
tego przekroju od końca części pomiarowej próbki. Powstały wtedy stan odkształcenia próbki
określa wartość jednostkowego kąta skręcenia

φ′

odniesionego do jej długości pomiarowej.

Jest on równy

0

l

ϕ

φ

=

′

(1)

gdzie:

φ′

– jednostkowy kąt skręcenia odniesiony do długości pomiarowej próbki,

ϕ

–

całkowity kąt skręcenia próbki, l

0

– długość pomiarowa próbki.

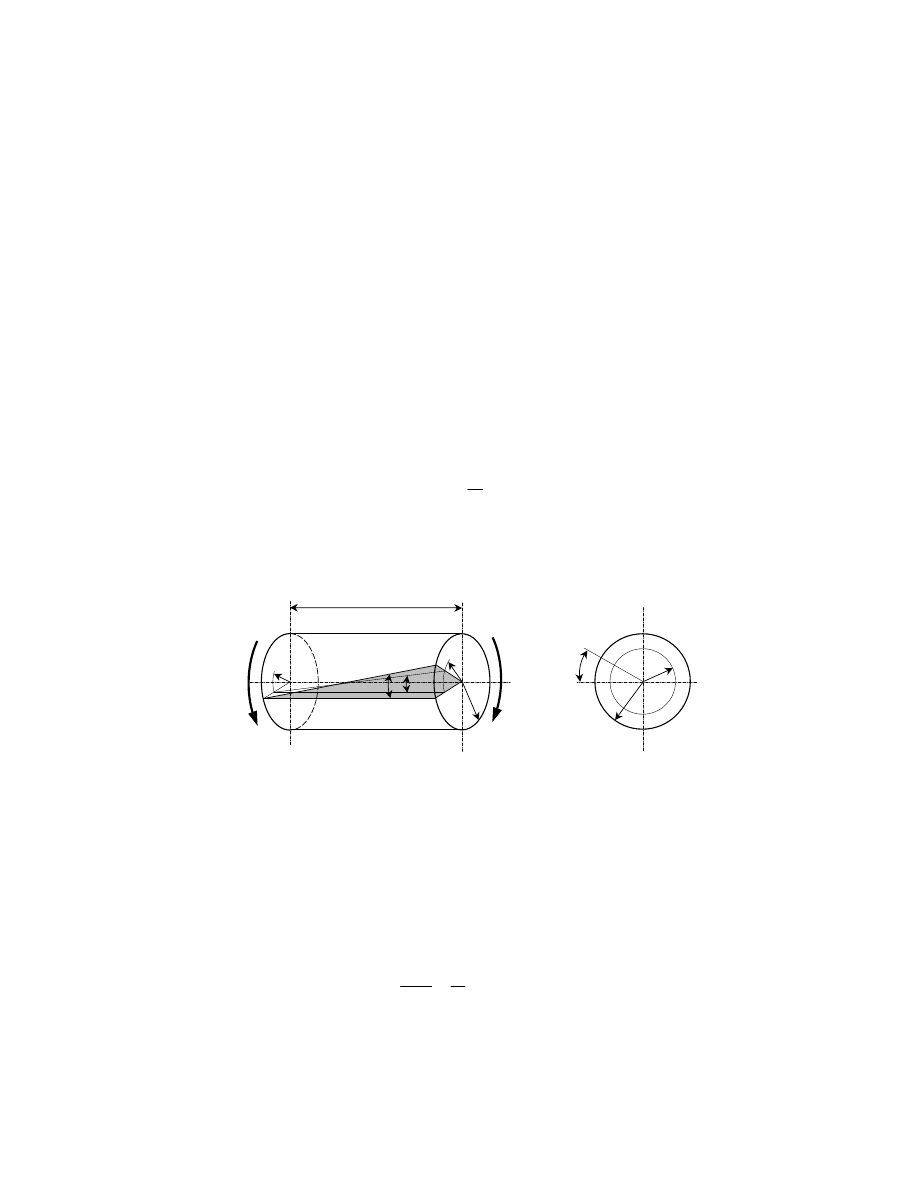
Rys. 1. Skręcanie próbki okrągłej

Powyższa równość wynika z założenia, słusznego dla materiałów jednorodnych, że

podczas odkształcenia próbki nie ulegają deformacji jej kołowe przekroje płaskie ze względu
na symetrię obrotową, a jedynie obracają się względem siebie o kąt

ϕ

. Natomiast warstwy

równoległe do osi próbki układają się wzdłuż linii śrubowej, nachylonej pod kątem

γ

do

tworzącej próbki.
Ze związku (1) wynika, że kąty odkształcenia postaciowego współosiowych warstw
walcowych w próbce są proporcjonalne do odległości

ρ

tych warstw od środka próbki, czyli

ρ

γ

γ

=

r

max

=const,

(2)

gdzie:

γ

max

– kąt odkształcenia postaciowego włókien skrajnych,

γ

– kąt odkształcenia

postaciowego włókien leżących wewnątrz próbki w odległości

ρ

od osi próbki, r – promień

r

ρ

γ

max

M

s

M

s

l

0

ϕ

γ

ρ

ρ

r

2

przekroju poprzecznego próbki,

ρ

– promień przekroju poprzecznego warstwy wewnętrznej

próbki.
Ponieważ w obszarze sprężystości obowiązuje prawo Hooke'a wyrażające się w przypadku
skręcania wzorem

γ

τ

G

=

(3)

oraz

max

max

γ

τ

G

=

(4)

przy czym: G – moduł sprężystości postaciowej materiału próbki (moduł Kirchhoffa),

τ

–

naprężenie tnące od skręcania.
Ze wzorów (2) i (3) wynika zależność

=

= C

ρ

τ

const.

(5)

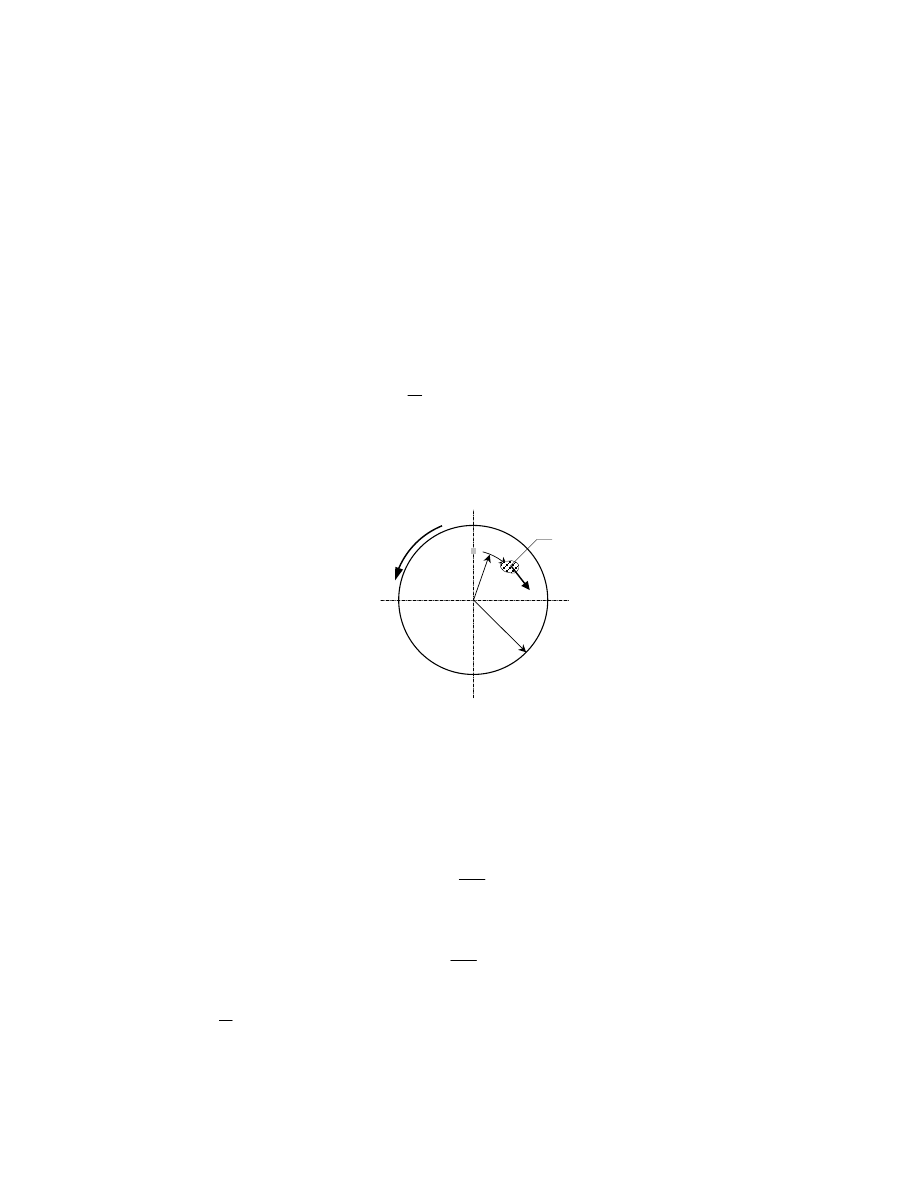
Wartość stałej C we wzorze (5) można otrzymać z warunku równości momentów sił
zewnętrznych i wewnętrznych o postaci (rys. 2)

Rys. 2. Moment skręcający sił zewnętrznych i naprężenia styczne

( )

( )

O

A

A

s

J

C

dA

C

dA

M

⋅

=

=

=

∫

∫

2

ρ

ρτ

,

(6)

gdzie

( )

∫

=

A

O

dA

J

2

ρ

– biegunowy moment bezwładności przekroju.

Stąd

O

s

J

M

C

=

,

(7)

czyli równanie (5) przyjmuje postać

ρ

τ

O

s

J

M

=

.

(8)

Dla

2

d

r

=

=

ρ

otrzymuje się największe naprężenia tnące, działające na konturze

zewnętrznym próbki równe

M

s

τ

r

ρ

dA
ρ

3

O

s

O

s

W

M

d

J

M

=

=

2

max

τ

,

(9)

gdzie W

O

– biegunowy wskaźnik przekroju na skręcanie równy

2

d

J

W

O

O

=

.

(10)

Biegunowy moment bezwładności J

O

pełnego przekroju kołowego wynosi (rys. 2)

( )

4

4

4

0

2

2

1

,

0

32

2

2

d

d

r

d

dA

J

r

A

O

≅

=

=

⋅

⋅

=

⋅

=

∫

∫

π

π

ρ

πρ

ρ

ρ

[m

4

],

(11)

natomiast biegunowy wskaźnik przekroju na skręcanie W

O

pełnego przekroju kołowego

wynosi

3

3

2

,

0

16

d

d

W

O

≅

=

π

[m

3

].

(12)

Podstawiając (12) do (9) otrzymujemy

3

3

max

2

,

0

16

d

M

d

M

s

s

≅

=

π

τ

.

(13)

Związek między kątem skręcania

ϕ

, a kątem odkształcenia postaciowego

γ

jest

następujący (rys. 1)

0

l

r

max

⋅

=

⋅

γ

ϕ

,

(14)

czyli

G

l

W

M

l

G

l

d

O

s

max

max

0

0

0

2

⋅

=

⋅

=

⋅

=

⋅

τ

γ

ϕ

,

(15)

albo

O

s

GJ

l

M

0

=

ϕ

,

(16)

sk

ą

d

ϕ

0

l

GJ

M

O

s

=

.

(17)

Dla pełnego przekroju kołowego wzory (15) i (16) przyjmuj

ą

posta

ć

G

d

l

M

G

d

l

M

s

s

4

0

4

0

10

32

≅

=

π

ϕ

,

(18)

ϕ

ϕ

π

0

4

0

4

1

0

32

l

G

d

,

l

G

d

M

s

≅

=

.

(19)

4

2. Cel ćwiczenia

2.1. Cel ogólny

Celem ogólnym jest zapoznanie si

ę

ze sposobem przeprowadzenia tzw. statycznej próby

skr

ę

cania pr

ę

tów okr

ą

głych, sposobem prowadzenia pomiarów, zapoznanie si

ę

ze zjawiskiem

histerezy spr

ęż

ystej, nabycie umiej

ę

tno

ś

ci wyznaczania wielko

ś

ci charakterystycznych przy

skr

ę

caniu dla stali w

ę

glowej.

2.2. Cele szczególne

1. Wyznaczenie modułu spr

ęż

ysto

ś

ci postaciowej Kirchhoffa G i liczby Poissona

ν

,

2. Wykonanie dla próbki stalowej wykresów:

a. histerezy spr

ęż

ystej

τ

(

γ

) w zakresie liniowo – spr

ęż

ystym,

b. napr

ęż

enie

τ

(

γ

) – k

ą

t odkształcenia postaciowego

γ

.

3. Wyznaczenie wielko

ś

ci charakteryzuj

ą

cych stal pod wzgl

ę

dem wytrzymało

ś

ciowym

przy skr

ę

caniu (granica plastyczno

ś

ci na skr

ę

canie: R

es

i wytrzymało

ść

na skr

ę

canie

R

ms

).

3. Wykres skręcania

Do celów praktycznych wykres skr

ę

cania sporz

ą

dza si

ę

w układzie współrz

ę

dnych M

s

–

ϕ

, gdzie: M

s

– moment skr

ę

caj

ą

cy próbk

ę

,

ϕ

– k

ą

t skr

ę

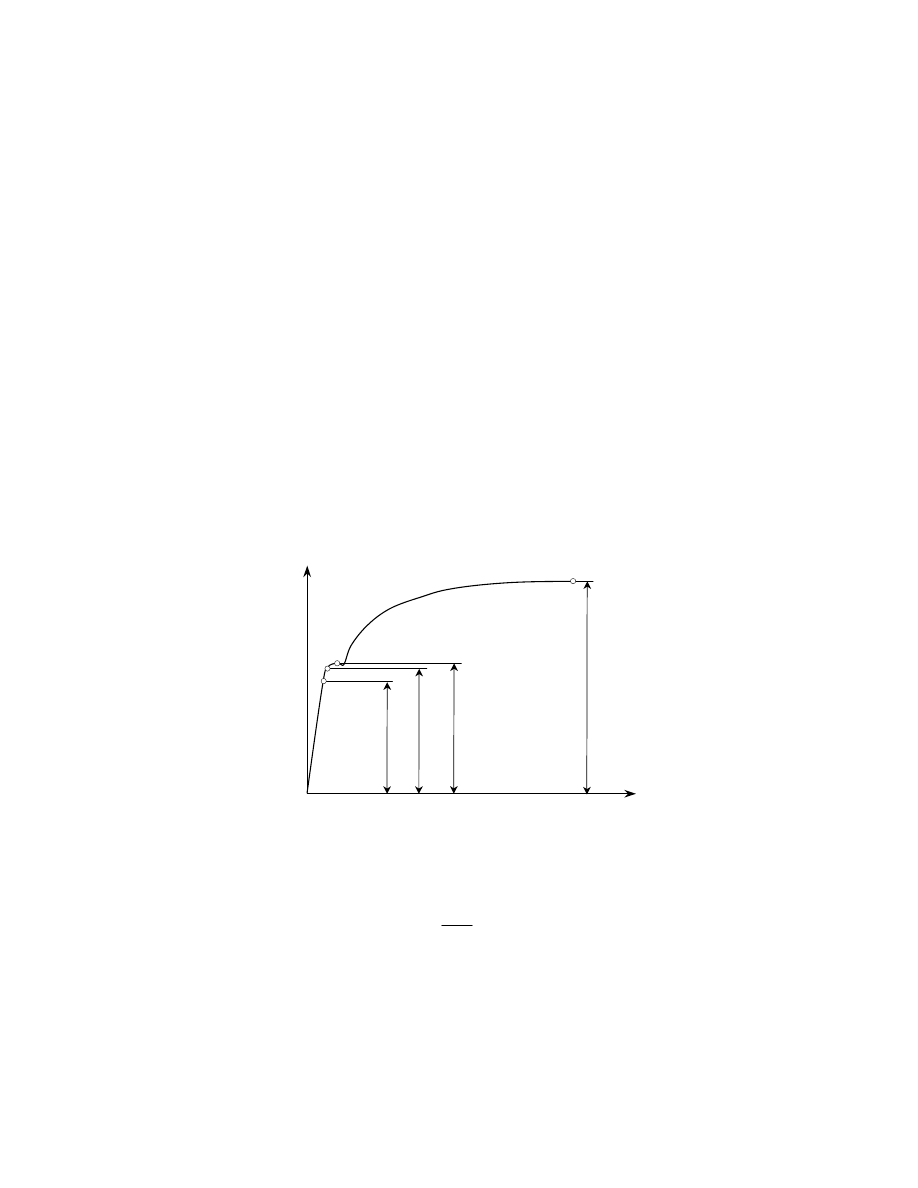
cenia próbki (rys. 3)

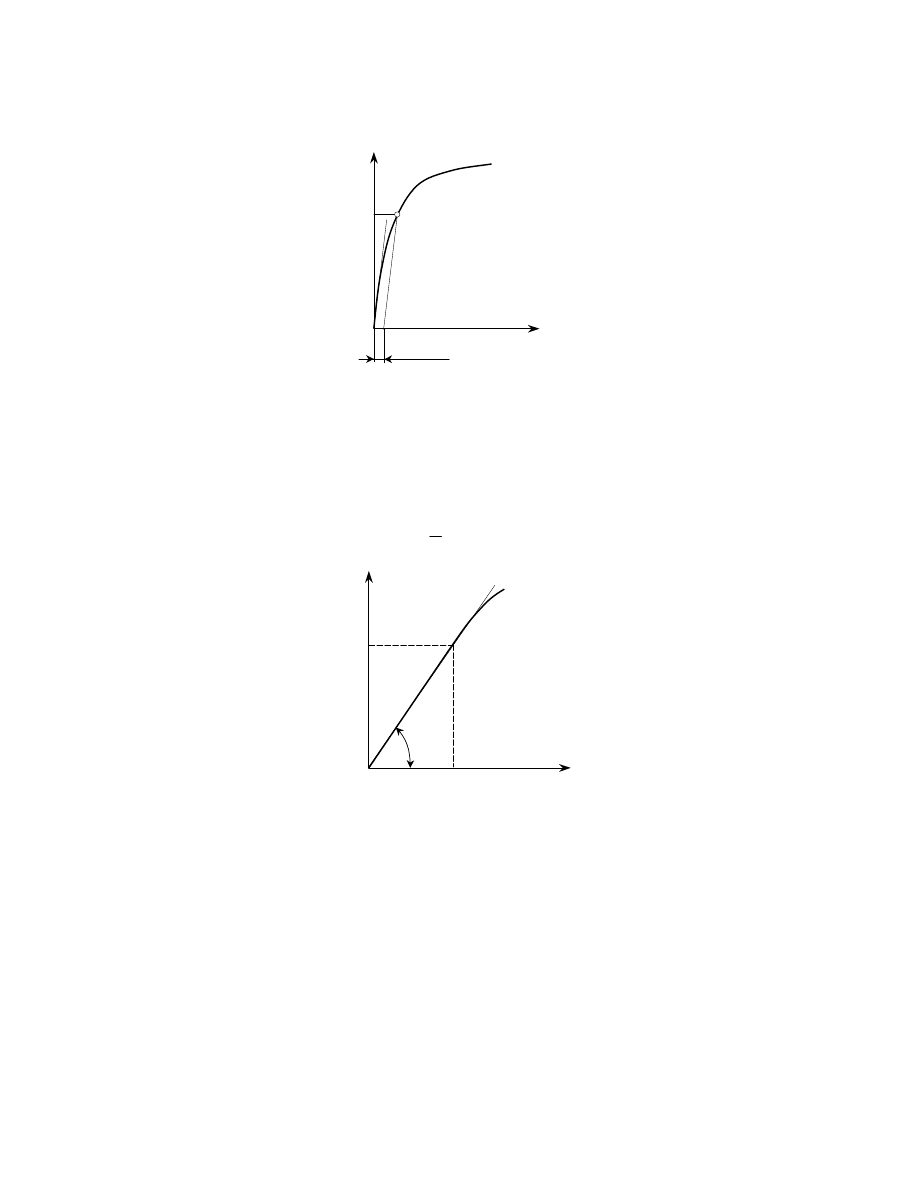
Rys. 3. Wykres skręcania próbki stalowej o średniej zawartości węgla

3. Definicje

3.1. Granica proporcjonalności na skręcanie

O

H

Hs

W

M

R

=

[MPa = N/mm

2

],

(20)

gdzie: M

H

− najwi

ę

ksza warto

ść

momentu skr

ę

caj

ą

cego, przy którym odkształcenie materiału

pozostaje jeszcze proporcjonalne do k

ą

ta skr

ę

cenia (spełnione jest prawo Hooke’a) (rys. 3),

W

O

− wska

ź

nik przekroju na skr

ę

canie.

ϕ

M

s

M

H

M

sp

M

Rs

M

pl

5

3.2. Granica sprężystości na skręcanie

0

W

M

R

sp

sps

=

[MPa = N/mm

2

],

(21)

gdzie: M

sp

− najwi

ę

kszy moment skr

ę

caj

ą

cy, przy którym jeszcze nie pojawia si

ę

odkształcenie plastyczne (trwałe) materiału (rys. 3), W

0

− wska

ź

nik przekroju na skr

ę

canie.

3.3. Granica plastyczności na skręcanie

O

pl

es

W

M

R

=

[MPa = N/mm

2

],

(22)

gdzie: M

pl

− moment skr

ę

caj

ą

cy, kiedy nast

ę

puje jego pierwszy spadek (rys. 3), W

0

−

wska

ź

nik przekroju na skr

ę

canie.

3.4. Wytrzymałość na skręcanie

O

Rs

ms

W

M

R

=

[MPa = N/mm

2

],

(23)

gdzie: M

Rs

− najwi

ę

kszy moment skr

ę

caj

ą

cy wyst

ę

puj

ą

cy w próbce, po przekroczeniu granicy

plastyczno

ś

ci (rys. 3), W

0

− wska

ź

nik przekroju na skr

ę

canie.

Wielko

ś

ci wyst

ę

puj

ą

ce w (20)

÷ (23) s

ą

napr

ęż

eniami (umownymi), odpowiadaj

ą

cymi

charakterystycznej warto

ś

ci momentu, odniesionemu do pocz

ą

tkowego przekroju

poprzecznego próbki.

4. Obliczanie wartości charakterystycznych

4.1. Obliczanie granic wytrzymałościowych

W praktyce przeprowadza si

ę

wyznaczanie:

−

granicy proporcjonalno

ś

ci na skr

ę

canie,

−

granicy spr

ęż

ysto

ś

ci na skr

ę

canie,

−

granicy plastyczno

ś

ci na skr

ę

canie,

−

wytrzymało

ś

ci na skr

ę

canie.

Granica proporcjonalno

ś

ci jest granic

ą

stosowalno

ś

ci prawa Hooke'a. W pobli

ż

u tej

granicy le

ż

y granica spr

ęż

ysto

ś

ci, przez któr

ą

rozumiemy tak

ą

warto

ść

napr

ęż

enia tn

ą

cego, po

przekroczeniu którego pojawia si

ę

trwałe odkształcenie materiału. Przy granicy plastyczno

ś

ci

pojawiaj

ą

si

ę

wyra

ź

ne odkształcenia trwałe, które zmieniaj

ą

kierunek przebiegu krzywej

skracania. Cechy granicy plastyczno

ś

ci przy skr

ę

caniu nie wyst

ę

puj

ą

tak wyra

ź

nie jak przy

próbie rozci

ą

gania mi

ę

kkiej stali, gdy

ż

odkształcania plastyczne pojawiaj

ą

si

ę

najpierw w

zewn

ę

trznej warstwie próbki a zatem nie powstaj

ą

równocze

ś

nie w całym przekroju.

Pocz

ą

wszy od załamania, charakteryzuj

ą

cego granic

ę

plastyczno

ś

ci, krzywa skr

ę

cania

wzrasta na ogół bardzo łagodnie a

ż

do zniszczenia próbki.

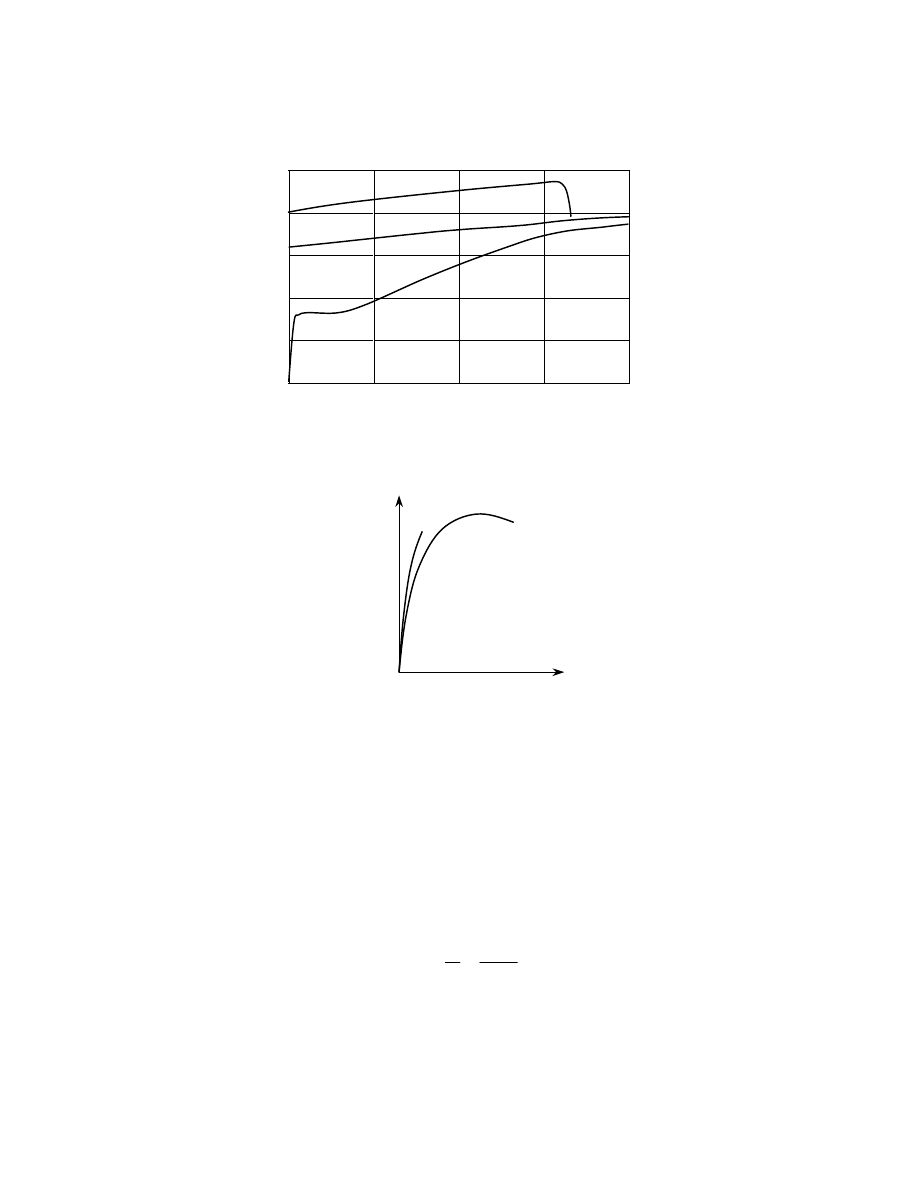
6

Ms [kNm]

1,5

1,2

0,9

0,6

0,3

Obroty

bębna

0

0,25

0,5

0,75 1

Rys. 4. Wykresy skręcania dla materiałów plastycznych

Na szczególn

ą

uwag

ę

zasługuje wykres skracania dla

ż

eliwa i dla stali hartowanej.

Rys. 5. Wykresy skręcania dla: 1) żeliwa, 2) stali nawęglanej i zahartowanej

Je

ś

li granica spr

ęż

ysto

ś

ci i plastyczno

ś

ci nie przebiega wyra

ź

nie na wykresie skracania,

to mo

ż

na j

ą

wyznaczy

ć

korzystaj

ą

c z zale

ż

no

ś

ci pomi

ę

dzy k

ą

tem odkształcenia postaciowego

γ

i wydłu

ż

eniem wzgl

ę

dne

ε

1

1

2

ε

γ

=

.

(24)

Poniewa

ż

dla oznaczenia umownej granicy plastyczno

ś

ci przy rozci

ą

ganiu przyjmuje si

ę

ε

= 0,2%, a zatem dla umownej granicy plastyczno

ś

ci na skracanie

γ

= 0,4%, st

ą

d

odpowiednikiem R

0,2

b

ę

dzie R

es

0,4

przy skr

ę

caniu. Wszystkie wska

ź

niki przy oznaczeniach

wa

ż

nych dla rozci

ą

gania nale

ż

y wi

ę

c pomno

ż

y

ć

przez 2, czyli

r

l

r

l

0

1

0

2

ε

γ

ϕ

=

⋅

=

.

(25)

Otrzymamy wtedy wielko

ść

dopuszczalnego k

ą

ta skr

ę

cania wyra

ż

onego w radianach.

Wielko

ść

k

ą

ta

ϕ

, odpowiadaj

ą

cego umownej warto

ś

ci

γ

, odmierzamy na wykresie podobnie

jak przy próbie rozci

ą

gania. Wyznaczona w ten sposób warto

ść

momentu M

0,4

, posłu

ż

y do

umownego obliczenia R

es

0,4

.

M

om

en

t s

kr

ę

ca

ją

cy

M

s

Jednostkowy kąt skręcenia φ′

1

2

7

Wykre

ś

ln

ą

metod

ą

wyznaczania przybli

ż

onej warto

ś

ci umownej granicy plastyczno

ś

ci

R

es

0,4

przedstawiono na rys. 7.

Rys. 6. Wykreślna metoda wyznaczania przybliżonej wartości umownej granicy plastyczności R

es0,4

4.2. Obliczanie modułu sprężystości postaciowej G

Moduł spr

ęż

ysto

ś

ci postaciowej (moduł Kirchhoffa) G w zakresie odkształce

ń

spr

ęż

ystych i proporcjonalnych przy skr

ę

caniu definiuje si

ę

moduł jako stosunek napr

ęż

enia

stycznego

τ

przy jednoosiowym stanie napr

ęż

enia do odpowiadaj

ą

cego mu odkształcenia

postaciowego wzgl

ę

dnego

γ

(rys. 7):

γ

τ

=

G

.

(26)

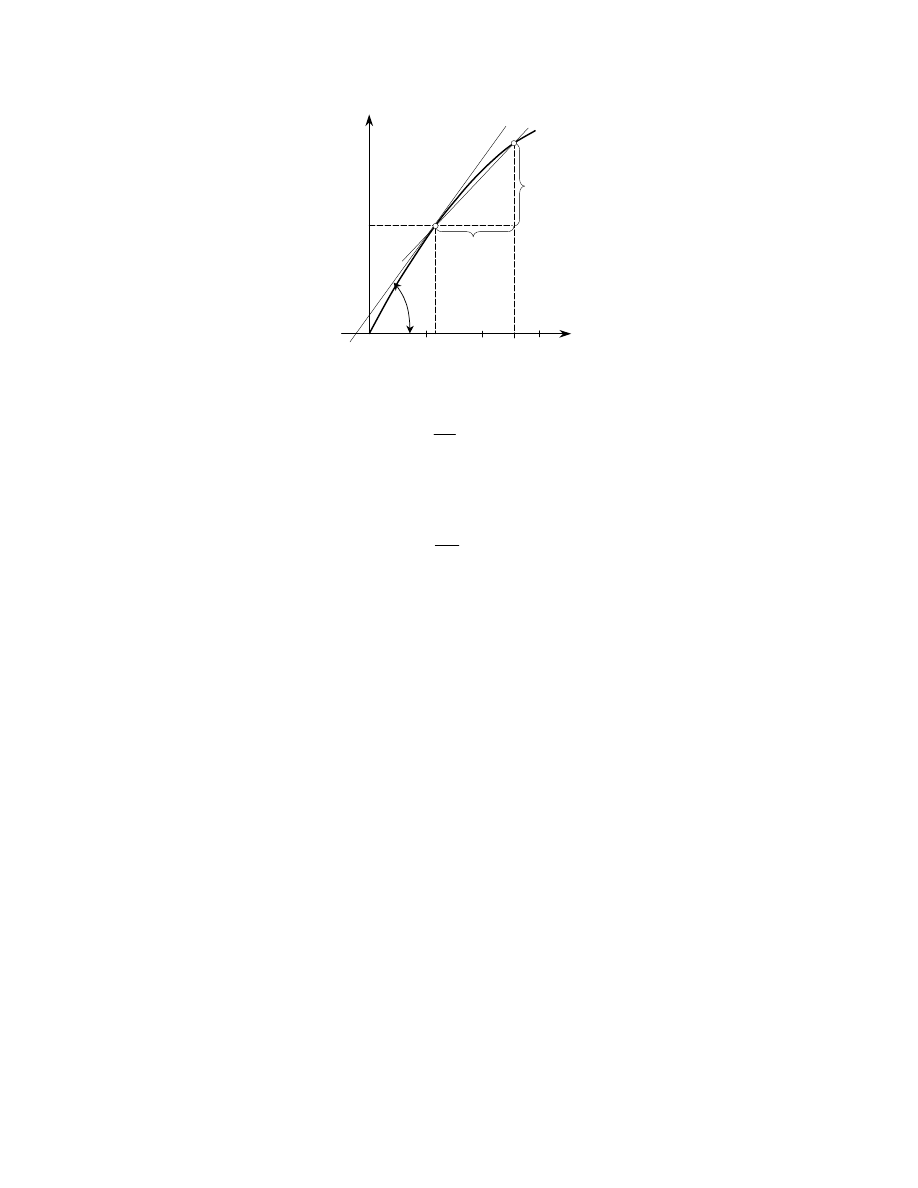
Rys. 7. Zależność

τ

= f(

γ

)

w przypadku odkształceń sprężystych i proporcjonalnych

Graficzna interpretacja modułu G: jest to współczynnik kierunkowy prostoliniowego

odcinka wykresu rozci

ą

gania

τ

= f(

γ

) i jest równy co do warto

ś

ci liczbowej tangensowi k

ą

ta

α

nachylenia prostoliniowej cz

ęś

ci wykresu skr

ę

cania.

Uwaga 1

: W przypadku odkształce

ń

spr

ęż

ystych i nie proporcjonalnych, kiedy wykres

skr

ę

cania nie wykazuje odcinka o przebiegu prostoliniowym (jak w przypadku

ż

eliwa lub

stali spr

ęż

ynowej), oblicza si

ę

moduł spr

ęż

ysto

ś

ci styczny lub sieczny.

γ

τ

O

α

γ

1

τ

1

M

om

en

t s

kr

ę

ca

ją

cy

M

s

Jednostkowy kąt skręcenia φ′

M

0,4

φ′ = 0,004

8

Rys. 8. Moduł styczny G

t

i moduł sieczny G

s

Moduł styczny G

t

definiuje si

ę

jako

γ

τ

d

d

G

t

=

.

(27)

G

t

jest równy tangensowi k

ą

ta nachylenia stycznej do krzywej skr

ę

cania w okre

ś

lonym

punkcie (rys. 8, graficzna interpretacja modułu G

t

).

Moduł sieczny G

s

definiuje si

ę

jako

γ

τ

∆

∆

=

s

G

.

(28)

Jest on równy tangensowi k

ą

ta nachylenia siecznej krzywej skr

ę

cania poprowadzonej przez 2

punkty wykresu (rys. 8). Moduły G

t

i G

s

wyznacza si

ę

w zakresie obci

ąż

e

ń

odpowiadaj

ą

cych

napr

ęż

eniom w przedziale 10%

÷ 90% umownej granicy spr

ęż

ysto

ś

ci.

Uwaga 2

: W niektórych zagadnieniach analitycznych wytrzymało

ś

ci materiałów stosuje

si

ę

poj

ę

cia: modułu stycznego lub siecznego – w odniesieniu do zakresu odkształce

ń

poza

zakresem spr

ęż

ysto

ś

ci – wówczas definicje i graficzne interpretacje modułów s

ą

analogiczne

jak podano wy

ż

ej.

4.3. Obliczanie momentu skręcającego w obszarze plastycznym

Po przekroczeniu obszaru proporcjonalno

ś

ci przestaje obowi

ą

zywa

ć

prawo Hooke'a.

Wraz z osi

ą

gni

ę

ciem stanu plastyczno

ś

ci pojawia si

ę

inny rozkład napr

ęż

e

ń

ni

ż

w stanie

spr

ęż

ystym. Nakładanie si

ę

odkształce

ń

plastycznych na spr

ęż

yste wywołuje napr

ęż

enia

wst

ę

pne zniekształcaj

ą

c prawdziwy obraz przej

ś

cia materiału ze stanu spr

ęż

ystego do

plastycznego. Dla próbki o przekroju kołowym obliczenie wielko

ś

ci napr

ęż

enia tn

ą

cego, przy

której zewn

ę

trzna warstewka próbki osi

ą

ga granic

ę

plastyczno

ś

ci, nie nastr

ę

cza trudno

ś

ci.

Pocz

ą

wszy bowiem od momentu M

pl

, nie zmieniaj

ą

swej wielko

ś

ci napr

ęż

enia

τ

max

ze

zwi

ę

kszeniem si

ę

warto

ś

ci M, je

ż

eli pomin

ąć

na ogół niezbyt silne umocnienie zaznaczaj

ą

ce

si

ę

podczas skr

ę

cania metali plastycznych. Wykres napr

ęż

e

ń

stycznych z trójk

ą

tnego

przechodzi na trapezowy, a

ż

eby ostatecznie zamieni

ć

si

ę

na prostok

ą

tny (rys. 10).

W przypadku całkowitego uplastycznienia przekroju warto

ść

momentu M

pl

mo

ż

na

otrzyma

ć

z warunku równo

ś

ci momentów sił zewn

ę

trznych i wewn

ę

trznych o postaci (rys. 9)

γ

O

∆

γ

A

B

G

t

G

s

∆

τ

τ

α

9

Rys. 9. Rozkład naprężeń tnących w obszarze plastycznym

( )

3

2

2

3

0

pl

r

pl

A

pl

pl

r

d

dA

M

τ

π

ρ

πρ

τ

ρ

τ

ρ

=

⋅

⋅

⋅

=

⋅

⋅

=

∫

∫

,

czyli

12

2

3

3

3

d

M

r

M

pl

pl

pl

π

π

τ

=

=

.

(29)

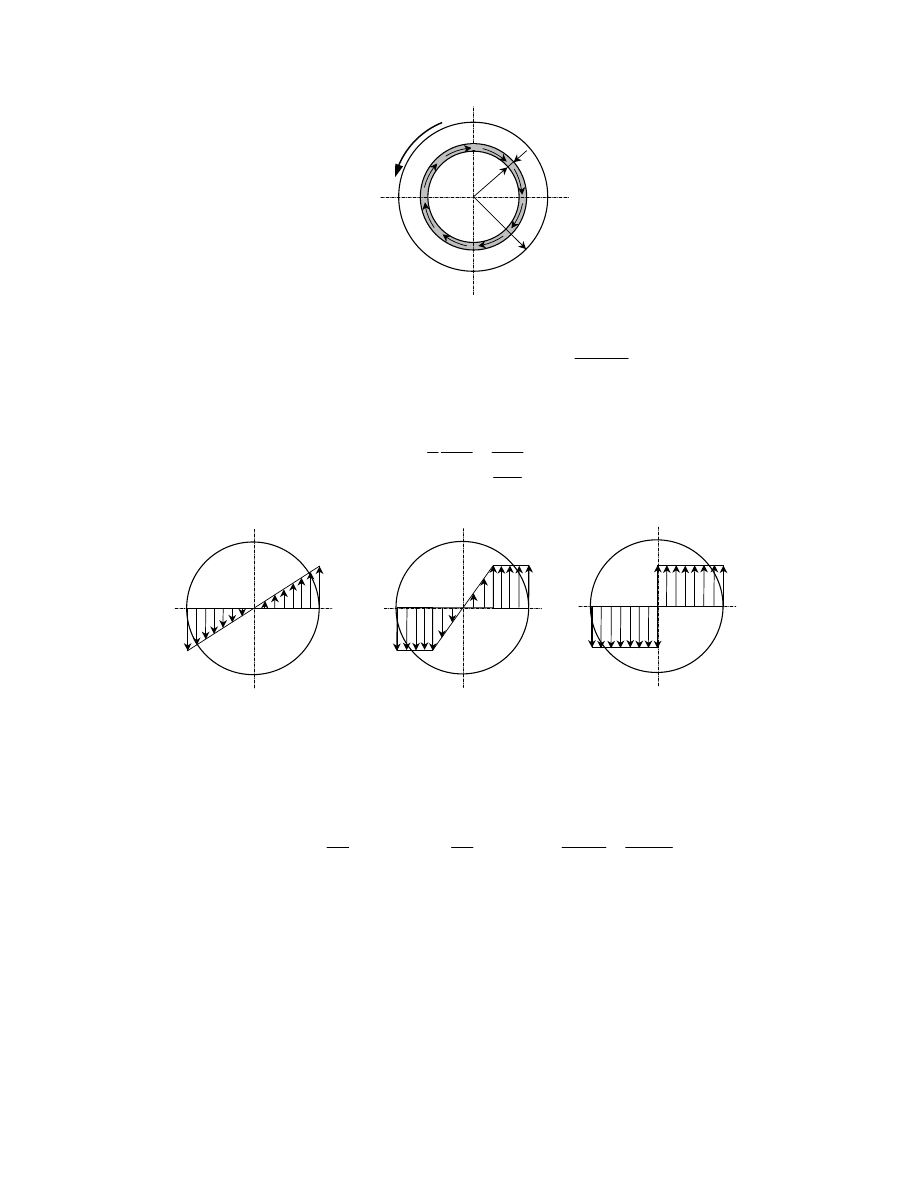
Rys. 10. Schemat naprężeń stycznych w poprzecznym przekroju skręconej próbki (dla materiału doskonale

jednorodnego i przy pominięciu umocnienia): a) w obszarze czysto sprężystym, b) w obszarze odkształceń

sprężysto

−plastycznym, c) w obszarze odkształceń czysto plastycznych (przegub plastyczny)

W przypadku uplastycznienia si

ę

tylko warstwy zewn

ę

trznej przekroju warto

ść

momentu M

pl

jest równa (rys. 10)

( )

16

2

2

3

3

0

2

pl

pl

r

pl

A

pl

pl

d

r

d

r

dA

r

M

τ

π

τ

π

ρ

πρ

τ

ρ

ρ

τ

ρ

=

=

⋅

⋅

⋅

=

⋅

⋅

=

∫

∫

.

(30)

Dla tych obu warto

ś

ci momentu skr

ę

caj

ą

cego okre

ś

la si

ę

dwie granice plastyczno

ś

ci materiału

na skr

ę

canie: teoretyczn

ą

i rzeczywist

ą

.

5. Próbki do próby skręcania

Do próby skr

ę

cania u

ż

ywa si

ę

próbek o długo

ś

ci pomiarowej (5

÷ 20)d

0

. Najcz

ęś

ciej

przyjmuje si

ę

L

0

= 10d

0

. Kształt próbki do prób skr

ę

cania przedstawiono na rys. 11.

M

pl

τ

pl

r

ρ

dρ

a)

τ

b)

τ

pl

c)

τ

pl

10

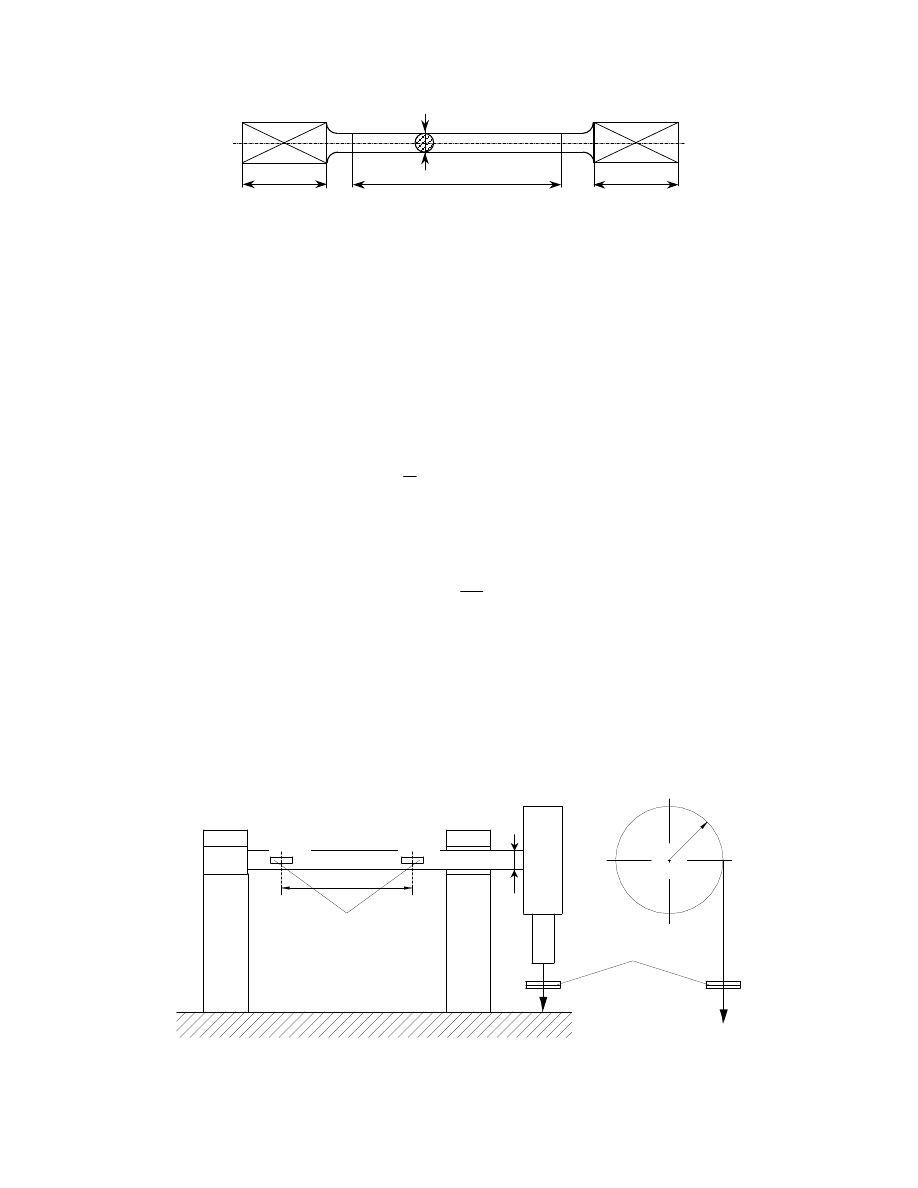
Rys. 11. Próbka do prób skręcania prętów okrągłych

6. Przeprowadzenie próby

Ć

wiczenie wykonywane jest na dwóch stanowiskach:

− stanowisko, na którym k

ą

t skr

ę

cania w danym przekroju próbki mierzymy za pomoc

ą

aparatu Martensa,

− maszyna do skr

ę

cania zwana skr

ę

cark

ą

.

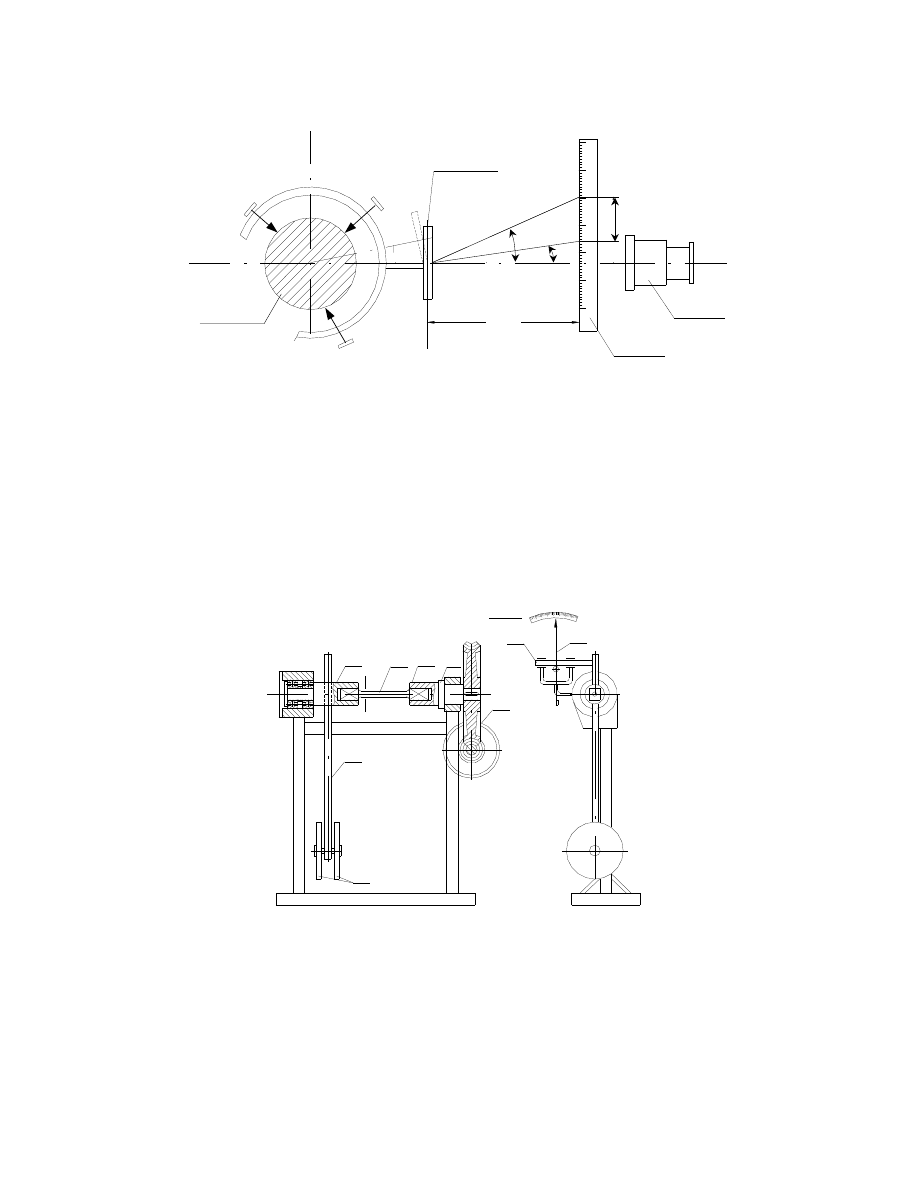
6.1. Pomiar kąta skręcenia za pomocą aparatu Martensa

K

ą

t skr

ę

cania w danym przekroju próbki obliczamy za pomoc

ą

aparatu Martensa w

sposób nast

ę

puj

ą

cy (rys. 12):

ϕ

ϕ

2

2

≅

= tg

L

S

,

(31)

gdzie

S

= S

2

– S

1

.

(32)

St

ą

d

L

S

2

≅

ϕ

,

(33)

gdzie: S

1

, S

2

− warto

ść

odczytów na skalach 1 i 2 aparatu Martensa w [mm] z dokładno

ś

ci

ą

do

0,1 mm, L

− odległo

ść

skali od lusterka równa 1 m.

Podczas próby stosuje si

ę

próbk

ę

o

ś

rednicy d = 10 mm, natomiast promie

ń

R tarczy, na

której zawieszamy ci

ęż

arki jest równy R = 152 mm.

K

ą

t skr

ę

cenia próbki jest równy (rys. 13)

2

1

ϕ

ϕ

ϕ

−

=

[rad].

(34)

R

LUSTERKA

F

l

0

CIĘŻARKI

F

1

2

Rys. 12. Schemat urządzenia do pomiaru kąta skręcenia

a

d

0

l

0

= (5÷20)d

0

a

φ

1

φ

2

d

11

PRÓBKA

0

l

SKALA

LUNETA

S

2

LUSTERKO

S

S

1

2

Rys. 13. Schemat aparatu Martensa do pomiaru kąta skręcenia

6.2. Wykonanie statycznej próby skręcania na skręcarce

Skr

ę

carka składa si

ę

z nast

ę

puj

ą

cych zespołów: urz

ą

dzenia nap

ę

dowego 1 z przekładni

ą

o nap

ę

dzie r

ę

cznym lub mechanicznym, uchwytów do próbek 3, 4, siłomierza 8 mierz

ą

cego

warto

ść

momentu skr

ę

caj

ą

cego i samoczynnego zapisu wykresu.

Pokazana na rys. 14 skr

ę

carka wyposa

ż

ona jest w przekładni

ę

ś

limakow

ą

1 o nap

ę

dzie

r

ę

cznym lub mechanicznym z odpowiednio dobranym przeło

ż

eniem.

4

2 3

9

1

7

8

5

6

A
A

A-A

Rys. 14. Schemat skręcarki

Próbk

ę

2 o odpowiednich ko

ń

cówkach umieszcza si

ę

w uchwytach: nap

ę

dowym 3 i

pomiarowym 4, z którym poł

ą

czona jest d

ź

wignia 5. Na d

ź

wigni tej osadza si

ę

wymienne

obci

ąż

niki 6, odpowiednio do obranego i przewidzianego dla danej maszyny zakresu

momentu skracaj

ą

cego. Wychylenie d

ź

wigni ci

ęż

arowej podczas obci

ąż

enia próbki z

poło

ż

enia pionowego wykorzystuje si

ę

do pomiaru warto

ś

ci momentu skracaj

ą

cego. Obrót

d

ź

wigni poprzez z

ę

batk

ę

7 powoduje obrót wskazówki siłomierza 8, wyskalowanej w

L

PRÓBKA

S

φ

1

φ

2

12

jednostkach momentu skr

ę

caj

ą

cego. Wykres skr

ę

cania wykre

ś

lany jest na b

ę

bnie przez rysik

sprz

ęż

ony ze wskazówk

ą

siłomierza. Nap

ę

d b

ę

bna uzyskuje si

ę

za pomoc

ą

linki poł

ą

czonej z

uchwytem 3 i 4.

7. Obliczenia

7.1. Moduł sprężystości postaciowej G

−

−

−

−

materiał o charakterystyce liniowo

−

−

−

−

sprężystej

Moduł spr

ęż

ysto

ś

ci postaciowej (moduł Kirchhoffa) G obliczamy jako (rys. 8)

γ

τ

∆

∆

=

G

,

(35)

gdzie:

O

s

W

M

∆

=

∆

τ

,

(36)

ϕ

γ

∆

≅

∆

0

l

r

.

(37)

Po podstawieniu (36) i (37) do (35) otrzymujemy

(

)

0

0

,

J

l

M

M

G

s

s

ϕ

ϕ

∆

∆

≅

∆

∆

.

(38)

Korzystamy ze zbioru punktów w układzie

τ

(

γ

) (napr

ęż

enie

−

−

−

− odkształcenie postaciowe

wzgl

ę

dne całkowite).

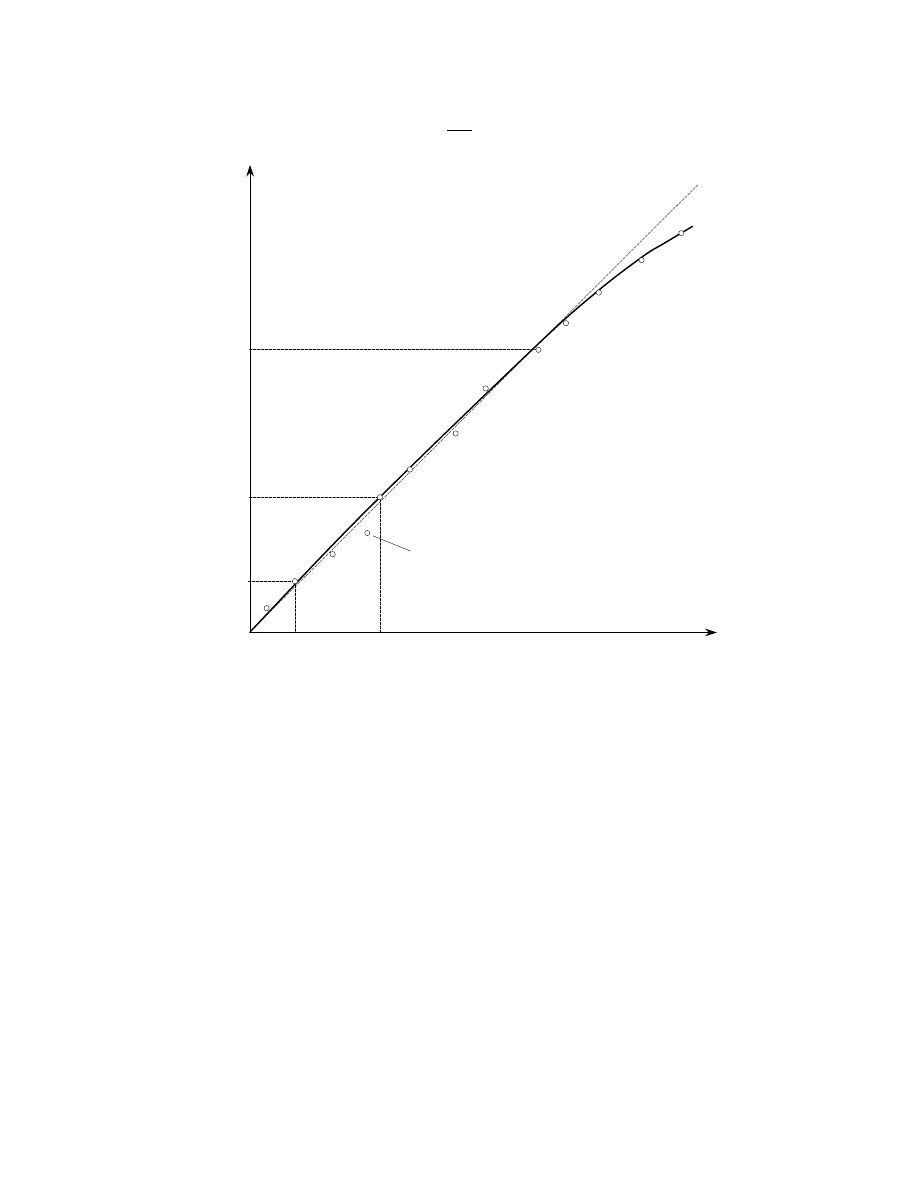
Po naniesieniu punktów w układzie współrz

ę

dnych ustalamy zbiór punktów znajduj

ą

cych

si

ę

w zakresie liniowo –spr

ęż

ystym charakterystyki materiału; pomijamy ostatni punkt z tego

zakresu. W przypadku, kiedy punkty uło

ż

one s

ą

na linii prostej, moduł G obliczamy

1

2

1

2

γ

γ

τ

τ

γ

τ

−

−

=

∆

∆

=

G

,

(39)

gdzie odległo

ść

punktów 2 i 1jest mo

ż

liwie du

ż

a. Natomiast kiedy wyniki pomiarów s

ą

obarczone wi

ę

kszymi bł

ę

dami i wyst

ę

puj

ą

odchylenia punktów od zakładanej linii prostej,

mo

ż

na otrzyma

ć

wynik w pewnym stopniu niezale

ż

ny od bł

ę

dów, przyjmuj

ą

c (rys. 15):

1. punkty pomiarowe z zakresu 10

÷ 90% przedziału liniowego;

2. z pomini

ę

ciem punktów znacznie odległych od zakładanej linii prostej.

Wówczas

−

−

−

−

dla n + 1 uwzgl

ę

dnianych punktów – moduł G mo

ż

na obliczy

ć

jako:

∑

=

−

−

−

−

=

n

i

i

i

i

i

n

G

1

1

1

1

γ

γ

τ

τ

.

(40)

7.2. Współczynnik Poissona

ν

ν

ν

ν

Obowi

ą

zuje zale

ż

no

ść

[9, 10]

(

)

ν

+

=

1

2

E

G

,

(41)

po przekształceniu której, otrzymujemy zale

ż

no

ść

, z której mo

ż

na obliczy

ć

Współczynnik

Poissona

ν

13

1

2

−

=

G

E

ν

.

(42)

Rys. 15. Obliczanie modułu G – odchylenia punktów od linii prostej (n = 5)

8. Wykonanie sprawozdania

W sprawozdaniu nale

ż

y umie

ś

ci

ć

:

1. tytuł i cele

ć

wiczenia,

2. definicje: modułu spr

ęż

ysto

ś

ci oraz umownych granic spr

ęż

ysto

ś

ci i plastyczno

ś

ci,

3. schemat aparatu Martensa do pomiaru k

ą

ta skr

ę

cania – rysunek z obja

ś

nieniami cz

ęś

ci

składowych,

4. poda

ć

definicj

ę

modułu G oraz sposób jego obliczenia,

5. poda

ć

zale

ż

no

ść

mi

ę

dzy modułem G i E oraz

ν

.

6. sposób obliczenia liczby Poissona

ν

,

7. poda

ć

zestawienie wyników bada

ń

i wielko

ś

ci obliczanych w tabeli pomiarowej 1; pod

tabel

ą

pomiarow

ą

1 poda

ć

przykład obliczenia warto

ś

ci z jednego wiersza,

8. narysowa

ć

wykresy:

τ

(

τ

) – ¼ p

ę

tli histerezy spr

ęż

ystej,

9. narysowa

ć

wykres

τ

= f(

γ) przy obci

ąż

eniu stale rosn

ą

cym i stale malej

ą

cym,

10. wykona

ć

obliczenie wielko

ś

ci charakterystycznych, stanowi

ą

cych cel

ć

wiczenia; zapisa

ć

wyniki w sprawozdaniu,

11. zamie

ś

ci

ć

wykres skr

ę

cania próbki uzyskany na skr

ę

carce.

γ

τ

i=1

punkt pominięty

0,9τ

H

0,1τ

H

τ

i

τ

0

γ

γ

i

i=2

i=3

i=4

i=5

14

Tabela pomiarowa 1

. Wykres

τ = f(γ)

Lp

F

M

s

S

1

S

2

ϕ

γ

τ

−

[N]

[Nm]

[mm]

[mm]

[rad

⋅10

3

]

[rad

⋅10

3

]

[MPa]

1

0

2

10

3

20

…

…

12

100

13

110

14

100

…

…

27

20

28

10

27

0

Literatura

[1] Bachmacz W.: Wytrzymało

ść

materiałów. Badania do

ś

wiadczalne. Skrypt Politechniki Cz

ę

stochowskiej,

Cz

ę

stochowa 1973.

[2] Banasik M.:

Ć

wiczenia laboratoryjne z wytrzymało

ś

ci materiałów. PWN, Warszawa 1977.

[3] Boruszak A., Sykulski R., Wrze

ś

niowski K.: Wytrzymało

ść

materiałów. Do

ś

wiadczalne metody bada

ń

.

Wydawnictwo Politechniki Pozna

ń

skiej, Pozna

ń

1977.

[4] Dyl

ą

g Z., Orło

ś

Z.: Wytrzymało

ść

zm

ę

czeniowa materiałów. Warszawa. WNT 1962.

[5] Jastrz

ę

bski P., Mutermilch J., Orło

ś

W.: Wytrzymało

ść

materiałów. Warszawa. Arkady 1985.

[6] Katarzy

ń

ski S., Koca

ń

da S., Zakrzewski M.: Badania wła

ś

ciwo

ś

ci mechanicznych metali. WNT, Warszawa

1967.

[7] Ł

ą

czkowski R.: Wytrzymało

ść

materiałów. Gda

ń

sk. WPG 1988.

[8] Mazurkiewicz S.: Laboratorium z wytrzymało

ś

ci materiałów. Wydawnictwo Politechniki Krakowskiej,

Kraków 1978.

[9] Niezgodzi

ń

ski M.E., Niezgodzi

ń

ski T.: Wzory wykresy i tablice wytrzymało

ś

ciowe. Warszawa. WNT

1996.

[10] Orło

ś

Z.: Do

ś

wiadczalna analiza odkształce

ń

i napr

ęż

e

ń

. PWN, Warszawa 1977.

[11] Walczyk Z.: Wytrzymało

ść

materiałów. Gda

ń

sk. WPG 1998.