1
Zastosowania geometryczne całki oznaczonej
(A)
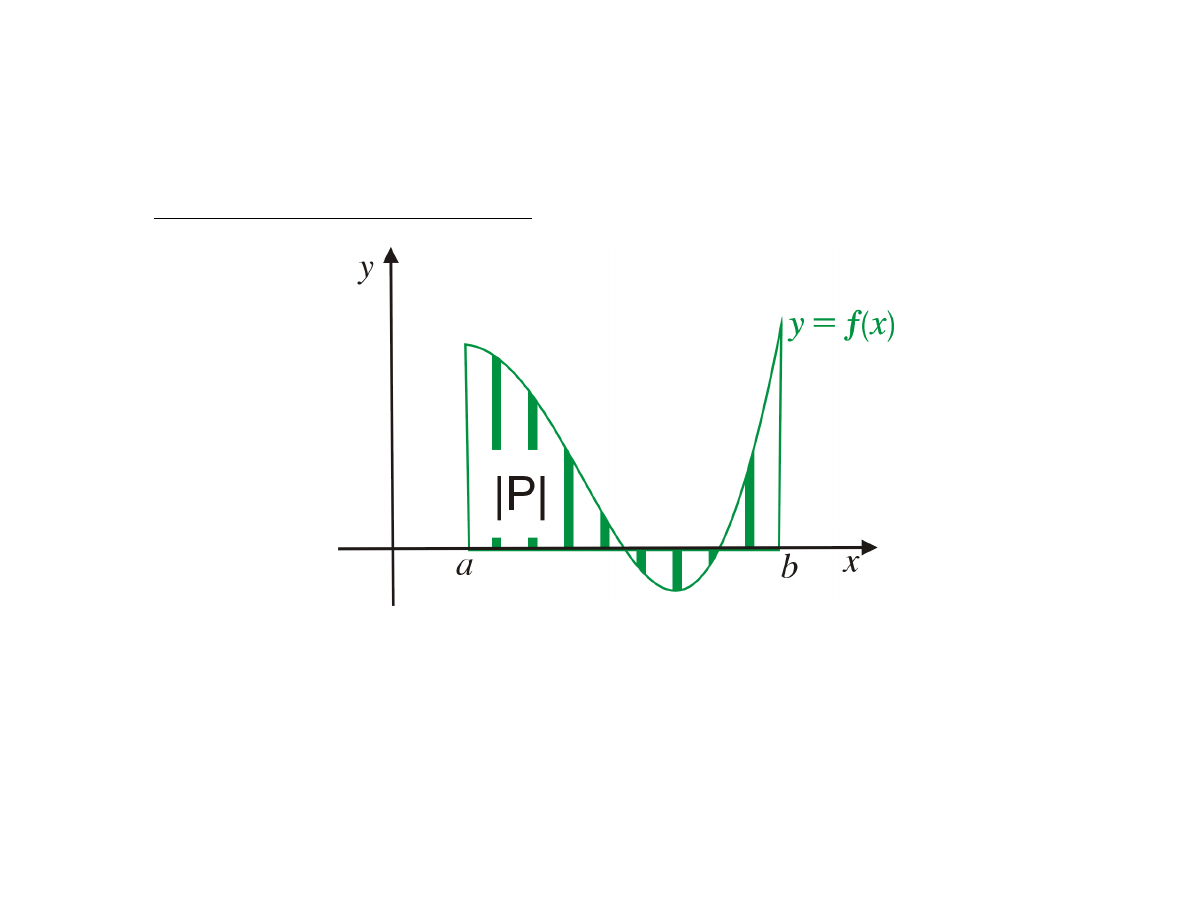
Pole obszararu płaskiego
|P | =
b
Z
a
|f (x)| dx
Założenie: funkcja
f (x)
jest ciągła dla
x ∈ [a, b]
.
1
Zastosowania geometryczne całki oznaczonej
(A)
Pole obszararu płaskiego
|P | =
b
Z
a
|f (x)| dx
Założenie: funkcja
f (x)
jest ciągła dla
x ∈ [a, b]
.
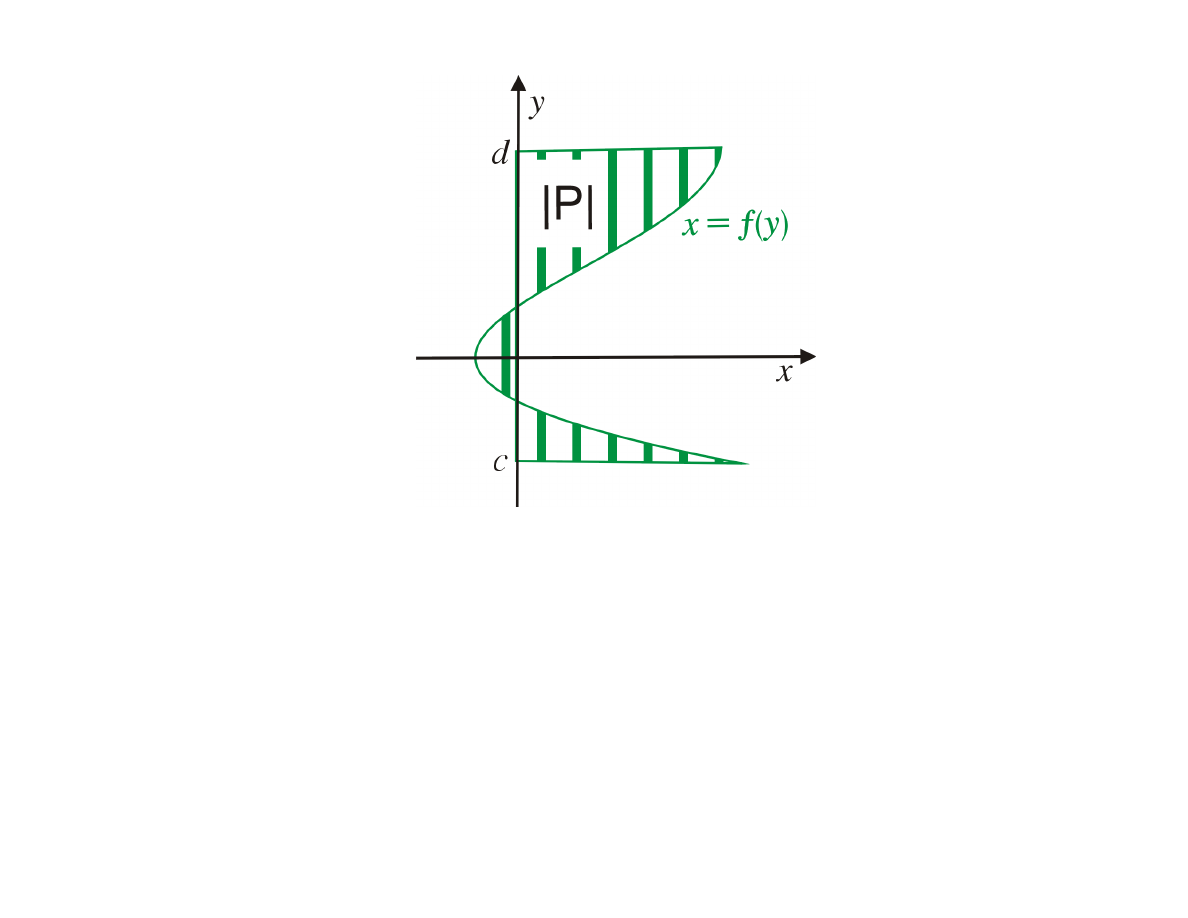
2
|P | =
d
Z
c
|f (y)| dy
Założenie: funkcja
f (y)
jest ciągła dla
y ∈ [c, d]
.
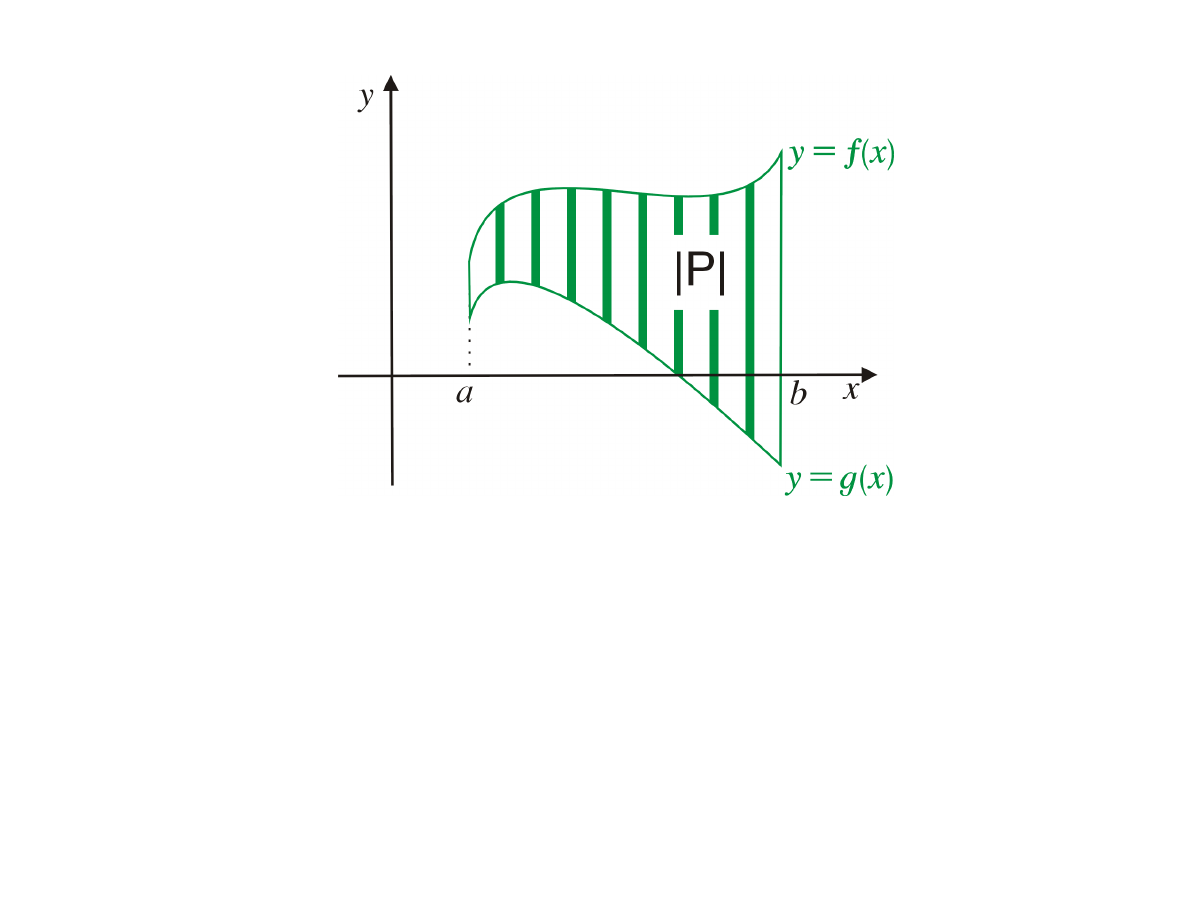
3
|P | =
b
Z
a
( f (x) − g(x) ) dx
Założenie: funkcje
f (x)
i
g(x)
są ciągłe dla
x ∈ [a, b]
oraz dla
każdego
x ∈ [a, b] f (x) > g(x)
.
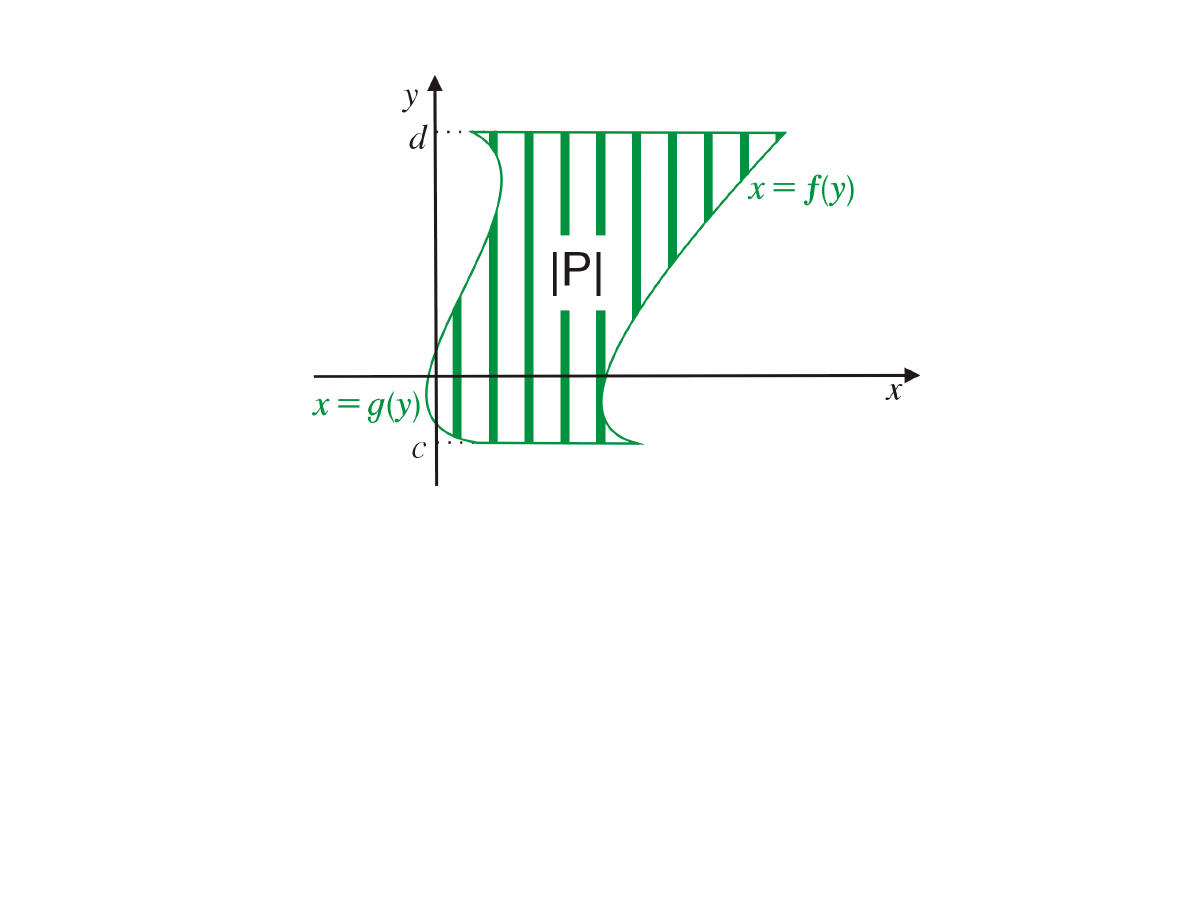
4
|P | =
d
Z
c
( f (y) − g(y) ) dy
Założenie: funkcje
f (y)
i
g(y)
są ciągłe dla
y ∈ [c, d]
oraz dla
każdego
y ∈ [c, d] f (y) > g(y)
.
5
Przykład Oblicz pola obszarów ograniczonych wykresami funkcji:
a)
y = arctg x,
y = 1 − e
x
,
x = 1
b)
y = ln x,
y = −1,
y = 1,
x = 0
(B)
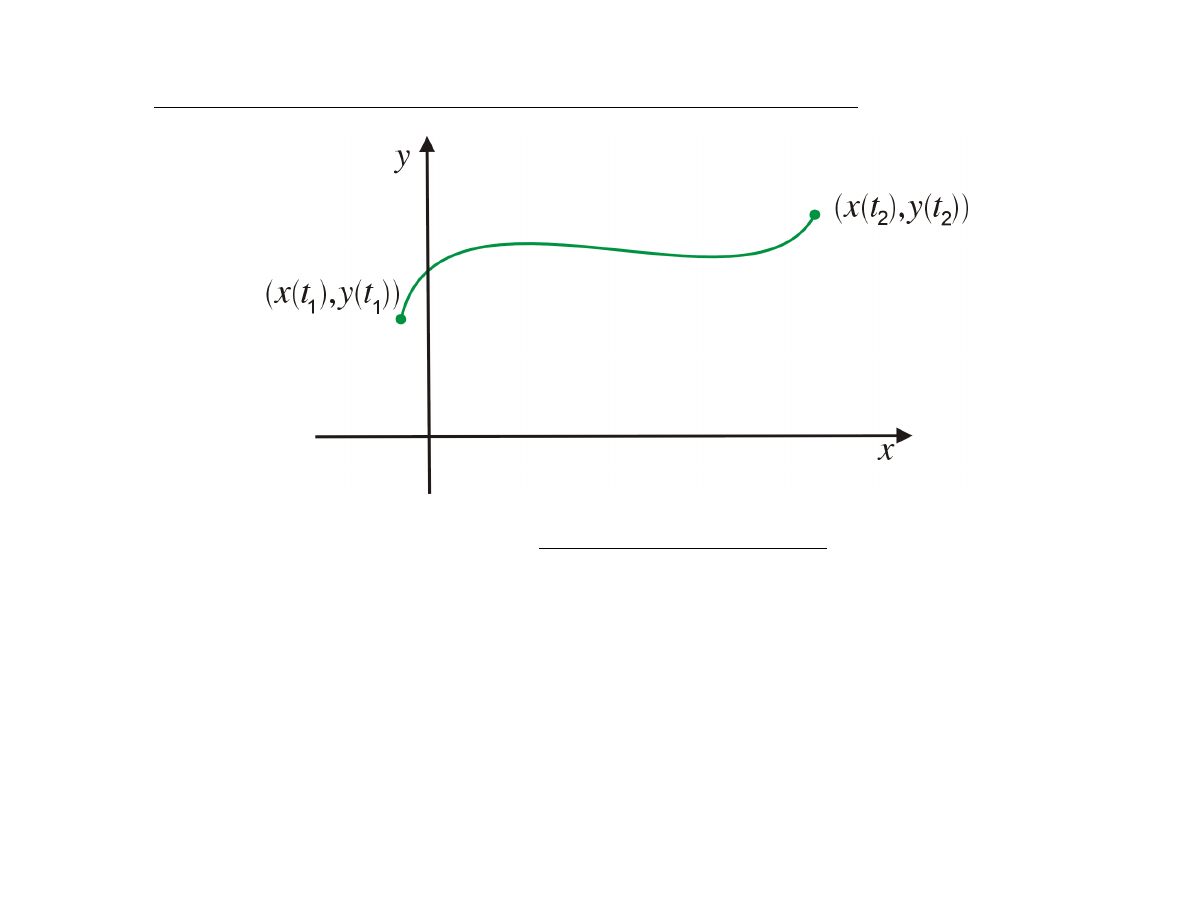
Krzywa płaska zadana parametrycznie
Definicja
Zbiór punktów płaszczyzny
(x, y) ∈ R
2 taki, że
x = x(t)
t ∈ [t
1
, t
2
]
y = y(t)
gdzie
x(t)
i
y(t)
są funkcjami ciągłymi dla
t ∈ [t
1
, t
2
]
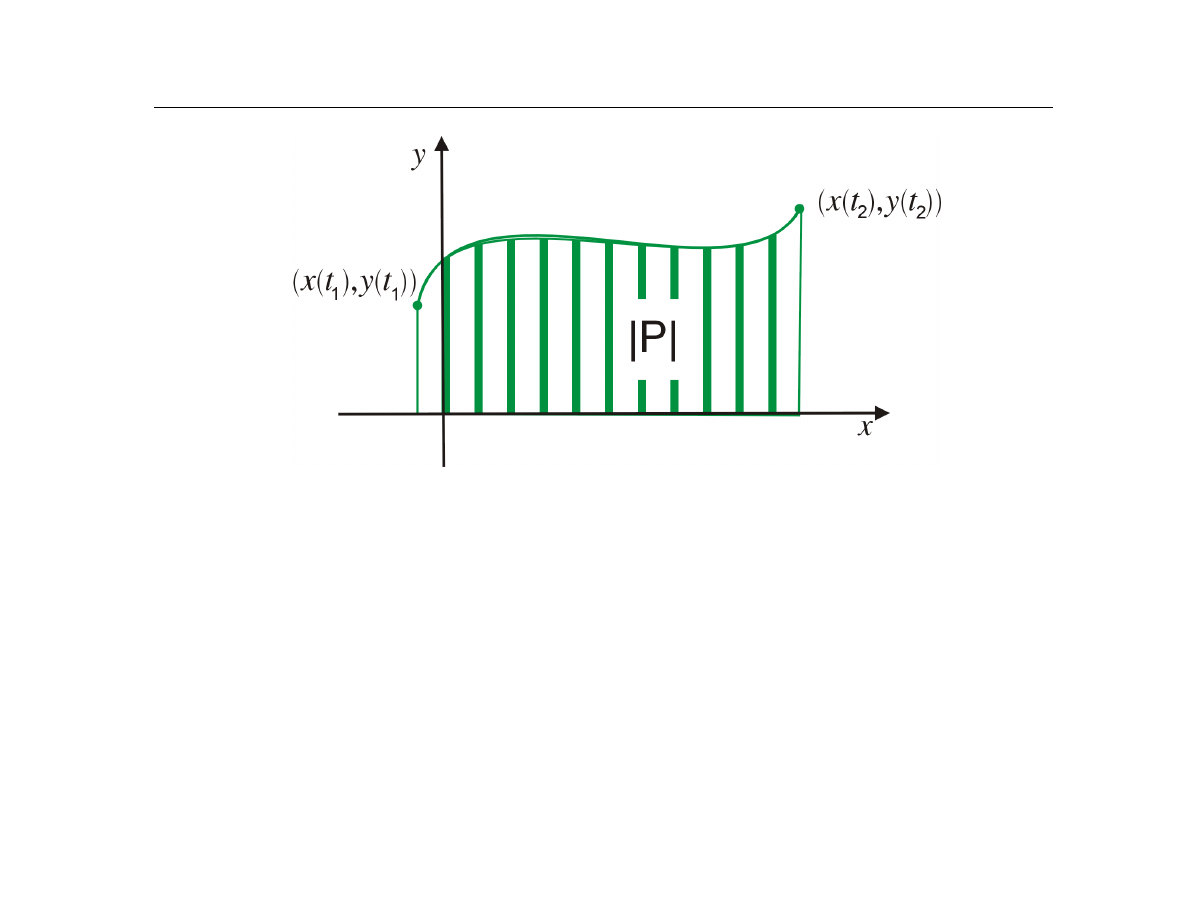
nazywamy krzywą płaską daną parametrycznie.
Punkt
(x(t
1
), y(t
1
))
nazywamy początkiem krzywej, punkt
(x(t
2
), y(t
2
))
- końcem.
6
Przykład
• Prosta przechodząca przez punkt
P (x
0
, y
0
)
i równoległa do
wektora
~a = [a
1
, a
2
]
ma parametryzację:
x(t) = x
0
+ a
1
t
t ∈ R
y(t) = y
0
+ a
2
t
Jeżeli
y ∈ [t
1
, t
2
]
, to wzór powyższy przedstawia parametryzację
odcinka o początku w punkcie
(x(t
1
), y(t
1
))
i końcu w punkcie
(x(t
2
), y(t
2
))
.
• Odcinek o początku w punkcie
A(x
A
, y
A
)
i końcu w punkcie
B(x
B
, y
B
)
ma parametryzację:
x(t) = x
A
+ (x
B
− x
A
) t
t ∈ [0, 1]
y(t) = y
A
+ (y
B
− y
A
) t
7
• Okrąg o środku w punkcie
P (x
0
, y
0
)
i promieniu
R > 0
ma
parametryzację:
x(t) = x
0
+ R cos t
t ∈ [0, 2π]
y(t) = y
0
+ R sin t
• Elipsa o równaniu
x
2
a
2
+
y
2
b
2
= 1
ma parametryzację:
x(t) = a cos t
t ∈ [0, 2π]
y(t) = b sin t
8
(C)
Pole obszaru płaskiego pod krzywą zadaną parametrycznie
|P | =
t
2
Z
t
1
| y(t) · x
0
(t) | dt
Założenie: funkcje
x(t)
,
x
0
(t)
i
y(t)
są ciągłe dla
t ∈ [t
1
, t
2
]
oraz
x
0
(t)
i
y(t)
mają stały znak.
9
Przykład
Oblicz pole obszaru ograniczonego osią OX i krzywą
zadaną parametrycznie
x(t) = t e
t
,
y(t) = t e
−t
,
t ∈ [0, 1]
.
Przykład
Wyprowadź wzór na pole elipsy o półosiach
a
i
b
.
10
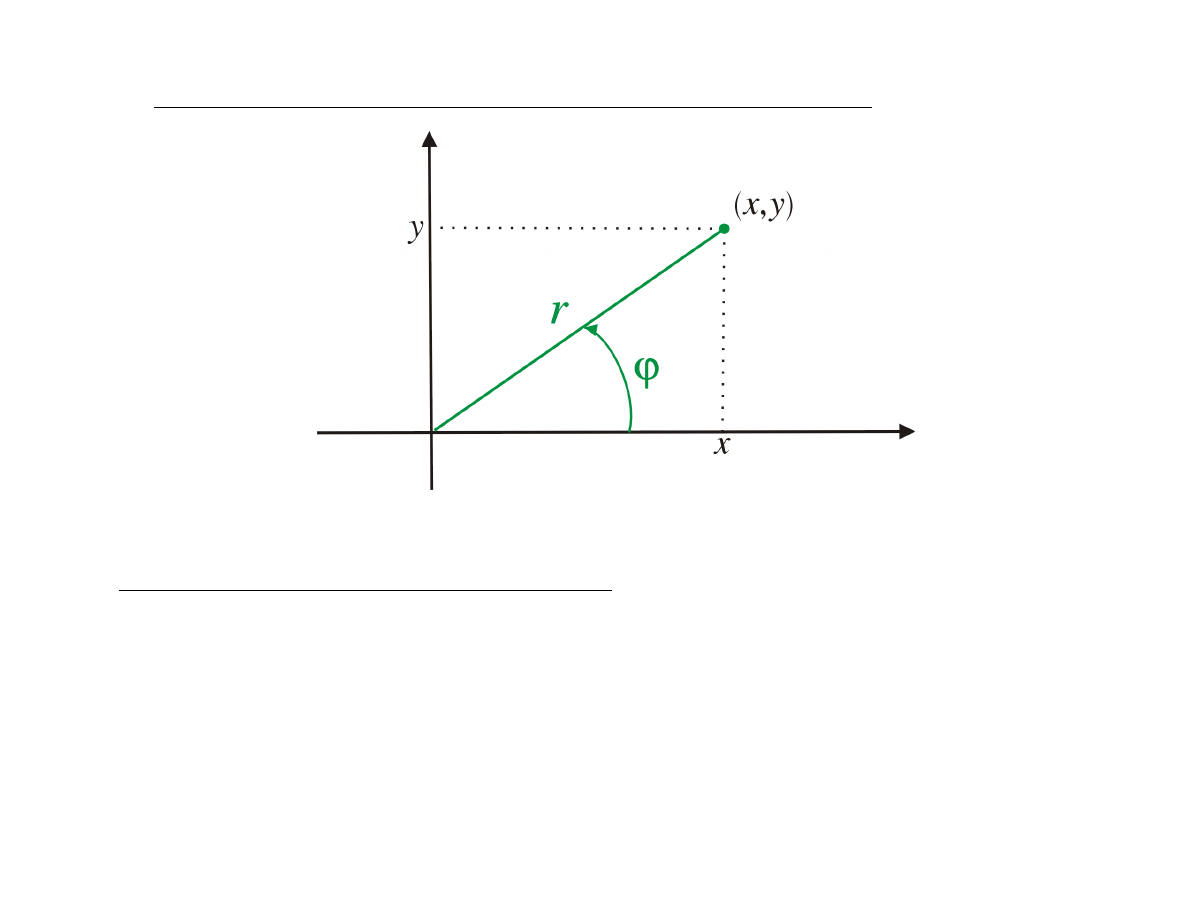
(D)
Krzywa płaska we współrzędnych biegunowych
Współrzędne biegunowe
(r, ϕ)
:
x = r cos ϕ
r ∈ [0, +∞)
y = r sin ϕ
ϕ ∈ [0, 2π]
r
2
= x
2
+ y
2
11
Przykład Zapisz równania krzywych we współrzędnych biegunowych:
a)
x
2
+ y
2
= R
2
b)
( x
2
+ y
2
)
2
= a
2
( x
2
− y
2
),
a > 0
12
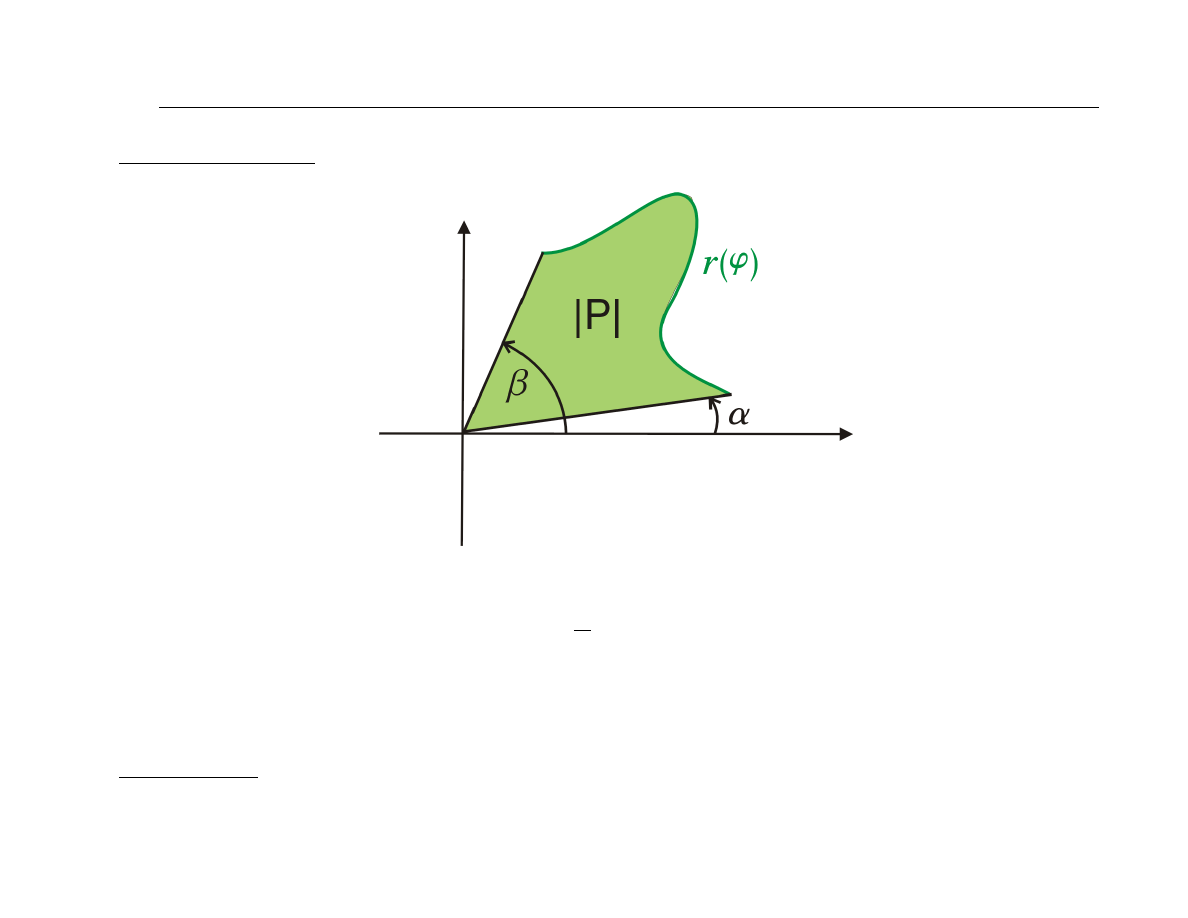
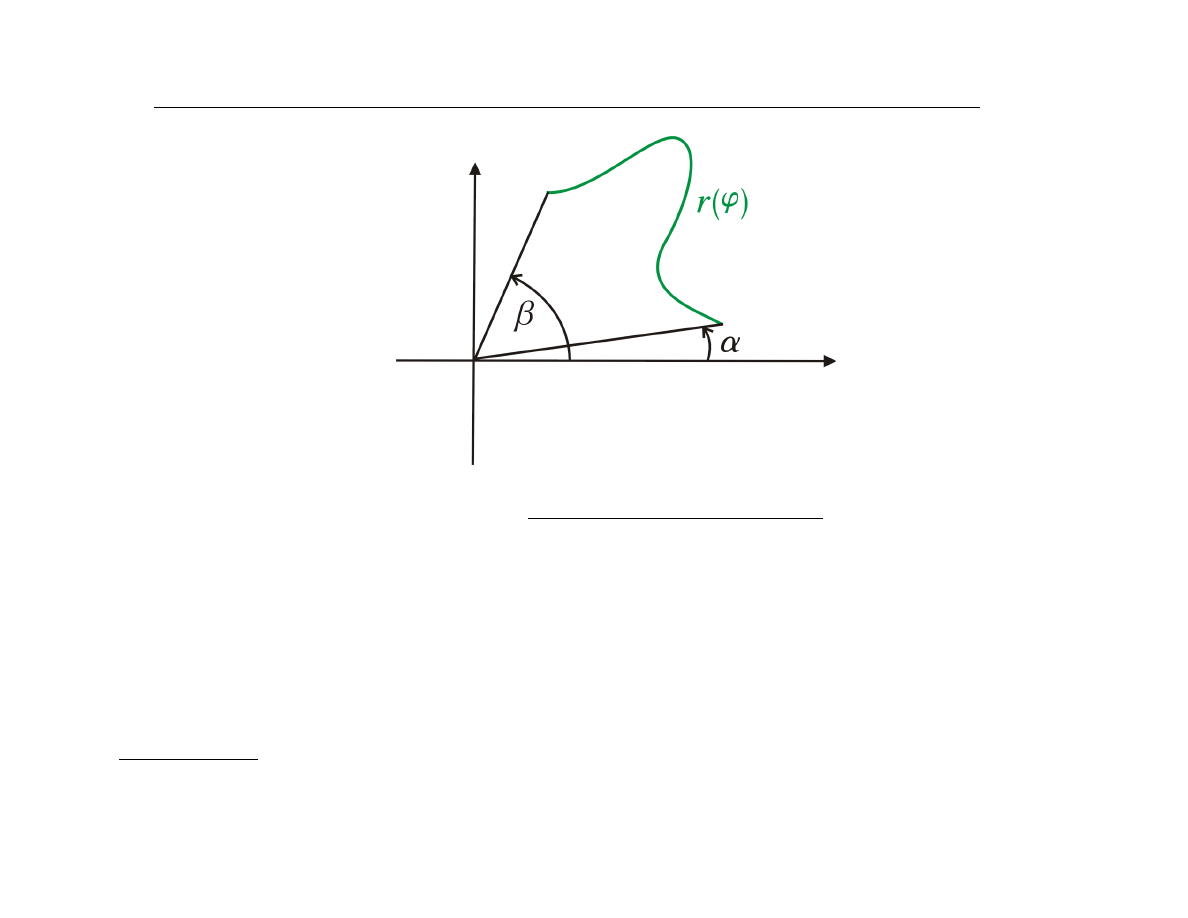
(E)
Pole obszaru płaskiego pod krzywą zadaną we współrzędnych
biegunowych
|P | =
1
2
β
Z
α
r
2
(ϕ) dϕ
Założenie: funkcja
r(ϕ)
jest ciągła i nieujemna dla
ϕ ∈ [α, β]
.
Przykład
Oblicz pole obszaru ograniczonego krzywą z punktu b)
z poprzedniego przykładu.
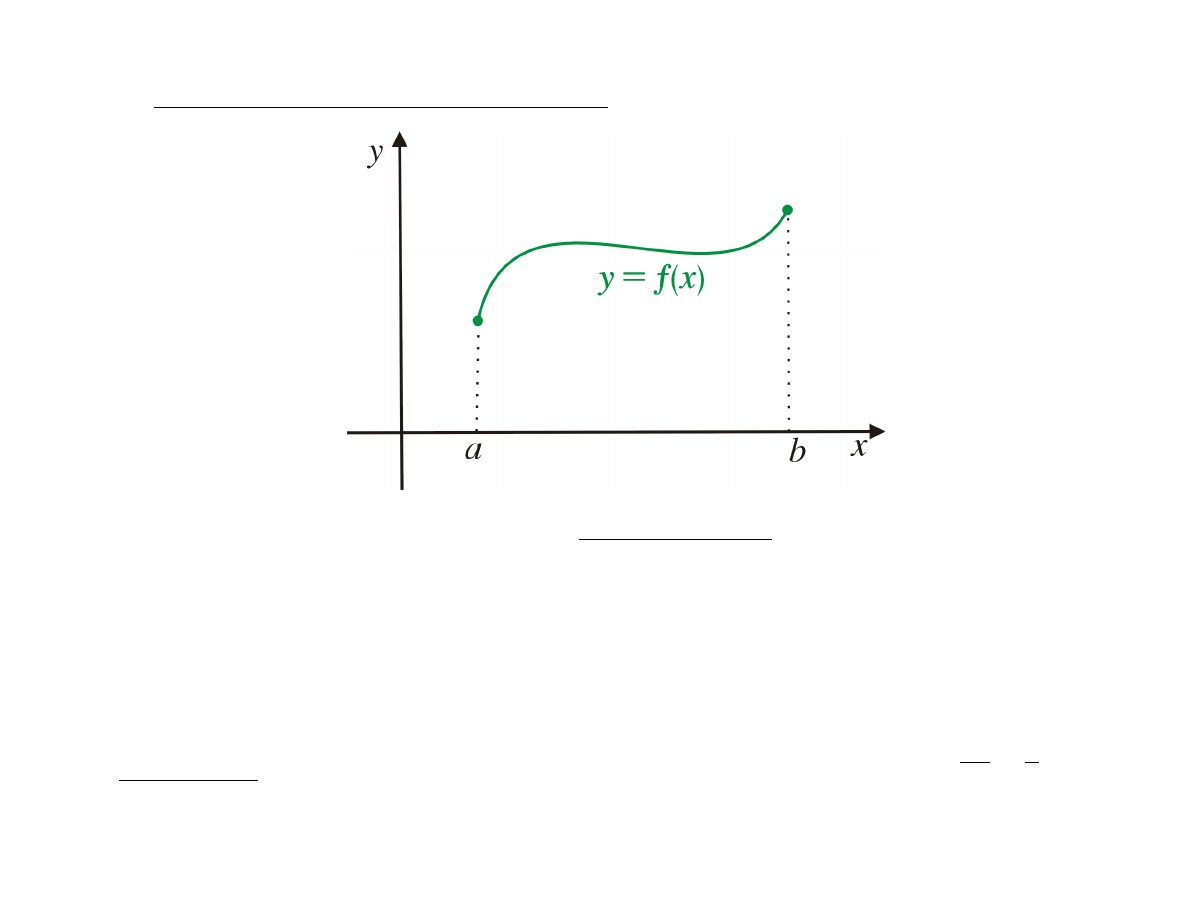
13
(F)
Długość łuku wykresu funkcji
|L| =
b
Z
a
v
u
u
t
1 + (f
0
(x))
2
dx
Założenie: funkcje
f (x)
i
f
0
(x)
są ciągłe dla
x ∈ [a, b]
.
Przykład Oblicz długość łuku wykresu funkcji
f (x) =
x
2
4
−
1
2
ln x
dla
x ∈ [1, e]
.
14
(G)
Długość łuku krzywej zadanej parametrycznie
|L| =
t
2
Z
t
1
v
u
u
t
(x
0
(t))
2
+ (y
0
(t))
2
dt
Założenie: funkcje
x(t)
,
x
0
(t)
,
y(t)
i
y
0
(t)
są ciągłe dla
t ∈ [t
1
, t
2
]
.
15
Przykład
Oblicz długość łuku krzywej zadanej dla
t ∈ [−4, −1]
parametrycznie:
x(t) =
t
R
−2
cos z
z
dz
y(t) =
3
R
t
sin z
z
dz
16
(H)
Długość łuku krzywej we współrzędnych biegunowych
|L| =
β
Z
α
v
u
u
t
(r(ϕ))
2
+ (r
0
(ϕ))
2
dϕ
Założenie: funkcje
r(ϕ)
i
r
0
(ϕ)
są ciągłe dla
ϕ ∈ [α, β]
.
Przykład
Oblicz
długość
łuku
krzywej
o
równaniu
r(ϕ) = a(1 + cos ϕ)
, gdzie
a > 0
i
ϕ ∈ [0, 2π]
.
17
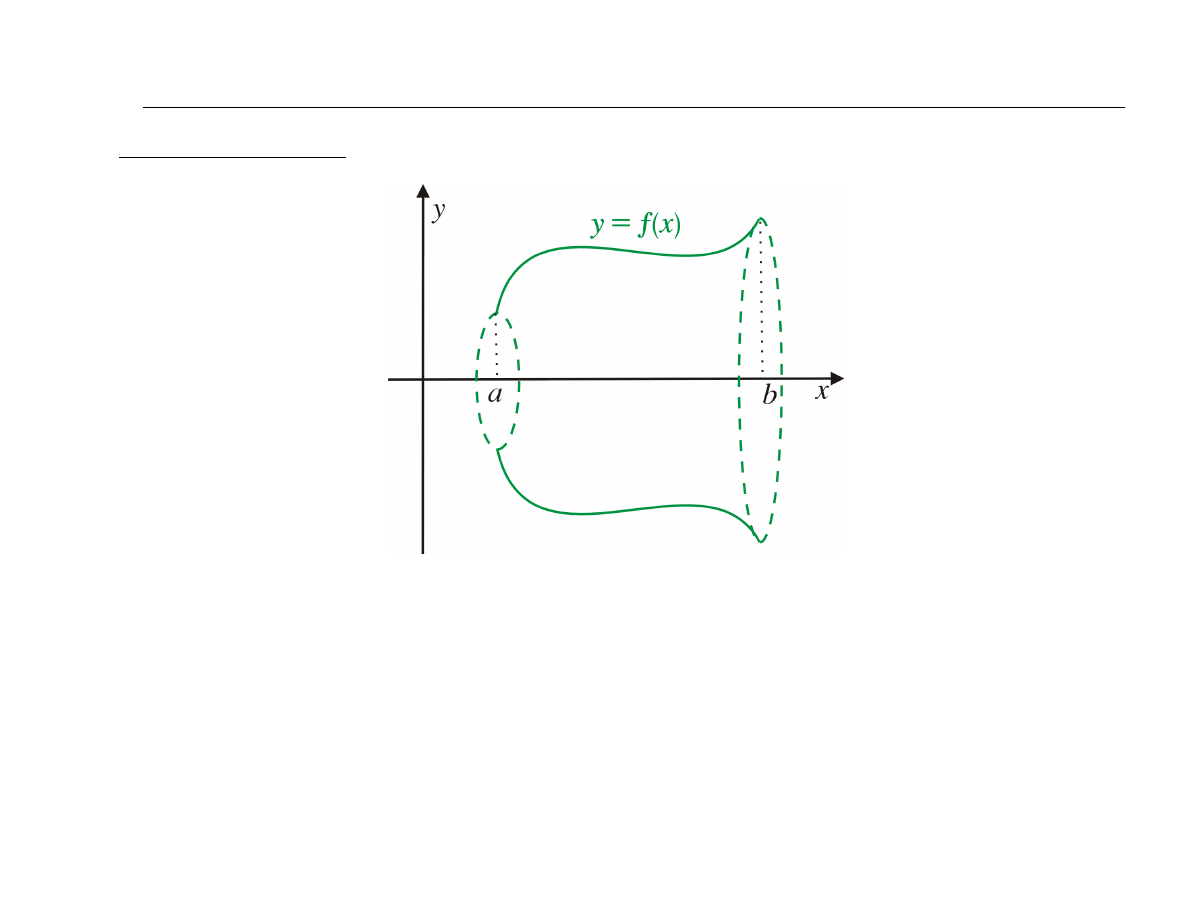
(I)
Objętość bryły obrotowej powstałej przez obrót wykresu funkcji
dookoła osi 0X
|V | = π
b
Z
a
(f (x))
2
dx
Założenie: funkcja
f (x)
jest ciągła dla
x ∈ [a, b]
.
18
Przykład
Oblicz objętość bryły powstałej przez obrót wykresu
funkcji
f (x) =
1
√
x
2
− 3x + 2
dookoła osi 0X dla
x ∈ [3, 4]
.
Przykład Wyprowadź wzór na objętość stożka ściętego, powstałego
przez obrót prostej
f (x) = cx
dookoła osi 0X dla
x ∈ [a, b]
,
gdzie stałe
a, b, c > 0
.
(J)
Objętość bryły obrotowej powstałej przez obrót krzywej zadanej
parametrycznie dookoła osi 0X
|V | = π
t
2
Z
t
1
(y(t))
2
· | x
0
(t) | dt
19
Założenie: funkcje
x(t)
,
x
0
(t)
i
y(t)
są ciągłe dla
t ∈ [t
1
, t
2
]
oraz
x
0
(t)
i
y(t)
mają stały znak.
Przykład
Oblicz objętość bryły powstałej przez obrót krzywej
x(t) =
1
2
t
2
+
1
2
t,
y(t) = t
3 dookoła osi 0X dla
t ∈ [0, 1]
(K)
Pole powierzchni bocznej bryły obrotowej powstałej przez obrót
wykresu funkcji dookoła osi 0X
|S| = 2π
b
Z
a
|f (x)|
v
u
u
t
1 + (f
0
(x))
2
dx
Założenie: funkcje
f (x)
i
f
0
(x)
są ciągłe dla
x ∈ [a, b]
.
20
Przykład Wyprowadź wzór na pole powierzchni sfery o promieniu
R
.
(L)
Pole powierzchni bocznej bryły obrotowej powstałej przez obrót
krzywej zadanej parametrycznie dookoła osi 0X
|S| = 2π
t
2
Z
t
1
|y(t)|
v
u
u
t
(x
0
(t))
2
+ (y
0
(t))
2
dt
Założenie: funkcja
x(t), y(t), x
0
(t), y
0
(t)
jest ciągła dla
t ∈
[t
1
, t
2
]
.
21
Przykład
Oblicz pole powierzchni powstałej przez obrót dookoła
osi 0X asteroidy:
x(t) = a cos
3
t
t ∈ [0, 2π]
y(t) = a sin
3
t
Przykład
• Oblicz pole obszaru zawartego pomiędzy krzywą
f (x) =
1
5
√
(x−3)
2
oraz prostymi
x = 3,
x = 4,
y = 0
.
• Oblicz długość łuku wykresu funkcji:
f (x) = arcsin x +
s
1 − x
2
.
• Oblicz objętość bryły powstałej przez obrót dookoła osi 0X
krzywej
f (x) = ln x
dla
0
6 x 6 1
.
22
• Oblicz objętość bryły powstałej przez obrót dookoła osi 0X
krzywej
f (x) = x e
−x
dla
x > 0
.
• Oblicz pole obszaru zawartego pomiędzy krzywą
f (x) =
1
1+x
2
a osią 0X.
• Krzywa
f (x) =
1
x , gdzie
1
6 x 6 +∞
obraca się wokół
osi 0X. Wykazać następujący pardoksalny fakt: pole uzyskanej
powierzchni obrotowej wynosi
+∞
zaś objętość bryły ograniczonej
tą powierzchnią wynosi tylko
π
.