TEORIA ERGODYCZNA

Bartosz Frej

Instytut Matematyki i Informatyki

Politechniki Wrocławskiej

Przedmiot zainteresowania

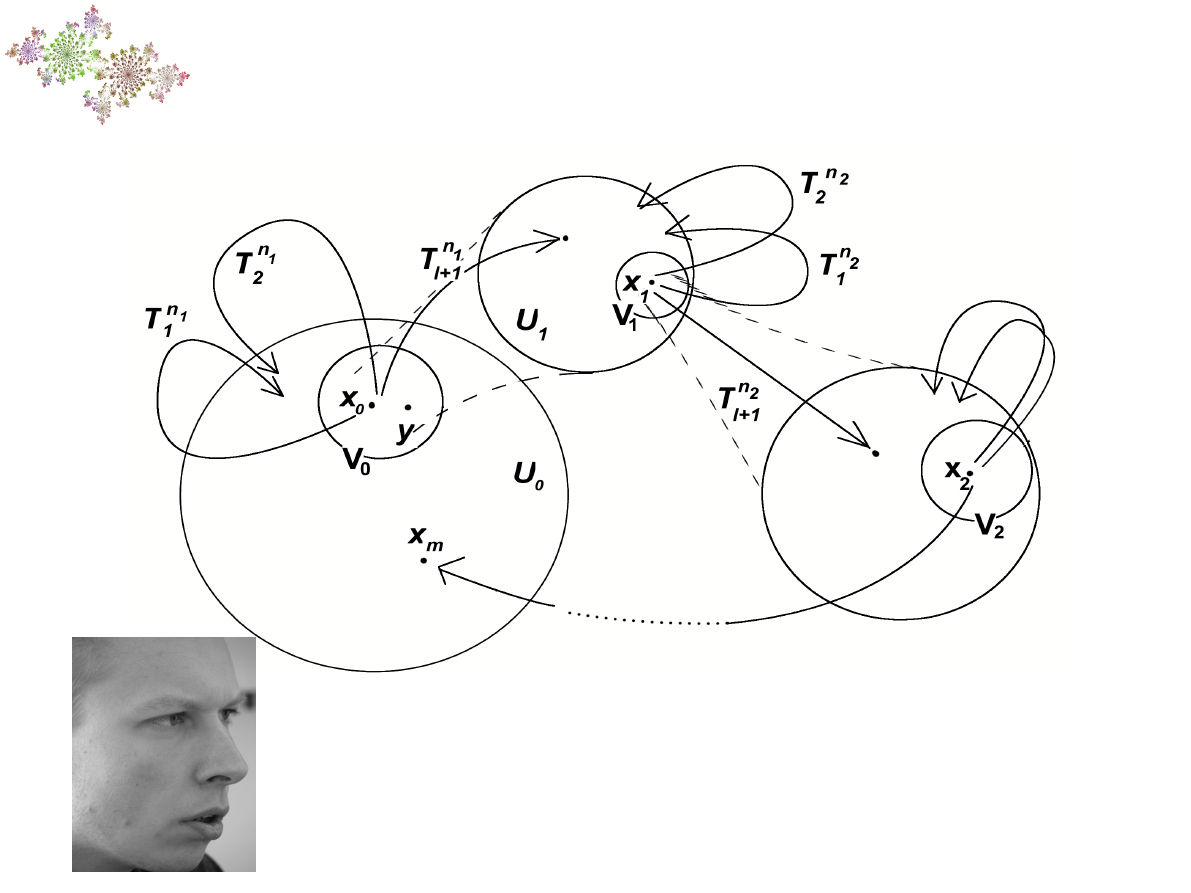
Teoria ergodyczna to dziedzina matematyki

zajmująca się badaniem przekształceń

określonych na pewnych abstrakcyjnych

przestrzeniach,

ze szczególnym

uwzględnieniem

asymptotycznych

własności tych

przekształceń.

Pomimo takiej definicji celu badań jest to

nauka mocno zakorzeniona w

rzeczywistych problemach.

Trochę mechaniki

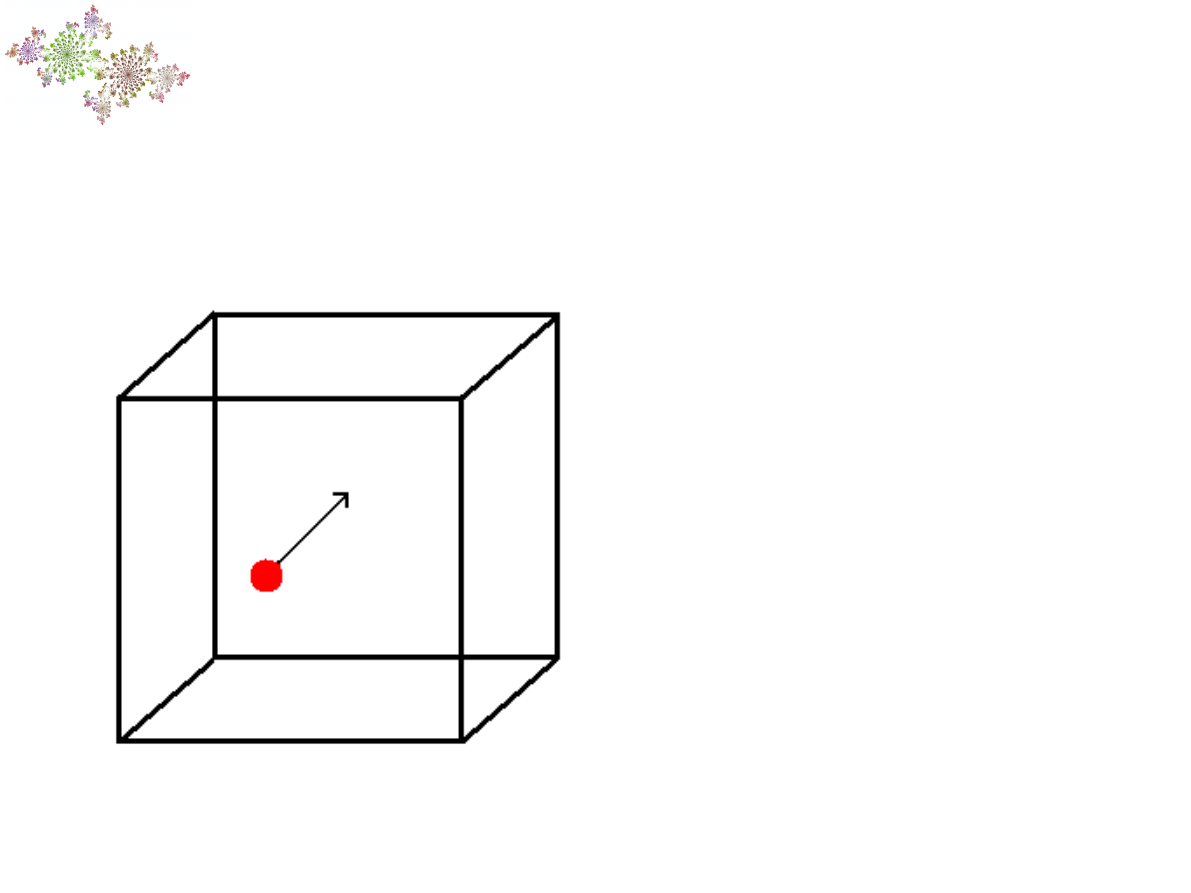
Jeden z klasycznych

modeli fizycznych –

cząstka w

zamkniętym pudle.

Do jej opisu

potrzebujemy 6

współrzędnych: trzy

współrzędne

położenia i trzy

prędkości (lub

pędu).

Trochę mechaniki

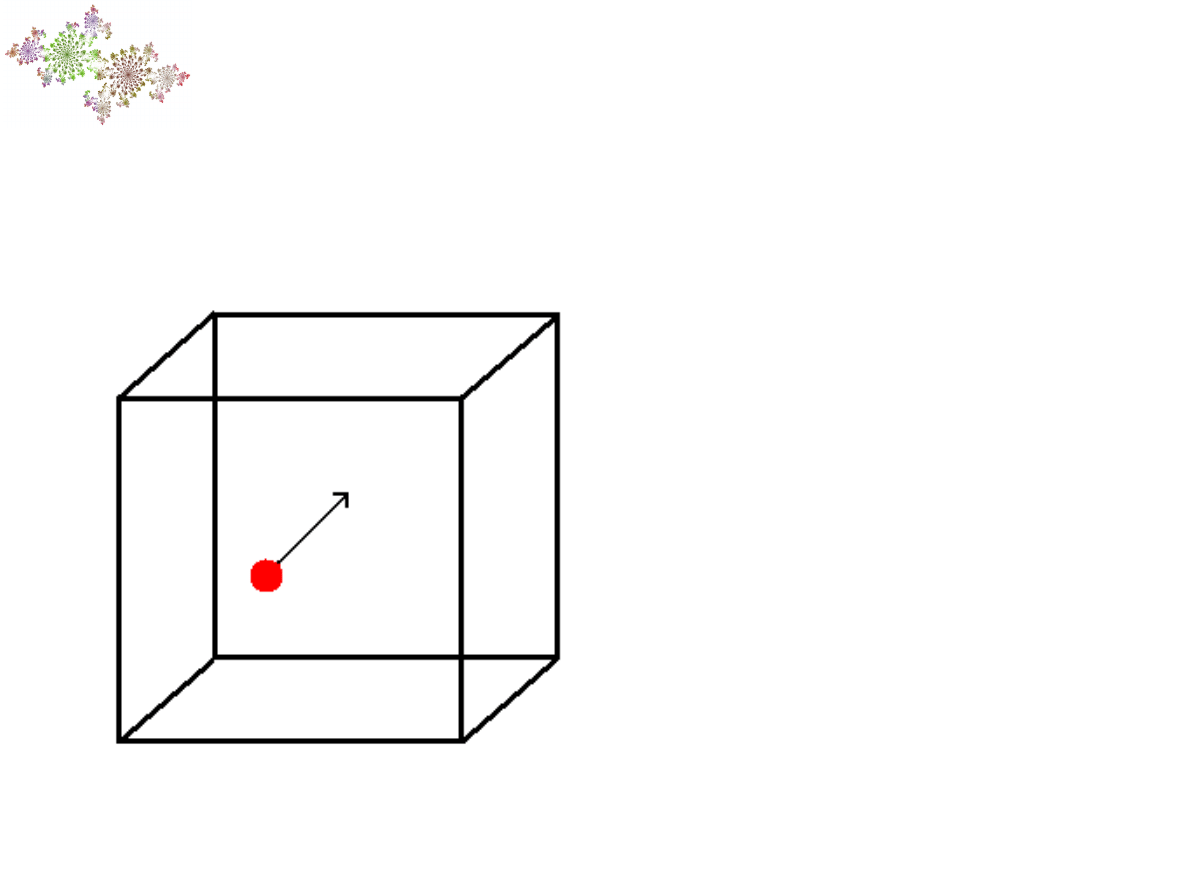
Znając te

współrzędne i

znając siły jakie

działają na naszą

cząstkę możemy z

odpowiednich

równań obliczyć,

jak będzie się

poruszała.

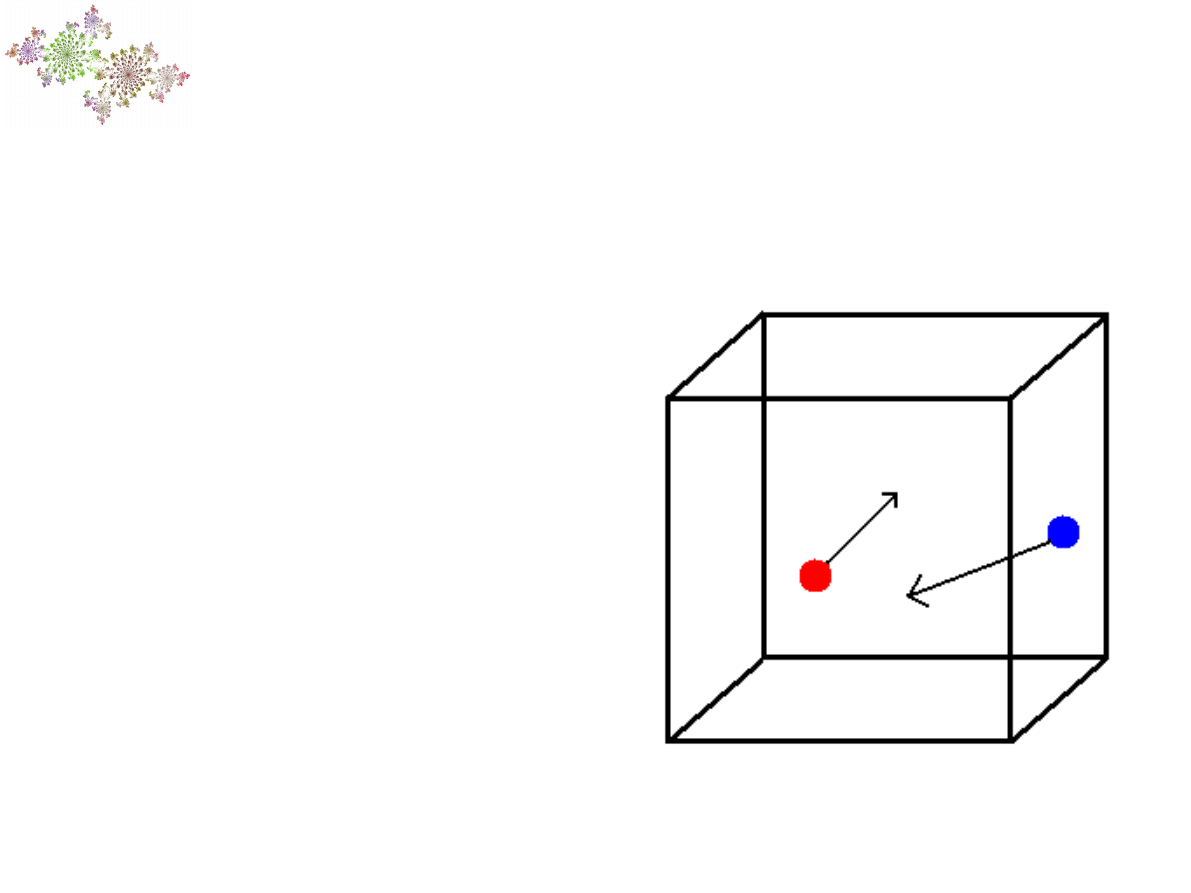
Trochę mechaniki

Jeśli rozważymy dwie

cząstki, będziemy

mieć dwanaście

współrzędnych w

opisie – sześć dla

jednej i sześć dla

drugiej cząstki.

Ogólnie – k cząstek to

6k współrzędnych w

równaniach.

Trochę mechaniki

Ale co zrobić gdy mamy tyle cząstek, ile

dyktuje liczba Avogadra?

W praktyce nigdy nie uzyskamy dokładnej

informacji o współrzędnych pędu i

położenia tylu cząstek, a nawet gdyby, to

jaką wartość miałoby w istocie rozwiązanie

równań, które mają 10

23

niewiadomych?

Zakładając, że dałoby się to zrobić...

Mechanika statystyczna

Zamiast pytać o szczegółową historię cząstek

możemy zadawać pytania innej natury:



jakie jest prawdopodo-

bieństwo, że układ

w trakcie swojej ewolucji

będzie się znajdował

w jednym ze stanów

z wyróżnionego zbioru

(np. wszystkie cząstki

w jednej połówce

pudełka)?

Ludwig Boltzmann (1844-1906)

Mechanika statystyczna



czy układ będzie

miał tendencję do

powracania do

stanu

początkowego?



czy stan układu

będzie dążył do

jakiegoś położenia

równowagi?

Josiah Willard Gibbs (1839-1903)

Układ dynamiczny

Matematyczny model:



X – zbiór wszystkich stanów układu



T

t

– przekształcenia przestrzeni X, które

odpowiadają upływowi czasu t



Zakładamy, że T

t+s

(x)=T

t

(T

s

(x)) dla

każdego stanu x

Układ dynamiczny

W ogóle nie zajmujemy się pytaniem, jaki

jest wymiar naszej przestrzeni!

Dzięki temu zyskujemy uniwersalność.

Dla mola cząstek wymiar będzie duży. Ale

dla ruchu wahadła zbiór stanów X może

być odcinkiem [-α,α], gdzie α jest

maksymalnym wychyleniem wahadła.

Układ dynamiczny

Upraszczając sytuację możemy umówić się,

że mierzymy stan układu jedyne co

pewien czas t', np. co sekundę, i zamiast

zestawu przekształceń T

t

rozważać tylko

to jedno T=T

t'

.

Otrzymujemy układ dynamiczny (X,T),

czyli zbiór z działaniem pewnego

przekształcenia – główny obiekt

zainteresowania teorii ergodycznej.

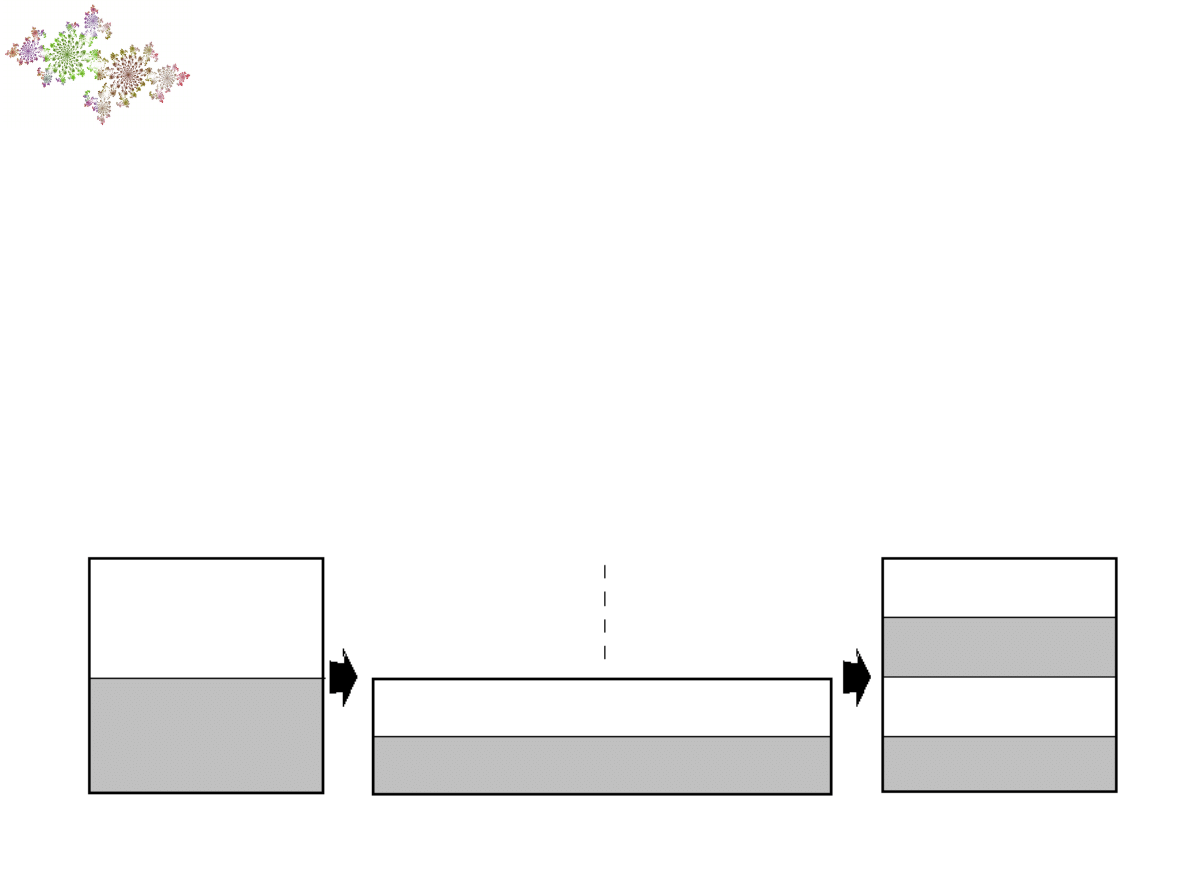
Przekształcenie piekarza

Znany przykład układ dynamicznego:



X = kwadrat, którego bokami są odcinki [0,1)



T = przekształcenie kwadratu, w którym

kwadrat najpierw ściskamy dwukrotnie w

pionie, a następnie przekrawamy na pół i

jedną połówkę ustawiamy na drugiej.

Przekształcenie piekarza

Ponieważ powyższe przekształcenie

kwadratu przypomina czynności

wykonywane przy wyrabianiu ciasta,

nazywa się je czasem przekształceniem

piekarza.

Wzór tego przekształcenia:

T(x,y)=(2x, 1/2y) dla x<1/2
T(x,y)=(2x - 1, 1/2y + 1) w przeciwnym razie

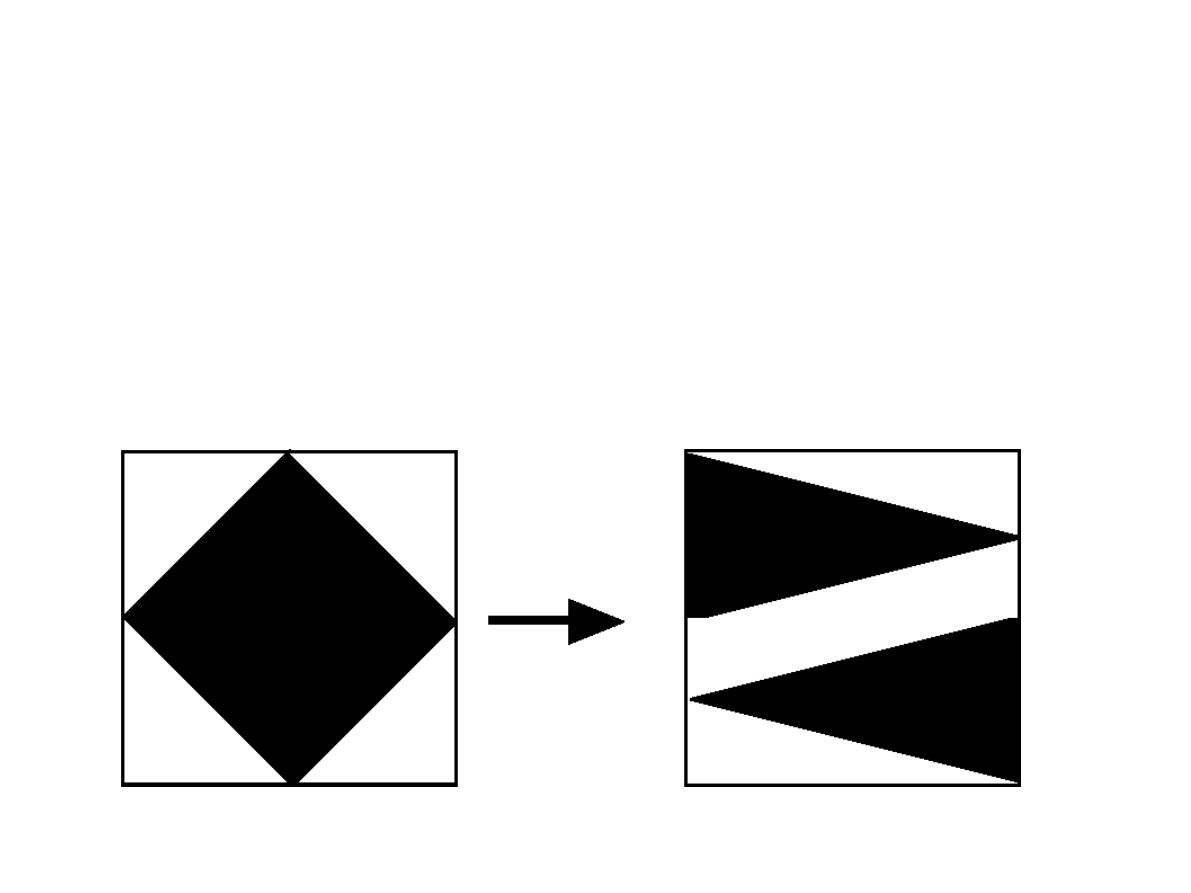
Co robi przekształcenie

piekarza?

Rozważmy ciasto-kwadrat z nadzieniem.

Zadziałajmy kilkakrotnie przekształceniem

piekarza.

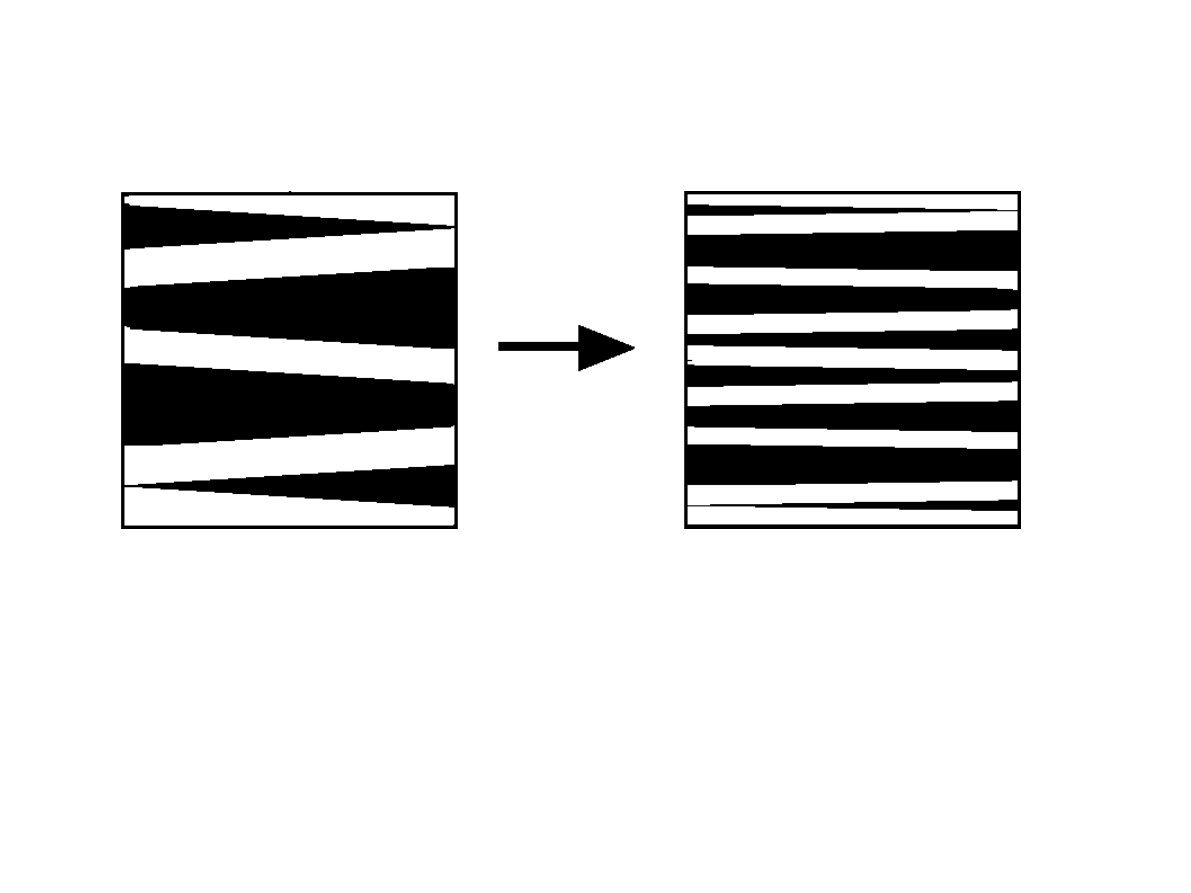
To przekształcenie nieźle

miesza

Jak widać nadzienie zostało równomiernie

rozłożone w całym cieście.

Mówimy, że przekształcenie piekarza ma

własność mieszania. Nie wszystkie

przekształcenia kwadratu mają tę cechę!

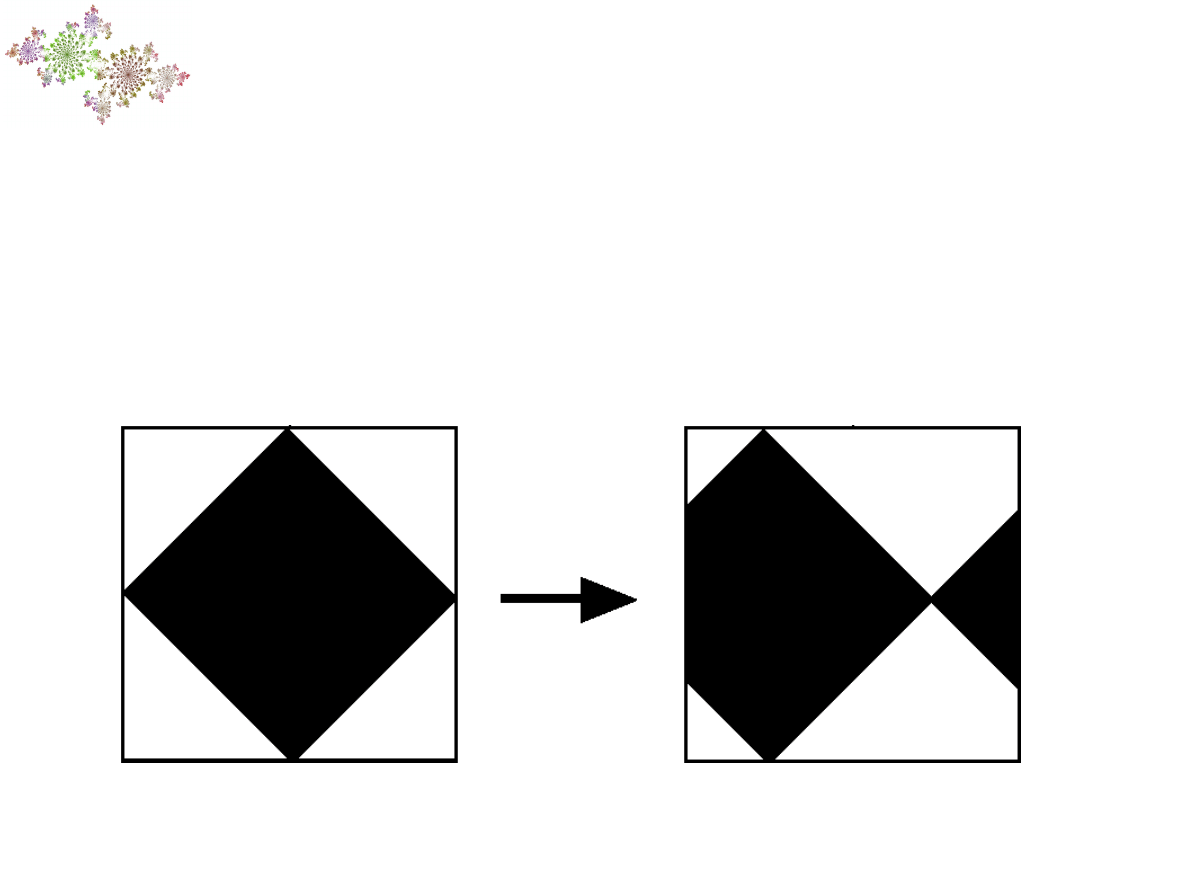
Kiepskie mieszanie

Na przykład

T(x,y)=(x+r,y) gdy x+r<1

T(x,y)=(x+r-1,y)

w przeciwnym razie

tylko przesuwa nadzienie poziomo

Mieszanie

Mieszanie jest ważnym pojęciem w teorii

ergodycznej.

Jeśli przez P(A) oznaczymy pole zbioru A, to

przekształcenie kwadratu T ma własność

mieszania, gdy dla dowolnych zbiorów A i

B zachodzi

P(A∩T

-n

B) → P(A)∙P(B), gdy n→∞.

Mieszanie

Innymi słowy, przekształcenie T ma własność

mieszania, gdy każdy zbiór B jest po

odpowiednio wielu iteracjach T równomiernie

rozłożony w całej przestrzeni.

Jego pole w dowolnym wycinku przestrzeni jest

wprost proporcjonalne do pola całego zbioru.

Dla ergodyków ciekawe są też pytania jakie

jest tempo zbieżności w definicji mieszania i

jak zależy ono od wyboru zbiorów A i B.

Wrocławska grupa ergodyków

W Instytucie Matematyki i Informatyki PWr

teorią ergodyczną zajmuje się grupa 10

osób (w tym 5 doktorantów) pod

kierunkiem profesorów Tomasza

Downarowicza i Zbigniewa Kowalskiego.

Badamy jeszcze ciekawsze rzeczy niż

przekształcenie piekarza.

Ciastem chętnie zajmujemy się w wolnych

chwilach.

Zapraszamy!