ANALIZA POPYTU
I OPTYMALNA POLITYKA CENOWA

Ćwiczenia 2 – Ekonomia menedżerska

mgr Krzysztof Sobczak

Katedra Ekonomii i Polityki
Gospodarczej
krzysztof_sobczak@sggw
.pl

Czynniki określające popyt

•

Dotychczas był jeden czynnik – cena

•

Przykład 1: Linia lotnicza konkuruje w przewozach na trasie
Teksas-Floryda. Liczba sprzedanych biletów na lot zależy od ceny
biletu (

P

), ceny biletu konkurenta na tej trasie (

P

k

) oraz poziomu

dochodu w regionie (

Y

).

•

Funkcja popytu określa zależność między ilością
sprzedanych dóbr a wieloma zmiennymi ją określającymi.

Q = f(

P

,

P

k

,

Y

)

Czynniki określające popyt c. d.

Linia lotnicza part II.
Dział ekonomii menadżerskiej oszacował funkcję popytu:

Q = 25 + 3

Y

+

P

k

– 2

P

Czy wzór jest potrzebny?
Równanie pozwala analizować wpływ zmian
poszczególnych składowych na wolumen sprzedaży
Rozważmy:
Zakładamy, że tylko jeden czynnik się zmienia a reszta
nie.

•

Wzrost wskaźnika dochodu o 1 punkt procentowy…

•

Podwyżka ceny o 10$...

•

Podwyżka ceny konkurenta o 10$...

Czynniki określające popyt c. d.

Linia lotnicza part III.
Jeżeli wszystkie czynniki ulegną zmianie otrzymujemy
równanie
Q = 3

Y

+

P

k

– 2

P

(zmiana pomija czynnik stały „25”)

Przykład 1:
Wskaźnik dochodu wzrośnie o 5 punktów procentowych, a
obie linie obniżą ceny o 15$.

Q = 3 * + – 2

=

30 miejsc

Linia powinna sprzedać dodatkowo 30 miejsc.
Przykład 2:
Oblicz wielkość zmiany wolumenu sprzedaży, gdy dochód
spadł o 8 punktów procentowych, cena konkurenta wzrosła o
12$ a cena naszej linii lotniczej wzrosła o 20$.

•

 

Czynniki określające popyt c. d.

Klasyfikacja dóbr

•

Dobra normalne – wzrost dochodu powoduje wzrost sprzedaży
(bilety lotnicze).

•

Dobra niższego rzędu – wzrost dochodu zmniejsza wydatki
(stać nas na co innego, kupujemy produkty lepsze jakościowo).

•

Dobro substytucyjne – konkuruje z dobrem i może je zastąpić
(wzrost ceny dobra zwiększa popyt na dobro substytucyjne;
różne marki jogurtów o podobnym składzie).

•

Dobro komplementarne – współistnieje z innym dobrem
(opony i samochody; wzrost popytu na jedno dobro spowoduje
wzrost popytu na drugie, wzrost ceny dobra
komplementarnego spowoduje spadek popytu na dane dobro).

Elastyczność cenowa popytu

Definicja: zmiana (reakcja) sprzedaży na zmianę ceny dobra.

Obecna cena na przelot wynosi 240$ ze sprzedażą 100
miejsc. Jaki będzie efekt obniżenia ceny o 5$ przy popycie na
110 miejsc?

?

!

Zmiana tylko jednego czynnika – warunek stałości

pozostałych czynników dla definicji elastyczności cenowej
popytu.

•

 

Rodzaje elastyczności

Elastyczność równa jedności: = (-1)

Zmiana ceny powoduje analogiczną zmianę ilości.

Popyt nieelastyczny:

Popyt niewrażliwy na zmianę ceny.

Popyt elastyczny: < (-1)

Zmiana ceny powoduje większą niż proporcjonalnie zmianę
ilości.

•

 

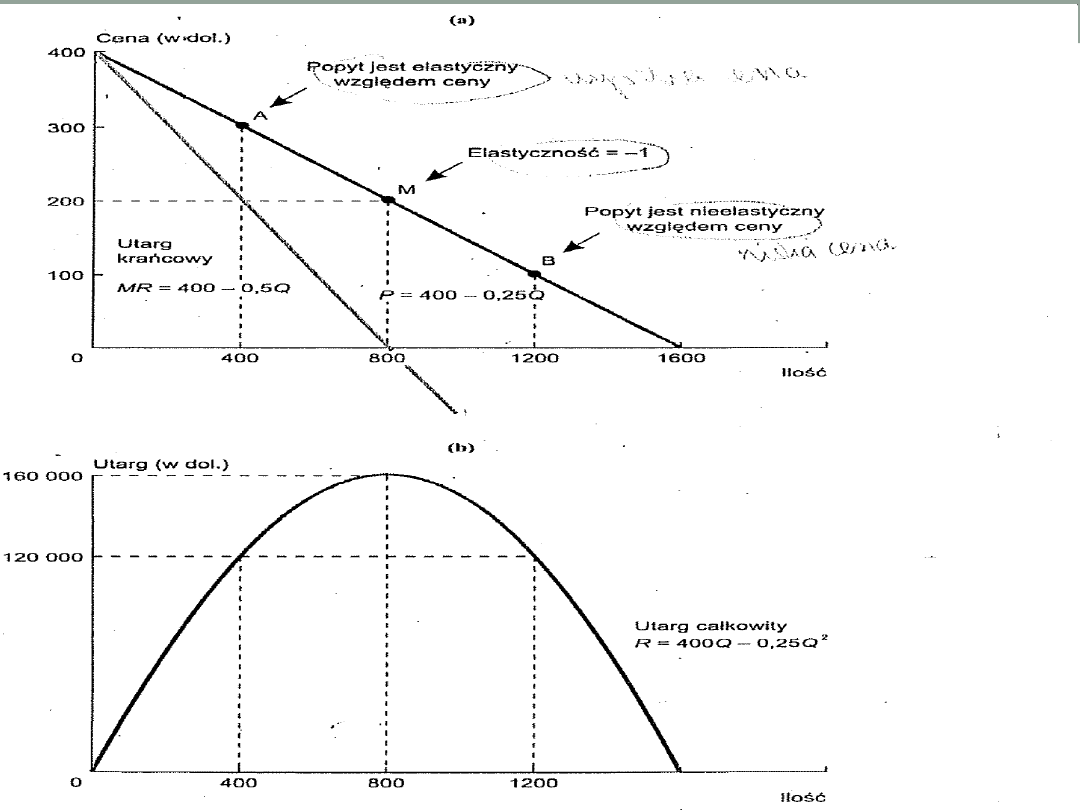
Optymalna polityka cenowa

Przykład 2: Przedsiębiorstwo sprzedaje oprogramowanie i
chce określić optymalny poziom ceny dla danego
programu.

Krzywa popytu: Q = 1600 – 4P.

S

a

m

u

e

ls

o

n

…

(2

0

0

9

),

s

.1

1

2

Optymalna polityka cenowa

W pkt. (A) E

p

= (-3); (dla P = 300, Q = 400).

Przedsiębiorstwo może osiągnąć wyższe przychody ?
Tak: Popyt jest elastyczny, więc procentowa obniżka ceny
zostanie zrekompensowana przez dodatnią zmianę
wolumenu sprzedaży.

W pkt. (B) E

p

= (-0,33); (dla P = 100, Q = 1200).

Tak: Przedsiębiorstwo funkcjonuje na nieelastycznym
odcinku krzywej popytu. Procentowy wzrost ceny jest większy
niż procentowa zmiana ilości sprzedaży. Dlatego przewaga
wzrostu ceny nad spadkiem ilości spowoduje zwiększenie
utargu.

Maksymalizacja utargu

Dla dowolnej krzywej popytu istnieje zależność:

Szczególny przypadek, gdy przedsiębiorstwo nie ponosi
kosztów zmiennych. W takiej sytuacji menedżer chcąc
maksymalizować zysk ustali cenę i ilość na poziomie
zapewniającej największy możliwy utarg.

•

 

Czysty problem sprzedaży

– przedsiębiorstwo

wytwarzając dobro lub usługę nie ponosi kosztów
zmiennych lub są one na tyle niskie, że zostają
pominięte w analizie.

Maksymalizacja utargu

Przykład 3:
Zarząd drużyny sportowej dysponuje obiektem na 36
000 miejsc.
Liczba biletów silnie zależy od ceny. Funkcja popytu ma
postać:

Q

= 60 000 – 3000

P

. Koszty są stałe i nie ulegają

zmianie względem liczby sprzedanych miejsc. Jak
powinna być optymalna polityka cenowa?

Cel: MR = 0

Q = 30 000? Dlaczego nie 36 000?

Optymalna polityka cenowa

Zasada optymalnego narzutu

Jaka ma być cena, by zmaksymalizować

wielkość nadwyżki na pokrycie kosztów, gdzie koszt
krańcowy jest stały.

Przedsiębiorstwo w zależności od elastyczności popytu
na dobro/usługę podnosi lub opuszcza ceny manipulując
narzutem

*

MR = MC, z poprzednich zajęć; optymalna wielkość

produkcji.

•

 

optymalny
narzut

maksymalny
utarg

maksymalny zysk

Optymalna polityka cenowa

Zasada optymalnego narzutu c. d.

•

Wielkość stosowanego przez przedsiębiorstwo narzutu
(narzutu ponad koszt krańcowy wyrażonego jako
procent ceny), jest

odwrotnie proporcjonalna

do

cenowej elastyczności popytu na dane dobro czy
usługę.

•

Narzut jest

zawsze dodatni

.

•

Narzut na cenę ponad koszt krańcowy jest tym
mniejszy im bardziej elastyczny jest popyt względem
ceny.

Optymalna polityka cenowa

Zasada optymalnego narzutu c. d.

•

Zasada ma zastosowanie dla popytu elastycznego. Gdy
popyt jest nieelastyczny

żadna cena nie zapewni

maksymalnego zysku

.

•

Przedsiębiorstwo nie powinno znaleźć się w obszarze
nieelastyczności na krzywej popytu. Powinno natomiast
przesuwać się do obszaru elastyczności podwyższając
cenę i zwiększając zyski.

•

Zasada opt. narz. Umożliwia określenie jak daleko
należy się przesunąć po krzywej poptyu.

Przykład 4:

Zarząd sieci sklepów spożywczych McPablo‘s Food Shops dokonał
analizy tygodniowego popytu na swoje tradycyjne tacos na 53
rynkach lokalnych. Z analizy wynika, że

Q= 400 – 1200P + 0,8A + 55Pop + 800P

k

Q: liczba tacos sprzedawanych przez jeden sklep w ciągu tygodnia;
A: wydatki na reklamę w danym regionie
Pop: liczba ludności w tym regionie (w tysiącach)
P

k

: przeciętna cena tacos pobierana przez konkurentów

Ustalono, że dla typowego sklepu sieci McPablo‘s:
P=1,50$; A= 1000$; Pop=40$; Pk=1$

a)

Oblicz wielkość tygodniowej sprzedaży typowego sklepu
McPablo’s

b)

Jaka jest obecnie elastyczność cenowa popytu na tacos? Jaka
jest elastycznośc popytu względem wydatków na reklamę?

c)

Czy sieć McPablo’s powinna podnieść ceny swoich tacos?

Przykład 4: ODP.

a)

Q=2400

b)

= -0,75,

= 0,33

c)

Tak. Przedsiębiorstwo znajdując się w obszarze
nieelastycznego popytu ( = -0,75) powinno
zwiększyć cenę.

 

Przykład 5:

General Motors (GM) produkuje małe ciężarówki w kilku fabrykach w stanie Michigan.
Stałe koszty produkcji wynoszą 180 mln USD rocznie a krańcowy koszt produkcji jednej
ciężarówki to 20 000 USD. Funkcja popytu na ciężarówki w tym stanie to: P = 30 000 –
0.1Q, gdzie P to cena w USD a Q roczna produkcja.

a)

Jaka jest wielkość produkcji która maksymalizuje zysk GM? Jaki jest roczny zysk?

b)

GM planuje eksportować ciężarówki do Ameryki Południowej. Bazując na badaniu
marketingowym, GM oszacowało, że elastyczność cenowa popytu w tych krajach
wynosi Ep = -9 dla szerokiego zakresu cen (od 20 000 USD do 30 000 USD).
Dodatkowe koszty transportu (włączając wszelkie opłaty impotowe i cła) wynoszą ok
800 USD za ciężarówkę. Jeden z menedżerów uważa, że cena powinna przewyższać
cenę krajową o 800 USD, aby pokryć koszty transportu. Czy zgadzasz się?

c)

GM produkuje ekonomiczną wersję małych ciężarówek. Krańcowy koszt tej wersji to
12 000 USD za ciężarówkę. Okazało się, że cena ustalona przez producenta na
poziomie 20 000 USD odstrasza potencjalnych klientów a sprzedaż idzie naprawdę
źle. GM zdecydowało zaprzestać produkcji tego modelu, ale pozostało im 18 000 nie
sprzedanych ciężarówek w magazynach. Szacowany popyt dla tej ilości ciężarówek
wynosi: P = 30000 – Q. Jeden z menedżerów sugeruje, aby utrzymać cenę na
bieżącym poziomie, inny sugeruje, aby wysprzedać cały zapas magazynowy. Jaką
cenę powinno ustalić GM?

Przykład 5: ODP.

a)

MR=MC, MC=20 000 => 30000 -0.2Q=20000
Q = 50 000,

P = 25 000 $,

π = 70 mln $

b)

Zasada optymalnego narzutu na koszty krańcowe:

(MC = 20 800, bo dodatkowo 800 za ciężarówkę, Ep = -9)
P = [-9/(-9+1)]*20800 = 23 400. GM powinno obniżyć cenę na

rynkach zagranicznych, a nie podnieść o 800, co wynika z wysokiej
elastyczności popytu.

c)

Czysty problem sprzedaży:

Nie interesują nas koszty, a celem jest maks. utarg MR=0, więc
30000-2Q=0 =>
Q = 15 000
P = 15 000 USD.

GM powinno obniżyć cenę, co spowoduje to sprzedaż 15 000 z 18
000 ciężarówek. Pozostałe 3000 sprzeda w następnym roku po
wyższej cenie P=30000-3000 = 27000 $.

Dziękuję za uwagę!