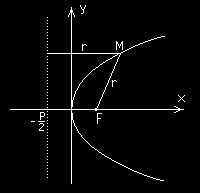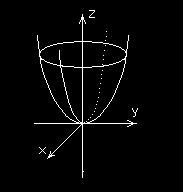
Niektóre krzywe na płaszczyźnie R2 (notatki z wykładu) 1. Okrąg o promieniu r i środku S = ( x , y ) ma równanie kanoniczne: 0
0
2
2
2
( x − x ) + ( y − y ) = r .
0
0
Okrąg o promieniu r i środku S = ( x , y ) można też zapisać w postaci 0
0
parametrycznej:
x = x
r
t
0 +
cos
y = y
r
t
t
0 +
sin , ∈<
π
2
;
0
>
Postać parametryczną najwygodniej jest stosować przy opisie fragmentów okręgów. Np. łuki l
i l przedstawione na rysunku powyżej mają postać parametryczną: 1
2
x = 2cos t
x = cos t
l :
l :
1
π
2
y = 2sin t , t ∈<
; π >,
y = sin t , t ∈< π 2
; π >
2
.
Zadanie. Zapisać ogólne równanie okręgu: 2
2
x − 2 x + y + 4 y −1 = 0 w postaci kanonicznej i w postaci parametrycznej.
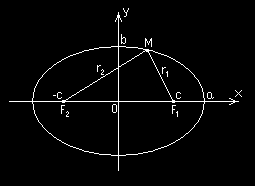
2. Elipsa o środku S = (
)
0
,
0
i półosiach a i b ma równanie kanoniczne:
2
2
x + y = 1,
2
2
a
b
i następującą postać parametryczną:
x = a cos t
y = b sin t , t ∈< 2
;
0 π > .
F = ( c 0
, )
, F = (− c 0
, ) to ogniska elipsy; c to połowa odległości między ogniskami. Jeżeli a jest 1
2
dużą półosią elipsy, b małą półosią elipsy, to zachodzą zależności: 2
2
2
a = b + c ;
r + r = 2 a .
1
2
( r
, r to odległości dowolnego punktu elipsy od ognisk F i F ).
1
2
1
2
c
Określa się też mimośród e =
e <
a , który jest miarą „ściśnięcia” elipsy. Dla elipsy mamy 1.
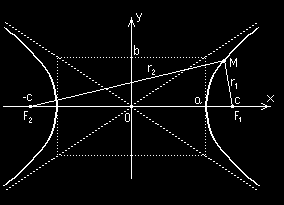
3. Hiperbola o środku S = (
)
0
,
0
i półosi rzeczywistej a oraz
półosi urojonej b ma równanie kanoniczne: 2
2
x − y = 1,
2
2
a
b
F = ( c 0
, )
, F = (− c 0
, ) to ogniska hiperboli;
1
2
r − r = 2 a ;
1
2
c
mimośród e =
> 1
a
.

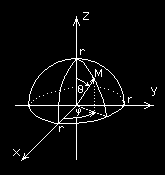
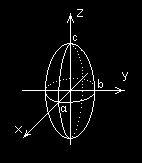
4. Parabola.
Parabolą nazywamy zbiór punktów równoodległych od punktu F
(ogniska) i prostej (zwanej kierownicą).
p
p
Jeżeli F = (
0
, ) , to kierownica ma równanie x = −
,
2
2
a równanie paraboli ma wtedy postać
y 2 = 2 px .
Niektóre powierzchnie w przestrzeni R3.
1. Powierzchnia sferyczna (sfera) o promieniu r i środku S = ( x , y , z ) ma równanie kanoniczne: 0
0
0
2
2
2
2
( x − x ) + ( y − y ) + ( z − z ) = r .
0
0
0
Natomiast w przypadku środka w punkcie (
)
0
,
0
,
0
mamy równanie
2
2
2
2
x + y + z = r .
Taką sferę możemy zapisać też w postaci parametrycznej (dwoma parametrami są tu odpowiednie kąty):
x = r cosϕ sinθ ,
y = r sinϕsinθ ,
z = r cosθ 0
,
≤ ϕ ≤ 2π 0
,
≤ θ ≤ π.
Jeśli M jest dowolnym punktem sfery, to kąt ϕ jest kątem między r
rzutem wektora
M
O
na płaszczyznę Oxy a osią Ox , kąt θ jest kątem r
między wektorem M
O
a osią Oz .
Półsferę o środku (
)
0
,
0
,
0
i promieniu r dla z ≥ 0 (jak na rysunku obok) możemy opisać równaniem
2
2
2
z = r − x − y otrzymanym z postaci kanonicznej sfery.
Taka półsfera ma równania parametryczne jak dla sfery przy kącie θ z zakresu <
π
;
0
> .
2
Elipsoida o środku w punkcie (
)
0
,
0
,
0
o półosiach odpowiednio a b
,
c
, ma
postać kanoniczną
2
2
y
2
x +
+ z = 1.
2
2
2
a
b
c
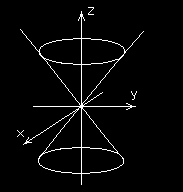


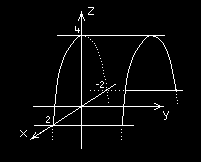
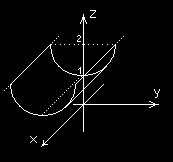
Przykłady różnych powierzchni.
Paraboloida obrotowa:
Powierzchnia stożkowa (stożek obrotowy), Powierzchnia stożkowa o
której tworząca jest nachylona do płasz-równaniu
2
2
z = x + y
π
czyzny xOy pod kątem
, a wierzchołek
2
2
4
z = a − x + y znajduje się w punkcie (
)
0
,
0
,
0
:
2
2
2
z = x + y
Powierzchnia walcowa – walec
Powierzchnia walcowa – (część
Powierzchnia walcowa
paraboliczny (kierownicą jest tu walca obrotowego) o równaniu: (walec obrotowy):
parabola, a tworzące są równoległe
2
2
2
2
x + y = r
z = 2 − 1− y
do osi Oy):
(oś obrotu pokrywa się z osią
2
(kierownicą jest tu półokrąg, a
z = 4 − x .
Oz).
tworzące są równoległe do osi
Ox).