ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ
Semestr zimowy 2006/2007
Egzamin na ocenę celującą, rozwiązania zadań
Zadanie 1*
Niech
n
n 1
W ( x) = a x + a
x −
∪
−
+ ... + a x + a , gdzie a , a ,..., a N
}
0
{
, n ∈N. Pytając naj-
0
1
n ∈
n
n 1
1
0
pierw o wartość W (1) Bartek pozna sumę a
wszystkich współczynników
0 + a + ...
1
+ an
wielomianu. Z niej wywnioskuje, że a , a ,..., a ∈{ , 0 ,
1 ,
2 ..., W (1)} . Jeżeli W 1
( ) = 0 , to
0
1
n
a + a = ... = a
, więc drugiego pytania już nie musi zadawać. Jeżeli nie, to wyznacza
n = 0
0
1
liczb
−
ę naturalną k spełniającą warunek
k
k
10 1 ≤ W 1
( ) < 10 . Pyta wówczas o wartość
(10 k
W
) .
Liczby a , a ,..., a są bowiem współczynnikami rozwinięcia liczby (10 k
W
) w systemie
0
1
n
liczbowym o podstawie
k
10 . Zapisując tę liczbę w systemie dziesiętnym szukane współ-
czynniki znajdą się w kolejnych k -cyfrowych blokach cyfr licząc od prawej strony.
Na przykład dla W ( x ) = 5 3
x + 7 x + 13 mamy W (1) = 25 ,
1
2
10 ≤ 25 < 10 , k = 2 , więc
(10 k
W
) = 5 ⋅106 + 7 ⋅102 + 13 = 5 000 713 = 05 | 00 | 07 |13 =
2 3
2 2
2 1
2 0
5 ⋅ 1
( 0 ) + 0 ⋅ 1
( 0 ) + 7 ⋅ 1
( 0 ) + 13 ⋅ 1
( 0 ) .
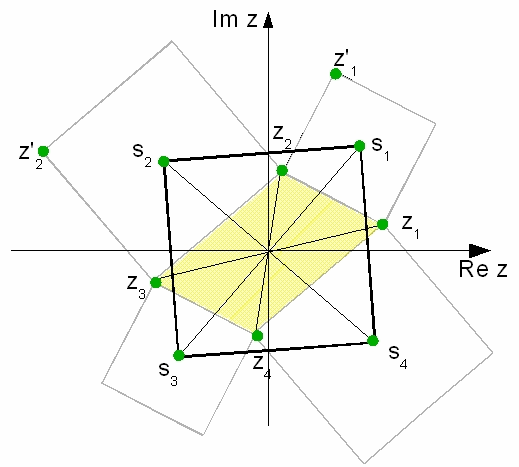
Zadanie 2*
Niech środek równoległoboku znajduje się w punkcie z = 0 oraz niech z , z , z , z będą 0
1
2
3
4
wierzchołkami tego równoległoboku. Wtedy oczywiście z = − z , z = − z . Przez 3
1
4
2
K1, K2, K3, K4 oznaczamy kwadraty zawierające kolejne pary wierzchołków z i z , 1
2
z i z , z i z , z i z . Niech s , s , s , s będą środkami kolejnych kwadratów, zaś 2
3
3
4
4
1
1
2
3
4
z ', z ' wierzchołkami tych kwadratów leżącymi po przekątnej do z , z . Z symetrii figury 1
2
1
2
wynika, że s = − s , s = − s . Punkty s , s , s , s tworzą zatem równoległobok o środku 3
1
4
2
1
2
3
4
z = 0 . Wystarczy więc uzasadnić, że s = i s i otrzymamy kwadrat. Interpretując dodawa-0
2
1
nie liczb zespolonych jako dodawanie ich wektorów wodzących otrzymujemy wzory 1
1
s = z + ( z '− z ) , s = z + ( z '− z ) .
1
1
2
1
1
2
2
2
2
2
Wierzchołki z ', z ' można otrzymać przez obrót wierzchołków z , z o kąt π wokół
1
2
1
2
z , z . Stąd z '= i ( z − z ) + z , z '= i ( z − z ) + z . Ostatecznie więc 2
3
1
1
2
2
2
2
3
3
1 + i
1 − i
i −1
i + 1
s =
z +
z , s =
z +
z = i s .
1
1
2
2
2
2
1
2
1
2
2
Zadanie 3*
Wszystkie rozważanie macierze muszą być macierzami kwadratowymi ustalonego stopnia n ≥ 1 , przy czym I jest macierzą jednostkową, zaś O macierzą zerową. Niech 2
2006
B = I + A + A + ... + A
.
Wówczas B ( I − A = I − A 2007
)
= I − O = I . Stąd i z twierdzenia Cauchy’ego o wyznacz-niku iloczynu macierzy wynika, że det[ B ( I − A) ] = det B ⋅ det ( I − A) = det I = 1, zatem det B ≠ 0 .
Zadanie 4*
Wektor wodzący położenia danego punktu w chwili t ma postać
r ( t ) = (
2
a t + a t + a ,
2
b t + b t + b ,
2
c t + c t + c ),
2
1
0
2
1
0
2
1
0
przy czym a , b , c , gdzie i = ,
0 ,
1 2 , są ustalone, t ∈ R. Przyjmując u = ( a , b , c ) , i
i
i
2
2
2
v = ( a , b , c ) , w = ( a , b , c ) otrzymujemy postać r ( t = t 2
)
u + tv + w . Jeżeli u× v ≠ 0 , to 1
1
1
0
0
0
r ( t ) jest wektorem wodzącym punktu płaszczyzny π : r = su + tv + w , gdzie s, t ∈ R. Jeżeli u × v = 0 i v ≠ 0 , to wektory u , v są współliniowe oraz u = α v dla pewnego α ∈ R i wówczas r ( t ) = ( t 2
α + t ) v + w jest wektorem wodzącym punktu prostej l : r = sv + w , gdzie t ∈ R, zawartej w płaszczyźnie π . Jeżeli na koniec u× v = 0 i v = 0 , to r ( t ) = w jest wektorem wodzącym punktu płaszczyzny π .
Teresa Jurlewicz, 14.02.2007
Wyszukiwarka
Podobne podstrony:
azg cel 07
azg cel 07
Merry Gentry 07 roz 14
Merry Gentry 07 roz 18
Merry Gentry 07 roz 8
Merry Gentry 07 roz 12 13
Merry Gentry 07 roz 19 20
Merry Gentry 07 roz 24 25
Merry Gentry 07 roz 9
Merry Gentry 07 roz 16
Merry Gentry 07 roz 17
30 ROZ książka obiektu budowlanego [M I ][3 07 2003][Dz U
112 ROZ stawki za zajęcie pasa drogowego[M I ][18 07 2011
pato v1.07 by El Prezidente do roz, patomorfologia TESTY
30 ROZ książka obiektu budowlanego [M I ][3 07 2003][Dz U
MG 07 Podazajac za Ciemnoscia roz 1
więcej podobnych podstron