OPRACOWANIE WYNIKÓW POMIARU

1. CEL ĆWICZENIA

Celem ćwiczenia jest poznanie podstawowych zagadnień związanych z opracowaniem

wyników pomiaru.

2. WPROWADZENIE

2.1. Wstęp

Umiejętność właściwego opracowania wyników pomiaru jest niezbędna w wielu dziedzinach

nauki, techniki oraz gospodarki. O wysokiej randze tej problematyki świadczą prace

międzynarodowych komisji, których celem jest znalezienie i ujednolicenie metod

opracowania wyników pomiaru. Wyniki tych prac są publikowane i z czasem zyskują

charakter normatywny, jak np. [1].

W wielu przypadkach surowy wynik pomiaru, bez jego właściwego opracowania, jest

uważany za bezużyteczny.

Pomiary można ogólnie podzielić na bezpośrednie lub pośrednie. Pomiarem bezpośrednim

jest na przykład pomiar napięcia stałego za pomocą woltomierza. Przykładem pomiaru

pośredniego jest pomiar rezystancji metodą techniczną: prąd płynący przez mierzony rezystor

jest mierzony za pomocą amperomierza, a spadek napięcia na rezystorze – za pomocą

woltomierza. Rezystancja obliczana jest z prawa Ohma.

2.2. Błąd i poprawka

Najczęściej surowy wynik pomiaru x jest jedynie przybliżeniem wartości rzeczywistej

(prawdziwej) x wielkości mierzonej X. Różnica pomiędzy wynikiem pomiaru x a wartością rz

rzeczywistą nazywana jest rzeczywistym błędem bezwzględnym ∆ x

rz

∆ x = x − x

(1)

rz

rz

Wartość rzeczywista wielkości mierzonej jest znana tylko w wyjątkowych przypadkach.

Dlatego pojęcie rzeczywistego błędu bezwzględnego ∆ x ma niewielkie znaczenie

rz

praktyczne. W praktyce, w zależności od wymaganej dokładności pomiaru, doświadczenie

pomiarowe modyfikuje się tak, aby otrzymać wartość najbliższą x . Wartość tę nazywa się rz

wartością poprawną xpopr. Wtedy wyrażenie na błąd bezwzględny przyjmuje postać .

∆ x = x − x

(2)

popr

Bezwzględny błąd ze zmienionym znakiem nazywany jest poprawką (

p x)

2

( px) = −∆ x

(3)

Poprawka dodana do wyniku pomiaru daje tzw. wynik skorygowany - czyli wartość

poprawną.

Błąd względny δ x jest to stosunek błędu bezwzględnego do wartości poprawnej

x

∆

x

δ =

(4)

x popr

Błąd względny jest często wyrażany w procentach (1 % = 10-2) lub promilach (1 ‰ = 10-3).

Spotykane są także mnożniki: ppm (ang. part per million; 1 ppm = 10-6) oraz ppb (ang. part

per billion; 1 ppb = 10-9), jednak ich stosowanie do wyrażania błędu wielkości elektrycznych

nie jest zalecane. Na przykład względny błąd pomiaru napięcia należy zapisać w postaci U

δ

= 1 µV/V zamiast U

δ = 1 ppm.

Błąd może być spowodowany różnymi czynnikami. Z tego powodu do słowa „błąd”

dodaje się określenie wskazujące na jego przyczynę lub charakter. Na przykład błąd

rozdzielczości jest błędem spowodowanym ograniczoną rozdzielczością, błąd przypadkowy -

błędem wynikającym z losowej zmienności wyników powtarzanego doświadczenia

pomiarowego itp.

2.3. Klasyfikacja błędów

Ogólnie błędy dzieli się na:

1) systematyczne,

2) przypadkowe,

3) nadmierne (grube).

Powyższy podział powstał na podstawie obserwacji zachowania się wyników pomiaru przy

powtarzaniu doświadczenia pomiarowego.

Ad.1. Błędy systematyczne można podzielić na:

a) błędy systematyczne stałe,

b) błędy systematyczne zmienne.

Błąd systematyczny stały można wykryć po powtórzeniu doświadczenia pomiarowego w

celowo zmienionym (zmodyfikowanym) układzie warunków fizycznych.

Wykrycie stałego błędu systematycznego przez powtarzanie doświadczenia pomiarowego w

niezmiennym układzie warunków fizycznych jest niemożliwe.

Jeśli wyniki powtarzanego doświadczenia pomiarowego w pozornie niezmiennym układzie

warunków fizycznych charakteryzują się systematyczną zmianą (dryfem), to wyniki pomiaru

3

obarczone są błędem systematycznym zmiennym. Ten rodzaj błędów powstaje np. w

wyniku zmian jakiejś dominującej wielkości zakłócającej (wpływającej) np. temperatury

otoczenia. Występowanie błędu systematycznego zmiennego świadczy o tym, że podstawowy

układ warunków fizycznych doświadczenia pomiarowego nie jest niezmienny. Cechą

charakterystyczną tego błędu jest możliwość wyznaczenia (zdeterminowania) zależności

między tym błędem i wywołującym go czynnikiem. Błąd systematyczny zmienny może być

monotoniczny (rosnący albo malejący) lub okresowy.

Inny podział błędów systematycznych bierze pod uwagę ogniwo doświadczenia

pomiarowego, w którym powstaje błąd. Na rys.1 przedstawiono strukturalny schemat

doświadczenia pomiarowego, przydatny do sklasyfikowania błędów systematycznych.

Rys.1. Strukturalny schemat doświadczenia pomiarowego

Pierwsza składowa błędu systematycznego jest związana z obiektem pomiaru. Dołączenie

przyrządu pomiarowego powoduje zmianę równowagi energetycznej w obiekcie badanym.

Dochodzi zatem do naruszenia podstawowego układu warunków fizycznych, w jakich

odbywa się doświadczenie pomiarowe i - w konsekwencji - do zmiany miary wielkości

mierzonej. Błąd spowodowany zmianą równowagi energetycznej jest nazywany czasem

błędem metody. Nazwa ta jest zbyt ogólna. Bardziej właściwe jest stosowane określenia „błąd

spowodowany zmianą równowagi energetycznej”. Błąd ten zazwyczaj wyznacza się

teoretycznie (oblicza).

Druga składowa błędu systematycznego jest związana z właściwościami narzędzia

pomiarowego. Nazywana jest błędem instrumentalnym. Jeśli błąd systematyczny narzędzia

pomiarowego występuje w znamionowych warunkach użytkowania, to nazywany jest

błędem podstawowym narzędzia pomiarowego. Przez znamionowe warunki użytkowania

rozumie się podstawowy układ warunków fizycznych, podany w normach lub przez

producenta przyrządu, a także układ warunków, w których dokonano wzorcowania przyrządu

lub w których przyrząd charakteryzuje się największą dokładnością. Błąd dodatkowy

narzędzia pomiarowego powstaje, gdy warunki fizyczne odbiegają od określonych przez

znamionowe warunki użytkowania. Błąd instrumentalny ma dwie składowe: błąd modelowy

oraz błąd wykonania narzędzia pomiarowego. Pierwszy powstaje na skutek rozbieżności

między fizyczną zasadą pomiaru (modelem) a rzeczywistymi zjawiskami zachodzącymi w

narzędziu pomiarowym. Drugi jest spowodowany ograniczoną dokładnością z jaką wykonano

lub wzorcowano narzędzie pomiarowe. Błąd instrumentalny można wyznaczyć przez

wzrorcowanie przyrządów przyrządów pomiarowych użytych w doświadczeniu.

4

Trzecia

składowa

błędu

systematycznego

jest

związana

z

subiektywizmem

(tendencyjnością) pomiarowca. Jest szczególnie istotna w przypadku przyrządów

analogowych.

Przykład 1

Do pomiaru siły elektromotorycznej E ogniwa o rezystancji wewnętrznej R = 8

,

0

użyto

w

Ω

woltomierza o rezystancji wewnętrznej R = 1500

. Woltomierz wskazał napięcie U

.

V =

8

,

2 75 V

V

Ω

Obliczyć:

a) wartość poprawną siły elektromotorycznej E ,

b) bezwzględny błąd systematyczny ∆ E pomiaru E ,

c) poprawkę p( E) pomiaru E ,

d) względny błąd systematyczny E

δ pomiaru E .

Rozwiązanie:

a) na podstawie schematu zastępczego, przedstawionego na rys.2, wartość poprawną E oblicza się ze wzoru





R



8

,

0



E = U 1

 + w

V

 = 8

,

2 75 ⋅ 1 +

 ≈ 8

,

2 765 V



RV 



1500 

Rys.2 Schemat zastępczy układu do pomiaru siły elektromotorycznej ogniwa

b) bezwzględny błąd systematyczny ∆ E = U

V − E ≈

8

,

2 75 − 8

,

2 765 ≈ − 5

,

1 mV

c) poprawka p( E) = −∆ E = 5

,

1 mV

∆ E − 5

,

1 ⋅10 3

−

d) względny błąd systematyczny E

δ =

=

≈ − 0

,

0

%

6

E

8

,

2 765

Ad. 2) Błędy przypadkowe występują, gdy powtarzanie doświadczenia pomiarowego w

pozornie niezmiennym układzie warunków fizycznych ujawnia losową zmienność wyników.

Słowo „pozornie” ma w tym przypadku szczególne znaczenie, gdyż błędy przypadkowe są

spowodowane oddziaływaniem wielu zmiennych i z reguły niezależnych od siebie

czynników. Deterministyczny opis takiego oddziaływania jest z reguły niemożliwy gdyż

przekracza ludzkie możliwości poznawcze. Przykładem pomiaru zdominowanego czynnikiem

losowym jest np. pomiar wartości chwilowej napięcia szumów rezystora. Do opisu błędów

przypadkowych stosuje się modele probabilistyczne.

5

Ad. 3) Błędy nadmierne mogą być spowodowane błędem odczytu, chwilowym silnym

zaburzeniem lub innymi czynnikami. Najprostszy sposób postępowania polega na odrzuceniu

wyników rażąco różniących się od spodziewanych. Bardziej właściwe jest zastosowanie

odpowiedniego testu statystycznego.

Końcowy wynik pomiaru powinien być wynikiem skorygowanym, tj. nie powinien zawierać

znanych błędów systematycznych oraz nadmiernych.

2.4. Niepewność

Graficzną interpretację relacji występujących między parametrami wyniku przedstawiono

na rys.3.

x

- u x

( )

x

x

x

+ u x

( )

popr

popr

rz

popr

x

∆ x rz

u x

( )

u( x)

Rys.3. Interpretacja relacji występujących między parametrami wyniku pomiaru

Na rys.3. punkty x

− u

i x

+ u

wyznaczają granice przedziału, w którym

popr

( x)

popr

( x)

z określonym prawdopodobieństwem znajduje się wartość rzeczywista x . Parametr u( x) jest rz

nazywany niepewnością bezwzględną.

Niepewność ma zawsze znak dodatni, gdyż wyraża długość jednostronnego przedziału.

Często niepewność wyniku pomiaru zapisuje się jako x

± u

, co oznacza iż wynik

popr

( x)

pomiaru, z określonym prawdobodobieństwem, znajduje się w przedziale o szerokości u

2 ( x) ,

symetrycznym względem wartości poprawnej.

Niepewność względną u

definiuje się jako stosunek niepewności bezwzględnej do

r ( x )

wartości poprawnej:

u x

u x =

(5)

r ( )

( )

x popr

2.5. Klasyfikacja niepewności

Zgodnie z ustaleniami międzynarodowymi [1] wyróżnia się dwa typy niepewności:

1) niepewność typu A,

2) niepewność typu B.

6

Ad.1) do niepewności typu A zalicza się niepewności, których rozkłady są znane lub mogą

być oszacowane na podstawie powtarzalnych pomiarów, wykonanych w nominalnie takich

samych warunkach. Ocena niepewności typu A wykorzystuje ustalony algorytm: wyznacza

się wartość średnią, niepewność pojedynczego wyniku oraz niepewność wartości średniej.

Wyznaczenie niepewności typu A wymaga wykonania serii pomiarów, w celu ujawnienia

losowego charakteru ich zmian.

Ad.2) jeśli niepewność szacowana jest nie na podstawie powtarzalnych pomiarów, ale innych

danych, to nazywa się ją niepewnością typu B. Do niepewności typu B zaliczyć można

niepewności przyrządów podane w ich dokumentacji, świadectwach kalibracji, wartości

współczynników podane w normach i tablicach. Jeśli niepewność wyniku nie jest określona i

nie ma możliwości jej oceny, to przedział niepewności określa się na podstawie liczby cyfr

znaczących wyniku.

2.6. Szacowanie standardowej niepewności typu A

Oszacowanie niepewności typu A jest możliwe jedynie wtedy, gdy wykonano serię pomiarów

x1, x2, .... xN, gdzie N>1. Przede wszystkim należy w serii wykryć i usunąć wyniki obarczone błędem nadmiernym. Gdy liczba czynników zakłócających pomiar jest duża i żaden z nich nie

dominuje, to można założyć, iż rozkład losowy błędu pomiaru jest rozkładem zbliżonym do

rozkładu normalnego (Gaussa). Wyróżnia się dwa przypadki:

1) seria pomiarów jest długa ( N ≥ 10),

2) seria pomiarów jest krótka ( N < 10).

Ad.1) dla długiej serii pomiarów, korzystając z metody estymacji punktowej oblicza się:

- wartość poprawną wyniku, którą jest średnia arytmetyczna:

N

1

x =

∑ x ,

(6)

n

N n=1

-

odchylenie standardowe średniej arytmetycznej:

s

s

x

=

,

(7)

x

N

gdzie

2

1

N

s

x

x

(8)

x =

∑( n − )

N − 1 n 1

=

jest odchyleniem standardowym pojedynczego wyniku.

Standardowa niepewność typu A u

jest równa:

A ( x )

7

u x = s

(9)

A ( )

x

Ad.2) dla krótkiej serii wyników pomiaru o błędach przypadkowych będących zmienną

losową o rozkładzie normalnym obliczone wartości x i s mogą się znacznie różnić od x

parametrów tego rozkładu. W tym przypadku, w celu zwiększenia wiarygodności wyników,

korzysta się z rozkładu t-Studenta [1].

Gdy liczba wyników pomiaru N wzrasta, to rozkład Studenta staje się bliski rozkładowi normalnemu. Dla N ≥ 10 można w większości przypadków korzystać z rozkładu normalnego.

W rozkładzie Studenta występuje pojęcie liczby stopni swobody k :

k = N −1

(10)

gdzie N jest liczbą wyników pomiaru w serii.

Standardową niepewność typu A wyznacza się następująco:

1. Dla

standardowej

niepewności

typu

A

przyjmuje

się

poziom

ufności

(prawdopodobieństwo) α =0,6827. Jest to poziom ufności, któremu w rozkładzie

normalnym odpowiada kwantyl równy odchyleniu standardowemu pojedynczego

wyniku pomiaru.

2. Oblicza się liczbę stopni swobody k ze wzoru (10) .

3. Korzystając z tablicy rozkładu Studenta dla obliczonego k i przyjętego α wyznacza

się kwantyl t

.

k α

,

4. Oblicza się standardową niepewność typu A ze wzoru

u

x = t

s

(11)

A (

) k α, x

Wartości kwantyli t

dla rozkładu Studenta w zależności od liczby stopni swobody ν

k α

,

zamieszczono w tablicy 1.

Tablica 1

Wartości kwantyli t

dla rozkładu Studenta dla poziomu ufności α =0,6827 w zależności od liczby

k α

,

stopni swobody k

k

1

2

3

4

5

6

7

8

9

10

11

12

50

100

t

1,84 1,32 1,20 1,14 1,11 1,09 1,08 1,07 1,06 1,05 1,05 1,04 1,01 1,005

k α

,

2.7. Ocena niepewności typu B w pomiarach bezpośrednich

W niektórych przypadkach rozrzut wyników jest bardzo mały i dominującą niepewnością jest

niepewność związana z niedoskonałością aparatury lub przyjętej metody pomiarowej, zwana

niepewnością typu B. Nie można jej scharakteryzować metodami statystycznymi, jak w

przypadku niepewności typu A, ponieważ nie dysponuje się serią wyników. Z tego powodu

8

do oceny niepewności typu B wykorzystuje się wszelkie dostępne informacje, którymi mogą

być:

-

znajomość zjawisk występujących w pomiarach;

- właściwości przyrządów i metod pomiarowych;

- informacje zawarte w dokumentacji przyrządów;

- dokumenty i certyfikaty kalibracyjne przyrządów;

- dane z wcześniej przeprowadzonych pomiarów;

- doświadczenie lub intuicja eksperymentatora.

Najczęściej przyjmuje się, że niepewność typu B charakteryzuje się rozkładem jednostajnym i

z poziomem ufności α =1 zawiera się w przedziale ± a wokół wartości poprawnej. Wówczas

standardowa niepewność typu B jest równa [1]

u

=

.

(12)

B ( )

a

x

3

Przykład 2

Obliczyć niepewność typu B woltomierza wskazówkowego klasy 0,5 o zakresie 100 V.

Rozwiązanie:

Można przyjąć, że wewnątrz symetrycznego przedziału wokół wartości poprawnej zmierzonego

napięcia, o szerokości połówkowej równej

klasa ⋅ zakres

5

,

0 ⋅100

∆ U =

=

= 5

,

0

V

100

100

prawdopodobieństwo wystąpienia wartości prawdziwej mierzonego napięcia, którą reprezentuje

wartość poprawna, jest w każdym punkcie jednakowe (opisuje je rozkład jednostajny). Standardowa

niepewność typu B jest równa

u

V

B (

) ∆

5

,

0

= U

U

=

= ,

0 287

3

3

Jedną ze składowych niepewności typu B jest składowa spowodowana ograniczoną

rozdzielczością pomiaru. Jeśli producent nie podał sposobu jej obliczania, to dla przyrządów z

odczytem cyfrowym, wykorzystujących wbudowany mikroprocesor do przeliczania wyniku

przyjmuje się, iż maksymalny błąd rozdzielczości jest równy wartości odpowiadającej ± 5

,

0

najmniej znaczącej cyfry wyświetlacza. Wynika to z założenia, że wynik pomiaru jest przed

wyświetleniem prawidłowo zaokrąglony. W przypadku tanich multimetrów wyposażonych w

przetwornik analogowo-cyfowy o podwójnym całkowaniu przyjmuje się, iż maksymalny błąd

rozdzielczości jest równy wartości odpowiadającej ± 1 najmniej znaczącej cyfry

wyświetlacza. We wszystkich przypadkach przyjmuje się, iż rozkład tego błędu w

9

określonym przedziale jest jednostajny Związaną z tą składową niepewność typu B oblicza

się ze wzoru (12).

Przykład 3

Obliczyć niepewność typu B woltomierza cyfrowego, który na zakresie U

=20 V charakteryzuje się

zakr

rozdzielczością 4½ cyfr znaczących. W dokumentacji przyrządu zawarta jest informacja, iż

maksymalny błąd pomiaru jest równy 0,05% U

+ 0,005% U

, gdzie U

=4,324 V jest

odczyt

zakr

odczyt

wartością napięcia wyświetloną na wyświetlaczu przyrządu. Ponadto z dokumentacji wynika, że

przyrząd zawiera mikroprocesor przeliczający wynik pomiaru przed jego wyświetleniem.

Rozwiązanie:

Rozdzielczość pomiaru jest równa U

=1 mV. Można przyjąć, iż wewnątrz symetrycznego

rozdz

przedziału wokół napięcia U

, o szerokości połówkowej równej

odczyt

,

0 05

,

0 005

1

∆ U =

U

U

U

odczyt +

zakr +

rozdz =

100

100

2

,

0 05

,

0 005

1

=

⋅ 3

,

4 24 +

⋅ 20 + ⋅ ,

0 001 = ,

3 662 mV

100

100

2

prawdopodobieństwo wystąpienia wartości prawdziwej mierzonego napięcia, którą reprezentuje

wartość poprawna, jest w każdym punkcie jednakowe (opisuje je rozkład jednostajny). Standardowa

niepewność typu B jest równa

u

mV

B (

) ∆

,

3 662

= U

U

=

= 1,

2 1

3

3

2.8. Obliczanie standardowej niepewności złożonej w pomiarach bezpośrednich

Obliczanie standardowej niepewności złożonej często występuje w praktyce: występują

błędy losowe reprezentowane przez niepewność uA typu A, której przypisać można rozkład normalny, oraz błędy przyrządów pomiarowych, którym można z reguły przypisać rozkład

jednostajny, a które są scharakteryzowane przez niepewność u typu B. Błędy te są z reguły

B

nieskorelowane (niezależne od siebie).

Standardową niepewność złożoną u pomiaru, z uwzględnieniem niepewności przyrządu

c

pomiarowego (czyli niepewności typu B), oblicza się wg następującego algorytmu:

1.

Oblicza się standardową niepewność u typu A;

A

2.

Oblicza się standardową niepewność u typu B;

B

3.

Oblicza się standardową niepewność złożoną u ze wzoru

c

10

2

2

u = u + u ;

(13)

c

A

B

4.

Podaje się końcowy wynik w następującej postaci:

x = x ± u ,

c

z dodanym następującym komentarzem: „gdzie liczba zapisana za symbolem ± jest

wartością złożonej niepewności standardowej uc, a nie jest przedziałem ufności”.

Podany wyżej sposób zapisu wyniku pomiaru jest zalecany przez [1].

Przykład 4

Woltomierzem cyfrowym o rozdzielczości 4½ cyfry dokonano, na zakresie U

=750 V, pomiaru

zakr

napięcia sieci elektroenergetycznej. Średnia z N = 20 pomiarów wynosiła U = 23 , 0 4 V z

odchyleniem standardowym s

1,8 V. W dokumentacji przyrządu zawarta jest informacja, iż

U =

maksymalny błąd pomiaru jest równy 0,5% U

+ 0,05% U

. Prawidłowo zapisać wynik

odczyt

zakr

pomiaru.

Rozwiązanie:

Niepewność typu A pomiaru jest równa

u ( U )

s

8

,

1

= U

V

A

=

≈ ,

0 402

N

20

Rozdzielczość pomiaru jest równa U

=0,1 V. Można przyjąć, że wewnątrz symetrycznego

rozdz

przedziału wokół U

, o szerokości połówkowej równej

odczyt

5

,

0

,

0 05

1

∆ U =

U

U

U

odczyt +

zakr +

rozdz =

100

100

2

5

,

0

,

0 05

1

=

⋅ 23 ,

0 4 +

⋅ 750 + ⋅ 1

,

0 = ,

1 2395 V

100

100

2

prawdopodobieństwo wystąpienia wartości prawdziwej mierzonego napięcia, którą reprezentuje

wartość poprawna, jest w każdym punkcie jednakowe (opisuje je rozkład jednostajny). Standardowa

niepewność typu B jest równa

u

V.

B (

) ∆

,

1 2395

= U

U

=

= ,

0 716

3

3

Standardowa niepewność złożona pomiaru jest równa

2

2

u

u

u

V.

c =

A +

B =

( ,0402)2 + ( ,0716)2 ≈ 8,

0 21

Ostatecznie wynik zapisuje się jako U = (23 ,

0 4 ± 8

,

0 )V , gdzie liczba zapisana za symbolem ± jest

wartością złożonej niepewności standardowej, a nie jest przedziałem ufności.

11

2.9. Obliczanie rozszerzonej niepewności złożonej w pomiarach bezpośrednich

Opcjonalnie można rozszerzyć (ang. expand) złożoną niepewność standardową u czyli

c

obliczyć połówkową szerokość przedziału, w którym znajdzie się błąd pomiaru ze

zwiększonym prawdopodobieństwem w stosunku do prawdopodobieństwa przyjętego dla

niepewności standardowej. W tym celu:

1. Rozszerza się złożoną niepewność standardową u do żądanego poziomu ufności α ,

c

mnożąc u przez odpowiedni współczynnik (kwantyl) k . Dokładne wyznaczenie

c

α

współczynnika kα , zależnego od żądanego poziomu ufności, jest zagadnieniem trudnym

[2]. W celu uproszczenia rozważa się dwa przypadki:

- u ≥ u , czyli dominuje niepewność typu A o rozkładzie normalnym lub

A

B

niepewność typu A jest bliska niepewności typu B;

- u < u , czyli dominuje niepewność typu B o rozkładzie jednostajnym.

A

B

Wartości kα wyznacza się z tablicy 2. dla jednej z trzech wybranych wartości

poziomu ufności α: 0,68; 0,95 i 0,99, które są zalecane przez [1].

Tablica 2

Wartości kα w zależności od poziomu ufności α [2]

Poziom ufności α

0,68

0,95

0,99

u ≥ u

A

B

0,994

1,960

2,576

u < u

A

B

1,179

1,645

1,715

2. Zapisuje się końcowy wynik pomiaru w postaci x = x ± k u

α

dodając komentarz o

c

przyjętym poziomie ufności oraz informację, że jest to niepewność złożona.

Sposób ten jest przybliżony.

Dla dużej serii wyników pomiaru, których rozrzut można scharakteryzować za pomocą

rozkładu normalnego, kwantyl kα wyznaczyć można z tablic funkcji Laplace’a [2].

Publikacja [1] zaleca stosowanie tylko kilku wartości poziomów ufności. Odpowiadające im

kwantyle kα zestawiono w tablicy 3.

Tablica 3

Wartość współczynnika kα określającego dla rozkładu normalnego przedział o

poziomie ufności α.

Poziom ufności α

% 68,27

90

95

95,45

99

99,73

Współczynnik rozszerzenia kα

-

1

1,645 1,960

2

2,576

3

12

2.10. Obliczanie niepewności pomiarów pośrednich

W przypadku pomiaru pośredniego mierzona wielkość Y jest funkcją M wielkości Xm mierzonych bezpośrednio:

y = f ( x

m )

gdzie m = 1, 2, ... M.

Dla każdej wielkości Xm dokonuje się serii pomiarów, a następnie oblicza się średnią arytmetyczną x , standardową niepewność złożoną u

oraz koryguje się x przez

m

c, m

m

uwzględnienie odpowiedniej poprawki. Następnie oblicza się:

- wartość średnią wielkości Y, która jest wartością poprawną :

y = f ( x

(14)

m )

- złożoną niepewność standardową dla średniej y :

M

u y

c 2 u 2

,

(15)

c (

)= ∑ m ⋅ c, m

m =1

gdzie

y

∂

c =

(16)

m

x

∂ m

są tzw. współczynnikami wrażliwości.

Niepewność u

jest dobrze oszacowana jedynie przy spełnieniu następujących warunków:

c ( y )

- liniowość funkcji y = f ( x jest wystarczająca na tyle, aby nie uwzględniać wyrazów m )

wyższych rzędów w rozwinięciu w szereg Taylora;

- zmienne losowe X oraz ich wartości średnie x są wzajemnie niezależne.

m

m

Przyjęcie założenia liniowości w przypadku silnie nieliniowych funkcji prowadzi do

zaniżenia oceny niepewności. Gdy zmienne losowe X lub X są wzajemnie zależne oblicza m

m

się tzw. kowariancję [3].

Przy obliczaniu niepewności wielkości mierzonych pośrednio sporządza się tak zwany

budżet niepewności. Ma on postać tablicy, zawierającej w podstawowej postaci wartości

poprawne poszczególnych wielkości mierzonych bezpośrednio, ich złożone niepewności

standardowe, współczynniki wrażliwości oraz udział standardowej niepewności każdej

wielkości mierzonej bezpośrednio w niepewności wielkości mierzonej pośrednio. W tabelach

bardziej zaawansowanych budżetów niepewności podaje się dodatkowe informacje o

rozkładzie prawdopodobieństwa błędów losowych, liczbie stopni swobody oraz kowariancji

poszczególnych zmiennych [1].

13

Przykład 5

Moc wydzielaną na pewnym obwodzie prądu stałego zmierzono za pomocą woltomierza i

amperomierza. Zmierzona wartość napięcia wyniosła (4,000 ±0,002) V, a zmierzona wartość prądu (1,000 ±0,004) A. W obu wynikach liczba za symbolem ± jest wartością złożonej niepewności

standardowej. Obliczyć standardową niepewność pomiaru rezystancji i sporządzić jej budżet przy założeniu, iż można zaniedbać wpływ błędu systematycznego, spowodowanego wpływem rezystancji

przyrządów.

Rozwiązanie:

Poprawną wartość mocy oblicza się ze znanego wzoru:

P = U ⋅ I = 4,000 ⋅1,000 = 4,000 W

Ponieważ pomiar napięcia i prądu był realizowany różnymi przyrządami, można przyjąć, iż wyniki pomiaru obu wielkości są od siebie niezależne. Wówczas standardową niepewność pomiaru mocy

oblicza się z zależności

u

2

2

2

2

=

+

,

(18)

c ( P)

c u

U

c ( U )

c u

I

c ( I )

gdzie współczynniki wrażliwości c oraz c są równe

U

I

∂

= P

c

A,

U

= I = ,1000

∂ U

∂

= P

c

V.

I

= U = ,

4 000

∂ I

Po podstawieniu do (18) otrzymuje się

u

W.

c ( P ) =

( ,1000)2( ,0002)2 + ( ,4000)2( ,0004)2 = ,0000004 + ,0000256 = ,00161≈ ,002

Zatem zmierzona moc jest równa (4,00±0,02) W, gdzie liczba za symbolem ± jest wartością złożonej

niepewności standardowej, a nie jest przedziałem ufności.

Budżet niepewności pomiaru mocy przedstawiono w tablicy 4.

Tablica 4

Przykład budżetu niepewności dla pomiaru mocy prądu stałego

Symbol

Oszacowanie Niepewność Współczynnik Niepewność

Udział w

wielkości

wielkości

standardowa

wrażliwości

składowa

niepewności

mocy

złożonej

X

x

u( x

c

u

u

/ u( y)

i ( y )

i ( y )

i )

i

i

i

U

4,000 V

2 mV

1,000 A

2 mW

11%

I

1,000 A

4 mA

4,000 V

16 mW

89%

P

4,00 W

0,02 W

14

2.11. Reguły zaokrąglania wyniku pomiaru i niepewności

Ogólnie zapis końcowego wyniku pomiaru powinien mieć postać następującą:

x = x

± u

(informacja o poziomie ufności)

popr

( x)

Końcowy wynik pomiaru powinien składać się z dwóch liczb przybliżonych, z których

pierwsza wyraża poprawną wartość wielkości mierzonej, a druga określa jej niepewność.

Istotny jest sposób zaokrąglania tych liczb. Obowiązują następujące zasady:

1. Liczbę wyrażającą niepewność zaokrągla się najczęściej w górę, do liczby o jednej

cyfrze znaczącej. Wynika to z faktu, że wartość niepewności nie jest dokładnie

określona. W szczególnych przypadkach pozostawia się dwie cyfry znaczące. Czyni

się tak gdy:

- liczba będzie używana do dalszych obliczeń;

- w przypadku podawania niepewności stałych fizycznych;

- w przypadku pomiarów dokładnych;

- jeśli po zaokrągleniu do 1 cyfry znaczącej błąd zaokrąglenia byłby większy od

20%. Na przyklad 0,1111 można zaokrąglić do 0,11 a nie do 0,2. W tym

przypadku nie zaokrągla się tej liczby w górę, lecz zgodnie z ogólnymi

regułami zaokrąglania.

2. Liczbę wyrażającą wynik pomiaru zaokrągla się pozostawiając najmniej znaczącą

cyfrę na tym miejscu, na którym występuje najmniej znacząca cyfra niepewności.

Obowiązują następujące reguły postępowania przy zaokrąglaniu wyników pomiaru:

a) Zastępuje się przez 0 zbędne cyfry liczb całkowitych, a zbędne cyfry po przecinku

dziesiętnym odrzuca się.

b) Jeżeli pierwsza zbędna cyfra (licząc od lewej strony) ma wartość <5, to pozostających

cyfr się nie zmienia. Jeżeli ta cyfra jest >5, to najmniej znaczącą pozostającą cyfrę

powiększa się o 1.

c) Jeżeli pierwszą zbędną cyfrą (licząc od lewej strony) jest 5, a cyfry z prawej strony od

5 nie są zerami, to najmniej znaczącą pozostającą cyfrę powiększa się o 1.

d) Jeżeli pierwszą zbędną cyfrą (licząc od lewej strony) jest 5, a cyfry z prawej strony od

5 są zerami, to najmniej znaczącej pozostającej cyfry nie zmienia się, jeżeli jej wartość

jest liczbą parzystą. Jeżeli jej wartość jest liczbą nieparzystą, to powiększa się ją o 1.

2.12. Opracowanie wyników pomiaru prezentowanych w postaci wykresów

Często wyniki pomiaru prezentowane są postaci wykresów. Także w tym przypadku wykres

powinien zawierać informację o niepewności przedstawionych na nim wyników pomiaru. Na

rysunku 4 przedstawiono przykładowy wykres charakterystyki prądowo-napięciowej. Na

uwagę zasługują charakterystyczne słupki („wąsy”), które reprezentują złożone niepewności

15

pomiaru obu wielkości. Podpis pod rysunkiem powinien informować o sposobie interpretacji

słupków niepewności.

Rys.4. Przykładowy wykres charakterystyki prądowo-napięciowej. Słupki błędów

reprezentują złożone niepewności standardowe pomiaru.

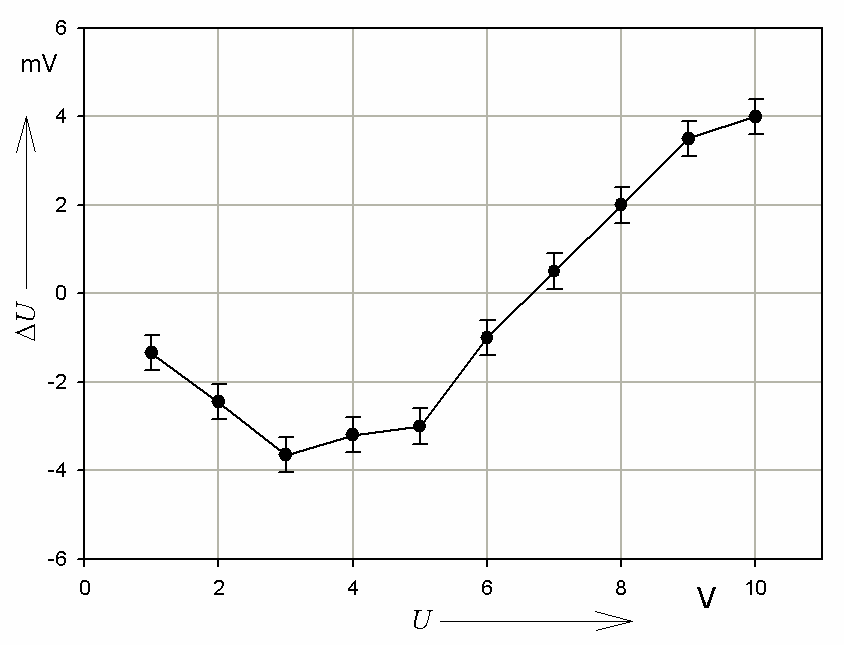
Podobnie należy sporządzać wykresy błędów lub poprawek. Na rysunku 5 przedstawiono

przykładowy wykres błędu. W tym przypadku zazwyczaj na wykresie zamieszcza się jedynie

słupki błędów reprezentujące niepewność wyznaczenia błędu lub poprawki.

Rys.5. Przykładowy wykres błędu. Słupki błędu reprezentują złożone niepewności

standardowe wyznaczenia błędu.

Na uwagę zasługuje także sposób opisania osi wykresów przedstawionych na rys.4 oraz rys.5.

16

3. PROGRAM ĆWICZENIA

1. Za pomocą cyfrowego woltomierza napięcia przemiennego o rozdzielczości minimum

5 cyfr znaczących wykonać serię a) N=2, b) N= 4, c) N=10 , d) N=30 pomiarów napięcia na wyjściu autotransformatora regulowanego. Prawidłowo zapisać końcowe

wyniki pomiaru.

2. Wykonać pomiar jak w p.1, ale przy wykorzystaniu cyfrowego woltomierza napięcia

przemiennego o mniejszej rozdzielczości (np. 3,5 cyfry). Prawidłowo zapisać

końcowe wyniki pomiaru.

3. Wykonać pomiar jak w p.1, zastępując autotransformator programowanym

generatorem funkcyjnym, wytwarzającym napięcie sinusoidalne o wartości skutecznej

zbliżonej do napięcia na wyjściu autotransformatora i o częstotliwości 50 Hz.

Prawidłowo zapisać końcowe wyniki pomiaru.

4. Wykonać pomiar jak w p.2, zastępując autotransformator programowanym

generatorem funkcyjnym, wytwarzającym napięcie sinusoidalne o wartości skutecznej

zbliżonej do napięcia na wyjściu autotransformatora i o częstotliwości 50 Hz.

Prawidłowo zapisać końcowe wyniki pomiaru.

5. Porównać wyniki uzyskane w p.1, 2, 3 i 4. Wyciągnąć wnioski.

6. Dokonać pomiaru mocy prądu a) stałego b) przemiennego, wydzielanej na odbiorniku

wskazanym przez prowadzącego ćwiczenie. Pomiar wykonać w układzie a) poprawnie

mierzonego napięcia, b) poprawnie mierzonego prądu. Obliczyć wartość poprawną

mocy, bezwzględny błąd systematyczny, poprawkę oraz względny błąd

systematyczny. Sporządzić budżet niepewności i prawidłowo zapisać końcowy wynik

pomiaru.

7. Dokonać pomiaru rezystancji metodą techniczną obiektu wskazanego przez

prowadzącego ćwiczenie. Pomiar wykonać w układzie a) poprawnie mierzonego

napięcia, b) poprawnie mierzonego prądu. Obliczyć wartość poprawną rezystancji,

bezwzględny błąd systematyczny, poprawkę oraz względny błąd systematyczny.

Sporządzić budżet niepewności i prawidłowo zapisać końcowy wynik pomiaru.

8. Wyznaczyć charakterystykę napięciowo-prądową żarówki zasilanej napięciem

przemiennym uzyskiwanym z autotransformatora. Wynik pomiaru przedstawić w

postaci wykresu.

9. Za pomocą cyfrowego woltomierza napięcia przemiennego o rozdzielczości minimum

5 cyfr znaczących wyznaczyć błąd nastawy napięcia przemiennego i stałego

programowanego generatora funkcyjnego. Pomiar błędu nastawy napięcia

17

przemiennego wykonać dla kilku wartości częstotliwości z przedziału od 40 Hz do

100 kHz. Wynik pomiaru błędu nastawy przedstawić w postaci wykresu.

Uwaga: obliczenia błędów i niepewności powinny być wykonywane w trakcie

przeprowadzania ćwiczenia. Zalecane jest przyniesienie na zajęcia kalkulatorów inżynierskich

realizujących proste obliczenia statystyczne.

4. PYTANIA KONTROLNE

1. Podać definicję błędu bezwzględnego, poprawki oraz błędu względnego.

2. Opisać rodzaje błędów i ogólne sposoby ich wyznaczania.

3. Wymienić typy niepewności i scharakteryzować je.

4. Opisać metody wyznaczania standardowej niepewności typu A.

5. Opisać metody wyznaczania standardowej niepewności typu B.

6. Opisać metodę wyznaczania niepewności złożonej.

7. Opisać sposób sporządzania budżetu niepewności.

5. LITERATURA

[1] „Wyrażanie niepewności pomiaru“. Przewodnik. Główny Urząd Miar, Warszawa 1999

[2] Turzeniecka D., „Ocena niepewności wyniku pomiaru”, Wydawnictwo Politechniki

Poznańskiej, Poznań 1997

[3] Skubis T., „Podstawy metrologicznej interpretacji wyników pomiaru”, Wydawnictwo

Politechniki Śląskiej, Gliwice 2004

Opracował: dr inż. Marian Kampik

v.1 / 14 XI 2008