WNUM Lab 6: całkowanie i różniczkowanie funkcji.
I. Zakres
materiału:
1. Zapis podanego układu równań różniczkowych (np. opisującego zachowanie prostej sieci elektrycznej) w postaci równań stanu: dy = f ( t, y) dt
2. Rozwiązywanie równań różniczkowych
a. nieliniowych - za pomocą funkcji programu MATLAB: ode23, ode45, ode15s, ode23s
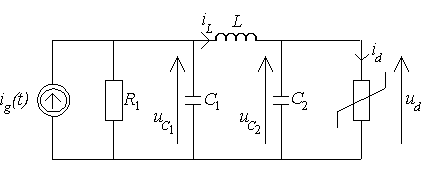
b. liniowych - za pomocą stałokrokowych metod: Eulera (otwartej i zamkniętej), trapezów II. Przykładowe zadania (do przygotowania przed zajęciami): 1. Dany jest układ elektryczny o schemacie jak na rysunku duC
i
= u /
1
R + C
+ i
g
C
1
1
L
1
dt
diL
u
− u
=
L
C
C 2
1
dt
duC 2
i
=
C
+ i ( u )
L
2
d
C 2
dt
w którym: R 1=10kΩ, C 1=1pF, C 2=1pF, L=1H, i d=f( u d), gdzie f( u d)= u d(2( u d)2-9 u d+12) [mA], a
, przy czym T=100 ns
Polecenia:
A. Wykreśl przebieg prądu generatora ig(t) w przedziale [-T,2T] dla I0= 1mA.
B. Ułóż układ równań stanu: y ’(t)=f (t, y (t)), y (0)=y , gdzie: y=[
0
i L u C1 u C2]T.
C. Korzystając z funkcji ode23 i ode45 programu MATLAB rozwiąż ten układ równań w przedziale czasu [0,T], z błędem nie przekraczającym wartości 10-3 , dla I 0=0 i zerowych warunków początkowych y(0)=0. Dla każdej z metod przedstaw graficznie ( plot) rozwiązanie.
D. Rozwiąż układ równań różniczkowych przy pomocy obydwóch metod (ode23, ode45), dla wartości tolerancji względnych (RelTol) równych kolejno 1e-1,1e-2,1e-3,1e-4,1e-5,1e-6. Dla każdej wartości tolerancji wyświetl przebieg prądu iL. Następnie wykreśl zależność liczby punktów czasowych w otrzymanym rozwiązaniu od wartości tolerancji E. Rozwiąż (za pomocą ode23 i ode45) ten sam układ równań dla: i g= const=19.5mA, R 1=100
oraz t z przedziału [0, 0.3T]. Przedstaw graficznie uzyskane rozwiązania.
2. Wyznacz rozwiązanie równania różniczkowego dx + 0.5 x − 2 = 0 , x(0) = 0
dt
w przedziale t ∈[ 10
,
0
] za pomocą otwartej i zamkniętej stałokrokowej metody Eulera. Obliczenia wykonaj dla czterech wartości kroku całkowania: h=1,1e-1,1e-2,1e-3. W każdym przypadku
⎛
− t ⎞
wykreśl otrzymane rozwiązania i porównaj graficznie z rozwiązaniem dokładnym x = ⎜⎜
4
− 2
1 e
⎟⎟ .
⎝
⎠
Na wspólnym rysunku wykreśl zależność błędów maksymalnych badanych metod od długości kroku.
Document Outline
Wyszukiwarka
Podobne podstrony:
lab6, SWBlab6
lab6
lab6
lab6 NHIP pyt
lab6 doc
Lab6 PSN cd 2015
AKiSO lab6
rownania nieliniowe, Automatyka i robotyka air pwr, VI SEMESTR, Notatki.. z ASE, metody numeryczne,
Lab6 5 id 260087 Nieznany
AK lab6 (2)
lab6 7
lab6
konspekt lab6 id 245555 Nieznany
Sprawozdanie EM lab6
lab6, Edukacja, ZiIP, sem. I, Podstawy programowania, Laborki i inne, Podstawy Programowania
lab6, MECHATRONIKA 1 ROK PWSZ, SEMESTR II, Metrologia techniczna i systemy pomiarowe, Laborki
Sprawozdanie kartka, AGH WIMIR AiR, Semestr 3, JPO, lab6 JPO
Lab6, Visual Basic Lab 6a, Visual Basic Lab 3
kurs matlaba, Lab6 KURS MATLAB 2003, KURS MATLABa
więcej podobnych podstron