Wprowadzenie do równań dynamiki maszyn asynchronicznych:

Zgodnie z zasadami transformacji układu trójfazowego do zastępczego układu dwufazowego, o właściwościach maszyny decydują równania strumieniowo-prądowe.

Dla maszyny asynchronicznej przy stosowaniu założeń upraszczających uwzględniających jedynie pierwszą harmoniczną pola magnetycznego w szczelinie powietrznej i idealnej symetrii maszyny, równania te w układzie współrzędnych naturalnych mają postać:

[ψ ] = [ L ][ i ] + [ M ][ i ] + [ M ][ i ]

s

σ s

s

ss

s

sr

r

[ψ ] = [ L ][ i ] + [ M ][ i ] + [ M ] T [ i ]

r

σ r

r

rr

r

sr

s

gdzie poszczególne macierze mają postać:

⎡1 0 0⎤

⎢

⎥

[ L ] = L

σ s

σ s ⎢0 1 0⎥

⎢

0

0

1⎥

⎣

⎦

- macierz indukcyjności związanych ze strumieniem rozproszenia stojana

⎡

1

cos120°

cos 240°⎤

⎢

⎥

[ M ] = M

ss

ss ⎢cos 240°

1

cos120°⎥

⎢cos120° cos 240°

1

⎥

⎣

⎦

⎡

1

1 ⎤

⎢ 1

−

− ⎥

⎢

2

2 ⎥

[ M ] = M ⎢− 1

− 1

1

⎥

ss

ss ⎢ 2

2 ⎥

⎢

1

1

⎥

⎢−

−

1 ⎥

⎣ 2

2

⎦

-macierz indukcyjności związanych ze strumieniem głównym w obrębie stojana.

Po transformacji polegającej na lewostronnym mnożeniu równań przez macierz transformacji uzyskamy (niezależnie od przyjętych współczynników w macierzach transformacyjnych) równania w postaci:

[ s][ψ ] = [ s][ L ][ s]− [

1 s][ i ] + [ s][ M ][ s]− [

1 s][ i ] + [ s][ M ][ s]− [

1 s][ i ]

s

σ s

s

ss

s

sr

r

[ s][ψ ] = [ s][ L ][ s]− [

1 s][ i ] + [ s][ M ][ s]− [

1 s][ i ] + [ s][ M ] T [ s]− [

1 s][ i ]

r

σ r

r

rr

r

sr

s

Co sprowadza się do transformacji wartości poszczególnych macierzy indukcyjności:

-1-

1

[ L ] [ s][ L][ ]−

=

s

αβ

Macierz diagonalna nie zmienia swojej postaci, natomiast macierz indukcyjności wzajemnych po transformacji uzyska postać:

⎡1 0 0⎤

αβ

3

⎢

⎥

[

0

M

] =

M ss

ss

⎢0 1 0⎥

2

⎢

0

0

0⎥

⎣

⎦

Macierz indukcyjności wzajemnych stojan-wirnik zależy od liczby faz wirnika.

Można udowodnić, że każde symetryczne uzwojenie wielofazowe, przy uwzględnieniu jedynie podstawowej harmonicznej pola, można przedstawić w postaci równoważnego układu dwufazowego. Dla wirnika klatkowego jako liczbę faz przyjmuje się liczbę prętów klatki wirnika. Dla uproszczenia analizy przyjmijmy, że liczba faz wirnika jest równa liczbie faz stojana (silnik pierścieniowy). Przy takich założeniach macierze indukcyjności wirnika mają postać identyczną jak w stojanie:

⎡1 0 0⎤

⎢

⎥

[ L ] = L

σ r

σ r ⎢0 1 0⎥

⎢

0

0

1⎥

⎣

⎦

- macierz indukcyjności związanych ze strumieniem rozproszenia wirnika

⎡

1

1 ⎤

⎢ 1

−

− ⎥

⎢

2

2 ⎥

[ M ] = M ⎢− 1

− 1

1

⎥

rr

rr ⎢ 2

2 ⎥

⎢ 1

1

⎥

⎢−

−

1 ⎥

⎣ 2

2

⎦

- Macierz indukcyjności związanych ze strumieniem głównym w obrębie wirnika Po transformacji otrzymamy podobnie jak dla stojana:

⎡1 0 0⎤

αβ

3

⎢

⎥

[

0

M

] =

M

rr

rr ⎢0

1

0⎥

2

⎢

0

0

0⎥

⎣

⎦

Macierz indukcyjności wzajemnych stojan-wirnik ma postać zależną od kąta pomiędzy uzwojeniem stojana i wirnika:

⎡

cosα

α

cos( +

°

120 )

α

cos( +

°

240 )⎤

⎢

⎥

[ M ] = M

sr

sr ⎢

α

cos( +

°

240 )

cosα

α

cos( +

°

120 )⎥

⎢

α

cos( +

°

120 )

α

cos( +

°

240 )

cosα

⎥

⎣

⎦

-2-

Zastosowanie transformacji opisanej wyżej dla równań opisujących maszynę indukcyjną prowadzi do diagonalizacji macierzy indukcyjności własnych w stojanie i wirniku. Macierz indukcyjności wzajemnych stojan-wirnik przyjmuje po transformacji postać:

⎡cosα − sinα 0⎤

αβ

3

⎢

⎥

[

0

M

] =

M sr

sr

⎢sinα

cosα

0⎥

2

⎢

0

0

0⎥

⎣

⎦

Uzwojenie wirnika i stojana różnią się liczbą zwojów, liczbą faz (w silniku klatkowym liczba faz jest równa liczbie prętów wirnika) oraz sposobem rozłożenia uzwojeń w przestrzeni. Efekt rozłożenia uzwojeń w przestrzeni uwzględnia się poprzez stosowanie współczynników uzwojenia. Stąd wygodnie jest przekształcić równania wirnika w taki sposób, aby wielkości występujące w równiach stojana i wirnika były porównywalne. Zwykle operacje taką przeprowadza się, podobnie jak w transformatorach, przez zastosowanie przekładni prądowej i napięciowej: m z k

z k

r

r

r

ϑ =

s

s

ϑ =

i

m z k u

z k

s

s s

r

r

Przyjęcie takich wartości przekładni prądowej wynika z dostosowania przepływu wirnika do przepływu stojana, natomiast przekładni napięciowej wynika z wyrównania sił elektromagnetycznych fazowych wirnika do fazy stojana. Równania w jednej fazie wirnika można wówczas przedstawić jako: ϑ

dψ ϑ

u ϑ = R

i

ϑ

i

r

u

+

r

u

r

u

r

ϑ

dt

i

Wielkości wirnika należy przeliczać wg zależności: u' = u ϑ

r

r

u

i' = i ϑ

r

r

i

ϑ

m

z k

'

u

s

s

s

2

R = R

=

(

)

r

r ϑ

m

z k

i

r

r

r

ϑ

m

z k

'

u

s

s

s

2

L = L

=

(

)

r

r ϑ

m

z k

i

r

r

r

Biorąc pod uwagę definicje współczynnika indukcyjności wzajemnej Msr można wykazać, że:

-3-

ϑ u

=

M

= ϑ M

M

M

ss

rr

ss

u

sr

ϑ

i

Wygodnie jest, po przeliczeniu wielkości strony wirnika na stronę stojana, oznaczyć wielkości występujące w równaniach jako: 3

L =

M

µ

ss

2

L =

+

s

σ

L s

µ

L

L' = ' +

r

σ

L r

µ

L

Po wykonaniu takich podstawień otrzymamy równania opisujące zastępczy silnik posiadający dwa uzwojenia w stojanie i dwa w wirniku.

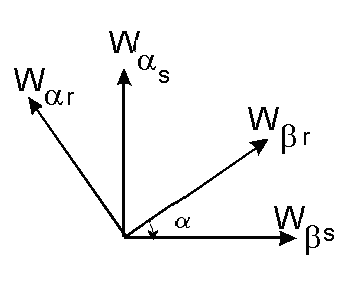
Uzwojenia zastępczej (równoważnej) maszyny dwufazowej można przedstawić w postaci:

Równania maszyny (przy pominięciu składowej zerowej) mają postać: dψ

dψ

α

β

u

= R i

s

+

u

= R i

s

+

sα

s sα

β

β

dt

s

s s

dt

d '

ψ

d '

ψ

u' = R' i'

rα

+

u'

= R' i'

rβ

+

rα

r

rα

dt

rβ

r

rβ

dt

W dalszych równaniach dla uproszczenia opuścimy znak ‘ oznaczający zastosowanie przekładni prądowej i napięciowej maszyny. Zależności strumieniowo-prądowe przyjmują postać:

-4-

ψ = L i + L i cosα − L i sinα

sα

s sα

µ rα

µ β

r

ψ = L i + L i sinα + L i cosα

sβ

s sβ

µ rα

µ β

r

ψ = L i + L i cosα + L i sinα

α

r

r rα

µ sα

µ sβ

ψ = L i − L i sinα + L i cosα

β

r

r β

r

µ α

s

µ sβ

Po pomnożeniu równań z indeksem β przez j i dodaniu stronami odpowiednich równań otrzymamy:

ψ + jψ = L ( i + ji ) + L cosα( i + ji ) +

sα

sβ

s

α

s

β

s

µ

rα

β

r

+ jL sinα( i + ji ) µ

rα

rβ

ψ + jψ = L ( i + ji ) + L cosα( i + ji ) −

rα

β

r

r

rα

rβ

µ

sα

sβ

− jL sinα( i + ji ) µ

sα

sβ

Otrzymamy opis równań strumieniowo-prądowych w postaci zespolonej: jα

ψ = L i + L i e

s s

µ r

s

− α

ψ

j

= L i + L i e

r r

µ s

r

Pomnożenie równań wirnika przez wielkość ejα jest równoznaczne z transformacją równań opisujących wirnik do układu stacjonarnego, otrzymamy: ψ =

'

α

j

L i + L i'

i = i e

s s

µ

r

s

r

r

ψ ' =

'

jα

L i' + L i

ψ

=ψ e

r

µ s

r

r

r

r

Oraz:

dψ

u = R i

s

+

s

s s

dt

dψ

α

α

α

u e j = R e j i + e j r

r

r

r

dt

dψ

'

'

α

u = R i + e j

r

r

r

r

dt

-5-

'

α

dψ

d ( e j ψ )

dψ

α

α

r

r

j

de j

=

= e

r

+ψ

dt

dt

dt

r

dt

dψ '

dψ

α

α

α

r

j

r

j

d

= e

+ψ je

dt

dt

r

dt

'

dψ

dψ

α

dα

'

e j

r

r

=

− j

ψ r

dt

dt

dt

Równana maszyny asynchronicznej przyjmują postać: ψ = L i + L i'

s s

µ

s

r

ψ ' = L i' + L i

r

µ s

r

r

dψ

u = R i

s

+

s

s s

dt

dψ '

'

'

dα

u = R i

r

+

ψ '

- j

r

r

r

dt

r

dt

Wzór na moment elektromagnetyczny uzyskamy po analizie następujących zależności:

dψ

u i* = R i i*

s

+

i*

s

s s

s

s

dt

s

d

'

ψ

dα

u i'* = R i i'*

r

+

i'*

'

- j

ψ i'*

r r

r r r

dt

r

r r

dt

Występujące w równaniach wielkości to:

-6-

Re{

*

u i } −

a

dostarczon

moc

stojana

obwodu

do

s s

*

R i i −

stojana

h

uzwojeniac

mocy w

straty

s s s

dψ

Re{

*

s i } −

ego

magnetyczn

pola

moc

dt

s

Re{ u i }

'*

−

a

dostarczon

moc

nika

obwodu wir

do

r r

*

R i i −

h wirniku

uzwojaniac

mocy w

straty

r r r

'

dψ

Re{

r i }

'*

−

ego

magnetyczn

pola

moc

dt

r

dα

Re{-j

'

ψ i }

'*

−

a

mechaniczn

moc

dt

r

r

Moment mechaniczny jest zatem równy:

P

p

dα

'

'*

m

M =

=

Im{-

ψ i }

e

ω

ω

dt

r

r

m

dα =ω

dt

'

'*

M = − p Im{ψ i }

e

r

r

'* '

M = p Im{ψ i }

e

r

r

ω = ω

p m

Jako, że:

'*

'*

*

ψ

= L i + L i

r

r

µ

s

r

-7-

Otrzymamy:

M = p Im{

'* '

L i i } = pL Im{ * '

i i }

e

r r

r

µ

s r

Bardzo często operujemy wielkością strumienia wypadkowego wynikającego z wypadkowego prądu magnesującego:

i = i + i

µ

s

r

M = pL Im{ *

*

i i + i i } = pL Im{ *

i i }

e

µ

s µ

s s

µ

s µ

M = p Im{ *

i L i } = p Im{ *

i ψ }

e

s

µ µ

s

µ

Wyprowadzone równania należy uzupełnić równaniem dynamiki masy wirującej: dω

1

m =

( M − M )

dt

J

e

0

Równania wyprowadzono przy zastosowaniu transformacji zachowującej moc, tzn:

⎡

1

1 ⎤

⎢ 1

−

− ⎥

⎢

2

2 ⎥

[ S]= 2 ⎢

3

0

− 3 ⎥

3 ⎢

2

2 ⎥

⎢

1

1

1 ⎥

⎢

⎥

⎣ 2

2

2 ⎦

Przy stosowaniu macierzy:

⎡

1

1 ⎤

⎢ 1

−

− ⎥

⎢

2

2 ⎥

[ S]= 2 ⎢

3

0

− 3 ⎥

3 ⎢

2

2 ⎥

⎢ 1

1

1 ⎥

⎢

⎥

⎣ 2

2

2 ⎦

Wzór na moment ma wartość zaniżoną, stąd: 3

M = − p Im{ ' '*

ψ i }

2

r

r

-8-

Uwaga!!!

Dostępne są programy symulacyjne dynamiki maszyn asynchronicznych:

-

ASYNCH.EXE – zasilanie sinusoidalne

-

ASYNCH_PWM.EXE – zasilanie z falownika napięcia sterowanego metodą modulacji szerokości impulsów (PWM)

W obu programach dostępne są wielkości w różnych układach odniesienia:

-

ABC – układ trójfazowy

-

alfa, beta – układ stacjonarny

-

xy – układ wirujący z prędkością synchroniczną

-

dq – układ związany z wirnikiem, wirujący z prędkością wirowania wirnika Wartość napięcia U określa wartość skuteczną napięcia fazowego, natomiast w przypadku zasilania z falownika PWM jest to wartość napięcia stałego zasilającego falownik. Wielkości oznaczone przyrostkiem _i są to wielkości orientowane względem wektora prądu stojana, _psi – wektora strumienia stojana.

W przypadku zasilania z falownika oprócz częstotliwości napięcia wyjściowego podawana jest wartość częstotliwości modulacji oraz współczynnik gamma określający wartość względną napięcia sterującego. Tym współczynnikiem możemy zmieniać wartość amplitudy pierwszej harmonicznej napięcia wyjściowego z falownika.

W programach przyjęto transformację w postaci:

⎡

1

1 ⎤

⎢ 1

−

− ⎥

⎢

2

2 ⎥

[ S]= 2 ⎢

3

0

− 3 ⎥

3 ⎢

2

2 ⎥

⎢

1

1

1 ⎥

⎢

⎥

⎣ 2

2

2 ⎦

-9-