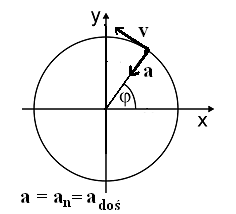
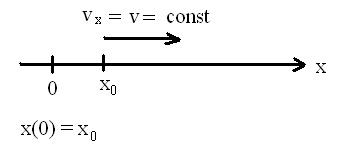Kinematyka

TOR RUCHU

Punkty materialne to obiekty obdarzone masą, których rozmiary (objętość) możemy zaniedbać.

Pod pojęciem ruchu rozumiemy zmiany wzajemnego położenia jednych ciał względem drugich wraz z upływem czasu.

Tor ruchu to krzywa jaką w przestrzeni zakreśla punkt materialny.

POŁOśENIE

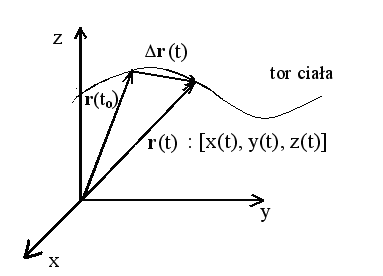
r (t) [

=

x( t), y( t), z( t)]

lub

 x = x( t) kinematyczne



równania

 y = y( t) ruchu

 z = z( t) Układ kartezjański

PRZEMIESZCZENIE

∆r (t) [

=

∆ x( t), ∆ y( t), ∆ z( t)]

1

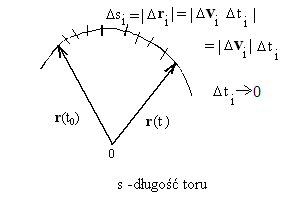
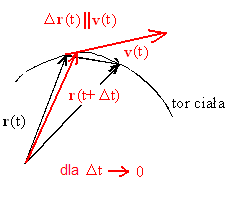
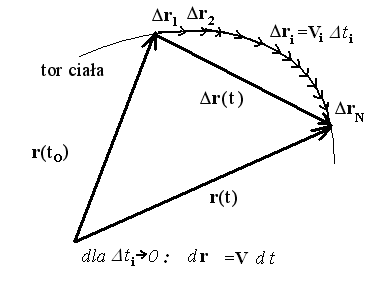
∆r(t)

tor ciała

r(t)

r(t+∆t)

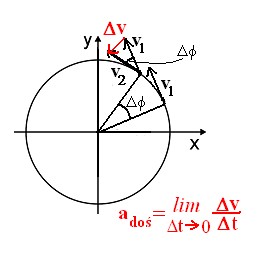
PRĘDKOŚĆ CHWILOWA PRZYSPIESZENIE CHWILOWE

d (

r t)

2

dv( t)

d r( t)

(

v t)

=

a( t) =

=

dt

2

dt

dt

t

t

r( t) = r( t ) + ∫ v( t') dt'

v t

( ) = v t

( )

a

0

+ ∫ t(') dt'

0

t

t

0

0

DROGA

t

s( t) = ∫ v t ( ') dt'

t 0

ds

v( t) =

Wartość prędkości dt

to szybkość

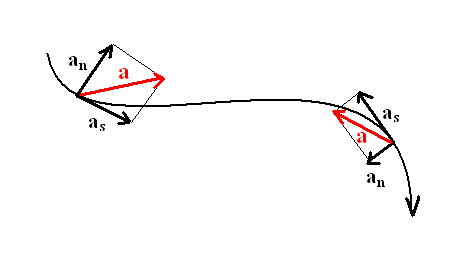
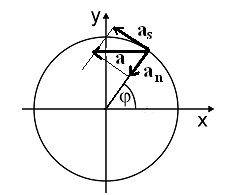
PRZYSPIESZENIE STYCZNE

I NORMALNE

dv t

( )

a ( t) =

s

dt

a ( t)

2

= a ( t)

2

− a ( t)

n

s

2

PRĘDKOŚĆ I PRZYSPIESZENIE ŚREDNIE

Wektorowe:

r t

( ) − r t

( )

r

0

∆ t

v

=

=

( )

ś r

t − t

t

0

∆

v t

( ) − v t

( )

v

0

∆ t

a

=

=

( )

ś r

t − t

t

0

∆

Liniowe:

Uwaga:

≠

s( t)

s t

( )

( v)

| v |

ś r

ś r

( v) =

=

ś r

t − t

t

≠

0

∆

( a )

| a |

st

ś r

ś r

v t

( ) − v t

( )

0

∆ v t()

( a ) =

=

st

ś r

t − t

t

0

∆

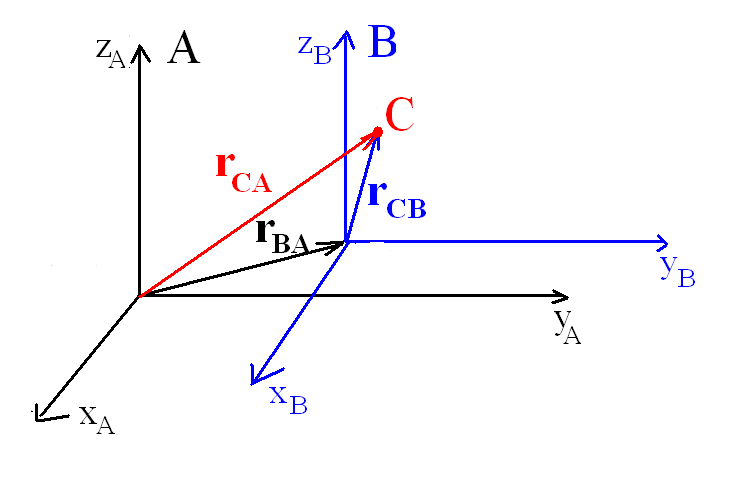
WZGLĘDNOŚĆ RUCHU

Względne położenie: r (t)

=

r (t) + r (t) CA

CB

BA

Względna prędkość: Względne przyspieszenie: dr (t)

dr (t)

dr (t)

dv

(t)

dv

(t)

dv

(t)

CA

=

CB

BA

+

CA

=

CB

BA

+

dt

dt

dt

dt

dt

dt

v

(t)

=

v

(t) + v (t) a

(t)

=

a

(t) + a (t) CA

CB

BA

CA

CB

BA

3

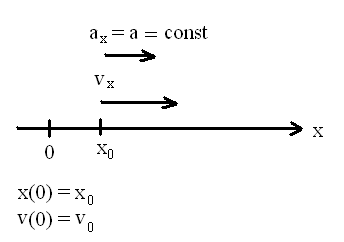
PRZYKŁADY RUCHU

Ruch w jednym wymiarze:

Ruch jednostajny prostoliniowy v = o

c

nst

x

= x ± v

t

równanie ruchu

0

Ruch jednostajnie zmienny prostoliniowy a = o

c

nst

v = v 0 ± a t 2

at

x = x ± v t ±

równanie ruchu

0

0

2

Ruch w dwóch wymiarach:

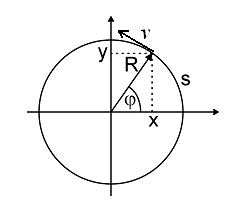
Ruch po okrę gu

Układ kartezjański:

Układ biegunowy:



 r t

( )

x( t) = R cosϕ( t)

= R = const.

równania



 y( t) = R sinϕ( t) ruchu





s( t)

ϕ t

( ) =



R

 vx = − Rωsinϕ



d

v

 v

= ϕ

ω

=

y = Rω cosϕ

dt

R



x = ε

a

vx −

2

xω



ω

dω

ε =



ε

2

 a

dt

y =

vy − yω



ω

lub inaczej:

ε

ε

2

a =

v ,

a = a

= − rω

a =

v

2

− ω r

S

n

doś

ω

ω

4

Ruch w dwóch wymiarach:

Ruch po okrę gu – stała prę dkość ką towa Układ kartezjański:

Układ biegunowy:

 x t

R

ϕ ω

0



( ) =

cos(

+ t)

r( t) = R = const.

równania





 y( t) = R sin(ϕ

ω

ruchu

0 +

t)

ϕ( t) = ω t + ϕ0

 v

ϕ ω

x = − Rω sin(

0 +

t)



ω = const

 v

ϕ ω

y = Rω cos(

0 +

t)

 a

ε = 0

x = −

2

xω



2

 ay = − yω

lub inaczej:

2

a

2

= −ω r

a = 0 , a = a

= − rω

S

n

doś

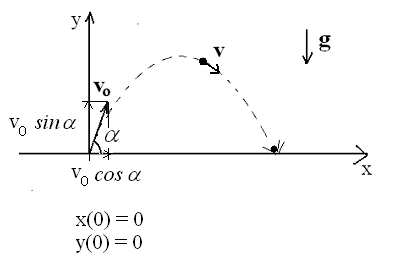
Ruch w dwóch wymiarach:

Rzut ukoś ny

 g

0

x =

 gy = − g

g

2

y = ( tgα ) x −

x

2

2( v cosα )

0

 v

cos

0

α

x = v



− v

θ

 v

sin

dv

gt

sin

0

0

α

y = v

− gt

a =

=

g

S

dt

2

v − 2 v gt sinθ + g 2 t 2

0

0

v cosθ

0



=

x = ( v cosα ) t a

g

n



0

2

v − 2 v gt sinθ + g 2 t 2

0

0



2

równania

gt

 y = ( v sinα ) t ruchu

0

−



2

5

Ćwiczenie 1.

Oblicz średnią szybkość i średnią prędkość samochodu, który przejeżdża odcinek 120 km z prędkością 60 km/h, a potem, zawraca i jedzie 240 km z prędkością 80 km/h.

Ćwiczenie 2.

Z wieży o wysokości H wyrzucono w dół piłkę z zerową prędkością początkową. W tym samym momencie spod wieży wystrzelono pionowo w górę, w kierunku piłki, pocisk nadając mu prędkość początkowa v . Po jakim czasie pocisk uderzy w 0

piłkę? Zaniedbać opory ruchu.

6